流体力学大作业
西工大-计算流体力学大作业
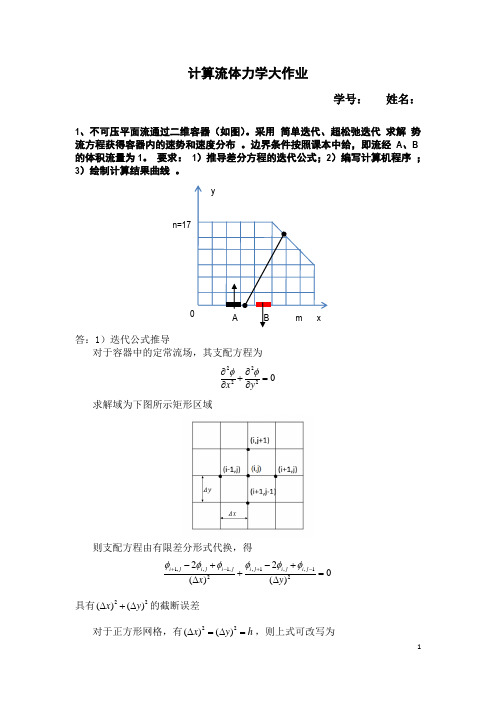
计算流体力学大作业学号: 姓名:1、不可压平面流通过二维容器(如图)。
采用 简单迭代、超松弛迭代 求解 势流方程获得容器内的速势和速度分布 。
边界条件按照课本中给,即流经 A 、B 的体积流量为1。
要求: 1)推导差分方程的迭代公式;2)编写计算机程序 ; 3)绘制计算结果曲线 。
答:1)迭代公式推导对于容器中的定常流场,其支配方程为22220x yφφ∂∂+=∂∂ 求解域为下图所示矩形区域则支配方程由有限差分形式代换,得1,,1,,1,,122220()()i j i j i ji j i j i j x y φφφφφφ+-+--+-++=∆∆具有22()()x y ∆+∆的截断误差对于正方形网格,有22()()x y h ∆=∆=,则上式可改写为n=17,1,1,,1,11()4i j i j i j i j i j φφφφφ+-+-=+++若采用简单迭代公式,即Liebmann 公式,则有(1)()(1)()(1),1,1,,1,11()4n n n n n i j i j i j i j i j φφφφφ++++-+-=+++若采用超松弛迭代,即SOR 公式,则有(1)()()(1)()(1),,1,1,,1,1(1)()4n n n n n n i j i j i j i j i j i j ωφωφφφφφ++++-+-=-++++其中松弛因子12ω<<。
ω最佳值opt ω为opt ω=式中cos(/)cos(/)m n αππ=+,m ,n 分别表示在网格系统中垂直线和水平线的总数。
2)计算机程序本程序采用C 语言编写。
程序源代码如下: #include<stdio.h> #include<math.h> void main() { int m=25,n=17,ilast[17],jlast[25]; int step1,step2; double h=0.25; double psi_j[25][17],psiprv_j,vel_j[25][17],velx_j[25][17],vely_j[25][17]; double psi_c[25][17],psiprv_c,vel_c[25][17],velx_c[25][17],vely_c[25][17]; double Pi,Alpha,Omega,Error; int i,j; for(i=0;i<17;i++) jlast[i]=17; for(i=17;i<m;i++) jlast[i]=17-(i-16); for(j=0;j<9;j++) ilast[j]=25; for(j=9;j<n;j++) ilast[j]=25-(j-8); //数据初始化 for(j=0;j<n;j++) { psi_j[0][j]=1.0; psi_c[0][j]=1.0;}for(i=1;i<m;i++){psi_j[i][jlast[i]-1]=1.0;psi_c[i][jlast[i]-1]=1.0; }for(j=0;j<8;j++){psi_j[m-1][j]=1.0;psi_c[m-1][j]=1.0;}for(i=1;i<m-1;i++){if(i>6 && i<21){psi_j[i][0]=0.0;psi_c[i][0]=0.0;}else{psi_j[i][0]=1.0;psi_c[i][0]=1.0;}}for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psi_j[i][j]=0.5;psi_c[i][j]=0.5;}}//处理右上角数据for(i=0;i<m;i++){for(j=0;j<n;j++){if(j>jlast[i]-1){psi_j[i][j]=0;vel_j[i][j]=3;psi_c[i][j]=0;vel_c[i][j]=3;}}}Pi=4.0*atan(1.0);Alpha=cos(Pi/m)+cos(Pi/n);Omega=(8.0-4*sqrt(4-pow(Alpha,2)))/pow(Alpha,2);//计算速势step1=0;step2=0;//简单迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_j=psi_j[i][j];psi_j[i][j]=(psi_j[i-1][j]+psi_j[i+1][j]+psi_j[i][j-1]+psi_j[i][j+1])/4.0;Error=Error+fabs(psi_j[i][j]-psiprv_j);}}step1++;if(step1>1000)break;if(Error<=0.001)break;}//超松弛迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_c=psi_c[i][j];psi_c[i][j]=(1-Omega)*psi_c[i][j]+Omega*(psi_c[i-1][j]+psi_c[i+1][j]+psi_c[i][j-1]+psi_c[i][j+1])/4.0;Error=Error+fabs(psi_c[i][j]-psiprv_c);}}step2++;if(step2>1000)break;if(Error<=0.001)break;}//计算速度for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){if(j==0){vely_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i][j+1]-psi_j[i][j+2])/2/h;vely_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i][j+1]-psi_c[i][j+2])/2/h;}else if(j==jlast[i]-1){vely_j[i][j]=(psi_j[i][j-2]-4*psi_j[i][j-1]+3*psi_j[i][j])/2/h;vely_c[i][j]=(psi_c[i][j-2]-4*psi_c[i][j-1]+3*psi_c[i][j])/2/h;}else{vely_j[i][j]=(psi_j[i][j+1]-psi_j[i][j-1])/2/h;vely_c[i][j]=(psi_c[i][j+1]-psi_c[i][j-1])/2/h;}}}for(j=0;j<n;j++){for(i=0;i<ilast[j];i++){if(i==0){velx_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i+1][j]-psi_j[i+2][j])/2/h;velx_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i+1][j]-psi_c[i+2][j])/2/h;}else if(i==ilast[j]-1){velx_j[i][j]=(psi_j[i-2][j]-4*psi_j[i-1][j]+3*psi_j[i][j])/2/h;velx_c[i][j]=(psi_c[i-2][j]-4*psi_c[i-1][j]+3*psi_c[i][j])/2/h;}else{velx_j[i][j]=(psi_j[i+1][j]-psi_j[i-1][j])/2/h;velx_c[i][j]=(psi_c[i+1][j]-psi_c[i-1][j])/2/h;}}}for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){vel_j[i][j]=sqrt(pow(velx_j[i][j],2)+pow(vely_j[i][j],2));vel_c[i][j]=sqrt(pow(velx_c[i][j],2)+pow(vely_c[i][j],2));}}//输出结果分布FILE *fp;fp=fopen("f:\\ESL\\YFresult.txt","w");fprintf(fp,"简单迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_j[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_j[i][j]);}}fprintf(fp,"超松弛迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_c[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_c[i][j]);}}fclose(fp);//输出tecplot数据FILE *fp1;fp1=fopen("f:\\ESL\\TECPLOT-result.txt","w");fprintf(fp1,"title=erwei grid\n");fprintf(fp1,"variables=x, y, psi_easy, velocity_easy, psi_SOR\n, velocity_SOR\n");fprintf(fp1,"zone t=grid,i=25,j=17,f=point\n");for(j=0;j<n;j++){for(i=0;i<m;i++){fprintf(fp1,"%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f\n",i*h,j*h,psi_j[i][j],vel_j[i][j],p si_c[i][j],vel_c[i][j]);}}fclose(fp1);}3)计算结果采用简单迭代,容器内的速势和速度分布速势分布(简单迭代)速度分布(简单迭代)采用超松弛迭代,容器内的速势和速度分布速势分布(SOR ) 速度分布(SOR )2、用点源(汇)分布在对称轴的源汇模拟流体绕过NACA0012旋称体的二维轴对称势流解。
流体力学 大作业

一.选择题1.牛顿内摩擦定律适用于()。
A.任何流体B.牛顿流体C.非牛顿流体2.液体不具有的性质是()。
A.易流动性B.压缩性C.抗拉性D.粘滞性3连续介质假定认为流体()连续。
A.在宏观上B.在微观上C.分子间D.原子间4.在国际单位制中流体力学基本量纲不包括()。
A.时间B.质量C.长度D.力.5.在静水中取一六面体,作用在该六面体上的力有()A.切向力、正压力B.正压力C.正压力、重力D.正压力、切向力、重力6.下述哪些力属于质量力( )A.惯性力B.粘性力C.弹性力D.表面张力E.重力7.某点存在真空时,()()A.该点的绝对压强为正值B.该点的相对压强为正值c.该点的绝对压强为负值D.该点的相对压强为负值8.流体静压强的()。
A.方向与受压面有关B.大小与受压面积有关B.大小与受压面方位无关9.流体静压强的全微分式为()。
A.B.C.10.压强单位为时,采用了哪种表示法()。
A.应力单位B.大气压倍数C.液柱高度11.密封容器内液面压强小于大气压强,其任一点的测压管液面()。
A.高于容器内液面B.低于容器内液面C.等于容器内液面12.流体运动的连续性方程是根据()原理导出的。
A.动量守恒B. 质量守恒C.能量守恒D. 力的平衡13. 流线和迹线重合的条件为()。
A.恒定流B.非恒定流C.非恒定均匀流14.总流伯努利方程适用于()。
A.恒定流B.非恒定流C.可压缩流体15. 总水头线与测压管水头线的基本规律是:()、()A.总水头线总是沿程下降的。
B.总水头线总是在测压管水头线的上方。
C.测压管水头线沿程可升可降。
D.测压管水头线总是沿程下降的。
16 管道中液体的雷诺数与()无关。
A. 温度B. 管径C. 流速D. 管长17.. 某圆管直径d=30mm,其中液体平均流速为20cm/s。
液体粘滞系数为0.0114cm3/s,则此管中液体流态为()。
A. 层流B. 层流向紊流过渡C.紊流18.等直径圆管中紊流的过流断面流速分布是()A呈抛物线分布B. 呈对数线分布 C.呈椭圆曲线分布 D. 呈双曲线分布19.等直径圆管中的层流,其过流断面平均流速是圆管中最大流速的()A 1.0倍B.1/3倍C. 1/4倍D. 1/2倍20.圆管中的层流的沿程损失与管中平均流速的()成正比.A. 一次方B. 二次方C. 三次方D. 四次方21..圆管的水力半径是( )A. d/2B. d/3C. d/4D. d/5.22谢才公式中谢才系数的单位是()A. 无量纲B. C. D. .23. 判断层流和紊流的临界雷诺数是()A.上临界雷诺数B.下临界雷诺数C.上下临界雷诺数代数平均D.上下临界雷诺数几何平均24.. 对于管道无压流,当充满度分别为()时,其流量和速度分别达到最大。
(完整版)流体力学作业试题库及答案

第一章 绪论思考题1-1 何谓流体连续介质模型?含有气泡的液体是否适用连续介质模型? 答:所谓流体的连续介质模型,即把流体视为没有间隙地由流体质点充满它所占据的整个空间的一种连续介质其物理性质和物理量也是连续的。
若气泡相对于液体而言可以看作孤立的点的话,则含有气泡的液体可以适用连续介质模型。
习题11-3 如题图所示,设平行板间隙为0.5mm ,中间充满液体,上板以U =0.25m/s 的速度平移,施于单位面积的力为2Pa ,试求液体的粘度为多少?解:YU dy du A F μμτ===液体粘度s Pa AU FY ⋅⨯=⨯⨯==--3310425.0105.02μ1-4 求题图所示的轴与轴套之间的流体粘度。
解:s Pa dLU FY dLA Y U dy du A F ⋅=⨯⨯⨯⨯⨯⨯==⇒====--0648.0493.010)140120(14.3102.034.863πμπμμτ第二章 流体静力学习题22-5 用多管水银测压计测压,,题图中标高的单位为m ,试求水面的压强p 0。
解:Pam g m g p pap m m g p p m m p p m m g p p m m g p p D D CC B B A A 5001065.29.298002.21334169.22.20)2.13.2()2.15.2(g )4.15.2()4.10.3(⨯=⨯-⨯=⨯-⨯=⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+=--=-+=-+=水汞汞水汞水ρρρρρρ2-9 一盛水的敞口容器作加速运动,试求下列两种情况下容器内静压强的分布规律:(1)自由降落;(2)以等加速度a 向上运动。
解:h a g p p )sin (0αρ++=(1)0,900=∴=︒-=p p 相对压强α(2))(,900a g h p p p p a a ++=∴=︒=ρα绝对压强2-12 试求开启题图所示水闸闸门所需的单宽拉力F 。
不计闸门自重及转轴摩擦力。
流体力学作业
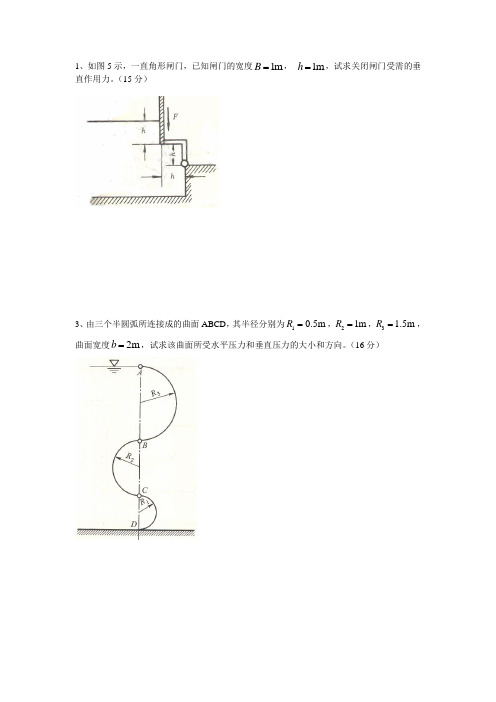
1、如图5示,一直角形闸门,已知闸门的宽度1m B =, 1m h =,试求关闭闸门受需的垂直作用力。
(15分)
3、由三个半圆弧所连接成的曲面ABCD ,其半径分别为10.5m R =,21m R =,3 1.5m R =,曲面宽度2m b =,试求该曲面所受水平压力和垂直压力的大小和方向。
(16分)
2、如图5示,一半球形闸门,已知球门的半径1m R =,上下游水位差1m H =,试求闸门受到的水平作用力和竖直作用力的大小和方向。
(16分)
图5
4、将圆柱弧形闸门吊到如图1所示位置,恰能挡住一定深度的水。
闸门宽度为B ,半径为R ,中心角为α。
已知水的密度为ρ,闸门自重为G 。
求闸门受到向下的合力。
图1
5、一矩形平板闸门AB ,门的转轴位于A 端,已知闸门宽3m ,门重9.8kN ,门与水平面夹角0
30α=,闸门左右水位分别为11m h =,23 1.73m h h ==,若不计门轴的摩擦,在门的B 点用钢索起吊,试求闸门启动时所需的拉力F 。
2023年流体力学作业题库及答案

第一章绪论思索题l—l何谓流体持续介质模型?具有气泡的液体与否合用持续介质模型?竺.仁丁•所谓流体向持续介质模型,即把流体视为没有间隙地由流体质点充斥它所占据的整个空间的一种持续介质其物理性质和物理量也是持续的。
若气泡相对千液体而言可以看作孤立的点的话,则具有气泡的液体可以合用持续介质模型。
习题l1 -3如题图所示,设平行板间隙为0.5m m,中间充斥液体,上板以U=O.25m/s的速度平移,施千单位面积的力为2Pa,试求液体的粘度为多少?解:F du UT=—=µ —=µ —A d y YF Y 2x0.5x10-3液体粘度µ== =4x10-3Pa·sAU 0.25I-4求题图所示的轴与轴套之间向流体粘度。
解:F du U1=—=µ —=µ —A d y YA=冗dL⇒ µ= = =0.0648Pa·sF Y 8.34x0.2x10-3动LU 3.14x(120x140)x10-6 x0.493第二章流体静力学习题22—5 用多管水银测压计测压,,题图中标高的单位为m,试求水面的压强p广解:p=p+ p g(3.0m-1.4m)A 0水p=p+p g(2.5m-1.4m)A B采p =p-p g(2.5m -1.2m)⇒B C水p=p+p g(2.3m-1.2m)C D采p =O p ap = p g x 2.2m-p g x 2.9m =133416x 2.2-9800x 2.9 = 2.65 x10s P a 0采水2-9 一盛水的敞口容器作加速运动,试求下列两种状况下容器内静压强的分布规律:(1) 自由降落;(2)以等加速度a向上运动。
解:p=p +p(g+as in a)h。
顶=-90°,相对压强p=0(1)。
:. p=O..双=90°,绝对压强p=p(2) 0 a: .p=p+ p h(g +a)a2-1 2试求启动题图所示水闸闸门所需的单宽拉力F。
流体力学大作业实验报告

END DO PRINT*,"摩擦系数为:",S END PROGRAM
运行结果:
∴ = 0.033379640, ∴ V = 58.8 ÷ (1.8 + 70 ) /s = 3.77m/s 经检验, = = 433001 > 4000,为紊流,符合假设。 ∴流量Q = AV = × V = 0.0666 /s
S=(1/(-2.0*LOG10((A/D)/3.7+2.51/(SQRT(58.8/(1.8+70*T))*D/U*SQRT(T)))))**2
DO WHILE(ABS(S-T)>E) PRINT*,"摩擦系数为:",S T=S S=(1/(-2.0*LOG10((A/D)/3.7+2.51/(SQRT(58.8/(1.8+70*T))*D/U*SQRT(T)))))**2
∴ V = 58.8 ÷ (1.8 + 70 ) /s
由科尔布鲁克公式 = −2.0 ( . + . ),其中 =
查表得, = 10℃时,运动粘性系数 = 1.306 × 10 /s D=150mm, Δ = 1 将V的表达式代入科尔布鲁克公式得:
= −2.0 ( + . )=−2.0 ( +
.
.
.
==6−.31606mm//ss,
流体力学大作业
7-36
题目:设有一虹吸管,其装置如图所示,设管径为 150mm。
试求通过该管的流量。已知水温为 10℃,∆=
,
弯头 = . ,, 进口 = . 。
推导过程:
选取截面 1-1,2-2 如右图所示, = 0 , = −3 , = = 由总流伯努利方程
计算流体力学课程大作业

《计算流体力学》课程大作业——基于涡量-流函数法的不可压缩方腔驱动流问题数值模拟张伊哲 航博1011、 引言和综述2、 问题的提出,怎样使用涡量-流函数方法建立差分格式3、 程序说明4、 计算结果和讨论5、 结论1引言虽然不可压缩流动的控制方程从形式上看更为简单,但实际上,目前不可压缩流动的数值方法远远不如可压缩流动的数值方法成熟。
考虑不可压缩流动的N-S 方程:01()P t νρ∇⋅=⎧⎪∂⎨+∇⋅=-∇+∆⎪∂⎩U UUU f U (1.1)其中ν是运动粘性系数,认为是常数。
将方程组写成无量纲的形式:01()Re P t∇⋅=⎧⎪∂⎨+∇⋅=-∇+∆⎪∂⎩U UUU f U (1.2) 其中Re 是雷诺数。
从数学角度看,不可压缩流动的控制方程中不含有密度对时间的偏导数项,方程表现出椭圆-抛物组合型的特点;从物理意义上看,在不可压缩流动中,压力这一物理量的波动具有无穷大的传播速度,它瞬间传遍全场,以使不可压缩条件在任何时间、任何位置满足,这就是椭圆型方程的物理意义。
这就造成不可压缩的N-S 方程不能使用比较成熟的发展型...偏微分方程的数值求解理论和方法。
如果将动量方程和连续性方程完全耦合求解,即使使用显示的离散格式,也将会得到一个刚性很强的、庞大的稀疏线性方程组,计算量巨大,更重要的问题是不易收敛。
因此,实际应用中,通常都必须将连续方程和动量方程在一定程度上解耦。
目前,求解不可压缩流动的方法主要有涡量-流函数法,SIMPLE 法及其衍生的改进方法,有限元法,谱方法等,这些方法各有优缺点。
其中涡量-流函数法是解决二维不可压缩流动的有效方法。
作者本学期学习了研究生计算流体课程,为了熟悉计算流体的基本方法,选择使用涡量-流函数法计算不可压缩方腔驱动流问题,并且对于不同雷诺数下的解进行比较和分析,得出一些结论。
本文接下来的内容安排为:第2节提出不可压缩方腔驱动流问题,并分析该问题怎样使用涡量-流函数方法建立差分格式、选择边界条件。
计算流体力学大作业

计算液体力学基础及应用课程期末作业-----程序调试最终版学号:134212059 姓名:徐影ContentsCFD模型示意图一、拟一维喷管理论解求解二、拟一维喷管的CFD求解三、理论值与CFD解的对比CFD模型示意图两圆弧直径为10米,喉部直径为0.59米,长为3米clear all;I=imread('xuying.png'); imshow(I)一、拟一维喷管理论解求解喷管内马赫数的变化公依赖于面积比A/A0,所以可以将Ma作为x的函数1.2.采用隐函数绘图给出理论的马赫数解gamma=1.4;h0=59/100;% 取学生学号后两位数的十分之一作喉部直径syms x Ma A_x y;% xz为x坐标,Ma为马赫数A_x=((10.59-2*sqrt(25-(x-1.5)^2))/0.59)^2;% A_x为面积系数figure('Color',[1 1 1]);set(gcf,'position',[0,0,1.5*468,468]);plot_Ma=A_x^2-(2/(gamma+1)+(gamma-1)/(gamma+1)*y^2)^((gamma+1)/(gamma-1))/y^2;subplot(1,2,1);gca=ezplot(plot_Ma,[0,3]);xlabel('x');ylabel('马赫数');title('采用隐函数求解的马赫数结果');grid on; % 得到两条曲线,由递增规律选取上升曲线段,从该曲线上得到一系列点的坐标为[x0,Ma0]load tk.mat;x_0=tk(:,1);Ma_0=tk(:,2);% 这里load的数据采用某算法从上面出的图取点拟合得到,用到polyval和polyfit函数subplot(1,2,2);plot(x_0,Ma_0);xlabel('x');ylabel('马赫数');title('马赫数的理论解');grid on;求出马赫数后,压力、密度、温度的变化都是Ma的函数,求出理论值并绘图1.2.3.p_0=(1+(gamma-1)/2*Ma_0.^2).^(-gamma/(gamma-1));rho_0=(1+(gamma-1)/2*Ma_0.^2).^(-1/(gamma-1));t_0=(1+(gamma-1)/2*Ma_0.^2).^-1;figure('Color',[1 1 1]);set(gcf,'position',[0,0,1.5*468,1.5*468]);subplot(3,1,1);plot(x_0,p_0);title('压力比理论值');xlabel('x');ylabel('p');grid on; subplot(3,1,2);plot(x_0,rho_0);title('密度比理论值');xlabel('x');ylabel('rho');grid on; subplot(3,1,3);plot(x_0,t_0);title('温度比理论值');xlabel('x');ylabel('T');grid on;二、拟一维喷管的CFD求解clear all;L=3;N=31;dx=L/(N-1);x=linspace(0,L,N);C=0.5;n=2000;student_num=59;A=((10+student_num/100-2*((25-((x-1.5).^2))).^0.5)/(student_num/100)).^2;%面积比A/A_0与x坐标的关系第一步,密度比、温度比、速度比的初始条件设定1.2.3.Rou=1-0.3146*x;rhobi=zeros(1,n);T=1-0.2314*x;V=(0.1+1.09*x).*sqrt(T);P_rou_t=zeros(size(Rou));P_v_t=zeros(size(Rou));P_T_t=zeros(size(Rou));P_rou_t_2=zeros(size(Rou));P_v_t_2=zeros(size(Rou));P_T_t_2=zeros(size(Rou));第二步,预估步第三步,并求Δt,求rou, V, T的预测量1.2.3.第四步,修正步第五步,求平均时间导数1.2.3.最后,得到t+Delta t时刻流动参数的修正值为1.2.3.第七步,边界条件处理for j=1:ntemp=Rou(16);% 第二步,预估步for i=2:30P_rou_t(i)=-V(i)*((Rou(i+1)-Rou(i))/dx)-Rou(i)*((V(i+1)-V(i))/dx)-Rou(i)*V(i)*((log(A(i+1))-log(A(i)))/dx);P_v_t(i)=-V(i)*((V(i+1)-V(i))/dx)-((T(i+1)-T(i))/dx+((Rou(i+1)-Rou(i))/dx)*T(i)/Rou(i))*1/1.4;P_T_t(i)=-V(i)*((T(i+1)-T(i))/dx)-0.4*T(i)*(((V(i+1)-V(i))/dx)+V(i)*((log(A(i+1))-log(A(i)))/dx));end% 第三步,并求Δt,求rou, V, T的预测量dt=C*(dx./(V(2:30)+sqrt(T(2:30))));dt=min(dt);Rou1(2:30)=Rou(2:30)+P_rou_t(2:30).*dt;V1(2:30)=V(2:30)+P_v_t(2:30).*dt;T1(2:30)=T(2:30)+P_T_t(2:30).*dt;V1(1)=V(1);T1(1)=T(1);Rou1(1)=Rou(1);% 第四步,修正步%for i=2:30P_rou_t_2(i)=-V1(i)*((Rou1(i)-Rou1(i-1))/dx)-Rou1(i)*((V1(i)-V1(i-1))/dx)-Rou1(i)*V1(i)*((log(A(i))-log(A(i-1)))/dx); P_v_t_2(i)=-V1(i)*((V1(i)-V1(i-1))/dx)-((T1(i)-T1(i-1))/dx+((Rou1(i)-Rou1(i-1))/dx)*T1(i)/Rou1(i))*1/1.4;P_T_t_2(i)=-V1(i)*((T1(i)-T1(i-1))/dx)-0.4*T1(i)*(((V1(i)-V1(i-1))/dx)+V1(i)*((log(A(i))-log(A(i-1)))/dx));end% 第五步,求平均时间导数P_rou_av=(P_rou_t+P_rou_t_2)/2;P_v_av=(P_v_t+P_v_t_2)/2;P_T_av=(P_T_t+P_T_t_2)/2;% 最后,得到t+Delta t时刻流动参数的修正值为Rou(2:30)=Rou(2:30)+P_rou_av(2:30).*dt;T(2:30)=T(2:30)+P_T_av(2:30).*dt;V(2:30)=V(2:30)+P_v_av(2:30).*dt;P(2:30)=Rou(2:30).*T(2:30);% 第七步,边界条件处理V(1)=2*V(2)-V(3);V(31)=2*V(30)-V(29);Rou(31)=2*Rou(30)-Rou(29);T(31)=2*T(30)-T(29);p=Rou.*T;Ma=V./sqrt(T);rhobi(j)=abs((temp-Rou(16))/temp); % 计算后一次时间步与前一时间步之间的密度比的变化情况,以此检验CFD过程收敛性质end最终结果的绘图figure('Color',[1 1 1]);set(gcf,'position',[0,0,1.2*468,1.5*468]);subplot(3,1,1);plot(1:n,rhobi);xlabel('x');ylabel('Ma');title('相对密度比');grid on;% 密度比收敛情况绘图subplot(3,1,2);plot(x,Ma);title('喷管内马赫数分布');xlabel('x');ylabel('Ma');grid on;% 马赫数CFD值绘图subplot(3,1,3);plot(x,p);title('喷管内压力分布');xlabel('x');ylabel('p');grid on; % 压力分布CFD值绘图shu=[x;A;Ma;V;T;p;Rou];显示各参量最终计算结果fprintf('%6s\t%12s\t%12s\t%12s\t%12s\t%12s\t%12s\r\n','x','A/A_0','Ma','v/v_0','T/T_0','p/p_0','rho')% 依次显示坐标点、形状参数、马赫数、速度、温度、压力的结果fprintf('%6.1f\t%12.4f\t%12.4f\t%12.4f\t%12.4f\t%12.4f\t%12.4f\r\n',shu)x A/A_0 Ma v/v_0 T/T_0 p/p_0 rho0.0 3.1709 0.1859 0.1859 1.0000 1.0000 1.00000.1 2.8156 0.2124 0.2121 0.9975 0.9915 0.99390.2 2.5056 0.2389 0.2383 0.9956 0.9847 0.98900.3 2.2361 0.2711 0.2700 0.9922 0.9728 0.98050.4 2.0030 0.3056 0.3038 0.9885 0.9602 0.97140.5 1.8022 0.3451 0.3422 0.9834 0.9433 0.95910.6 1.6303 0.3882 0.3838 0.9775 0.9234 0.94470.7 1.4844 0.4364 0.4298 0.9700 0.8989 0.92670.8 1.3617 0.4891 0.4794 0.9611 0.8701 0.90540.9 1.2600 0.5469 0.5331 0.9502 0.8362 0.88001.0 1.1771 0.6096 0.5903 0.9374 0.7974 0.85071.1 1.1116 0.6776 0.6508 0.9224 0.7536 0.81701.2 1.0620 0.7507 0.7142 0.9051 0.7053 0.77921.3 1.0273 0.8289 0.7800 0.8855 0.6532 0.73761.4 1.0068 0.9119 0.8475 0.8636 0.5982 0.69271.5 1.0000 0.9998 0.9160 0.8394 0.5416 0.64521.6 1.0068 1.0921 0.9849 0.8132 0.4847 0.59601.7 1.0273 1.1887 1.0534 0.7853 0.4288 0.54611.8 1.0620 1.2893 1.1210 0.7559 0.3753 0.49641.9 1.1116 1.3934 1.1869 0.7255 0.3250 0.44802.0 1.1771 1.5009 1.2507 0.6943 0.2788 0.40152.1 1.2600 1.6113 1.3119 0.6629 0.2371 0.35762.2 1.3617 1.7245 1.3705 0.6315 0.2001 0.31682.3 1.4844 1.8398 1.4258 0.6006 0.1678 0.27952.4 1.6303 1.9576 1.4782 0.5702 0.1400 0.24552.5 1.8022 2.0764 1.5269 0.5408 0.1163 0.21512.6 2.0030 2.1983 1.5732 0.5122 0.0962 0.1879。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“水流动力学基本原理的应用”大作业
姓名:
学号:
专业班级:
成绩:
教师评语:
年月日
1、对水流流向问题有如下一些说法:“水一定从高处向低处流”,“水一定从压强大的地方向压强小的地方流”,“水一定从流速大的地方向流速小的地方流”。
这些说法是否正确?为什么?
2、在写总流能量方程221112221222p p z z h g g g g
ωαυαυρρ++=+++ 时,过水断面上的计
算点、基准面、压强标准是否可以任意选取?为什么?
3、液流通过如图所示管道流入大气中,已知:U 形测压管中水银柱高差m h Hg 2.0=∆,
10.72h m =水柱高,管径m d 1.01=,管嘴出口直径m d 05.02=,不计管中水头损失,试
求:管中流量Q 。
4、如图所示为一水平面上的渐变弯管,已知:
断面1-1处的压强2
3
1/1098m N p ⨯=,流速14/m s υ=,管径mm d 2001=,管径mm d 1002=,转角
45=α,不计弯管的水头损失。
试求:水流作用在弯管上的力
5、如图所示为闸下底板上的消力墩,已知:跃前断面水深h 1=0.6m ,流速v 1=15m/s ,跃后断面水深h 2=4m ,墩宽b=1.6m ,试求:水流对消力墩的作用力。
题2.9图
6、学过恒定总流能量方程及动量方程及其应用这部分内容以后,你觉得有些什么收获?有什么疑惑或者模糊的地方?。
