系统辨识与自适应控制硕士研究生必修课程考核
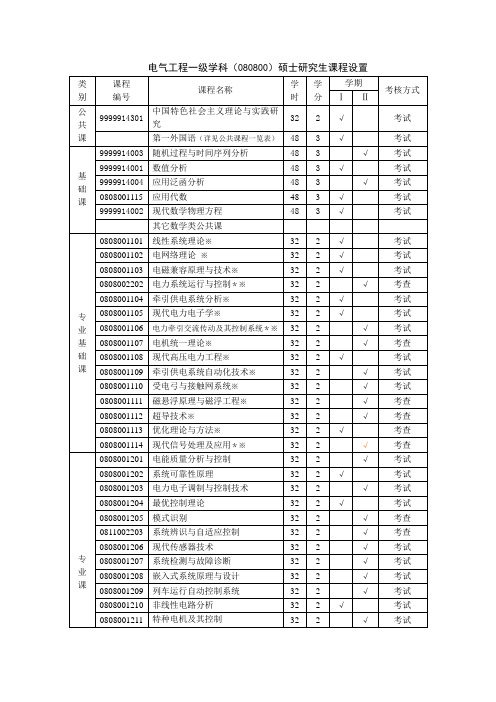
电气工程一级学科080800硕士研究生课程设置
2
√
考试
0808001109
牵引供电系统自动化技术※
32
2
√
考试
0808001110
受电弓与接触网系统※
32
2
√
考试
0808001111
磁悬浮原理与磁浮工程※
32
2
√
考查
0808001112
超导技术※
32
2
√
考查
0808001113
优化理论与方法※
32
2
√
考查
0808001114
现代信号处理及应用*※
工程电磁场中的数值方法
32
2
√
考试
0808001225
过电压防护与绝缘配合
32
2
√
考试
0808001226
工程电介质理论及其应用
32
2
√
考试
0808001227
电气工程材料导论
32
2
√
考查
0808001228
工程项目管理
32
2
√
考查
0808001229
电器原理与应用
32
2
√
考试
0808001230
工业监控技术
√
考试
0808002202
电力系统运行与控制*※
32
2
√
考查
0808001104
牵引供电系统分析※
32
2
√
考试
0808001105
现代电力电子学※
32
2
√
考试
0808001106
电力牵引交流传动及其控制系统*※
系统辨识与自适应控制硕士研究生必修课程考核

《系统辨识与自适应控制》硕士研究生必修课程考核(检测技术与自动化装置专业)2003.5. 22可下载自/xuan/leader/mrj/ 学生姓名:考核成绩:一、笔试部分 (占课程成绩的 80% )考试形式:笔试开卷答卷要求:笔答,可以参阅书籍,要求简明扼要,不得大段抄教材,不得相互抄袭试题:1 简述系统辨识的基本概念(概念、定义和主要步骤)(10分)2 简述相关辨识的基本原理和基于二进制伪随机序列的相关辩识方法(原理、框图、特点)。
(10分)3 简述离散线性动态(SI / SO)过程参数估计最小二乘方法(LS法)的主要内容和优缺点。
带遗忘因子递推最小二乘估计(RLS法)的计算步骤和主要递推算式的物理意义(10分)4 简述什么是时间序列?时间序列建模如何消除恒定趋势、线性趋势和季节性的影响?(10分)5 何谓闭环系统的可辨识性问题,它有那些主要结论?(10分)6 何谓时间离散动态分数时滞过程?“分数时滞”对过程模型的零点和极点有什么影响?(10分)7 简述什么是自适应控制,什么是模型参考自适应控制(MRAC)?,试举一例说明MRAC的设计方法(10分)。
8 请设计以下过程( yr = 0 )y(k) -1.6y(k-1)+0.8y(k-2) = u(k-2)- 0.5u(k-3)+ε(k)+1.5ε(k-1)+0.9ε(k-2) 的最小方差控制器(MVC)和广义最小方差控制器(GMVC), 并分析他们的主要性能。
(10分)二、上机报告RLS仿真(占课程成绩的 20%)交卷时间:6月9日下午试题标准答案1 简述系统辨识的基本概念(概念、定义和主要步骤)(10分)系统辩识是研究怎样利用未知系统的试验或运行数据(输入/输出数据)建立系统的数学模型的科学,是现代控制理论的一个分支。
数学模型具有近似性和非唯一性,依据辩识的不同目的,系统辨识的结果也能有不同答案。
(3分)定义:按照数学等价的观点定义为“系统辩识是在输入/输出数据的基础上,从一类模型中确定一个与所测系统等价的模型”。
最新系统辨识与自适应控制试卷

系统辨识与自适应控制试卷------------------------------------------作者xxxx------------------------------------------日期xxxx北方工业大学《系统辨识与自适应控制》课程试卷2010年秋季学期开课学院: 机电工程考试方式:开卷考试时间:120 分钟班级姓名学号装说明:试题中{ek}是均值为零的白噪声序列一)(20分)已知静态非线性系统模型为y= a0+ a1x1+a2x1x2+ a3 x2 + ε(1)(10分)给出该系统参数无偏估计的一种方案,要求说明你给出的方案是一定可行的(有解).订(2)(10分)证明你的方案是无偏的。
二) (15分)系统的动态过程为:线三)(20分)2010年4月6日作业为:“给出如下系统y(k)+a1*y(k—1)+a2*y(k-2)=b1*u(k-1)+b2*u(k-2)+e(k)+c1*e(k—1)+ c2*e(k-2)的输入输出试验数据(501组),1)试用两种不同的方法求出系统参数。
2)尝试各种改进辩识精度的方法,并给出评价。
”1)(10分)请用简要说明一种你采用的辩识方案。
可以附加框图说明.2)(10分)你的辩识结果与参考答案基本相符吗?(改卷时会参考作业结论)。
如果不相符,你认为你的结果是正确的吗?为什么?四)(15分)在对股票做时间序列模型的作业中,需要对原始数据先做差分处理。
1)(6分)为什么要对原始数据先做差分处理?2)(9分)你的作业中选了几阶差分?与一阶差分的辩识结果相比,有什么不同?五)(15分)考虑CARMA 过程A(z-1) y(k) = z—d B(z—1) - u(k)+λ C (z-1) ε(k)(1)求闭环系统极点(10分)(2)试说明为什么最小方差控制仅适用于最小相位系统(5分)六)(15分)在模型参考自适应方法中,若单输入单输出系统为:Y=Ko * G(s) * U采用的参考模型为:Ym= Km * G(s) * Uc系统采用采用前馈控制 U = K * Uc如果取e=Y-Ym, J= (1/2)* e2 , 求基于MIT方案的自适应控制率.。
系统辨识与自适应控制实验

中南大学系统辨识及自适应控制实验指导老师贺建军姓名史伟东专业班级测控1102班0909111814号实验日期2014年11月实验一 递推二乘法参数辨识设被辨识系统的数学模型由下式描述:2341231232.0 1.51()()()1 1.50.70.11 1.50.70.1z z z y k u k k z z z z z zξ---------++=+-++-++ 式中ξ(k )为方差为0.1的白噪声。
要求:(1) 当输入信号u (k )是方差为1的白噪声序列时,利用系统的输入输出值在线辨识上述模型的参数;(2) 当输入信号u (k )是幅值为1的逆M 序列时,利用系统的输入输出值在线辨识上述模型的参数;分析比较在不同输入信号作用下,对系统模型参数辨识精度的影响。
(1)clear all; close all;a=[1 -1.5 0.7 0.1]';b=[1 2 1.5]';d=3; %对象参数na=length(a)-1;nb=length(b)-1; %计算阶次L=500; %数据长度uk=zeros(d+nb,1);yk=zeros(na,1); %输入输出初值u=randn(L,1); %输入采用方差为1的白噪声序列xi=sqrt(0.1)*randn(L,1); % 方差为0.1的白噪声干扰序列theta=[a(2:na+1);b]; %对象参数真值thetae_1=zeros(na+nb+1,1); %参数初值P=10^6*eye(na+nb+1);for k=1:Lphi=[-yk;uk(d:d+nb)]; %此处phi为列向量y(k)=phi'*theta+xi(k); %采集输出数据%递推公式K=P*phi/(1+phi'*P*phi);thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);P=(eye(na+nb+1)-K*phi')*P;%更新数据thetae_1=thetae(:,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endplot([1:L],thetae); %line([1:L],[theta,theta]); xlabel('k');ylabel('参数估计a,b');legend('a_1','a_2','a_3','b_0','b_1','b_2');axis([0 L -2 2]);(2)clear all;a=[1 -1.5 0.7 0.1]';b=[1 2 1.5]';d=2; %对象参数na=length(a)-1;nb=length(b)-1; %计算阶次L=20; %数据长度uk=zeros(d+nb,1);yk=zeros(na,1); %输入初值x1=1;x2=1;x3=1;x4=0;S=1;%移位寄存器初值,方波初值xi=rand(L,1);%白噪声序列theta=[a(2:na+1);b]; %对象参数真值for k=1:Lphi(k,:)=[-yk;uk(d:d+nb)]'; % phi(k,:)为行向量,便于组成phi矩阵y(k)=phi(k,:)*theta+xi(k); %采集输出数据IM=xor(S,x4);if IM==0u(k)=-1;elseu(k)=1;endS=not(S);M=xor(x3,x4); %产生M序列%更新数据x4=x3;x3=x2;x2=x1;x1=M;for i=nb+d:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);End实验二 最小方差自校正控制实验设二阶纯滞后被控对象的数学模型参数未知或慢时变,仿真实验时用下列模型:34112122.5 1.510.5()()()1 1.50.71 1.50.7z z z y k u k k z z z zξ-------++=+-+-+ 式中ξ(k )为方差为0.1的白噪声。
(整理)系统辨识自适应控制

1.1讨论系统方程为:(信噪比)至少30%)()1()()1()(k e k u k b k ay k y +-=-+)(k e 为零均值白噪声, =)(k a=)(k b 要求对系统参数辨识进行讨论(1) 定常系统 a=0.8,b=0.5参数递推估计 (2) 时变系统 取不同值是的不同结果并讨论。
(1)取初值P (0)=I 、∧θ(0)=0选择方差为1的白噪声作为输入信号u (k ),L=300,采用RLS 算法进行参数估计,代码及仿真结果图如下: clear all ;close all ;a=[1 0.8]';b=[0.5]';d=1; %对象参数na=length(a)-1;nb=length(b)-1; %na 、nb 为A 、B 阶次L=300; %仿真长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i) yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列 xi=sqrt(0.1)*randn(L,1); %白噪声序列theta=[a(2:na+1);b]; %对象参数真值thetae_1=zeros(na+nb+1,1); %thetae 初值 P=10^6*eye(na+nb+1); for k=1:Lphi = [-yk;uk(d:d+nb)]; %´此处phi 为列向量 y(k)=phi'*theta + xi(k); %采集输出数据%递推最小二乘法K=P*phi/(1+phi'*P*phi);thetae( : ,k)=thetae_1 + K*(y(k)-phi'*thetae_1); P=(eye(na+nb+1)-K*phi')*P;%更新数据thetae_1 = thetae( : ,k);for i=d+nb:-1:2 uk(i)=uk(i-1); enduk(1)=u(k); for i=na:-1:2yk(i)=yk(i-1); endyk(1)=y(k); endplot([1:L],thetae); %line([1,L],[theta,theta]); xlabel('k');ylabel('参数估计a 、b'); legend('a_1','b_0');axis([0 L -2 2]);图1-1 递推最小二乘法的参数估计结果(2))取初值P (0)=I 、∧θ(0)=0选择方差为1的白噪声作为输入信号u (k ),取 分别为0.91,0.95,0.98,1.00时,L=600,采用FFRLS 算法进行参数估计,代码及仿真图如下所示:clear all ;close all ;a=[1 0.8]';b=[0.5]';d=1; %对象参数na=length(a)-1;nb=length(b)-1; %na 、nb 为A 、B 阶次L=600; %仿真长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i) yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列thetae_1=zeros(na+nb+1,1); %thetae初值P=10^6*eye(na+nb+1);lambda=0.98; %遗忘因子范围[0.9 1]for k=1:Lif k==301a=[1 0.6]';b=[0.3]'; %对象参数突变endtheta( : ,k)=[a(2 : na+1);b]; %对象参数真值phi = [-yk;uk(d:d+nb)]; %´此处phi为列向量y(k)=phi'*theta( : ,k) + xi(k); %采集输出数据%遗忘因子递推最小二乘法·¨K=P*phi/(lambda+phi'*P*phi);thetae( : ,k)=thetae_1 + K*(y(k)-phi'*thetae_1);P=(eye(na+nb+1)-K*phi')*P/lambda;%更新数据thetae_1 = thetae( : ,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endsubplot(1,2,1)plot([1:L],thetae(1:na,:));hold on;plot([1:L],theta(1:na,:),'k:'); xlabel('k');ylabel('参数估计a');legend('a_1');axis([0 L -2 2]);subplot(1,2,2)plot([1:L],thetae(na+1:na+nb+1,:));holdon;plot([1:L],theta(na+1:na+nb+1,:),'k:');xlabel('k');ylabel('参数估计b');legend('b_0');axis([0 L -0.5 2]);图1-2-1 遗忘因子递推最小二乘法的参数估计结果(λ=0.91)图1-2-2 遗忘因子递推最小二乘法的参数估计结果(λ=0.95)图1-2-3遗忘因子递推最小二乘法的参数估计结果(λ=0.98)图1-2-4 遗忘因子递推最小二乘法的参数估计结果(λ=1)由以上可以看出,技术对于参数突变的系统,采用FFRLS算法也能够有效地进行参数估计。
控制工程(085210)硕士研究生培养方案

四、领域范围 (1)运动控制系统的分析与设计; (2)节能技术及装置; (3)先进传感与检测技术; (4)智能信息处理及应用
五、课程设置与培养环节
课程性质
课程名称
公
英语
共
学 中国特色社会主义理论与实践研究
位
学
课
自然辩证法
位
矩阵理论
课
线性系统理论
专业 程 学位课 计算机控制技术
智能控制理论
现代检测理论与技术 公共选
跨文化交际(英语) 修课
自适应控制
系统辨识与参数估计
鲁棒控制理论与方法
非
现代电力电子技术
学
运动控制系统的先进控制策略
现代传感器技术 位
专业 现代数字信号处理
选修课 课
网络控制系统及应用
程
信息融合理论与技术
鲁棒控制理论与方法
√
40/2
√
40/2
√
40/2
√
40/2
选修
√
40/2
≥11 学分
√
40/2
√
40/2
√
40/2
√
40/2
√
40/2
√
40/2
小波分析与应用 DSP 技术及应用 VHDL 与 FPGA 技术及应用 虚拟仪器技术及应用 控制网络与现场总线系统 现代计算机网络 嵌入式系统及应用 控制理论发展综述
√
40/2
√
40/2
√
40/2
√
40/2
√
40/2
√
40/2
√
40/2
√
系统辨识及自适应控制 教学大纲

系统辨识及自适应控制一、课程说明课程编号:090148Z10课程名称:系统辨识及自适应控制/ System Identification and Adaptive Control课程类别:专业课学时/学分: 32/2(其中实验学时:6 )先修课程:自动控制理论、线性代数适应专业:自动化、测控技术与仪器、智能科学与技术、电气工程及其自动化教材、教学参考书:1.杨承志、孙棣华等.系统辨识与自适应控制.重庆:重庆出版社.2003年;2.徐湘元.自适应控制理论与应用.北京:电子工业出版社.2007年;3.庞中华,崔红.系统辨识与自适应控MATLAB 仿真.北京:北京航空航天大学出版社.2009年二、课程设置的目的意义系统辨识与自适应控制是电气信息类专业大学本科高年级学生的一门专业选修课程,是现代控制理论的一个重要组成部分。
通过该课程的学习,帮助学生了解系统辨识与自适应控制的基本原理和算法,掌握系统数学模型的建立方法及自适应控制系统的设计方法和技巧,为培养学生成为控制学科的高级工程技术人才奠定基础。
三、课程的基本要求知识:掌握系统辨识与自适应控制的基本概念和基本原理,最小二乘参数辨识方法,最小方差自校正控制方法,广义最小方差自校正控制方法,极点配置自校正控制方法,自校正PID控制方法,自校正内膜控制方法,自校正模型算法控制方法,基于Lyapunov稳定性理论的模型参考自适应控制方法等。
能力:从实际应用的角度出发,针对具有一定程度不确定性的被控对象,能够运用上述方法和知识设计一般的自适应控制系统,满足控制系统的基本控制要求。
素质:拓展学生在控制工程领域的设计思路,丰富学生对控制系统的设计方法;通过对不确定性被控对象特点的分析、难于控制问题的解决培养学生发现问题、分析问题、解决问题的科研素养。
四、教学内容、重点难点及教学设计注:实践包括实验、上机等五、实践教学内容和基本要求通过实验,帮助学生巩固、加深理解课堂所学基本理论知识,在Matlab/SimuLink仿真计算平台中实现系统模型参数辨识和含噪声干扰系统的自六、考核方式及成绩评定1、平时成绩占40%:包括作业、上机实验考核以及平时上课考核;七、大纲主撰人:大纲审核人:。
自适应作业1--系统辨识

Adaptive ControlAssignment 1System Identification姓名: ****学号: *************班级: ***********Answers :1. a) Obtain the system model equation and write it in linear regression form.The system model equation:1111()*()*()10.810.8q y k u k e k q q ---=+--It ’s auto regressive form:()0.8(1)(1)()y k y k u k e k =-+-+b) Simulate the system by generating 1000 data points. Plot u(t) and y(t).Th e in pu t s u (k )时刻-k输入信号-u (k )时刻-k输出信号-y (k )c) Obtain the least squares estimator for this system.The least squares estimator for the parameter vector is:The estimated value of system parameters are:2.a) Generate any input and get the response. Plot u(t) and y(t). Ignore the system noiseThe ARX models :11()()()()(k A q y k B q u k e --=+)It ’s auto regressive form:() 1.5363(1)0.8607(2)0.0416(1)0.0395(2)()y k y k y k u k u k e k =---+-+-+When input is a step function, the output is:t h e mo d el r es po n s e t o a s t ep in pu t时刻-k输出响应-y (k )When input is a sin wave, the output is:t h e mo d el r es po n s e t o s in wav e时刻-k输入信号-s i n (k *0.0628) 输出响应-y (k )b) Write a recursive least squares program to identify this model and test your program.The least squares estimatecan be obtained from :The estimated value of system parameters are:Test my recursive least squares program :时刻-k模型输出z (k ) 系统输出-y (k )Clearly, the response with the least squares estimate is almost as same as the original system response.c) Test the response and the recursive least squares program if a white noise is added.时刻-k模型输出z (k ) 系统输出-y (k )Obviously, the response with the least squares estimate is almost as same as the original system response. So I think it is predicting the correct system parameters.d) Comment on how different types of inputs, initial LN, and length of dataaffect the final estimation.Conclusion:1)The error of parameter estimation will be smaller with bigger initial LN. So the system identification will be more accurate.2) Different types of inputs can affect the final estimation, in this case, a Step function signal is better then A sin wave signal.Case two: recursive least squares with a forgetting factorConclusion:1)when c is smaller, the estimated values are more precise, but the smaller c could make System Identification instability. For sinusoidal signals, when c <0 .5, the estimated values become the divergence. Therefore, the general range of c is 0.95 to 0.98.2)For this system,RLS- with a forgetting factor is more accurate then recursive least squares. 3)The error of parameter estimation will be smaller with bigger initial LN. So the system identification will be more accurate.e) Show how the system parameters in the θ track towards the true values A and B as each new iteration occurs.Case one: RLS,without interruptt h e t r ac k o f t h e a1-s t ep f u c t io n时刻-k系统参数-a 1t h e t r ac k o f t h e a1-s in wav e时刻-k系统参数-A 1t h e t r ac k o f t h e a1-r an d m时刻-k系统参数-a 1Case two:RLS- withinterruptt h e t r ac k o f t h e a1-s t ep f u c t io n时刻-k系统参数-a1t h e t r ac k o f t h e a1-s in wav e时刻-k系统参数-a1t h e t r ac k o f t h e a1-r an d m时刻-k系统参数-a 1Conclusion :1. when the input is the random signal, the speed of identification is the fastest.2.The speed of identification is faster and more accurate when there isn ’t interrupt.3. Find the order of the following input signals:• To obtain estimates of a parametric model, the input signal has to be “rich” enough to excite all modes of the system.• An input signal is said to be persistently exciting (P.E.) of order n if the following limit exists:11()lim ()()tt i c k u i u i k t →∞==-∑and the matrix is positive semi-definite (non-singular).(0)(1)...(1)(1)(0)...(2).1lim ..(1)(2)...(0)TN t c c c n c c c n C t c n c n c φφ→∞-⎡⎤⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦• The signal u with the property c(k) is persistently exciting of order n if and only if()211lim ()()0tt k U A q u k t →∞==>∑a) A step function signal;Let u(t)=1 for t>0 and zero otherwise. It follows that10(1)()00t q u t t =⎧-=⎨≠⎩A step can be thus at most be PE of order 1. Since11(k)lim ()()tt i c u i u i k t →∞==-∑1l i m ()()1l i m 1*1l i m 1tt i k tt i kt u i u i k t t t k t →∞=→∞=→∞=-=-==∑∑So:123[(0)]1(0)(1)110(1)(0)11(0)(1)(2)111(1)(0)(1)1110(2)(1)(0)111...C c c c C c c c c c C c c c c c c ==⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(0)(1)...(1)(1)(0)...(2)...(1(2)...(0)n c c c n c c c n C c n c n c -⎡⎤⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦) 11...111...1.0..11...1⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦It follows that it is PE of order 1.b) A pulse function signal;It follows from Eq()211lim ()()0tt k U A q u k t →∞==>∑that Cn →0 for all n if u is a pulse. A pulse thus is not PE for any n.c) A sinusoid function signal;Let u(t)=sin wt. It follows that2(2cos 1)()0q q w u t -+=A sinusoid can thus at most be PE of order 2. Since 21cos 1cos 12w C w⎛⎫= ⎪⎝⎭ it follows that a sinusoid is actually PE of order 2.d) A random signal.Consider the stochastic processU(t)=H(q)e(t)Where e(t) is white noise and H(q) is a pulse transfer function. It follows from the definition of white noise that Eq()211lim ()()0t t k U A q u k t →∞==>∑ is satisfied for the signal e for any nonzero polynomial A(q). This property also holds for the signal u. So the signal u is thus PE of any order.Appendix:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《系统辨识与自适应控制》硕士研究生必修课程考核(检测技术与自动化装置专业)2003.5. 22可下载自/xuan/leader/mrj/ 学生姓名:考核成绩:一、笔试部分 (占课程成绩的 80% )考试形式:笔试开卷答卷要求:笔答,可以参阅书籍,要求简明扼要,不得大段抄教材,不得相互抄袭试题:1 简述系统辨识的基本概念(概念、定义和主要步骤)(10分)2 简述相关辨识的基本原理和基于二进制伪随机序列的相关辩识方法(原理、框图、特点)。
(10分)3 简述离散线性动态(SI / SO)过程参数估计最小二乘方法(LS法)的主要内容和优缺点。
带遗忘因子递推最小二乘估计(RLS法)的计算步骤和主要递推算式的物理意义(10分)4 简述什么是时间序列?时间序列建模如何消除恒定趋势、线性趋势和季节性的影响?(10分)5 何谓闭环系统的可辨识性问题,它有那些主要结论?(10分)6 何谓时间离散动态分数时滞过程?“分数时滞”对过程模型的零点和极点有什么影响?(10分)7 简述什么是自适应控制,什么是模型参考自适应控制(MRAC)?,试举一例说明MRAC的设计方法(10分)。
8 请设计以下过程( yr = 0 )y(k) -1.6y(k-1)+0.8y(k-2) = u(k-2)- 0.5u(k-3)+ε(k)+1.5ε(k-1)+0.9ε(k-2) 的最小方差控制器(MVC)和广义最小方差控制器(GMVC), 并分析他们的主要性能。
(10分)二、上机报告RLS仿真(占课程成绩的 20%)交卷时间:6月9日下午试题标准答案1 简述系统辨识的基本概念(概念、定义和主要步骤)(10分)系统辩识是研究怎样利用未知系统的试验或运行数据(输入/输出数据)建立系统的数学模型的科学,是现代控制理论的一个分支。
数学模型具有近似性和非唯一性,依据辩识的不同目的,系统辨识的结果也能有不同答案。
(3分)定义:按照数学等价的观点定义为“系统辩识是在输入/输出数据的基础上,从一类模型中确定一个与所测系统等价的模型”。
按照逼近的观点定义为“系统辩识有三个要素——数据、模型类和准则。
系统辩识是按照一个准则,在模型类中选择一个与数据拟合得最好的模型”。
(4分)辨识的主要步骤:(3分)1、明确目的,尽可能多的获取先验知识;2、实验设计;3、模型结构的确定(假设与检验);4、参数估计;5、模型验证。
2、简述相关辨识的基本原理和基于二进制伪随机序列的相关辩识方法(原理、框图、特点)。
(10分)相关辩识的理论基础是维纳—何普方程:R xy ( τ ) =⎰o∞ g (ν)R xx ( τ - ν) dν(3分)基于二进制伪随机序列的相关辩识方法用二位式周期性伪随机信号x(t),大大缩短积分时间并使乘法运算简化。
(3分)优点:(1)辨识结果与(t)不相关;(2)x(t)幅值±a比直接测量g(t) 时小,可在线辩识;(3)方法简单,容易实现。
(2分)缺点:(1)辩识时间长(解决办法——多路并行);(2)在线辩识时对f(t) 有严格限制(0或常数); (3)得到的是非参数模型。
(2分)3 简述离散线性动态(SI / SO )过程参数估计最小二乘方法(LS法)的主要内容和优缺点。
带遗忘因子递推最小二乘估计(RLS法)的计算步骤和主要递推算式的物理意义(10分) 考虑过程模型(CAR ):其中{ y(k) }和{ u(k) }为可测的输出和输入,{ ε(k) }为不可测的随机干扰。
估计准则:使得以下目标函数达到最小:解出:NT N N T N Ny--∧-=φφφθ1)(可视为以下正则方程NT N N N TNy -∧-=φθφφ.)(的解,称为最小二乘的“一次完成算法”。
其优点是:(1) 不要求对{ (k )} 的统计特性有任何验前知识;(2) 如果{(k )}为零均值白噪声,则可得渐进无偏估计,即当 N → ∞时, --∧-=-0)(2θθNE , 且 -∧-→θθN。
(3) 算法简单可靠,应用广泛; (4) 可推广到多输入 多输出系统。
缺点(1)如果{(k )}为有色噪声,则得出的估计是有偏的;(2)仅适于离线辩识,要记忆全部测量数据,程序长。
(5分)∑∑==+-=-+n i n i i i k i k u b i k y a k y 11)()()()(ε∑=∧-=Nk Tk k y J 12])([θϕ带遗忘因子递推最小二乘估计(RLS法)的计算步骤共由以下八个步骤组成:(1)置初值,令:-∧-=00θ 和 P 0 =I 2n ⨯2n ,其中= 103 ~ 106 ;设定遗忘因子( 0 < < 1 ),取值范围 (0.95~0.995),值愈小,“遗忘”愈快。
(2)构成数据向量N+1 ;(3)进行新的第N+1次采样; (4)计算 K N+1 ; (5)计算新的参数估计 !+∧-N θ;(6)计算估计误差的协方差阵 P N+1 ; (7)终点判断,如果未到终点,置 N N+1,返回到步骤 (2),如果已到终点则转到下一步骤; (8)输出模型辨识结果。
主要递推算式 ])1([111NTN N NN N y K-+-+-∧-+∧--++=θϕθθ有明显的物理意义如下:用 NTN N N y ∧-+-∧=+θϕ1)1(表示N 时刻对N+1时刻输出量的预报。
预报误差( 被称为 新息 ) 为()NTN N y N N y N y N N y ∧-+-∧-+=+-+=+θϕ1)1()1()1(1~第N+1步的参数估计可表达成)1(~11N N y KN NN ++=+-∧-+∧-θθ物理意义:新的参数估计1+∧-N θ是对上次老的估计 N∧-θ进行修正而得出的,修正的依据是利用在N∧-θ对新的输出 y(N+1) 预报的预报误差。
K N+1是修正系数向量,它需要递推计算得出,在递推计算K N+1时要用到估计误差的协方差阵P N ,而后者也是递推得出的。
(5分)4 简述什么是时间序列?时间序列建模如何消除恒定趋势、线性趋势和季节性的影响?(10分)对系统观测得出的按照时间顺序排列的数据称之为时间序列。
时间序列分析建模是基于时间序列,通过曲线拟合和参数估计或者谱分析,建立数学模型的理论与方法,理论基础是数理统计。
(5分)通过引入算子,定义为: =(1 - B ) , 即x t = x t - x t-1 可以消除恒定趋势。
利用算子 2= ( 1 – B ) 2 可以消除线性趋势。
引入算子:s = 1 – Bs消除按照一定周期波动的季节性的影响。
(5分)5 何谓闭环系统的可辨识性问题,它有那些主要结论?(10分)开环系统的输入量 u 是外加的,而闭环系统 u 是由输出 y 经过某种反馈联系产生的。
因此,从闭环系统的输入——输出数据中获得的信息比从开环系统中得到的少,由此带来了闭环情况下系统的可辨识性问题。
(4分)主要结论有:(1)在闭环状态下,不能由实验数据来辨识出模型的阶数,即在纯闭环下的阶数的不可辨识。
(2)如果模型阶数已知,能否由实验数据来估计过程参数呢?结论是有条件的。
如不满足一定的条件,参数亦是不可辨识的。
闭环系统的参数可辨识条件是:n f ≥ n b – p + 1 或者 n d ≥ n a – p + 1上两式给出闭环系统参数可以辨识的充分条件,如若以上两个条件之一能够被满足,则A (z -1) 、B(z -1)和C (z -1) 的参数是可以辨识。
如果n = n a = n b , m = n f = n d , p = 1,则以上条件可合并概括为为 m ≥ n , 即:反馈通道的阶次不低于正向通道的阶次。
时滞大,有利于闭环可辨识性。
如果存在外激励信号,或者反馈通道中有干扰存在,则参数是可辨识的。
(6分)7 何谓时间离散动态分数时滞过程?“分数时滞”对过程模型的零点和极点有 什么影响?(10分)考虑带纯滞后T t 的线性过程以采样间隔T 进行离散化,如若T t 与T 之间不是整数倍的关系,即:T t =(d+)T , d = 0, 1, 2 , … ;0< 1,则离散化后的过程为“分数时滞”过程。
(4分)“分数时滞”不影响离散过程的极点;由于“分数时滞”的影响,离散化的过程零点数比“整数时滞”离散过程的零点数增多了一个,而增加的零点很可能位于单位圆之外。
(6分)8 简述什么是自适应控制,什么是模型参考自适应控制(MRAC )?,试举一例说明MRAC 的设计方法(10分)。
能在系统和环境的新息不完备的情况下改变自身特性来保持良好工作品质的控制系统,称自适应控制系统。
一个典型的比较完善的自适应控制系统包含:辨识——决策——调整三个部分组成。
自适应控制系统是本质非线性系统。
(2分)模型参考自适应控制(MRAC )系统包含一个参考模型,模型动态表征了对系统动态性能的理想要求,MRAC 通过与参考模型的比较,察觉被控对象特性的变化,力求使被控系统的动态响应与模型的响应相一致。
MRAC 具有跟踪迅速的突出优点。
系统的难点在于如何保证自适应控制回路的稳定性。
(2分)MRAC 有两类设计方法:一类是“局部参数最优化设计方法”,目标是使得ST t e )s (Q )s (P )s (u )s (y )s (G -==性能指标J 达到最优化;另一类是使得自适应控制系统能够确保稳定工作,称之为“稳定性理论的设计方法。
以具有一个时变参数——可调增益(MIT 方案)为例说明MRAC 设计。
定义广义误差为 e = y m – y s ,用梯度法的局部参数最优化的设计方法,自适应控制的目标是使得以下与广义误差有关的自适应控制性能指标 J 达到最小:由梯度法有:⎰∂∂-∂∂-=∆tt cc cd K ee K J K 02τλλ得出其中:B = 2 λ K s / K m , 当K s 与K m 同号时B 为正值常系数,即自适应回路的积分时间常数。
实现的方案如下图,自适应回路由乘法器与积分器组成。
该方案能够使得J 为最小,但是不能确保自适应回路是稳定的。
方案实现如下图:J e d t=⎰20()ττ(也可以选择用稳定性理论的设计方法为例)(6分)8 请设计以下过程( yr = 0 )y(k) -1.6y(k-1)+0.8y(k-2) = u(k-2)- 0.5u(k-3)+ε(k)+1.5ε(k-1)+0.9 ε(k-2)的最小方差控制器(MVC)和广义最小方差控制器(GMVC), 并分析他们的主要性能。
(10分)过程 A y(k)=z-d Bu(k)+λCε(k) 其中A = 1-1.6 z-1+0.8 z-2 ;B = 1- 0.5z-1 ;C = 1+1.5 z-1+0.9 z-2;d=2 ; n=2 由长除法得:F = 1+ 3.1z-1; G = 5.06- 2.48z-1最小方差控制器(MVC)的设计:由k 时刻的控制量u(k) 由如下控制目标J=E[ y2(k+d)-y r ] ∣u(k)=u*(k) = min得出MVC控制律为(当y r =0时)其中:G =5.06- 2.48z-1 B F =1+2.6 z-1 -1.55 z-2最小方差控制器(MVC)的主要性能是:(1)调节误差的方差为:E y2(k+d) = λ2 E [Fε(k+d)]2 = λ2 (1+f12) = λ2(2)(2)算法简单,容易实现;(3)只适用于逆稳定(最小相位)过程;(4)控制的目标函数中仅考虑使得E y2为最小,没有考虑对u 的约束,有可能因导致过大的控制动作而不能实现。
