4第四章 描述统计分析
统计学第4章数据特征的描述

极差计算简单,但容易受到极端值的影响,不能全面 反映数据的离散程度。
四分位差
定义
四分位差是第三四分位数与第 一四分位数之差,用于反映中
间50%数据的离散程度。
计算方法
四分位差 = 第三四分位数 第一四分位数
优缺点
四分位差能够避免极端值的影 响,更稳健地反映数据的离散
程度,但计算相对复杂。
方差与标准差
统计学第4章数据特征 的描述
https://
REPORTING
• 数据特征描述概述 • 集中趋势的度量 • 离散程度的度量 • 偏态与峰态的度量 • 数据特征描述在统计分析中的应用 • 数据特征描述的注意事项
目录
PART 01
数据特征描述概述
REPORTING
WENKU DESIGN
数据特征描述在推断性统计中的应用
参数估计 假设检验 方差分析 相关与回归分析
基于样本数据特征,对总体参数进行估计,如点估计和区间估 计。
通过比较样本数据与理论分布或两组样本数据之间的差异,对 总体分布或总体参数进行假设检验。
研究不同因素对总体变异的影响程度,通过比较不同组间的差 异,分析因素对总体变异的贡献。
定义
方差是每个数据与全体数据平均数之方根,用于衡量数据的波动大小。
计算方法
方差 = Σ(xi - x̄)² / n,标准差 = √方差
优缺点
方差和标准差能够全面反映数据的离散程度,且计算相对简单,但容易受到极端值的影响。同时,方差 和标准差都是基于均值的度量,对于非对称分布的数据可能不够准确。
适用范围
适用于数值型数据,且数据之间可能 存在极端异常值的情况。
特点
中位数不受极端值影响,对于存在极 端异常值的数据集,中位数能够更好 地反映数据的集中趋势。
第四章 SPSS的基本统计分析知识讲解

多选项分析
多选项分析的基本思路
– 定义多选项变量集 – 多选项频数分析 – 多选项交叉分组下的频数分析
多选项分析
定义多选项变量集
目的:将已分解的变量定义为一个集合,便于进行多选 项分析
– 菜单选项:analyze->multiple response->define sets – 从原变量中选取被分解的变量(数值型)到variables in
进一步计算
– cells选项:选择在频数分析表中输出各种百分比.
row:行百分比(Row pct); column:列百分比(Col pct); total:总百分比(Tot pct);
分析列联表中变量间的关系
目的:
通过列联表分析,检验行列变量之间是否独立。
方法:
– 卡方检验:对品质数据的相关性进行度量
频数分析
基本操作步骤
(1)菜单选项:analyze->descriptive statistics->frequencies (2)选择几个待分析的变量到variables框. (3)chart选项,选择所需要的图形
计算描述统计量
目的
– 精确把握变量的总体分布状况,了解数据的集中趋 势、离散趋势、对称程度、陡峭程度。
– 菜单选项:analyze->multiple response->crosstabs
频数分析
目的
粗略把握变量值的分布状况。
例:研究被调查者的特征(如:性别、年龄、收入) 研究被调查者对某个问题的总体看法(如:教学方式、选修课程) 研究被调查者某方面的状态(如:购买家电的类型、居民月支出状况)
采用的方法
– 计算频分布表:包括计算 频数、累计频数、百分比、累 计百分比
spss第四章描述统计简介PPT课件

当n 为奇数时:正中间位置号码=(n+1)/2 样本中位数=X(n+1)/2
当n为偶数时:正中间位置号码=(n+1)/2是小数,处于n/2与(n/2)+1之间。 样本中位数=(Xn/2+X(n/2)+1)/2 如5位同学的学习成绩:3,3,3,4,5。中间位置是第三位,中位数:3。 如果六位同学: 3,3,4,5,5,5。中间位置是3与4位中间的位置,中位数为: (4+5)/2=4.5
第四章 描述统计量简介
2024/10/23
第三章 样本数据特征的初步分析
1
调查杭州市居民收入情况,得到
调查顾客对产品的满意第度情四况章, 获得100个样本数据,能分
样本100统个计样本量数描据,述根据这些数据,
析出哪些信息?
你最想得到哪些信息?
调查大学生群体中对手机品牌的偏 好程度,你如何描述调查结果?
• 选择Percentile Values 栏中的 选项,输出所选变量的百分值
• Dispersion(离差)栏,用于
指定输出反映变量离散程度的 统计量
• Central Tendency (集中趋势)
栏,用于指定输出反映变量集 中趋势的统计量
• Distribution (分布特征)栏,
用于指定输出描述分布形状和
如果样本容量为n,那么,某个样本值出现 的频率=该样本值出现的频次/n
2024/10/23
第三章 样本数据特征的初步分析
9
分类数据或顺序数据描述频次与 频率的图形方法
第四章 数据分析

6、数据导出
• (1)导出CSV文件: to_csv(file_path,sep=",",index=True,header=True) • (2)导出Excel文件: to_excel(file_path,index=True,header=True) • (3)导出到MySQL库: to_sql(tableName,con=数据库链接)
7、数据处理
• 在数据分析前需要对数据进行处理,剔除其中噪声、恢复数据的完整性和一致性后 才能进行数据分析
数据 数据 数据 数据 清洗 合并 计算 分组
8、数据的清洗
• 1.重复数据的处理:
• 使用duplicated( )可以获取哪些是重复的元素,使用drop_duplicates( )能够删除重复元素。
• 2.缺失数据的处理:
• 缺失值的处理包括两个步骤,即缺失数据的识别和缺失值处理,缺失值处理常用的方法有 删除法、替换法、插补法等。
• 3.噪声数据的处理:
• 在实际操作中常用分箱(binning)、回归(regression)、聚类(clustering)、计算机与人工检查 相结合等方法“光滑”数据,去掉数据中的噪声。
3、数据分析的工具
• 数据分析的工具数量众多,根据分析数据层次结构的不同,常用数据分析软件可分 为四类
4、PYTHON的PANDAS数据分析包
• Numpy科学计算模块 • Matplotlib绘图模块。
数据导入
数据导出
5、数据导入
• (1)导入TXT文件:read_table(file,names=[列名1,列名2,...],sep="",...) • (2)导入CSV文件:read_csv(file,names=[列名1,列名2,...],sep="",...) • (3)导入excel文件:read_excel(file,sheetname,header=0) • (4)导入MySQL库:read_sql(sql,con=数据库)
spss第四章,描述性统计分析。。
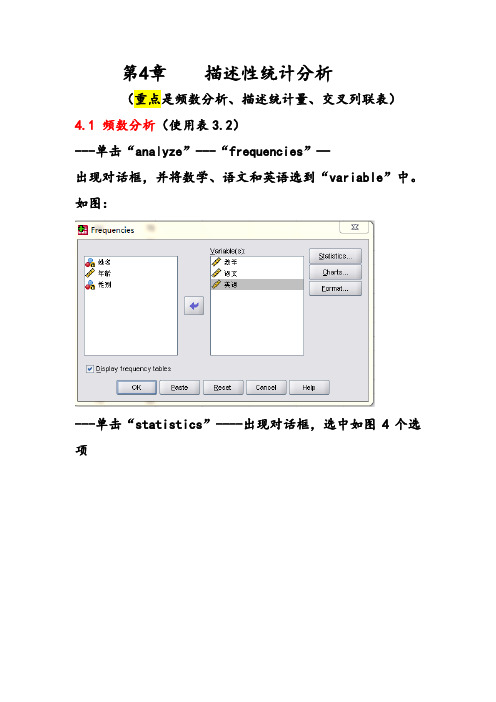
第4章描述性统计分析(重点是频数分析、描述统计量、交叉列联表)4.1 频数分析(使用表3.2)---单击“analyze”---“frequencies”—出现对话框,并将数学、语文和英语选到“variable”中。
如图:---单击“statistics”----出现对话框,选中如图4个选项-----单击“continue”回到前一对话框----单击“OK”结果如表4.1-----如图,重新选择语文---单击“charts”---得到一个对话框,如图选中2个选项----单击“continue”----回到前一对话框---单击“OK”。
结果如表4.24.2 基本描述统计量(使用表3.2)---单击“analyze”---“descriptive statistics”—“Descriptives”---得到对话框,并将数据进行如图选入:-----单击“options”—得到对话框,并选中如图6个选项:----单击“continue”----回到前一对话框---单击“OK”。
结果如表4.34.3 探索性分析(使用表3.2)---单击“analyze”---“descriptive statistics”—“Explore”---得到对话框,并将数据进行如图选入:----单击“Plots”—得到对话框,并选中如图4个选项:----单击“continue”----回到前一对话框---单击“OK”。
结果如表4.6(与书有不同)4.4交叉列联表分析(使用表化环0708)(1)T ransform(修改)----Recode into Different variable----选定身高------点击“向右箭头”------在“name”下写个名字:eg:T1-------change-------(此处T1和T2是已经做好的分组)点击-----old and new values对其分组---例:Range LOWEST through values :160 new values :1Rang :160 through :170 2Range HIGHEST through values :170 3 点击continue-----回到前一个对话框点击------OK同样的方法做好T2---------点击“analyze(分析)”-----“Descriptive Statistics(描述性统计)”------“Crosstabs(交叉列联表)”选中行列------点击“Exat….“则弹出“exct tests(精确检测)对话框”点“Statistics…”则弹出“Crosstabs:statistics(交叉表统计)对话框”-------点击“Chi—square(卡方检验)”----“continue”点“Cells…”则弹出“Crosstabs:Cells display(交叉表统计)对话框”-------选择“Counts”中的“Observed”和“Expected”为期望频数,-------选择“Percentages”中的“Row”“Column”“Total”选项,分别计算“频数”“列频数”“总频数”-------选择“Residuals”中的“Standardized”分别计算单元格的非标准化残差、标准化残差、调整后的残差----“continue”回到前一页点----“OK”4.5比率分析(课本71页)不需要掌握英语未写完作业:1-10,11-25,26-30。
《医学统计学》第四章定性资料的统计描述

1、不要把构成比与率相混淆。即分析时不能以构成 比代率;这是常见的错误。
某文章作者根据上述资料认为,沙眼在20~组的患病率最高,以后随年 龄增大而减少。该作者把构成比当作率进行分析,犯了以比代率的错误。
2、使用相对数时分母不宜过小。分母过小时相对数 不稳定。
3、注意资料的可比性;
不同时期、不同地区、不同条件下的资料比较时应注意具有 可比性。
12965.2
46.3
否
265
660291.4
40.1
说明该地市区非吸烟女性饮酒者的肺癌发病率是
非吸烟女性不饮酒者的1.15倍。
3.比数比
比数比( Odds ratio ,OR) : 常用于流行病学
中病例-对照研究资料,表示病例组和对照组中的 暴露比例与非暴露比例的比值之比,是反映疾病 与暴露之间关联强度的指标。其计算公式为
一般的,两个地方的出生率、死亡率、发病率、不同级别 医院某病的治愈率等不能直接比较。
无可比性的实例:
由表2-7可见,无论有无腋下淋巴结转移,省医院的5年生存 率均高于市医院,但从总生存率看,省医院的5年生存率低于市 医院。这不符合常理。因此,省医院与市医院的总生存率就不能 直接比较(标准化后再比)。
感谢聆听
率
某事物或现象发生的实 际数 某事物或现象发生的所 有可能数
比例基数
公式中的“比例基数”通常依据习惯而定。
需要注意的是,率在更多情况下是一个具有时间 概念的指标,即用于说明在某一段时间内某现象 发生的强度或频率,如出生率、死亡率、发病率 、患病率等,这些指标通常是指在1年时间内发 生的频率。
例4-1 某单位在2009年有3128名职工,该单位 每年对职工进行体检,在这一年新发生高血压 病人12例,则
第4章 SPSS基本统计分析

练习3
• 完成上例
提纲
1
频数分析
2
计算基本描述统计量
复合分组下的频数分析 多选项分析
3
4
5
比率分析
多选项分析
实现思路 1)按多选项二分法或多选项分类法将多选项问题 分解成若干的问题,并设置若干个SPSS变量 2)采用多选项频数分析或多选项交叉分组下的频
• 选择若干个频数分析的变量
• 选择绘制统计图形
4、频数分析的扩展功能
计算分位数 • 分位数:是变量在不同百分位点上的取值。分位 点在0~100之间。 • 分位数差是一种描述数据离散程度的方式。分位 数差越大,表示数据在相应分位上的离散程度越 大
4、频数分析的扩展功能
频数分布表格式的定义 • 调整频数分布表中数据的输出顺序
– 按变量值的升序或降序输出 – 按频数值的升序或降序输出
• 压缩频数分布表
– SPSS默认如果变量取值的个数或取值区间的个数大于10,则 不输出相应的频数分布表
5、频数分析应用举例
分析月住房开销的分布,并对不同居住类型进行比较 • 1)“月住房开销”为定距型变量→先分组,再编 制频数分布表
• 2)计算月住房开销的四分位数→按照“居住类型” 将数据拆分,并重新计算四分位数→进行比较
• 累计百分比:即各百分比逐级累加起来的结果,
最终取值为100%。
2、频数分析中常用统计图
• 条形图:适用于定序和定类变量的分析。条形图
的纵坐标可以是频数,也可以是百分比。
• 饼图:饼图中圆内的扇形面积可以表示频数,也可
以表示百分比。
• 直方图:适用于定距型变量的分析。
3、频数分析的基本操作
第 章 SPSS 基本统计量的描述

存 (取 )款 金 额
直方图
二、计算基本描述统计量
目的:精确把握变量的总体分布状况。 基本操作: ✓ 描述统计-频率过程:统计 ✓ 描述统计- 描述过程 ✓ 描述统计- 探索过程 ✓ 均值比较-均值 过程(分组显示) 用途:计算变量的集中趋势、离散趋势、偏度、
峰度等指标,绘制统计图。
几个过程的基本描述统计量比较
农村户口
户口
城镇户口
饼图
Frequency
100
0 0.0
Std. Dev = 10945.57 Mean = 4738.1 10000.0 20000.0 30000.0 40000.0 50000.0 60000.0 70000.0 80000.0 90000.0N10=000208.02.00
McNemar:配对计数资料的卡方检验。零假设
为两变量的阳性率无差别源自2(bc 1)2
bc
Kappa一致性检验:系数取值-1~1。测量同 一观测对象在两变量(两变量服从二项分布) 上取值的一致性程度。其绝对值越接近1,说明 一致性程度越高。一般来说:
✓ 系数>=0.7,一致性程度较高;
✓ 0.4~0.7,一致性程度一般;
卡方检验操作:统计量选项
【单元格】:用于定义列联表单元格中需 要计算的指标:
计数:是否输出实际观察数和理论数;
百分比:是否输出行百分数、列百分数以及合 计百分数;
残差:选择残差的显示方式;
【格式】:用于选择行变量是升序还是降 序排列。
结果:城乡储户的收入水平没有明显差异。
Pearson卡方值的影响因素
C
2 2 n
A11A22A12A21
R1R2C1C2
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七个统计图:直方图。(省略) 第八个统计图:茎叶图。
茎叶图描述,在男孩的智力测验 分数的茎叶图中的第二行,频率是数 量为1,也就是有1个数值,茎(Stem )为8,叶(Leaf)为5,其实该数值 是85;第三行,频率是数量为5,有5 个数值是茎为9,叶为16889,其实这 5个数值是91、96、98、98、99。 其 余数据依此类推。
第4步:设置绘图。点击【图】按钮,弹出“探索 :图”对话框。
在“描述”栏内,同时选择“ 茎 叶图”、“直方图”两个复选框,要 求作茎叶描述,以及直方图显示。 同时,选择“含检验的正态图”。
第5步:设置选项。点击【选项】按钮,弹出“探 索:选项”对话框。
第6 步:在主对话框中点击【确定】按钮 。SPSS 在输出窗口的输出结果。 第7 步:结果分析。 第一个统计表:个案处理摘要(略) 第二个统计表:描述统计表。
第十章 信度和效度分析 第十一章 非参数检验 第十二章 多选变量分析 第十三章 SPSS应用案例——问卷调查分析 第十四章 SPSS应用案例——测验质量分析 第十五章 探索性因子分析及案例应用 第十六章 基本统计图表的制作 第十七章 SPSS应用分析归纳小结
第四章 描述统计分析
第3 步:设置分析变量。从左边的源变量框里选 择一个和多个变量进入右边的“变量:”框里。在 本例中选“总分”变量进入“变量:”框。 第4 步:输出频率分布表。在主界面中“ 显示频 率表”,系统默认为选中显示,在本例中也选中 。 第5 步:设置输出的统计量。
第6 步:统计图形输出设置。
在该表中,性别变量分 男、女分别输出均数为 、中位数、方差、标准 差、极小值、极大值、 全距、四分位距、偏度、 峰度等一些统计量。通 过此表,能较全面的反 映数据的集中趋势、离 散趋势。
第三个统计表:M-估计
输出四个不同权重下作中心趋势的粗略最大似然确定数,对于伴有长拖 尾的对称分布数据或带有个别极端数值的数据,用粗略最大似然确定数 替代均数或中位数,结果更准确。
案例:【例4-3】试对10岁少儿的智力测验分数进 行探索分析,对该测验分数进行正态分布检验、 分析茎叶图。
第1 步:打开分析数据。打开“10岁少儿的智力 测验分数.sav”文件。 第2 步:启动分析过程。点击【分析】【描述统 计】【探索】命令,打开如图所示的对话框。
第3 步:统计量选择。点击【统计】按钮,弹出 “探索:统计量”对话框
第一节 第二节 第三节 第四节 第五节
频数分析 描述分析 探索分析 P-P图 SPSS表格处理:三线表的制作
第三节 探索分析
调用探索性分析过程可对变量的分布进行更为深 入详尽的描述性分析。 它在一般描述统计指标的基础上,增加观察数据 的分布描述、发现数据是否有异常值或极值,以 及有关数据其他特征的文字与图形描述,显得更 加细致与全面,有助于用户思考对数据进行进一 步分析的方案。
第十个统计图:箱图。
图中方箱为四分位数的箱图,中心粗线为中位数(50%百分位的观察值 ),箱图的上线、下线为(25%、75%百分位的观察值),外部的两端线 为最大值与最小值。
第四节 P-P图
P-P图通过变量分布累计比与某一分布累计比生成 的图形。通过P-P图可以检验数据是否符合指定的分 布。原假设H0为:观察变量的数据完全符合指定分 布时,P-P图中各点近似呈一条直线。如果P-P图中 各个观测点不呈直线,但有一定规律,可以对变量 数据进行转换,使转换后的数据更接近指定分布或 另外指定的分布。 Q-Q图同样可以用于检验数据的分布,其检验效果是 一样的。所不同的是,Q-Q图是用变量数据分布的分 位数与所指定分布的分位数之间的关系曲线来进行 检验的。在本章中仅介绍P-P图。
SPSS 23.0 统计分析
——在心理学与教育学中的应用
2016-8-4
第四章 描述统计分析
全书目录
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 第九章
SPSS 23.0 简介与基本操作 数据编辑与整理 数据转换 描述统计分析 交叉表分析 比较平均值 方差分析 相关分析 回归分析
□描述:输出均数、中位数、众数、5% 修正均数、标准误、方差、标准差、最小 值、最大值、范围、四分位全距、峰度系 数、峰度系数的标准误、偏度系数、偏度 系数的标准误; □ M- 估计量:作中心趋势的粗略最大似 然确定,输出四个不同权重的最大似然确 定数; □离群值:输出五个最大值与五个最小 值; □百分位数:输出第5%、10%、25%、50% 、75%、90%、95%位数; 本例以上四个复选框全部选择
第 4 步:设置分析参数。在对话框的“转换(Transform) ”栏:“ 自然对数转换”,对当前变量的数据取自然对 数,即将原有变量转换成以自然数e为底的对数变量。“ 将值标准化”,将当前变量的数据转换为标准值,即转换 后变量数据的均值为0,方差为1。“ 差异”,对当前变 量的数据进行差分转换,即利用变量中连续数据之间的差 值来转换数据。选择此项以后,后面的文本框变为可用, 在其中输入一个正整数,以确定转换的差分度,默认值为 1。“ 季节性差异”,用于确定指明计算时间序列的季节 差分。只有在对当前变量的数据序列定义了周期以后才可 用,如果当前周期为0,将不能计算季节差分。 需要注意的是,这些数据转换并不改变变量中的变量 值,只影响正态概率图。
第二个表: 频率表
第三个图:频率分布的条形图
图中的右边标明了标准差、平均数、样本量。 此图就表明,这批数据基本接近正态分 布曲线。
【思考题】
在智力测验分析中,往往根据分数将智力分为几个等级, 然后再统计报告各个智力等级的人数,如下表所示(在下 表的数据仅为参考,实际统计数字以数据文件的统计结果 为准)。以“智力测验分数.sav”文件为例,在SPSS中如 何实现如下分析结果?
第一节 频数分析
频率分布分析主要通过频率分布表、条形图和直 方图,以及集中趋势和离散趋势的各种统计量来 描述数据的分布特征。
案例:【例4-1】试对某一次测验的测验总分进
行频率分析,描述测验分数的分布表,以及累计 百分比表,并绘制分数分布直方图。 第1 步:打开分析数据。打开“测验数据文件 .sav”文件。 第2 步:启动分析过程。点击【分析】 【描述 统计】 【频率】菜单命令 。
第 四 章 描 述 统 计 分 析
第一节 第二节 第三节 第四节 第五节
频数分析 描述分析 探索分析 P-P图 SPSS表格处理:三线表的制作
第二节 描述分析源自描述统计分析(Descriptives)过程是对变量进行 描述统计分析,包括计算集中趋势、离散趋势、分 布等统计指标,而且可将原始数据转换成标准Z分 值并存入数据集中。 所谓Z分值是指某原始数值比其均值高或低多少个 标准差,高时为正值,低时为负值,相等时为零。
第 四 章 描 述 统 计 分 析
从第四章开始讲解【分析】菜单命令下的数 据分析方法,点击【分析】菜单命令下拉子 菜单。 包括:【报告】,【描述统计】,【定制表 】,【比较平均值】,【一般线性模型】, 【广义线性模型】,【混合模型】,【相关 】,【回归】,【对数线性】,【神经网络 】,【分类】,【降维】,【标度】,【非 参数检验】,【时间序列预测】,【生存分 析】,【多重响应】,【缺失值分析】,【 多重插补】,【复杂抽样】,【质量控制】 ,【ROC曲线图】,【时间和空间建模】。
案例:【例4- 2】试对某一次测验的测验总分进
行分析,描述该测验分数的基本描述信息,以及将 每个被试的分数转化为标准化分数。
第1 步:打开分析数据。打开“测验数据文件 .sav”文件。 第2 步:启动分析过程。点击【分析】【描述统 计】【描述】菜单命令,打开如图所示的对话 框。
第3 步:设置分析变量。从左边的源变量框里选 择一个和多个变量进入右边的“变量:”框里。在 本例中选“总分”、“智商分数”变量进入“变 量:”框。 选中 “□将标准化值另存为变量” 复选框, 将计算该变量的z值并保存结果到当前数据集中。 第4 步:选定统计分析选项。单击【选项】按钮 ,打开图 所示的对话框,该对话框用于选择统计 量:
第九个统计图:正态Q-Q图。 Q-Q图是用变量数据分布的分位数与所指定分布的 分位数之间的关系曲线来进行检验的。这里是与 正态分布进行检验,因而称为正态Q-Q图。原假设 H0:一个变量的数据服从正态分布,正态Q-Q图将 是一条直线。
当性别为男时,正态Q-Q图中的点都是在直线附近,也就是说,智 力测验分数服从正态分布的假设可以接受。 当性别为女时,正态Q-Q图中的点也都是在直线附近,也就是说, 智力测验分数服从正态分布的假设可以接受。
第四个统计表:输出百分位数。
有两种计算方式:加权平均、图基枢纽。计算的百分位数能 较好分析数据的百分位参照点。
第五个统计表:输出极值。
按男、女分组,分别 输出最大五个数和最小五 个数。
第六个统计表:正态性检验。
( 1) 柯尔莫戈洛夫-斯米诺夫的检验所对应的显著性水平sig为0.200 ,大于0.05,接受原假设,即男生、女生的智力测验分数服从正态分布 ( 2) 夏皮洛 -威尔克的检验所对应的显著性水平sig为0.368,和0.598 ,大于0.05,接受原假设,即男生、女生的智力测验分数服从正态分布
第四章 描述统计分析
第 四 章 描 述 统 计 分 析
第一节 第二节 第三节 第四节 第五节
频数分析 描述分析 探索分析 P-P图 SPSS表格处理:三线表的制作
