第7章 图单元测试(答案)
人教版七年级数学下册第7章-平面直角坐标系-单元测试卷(解析版)

第7章平面直角坐标系期末考好题精选训练一、选择题1.已知点P(2a﹣5,a+2)在第二象限,则符合条件的a的所有整数的和的立方根是()A.1 B.﹣1 C.0 D.2.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为()A.6,(﹣3,4)B.2,(3,2) C.2,(3,0) D.1,(4,2)3.已知点P(2﹣a,3a+6)到两坐标轴距离相等,则P点坐标为() A.(3,3)B.(6,﹣6)C.(3,3)或(6,﹣6)D.(3,﹣3)4.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标是()A.(﹣4,0) B.(6,0)C.(﹣4,0)或(6,0) D.(0,12)或(0,﹣8)5.已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是()A.B.C.D.6.下列命题是真命题的是()①a,b为实数,若a2=b2,则=②的平方根是±4③三角形ABC中,∠C=90°,则点到直线的距离是线段BC④建立一个平面直角坐标,点A(﹣2,4),点B(3,4),画直线AB,若点C在直线AB上,且AC=4,则C点坐标(1,4),(﹣6,4)A.0 B.1 C.2 D.37.如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(﹣1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(﹣2,2),第四次向左跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标()A.(50,49)B.(51,50)C.(﹣50,49)D.8.下列说法正确的是()A.若ab=0,则点P(a,b)表示原点B.点(1,﹣a2)在第四象限C.已知点A(2,3)与点B(2,﹣3),则直线AB平行x轴D.坐标轴上的点不属于任何象限9.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n 被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是()A.(66,34)B.(67,33)C.D.(99,34)10.在△ABC内任意一点P(a,b)经过平移后对应点P1(c,d),已知A(3,2)在经过此次平移后对应点A1的坐标为(5,﹣1),则a+b﹣c﹣d的值为()A.﹣5 B.﹣1 C.1 D.511.周末,小明与小文相约一起到游乐园去游玩,如图是他俩在微信中的一段对话:根据上面两人的对话纪录,小文能从M超市走到游乐园门口的路线是()A.向北直走700米,再向西直走300米B.向北直走300米,再向西直走700米C.向北直走500米,再向西直走200米D.向南直走500米,再向西直走200米二、填空题12.如图,将边长为1个单位长度的正方形ABCD置于平面直角坐标系内,如果BC与x轴平行,且点A的坐标是(2,2),那么点C的坐标为.第12题图第13题图13.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是.14.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.则A20(,);点A4n的坐标为(,)(n是正整数).15.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,﹣5),A(4,0),则AD•BC=.16.平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形",现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是.17.如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是m.18.定义:若点M、N分别是两条线段a和b上任意一点,则线段MN长度的最小值叫做线段a与线段b的“理想距离”.已知O(0,0),A(1,1),B(3,k),C(3,k+2)是平面直角坐标系中的4个点.根据上述概念,若线段BC与线段OA的理想距离为2,则k的取值范围是.三、解答题19.如图,这是某市部分简图,为了确定各建筑物的位置:(1)请你以火车站为原点建立平面直角坐标系.(2)写出市场、超市的坐标.(3)请将体育场、宾馆和火车站看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.20.如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a ﹣2|+(b﹣3)2=0.(1)求a,b的值;(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;(3)在(2)条件下,当m=﹣时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.21.如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A(1,1),点C(a,b),满足+|b﹣3|=0.(1)求长方形ABCD的面积.(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.①当t=4时,直接写出三角形OAC的面积为;②若AC∥ED,求t的值;(3)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,A n.①若点A1的坐标为(3,1),则点A3的坐标为,点A2014的坐标为;②若点A1的坐标为(a,b),对于任意的正整数n,点A n均在x轴上方,则a,b 应满足的条件为.22.在平面直角坐标系xOy中,对于点P(x,y),我们把P'(y﹣1,﹣x﹣1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,…,这样依次得到点.(1)当点A1的坐标为(2,1),则点A3的坐标为,点A2016的坐标为;(2)若A2016的坐标为(﹣3,2),则设A1(x,y),求x+y的值;(3)设点A1的坐标为(a,b ),若A1,A2,A3,…A n,点A n均在y轴左侧,求a、b的取值范围.23.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底"a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底"a=5,“铅垂高"h=4,“矩面积”S=ah=20.已知点A(1,2),B(﹣3,1),P(0,t).(1)若A,B,P三点的“矩面积"为12,求点P的坐标;(2)直接写出A,B,P三点的“矩面积”的最小值.一、选择题1.已知点P(2a﹣5,a+2)在第二象限,则符合条件的a的所有整数的和的立方根是()A.1 B.﹣1 C.0 D.【解答】解:∵点P(2a﹣5,a+2)在第二象限,∴解得:符合条件的a的所有整数为﹣1,0,1,2,∴﹣1+0+1+2=2,∴2的立方根为:,故选:D.2.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为()A.6,(﹣3,4)B.2,(3,2)C.2,(3,0) D.1,(4,2)【解答】解:如图所示:由垂线段最短可知:当BC⊥AC时,BC有最小值.∴点C的坐标为(3,2),线段的最小值为2.故选:B.3.已知点P(2﹣a,3a+6)到两坐标轴距离相等,则P点坐标为()A.(3,3) B.(6,﹣6)C.(3,3)或(6,﹣6)D.(3,﹣3)【解答】解:∵点P(2﹣a,3a+6)到两坐标轴距离相等,∴|2﹣a|=|3a+6|,∴2﹣a=3a+6或2﹣a=﹣(3a+6),解得a=﹣1或a=﹣4,当a=﹣1时,2﹣a=2﹣(﹣1)=3,3a+6=3×(﹣1)+6=3,当a=﹣4时,2﹣a=2﹣(﹣4)=6,3a+6=3×(﹣4)+6=﹣6,∴点P的坐标为(3,3)或(6,﹣6).故选C.4.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标是()A.(﹣4,0)B.(6,0)C.(﹣4,0)或(6,0) D.(0,12)或(0,﹣8)【解答】解:∵A(1,0),B(0,2),点P在x轴上,∴AP边上的高为2,又△PAB的面积为5,∴AP=5,而点P可能在点A(1,0)的左边或者右边,∴P(﹣4,0)或(6,0).故选C5.已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是()A.B.C.D.【解答】解:根据岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,故D 符合.故选:D.6.下列命题是真命题的是()①a,b为实数,若a2=b2,则=②的平方根是±4③三角形ABC中,∠C=90°,则点到直线的距离是线段BC④建立一个平面直角坐标,点A(﹣2,4),点B(3,4),画直线AB,若点C在直线AB上,且AC=4,则C点坐标(1,4),(﹣6,4)A.0 B.1 C.2 D.3【解答】解:a,b为实数,若a2=b2,则a=b或a=﹣b,所以①错误;的平方根是±2,所以②错误;三角形ABC中,∠C=90°,则点B到直线AC的距离是线段BC的长,所以③错误;建立一个平面直角坐标,点A(﹣2,4),点B(3,4),画直线AB,若点C在直线AB上,且AC=4,则C点坐标(2,4),(﹣6,4),所以④错误.故选A.7.如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(﹣1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(﹣2,2),第四次向左跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标()A.(50,49)B.(51,50)C.(﹣50,49)D.【解答】解:观察发现,第2次跳动至点的坐标是(2,1),第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是(4,3),第8次跳动至点的坐标是(5,4),…第2n次跳动至点的坐标是(n+1,n),∴第100次跳动至点的坐标是(51,50).故选B.8.下列说法正确的是()A.若ab=0,则点P(a,b)表示原点B.点(1,﹣a2)在第四象限C.已知点A(2,3)与点B(2,﹣3),则直线AB平行x轴D.坐标轴上的点不属于任何象限【解答】解:A、a=0,b≠0时,点P(a,b)在y轴上,a≠0,b=0时,点P(a,b)在x轴上,a=b=0时,点P(a,b)表示原点,故本选项错误;B、a=0时,点(1,﹣a2)在x轴上,a≠0时,点(1,﹣a2)在第四象限,故本选项错误;C、∵点A(2,3)与点B(2,﹣3)的横坐标相同,∴直线AB平行y轴,故本选项错误;D、坐标轴上的点不属于任何象限正确,故本选项正确.故选D.9.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是()A.(66,34)B.(67,33) C.D.(99,34)【解答】解:由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,∵100÷3=33余1,∴走完第100步,为第34个循环组的第1步,所处位置的横坐标为33×3+1=100,纵坐标为33×1=33,∴棋子所处位置的坐标是.故选:C.10.在△ABC内任意一点P(a,b)经过平移后对应点P1(c,d),已知A(3,2)在经过此次平移后对应点A1的坐标为(5,﹣1),则a+b﹣c﹣d的值为()A.﹣5 B.﹣1 C.1 D.5【解答】解:∵A(3,2)在经过此次平移后对应点A1的坐标为(5,﹣1),∴△ABC的平移规律为:向右平移个单位,向下平移3个单位,∵点P(a,b)经过平移后对应点P1(c,d),∴a+2=c,b﹣3=d,∴a﹣c=﹣2,b﹣d=3,∴a+b﹣c﹣d=﹣2+3=1,故选C.11.周末,小明与小文相约一起到游乐园去游玩,如图是他俩在微信中的一段对话:根据上面两人的对话纪录,小文能从M超市走到游乐园门口的路线是()A.向北直走700米,再向西直走300米B.向北直走300米,再向西直走700米C.向北直走500米,再向西直走200米D.向南直走500米,再向西直走200米【解答】解:根据题意建立平面直角坐标系如图所示,小文能从M超市走到游乐园门口的路线是:向北直走700米,再向西直走300米.故选A.二、填空题12.如图,将边长为1个单位长度的正方形ABCD置于平面直角坐标系内,如果BC与x轴平行,且点A的坐标是(2,2),那么点C的坐标为.【解答】解:∵点A的坐标是(2,2),BC∥x轴,且AB=1,∴点B坐标为(2,1),又BC=1,∴点C的坐标为(3,1),故答案为:(3,1).13.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是.【解答】解:∵每个正方形都有4个顶点,∴每4个点为一个循环组依次循环,∵2018÷4=504…2,∴点A2018是第505个正方形的第2个顶点,在第二象限,∵从内到外正方形的边长依次为2,4,6,8,…,∴A2(﹣1,1),A6(﹣2,2),A10(﹣3,3),…,A2018(﹣505,505).故答案为(﹣505,505).14.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.则A20(,);点A4n的坐标为(,)(n是正整数).【解答】解:由图可知,A4,A8都在x轴上,∵小蚂蚁每次移动1个单位,∴OA4=2,OA8=4,则OA20=10,∴A20(10,0);根据以上可得:OA4n=4n÷2=2n,∴点A4n的坐标(2n,0).故答案为:10,0;2n,0.15.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,﹣5),A(4,0),则AD•BC=.【解答】解:过B作BE⊥x轴于E,过C作CF⊥y轴于F,∵B(m,3),∴BE=3,∵A(4,0),∴AO=4,∵C(n,﹣5),∴OF=5,∵S△AOB=AO•BE=×4×3=6,S△AOC=AO•OF=×4×5=10,∴S△AOB +S△AOC=6+10=16,∵S△ABC=S△AOB+S△AOC,∴BC•AD=16,∴BC•AD=32,故答案为:32.16.平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形",现有点A(2,5),B (﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是.【解答】解:∵以O,A,B,C四点为顶点的四边形是“和点四边形”,①当C为A、B的“和点”时,C点的坐标为(2﹣1,5+3),即C(1,8);②当B为A、C的“和点”时,设C点的坐标为(x1,y1),则,解得C(﹣3,﹣2);③当A为B、C的“和点"时,设C点的坐标为(x2,y2),则,解得C(3,2);∴点C的坐标为(1,8)或(﹣3,﹣2)或(3,2).故答案为:(1,8)或(﹣3,﹣2)或(3,2).17.如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是m.【解答】解:根据题意可知当机器人走到A6点时,A5A6=18米,点A6的坐标是(6+3=9,18﹣6=12),即(9,12).所以,当机器人走到点A6时,离点O的距离是=15.故答案为:15.18.定义:若点M、N分别是两条线段a和b上任意一点,则线段MN长度的最小值叫做线段a与线段b的“理想距离".已知O(0,0),A(1,1),B(3,k),C(3,k+2)是平面直角坐标系中的4个点.根据上述概念,若线段BC与线段OA的理想距离为2,则k的取值范围是.【解答】解:由题意可得,,解得,﹣1≤k≤1,故答案为:﹣1≤k≤1.三、解答题19.如图,这是某市部分简图,为了确定各建筑物的位置:(1)请你以火车站为原点建立平面直角坐标系.(2)写出市场、超市的坐标.(3)请将体育场、宾馆和火车站看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.【解答】解:(1)如图所示:(2)如图所示:市场(4,3)、超市(2,﹣3);(3)如图所示,△A1B1C1的面积是:3×6﹣×1×6﹣×2×2﹣×3×4=7.20.如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.(1)求a,b的值;(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;(3)在(2)条件下,当m=﹣时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.【解答】解:(1)∵a ,b 满足|a ﹣2|+(b ﹣3)2=0, ∴a ﹣2=0,b ﹣3=0,解得a=2,b=3.故a 的值是2,b 的值是3;(2)过点M 作MN 丄y 轴于点N .四边形AMOB 面积=S △AMO +S △AOB =MN•OA +OA•OB =×(﹣m )×2+×2×3=﹣m +3;(3)当m=﹣时,四边形ABOM 的面积=4。
2020--2021学年人教版数学七年级下册第7章《平面直角坐标系》单元测试题(含答案)

人教版数学七年级下册《平面直角坐标系》单元测试题一、选择题1.下列关于有序数对的说法正确的是( )A.(3,2)与(2,3)表示的位置相同B.(a,b)与(b,a)表示的位置一定不同C.(3,-2)与(-2,3)是表示不同位置的两个有序数对D.(4,4)与(4,4)表示两个不同的位置2.点P在第三象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )A.(-4,3)B.(-3,-4)C.(-3,4)D.(3,-4)3.如果点P(m+3,m+1)在直角坐标系的x轴上,那么P点坐标为( )A.(0,2)B.(2,0)C.(4,0)D.(0,-4)4.如果一个图案沿x轴负方向平移3个单位长度,那么这个图案上的点的坐标变化为( )A.横坐标不变,纵坐标减少3个单位长度B.纵坐标不变,横坐标减少3个单位长度C.横纵坐标都没有变化D.横纵坐标都减少3个单位长度5.如图,线段AB经过平移得到线段A1B1,其中点A,B的对应点分别为点A1,B1,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P′的坐标为( )A.(a-2,b+3)B.(a-2,b-3)C.(a+2,b+3)D.(a+2,b-3)6.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(﹣2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为()A.(﹣4,3)B.(3,4)C.(﹣3,4)D.(4,3)7.如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)8.已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )A.(4,0) B.(0,4) C.(﹣4,0) D.(0,﹣4)9.已知点A(﹣3,2)与点B(x,y)在同一条平行y轴的直线上,且B点到x轴的矩离等于3,则B点的坐标是()A.(﹣3,3)B.(3,﹣3)C.(﹣3,3)或(﹣3,﹣3)D.(﹣3,3)或(3,﹣3)10.已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A.﹣3B.﹣5C.1或﹣3D.1或﹣511.若m是任意实数,则点P (m-4,m+1) 一定不在( )A.第一象限B.第二象限C.第三象限D.第四象限12.将一组整数按如图所示的规律排列下去.若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是()A.32B.24C.25D.-25二、填空题13.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(-4,-1),N(0,1),将线段MN平移后得到线段M′N′(点M,N分别平移到点M′,N′的位置).若点M′的坐标为(-2,2),则点N′的坐标为____________.14.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是.15.点N(x,y)的坐标满足xy<0,则点N在第象限.16.在平面直角坐标系中,若将点P (-1,4) 向右平移2个单位长度后,再向下平移3个单位长度,得到点P1,则点P1的坐标为.17.已知点P在第四象限,它的横坐标与纵坐标之和为1,则点P的坐标为(写出一个即可)18.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后,动点P的坐标是.三、作图题19.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.(1)点A的坐标为,点C的坐标为;(2)将△ABC向左平移7个单位,请画出平移后的△A′B′C′,若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M'的坐标为.四、解答题20.已知平面直角坐标系中有一点M(m-1,2m+3).(1)当m为何值时,点M到x轴的距离为1?(2)当m为何值时,点M到y轴的距离为2?21.如图,机械手要将一个工件从图中的A处移动到B处,但是这个工件不能碰到图中的障碍(不包括坐标轴所表示的直线),试用坐标写出一条机械手在移动中可能要经过的路线(机械手的行走路线均经过格点).22.已知:A(0,1),B(2,0),C(4,3).(1)在坐标系中描出各点,画出△ABC;(2)求△ABC的面积;(3)若点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.23.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).(1)填空:四边形ABCD内(边界点除外)一共有个整点(即横坐标和纵坐标都是整数的点);(2)求四边形ABCD的面积.24.如图,在平面直角坐标系中,A(-2,2),B(-3,-2).(1)若点D与点A关于y轴对称,则点D的坐标为___;(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为____;(3)求A,B,C,D组成的四边形ABCD的面积.25.如图所示,A(1,0),点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).(1)直接写出点E的坐标;(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:①当t= 秒时,点P的横坐标与纵坐标互为相反数;②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.参考答案1.C.2.B.3.B.4.B5.B.6.D.7.C.8.A.9.C.10.C.11.D12.D13.答案为:(2,4);14.答案为:(-3,5).15.答案为:二、四.16.答案为:(1,1)17.答案为:(2,﹣1)18.答案为:(504,2).19.解:(1)利用图形得出:点A的坐标为:(2,8),点C的坐标为:(6,6);(2)∵将△ABC向左平移7个单位,M为△ABC内的一点,其坐标为(a,b),∴平移后点M的对应点M'的坐标为:(a﹣7,b).20.解:(1)∵|2m+3|=1,∴2m+3=1或2m+3=-1,解得m=-1或m=-2.(2)∵|m-1|=2,∴m-1=2或m-1=-2,解得m=3或m=-1.21.解:答案不唯一,如:A(1,-2)→(5,-2)→(5,5)→(-4,5)→B(-4,3).22.解:(1)如图所示.(2)S△ABC=3×4-×2×3-×2×4-×2×1=12-3-4-1=4.(3)当点P在x轴上时,S△ABP=AO·BP=4,即×1·BP=4,解得BP=8,∴点P的坐标为(10,0)或(-6,0);当点P在y轴上时,S△ABP=BO·AP=4,即×2AP=4,解得AP=4,∴点P的坐标为(0,5)或(0,-3),∴点P的坐标为(0,5)或(0,-3)或(10,0)或(-6,0).23.解:(1)填空:四边形ABCD内(边界点除外)一共有 13个整点.(2)如下图所示:∵S四边形ABCD=S△ADE+S△DFC+S四边形BEFG+S△BCGS△ADE=×2×4=4 S△DFC=×2×5=5 S四边形BEFG=2×3=6 S△BCG=×2×2=2 ∴S四边形ABCD=4+5+6+2=17 即:四边形ABCD的面积为1724.解:_(2,2) (2,-1)(3)15.5.25.解:(1)根据题意,可得三角形OAB沿x轴负方向平移3个单位得到三角形DEC,∵点A的坐标是(1,0),∴点E的坐标是(-2,0);故答案为:(-2,0);(2)①∵点C的坐标为(-3,2).∴BC=3,CD=2,∵点P的横坐标与纵坐标互为相反数;∴点P在线段BC上,∴PB=CD,即t=2;∴当t=2秒时,点P的横坐标与纵坐标互为相反数;故答案为:2;②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);③能确定,如图,过P作PE∥BC交AB于E,则PE∥AD,∴∠1=∠CBP=x°,∠2=∠DAP=y°,∴∠BPA=∠1+∠2=x°+y°=z°,∴z=x+y.。
北师大版八年级上册数学第七章平行线的证明单元测试(含答案)

八年级上册数学第七章单元测试一、选择题(每题3分,共30分)1.命题“负数没有平方根”的条件是()A.如果一个数是正数B.如果一个数没有平方根C.如果一个数是负数D.如果一个数是非负数2.如图,下列能判定AB∥CD的条件有()(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1个B.2个C.3个D.4个3.如图,直线AB∥CD,OG是∠EOB的平分线,∠EFD=70°,则∠BOG的度数是()A.70°B.20°C.35°D.40°4.如图所示,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是()A.∠2=45°B.∠1=∠3C.∠AOD与∠1互为补角D.∠1的余角等于75°30′5.如图,下列选项中,不可以得到l1∥l2的是()A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°6.如图,把△ABC纸片沿DE折叠,则()A.∠A=∠1+∠2 B.2∠A=∠1+∠2C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)7.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于()A.90°B.180°C.210°D.270°8.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE为()A.80°B.60°C.50°D.40°9.如图,在△ABC中,∠B=38°,∠C=54°,AD是BC边上的高,AE是∠BAC 的平分线,则∠DAE的度数为()A.8°B.10°C.12°D.14°10.在三角板拼角活动中,小明将一副三角板按如图方式叠放,则拼出的∠α度数为()A.65°B.75°C.105°D.115°二、填空题(每题3分,共15分)11.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,则∠A为________度.12.如图,AB∥CD,∠1=58°,FG平分∠EFD交AB于G,则∠FGB的度数为________.13.已知AD是△ABC的高,∠BAD=72°,∠CAD=21°,则∠BAC的度数是________.14.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于________.15.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=65°,则∠BEC =________度.三、解答题(16题10分,17题7分,第18~21题每题8分,第22~23题每题13分,共75分)16.如图,点A、B、C、D在同一条直线上,EC∥FD,∠F=∠E,求证:AE ∥BF.将证明过程补充完整,并在括号内填写推理依据.证明:∵EC∥FD,()∴∠________=∠1.()∵∠F=∠E,(已知)∴∠________=∠________,()∴AE∥BF.()17.如图,D、E、F分别在△ABC的三条边上,DE∥AB,∠1+∠2=180°.(1)试说明:DF∥AC;(2)若∠1=100°,DF平分∠BDE,求∠C的度数.18.如图,∠AGF=∠ABC,∠1+∠2=180°.(1)试判断BF与DE的位置关系,并说明理由;(2)若BF⊥AC,∠2=145°,求∠AFG的度数.19.如图,已知BE∥CF,BE、CF分别平分∠ABC和∠BCD,求证:AB∥CD.20.如图,已知:DE⊥AO于点E,BO⊥AO于点O,∠CFB=∠EDO,证明:CF∥DO.21.如图,AD为△ABC的角平分线,DE∥AB,DE交AC于点E.若∠B=57°,∠C=65°,求∠ADE的度数.22.已知如图,点E在△ABC的边BC上,AD∥BC,∠DAE=∠BAC,∠1=∠2.(1)求证AB∥DE;(2)若已知AE平分∠BAC,∠C=35°,求∠2的度数.23.如图,点A、B分别在射线OM、ON上运动(不与点O重合).(1)如图1,若∠MON=90°,∠OBA、∠OAB的平分线交于点C,则∠ACB=________;(2)如图2,若∠MON=n°,∠OBA、∠OAB的平分线交于点C,则∠ACB=________;(3)如图2,若∠MON=n°,△AOB的外角∠ABN、∠BAM的平分线交于点D,求∠ACB与∠ADB之间的数量关系,并求出∠ADB的度数;(4)如图3,若∠MON=80°,BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E.试问:随着点A、B的运动,∠E的大小会变吗?如果不会,求出∠E的度数;如果会,请说明理由.答案一、1.C 2.C 3.C 4.D 5.C 6.B7.B8.D9.A10.C二、11.3012.151°13.51°或93°14.230°15.122.5三、16.已知;F;两直线平行,内错角相等;E;1;等量代换;内错角相等,两直线平行17.解:(1)∵DE∥AB,∴∠A=∠2.∵∠1+∠2=180°,∴∠A+∠1=180°,∴DF∥AC.(2)∵∠1=100°,∠1+∠2=180°,∴∠2=80°.∵AC∥DF,∴∠FDE=∠2=80°,∠C=∠BDF.∵DF平分∠BDE,∴∠BDF=80°,∴∠C=∠BDF=80°.18.解:(1)BF∥DE.理由如下:∵∠AGF=∠ABC,∴GF∥BC,∴∠1=∠3.∵∠1+∠2=180°,∴∠3+∠2=180°,∴BF∥DE.(2)∵BF⊥AC,∴∠BF A=90°.∵∠1+∠2=180°,∠2=145°,∴∠1=35°,∴∠AFG=90°-35°=55°.19.证明:∵BE∥CF,∴∠1=∠2.∵BE、CF分别平分∠ABC和∠BCD,∴∠ABC=2∠1,∠BCD=2∠2,∴∠ABC=∠BCD,∴AB∥CD.20.证明:∵DE⊥AO,BO⊥AO,∴∠AED=∠AOB=90°,∴DE∥BO,∴∠EDO=∠BOD.又∵∠EDO=∠CFB,∴∠BOD=∠CFB,∴CF∥DO.21.解:∵∠B=57°,∠C=65°,∴∠BAC=180°-57°-65°=58°.∵AD为△ABC的角平分线,∴∠BAD=∠DAC=29°.∵DE∥AB,∴∠ADE=∠BAD=29°.22. (1)证明:∵AD∥BC,∴∠DAE=∠2,∵∠1=∠2,∴∠DAE=∠1.∵∠DAE=∠BAC,∴∠BAC=∠1,∴AB∥DE.(2)解:∵∠DAE=∠BAC,∴∠BAE=∠DAC.∵AE平分∠BAC,∴∠EAC=∠BAE=∠DAC.∵AD∥BC,∴∠C=∠DAC=35°,∴∠EAC=∠DAC=35°,∴∠AEC=180°-∠EAC-∠C=110°,∴∠2=180°-∠AEC=70°.23.解:(1)135°(2)90°+12n°(3)∵BC、BD分别是∠OBA和∠NBA的平分线,∴∠ABC=12∠OBA,∠ABD=12∠NBA,∴∠ABC+∠ABD=12∠OBA+12∠NBA=12(∠OBA+∠NBA)=90°,即∠CBD=90°,同理:∠CAD=90°.∵四边形内角和等于360°,∴∠ACB+∠ADB=360°-90°-90°=180°,由(2)知:∠ACB=90°+12n°,∴∠ADB=180°-(90°+12n°)=90°-12n°,∴∠ACB+∠ADB=180°,∠ADB=90°-12n°.(4)∠E的度数不会变,∠E=40°.求解如下:∵∠NBA=∠AOB+∠OAB,∴∠OAB=∠NBA-∠AOB.∵AE、BC分别是∠OAB和∠NBA的平分线,∴∠BAE=12∠OAB,∠CBA=12∠NBA,∵∠CBA=∠E+∠BAE,∴12∠NBA=∠E+12∠OAB,∵12∠NBA=∠E+12(∠NBA-80°),即12∠NBA=∠E+12∠NBA-40°,∴∠E=40°.。
新人教版四年级上册《第7章_条形统计图》小学数学-有答案-单元测试卷
新人教版四年级上册《第7章条形统计图》单元测试卷一、填空题.1. 一张饼有________面,如果烙一面要花2分钟,烙熟一张饼需要________分钟。
2. 煮一个鸡蛋需要8分钟,一个锅一次可以煮10个鸡蛋,那么煮10个鸡蛋至少需要________分钟。
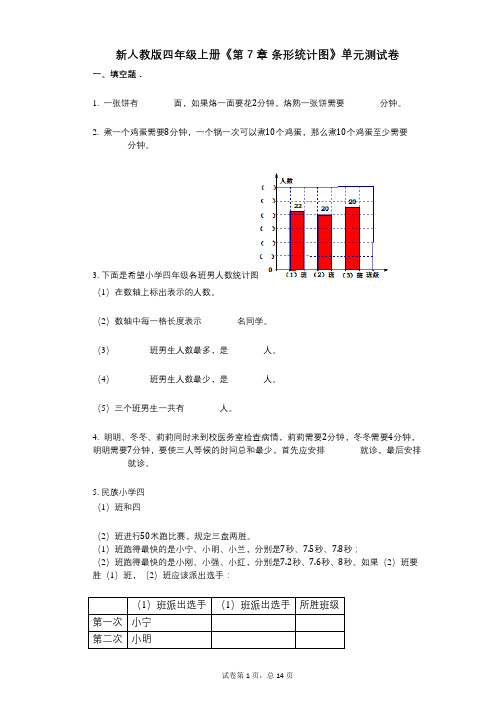
3. 下面是希望小学四年级各班男人数统计图(1)在数轴上标出表示的人数。
(2)数轴中每一格长度表示________名同学。
(3)________班男生人数最多,是________人。
(4)________班男生人数最少,是________人。
(5)三个班男生一共有________人。
4. 明明、冬冬、莉莉同时来到校医务室检查病情,莉莉需要2分钟,冬冬需要4分钟,明明需要7分钟,要使三人等候的时间总和最少,首先应安排________就诊,最后安排________就诊。
5. 民族小学四(1)班和四(2)班进行50米跑比赛,规定三盘两胜。
(1)班跑得最快的是小宁、小明、小兰,分别是7秒、7.5秒、7.8秒;(2)班跑得最快的是小刚、小强、小红,分别是7.2秒、7.6秒、8秒。
如果(2)班要胜(1)班,(2)班应该派出选手:加油站同时来了A、B、C三辆车,而且三辆车加满油的时间依次是8分钟、5分钟、10分钟。
现在只有一个油泵,那么它们全部加满油,等候时间和加油时间最少需要()分钟。
A.39B.41C.51D.44星期天妈妈要做以下家务事:擦玻璃要20分钟,收拾厨房要15分钟,用全自动洗衣机洗衣服需要30分钟,晾衣服要10分钟。
妈妈做完这些事最少需要()分钟。
A.75B.45C.55D.65四(1)班同学对他们所喜欢的故事进行了统计,统计结果如图:有30个同学所喜欢的故事是()故事。
A.历史B.成语C.童话D.寓言动物园的管理人员为动物们做了一次“体检”,下面是几种动物体重的统计图,最重的是________,最轻的是________.A.长颈鹿B.棕熊C.大猩猩D.东北虎下面是四(1)班同学最喜欢的一种早餐(不包括主食)统计表。
冀教版小学六年级上册数学第7单元扇形统计图单元测试题2(附答案)
冀教版小学六年级上册数学第7章扇形统计图单元测试题一.选择题(共8小题)1.六(1)班在“六一”儿童节前要评选一名区雏鹰队员,采取一名学生只投一票的方式进行评选,投票结果如下:姓名杨洋郑益刘强王华票数/张241284下图()能表示这个投票结果.A.B.C.2.新月小区有一个花坛,其中栽种了40平方米菊花,10平方米鸡冠花,20平方米芍药花和10平方米月季花.下面能正确反映四种鲜花栽种面积分布情况的是()A.B.C.D.3.六(1)班现有40名学生,选举班长的得票数为:小何20票,小赵10票,小邓6票,小李4票.下列四幅图中,()图准确的表示了这一结果.A.B.C.D.4.画统计图时,要根据信息的特点来画.在下面的信息中,适合用扇形统计图的是()A.六年级一班女同学的身高B.芳芳6﹣12岁的身高变化C.大豆的营养成分5.五年(1)班有40名学生,参加竞选班长投票,限定每人有且只能投票一次,结果的得票数为:小明20票,小何10票,小阳6票,小新4票.下列四幅图中,()图能准确地表达这一投票结果.A.B.C.D.6.如图是某小学六(1)班50名同学喜欢的体育运动统计图.下面说法不正确的是()A.喜欢篮球的人数占全班人数的40%.B.喜欢打乒乓球的有40人C.喜欢打乒乓球的人数是踢足球人数的2倍7.在一个有40个学生的班级里选出一名同学担任班长.选举结果如下表,下面()图表示了这一选举结果.姓名票数小李20票小赵10票小邓6票小何4票A.B.C.D.8.六(1)班共有48名同学,期末推选一名优秀毕业生,投票选举结果如表中,下面()图能大体表示出这个结果姓名小红小刚小芳小军票数241248A.B.C.二.填空题(共6小题)9.一个商城2013上半年收入中,家电收占55%,服装占25%,其他收入占20%,如此制成扇形统计图,其中表示家电收入的扇的圆心角是度.10.如图:是某校六年级学生某次数学竞赛的成绩统计图,若获得优秀成绩有60人,那么全年级有人,本次竞赛不及格人.11.六年级同学血型情况如图.AB型的占%;如果O型的共有60人,那么六年级共有人;A型的有人.12.一块菜地种植了4种蔬菜,分布情况如图.若油菜的种植面积是420m2.则(1)黄瓜的种植面积是平方米;(2)芹菜的种植面积比油菜少平方米.13.东林小学学生参加社团活动情况如图.(1)参加社团的人数最多.(2)参加体育类社团的学生占全校学生的%.(3)参加艺术类社团的有800人,参加综合实践类社团的学生有人.(4)参加综合实践类社团与学科类社团的学生人数之比是.14.某学校六年级某次考试中,成绩情况如图所示:不及格人数为20人,六年级总共有人,良好有人,良好人数比优秀人数少%.三.判断题(共5小题)15.扇形统计图和其他统计图一样也要有标题和图例..(判断对错)16.在一个扇形统计图中,经济作物的扇形圆心角是60度,则经济作物的面积占总面积的..(判断对错)17.在扇形统计图中是用整个圆来表示总数.(判断对错)18.扇形统计图可直观看出统计数据各部分占总体的比率..(判断对错)19.扇形统计图中,一个圆代表100%.(判断对错)四.应用题(共4小题)20.一块菜地四种蔬菜的种植面积分布情况如下:①你获得哪些信息请逐条写下来.②如果种植黄瓜的面积有90平方米,你能提出哪些用百分数解决的问题?并解答.21.调味酱里含有各种材料质量的百分比如图所示.在50g的调味酱里,含有辣椒酱的质量是多少克?22.红星果园三种果树种植面积所占百分比如图所示.苹果树种植面积12.6公顷.①三种果树种植总面积是多少公顷?②梨树的种植面积是多少公顷?23.我国四大海域的总面积大约有473万平方千米.根据如图中数据,计算我国南海海域的面积大约是多少万平方千米?五.操作题(共2小题)24.博物馆共有A、B、C、D四个展厅,第一天参观人数如图,第一天B展厅参观人数最多,A、C 展厅参观人数同样多.请根据这条信息,将统计图图例补充完整.25.某课题小组对“蓝点”电动自行车专卖店第一季度该品牌A、B、C、D四种不同型号电动自行车的销量做了统计,绘制成如下两幅统计图.(1)该店第一季度共售出这四种型号的电动自行车共辆.(2)把这两幅统计图补充完整.六.解答题(共3小题)26.绿水青山就是金山银山,北京市政府要坚决打赢蓝天保卫战,让人们乐享蓝天.下面是2017年北京市空气质量情况统计表.2017年北京市空气质量情况统计表等级优良轻度污染中重度污染天数7860(1)完成统计表.(2)结合统计表完成扇形统计图.27.笏石中心小学红领巾广播站每周播音2小时.如图表示各个节目的播音时间.(1)的播音时间最长.(2)每周播出《学法交流》专题节目24分钟,占每周播音总时间的.(3)《音乐欣赏》的播音时间占每周播音总时间的15%,它的播音时间是分钟.(4)学校广播站每周都要用的时间播报《校园新闻》,《故事天地》每周播音分钟.28.联合国规定每年的6月5日是“世界环境日”,为了配合2018年的“世界环境日”,某校课外活动小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将调查结果分析整理后,制成了下面两个统计图.其中,A.能将垃圾放到规定的地方,而且还会考虑垃圾的分类.B.能将垃圾放到规定的地方,但不会考虑垃圾的分类.C.偶尔会将垃圾放到规定的地方.D.随手乱扔垃圾.(1)该校课外活动小组共调查了多少人?并补齐图2的条形统计图.(2)如果该校共有师生2600人,那么随手乱扔垃圾的约有多少人?参考答案与试题解析一.选择题(共8小题)1.解:24+12+8+4=48,24÷48=,12÷48=,4÷48=,8÷48=,只有A答案能表示出投票结果;故选:A.2.解:40+10+20+10=80(平方米),40÷80=;10÷80=;20÷80=;10÷80=;由此可知:菊花的面积占花坛面积的,芍药花的面积占花坛面积的,鸡冠花和月季花的面积各占花坛面积的.所以图象A能正确反映四种鲜花栽种面积分布情况.故选:A.3.解:20÷40=50%10÷40=25%6÷40=15%4÷40=10%选项A、选项D没有表示50%的扇形,排除;选项B没有表示25%的扇形(圆心角是直角),排除;选项C符合题意.故选:C.4.解:根据统计图的特点可知:画统计图时,要根据信息的特点画.A、六年级一班女同学的身高,适合用条形统计图表示;B、芳芳6﹣12岁的身高变化,适合用折线统计图表示;C、大豆的营养成分,适合用扇形统计图表示;故选:C.5.解:20÷40=50%10÷40=25%6÷40=15%4÷40=10%选项A、选项D没有表示50%的扇形,排除;选项B没有表示25%的扇形(圆心角是直角),排除;选项C符合题意.故选:C.6.解:A.1﹣20%﹣40%=40%,答:喜欢篮球的人数占全班人数的40%.因此,喜欢篮球的人数占全班人数的40%.说法正确.B.50×40%=20(人),答:喜欢打乒乓球的有20人.因此,喜欢打乒乓球的有40人.这种说法是错误的.C.40%÷20%=2,答:喜欢打乒乓球的人数是踢足球人数的2倍.因此,喜欢打乒乓球的人数是踢足球人数的2倍.这种说法是正确的.故选:B.7.解:根据题意,计算小李得票率为20÷40=0.5=50%,小赵得票率为10÷40=0.25=25%,小邓得票率为6÷40=0.15=15%,小何得票率为4÷40=0.1=10%,符合这一特征的扇形统计图是:故选:C.8.解:24+12+8+4=48小红:24÷48=50%;小刚:12÷48=25%;小芳:4÷48≈8%;小军:8÷48≈17%;只有A答案能表示出投票结果;故选:A.二.填空题(共6小题)9.解:55%×360°=198°答:表示家电收入的圆心角是198°.故答案为:198.10.解:60÷30%=60÷0.3=200(人);200×(1﹣30%﹣40%﹣25%)=200×5%=200×0.05=10(人);答:全年级有200人,本次竞赛不及格的有10人.故答案为:200、10.11.解:1﹣28%﹣24%﹣40%=8%60÷40%=150(人)150×28%=42(人)答:AB型的占8%;六年级共有150人;A型的有42人.故答案为:8,150,42.12.解(1)420÷20%×(1﹣15%﹣20%﹣35%)=2100×30%=630(m2)答:黄瓜的种植面积是630平方米.(2)420÷20%×(20%﹣15%)=2100×5%=105(m2)答:芹菜的种植面积比油菜少105平方米.故答案为:630,105.13.解:(1)观察图可知:参加艺术类社团的人数最多.(2)1﹣(40%+25%+20%)=1﹣85%=15%答:参加体育类社团的学生占全校学生的15%.(3)800÷40%×25%=2000×25%=500(人)答:参加艺术类社团的有800人,参加综合实践类社团的学生有500人.(4)25%:20%=5:4答:参加综合实践类社团与学科类社团的学生人数之比是5:4.故答案为:艺术类,15,500,5:4.14.解:20÷(1﹣40%﹣35%﹣15%)=20÷10%=20÷0.1=200(人);200×35%=200×0.35=70(人);(40%﹣35%)÷40%=5%÷40%=0.05÷0.4=0.125=12.5%;答:六年级总共有200人,良好的有70人,良好人数比优秀人数少12.5%.故答案为:200、70、12.5.三.判断题(共5小题)15.解:扇形统计图和其他统计图一样也要有标题,但可以没有图例,所以上在的说法是错误.故答案为:×.16.解:由题意得:经济作物种植面积占总面积的:60°÷360°=.答:经济作物种植面积占总面积的.故答案为:√.17.解:扇形统计图是用整个圆表示整体(或总数),用圆内各个扇形的大小表示各部分.所以原题说法正确.故答案为:√.18.解:扇形统计图可直观看出统计数据各部分占总体的比率.原题说法是正确的.故答案为:√.19.解:扇形统计图是用整个圆的面积表示总数(即100%),用圆中各扇形的面积表示各部分占总数的百分比.所以,扇形统计图中,一个圆代表100%.这种说法是正确的.故答案为:√.四.应用题(共4小题)20.解:①可以获得的信息有:黄瓜的种植面积占总面积的30%;油菜的种植面积占总面积的20%;芹菜的种植面积占总面积的15%;西红柿的种植面积占总面积的35%.②可以选择下面其中的一、两个问题:问题一:种植的总面积是多少平方米?90÷30%=300(平方米)答:种植的总面积是300平方米.问题二:油菜的种植面积是多少平方米?300×20%=60(平方米)答:油菜的种植面积是60平方米.问题三:芹菜的种植面积是多少平方米?300×15%=45(平方米)答:芹菜的种植面积是45平方米.问题四:西红柿的种植面积是多少平方米?300×35%=105(平方米)答:西红柿的种植面积是105平方米.21.解:50×60%=30(克)答:含有辣椒酱的质量是30克.22.解:①三种果树种植总面积:12.6÷56%=22.5(公顷)答:三种果树种植总面积是22.5公顷.②梨树的种植面积是:22.5×30%=6.75(公顷)答:梨树的种植面积是6.75公顷.23.解:473×(1﹣1.6%﹣8.0%﹣16.4%)=473×74%=473×0.74=350.02(万平方千米)答:我国南海海域的面积大约是350.02万平方千米.五.操作题(共2小题)24.解:根据分析画图如下:25.解:(1)210÷35%=600(辆)答:该店第一季度共售出这四种型号的电动自行车共600辆.(2)C型号电动自行车的数量:600×30%=180(辆);A型号电动自行车所占百分比:150÷600=0.25=25%;D型号电动自行车所占百分比:60÷600=0.1=10%.补全完整的统计图如图所示:故答案为:600.六.解答题(共3小题)26.解:(1)2017÷4=504 (1)说明2017是平年,共有365天天气优良的天数:365﹣78﹣60=227(天)所以统计如下表:等级优良轻度污染中重度污染天数2277860(2)227÷365×100%≈62.2%78÷365×100%≈21.4%60÷365×100%≈16.4%绘制扇形统计图如下:故答案为:227.27.解:(1)答:《故事天地》的播音时间最长.(2)2小时=120分钟24÷120=答:占每周播音总时间的.(3)120×15%=120×0.15=18(分钟)答:它的播音时间是18分钟.(4)120×(1﹣﹣15%)=120×(1)=120×=48(分钟)答:《故事天地》每周播音48分钟.故答案为:《故事天地》;;18;48.28.解:(1)150÷50%=300(人),偶尔会将垃圾放到规定的地方的人数:300﹣150﹣30﹣30=90(人),作图如下:(2)30÷300=0.1=10%,2600×10%=2600×0.1=260(人),答:随手乱扔垃圾的约有260人.。
(中图版)初中地理七年级下册:第七章 认识我国的区域 单元测试(含答案)

第七章综合测试一、选择题雄安新区是继深圳特区和浦东新区之后又一具有全国意义的新区。
雄安新区规划建设以特定区域为起步区先行开发,起步区面积约100平方千米,中期发展区面积约200平方千米,远期控制区面积约2 000平方千米。
读图,结合所学区域地理知识,完成下面三题。
1.雄安新区位于我国()A.热带B.亚热带C.暖温带D.中温带2.与上海浦东新区和深圳经济特区相比,雄安新区()A.空气湿度更大B.发展空间更广C.人口素质更高D.交通条件更优3.雄安新区主要()A.集中疏解北京市非首都功能B.探索传统工业区优化开发新模式C.培育珠三角创新发展新引擎D.优化长三角城市布局和空间结构读图,回答下面两题。
4.下列有关台湾省的叙述,正确的是()A.北回归线从中部穿过,南部为北温带B.花莲位于板块内部,地震频发C.台湾省包括台湾岛、澎湖列岛、钓鱼岛等D.与大陆联系主要通过铁路运输5.关于台湾岛自然地理要素相互作用的表述,正确的是()A.受地势影响,河流自西向东流B.受气候影响,森林集中分布在西部C.岛屿面积小,植物类型单一D.受地形影响,降水东多西少我国某省位于祖国西南部,地处长江上游,全省面积48.5万平方千米。
宋代称为“川峡四路”,省内有一个盆地,盆地内气候温和多雨,盆地西部为平原,农业发达。
根据材料和图,回答下列两题。
6.图中①②③④位于盆地西部平原的是()A.①B.②C.③D.④7.下列关于该省的说法正确的是()A.地形复杂,地势东高西低B.地跨我国二三级阶梯,河流落差大C.人口分布东多西少,人口分布东密西疏D.气候以亚热带季风气候为主,气候类型单一8.关于泰宁县的叙述,错误的是()A.位于福建省西北部B.城区主要位于低山丘陵C.被列入世界文化遗产名录D.有“汉唐古镇,两宋名城”之誉黄土高原地貌千姿百态、地域文化丰富多彩、生态环境日益改善。
图中阴影区黄土层深厚,黄土高原是世界上最大的黄土堆积区。
读图,回答下面三题9.下列有关黄土高原的说法,正确的是()A.黄土是由风从沿海湿润地区吹到黄土高原堆积而成的B.流经黄土高原的黄河水质清澈、含沙量小C.黄土高原自然植被保存好,森林覆盖率高D.黄土高原地表千沟万壑、支离破碎10.下列属于“黄土风情”的是()①窑洞②碉房③信天游④京剧A.①②B.①③C.②④D.①④11.造成黄土高原水土流失严重的人为原因,主要是()A.退耕还林还草B.植被遭到人为破坏C.黄土土质疏松D.降水集中,多暴雨长江三角洲地区的人们往返于不同城市之间,就像生活在同一座城市,这种现象被称为“同城效应”。
【数学】人教版小学三年级数学上册 第7章 长方形和正方形 单元测试题(含答案)
人教版小学三年级数学上册第7章长方形和正方形单元测试题(含答案)第七单元测试卷一、我会填。
(24分)1.在下面的图形中,()是四边形,()是正方形,()是长方形。
2.长方形的周长=(),正方形的周长=()。
3.用4根长为8厘米的小棒摆出一个正方形,它的周长是()厘米。
4.一个长方形的长是5米,宽是1米,它的周长是()米。
5.正方形的周长是24分米,它的边长是()分米。
6.一个长方形的周长是18米,它的长是6米,宽是()米。
7.一个长方形,长和宽的和是12厘米,则它的周长是()厘米。
8.用两个周长12厘米的正方形拼成一个长方形,其周长是()厘米。
9.将一个边长是9厘米的正方形分成三个相同的长方形,这三个长方形的周长总和是()厘米。
二、我会判。
(正确的画“✔”,错误的画“×”)(10分)1.由四条边组成的图形就是四边形。
()2.长方形的长增加3厘米,周长就增加3厘米。
()3.长方形的周长比正方形的周长长。
()4.如果知道正方形的边长,那么就可以计算出它的周长。
()5.周长不相等的两个正方形,它们的边长也可能相等。
()三、我会选。
(10分)1.如图,从小明家到学校有两条路可以走,这两条路相比,()。
A.第①条路近B.第②条路近C.一样近2.从边长5厘米的正方形的一个角上剪去一个边长1厘米的小正方形,如图所示,剪后的图形的周长与原正方形的周长相比,()。
A.剪后的图形周长长B.原正方形的周长长C.周长一样长3.用两根同样长的铁丝,一根围成正方形,一根围成长方形,它们的周长相比, ()。
A.周长一样长B.正方形的周长长C.长方形的周长长4.用边长是1厘米的小正方形拼成的下列图形,周长最长的是()。
5.从一个长是10厘米、宽是8厘米的长方形中,剪下一个最大的正方形,正方形的边长是()。
A.10厘米B.2厘米C.8厘米四、操作天地。
(16分)1.量一量,并计算下面图形的周长。
(单位:厘米)(8分)(1)(2)2.计算下面图形的周长。
第7章 扇形统计图 单元测试 01-2024-2025学年数学人教版六年级上册(含答案解析)

2024-2025学年上学期六年级数学第7章扇形统计图单元测试分值:100分考试时间:60分钟学校:____________________________________________题号一二三四总分得分一、选择题(共5分)1.(本题1分)要反映各种果树的面积与果园总面积之间的关系,应绘制()较合适。
A.条形统计图B.扇形统计图C.折线统计图2.(本题1分)明明用50元钱刚好购买了甲、乙、丙三种物品(如图),则他用了总钱数的()%购买了物品丙。
A.78B.22C.42D.11 3.(本题1分)下面分别是五、六两个年级学生参加各类活动小组情况的统计图。
五年级和六年级参加艺术活动小组的人数相比,()。
A.五年级多B.六年级多C.一样多D.无法比较4.(本题1分)如果用整个圆表示某校学生人数,已知扇形B比扇形A多5%,恰好多60人,那么全校有()人。
A.240B.200C.12005.(本题1分)通过分析信息的特点,选择合适的统计图。
下列信息中适合用扇形统计图的是()。
A.六(1)班女生的身高B.一天中24个小时气温的变化C.玉米面的营养成分含量二、判断题(共5分)6.(本题1分)要清楚反应玉米中各种营养成分所占的百分比,可选用扇形统计图。
( )7.(本题1分)一个鸡蛋中蛋白的质量约占53%,在制作扇形统计图时,表示蛋白质量的扇形的圆心角是53°。
( )8.(本题1分)扇形统计图中,所有扇形的百分比之和可以大于1。
( ) 9.(本题1分)在扇形统计图甲和乙中,女生都占45%,那么甲乙两个统计图表示的女生人数一定相等。
( )10.(本题1分)要表示本校六年级各班学生的具体人数选用扇形统计图最合适。
( )三、填空题(共21分)11.(本题1分)对某地工人上班的交通方式进行调查,统计情况如图。
如果骑车人数是18人,那么坐地铁人数是( )人。
12.(本题1分)六年级一班在最近的一次小升初模拟考试中,得100分的同学有8人,得90分至99分的同学有14人,其余18人的得分都在90分以下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 图
姓名: 学号:
一、选择题
1.设无向简单图的顶点个数为n ,则该图最多有( B )条边。
A .n-1
B .n(n-1)/2
C . n(n+1)/2
D .n 2
2.一个n 个顶点的连通无向图,其边的个数至少为( A )。
A .n-1
B .n
C .n+1
D .nlogn ;
3.在一个无向图中,所有顶点的度数之和等于所有边数( B )倍,在一个有向图中,所有顶点的入度之和等于所有顶点出度之和的( C )倍。
A .1/2
B .2
C .1
D .4
4.下列哪一种图的邻接矩阵是对称矩阵?( )
A .有向图
B .无向图
C .AOV 网
D .AO
E 网
5.下列有关图的遍历的说法中,不正确的是( )。
A .用邻接表存储的图的深度优先搜索的时间复杂度为O(n +e)
B .图的广度优先搜索中邻接点的寻找具有“先进先出”的特征,需要采用队列结构来实现
C .非连通图不能用深度优先搜索法
D .图的遍历要求每一顶点访问且仅被防问一次
6. 求解最短路径的Floyd 算法的时间复杂度为( )。
A .O (n ) B. O (n+c ) C. O (n 2) D. O (n 3)
7. 在用邻接表表示图时,拓扑排序算法时间复杂度为( )。
A. O(n)
B. O(n +e)
C. O (n 2)
D. O (n 3) 8.右图所示的无向网的最小生成树的权为( )。
A .11 B . 9 C .14 D .12 9. 关键路径是AOE 网中( )。
A .从源点到汇点的最长路径
B .从源点到汇点的最短路径
C .最长回路
D .最短回路
10.下列关于AOE 网的叙述中,不正确的是( )。
A .关键活动不按期完成就会影响整个工程的完成时间
B .任何一个关键活动提前完成,那么整个工程将会提前完成
C .所有的关键活动提前完成,那么整个工程将会提前完成
D .某些关键活动提前完成,那么整个工程将会提前完成
二、判断题
1. 有e 条边的无向图,在邻接表中有e 个结点。
( × )
2. 强连通图的各顶点间均可达。
( √ )
42
3.十字链表是无向图的一种存储结构。
(×)
4.用邻接矩阵存储一个图时,在不考虑压缩存储的情况下,所占用的存储空间大小与图中
结点个数有关,而与图的边数无关。
(√)
5.带权的连通无向图的最小生成树是唯一的。
(×)
6.AOV网的含义是以边表示活动的网。
(×)
7.在表示某工程的AOE网中,加速其关键路径上的任意关键活动均可缩短整个工程的完
成时间。
(×)
三、应用题
1.已知一个无向图G的邻接表存储表示如下,试写出从顶点A出发进行深度和广度优先遍历得到的顶点序列,并判断该图的连通性。
答:深度优先遍历序列:ABDHECFG
广度优先遍历序列:ABCDEFGH
该图是连通图。
2.下图表示一个地区的通讯网,边表示城市间的通讯线路,边上的权表示架设线路花费的代价,如何选择能沟通每个城市且总代价最省的n-1条线路,画出你的选择,并写出这n-1条
答:本题就是寻找无向连通网的一棵最小生成树问题,你可以选择prim或Kruscal任一算法求解。
最小生成树(略)。
最小生成树的代价为:53
3.叙述拓扑排序的基本思想,并对如下的有向图,写出两个不同的拓扑序列。
答:拓扑排序的基本思想
a)在图中找一个没有前驱的顶点,并把它输出;
b)从图中删除该顶点及与它相关的弧;
c)重复第1、2步,直到所有顶点都输出(顶点输出序列为拓扑序列)或剩余顶点中
找不到没有前驱的顶点(图中存在回路)。
拓扑序列:v1,v6,v4,v3,v2,v5
v6,v1,v4,v3,v5,v2
四、算法设计题
1.已知图的邻接表存储定义如下:
#define MAX_VEX_NUM 20; //最大顶点个数
typedef struct ArcNode {
int adjvex; // 该弧所指向的顶点的位置
struct ArcNode *nextarc; // 指向下一条弧的指针
} ArcNode;
typedef struct VNode {
VertexType data; // 顶点信息
ArcNode *firstarc; // 指向第一条依附该顶点的弧
} VNode, AdjList[MAX_VERTEX_NUM];
typedef struct {
AdjList vertices;
int vexnum, arcnum; // 顶点个数和弧数
int kind; // 图的种类标志
} ALGraph;
(1)试写出计算图中所有顶点的入度算法,并将每个顶点的入度存入数组indegree中;
void FindIndegree(ALGraph G,int indegree[ ]){
for (i=0;i<G.vexnum;i++) indegree[i]=0;
for (i=0;i<G.vexnum;i++)
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
++indegree[p->adjvex];
}
(2)试写出计算图中所有顶点的出度算法,并将每个顶点的入度存入数组outdegree中;
void FindOutdegree(ALGraph G,int outdegree[ ]){
for (i=0;i<G.vexnum;i++) outdegree[i]=0;
for (i=0;i<G.vexnum;i++)
for(p=G.vertices[i].firstarc;p;p=p->nextarc)
++outdegree[i];
}
沁园春·雪 <毛泽东>
北国风光,千里冰封,万里雪飘。
望长城内外,惟余莽莽;
大河上下,顿失滔滔。
山舞银蛇,原驰蜡象,
欲与天公试比高。
须晴日,看红装素裹,分外妖娆。
江山如此多娇,引无数英雄竞折腰。
惜秦皇汉武,略输文采;
唐宗宋祖,稍逊风骚。
一代天骄,成吉思汗,
只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。
