格林高级计量经济学第二版
研究生《高级计量经济学》课程提纲

研究生《高级计量经济学》课程提纲【说明】这是非经济学院、一个学期的研究生《高级计量经济学》课程的指导性纲要,包括推荐的教材、教学内容、课时安排和教学要求。
教材:第一本可作为指定教材备案;后两本教材更适合学生阅读。
教师可根据需要补充其它参考资料。
[1] William H. Greene, Econometric Analysis, 5th edition。
(有中译本)。
[2] Jeffrey Wooldridge著,费剑平译,计量经济学导论(第三版)上下册,中国人民大学出版社,2007。
(英文原版:Introductory Econometrics: A Modern Approach,South-Western College Publishing, 2000)。
[3] Walter Enders (2004), Applied Econometric Time Series, 2nd edition, John Wiley & Sons, Inc. 中译本:应用计量经济学---时间序列分析(第2版),杜江和谢志超译,高等教育出版社,2006。
预备知识:经济学基础、微积分学、线性代数,概率论和数理统计。
授课对象:非经济学院的、仅上一个学期“高级计量经济学”的硕士、博士。
课时安排:每周3课时 17(周)=51课时。
考核方式:包括作业、期中考试和期末考试。
期中考试和期末考试均采用闭卷形式。
教学内容、课时安排和教学要求:课时安排说明:内容讲解约43课时(预估课时都标注在各章名称后面的括号内),复习约6课时,期中考试2课时,共计51课时。
助教职责:计量软件辅导(如Eviews、Stata等),问题答疑,批改作业,协助老师评判试卷。
一、课程概述及复习(预估6课时)主要内容:(一)计量经济学课程简介,包括计量经济学的学科性质、实证分析的步骤、经济数据的类型、因果关系概念介绍、本课程的学习内容、课程要求等。
计量经济学第二版课后习题答案
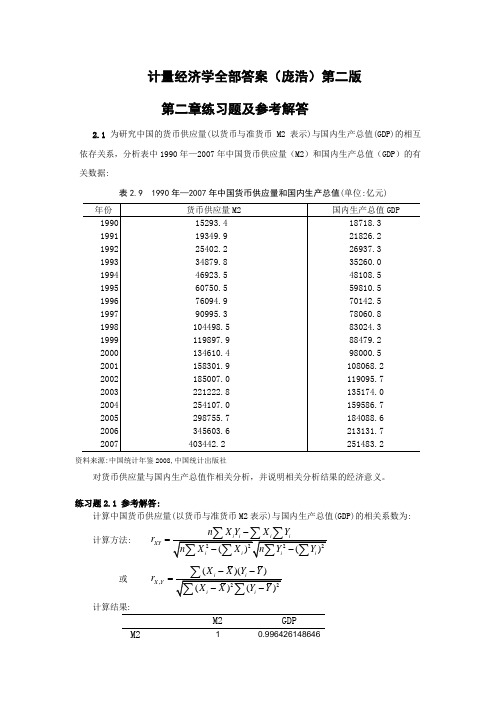
计量经济学全部答案(庞浩)第二版 第二章练习题及参考解答2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2007年中国货币供应量(M2)和国内生产总值(GDP )的有关数据:表2.9 1990年—2007年中国货币供应量和国内生产总值(单位:亿元)资料来源:中国统计年鉴2008,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明相关分析结果的经济意义。
练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或 ,()()X Y X X Y Y r --=计算结果:M2GDPM210.996426148646GDP 0.996426148646 1经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
2.2 为研究美国软饮料公司的广告费用X与销售数量Y的关系,分析七种主要品牌软饮料公司的有关数据表2.10 美国软饮料公司广告费用与销售数量资料来源:(美) Anderson D R等. 商务与经济统计.机械工业出版社.1998. 405绘制美国软饮料公司广告费用与销售数量的相关图, 并计算相关系数,分析其相关程度。
能否在此基础上建立回归模型作回归分析?练习题2.2参考解答美国软饮料公司的广告费用X与销售数量Y的散点图为说明美国软饮料公司的广告费用X与销售数量Y正线性相关。
若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。
回归结果表明,广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
《高级计量经济学 II》2014-2015(1)

论文研读和报告可分组进行,自选论文,在课堂进行报告。
课程要求:除非你能证明有特殊情况,例如疾病,否则不能以任何借口不参加考试和随 堂测验。如果无故不参加考试和测验,给予 0 分。你可以和同学讨论课后作业,但是不可以 抄袭别人的作业。助教可以不予批改迟交的作业。涉及学生的学术不诚实问题主要包括考试 作弊;抄袭;伪造或不当使用在校学习成绩;未经老师允许获取、利用考试材料;对于学术 不诚实的最低惩罚是考试给予 0 分。其他的惩罚包括通告学校相关部门并按照有关规定进行 处理。
©沈根祥(上海财大经济学院)
HW3
11/18 11/25
多元选择模型(I) 计数模型
参考书①Ch15 参考书①Ch20
HW4
12/2 12/9 12/16
BootStrap(I) BootStrap(II) 贝叶斯分析简介
参考书①Ch13 参考书①Ch13
12/23
论文研读报告(I)
12/30
论文研读报告(II)
注:1.本课程进度可根据实际教学进程做相应调整;2.论文研读报告可穿插进行。
预备知识:本课程需要计量经济学基础和统计学基础为前导,需要熟悉会计学和公司金 融的有关理论和实务。掌握计量经济学软件的应用将对本课程的学习有很大帮助。
©沈根祥(上海财大经济学院)
Advanced Econometrics II
课程结构:本课程基本内容分为两部分:第一部分为课堂教学,第二部分为应用,通过 有关科研论文的研读和报告探讨计量经济方法在会计学和公司金融实证分析中的应用。
课程网址:
©沈根祥(上海财大经济学院)
Advanced Econometrics II
第一讲_高级计量经济学_绪论

建模流程
下页
理论模型的设计
对所要研究的经济现象进行深 入的分析,根据研究的目的,选择 模型中将包含的因素,根据数据的 可得性选择适当的变量来表征这些 因素,并根据经济行为理论和样本 数据显示出的变量间的关系,设定 描述这些变量之间关系的数学表达 式,即理论模型。
设计理论模型的步骤
理论模型的设计主要包含三部分工作 1. 选择变量 2. 确定变量之间的数学关系 3. 拟定模型中待估计参数的数值范围
确定模型的数学形式
选择了适当的变量,接下来就要选择适当的 数学形式描述这些变量之间的关系,即建立理 论模型。 (1)借鉴前人的研究成果 (2)用散点图判断 (3)用多个模型模拟,再进行比较选择
拟定理论模型中待估参数的理 论期望值
理论模型中的待估参数一般都具有特定的 经济含义,它们的数值,要待模型估计、检验 后,即经济数学模型完成后才能确定,但对于 它们的数值范围,即理论期望值,可以根据它 们的经济含义在开始时拟定。这一理论期望值 可以用来检验模型的估计结果。
设计、非参数方法、生存分析、时间序列分析、谱分析、投影寻踪等。)
12.Ox V. 1.11, GAUSS V. 3.2.19 13.SPSS, SAS
学习要求及达到的目的
学习要求: 1.不迟到、不早退、不无故旷课 2.课内外学习时间比例至少为1︰3 3.课内的案例课后一定要自己动手做一遍 4.认真完成课后作业 达到的目的: 1.进入应用计量经济学的殿堂 2.充分了解计量经济学理论背景 3.熟练应用计量经济学方法解决实际问题
20世纪80年代至今计量经济学经典计量初级中级高级微观计量非参数半参数时间序列paneldata一理论模型的设计二样本数据的收集三模型参数的估计四模型的检验建模流程对所要研究的经济现象进行深入的分析根据研究的目的选择模型中将包含的因素根据数据的可得性选择适当的变量来表征这些因素并根据经济行为理论和样本数据显示出的变量间的关系设定描述这些变量之间关系的数学表达式即理论模型
高级计量经济学课程

高级计量经济学课程摘要:一、引言1.介绍高级计量经济学课程的背景和重要性2.阐述本课程的主要内容和目标二、高级计量经济学课程概述1.课程的核心概念和理论2.课程的主要方法论和工具三、高级计量经济学课程的主要内容1.多元回归分析2.异方差性、序列相关性和多重共线性3.工具变量和两阶段最小二乘法4.矩估计和广义矩估计5.非参数估计和半参数估计6.面板数据分析7.蒙特卡洛模拟和贝叶斯统计四、高级计量经济学课程的实践应用1.宏观经济政策的评估2.金融市场的风险管理3.产业组织和市场竞争分析4.人力资本和研发投资决策五、高级计量经济学课程的学习方法和建议1.掌握基本理论和方法2.动手实践和案例分析3.学术研究和论文写作六、总结1.强调高级计量经济学课程在现代经济学研究中的应用2.展望计量经济学未来的发展趋势和挑战正文:一、引言高级计量经济学课程是经济学专业研究生的核心课程之一,它涉及到现代经济学研究中许多重要的理论和方法。
本课程的主要目标是帮助学生掌握高级计量经济学的基本概念、理论和方法,并能够运用这些知识和技能进行独立的研究和论文写作。
二、高级计量经济学课程概述高级计量经济学课程主要涉及以下几个方面的内容:多元回归分析、异方差性、序列相关性和多重共线性、工具变量和两阶段最小二乘法、矩估计和广义矩估计、非参数估计和半参数估计、面板数据分析、蒙特卡洛模拟和贝叶斯统计等。
这些内容不仅包括高级计量经济学的基本理论和方法,还涵盖了许多现代计量经济学研究的前沿领域。
三、高级计量经济学课程的主要内容1.多元回归分析:介绍多元回归模型的建立、参数估计和假设检验等基本概念和方法。
2.异方差性、序列相关性和多重共线性:讲解这些问题的产生原因、影响和解决方法。
3.工具变量和两阶段最小二乘法:阐述工具变量理论及其在解决因果推断问题中的应用,以及两阶段最小二乘法的原理和应用。
4.矩估计和广义矩估计:介绍矩估计和广义矩估计的基本概念、性质和应用。
高级计量经济学2

第2章 经典线性回归模型Chapter 2 The Classical Multiple Linear Regression Model进行计量经济分析时,我们将首先通过经济理论来指定变量之间精确的和确定性的关系,然后利用模型方法经验地探索这些估计,再通过适当的检验判断估计的准确性,最后使用这样的模型来推断和判断经济行为。
无论当前的计量经济分析多么复杂,仍然大都从线性回归模型(linear regression model)开始进行分析。
因此多元线性模型可以作为计量经济分析的基石。
线性模型的估计方法可以推广到更为广泛的模型当中。
§2.1 线性回归模型多元线性回归模型主要用于研究一个相依变量与一个或者多个独立变量之间的关系。
线性模型的一般形式是:εβββε++++=+=K K K x x x x x x f y 221121),,,( (2.1) 这里y 是相依变量(dependent variable)或者被解释变量(explained variable),K x x ,,1 是独立变量(independent variable)或者解释变量(explain variable)。
一些理论将有助于指定函数),,,(21K x x x f 的形式,这个函数通常称为y 基于K x x ,,1 的母体回归方程(population regression equation)①。
ε被称为随机扰动项(random disturbance),如此定义是因为它是对原本稳定关系的扰动。
随机扰动项的出现主要有下述原因:首先,无论模型是多么精美,也无法完全表示穷尽对经济变量的各种影响,因此它们被忽略掉的因素所产生的净影响便体现在扰动项中;其次,在经验模型中还有很多对随机扰动产生影响的因素,其中最为显著的可能是模型度量的误差。
虽然我们可能在理论上很容易地得到变量之间准确的关系,但是却很难获得这些变量准确和合理的度量;更为困难的是,可能一些理论上的变量在现实中难以寻求到对应的观测数据。
计量经济学第二版第八章答案

计量经济学第二版第八章答案【篇一:庞皓计量经济学课后答案第八章】业1、①在给定的数据中可以看出人均收入的系数的t值t(?2)?0.857,di(lnxi?7)系数的t值t(?3)?2.42,在给定显著性水平??0.05下n=101,t0.025(101)?1.984。
所以人均收入对期望寿命并没有显著影响。
而di(lnxi?7)对期望寿命有显著影响。
当人均收入超过1097美元时,即di=1为富国时:???2.40?9.39lnx?3.36(lnx?7)?21.12?6.03lnx yiiii当人均收入未超过1097美元时,即di=0为穷国时:???2.40?9.39lnx yii②引入di(lnxi?7)的原因是从截距和斜率两个方面来考虑收入对期望寿命的影响。
③对穷国进行回归时,yi取xi?1097时的值。
对富国进行回归时,yi取xi?1097时的值④结论:富国的期望寿命高于穷国的期望寿命。
贫富国之间的期望寿命的确存在显著差异。
2、①d1t???1,t为1987年及以后?0,t为1987年以前 d2t??年及以后?1,t为1994年以前?0,t为1994年及以后年及以后?1,t为2006?1,t为2008 d3t?? d4t?? 0,t为2006年以前0,t为2008年以前??②从图形上看。
consume和income 及employment存在线性相关关系。
而与burden从图形上看不出线性关系。
所以对模型的设定保持怀疑态度。
③?umecons.16?0.63incomeconsume.51employmentt?1674t?0.0 86t?1?537t?202.50burden.27d2t?127.04d3t?172.2d4tt?7.22d1t?194r2?0.9998672?0.99979 2 f=13189.98 dw=2.921拟合效果好,且通过dw检验由回归可知consumet,d1td3t的系数未能通过显著性水平??0.05下的tt?1,burden检验。
高级计量经济学-1

步骤之一,即探索性的关系识别。 • 一些人为了获得预想的结果,常常有目的地进行“数据淘洗
〞 (data-cleaning) ,即删除那些不支持预想结果的观察值, 甚至修改数据。 • 因而应该认识到,利用计量经济学方法得出的结论都是有条 件的。
和归纳开展为探讨多因素间的数量关系和进行假说检 验
第十九页,编辑于星期六:十八点 十八分。
计量经济学与经验研究
• 传统研究方法侧重于得到模型参数的“精确〞估计, 但对于“数据生成过程〞未给予高度关注。
• 研究人员依据感觉或经验提出模型,然后利用“试错 法〞、逐步回归等手段估计变量之间的统计关系,在 此基础上,“选择〞出自己满意的模型。
o 高雪梅主编(2005).《计量经济分析方法与建模:EVIEWS应 用及实例》.北京:清华大学出版社.
4
第四页,编辑于星期六:十八点 十八分。
△ 初、中、高级计量经济学
• 初级以计量经济学的数理统计学基础知识和经典 的线性单方程模型理论与方法为主要内容;
• 中级以用矩阵描述的经典的线性单方程模型理论 与方法、经典的线性联立方程模型理论与方法, 以及传统的应用模型为主要内容;
8
第八页,编辑于星期六:十八点 十八分。
• 非经典计量经济学一般指20世纪70年代以来开展的计 量经济学理论、方法及应用模型,也称为现代计量经济 学。
• 非经典计量经济学主要包括:微观计量经济学、非参数 计量经济学、时间序列计量经济学和动态计量经济学等。
• 非经典计量经济学的内容体系:模型类型非经典的计量 经济学问题、模型导向非经典的计量经济学问题、模型 结构非经典的计量经济学问题、数据类型非经典的计量 经济学问题和估计方法非经典的计量经济学问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fY ( y ) = f X ( x ) dx . dy
Remark: LHS x=x(y) “Proof”: ! By the definition of probability, within an interval ∆x : Probability = f X ( x ) ∆x Probability = fY ( y ) ∆y ⇒ f X ( x ) ∆ x = fY ( y ) ∆ y ∆x fY ( y ) = f X ( x ) ∆y ∆y dx fY ( y ) = f X ( x ) (taking limit) dy dx as a proportional factor! dy
PDF : A Function of A Random Variable Motivating example: Image that two grading systems - Chianese and American Prob { X ∈ [ 0,100]} = 1 and Prob {Y ∈ [0, 4]} = 1 How to change the PDF from Chinese to American system? Then the transformation is y=x/25 . Special case of scalar: suppose that X : f X ( x ) is known and Y is a function of X, then
a1n x1 a2n x2 ann xn ( y1 , y2 ,..., yn ) .
n
1 1 − 2 y '( AA ')−1 y fY ( y1 , y2 ,..., yn ) = e || A−1 || (一般正态分布) 2π
be the joint probability density
function of X A ( X1 , X 2 ,..., X n ) , then the joint probability density function of Y is: X ,Y are randon vector, x y are vectorsAltern源自tively:derive
pdf through ∂ f ( y) = F ( y) ∂y
Suppuse σ =0.5 , then the density will be twice as stronger.
3
PDF created with pdfFactory Pro trial version
EX1: assume that X 1 , X 2 ,..., X n ~ iid N(0,1) then the PDF of X ≡ ( X 1 , X 2 ,..., X n ) is
x'x 1 −1 2 f X ( x1 , x2 ,..., xn ) = e 2π where iid stands for independently and identically distributed x ≡ ( x1 , x2 ,..., xn ) ' n
x2 1 −1 e 2 is preferred. 2π
2
PDF created with pdfFactory Pro trial version
2010.3.3 Nanqiang2 209 16:30-18:10
Univariate Normal Distribution How to derive the PDF of Y ~ N ( µ,σ 2 ) from
X ~ N ( 0,1) ? The PDF of Y ~ N ( µ , σ 2 ) is : f ( y) = Proof: recall F ( y ) = ∫ (? )dt
−∞ y
1 2πσ 2
e
1 y −µ − 2 σ
2
, need to find (?) cdf by using
Remark: image
4
PDF created with pdfFactory Pro trial version
PDF of A Function of A Random Vector Theorem: Let f X ( x1 , x2 ,..., xn )
− 1 x2 1 f ( x) = e 2 2π
Cumulative Distribution Function: CDF F ( x ) = Pr( X ≤ x ) =
−∞
∫
x
1 f ( t )dt = 2π
−∞
∫e
x
1 − t2 2
dt
Remark: to avoid using too many notations (X x t), simply using f ( x ) =
2010.3.1 Nanqiang2 208 16:30-18:10
Multivariate Distribution
Be very familiar with Distribution, Why? The foundation of econometrics. No distribution theory, no econometrics .
Using matrix notation: ∑ A var ( X ) A E [ ( X − µ )( X − µ ) '] Remarks: 1) ∑ is symmetric 2) ∑ is nnd . quadratic form is non-negative, n.n.d. , d=definite. That is, for any vector a, a ' ∑ a ≥ 0 Proof: let w ≡ a1 X 1 + ... + an X n = a ' X ( no assumptions of normality)
E ( X i ) ≡ µi E ( X ) =µ
then
Second Moment of a Multivariate Distribution Denote: σ ij ≡ E ( X i − µi )( X j − µ j ) σ 11 σ 12 σ σ 22 ∑ ≡ 21 σ n1 σ n 2 σ 1n σ 23 σ nn
−µ 1 1 − 2 yσ f ( y) = e 2 || σ || 2π
1 || ∑ ||
n 1
2
一般一元正态分布的密度函数 1 1 −2 f ( y) = e || σ 2 || 2π 1 1 −2 f ( y) = e || ∑ || 2π
EX21: x1 , x2 ,..., xn ~ iid N (0,1) , and
1
To make life easy, now we abused notations sometimes without producing ambiguities: we use the same notation for regular variable and for random variable; the same notation for row vector and column vector! 5
7
PDF created with pdfFactory Pro trial version
8
PDF created with pdfFactory Pro trial version
Construct a multivariate normal distribution2 Theorem: A linear transformation distribution is normal. of normal
1
PDF created with pdfFactory Pro trial version
Univariate Standard Normal Distribution Normal Distribution is universal distribution, why? Bernoulli, scaled symmetric random walk, brownian motion? Probability Density Function: PDF X ~ N ( 0,1)
PDF created with pdfFactory Pro trial version
y1 a11 a12 y a 2 = 21 a22 yn an1 an 2 Pls derive fY ( y1 , y2 ,..., yn ) , the PDF of Answer:
Non-parametric estimation -- the central issue is to estimate
PDF;
Parameter estimation -- distribution theory plays major roles:
1. Derive the Linear Regression Equation 2. Maximum likelihood estimation 3. Hypothesis Testing 4. Asymptotic Distribution 5. Bayesian estimation Cumulative Distribution Function & Probability Density Function
fY ( y ) = f X ( x ) ∂x ∂y '
x = x( y ) fY ( y1 , y2 ,..., yn ) = f X ( x1 , x2 ,..., xn ) || J ( y ) || fY ( y1 , y2 ,..., yn ) = f X ( x1 , x2 ,..., xn .) || J || where J is the Jacobian matrix ∂x1 / ∂y1 / ∂x1 / ∂y2 ... ... ∂x ≡ J ≡ J ( y) ≡ ... ... ∂y ' ∂xn / ∂y1 / ∂xn / ∂y2 ... ∂x1 / ∂yn ... ... ... ... ... ∂xn / ∂yn
