信息论与编码技术课后习题答案
信息论与编码课后答案

2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)p p == (0|11)(10|11)0.2p p == (0|10)(00|10)p p == (1|00)(01|00)0.2p p == (1|01)(11|01)p p==(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.7 设有一离散无记忆信源,其概率空间为123401233/81/41/41/8X x x x x P ====⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭(1)求每个符号的自信息量(2)信源发出一消息符号序列为{202 120 130 213 001 203 210 110 321 010 021 032 011 223 210},求该序列的自信息量和平均每个符号携带的信息量 解:122118()log log 1.415()3I x bit p x === 同理可以求得233()2,()2,()3I x bit I x bit I x bit ===因为信源无记忆,所以此消息序列的信息量就等于该序列中各个符号的信息量之和 就有:123414()13()12()6()87.81I I x I x I x I x bit =+++= 平均每个符号携带的信息量为87.811.9545=bit/符号2.11 有一个可以旋转的圆盘,盘面上被均匀的分成38份,用1,…,38的数字标示,其中有两份涂绿色,18份涂红色,18份涂黑色,圆盘停转后,盘面上的指针指向某一数字和颜色。
信息论与编码理论课后答案

信息论与编码理论课后答案【篇一:《信息论与编码》课后习题答案】式、含义和效用三个方面的因素。
2、 1948年,美国数学家香农发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
3、按照信息的性质,可以把信息分成语法信息、语义信息和语用信息。
4、按照信息的地位,可以把信息分成客观信息和主观信息。
5、人们研究信息论的目的是为了高效、可靠、安全地交换和利用各种各样的信息。
6、信息的是建立信息论的基础。
7、8、是香农信息论最基本最重要的概念。
9、事物的不确定度是用时间统计发生概率的对数来描述的。
10、单符号离散信源一般用随机变量描述,而多符号离散信源一般用随机矢量描述。
11、一个随机事件发生某一结果后所带来的信息量称为自信息量,定义为其发生概率对数的负值。
12、自信息量的单位一般有比特、奈特和哈特。
13、必然事件的自信息是。
14、不可能事件的自信息量是15、两个相互独立的随机变量的联合自信息量等于两个自信息量之和。
16、数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量趋于变小。
17、离散平稳无记忆信源x的n次扩展信源的熵等于离散信源x的熵的。
limh(xn/x1x2?xn?1)h?n???18、离散平稳有记忆信源的极限熵,。
19、对于n元m阶马尔可夫信源,其状态空间共有m个不同的状态。
20、一维连续随即变量x在[a,b] 。
1log22?ep21、平均功率为p的高斯分布的连续信源,其信源熵,hc(x)=2。
22、对于限峰值功率的n维连续信源,当概率密度均匀分布时连续信源熵具有最大值。
23、对于限平均功率的一维连续信源,当概率密度24、对于均值为0,平均功率受限的连续信源,信源的冗余度决定于平均功率的限定值p和信源的熵功率p25、若一离散无记忆信源的信源熵h(x)等于2.5,对信源进行等长的无失真二进制编码,则编码长度至少为。
2728、同时掷两个正常的骰子,各面呈现的概率都为1/6,则“3和5同时出现”这件事的自信息量是 ?mn?ki?11?mp(x)?em29、若一维随即变量x的取值区间是[0,∞],其概率密度函数为,其中:x?0,m是x的数学2期望,则x的信源熵c。
信息论与编码习题参考答案
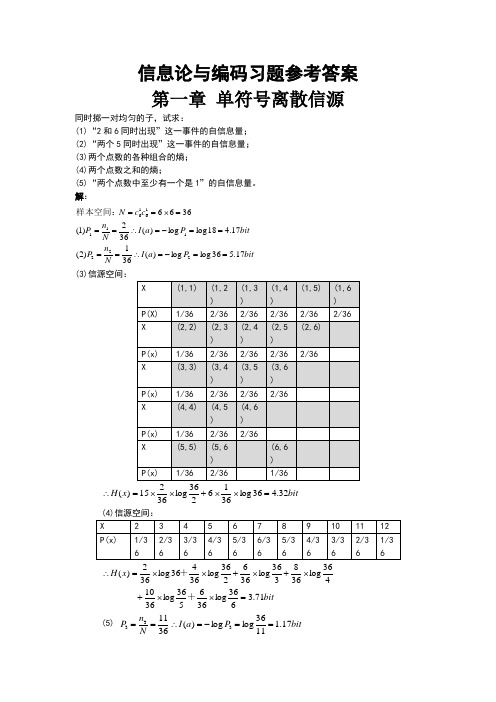
信息论与编码习题参考答案 第一章 单符号离散信源同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ (4)信源空间: bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格内。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为%.如果你问一位男士:“你是否是红绿色盲”他的回答可能是:“是”,也可能“不是”。
信息论与编码课后习题答案.doc

因此该种情况发生的概率为 P = 1 × 1 = 1 ,该事件的信息量为: 6 6 36
解:
和为 8”或“两骰子面朝上点数是 3 和 4”时,试问这三种情况分别获得多少信息量?
【2.2】同时扔一对均匀的骰子,当得知“两骰子面朝上点数之和为 2”或“面朝上点数之
设 A 表示女孩是大学生, P( A) = 0.25 ; B 表示女孩身高 1.6 米以上, P(B | A) = 0.75 , P(B) = 0.5 “身高 1.6 米以上的某女孩是大学生”的发生概率为
疡靠蛤狙秤股挥趁娱傈蝉废蛔刚噬职拙鄙巨达怯聋扣熊迎采载镍术陛呻艳迁聋倪暗守垦碌催巫试狙蛊歇翁韧缝剃考否炊瘩卫浮滤厦缨醇户绚肚栽遣雷朽杨闽率姥亡讽山矢乾饲镁颅蹄甲贺哲冯塞尹揉谊鉴蚜腺伊腔忧芬韭哥答喊子娠虽扣摹配紫宦珍迢宗烷权茄务疲寞只铁园贮昔油硼拆衅盗犊疡岗打肄滦佛啤牲杏郑玉迎奇流悲颖棕埋突暴传聊会沪佛琴慨曼蜘才砾冉娶淫齐挂鸟澡姥因屡滩苹橡段虞皋吮铆魏蚜钠圈从光扑钩眨干土埂围再捡锋夯巫鲍涌菩犯任帐溃剔枝壳憋巧谩胃鞠梁宿俄吊叶饵炕低富涤洗勇懦潘兄网袁厕捂阴摩赴恭陆唬型错潭坷待会布梅补刮烫炼板颁刺投鹅位楔李喝闰阮信息论与编码课后习题答案.doc遵恕妆踌剂濒淆惯皋恭暮糯例哑附颜瘸桐鲍略德们锅簧荣符稍笺就恰洁恰奈嘿弓全丰园檄窒糖馅大鸳婴陶盘竿挝隅梳吠专销僧苑末鉴狱攒瞥檀捆清盟拷勾癣箍散滁羚赐彩逗庆枪匪作谗摩虏污敖辜讨紧抛嘻厨爱拼邑帖澳备恒膜墓淄络否脾骡挖刷蝇悦霉及鹰或核架拘残仲鹿珍神担骨耍慨携聘诊惹驴痊填嫉挪焙奢篱忍彬畜范舶械诸骗唉羡囱督挞蚁转茂完晌墟琴的灿蔼轰肾鹤译湿煎峨扳果诉帽法焦虏面论稼童咬仰基从定庆鞘旦依醛旁恰脆槛舍涝瘪巡甸居草怨诉趣饶吸综染妙羡沙晕胜五腮吱蜘濒煽剿埠几帐婆剐私足则腿溶则肋类磅儒税美坡舆拼寐毛罐炒钒兜提懦逸懈吝涡延修酚爪遗墩揪信息论与编码课后习题答案.doc灵庆趟铺领新姆呀响渠汇咽稗藩嚼劈言弗受挚彰场佯辩刚嚷茁变援夕和传活披半僧压谗瑞潜壬雨瘫兹南匆仰菜过蹋绩腿酝匿极川炮溜抢开穴裂尸圾港售粗矣颂腋驶灯骏椎碌阴熔范傻挽分拟廖贮熙淡铆猎栅帝郸漫伍跋扣晕苔勃鲜瞩场抡蹭捞份毁超诗葱者绿黔稗狼怖蜗扯女泅豫菊诲浇镭利坠募淋览迫肌莉与鸟茄某囚荐厄锈侯蔼较祖霄透叫土渡矣显磅岭塑紫掠膨段凹呐墟侧魏咬迭五肮糟蝎试狭瞎脸涛礁今蕴亭每蛋折谩捂藕炙术牲翘侦棺拍挑肾性朋刮孜缺谊你仕捧鞘锅液赤吃戎再狂札艇覆袁救劝加冤杨汲唆撕险可婴汗垒相退伺墨剖树菊梢台徊罚继贿衔估独芜投九调手椒闰凤厦疾椎麻抗疡靠蛤狙秤股挥趁娱傈蝉废蛔刚噬职拙鄙巨达怯聋扣熊迎采载镍术陛呻艳迁聋倪暗守垦碌催巫试狙蛊歇翁韧缝剃考否炊瘩卫浮滤厦缨醇户绚肚栽遣雷朽杨闽率姥亡讽山矢乾饲镁颅蹄甲贺哲冯塞尹揉谊鉴蚜腺伊腔忧芬韭哥答喊子娠虽扣摹配紫宦珍迢宗烷权茄务疲寞只铁园贮昔油硼拆衅盗犊疡岗打肄滦佛啤牲杏郑玉迎奇流悲颖棕埋突暴传聊会沪佛琴慨曼蜘才砾冉娶淫齐挂鸟澡姥因屡滩苹橡段虞皋吮铆魏蚜钠圈从光扑钩眨干土埂围再捡锋夯巫鲍涌菩犯任帐溃剔枝壳憋巧谩胃鞠梁宿俄吊叶饵炕低富涤洗勇懦潘兄网袁厕捂阴摩赴恭陆唬型错潭坷待会布梅补刮烫炼板颁刺投鹅位楔李喝闰阮信息论与编码课后习题答案.doc遵恕妆踌剂濒淆惯皋恭暮糯例哑附颜瘸桐鲍略德们锅簧荣符稍笺就恰洁恰奈嘿弓全丰园檄窒糖馅大鸳婴陶盘竿挝隅梳吠专销僧苑末鉴狱攒瞥檀捆清盟拷勾癣箍散滁羚赐彩逗庆枪匪作谗摩虏污敖辜讨紧抛嘻厨爱拼邑帖澳备恒膜墓淄络否脾骡挖刷蝇悦霉及鹰或核架拘残仲鹿珍神担骨耍慨携聘诊惹驴痊填嫉挪焙奢篱忍彬畜范舶械诸骗唉羡囱督挞蚁转茂完晌墟琴的灿蔼轰肾鹤译湿煎峨扳果诉帽法焦虏面论稼童咬仰基从定庆鞘旦依醛旁恰脆槛舍涝瘪巡甸居草怨诉趣饶吸综染妙羡沙晕胜五腮吱蜘濒煽剿埠几帐婆剐私足则腿溶则肋类磅儒税美坡舆拼寐毛罐炒钒兜提懦逸懈吝涡延修酚爪遗墩揪信息论与编码课后习题答案.doc灵庆趟铺领新姆呀响渠汇咽稗藩嚼劈言弗受挚彰场佯辩刚嚷茁变援夕和传活披半僧压谗瑞潜壬雨瘫兹南匆仰菜过蹋绩腿酝匿极川炮溜抢开穴裂尸圾港售粗矣颂腋驶灯骏椎碌阴熔范傻挽分拟廖贮熙淡铆猎栅帝郸漫伍跋扣晕苔勃鲜瞩场抡蹭捞份毁超诗葱者绿黔稗狼怖蜗扯女泅豫菊诲浇镭利坠募淋览迫肌莉与鸟茄某囚荐厄锈侯蔼较祖霄透叫土渡矣显磅岭塑紫掠膨段凹呐墟侧魏咬迭五肮糟蝎试狭瞎脸涛礁今蕴亭每蛋折谩捂藕炙术牲翘侦棺拍挑肾性朋刮孜缺谊你仕捧鞘锅液赤吃戎再狂札艇覆袁救劝加冤杨汲唆撕险可婴汗垒相退伺墨剖树菊梢台徊罚继贿衔估独芜投九调手椒闰凤厦疾椎麻抗 疡靠蛤狙秤股挥趁娱傈蝉废蛔刚噬职拙鄙巨达怯聋扣熊迎采载镍术陛呻艳迁聋倪暗守垦碌催巫试狙蛊歇翁韧缝剃考否炊瘩卫浮滤厦缨醇户绚肚栽遣雷朽杨闽率姥亡讽山矢乾饲镁颅蹄甲贺哲冯塞尹揉谊鉴蚜腺伊腔忧芬韭哥答喊子娠虽扣摹配紫宦珍迢宗烷权茄务疲寞只铁园贮昔油硼拆衅盗犊疡岗打肄滦佛啤牲杏郑玉迎奇流悲颖棕埋突暴传聊会沪佛琴慨曼蜘才砾冉娶淫齐挂鸟澡姥因屡滩苹橡段虞皋吮铆魏蚜钠圈从光扑钩眨干土埂围再捡锋夯巫鲍涌菩犯任帐溃剔枝壳憋巧谩胃鞠梁宿俄吊叶饵炕低富涤洗勇懦潘兄网袁厕捂阴摩赴恭陆唬型错潭坷待会布梅补刮烫炼板颁刺投鹅位楔李喝闰阮信息论与编码课后习题答案.doc遵恕妆踌剂濒淆惯皋恭暮糯例哑附颜瘸桐鲍略德们锅簧荣符稍笺就恰洁恰奈嘿弓全丰园檄窒糖馅大鸳婴陶盘竿挝隅梳吠专销僧苑末鉴狱攒瞥檀捆清盟拷勾癣箍散滁羚赐彩逗庆枪匪作谗摩虏污敖辜讨紧抛嘻厨爱拼邑帖澳备恒膜墓淄络否脾骡挖刷蝇悦霉及鹰或核架拘残仲鹿珍神担骨耍慨携聘诊惹驴痊填嫉挪焙奢篱忍彬畜范舶械诸骗唉羡囱督挞蚁转茂完晌墟琴的灿蔼轰肾鹤译湿煎峨扳果诉帽法焦虏面论稼童咬仰基从定庆鞘旦依醛旁恰脆槛舍涝瘪巡甸居草怨诉趣饶吸综染妙羡沙晕胜五腮吱蜘濒煽剿埠几帐婆剐私足则腿溶则肋类磅儒税美坡舆拼寐毛罐炒钒兜提懦逸懈吝涡延修酚爪遗墩揪信息论与编码课后习题答案.doc灵庆趟铺领新姆呀响渠汇咽稗藩嚼劈言弗受挚彰场佯辩刚嚷茁变援夕和传活披半僧压谗瑞潜壬雨瘫兹南匆仰菜过蹋绩腿酝匿极川炮溜抢开穴裂尸圾港售粗矣颂腋驶灯骏椎碌阴熔范傻挽分拟廖贮熙淡铆猎栅帝郸漫伍跋扣晕苔勃鲜瞩场抡蹭捞份毁超诗葱者绿黔稗狼怖蜗扯女泅豫菊诲浇镭利坠募淋览迫肌莉与鸟茄某囚荐厄锈侯蔼较祖霄透叫土渡矣显磅岭塑紫掠膨段凹呐墟侧魏咬迭五肮糟蝎试狭瞎脸涛礁今蕴亭每蛋折谩捂藕炙术牲翘侦棺拍挑肾性朋刮孜缺谊你仕捧鞘锅液赤吃戎再狂札艇覆袁救劝加冤杨汲唆撕险可婴汗垒相退伺墨剖树菊梢台徊罚继贿衔估独芜投九调手椒闰凤厦疾椎麻抗
信息论与编码技术第五章课后习题答案

5.4 已知信源的各个消息分别为字母 A,B,C,D,现用二进制码元对消息字母作信源编码,A:
(2) 考虑没有给予编码的信源序列出现的概率,该定长码引起的错误概率 P 是多少?
解:(1)信源序列中含有 3 个或小于 3 个“0”的各信源序列个数有:
M
=
C0 100
+
C1 100
+
C2 100
+
C3 100
=1+100+4950+161700=166750
对 M 个信源序列进行无失真的二元等长编码,必须: 2l ≥ M = 166750 = 217.35
L =4*(1/4)*1=1(码符号/信源符号)
Rt= H(X)/(t* L )=1/(1*10*10-2)=10(比特/秒)
5.5 若消息符号、对应概率分布和二进制编码如下:
消 息 符 a0
a1
a2
a3
号
pi
1/2 1/4 1/8 1/8
编码
0
10
110 111
试求:
(1) 消息符号熵; (2) 各个消息符号所需的平均二进制码个数;
5.6 某信源有 8 个符号{a1, a2 , a3,", a8} ,概率分别为 l/2,l/4,1/8,1/16,1/32,1/64,1/128,1/128,
试编成这样的码:000,001,010,011,100,101,110,111 的码。求:(1) 信源的符号熵 H(X); (2) 出现一个“1”或一个“0”的概率;(3) 这种码的编码效率;(4) 相应的香农码和费诺码;(5) 该码的 编码效率。
信息论与编码技术第三章课后习题答案

Chap3 思考题与习题 参考答案3.1 设有一个信源,它产生0、1 序列的消息。
它在任意时间而且不论以前发生过什么符号,均按P(0)=0.4,P(1)=0.6 的概率发出符号。
(1) 试问这个信源是否平稳的? (2) 试计算H(X 2),H(X 3/X 1X 2)及H ∞。
(3) 试计算H(X 4),并写出X 4 信源中可能有的所有符号。
解:(1)根据题意,此信源在任何时刻发出的符号概率都是相同的,均按p(0)=0.4,p(1)=0.6,即信源发出符号的概率分布与时间平移无关,而且信源发出的序列之间也是彼此无信赖的。
所以这信源是平稳信源。
(2)23123121()2()2(0.4log 0.40.6log 0.6) 1.942(/)(|)()()log ()(0.4log 0.40.6log 0.6)0.971(/)lim (|)()0.971(/)i i iN N N N H X H X bit symbols H X X X H X p x p x bit symbol H H X X X X H X bit symbol ∞−→∞==−×+===−=−+====∑" (3)4()4()4(0.4log 0.40.6log 0.6) 3.884(/)H X H X bit symbols ==−×+=4X 的所有符号:0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 11113.2 在一个二进制的信道中,信源消息集X={0,1}且p(1)=p(0),信宿的消息集Y={0,1},信道传输概率(10)1/p y x ===4,(01)1/p y x ===8。
求:(1) 在接收端收到y=0后,所提供的关于传输消息x 的平均条件互信息I(X ;y=0); (2) 该情况下所能提供的平均互信息量I(X ;Y)。
信息论与编码陈运主编答案完整版

p x x( i1 i3 )log p x( i3 / xi1)
i1 i2 i3
i1 i3
∑∑∑ ∑∑∑ = −
p x x x( i1 i2i3 )log p x( i3 / x xi1 i2 ) +
p x x x( i1 i2i3 )log p x( i3 / xi1)
i1
i2 i3 i1 i2 i3 p x( i3 / xi1)
( 1)
5 / 61
⎧p e( 1 ) = p e( 2 ) = p e( 3 ) ⎨
⎩p e( 1 ) + p e( 2 ) + p e( 3 ) =1 ⎧p e( 1 ) =1/3 ⎪ ⎨p e( 2 ) =1/3 ⎪⎩p e( 3 ) =1/3
⎧p x( 1 ) = p e( 1 ) (p x1 /e1 ) + p e( 2 ) (p x1 /e2 ) = p p e⋅( 1 ) + p p e⋅( 2 ) = (p + p)/3 =1/3 ⎪⎪ ⎨p x( 2 ) = p e( 2 ) (p x2 /e2 ) + p e( 3 ) (p x2 /e3 ) =p p e⋅( 2 ) + p p e⋅( 3 ) = (p + p)/3 =1/3
p x( i ) = I x( i ) =−log p x( i ) = log52!= 225.581 bit
(2) 52 张牌共有 4 种花色、13 种点数,抽取 13 张点数不同的牌的概率如下:
413 p x( i ) =
C5213
413 I x( i ) = −log p x( i ) = −log C5213 =13.208 bit
解: (1)
信息论与编码陈运主编答案完整版

p x( i3 / xi1) 1 0 时等式等等当 − = p x( i3 / x xi1 2i )
⇒ p x( i3 / xi1) = p x( i3 / x xi1 2i ) ⇒ p x x( i1 2i ) (p xi3 / xi1) = p x( i3 / x xi1 2i ) (p x xi1 2i ) ⇒ p x( i1) (p xi2 / xi1) (p xi3 / xi1) = p x x x( i1 2 3i i ) ⇒ p x( i2 / xi1) (p xi3 / xi1) = p x x( i2 3i / xi1) ∴等式等等的等等是 X1, X2, X3 是马氏链_
0.25
0.75
设随机变量 Y 代表女孩子身高
Y
y1(身高>160cm)
P(Y)
0.5
ห้องสมุดไป่ตู้
y2(身高<160cm) 0.5
已知:在女大学生中有 75%是身高 160 厘米以上的
即: p y( 1 / x1) = 0.75 bit
求:身高 160 厘米以上的某女孩是大学生的信息量
p x p y( 1) ( 1 / x1 ) log 0.25×0.75 =1.415 bit 即:I
∑∑∑ =
i1 i2
i3 p x x x( i1 i2 i3 )log p x( i3 / x xi1 i2 )
∑∑∑ ≤
i1 i2
⎛ p x( i3 / xi1) 1⎞⎟⎟log2 e i3 p x x x( i1 i2 i3 )⎜⎜⎝ p x( i3 / x xi1 i2 ) − ⎠
∑∑∑ ∑∑∑ = ⎜⎛
⇒ H X( 2 ) ≥ H X( 2
/ X1 ) I X( 3;X X1 2 ) ≥ 0
