信息论与编码习题课
信息论与编码习题

1 0 1 1 1 0 0 H 1 1 1 0 0 1 0 0 1 1 1 0 0 1
13为提高通信系统传输消息有效性,信源编码采用的方法 是
A.压缩信源的冗余度 C.研究码的生成矩阵 B.在信息比特中适当加入冗余比特 D.对多组信息进行交织处理
14、给定xi条件下随机事件yj所包含的不确定度和条件自信 息量p(yj /xi),( ) A.数量上不等,单位不同 B.数量上不等,单位相同 C.数量上相等,单位不同 D.数量上相等,单位相同 15、条件熵和无条件熵的关系是: A.H(Y/X)<H(Y) B.H(Y/X)>H(Y) C.H(Y/X)≤H(Y) D.H(Y/X)≥H(Y)
8、对于相同的信息,不同的观察者所获得的信息量可能 不同,指的是信息的( ) A 可度量性 B 相对性 C 可替代性 D 可共享性 9、信源熵不满足以下哪个性质?( ) A 确定性 B 非负性 C 连续性 D 可加性 10、二进制通信系统使用符号0和1,由于存在失真,传输 时会产生误码,用符号表示下列事件,u0:一个0发出, u1:一个1发出,v0 :一个0收到,v1:一个1收到。则已知 收到的符号,被告知发出的符号能得到的信息量是 ( )。 A H(U/V) B H(V/U) C H(U,V) D H(UV)
2,二元对称信道如图。
2)求该信道的信道容量。
x3 x4 x5 x6 x7 X x1 x2 3,.信源空间为 P( X ) 0.2 0.19 0.18 0.17 0.15 0.1 0.01 ,试构造二元霍夫曼码,计算其平均码长和编码效率(要 求有编码过程)。
信息论与编码习题参考答案(全)
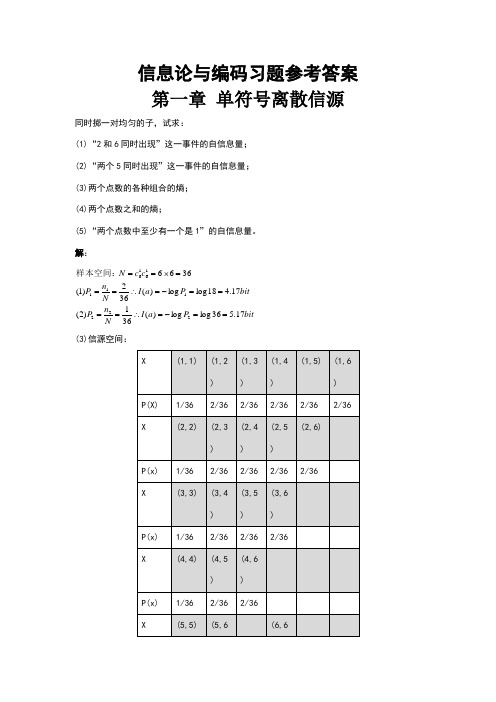
信息论与编码习题参考答案 第一章 单符号离散信源同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3616236log 36215)(=⨯⨯+⨯⨯=∴ (4)信源空间:bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格内。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为%.如果你问一位男士:“你是否是红绿色盲”他的回答可能是:“是”,也可能“不是”。
信息论与编码习题课

111 011000 01000000
1 01 000000010 10001
00
11
000111 110011 11000101 110011 01001101 110011 01110101 110011 00
01 000100 10011 10001
10
01
10
00101 10
00101 10
i
0.05 5 0.06 4 0.1 4 0.07 4 0.04 5
2.61码元 / 符号
编码效率为
H (X ) 2.55 0.977
K 2.61
(3)香农编码如下:
信源符号
x1 xx32 x4
x5
xx67
x8
符号概率 log p(xi ) 码字长度 Ki
0.4
1.32
00101 11
00101 00
00111 10
00100 1100100 1101101 1100100 0101001 1100100 0110101 1100100 01
10110 11
00111 010011
01
1
00111 010011
01
1
00111 010011
00
0
00111 010010
v0 u1 u2 u3
vv12
u0 u0
u1 u1
u2 u3
v3 u0 u2 u3
求该码的生成矩阵、校验矩阵及该码的最小距离, 并画出该编码器硬件逻辑连接图。 解:由(8,4)系统码,得n=8,k=4。
C (m3 m2 m1 m0 c3 c2 c1 c0 ) (u3 u2 u1 u0 v3 v2 v1 v0 )
《信息论与编码》部分课后习题参考答案

P ( y1 = 0 | M 1 ) P ( y1 = 0)
因为信道为无记忆信道,所以
P( y1 = 0 | M 1 ) = P( y1 = 0 | x11 x12 = 00) = P( y1 = 0 | x11 = 0) = P(0 | 0) = p
同理,得 I ( y1 = 0 | M i ) = P ( y1 = 0 | xi1 xi 2 ) = P ( y1 = 0 | xi1 ) 输出第一个符号是 y1=0 时, 有可能是四个消息中任意一个第一个数字传送来的。 所以
第二章
2.1 同时掷两个骰子,设每个骰子各个面向上的概率都是 1/6。试求: (1)事件“2 和 6 同时出现”的自信息量; (2)事件“两个 3 同时出现”的自信息量; (3)事件“两个点数中至少有一个是 5”的自信息量; (4)两个点数之和的熵。 答: (1)事件“2 和 6 同时出现”的概率为:
《信息论与编码》
部分课后习题参考答案
1.1 怎样理解消息、信号和信息三者之间的区别与联系。 答:信号是一种载体,是消息的物理体现,它使无形的消息具体化。通信系统中传输的是 信号。 消息是信息的载体, 信息是指消息中包含的有意义的内容, 是消息中的未知成分。 1.2 信息论的研究范畴可以分成哪几种,它们之间是如何区分的? 答:信息论的研究范畴可分为三种:狭义信息论、一般信息论、广义信息论。 1.3 有同学不同意“消息中未知的成分才算是信息”的说法。他举例说,他从三岁就开始背 诵李白诗句“床前明月光,疑是地上霜。举头望明月,低头思故乡。 ” ,随着年龄的增长, 离家求学、远赴重洋,每次读到、听到这首诗都会带给他新的不同的感受,怎么能说这 些已知的诗句没有带给他任何信息呢?请从广义信心论的角度对此现象作出解释。 答:从广义信息论的角度来分析,它涉及了信息的社会性、实用性等主观因素,同时受知识 水平、文化素质的影响。这位同学在欣赏京剧时也因为主观因素而获得了享受,因此属于广 义信息论的范畴。
《信息论与编码》课后习题答案

《信息论与编码》课后习题答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码习题参考答案(全)

已知信源X的信源空间为
某信道的信道矩阵为:
b1b2b3b4
试求:
(1)“输入?3,输出b2的概率”;
(2)“输出b4的概率”;
(3)“收到b3条件下推测输入?2”的概率。
解:
已知从符号B中获取关于符号A的信息量是1比特,当符号A的先验概率P(A)为下列各值时,分别计算收到B后测A的后验概率应是多少。
(1)在W4=011中,接到第一个码字“0”后获得关于a4的信息量I(a4;0);
(2)在收到“0”的前提下,从第二个码字符号“1”中获取关于a4的信息量I(a4;1/0);
(3)在收到“01”的前提下,从第三个码字符号“1”中获取关于a4的信息量I(a4;1/01);
(4)从码字W4=011中获取关于a4的信息量I(a4;011)。
(2)求信源的极限熵H∞;
(3)求当p=0,p=1时的信息熵,并作出解释。
解:
设某马尔柯夫信源的状态集合S:{S1S2S3},符号集X:{α1α2α3}。在某状态Si(i=1,2,3)下发发符号αk(k=1,2,3)的概率p(αk/Si) (i=1,2,3; k=1,2,3)标在相应的线段旁,如下图所示.
证明:
第三章 多符号离散信源与信道
设X=X1X2…XN是平稳离散有记忆信源,试证明:
H(X1X2…XN)=H(X1)+ H(X2/ X1)+H(X3/ X1X2)+…+H(XN/ X1X2…XN-1)。
(证明详见p161-p162)
试证明:logr≥H(X) ≥H(X2/ X1) ≥H(X3/ X1X2) ≥…≥H(XN/ X1X2…XN-1)。
(1,3)
(1,4)
(1,5)
信息论与编码习题1及答案1

一、dr)填空题(1)1948年.美国数学家_____________________ 发表了题为“通信的数学理论”的长篇论文,从而创立了信息论.(2)必然事件的自信息是_0 ___________ 。
(3)离散平稳无记忆信源X的N次扩展信源的嫡等于离散信源X的嫡的N倍°(4)对于离散无记忆信源,当信源爛有最大值时,满足条件为.信源符号等槪分術一(5)若一离散无记忆信源的信源爛H (X)等于2.5,对信源进行等长的无失真二进制编码,则编码长度至少为3 _____ ・(6)对于香农编码、费诺编码和霍夫曼编码,编码方法惟一的是 __________________ 。
(7)已知某线性分组码的最小汉明距离为3,那么这组码最多能检测出2 个码元错误.最多能纠正—1_个码元错误.(8)设有一离散无记忆平稳信道,其信道容董为C,只要待传送的信息传输率R_小于_C(大于、小于或者等于),则存在一种编码,当输入序列长度n足够大,使译码错误概率任意小。
(9)平均错误概率不仅与信道本身的统计特性有关,还与— ___________ 和_编码方巷—有关二、(9 )判斷题(1)信息就是一种消息。
( )(2)信息论研究的主要问题是在通信系统设计中如何实现信息传输、存储和处理的有效性和可靠性。
( )(3)概率大的事件自信息量大。
( )(4)互信息量可正、可负亦可为零。
( )(5)信源剩余度用来衡量信源的相关性程度,信源剩余度大说明信源符号间的依赖关系较小。
( )(6)对于固定的信源分布,平均互信息董是信道传递概率的下凸函数。
( )(7)非奇异码一定是唯一可译码,唯一可译码不一定是非奇异码。
( )(8)信源变长编码的核心问题是寻找紧致码(或最佳码),霍夫曼编码方法构造的是最佳码。
( )(9)信息率失真函数R(D)是关于平均失真度D的上凸函数. ( )三、(5 )居住在某地区的女孩中有25%是大学生,在女大学生中有75%是身高1o 6米以上的,而女孩中身爲1・6米以上的占总数的一半。
信息论与编码习题参考答案(全)

信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格内。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
G [Ik P] [I4 P]
由已知条件
v0 u1 u2 u3
vv12
u0 u0
u1 u1
u2 u3
v3 u0 u2 u3
得,
1 0 0 0
1 1 0 1
0 1 0 0 P1 0 1 1
0 0 1 0
信源各符号的对应哈夫曼曼码字如下:
0.1 0.18 0.4 0.05 0.06 0.1 0.07 0.04
011 001 1 0001 010 000 010 0001
平均码长为
0 1001
K p(xi )Ki 0.1 3 0.18 3 0.41
i
0.05 5 0.06 4 0.1 4 0.07 4 0.04 5
0
00
101000 11010
0
10
0101100 01100 011101
01
0
0101100 01100 011101
01
0
0101101 01100 011101
00
1
0101110 01100 011100
11
0
0100100 01110 011001
01
0
0101000 01101
110100 1101010
C12 (1100010)C13 (1101001)C14 (1110100)C15 (1111111)
伴随式有 2nk 23 8 种组合,除了全零图案外, 代表1个差错的差错图案有C71 7 种。
由
1 0 1 1 1 1
1 1 0
S eH T [e6 , e5 , e4 , e3, e2 , e1, e0 ]0 1 1 可得,
,则求: (1)该信源在每秒内发出1个符号,求该信源
的熵及信息传输速率。 (2)对这8个符号作哈夫曼编码,写出相应码
字,并求出编码效率。 (3)采用香农编码,写出相应码字,求出编
码效率。 (4)进行费诺编码,写出相应码字,求出编
码效率。
解:(1)信源熵
H (X ) p(xi )log p(xi )
11101100 011100
110100 1101010
10111100 001000
110100 1101010
00001100 100100
110101 1101011
1
0
011111 1011111 1111101 1011111 1010101 1011111 0001101 1011110 1
0 1 1 1
0 0 0 1
1 1 1 0
1 0 0 0 1 1 0 1 G 0 1 0 0 1 0 1 1
0 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0
H [PT Ink ] [PT I4]
1 1 0 1 1 0 0 0 1 0 1 1 0 1 0 0
i
0.1log2 0.1 0.18log2 0.18 0.4log2 0.4 0.05log2 0.05 0.06log2 0.06 0.1log2 0.1 0.07log2 0.07 0.04log2 0.04
2.55bit / symbol
信息传输速率为
Rt 2.55bit / s
2.61码元 / 符号
编码效率为
H (X ) 2.55 0.977
K 2.61
(3)香农编码如下:
信源符号
x1 xx32 x4
x5
xx67
x8
符号概率 log p(xi ) 码字长度 Ki
0.4
1.32
2
0.18 2.47
3
0.1
3.32
4
0.1
3.32
4
0.07 3.84
V2 {(0100 ), (1000 ), (0000 ), (1100 )} V2的一个两维4重对偶子空间为
V2' {(0010 ), (0001), (0000 ), (0011)}
6-3某系统(8,4)码,其四位校验位 vi , i 0,1, ,3
与四位信息位 ui ,i 0,1, ,3 的关系是
解:(1)信源符号熵为
H (X ) p(xi ) log p(xi )
i
0.37log2 0.37 0.25log2 0.25 0.18log2 0.18
0.10log2 0.10 0.07log2 0.07 0.03log2 0.03
2.23bit / symbol
(2)
符号 概率
x1 0.37
x2 0.25 x3 0.18 x4 0.10
x5 0.07 x6 0.03
0 1
0
0.10
1
0.62
0
0.20
1
0
0
1.00
0.38 1 1
编码 00 01 11 101
1000 1001
该哈夫曼码的平均码长为
K p(xi )Ki
i
0.37 2 0.25 2 0.18 2 0.10 3 0.07 4 0.03 4 2.3码元 / 符号
由切比雪夫不等式可得
L
2(X) 2
0.792 (0.07)2 103
信源符号一起编码才 能满足要求。
5-12 已知一信源包含8个消息符号,其出现的概率
P(X ) {0.1,0.18,0.4,0.05,0.06,0.1,0.07,0.04}
C0 (0000000)C1 (0001011)C2 (0010110)C3 (0011101)
C4 (0100111)C5 (0101100)C6 (0110001)C7 (0111010)
C8 (1000101)C9 (1001110)C10 (1010011)C11 (1011000)
v0 u1 u2 u3
vv12
u0 u0
u1 u1
u2 u3
v3 u0 u2 u3
求该码的生成矩阵、校验矩阵及该码的最小距离, 并画出该编码器硬件逻辑连接图。 解:由(8,4)系统码,得n=8,k=4。
C (m3 m2 m1 m0 c3 c2 c1 c0 ) (u3 u2 u1 u0 v3 v2 v1 v0 )
0
x3 0.1
x4 0.1
1
x 0.07 5
x6 0.06
x 0.05 7
x8 0.04
第二次 分组
0 1
0
1
第三次 分组
0 1 0
1
第四次 分组
0 1 0 1
码字
00 01 100 101 1100 1101 1110 1111
平均码长为
K p(xi )Ki 2.64码元/ 符号
i
编码效率为
解:由题意,可知
1 1 1 0 1 0 0 H 0 1 1 1 0 1 0
1 1 0 1 0 0 1
1 0 0 0 1 0 1 G 0 1 0 0 1 1 1
0 0 1 0 1 1 0 0 0 0 1 0 1 1
信息组m={(0000),(0001),(0010), (0011),(0100),(0101),(0110), (0111)(10000),(1001),(1010), (1011),(1100)(1101),(1110), (将1m11及1G)代} 入C=mG中求得16个对应的码字:
4
0.06 4.06
5
0.05 4.32
5
0.04 4.64
5
累加概率 二进制
码字
Pi
(Pi )
0
0
00
0.4 0.011001... 011
0.58 0.100101... 1001
0.68 0.101011... 1010
0.78 0.110001... 1100
0.85 0.110110... 11011
0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 1
从H看出,不相关的列数为3,即 dmin 1 3
所以
dmin 4
编码器逻辑连接图如下:
输入 u0 u1 u2 u3
++++
输出
v0 v1 v2 v3
6-5列出本章例6-4的(7,4)汉明码的标准阵列译码表。 若收码R=(0010100,0111000,1110010),由标准阵 列译码表判断发码是什么?
0
1
00 00000 000000 000101
1 01
1
0
01 00000 000001 000100
0 10
0
1
01 00010 000100 000001
1 00
0
1
10 00001 000010
0 S 00 E 0 10001
10 10000 10001000
1 00 000000000 10001
0.91 0.111010... 11101
0.96 0.111101... 11110
平均码长为
K p(xi )Ki 3.17码元/ 符号
i
编码效率为
H (X ) 2.55 0.804
K 3.17
(4)费诺编码
消息 符号概率 第一次
符号
分组
x1 0.4
x2 0.18
第五章
5-10 设有离散无记忆信源P(X ) {0.37,0.25,0.18,0.10,0.07,0.03}
