学而思2016秋季班尖子班第6讲,讲义差倍问题 奥数
三年级学而思奥数讲义精编版

目录第一讲加减法的巧算(一) (2)第二讲加减法的巧算(二) (7)第三讲乘法的巧算 (12)第四讲配对求和 (16)第五讲找简单的数列规律 (17)第六讲图形的排列规律 (19)第七讲数图形 (23)第八讲分类枚举 (26)能力测试(一) (26)第九讲填符号组算式 (28)第十讲填数游戏 (31)第十一讲算式谜(一) (35)第十二讲算式谜(二) (37)第十三讲火柴棒游戏(一) (39)第十四讲火柴棒游戏(二) (40)第十五讲从数量的变化中找规律 (45)第十六讲数阵中的规律 (45)第17讲时间与日期……………第18讲推理……………能力测试(二) (63)第19讲循环………………第20讲最大和最小…………………………第21讲最短路线…………………………第22讲图形的分与合…………………第23讲格点与面积……………………第24讲一笔画………………………阶段测试(三)……………………第25讲移多补少与求平均数………………第26讲上楼梯与植树………………第27讲简单的倍数问题……………………第28讲年龄问题……………………………第29讲鸡兔同笼问题……………………第30讲盈亏问题…………………第31讲还原问题……………………第32讲周长的计算……………………第33讲等量代换……………………第34讲一题多解……………………能力测试(四)………………………………第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小学奥数和倍差倍问题

和倍差倍问题考试要求1、该知识点不会单独出题,但是思路很重要;2、该知识点是典型应用题的基础,是必考内容。
知识框架一、基本运算律及公式1、和倍问题和倍问题就是已知两个数的和以及它们之间的倍数关系,求这两个数各是多少的问题.解答此类应用题时要根据题目中所给的条件和问题,画出线段图,使数量关系一目了然,从而找出解题规律,正确迅速地列式解答。
和倍问题的特点是已知两个数的和与大数是小数的几倍,要求两个数,一般是把较小数看作倍数,大数就是几倍数,这样就可知总和相当于小数的几倍了,可求出小数,再求大数.和倍问题的数量关系式是:和÷(倍数+1)=小数小数×倍数=大数或和一小数=大数如果要求两个数的差,要先求1份数:1份数×(倍数-1)=两数差.解决和倍问题,关键是学会画线段图,这样可以帮助我们更好的弄清各数量之间的关系。
2、差倍问题差倍问题就是已知大小两数的差,以及大小两数的倍数关系,求大小两数的问题.差倍问题的特点与和倍问题类似。
解答差倍问题的关键是要确定两个数量的差及相对应的倍数差,一般情况下,在题目中不直接给出,需要经过调整和计算才能得到。
解题思路:首先要在题目中找到1倍量,然后画图确定解题方法.被除数的数量和除数的倍数关系要相对应,相除后得到的结果是一倍量差倍问题的基本关系式:差÷(倍数- 1)=1 倍数(较小数)倍数×几倍=几倍数(较大数)或较小数+差=较大数解决差倍问题,关键是学会画线段图,这样可以帮助我们更好的弄清各数量之间的关系.年龄问题的和差问题主要利用的年龄差不变。
重难点重点:1、最基本的应用题,但是应用很广;2、如何画线段图,找等量关系;难点:1、画图和找等量关系;2、找到解题的思路和捷径。
课前预习购物圣诞节那一天,我与妈妈到百货大楼去买东西。
正巧,大楼正在举办返券销售活动,只见标牌上清清楚楚地写着:购买服装类每付现金100元,返回礼券80元;鞋类每付100元,返回礼券60元;用具类每付100元,返回礼券40元;所付现金不足100元部分不返券,所返的礼券可在返券销售活动期间在商场内购买任何商品。
学而思奥数第六级第六讲逻辑思维综合(邹、陈、罗)

学而思奥数第六级第六讲 逻辑推理综合逻辑推理作为数学思维中重要的一部分,经常出现在各种数学竞赛中,除此以外,逻辑推理还经常作为专项的内容出现在各类选拔考试,甚至是面向成年人的考试当中。
对于学生学习数学来说,逻辑推理既有趣又可以开发智力,学生自主学习研究性比较高。
本讲我们主要从各个角度总结逻辑推理的解题方法。
一、 列表推理法逻辑推理问题的显著特点是层次多,条件纵横交错.如何从较繁杂的信息中选准突破口,层层剖析,一步步向结论靠近,是解决问题的关键.因此在推理过程中,我们也常常采用列表的方式,把错综复杂的约束条件用符号和图形表示出来,这样可以借助几何直观,把令人眼花缭乱的条件变得一目了然,答案也就容易找到了.二、 假设推理用假设法解逻辑推理问题,就是根据题目的几种可能情况,逐一假设.如果推出矛盾,那么假设不成立;如果推不出矛盾,而是符合题意,那么假设成立.解题突破口:找题目所给的矛盾点进行假设三、 计算中的逻辑推理能够利用数论等知识通过计算解决逻辑推理题.一、 列表推理法【例 1】 刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刘刚和小丽对李强和小英;第二盘:李强和小红对刘刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【巩固】 王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:⑴张贝从未上过天;⑵跳伞运动员已得过两块金牌;⑶李丽还未得过第一名,她与田径运动员同年出生.请根据上述情况判断王文、张贝、李丽各是什么运动员?例题精讲知识结构【例2】张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:⑴张明不在北京工作,席辉不在上海工作;⑵在北京工作的不是教师;⑶在上海工作的是工人;⑷席辉不是农民.问:这三人各住哪里?各是什么职业?【巩固】甲、乙、丙三人,他们的籍贯分别是辽宁、广西、山东,他们的职业分别是教师、工人、演员.已知:⑴甲不是辽宁人,乙不是广西人;⑵辽宁人不是演员,广西人是教师;⑶乙不是工人.求这三人各自的籍贯和职业.【例3】甲、乙、丙、丁四个人的职业分别是教师、医生、律师、警察.已知:⑴教师不知道甲的职业;⑵医生曾给乙治过病;⑶律师是丙的法律顾问(经常见面);⑷丁不是律师;⑸乙和丙从未见过面.那么甲、乙、丙、丁的职业依次是:.【巩固】甲、乙、丙三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长.一次数学测验,这三个人的成绩是:⑴丙比大队长的成绩好.⑵甲和中队长的成绩不相同.⑶中队长比乙的成绩差.请你根据这三个人的成绩,判断一下,谁是大队长呢?【例4】甲、乙、丙、丁每人只会中、英、法、日四种语言中的两种,其中有一种语言只有一人会说.他们在一起交谈可有趣啦:⑴乙不会说英语,当甲与丙交谈时,却请他当翻译;⑵甲会日语,丁不会日语,但他们却能相互交谈;⑶乙、丙、丁找不到三人都会的语言;⑷没有人同时会日、法两种语言.请问:甲、乙、丙、丁各会哪两种语言?【巩固】宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:⑴数学博士夸跳高冠军跳的高⑵跳高冠军和大作家常与宝宝一起看电影⑶短跑健将请小画家画贺年卡⑷数学博士和小画家关系很好⑸贝贝向大作家借过书⑹聪聪下象棋常赢贝贝和小画家问:宝宝、贝贝、聪聪各有哪两个外号吗?【例5】六年级四个班进行数学竞赛,小明猜想比赛的结果是:3班第一名,2班第二名,1班第三名,4班第四名.小华猜想比赛的结果是:2班第一名,4班第二名,3班第三名,1班第四名.结果只有小华猜到的4班为第二名是正确的.那么这次竞赛的名次是班第一名,班第二名,班第三名,班第四名。
六年级学而思奥数

六年级学而思奥数11111+++++12342026122042036579111357612203042++++++1111112123123100+++++++++++222222222222233333333333331121231234122611212312341226L L L +++++++++-+-+-+++++++++测试题【例1】(★★)111111357911_____.612203042+++++=计算A .53614B .7512C .4121D .1712【例2】(★★★)计算:2337911345122030+++++=( )A .3227B .4112C .4121D .2312【例3】(★★★★)11111_____12123123412310+++++=+++++++++A .1113B .111C .712 D .2011【例4】(★★★★)计算:2222222222221324351820213141191++++++++=----( )A .72019B .15138190C .1402D .73620本讲学习重点:1.海哥、海马学奥数时的那点笑话~ 2.整体约分与连锁约分技巧(2010第8届·走进美妙的数学花园·六年级初赛)211354117997⎛⎫⎛⎫+÷+ ⎪ ⎪⎝⎭⎝⎭【附加练习】2129476122323791113791113⎛⎫⎛⎫+++÷+++ ⎪ ⎪⎝⎭⎝⎭(2009·数学解题能力展示·读者评选活动小学六年级组初赛试题)89109101110111211121378910111178910++++++++-+--+-124248361210020040013926183927100300900⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯【附加练习】1246248123612181002004006001369261218391827100300600900⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯一根铁丝,第1次截去总长度的212,第2次截去剩余长度的213,第3次截去剩余长度的214…第2008次截去剩余长度的212009,此时该铁丝还剩2010厘米,那么该铁丝原长为______厘米?【附加练习】1111111113243520072009⎛⎫⎛⎫⎛⎫⎛⎫+⨯+⨯+⨯⨯+ ⎪ ⎪ ⎪ ⎪⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭已知135979924698100A ⨯⨯⨯⨯⨯=,24696983579799B ⨯⨯⨯⨯⨯=,110C =。
学而思奥数2016秋季班提高班第6讲讲义
BC 边上靠近 B 点的三等分点,那么阴
影部分的面积为
.
A
B
F E
D
C
【答案】30 平方厘米 【分析】△BEC 的面积是梯形的一半, S△BEC 180 2 90(cm2),阴影面积 是90 3 30(cm2).
拓展 4
如图,在梯形 ABCD中,E 、F 分别是
AB、CD 的中点,S1和S2的面积分别是 5 和 15,求梯形 ABCD 的面积.
为面积相等的两部分,且每个三角形
中的两部分都分属于S1 S4、S2 S3这
两个不同的组合,所以S1 S4 S2 S3.
C G D
S1
S2 F
H
O
S3 S4
A
E
B
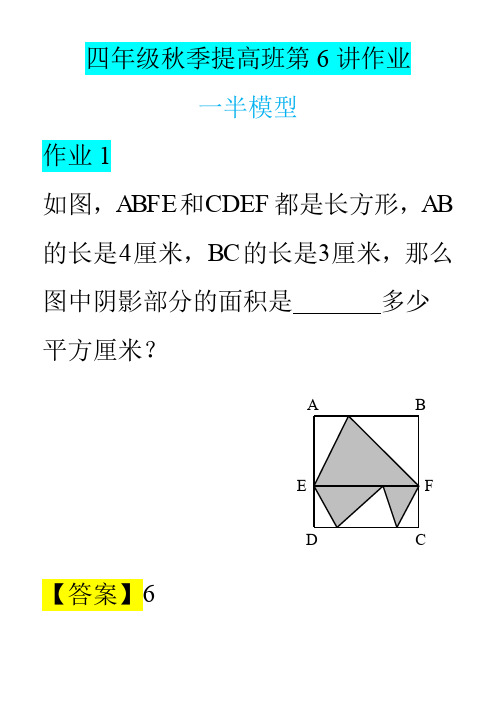
8.56 因为 ABFD 是平行四边形,所以 AD BF ,那么FC 22 14 8cm.又 CDEF 是正方形,所以
EF FC 8cm.三角形 ABF 的面积是 14 8 2 56cm2.因为三角形 ABF 在 平行四边形 ABFD,长方形 AGHF 中 都是一半,因此阴影部分面积为 56cm2.
四年级秋季提高班第 6 讲 一半模型
例1 (1)如图所示,一个长方形分成 4 个 不同的三角形,其中红色部分的面积 和为 50 平方厘米,黄色三角形面积是 21 平方厘米,则绿色三角形的面积是 ________平方厘米;
黄
红
红
绿
(2)如图所示,长方形的面积均为 20, 则下面两个图形中阴影部分的面积依
4.连 DC,S BDC 6S BDE 6, S ABC 2S BDC 12
5.如图,连接 CF,那么 CF 平行 BD ,所以,阴影面积 三角形 BDF 的面积 三角形 BCD 的面积=0.72(平 方厘米).
差倍问题(语音同步讲解)

难点:
和倍、差倍问题关键要找准倍数和或倍数 差所对应的数量关系 在分数、百分数应用题中应用广泛 用方程解决和倍、差倍问题较为简便 线段图是解决问题重要的方法
例题5、有两袋面粉,从第一袋中取8千克放入第 二袋,两袋重量相等,如果从第二袋中取10千克 放入第一袋,则第一袋的重量是第二袋的2倍,两 袋原来有面粉多少千克? 我想: 根椐题意画线段图 这时可求出第二袋有 取8 第一袋 36÷(2-1)=36千克 放8 第二袋 原来第二袋是 第一袋 36+10=46千克 放 取10 第二袋 10 原来第一袋是 从图中可得知: 2×36-10=62千克 第二次第一袋比第二袋多 10+8+8+10=36千克
花盆数是 188-25+188=351个 把长春园的杜鹃花盆数是1倍数
那么人民公园的杜鹃 花盆数是这样的5倍
171×4=684盆
例题4、两个书架所存书的本数相等,如果从第 一个书架取出200本书,而从第二个书架再放入40 本书,那么第二个书架的本数是第一个书架的3倍, 问第一个书架原来各存多少本? 我想: 根椐题意画线段图 第二书架比第一书架多240本 就相当于变化后第一 取出200本 1倍数 个书架的(3-1)倍 一书架 变化后第一个书架书 二书架 (200+40)÷(3-1) 40 从变化后的两个书架: =120本 第二书架比第一书架多240本 第一个书架原来有: 变化后第一个书架看作1倍数 2000+400=2400本
我想: 要点:先找出差所对应的倍数,先求1倍数,
再求几倍数. 一件皮衣价钱是一件 首先确定哪一个是1倍数 羽绒服价钱的5倍 那么;把羽绒服的人数看做1倍数 1倍数 羽绒服的4倍是960元 羽绒服 ? 多960元 所以用960÷4=240元 皮衣
三年级奥数.差倍问题例题及答案

三年级奥数第二讲差倍问题例题精讲教学目标:1.掌握差倍问题的基本解法以及相关的年龄等应用题.2.熟练应用通过图示来表示数量关系.知识点说明:差倍问题就是已知大小两数的差,以及大小两数的倍数关系,求大小两数的问题.差倍问题的特点与和倍问题类似。
解答差倍问题的关键是要确定两个数量的差及相对应的倍数差,一般情况下,在题目中不直接给出,需要经过调整和计算才能得到。
解题思路:首先要在题目中找到1倍量,然后画图确定解题方法.被除数的数量和除数的倍数关系要相对应,相除后得到的结果是一倍量差倍问题的基本关系式:差÷(倍数-1)=1倍数(较小数)1倍数×几倍=几倍数(较大数)或较小数+差=较大数解决差倍问题,关键是学会画线段图,这样可以帮助我们更好的弄清各数量之间的关系.年龄问题的和差与差倍问题主要利用的年龄差不变。
板块一、差倍问题【例1】李爷爷家养的鸭比鹅多18只,鸭的只数是鹅的3倍,你知道李爷爷家养的鸭和鹅各有多少只吗?【解析】引导学生画图,但是一定要强调差所对应的份数,这样我们就可以求一份量(一倍量),从而解决题目.与18只相对应,这样就可以求出一倍数也就是鹅的只数,求出了鹅的只数,鸭的只数就容易求出来了.鸭与鹅只数的倍数差是312÷= (只),鸭有-=(倍),鹅有1829⨯=(只).9327【巩固】两个书架,甲书架存书相当于乙书架存书量的5倍,甲书架比乙书架存书多120本,则乙书架存书多少本?【解析】多的120本相当于乙书架的4倍,则乙书架的书为:120430÷=(本).【巩固】某小学原来参加室外活动的人数比参加室内活动的人数多480人,现在把室内活动的50人改为室外活动,这样室外活动的人数正好是室内人数的5倍,则参加室内、室外活动的共有多少人?【解析】原来室外、室内活动人数相差480人,现把室内的50人改为室外活动,这样室外活动人数比室内人数多480502580+⨯=(人),这时室外活动人数正好是室内人数的5倍,580人相当于现在室内活动人数的514÷=,再求出-=(倍),这样可先求出现在室内活动人数为5804145室内、外人数之和:145(51)870⨯+=人.【巩固】师、徒两人共加工105个零件,师父加工的个数比徒弟的3倍还多5个,师父和徒弟各加工零件多少个?【解析】把徒弟加工的个数看作1份数,师父加工的个数就比3份数还多5个,如果师父少加工5个,两人加工的总数就少5个,总数变为(1055)-个,就可以求出师父和徒弟各加工多少个了.徒弟做了:100(31)25÷+=(个),师父做了:253580⨯+=(个).【巩固】甲班的图书本数比乙班多80本,甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?【解析】乙班的本数: 80÷(3-1)=40(本)甲班的本数: 40×3=120(本)或40+80=120(本)。
小学奥数之差倍问题解法(完整版)

小学奥数之差倍问题解法1. 掌握差倍问题的基本解法以及相关的年龄等应用题.2. 熟练应用通过图示来表示数量关系.差倍问题就是已知大小两数的差,以及大小两数的倍数关系,求大小两数的问题.差倍问题的特点与和倍问题类似。
解答差倍问题的关键是要确定两个数量的差及相对应的倍数差,一般情况下,在题目中不直接给出,需要经过调整和计算才能得到。
解题思路:首先要在题目中找到1倍量,然后画图确定解题方法.被除数的数量和除数的倍数关系要相对应,相除后得到的结果是一倍量差倍问题的基本关系式:差÷(倍数-1)=1倍数(较小数)1倍数×几倍=几倍数(较大数)或较小数+差=较大数解决差倍问题,关键是学会画线段图,这样可以帮助我们更好的弄清各数量之间的关系.年龄问题的和差问题主要利用的年龄差不变。
【例 1】 两个整数,差为l6,一个是另一个的5倍.这两个数分别是( )和( )【考点】差倍问题 【难度】1星 【题型】填空【关键词】走美杯,3年级,初赛【解析】 本题属于和差问题。
小数:16÷(5-1)=4;大数:4×5=20或4+16=20。
【答案】小数4,大数20【例 2】 李爷爷家养的鸭比鹅多18只,鸭的只数是鹅的3倍,你知道李爷爷家养的鸭和鹅各有多少只吗?【考点】差倍问题 【难度】1星 【题型】解答【解析】 引导学生画图,但是一定要强调差所对应的份数,这样我们就可以求一份量(一倍量),从而解决题目.与18只相对应,这样就可以求出一倍数也就是鹅的只数,求出了鹅的只数,鸭的只数就容易求出来了.鸭与鹅只数的倍数差是312-=(倍),鹅有1829÷= (只),鸭有 9327⨯=(只).【答案】鹅9只,鸭27只【巩固】 甲班的图书本数比乙班多80本,甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?【考点】差倍问题 【难度】1星 【题型】解答【解析】 乙班的本数: 80÷(3-1)=40(本)甲班的本数: 40×3=120(本)或40+80=120(本)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小大 大大
卖卖卖卖 卖卖卖卖
【分析】 卖出同样多的油,可知两个 桶里所有油的差总保持不变,因此这 是一个差倍问题.小桶所剩的油为l倍 数,大桶剩油是小桶剩油的4倍,所以 大桶剩油比小桶剩油多 4 1 3 (倍). 而大桶比小桶多的油总保持不变,是 60 30 30 (千克).再利用差倍问题 的公式就可解决.小桶剩下的油是: 30 3 10 (千克),大桶剩下的油是: 10 4 40 (千克).
大______桶多(填大或小) , 多_____60_______千克. (2)小强和小明卡片一样多,小强又 得到10张,小明得到5张,此时小强比 小明多_____5______张. (3)小强和小明卡片一样多,如果小 强丢了15张,小明丢了11张,那么小 明比小强多____4_______张. (4)小花和小红卡片一样多,如果小 红得到8张,小花丢了4张,那么小红 比小花多____12_______张. (5)小花和小红卡片一样多,小红给 小花4张,此时小花比小红多 ____8_______张. 【例4】大桶里有油60千克,小桶里有 油30千克.将两个桶的油卖出同样多 以后,所剩下的油中,大桶是小桶的4 倍.问:两个桶各剩油多少千克?
【例2】学而思学校买来白粉笔比彩色 粉笔多153箱,白粉笔的箱数比彩色笔 的4倍还多3箱,学校买来白粉笔和彩 色粉笔各多少箱?
彩白 白白 1倍倍 4倍倍 பைடு நூலகம்箱
【分析】 通过适当的变形,将其作为 一个典型的“差倍问题”来解决.见上 图,由于白笔比彩笔的4倍多3箱,故 (白笔-3)就相当于 把彩笔看做1倍数, 彩笔的4倍,即彩笔比(白笔 3 )少3 倍,注意此时白笔比彩笔多153-3=150 (箱) .彩色粉笔的箱数:150÷3=50 (箱),白色粉笔的箱数:50+153=203 (箱).
【练一练】甲、乙两班人数相等.如 果从甲班调27人到乙班,那么乙班的 人数正好是甲班人数的4倍.问两个班 原来各有多少人? 【分析】 “从甲班调27人到乙班”,这 时乙班比甲班多的人数是 27 27 54 (人),把甲班剩下的人数 作为l倍数,乙班现有人数比甲班剩下 人数多的倍数是 4 1 3 倍. 甲班剩下 的人数是: 54 3 18 (人),甲、乙两 班原来各有人数是: 18 27 45 (人).
【例5】两块同样长的花布,第一块卖 出31米,第二块卖出19米后,第二块 是第一块的4倍,求每块花布原有多少 米?
卖卖31米 卖卖19米
【分析】 已知两块花布同样长,由于 第一块卖出的多,第二块卖出的少, 因此.所剩的布第二块比第一块多 31 19 12 (米).又知第二块所剩下的 布是第一块的4倍,那么第二块比第一 块多出的12米正好相当于所剩布的 ( 4 1 )倍,第一块布剩下: 12 (4 1) 4 (米),第一块布原有: 4 31 35 (米).
【练一练】学而思男老师比女老师少 346人,女老师的人数是男老师的5倍 还少14人,学而思有男女老师各多少 人? 【分析】 如上题可知女老师比男老师 多346人,女老师只需补上14人就是男 老师人数的5倍,那么差也随之变成 346+14=360(人) ,女老师就比男老师 多4份,所以男老师有360÷(5-1)=90 (人) ,女老师有90+346=436(人). 【例3】你会找差吗? (1)大桶里有油100千克,小桶里有 油40千克.将两个桶的油卖出同样多 以后(都没有卖完) ,请问此时 _____________桶多(填大或小) ,多
2
【例6】有大小两桶一样多的油,如果 从小桶倒9千克油到大桶中,则大桶中 的油是小桶的4倍,那么原来大小两桶 各有油多少千克?
倒卖 9千千 小大 倒倒 9千千 大大
【分析】 开始时两桶油一样多,从小 桶倒入大桶9千克后,大桶中的油会比 小桶中的油多出 9 2 18 (千克),由 图可知,此时大桶中的油比小桶多出3 倍,18千克即为3倍量,所以,1倍数 为: 18 3 6 (千克),倒入油后大桶 中的油量为: 6 4 24 (千克), 24 9 15 (千克),即原来两桶中各有 油15千克.
2016年秋季三年级尖子班 第六讲:差倍问题
【例1】学而思学校三年级的图书本数 比四年级多80本,三年级的图书本数 是四年级的3倍,三年级和四年级各有 图书多少本? 【分析】 把四年级的图书本数看作1 倍,三年级的图书本数是四年级的3 倍,那么三年级的图书本数比四年级 多2倍.又知“三年级的图书比四年级多 80本”,即2倍与80本相对应,这样可 以算出1倍是多少本.所以四年级的本 数: 80 (3 1) 40 (本),三年级的 本数: 40 3 120 (本)或 40 80 120 (本).
【练一练】实验小学一校区人数比实 验小学二校区人数少540人,因为第三 校区建成,从两个校区各调走200人, 这时实验小学二校区人数恰好是实验 小学一校区人数的4倍,那么实验小学 一校区和实验小学二校区原来各有多 少人? 【分析】 两校区各调走200人之后还 是相差540人, 对应的倍数是:4 1 3 倍,实验小学一校区调走200人后剩下 的人数是: 540 (4 1) 180 (人),实 验小学一校区原有: 180 200 380 (人),实验小学二校区 为: 380 540 920 (人).
____________千克. (2)小强和小明卡片一样多,如果小 强又得到10张,小明得到5张,那么小 强比小明多___________张. (3)小强和小明卡片一样多,如果小 强丢了15张,小明丢了11张,那么小 明比小强多___________张. (4)小花和小红卡片一样多,如果小 红得到8张,小花丢了4张,那么小红 比小花多___________张. (5)小花和小红卡片一样多,小红给 小花4张,此时小花比小红多 ___________张. 【分析】 (1)大桶里有油100千克,小桶里有 油40千克.将两个桶的油卖出同样多 以后 (都没有卖完) , 请问此时_______
