六年级奥术数学求阴影部分面积超难题
小学六年级求阴影部分面积试题和答案

求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:?圆面积减去等腰直角三角形的面积,?例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r ,因为正方形的面积为7平方厘米,所以=7,=7-×7=1.505?π()=16-π(2π-π(例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5 所以阴影面积为:π÷4-12.5=7.125平方厘米?(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形, 所以阴影部分面积为:2×3=6平方厘米解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
(单位:厘米)解:这种图形称为环形,可以用两个同心圆的面积差或差的一部例12.求阴影部分的面积。
(单位:厘米)解:三个部分拼成一个半圆面积.解:梯形面积减去积,(4+10)×4=12,=6π÷2=3π。
阴影部分面积为:(3π-6)×=5.13平方厘米[-] =π(116-36)=40π=125.6平方厘米例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)解:上面的阴影部分以AB 为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED 、BCD 面积和。
小学六年级求阴影部分面积试题和答案

例5.求阴影部分的面积。(单位:厘米)
解:这是一个用最常用的方法解最常见的题,为方便起见,
我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,
π( )×2-16=8π-16=9.12平方厘米
另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?
例28.求阴影部分的面积。(单位:厘米)
解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,
三角形ABD的面积为:5×5÷2=12.5
弓形面积为:[π ÷2-5×5]÷2=7.125
所以阴影面积为:12.5+7.125=19.625平方厘米
解法二:右上面空白部分为小正方形面积减去 小圆面积,其值为:5×5- π =25- π
例14.求阴影部分的面积。(单位:厘米)
解:梯形面积减去 圆面积,
(4+10)×4- π =28-4π=15.44平方厘米.
例15.已知直角三角形面积是12平方厘米,求阴影 部分的面积。
分析:此题比上面的题有一定难度,这是"叶形"的一个半.
解:设三角形的直角边长为r,则 =12, =6
圆面积为:π ÷2=3π。圆内三角形的面积为12÷2=6,
求阴影部分面积
例1.求阴影部分的面积。(单位:厘米)
解:这是最基本的方法: 圆面积减去等腰直角三角形的面积,
× -2×1=1.14(平方厘米)
例2.正方形面积是7平方厘米,求阴影部分的面积。(单位:厘米)
解:这也是一种最基本的方法用正方形的面积减去 圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以 =7,
小学六年级阴影部分面积专题复习经典例题(含答案)

小学六年级阴影部分面积专题复习经典例题(含答案)欢迎下载研究必备资料,本文主要涉及组合图形的面积计算。
以下是各题的解答和点评:1.求如图阴影部分的面积。
(单位:厘米)分析:阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积。
利用梯形和半圆的面积公式代入数据即可解答。
解答:$(4+6)\times4\div2\div2-3.14\times2^2=10-6.28=3.72$(平方厘米)。
答案:阴影部分的面积是3.72平方厘米。
点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用。
2.如图,求阴影部分的面积。
(单位:厘米)分析:根据图形可以看出,阴影部分的面积等于正方形的面积减去4个扇形的面积。
正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积。
解答:扇形的半径是:$10\div2=5$(厘米);$10\times10-3.14\times5\times5=100-78.5=21.5$(平方厘米)。
答案:阴影部分的面积为21.5平方厘米。
点评:组合图形的面积计算需要注意各部分之间的关系,特别是涉及到圆形时需要注意半径的计算。
3.求如图阴影部分面积。
(单位:厘米)解答:该题缺少图形,无法回答。
4.求出如图阴影部分的面积:单位:厘米。
解答:该题缺少图形,无法回答。
5.求如图阴影部分的面积。
(单位:厘米)解答:该题缺少图形,无法回答。
6.求如图阴影部分面积。
(单位:厘米)解答:该题缺少图形,无法回答。
7.计算如图中阴影部分的面积。
单位:厘米。
解答:该题缺少图形,无法回答。
8.求阴影部分的面积。
单位:厘米。
解答:该题缺少图形,无法回答。
9.如图是三个半圆,求阴影部分的周长和面积。
(单位:厘米)分析:阴影部分可以看成是两个半圆和一个矩形组成的,可以分别计算各部分的周长和面积再相加。
解答:矩形的长和宽分别为$8-4\pi$和$4$,面积为$(8-4\pi)\times4=32-16\pi$(平方厘米);半圆的半径为$4$,周长为$2\pi r=8\pi$(厘米),面积为$\pi r^2=16\pi$(平方厘米)。
小学六年级求阴影部分面积试题和答案

解:将两个同样的图形拼在一起成为 圆减等腰直角三角形
[π ÷4- ×5×5]÷2
=( π- )÷2=3.5625平方厘米
解法二:补上两个空白为一个完整的圆.
所以阴影部分面积为一个圆减去一个叶形,叶形面积为:π( )÷2-4×4=8π-16
所以阴影部分的面积为:π( )-8π+16=41.12平方厘米
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?
解:把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,
所以面积为:2×2=4平方厘米
例22.如图,正方形边长为8厘米,求阴影部分的面积。
解法一:将左边上面一块移至右边上面,补上空白,则左 边为一三角形,右边一个半圆.
阴影部分为一个三角形和一个半圆面积之和. π( )÷2+4×4=8π+16=41.12平方厘米
求阴影部分面积
例1.求阴影部分的面积。(单位:厘米)
解:这是最基本的方法: 圆面积减去等腰直角三角形的面积,
× -2×1=1.14(平方厘米)
例2.正方形面积是7平方厘米,求阴影部分的面积。(单位:厘米)
解:这也是一种最基本的方法用正方形的面积减去 圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以 =7,
例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米。求阴影部分的面积。
解:三角形DCE的面积为: ×4×10=20平方厘米
梯形ABCD的面积为: (4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,阴影部分可补成 圆ABE的面积,其面积为:
六年级奥数图形难题
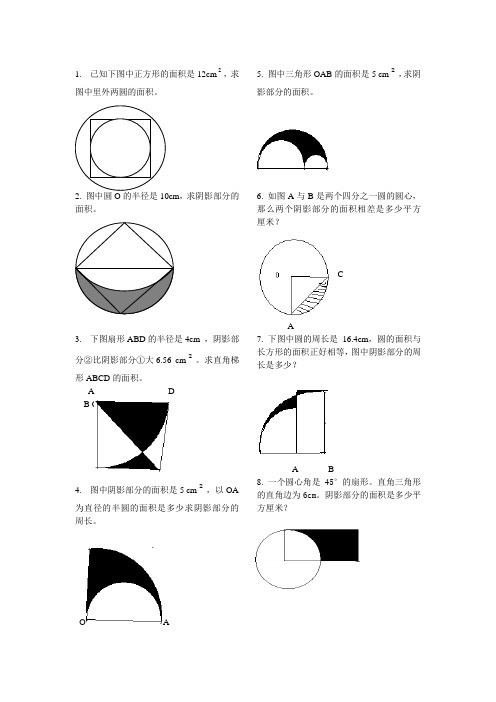
1.已知下图中正方形的面积是12cm2,求图中里外两圆的面积。
2. 图中圆O的半径是10cm,求阴影部分的面积。
3.下图扇形ABD的半径是4cm ,阴影部分②比阴影部分①大6.56 cm2。
求直角梯形ABCD的面积。
A DB C4.图中阴影部分的面积是5 cm2,以OA为直径的半圆的面积是多少求阴影部分的周长。
O A 5. 图中三角形OAB的面积是5 cm2,求阴影部分的面积。
6. 如图A与B是两个四分之一圆的圆心,那么两个阴影部分的面积相差是多少平方厘米?CA7. 下图中圆的周长是16.4cm,圆的面积与长方形的面积正好相等,图中阴影部分的周长是多少?A B8. 一个圆心角是45°的扇形。
直角三角形的直角边为6cm。
阴影部分的面积是多少平方厘米?9. 如图,P是等边三角形ABC的任意一点。
PD垂直于BC,PF垂直于AB,PE垂直于AC 已知三角形ABC的面积是2003cm2,三角形PBD的面积是284 cm2,求三角形APF和三角形PCE的面积之和。
10. 如图,边长为10cm的正方形ABCD中有一个最大的圆,E是CD的中点,求图中阴影部分的面积?11. 如图,正方形ABCD的边长是4cm,E、F 分别是BC、AD的中点,P是正方形内任意一点,求阴影部分的面积?12. 如图三角形ABC的面积是120 cm2,6AF =5AB,AC=4AD,BC=5CE.求三角形DEF的面积。
13. 如图在三角形ABC中,DC=3BD,AE=ED,若三角形ABC的面积是1,求阴影部分的面积。
14.如图,AB是AD的3倍,AC是AE的5倍,那么三角形ABC的面积是三角形ADE面积的多少倍?15. 如图,两个长方形叠放在一起,小长方形的宽是2米,点A是大长方形的一边的中点,求图中阴影部分的总面积。
16. 如图,梯形ABCD的上底AD为1cm,高CD为2.5cm,求梯形ABCD的面积。
17. 如图,已知长方形ADEF的面积是16,三角形ADB的面积为3,三角形ACF的面积是4,求三角形ABC的面积是多少?。
(完整版)小学六年级阴影部分面积专题复习典型例题(含答案)
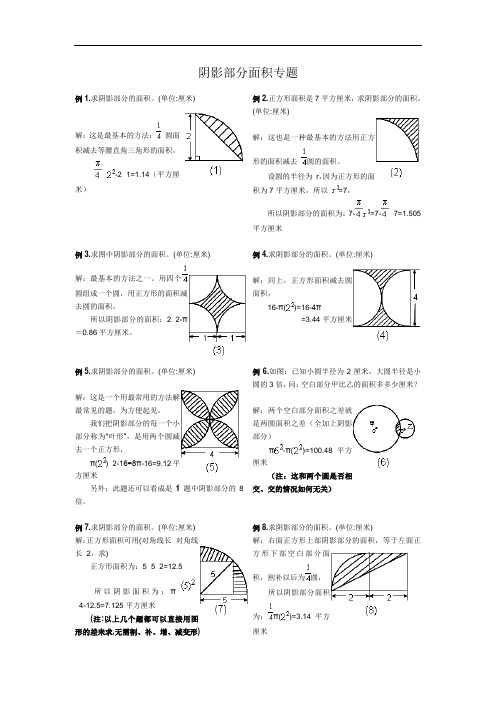
阴影部分面积专题例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六年级奥术数学求阴影部分面积_超难题

求阴影部分的面(奥数)1、求下图中阴影部分的面积。
2、下图两个正方形的边长分别是8厘米和10厘米,求阴影部分的面积。
3、下图中半圆直径为9厘米,求阴影部分的面积。
4、下图中长方形的长为10宽为4,求阴影部分的面积。
(单位:分米)
5、下图中等腰直角三角形的腰长为8厘米,求阴影部分的面积。
6、如下图扇形圆心角为90度,半径为8厘米,扇形内有一个正方形,求阴影部分的面积。
7、等腰直角三角形斜边长10厘米,求阴影部分的面积。
8、平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角
形EFG的面积大10平方厘米。
求CF的长。
小学六年级 阴影部分面积 专题复习 典型例题(含答案)

小学六年级阴影部分面积专题复习典型例题(含答案)work Information Technology Company.2020YEAR阴影部分面积专题例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米) 解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
