连续体力学课件
合集下载
第五章连续体力学

l2
O
dM
r d
f
2mg
l2
r
2
d
r
r
dr
0
f
(选z方向为正)
dM
M 0
dM
M
l 0
2mg
l2
r
2
d
r
2 mgl
3
3)由角动量原理:
t
0 M d t J J0
则
2 3
mglt
0
1 2
ml
20
t 3l0 4g
作业:5 – 1, 5--5, 5--7
§5-3 刚体的定轴转动定律
对于作定轴转动的刚体,满足:
第五章 连续体力学
连续体包括刚体、弹性固体、流体(液体和气体) 本章重点介绍刚体的力学规律。
§5-1 刚体运动学
一、刚体的平动与转动: 1、刚体 ─ 受力时形状和大小完全不变的的物体为刚体。刚体 上的任两点间的距离 始终保持不变。刚体是一种理想模型。
2、平动 ─ 刚体上任意两点的连线在运动中保持平行,这种 运动称为刚体的平动。
mi Rivi
zLioLiz来自Lzori
mi
o Ri
均匀细棒对OZ轴的角动量:
Lz mivi Ri cos miviri
miri2 ( miri2)
Lz J
定义:刚体转动惯量: J miri2
2、转动惯量的计算: 若质量离散分布:(质点,质点系)
J= miri2
i
若质量连续分布:
线速度与角速度之间的矢量关系为:
v
r
o r
v
[例1]一半径为R = 0.1m的砂轮作定轴转动,其角位置随时间t 的
高中物理奥林匹克竞赛专题连续体力学(共张)课件

能量守恒定理
系统的能量在变形过程中 保持不变。
动量守恒定理
系统的动量在变形过程中 保持不变。
弹性力学在连续体力学中的应用
弹性力学在材料力学中的应用
通过弹性力学可以研究材料的应力分布、应变分布等,从而为材料的设计和优 化提供依据。
弹性力学在结构力学中的应用
通过弹性力学可以研究结构的稳定性、振动等,从而为结构的设计和优化提供 依据。
连续体力学中的基本概念
要点一
总结词
连续体力学中的基本概念包括应力、应变、应力和应变关 系等。
要点二
详细描述
应力是指单位面积上的力,用于描述物质系统内部的作用 力。应变则是指物质系统的变形量或位移量,用于描述物 质系统的形变。应力和应变之间的关系可以通过本构方程 来描述,不同的物质材料具有不同的本构方程。这些基本 概念是描述物质系统形变和运动规律的基础,对于理解物 质系统的力学行为和解决实际问题具有重要的意义。
03
弹性力学
弹性力学基础
1 2
弹性力学定义
弹性力学是研究物体在弹性范围内变形和应力的 学科。
弹性力学的基本假设
连续性、均匀性、各向同性、小变形假设。
3
弹性力学的基本量
位移、应变、应力等。
弹性力学中的基本定理
01
02
03
胡克定律
在弹性范围内,物体的应 力和应变之间成正比,即 应力=弹性模量×应变。
高中物理奥林匹 克竞赛专题连续 体力学课件
目录
• 连续体力学基础 • 流体动力学 • 弹性力学 • 专题研究 • 习题与解答
01
连续体力学基础
连续体的定义与分类
总结词
连续体的定义是指物质在空间上连续分布的一种模型,没有明显的边界。连续体可以分为可变形连续体和不可变 形连续体。
第一章 连续体力学

(5)液晶态:在一定温度下,晶体变成清亮透明的液态。
特点:1)力学性质象液体。 2)光学性质象晶体。
4
二、应变与应力
1、应变:物体在外力作用下发生的相对形变。
5
2、两种基本形变: 拉伸压缩:在外力牵引或压缩下发生长度的变化。 剪切形变:在外力偶作用下,两个平行截面间发生 相对平移,只有形状变化而没有体积变化的形变。
p 1.46 10 ,46 10 ,46 10 pa 1. 1.
4 5 6
38
应用:毛细现象 Capillary
浸润液体在细管里上升和不浸润液体在细管里 下降的现象,称为毛细现象
管内液面上升的高度
2 cos h gr
39
【例4】汞对玻璃表面完全部润湿,若将直径为0.100mm的 玻璃毛细管插入大量汞中,试求管内汞面的相对位置。已 知汞的密度1.35×10-4Kg.m-3,表面张力0.520N.m-1。 解:完全不润湿时,cosθ=-1,
32
四、弯曲液面两侧压强差
33
1 、浸润与不浸润
接触角:在液体与 固体接触处,作液 体表面的切线与固 体表面的切线,这 两条切线通过液体 内部所成的角度θ 称为“接触角”。
/2 /2
液体润湿固体
液体不润湿固体
0
完全润湿
完全不润湿
34
2、拉普拉斯公式(掌握)
凸球形液面内外压强差
2 2 0.520 10 2 h 1.35 10 4 9.8 0.05 10 3 cm gR h -15.7cm
40
毛细现象的例子
下雨后,人走过潮湿的泥地,在地面上留下的脚 印里会渗出水来 建房子时在地基上铺防潮毡 画国画,毛笔由于有毛细管可吸较多墨汁,宣纸 由于毛细管的作用能使墨汁迅速散布开来
第四章连续体

u x, t ( A sin
'
a
x B cos
'
a
x) sin t
u 0, t B sin t 0
'
' sin t B 由于 不恒为零,故定有 0
u l , t A sin
'
a
l sin t
T '' T 0
U
''
a
2
U 0
只有 为负数才能确定振动运动,所以不妨设为
2 ,这样有
T T 0
'' 2
U U 0 a
''
2
T t C sin t
U x Asin x B cos x a a
则有
u x, t T t U x
' ' A sin x B cos x sin t a a
' ' A , B , , 为待定常数,由边界条件和初始条 这里
件确定。 其中 U x 相当于在 x 处截面(质点)的振动的 振幅,则 U x 也称振型函数。
对于等截面的杆,由同种材料构成的
A x A
, x
u u A 2 EA 2 t x
2 2
2 2u E 2u u 2 a 2 2 t x x 2
该方程为一维波动方程, a 为纵波在杆内的传播速 度。方程可用分离变量的方法求解
u x, t U x T t
《大学基础物理学》农科用教材自作ppt课件-01连续体力学

海 纳 百 川 大
无规则对称的外形,加热熔化时也没有确 定的熔点,在微观上分子排列无序(或近程有 序),这类固体称非晶体。 非晶体有许多类型,玻璃体、弹性体和塑 性体是其中最主要的类型。生物材料大多属于 非晶体。
道 致 远
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
大 道 致 远
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
二、 应变与应力
海 纳 百 川
1. 应变(strain)
在外力作用下,固体要产生形变。固体的形 变包括拉伸压缩、剪切、扭转和弯曲四种。在四 种形变中,拉伸压缩和剪切为基本形变,扭转和 弯曲可视为前两种形变的组合。
第一章 连续体力学(Mechanics of continuous medium)
(b)多晶体(Ploycrystal):由大量晶粒组成的晶体。 如:金属、岩石等。
海 纳 百 川 大 道 致 远
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
趣闻:千姿百态的水结晶
海 纳 百 川
大 道 致 远
图描绘了Be2O3晶体和 Be2O3玻璃的内部结构。 由图可以看出,两者间具有显著的不同,组成 Be2O3晶体的粒子在空间的排列具有周期性,是 长程有序的。
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
2. 非晶体(amorphous)
作业 练习题1-2
海 纳 百 川 大 道 致 远
海 南 大 学
§1.2 静止液体的力学性质
无规则对称的外形,加热熔化时也没有确 定的熔点,在微观上分子排列无序(或近程有 序),这类固体称非晶体。 非晶体有许多类型,玻璃体、弹性体和塑 性体是其中最主要的类型。生物材料大多属于 非晶体。
道 致 远
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
大 道 致 远
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
二、 应变与应力
海 纳 百 川
1. 应变(strain)
在外力作用下,固体要产生形变。固体的形 变包括拉伸压缩、剪切、扭转和弯曲四种。在四 种形变中,拉伸压缩和剪切为基本形变,扭转和 弯曲可视为前两种形变的组合。
第一章 连续体力学(Mechanics of continuous medium)
(b)多晶体(Ploycrystal):由大量晶粒组成的晶体。 如:金属、岩石等。
海 纳 百 川 大 道 致 远
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
趣闻:千姿百态的水结晶
海 纳 百 川
大 道 致 远
图描绘了Be2O3晶体和 Be2O3玻璃的内部结构。 由图可以看出,两者间具有显著的不同,组成 Be2O3晶体的粒子在空间的排列具有周期性,是 长程有序的。
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
2. 非晶体(amorphous)
作业 练习题1-2
海 纳 百 川 大 道 致 远
海 南 大 学
§1.2 静止液体的力学性质
第五章连续体力学共45页
四、 刚体的角动量原理
刚体→质点系(由无限多个质元构成的连续体)
质点系的角动量原理
M外
dL dt
即L , tt1 2M 外 dt
同样适用于刚体
五. 刚体的角动量守恒定律
若 M 外 0, L 则 J 常矢量
注意: (1)定轴转动时,M外=0时,J=常量,即刚体保持静止或匀
角速转动。
解:设面密度为σ 取半径为r 宽为dr 的薄圆环,
R O r dr
d m d s 2 rdr
Jr2 d m R r2 2 r2 d r 1 R 4 1 m 2R
0
2
2
(适用圆柱对轴线的转动惯量。)
[例3] 求长为L、质量为m的均匀细棒对图中不同轴的转动惯量。
解:取如图坐标,dm=dx
1. 作用于刚体的力对空间某点A的力矩
M Ar AF
2. 作用于刚体的力对转轴的力矩
z
A
rAF z
(1)力在转动平面内。
M Zr F
o r
大 小 M Zr: F sin
M z有两个方向,Mz有正负
(2)力不在转动平面内。
M Zr F 面
Fz 平行于转轴,对转轴产生的的力矩为零。
F
Ft
(2) Fi 0 不等价 Mi 0
F面
Fn
3. 当有n 个力作用于刚体,则
M zM 1zM 2z M nz
即定轴转动的刚体所受到的对转轴的合力矩应等于各
力对转轴的力矩的代数和。
z
4. 刚体中内力对给定转轴的力矩的 矢量和等于零,只需考虑外力矩 的作用。
O
d rr21
1 f21
f121 2
2
总结
《大学物理学》习岗主编农科教材课件pdf-01连续体力学
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
海 纳 百 川
应变是描述固体形变程度的 物理量,它是指物体在外力 作用下发生的相对形变。 拉伸应变
l0
l
大 道
Δl ε= l0
x d
致 远
剪切应变
体应变
x γ = d ΔV θ= V
海 南 大 学
γ
第一章 连续体力学(Mechanics of continuous medium)
海 大 纳 道 百 致 川 远
听到对美充满深深祈望的 莫扎特的《第40号交响 曲》的水,其结晶也竭尽 全力展现出一种华丽的美.
听到恶毒咒语的水结 晶显得杂乱而丑陋
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
(2)微观上分子呈有序排列(远程有序),
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
(1)宏观上具有规则对称的外形
海 纳 道 百 致 川 远
(a)单晶体(monocrystal):规则外形且各向异 性的单个大晶体。如水晶、金刚石、石英等。
大
水 晶
巴西蓝色黄宝石晶体
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
海 大 纳 道 百 致 川 远
听到美好祝词的 水结晶
听了贝多芬田园交响曲的水 呈现的结晶就像明快、清爽 的曲子一样美丽而工整
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
海 纳 百 川
应变是描述固体形变程度的 物理量,它是指物体在外力 作用下发生的相对形变。 拉伸应变
l0
l
大 道
Δl ε= l0
x d
致 远
剪切应变
体应变
x γ = d ΔV θ= V
海 南 大 学
γ
第一章 连续体力学(Mechanics of continuous medium)
海 大 纳 道 百 致 川 远
听到对美充满深深祈望的 莫扎特的《第40号交响 曲》的水,其结晶也竭尽 全力展现出一种华丽的美.
听到恶毒咒语的水结 晶显得杂乱而丑陋
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
(2)微观上分子呈有序排列(远程有序),
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
(1)宏观上具有规则对称的外形
海 纳 道 百 致 川 远
(a)单晶体(monocrystal):规则外形且各向异 性的单个大晶体。如水晶、金刚石、石英等。
大
水 晶
巴西蓝色黄宝石晶体
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
海 南 大 学
第一章 连续体力学(Mechanics of continuous medium)
海 大 纳 道 百 致 川 远
听到美好祝词的 水结晶
听了贝多芬田园交响曲的水 呈现的结晶就像明快、清爽 的曲子一样美丽而工整
海 南 大 学
Chap1连续体力学3_理想液体的流动性和粘滞流体的流动
( p2 p1 ) 0 dv R 2l rdr
v r
rR
v0
p1 p2 2 2 v R r 4ηl
p1 p2 2 2 v R r 4ηl
讨论
最大流速: p1 p2 2 R 当 r 0 时,得 v m
4ηl
2、泊肃叶流量公式
dqv vdS v 2rdr
解:设 S1 4m 2 , S2 10cm2 ,V2 2m / s
由连续性原理有 S1V1 S2V2 ,代入数据,得
V1 5 104 m / s
三、伯努利方程(Bernoulli’s equation)
1、伯努利方程是流体动力学的基本规律之一,它说 明了理想流体在管道中作稳定流动时,同一流线上各 点的压强p、流速v和高度h三者之间的关系。
v v 2 gh
2 B 2 A
S Av A S B v B
vB
2 2 ghS A 2 2 S A SB
qV S B v B S B S A
2 gh 2 2 S A SB
(3)从虹吸管管口吸出的液体速度
1 2 1 2 p A v A ghA pB v B ghB 2 2
对于一般的圆形 管道流,Re约为 2000~2600。
①层流或湍流的判据 ②流体相似律:两种流动的边界状况或边界条件相似 且具有相同的雷诺数,则流体具有相同的动力学特征。
雷诺数(Reynold number)
讨论
v D Re
液体的流动状态可以通过雷诺数来表征
通过雷诺数可以得到流体相似率(The similar law of fluid)
2、伯努利方程的推导过程 a、研究对象:取一段细流管,研究经过 t 时间流 体微团自ab运动到a’b’过程中的功能关系 b、受力分析:F1 p1 S1 c、应用功能原理:
工程物理 第三章连续体力学
在(SI)中,J 的单位:kgm2 质量为线分布 dm dl 其中、、分 别为质量的线密 质量为面分布 dm ds 度、面密度和体 质量为体分布 dm dV 密度。
线分布
面分布
体分布
注 意
只有对于几何形状规则、质量连续且均匀分布 的刚体,才能用积分计算出刚体的转动惯量
例 1、求质量为m、半径为R的均匀圆环的转动 惯量。轴与圆环平面垂直并通过圆心。
A
A
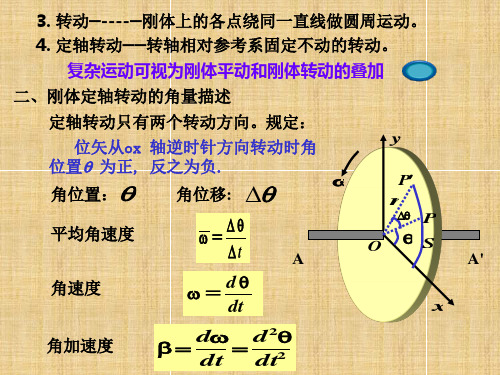
二、定轴转动的角量描述
P P X
参考 方向
X X
Q
参考平面
转轴
各质元的线速度、加速度一般不同, 但角量(角位移、角速度、角加速度)都相同。
描述刚体整体的运动用角量最方便。
常规定:逆时针方向为正。
刚体运动学中所用的角量关系: d d 2 d dt dt 2 dt 定轴转动角速度方向规定为沿轴 方向,指向用右手螺旋法则确定。 只有两个方向,用标量处理。
1 J dJ 2lr dr R 4 l 0 2 m 1 J mR 2 R 2 l 2
R 3
R
可见,转动惯量与l无关。所以,实心圆柱对 其轴的转动惯量也是mR2/2。
例3、求长为L、质量为m的均匀细棒对图中不 同轴的转动惯量。 解:取如图坐标,dm=dx λ=m / L
则角动量定理表示为
其中
M M i | ri Fi |
i i
dL M dt
L mi ri mi ri
2 i i
2
再定义转动惯量
J mi ri
i
2
则
d L J, M J dt
M=Jα 与 F ma 地位相当 =
第五章 连续体力学2
N
N为材料的剪切模量。
理论上还可推出杨氏模量Y、剪切模量N和泊松系数 μ之间的关系: Y N 2(1 ) 3、剪切形变的势能
用类似的方法可得出发生剪切形变的弹性势能密度
1 E N 2 2
0 P
三、弯曲和扭转形变
1、梁的弯曲 水平横梁都会在自身重力和两端 支持力作用下发生弯曲。可认为 梁的上半部受压缩而下半部受拉 伸,越靠边缘形变越大。
二、流线和流管 在有流体的空间中每点都有一个流速矢量v(x,y,z),它 们构成一个流速场。为直观地描述流体的运动状况, 在流速场中画出许多曲线,其上每一点的切线方向就 是该点的流速方向,这种曲线称为流线。任意两条流 线都不会相交。 假想在流体内由一些流线所围成的管子,叫做流管。 流管可粗可细,由于流线不会相交,流管内、外的流 体都不会穿越管壁,就象真有管子在流体内一样。
公元前3世纪希腊的阿基米德提出: 物体在流体中所受的浮力等于该物 体排开同体积流体的重量。
五.液体的表面现象
1.液体的表面张力 液体的表面像一张绷紧的弹性薄膜, 有收缩的趋势,在液体的表面层上 存在着一种沿着液体表面的应力— —表面张力。为研究液体表面张力 的大小,我们在液体表面上划一条 假想的线元Δl,把液面分割为两部 分,表面张力就是这两部分液面相 互之间的拉力。
5-1 固体的弹性
一、拉伸压缩形变 1、正应力与应变 以一个被拉伸(压缩)的直杆为例,此时杆 内各处张力Fn 均与横截面S相垂直,定义作 用在S面上的正应力: F
F Fn S
n
S
b
0
F
σ>0时为拉伸应力, σ<0时为压缩应力。 设一杆被拉伸发生形变如图所示,定义 纵向应变:
l l0 l l0 l0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、液体的表面张力(surface tension)
雨后初晴的礼物
液体的表面张力的成因解释
1、分子力
当分子间距离略大于平衡距离r0时, 分子力表现为引力( 108 m)
2、液体表面状况
汽化层 液体表面层
液体内部
表面层液体分子间距比液体内部 分子间距大,分子之间呈现引力
定义
f
存在于液体表面;由分子间的吸引 力引起的;使液体表面具有自发收 缩趋势的力称液体的表面张力;方 向沿着液面的切线方向。
Ⅱ、球形液面附加压强
如图球形液面上的一小 液面,在周界上取一线 元dl,作用在dl上的表面 张力 df dl
球 冠
df j dl r
//
c
R
df
df
^
R
j
o
df力的方向垂直dl且与球面相切。将df分解 为与半径r垂直和平行的两个分力 df 与 df
^
//
df df cos j dl cos j df df sin j dl sin j
R O
CB A
2 2 PC R R
4 PC PA R
膜内压强大于膜外压强,并与半径成反比。
【例2】一个肥皂泡的直径为圆形水珠的
二倍,设肥皂泡的 是水的三倍,求水滴 和肥皂泡的内外压强差之比。
【解】
P水 2 水 / R水 P肥 4 肥 / R肥
水 R肥 1 1 2 2 肥 R水 2 3
本章主要研究液体的表面性质、液体的流动性质和黏滞 性质,这些性质无疑对农业和生物学是非常重要的。
§1.2 静止液体的力学性质
一、液体的压强
压强(液体的正应力):经过某点的任一假想面 元上正压力与该面元面积之比在面元趋近于零时 的极限。 f f p lim p S 0 S S 液体中压强与面元ΔS的取向无关,即各向同性 ( isotropy)
P 内P 外?
p内-p外=2 /R
p内-p外=-2 /R
[例1]一个膜厚度很薄的圆形肥皂泡,假定泡内外均为 空气,泡内外的压强差为多少?
Ⅲ.球形液膜内、外压强差
如图,由于球形液膜很薄,内外 膜半径近似相等,设A、B、C 三 点压强分别为PA 、PB 、PC ,则:
PB PA PA 2 R PB PC 2 R
2r f^ R
附加压强
2
f ^ 2r 2 ps 2 2 r Rr R
2
——拉普拉斯球公式 球形液面附加压强与表面张力系数成正比,与球面半径R 成反比。半径越小,附加压强越大;半径越大,附加压强 越小;半径无限大时,附加压强等于零,这正是水平液面 的情况。
2 凸液面:p p0 R 2 凹液面:p p0 R
dS dS 表面张力系数在数值上等于增加单位液体表面积时,外力所 需做的功,或增加单位液体表面积时,表面能的增加。
dW Fdx 2ldx dS
【例1】 把一个半径为5cm的金属细圆环从液体中拉出,圆
环所在平面与液体表面平行。已知,刚拉出圆环时需用力 28.3×10-3N。若忽略圆环的重力,该液体的表面张力系数为 多少? 解: 作用在圆环上的液体表面张力为
第一章 连续体力学
(Mechanics of continuous medium)
引 言
连续体力学又称连续介质力学,包括固体的弹 性力学和流体力学。连续体的共同特点是其内部质 点之间可以有相对运动。处理连续体的办法是不再 把它看成一个个离散的质点,而是取“质元”,即 有质量的体积元。
连续介质假设
四、润湿与不润湿
液滴单独存在时由于表面张力的作用,表面总是凸起。 但是当液体与固体接触时可能表现出不同的表面现象, 由分子力不对称引起。
1. 定义
润湿: 液体沿固体表面 延展的现象,称液体润 湿固体。 不润湿:液体在固体表 面上收缩的现象,称液 体不润湿固体。
润湿、不润湿与相互接触的液体、固体的性质有关。 水——玻璃:润湿 水——石蜡:不润湿
1 3
例3 RA RB PSA PSB 空气由 A B
RA 、RB
膜内压强大于膜外压强,并 与半径成反比,与表面张力 系数成正比。
A
B
体积较大的肺泡表面积↑,表面活性剂的浓度↓, 肺泡的表面张力系数↑,产生的附加压强↑,对 抗由于半径增加对附加压强的减小;体积较小 的肺泡表面积↓,表面活性剂的浓度↑,肺泡的 表面张力系数↓,同理。
// ^
由圆对称性,在圆周界上 的其他线元上,作用着同 样大小的表面张力,这些 力的水平分力相互抵消, 垂直分力方向相同,合力 为:
//
j
dl df
^
r
c
df
R
j
o
f ^ df ^
2r 0
sin jdl sin j 2r
2
r 2r 由于 sin j , 则f ^ R R
(8 4 r 4 R ) 4 (8r R ) 1 4 4 3 3 r R R 8 r 2 3 3
dW 4 R
2
讨论
2. 测量表面张力系数的实验方法
拉脱法
液滴法
3. 影响表面张力系数的因素(Factors ) 液体种类(varieties of liquid) 温度(temperature) 温度越高,表面张力系数越小 表面活性物质(surface activator)
三、拉普拉斯公式(Laplace formula)
由于表面张力的存在,弯 曲液面内外(inside and outside)的压强不等,其压 强差服从拉普拉斯公式:
pout
pin
pin pout
2 R
R
拉普拉斯方程的推导:
Ⅰ:附加压强的产生1.液面弯曲P 01)凸液面时,如图 s 周界 上表面张力沿切线方向,合 力指向液面内, s 好象紧 压在液体上,使液体受一附 加压强 ps ,由力平衡条件, 液面下液体的压强:
p x p y p z pn
对于液体中的任一点,来自任何方向 的压强均相同。
液体压强的各向同性( isotropy)
等高的地方压强相等
p A pB
液体压强随高度的变化
h A
p A p0 gh
等高各点压强相等
在流体中取一柱状体元,在水平方向 应用平衡方程 pAS pB S , pA pB 表明:流体内等高各点压强相等, 即等压面与竖直方向垂直
f 2 2R
由题
f 28.3 103 N/m
28.3 10 3 3 4 . 5 10 N/m 2 4 5 10
4R 28.3 103
【例2】将一个半径为 R 的球型液珠
分散成 8 个半径相同的小液滴需作功多少? (设表面张力系数为) dW 【解】 dW dS dS2 2 2 2
在化妆品行业中,乳化剂是乳霜、乳液、洁面、 卸妆等护肤产品中不可或缺的成分。
表面张力的例子
a. 水面上的爬虫能不落入水中 b.把一根缝衣针放在一张薄餐巾纸上,用纸托 住缝衣针轻轻地放在水面上,纸被水浸透后 沉入水底,而缝衣针会浮在水面上。 c.在杯中装满水(注意杯口的外沿必须干燥),放在 桌上。将干净的分币轻轻地从水面投下,要求尽 量减少水面的扰动。随着投入的分币数增多,水 面会明显超出杯口,但水不溢出来。 d.雨伞的伞面织物都有细小的孔,下雨天 用撑开的 伞遮雨,雨水不会从小孔中漏下来
dF_ α
H dh
h
dl
α
dF
解:如图所示,取长为L,宽为dl的狭长面元,该 面元受力dF=ρghLdl,方向垂直该面元 dF在水平方向的分力: dF ghLdl sin gLhdh
2 坝受水平推力 F gL hdh 1 gLH 2 0 3 2 7 1 1 . 0 10 9 . 8 1088 5 13 . 3 10 N 2 H
p1 y1
如有自由表面,令p2=p0,p1=p,则 p = p0+ρgh
例题1、在密度为 的液体中竖直放置一个长为a,宽 为b的长方形平板,板的上边与水面相齐,求此板面所 受液体压力的大小(不考虑大气压的影响)
例2:已知坝长L=1088m, 水深H=5m,不计大气压, 求水对坝的水平推力
0 dF
A PAΔS y w z B PBΔS
(p+dp)ΔS dy pΔS
压强沿竖直方向的分布
取一高为dy的柱状体元,在竖直方向 应用平衡条件:
x dp pS ( p dp)S g Sdy 0, dp gdy, g , 设ρ,g与y无关, dy p2 y2 dp g dy , p2 p1 g ( y2 y1 ) gh, p1 p2 gh
表面活性剂的作用
I. 润湿作用
可湿性粉剂中原药多为有机化合物,具有憎水性,只有在表面活性剂存 在的条件下,降低水的表面张力,药粒才有可能被水所润湿,形成水悬 液; 在粒剂及供喷粉用的粉剂中,有的也含有一定量的表面活性剂,其目的 是为了提高药剂在受药表面的附着性和沉积量,提高有效成分在有水分 条件下的释放速度和扩展面积,提高防病、治病效果。
液体表面张力服从以 下基本规律:
l
f l
称表面张力系数( coefficient of surface tension), 1 其单位是 N m
讨论
1. 表面张力系数的物理意义(physical significance ) 力的属性(property of force) 作用在液体表面单位长 度直线上的表面张力 能的属性(property of energy) 增加单位液体表面积时所增加的表面能
