数字信号处理第三章-FFT
数字信号处理FFT

数字信号处理FFT数字信号处理中的FFT算法数字信号处理(Digital Signal Processing, DSP)是一门研究如何以数字方式对信号进行处理和分析的学科。
其中,FFT(Fast Fourier Transform)算法是数字信号处理中最为重要和常用的算法之一。
本文将介绍FFT算法的原理、应用以及一些常见的优化方法。
一、FFT算法原理FFT算法是一种高效地计算离散傅里叶变换(Discrete Fourier Transform, DFT)的方法。
DFT是将一个离散信号从时域(time domain)变换到频域(frequency domain)的过程。
在频域中,我们可以分析信号的频率成分和振幅,从而得到信号的频谱图。
FFT算法的原理是利用对称性和重复计算的方式,将一个需要O(N^2)次乘法运算的DFT计算降低到O(N*logN)的时间复杂度。
通过将N个点的DFT分解成多个规模较小的DFT计算,最终得到原始信号的频域表示。
二、FFT算法应用FFT算法在信号处理领域有着广泛的应用,其中包括但不限于以下几个方面:1. 信号的频谱分析:通过FFT算法,可以将时域信号转化为频域信号,进而分析信号的频率成分和振幅,为后续的信号处理提供依据。
例如,在音频处理中,我们可以通过FFT算法分析音频信号的频谱,用于音乐合成、音频降噪等应用。
2. 图像处理:图像信号也可以看作是一种二维信号,通过对图像的行、列分别进行FFT变换,可以得到图像的频域表示。
在图像处理中,FFT算法被广泛应用于图像增强、滤波、压缩等方面。
3. 通信系统:FFT算法在OFDM(正交频分复用)等通信系统中被广泛应用。
在OFDM系统中,多个子载波信号通过FFT变换合并在一起,实现信号的同时传输和接收。
4. 音频、视频压缩:在音频、视频等信号的压缩算法中,FFT算法也扮演着重要的角色。
通过对音频、视频信号进行频域分析,可以找到信号中能量较小的部分,并将其抛弃从而达到压缩的效果。
数字信号处理课后答案+第3章DFT+FFT

ej(02N πk)(N21)sin( 02N πk)N 2 sin(02N πk)/2
k0,1, ,N1
或
1ej0N X7(k)1ej(02 N k)
(8) 解法一 直接计算:
k0,1, ,N1
x 8 (n ) si0 n n )R (N (n ) 2 1 j[ej 0 n e j 0 n ]R N (n )
即 X 8 (k ) jX 7 o (k ) j1 2 [X 7 (k ) X 7 * (N k )]
结果与解法一所得结果相同。 此题验证了共轭对称性。
(9) 解法一 直接计算:
x9(n )co0 n s )R N ((n )1 2[ej 0 n e j 0 n]
N1
X9(k) x9(n)WNkn
x 7 ( n ) e j 0 n R N ( n ) [c 0 n ) o j ss i 0 n ) ( n R N ] ( n ( )
所以
x 8 (n ) si0 n )R N ( (n ) Im x 7 (n )[ ]
所以 D [ jx 8 ( F n ) D ] T [ j IF x m 7 ( n ) T ] X [ 7 o ] ( k )
(7) x(n)=ejω0nRN(n) (8) x(n)=sin(ω0n)RN(n) (9) x(n)=cos(ω0n)RN(N) (10) x(n)=nRN(n) 解: (1)
X(k)N n011WN knN n01ej2N πkn1 1 ee jj2 2N N π πkkN N
N k0 0 k1,2,,N1
(5)
X (k)
N 1 j 2π mn
eN
W Nkn
N 1 j 2π (mk )n
数字信号处理实验3 FFT算法应用

图 6-2
>> xlabel('n');ylabel('x[n]');
图 6-1
理论分析如下:
由欧拉公式得: x[n] cos(2 7n) 1 cos(2 19n)
N
2N
1
(e
j 2 7n N
e
j 2 ( N 7n) N
1
e
j 2 19n N
1
e
j 2 ( N 19n)
N
)
2
2
2
j 2 kn
对 p[n] e N ,其 2N 点的 DFT 变换为:
2N 1
j 2mn 2N 1 j 2n(2km)
X (k) 。
(2) 已知某序列 x(n) 在单位圆上的 N=64 等分样点的 Z 变换为
X (zk
)
X
(k)
1 1 0.8e j2k / N
,k
0,1,2,...,63
。
_
_
用 N 点 IFFT 程序计算 x(n) IDFT[ X (k)],绘出和 x(n) 。
实验要求:利用 MATLAB 编程完成计算,绘出相应图形。并与理论计算相比较,说明实验结 果的原因。 (1) 用以下代码实现可得图 6-1 所示的 DFT 图。 >> N=64; >> n=0:2*N-1; >> x=cos(2*pi*7*n/N)+1/2*cos(2*pi*19*n/N); >> X=fft(x,128); >> k=n; >> stem(k,abs(X)) >> grid >> xlabel('k');ylabel('|X[k]|');
数字信号处理之离散傅里叶变换

共轭对称性
对于实数输入信号,DFT 的结果X[k]满足共轭对称 性,即X[-k] = X[k]*。
离散傅里叶变换的矩阵表示
DFT可以表示为一个矩阵运算, 即X = W * x,其中X是DFT的输 出,x是输入信号,W是DFT的
权重矩阵。
权重矩阵W是一个复数矩阵,具 有特殊的结构,可以通过快速傅 里叶变换(FFT)算法进行高效
03
其他信号处理方法还包括短时 傅里叶变换、Wigner-Ville分 布等,可根据具体应用场景选 择合适的信号处理方法。
ቤተ መጻሕፍቲ ባይዱ 06
结论
离散傅里叶变换的重要性和应用价值
离散傅里叶变换(DFT)是数字信号处理领域 中的重要工具,它能够将信号从时域转换到频 域,从而揭示信号的频率成分和特征。
DFT在通信、雷达、声呐、图像处理、语音识 别等领域有着广泛的应用,是实现信号分析和 处理的关键技术之一。
图像压缩
通过对图像进行DFT变换,将图像从空间域变换到频域,可以提取出图像的主要频率成分 ,从而实现图像压缩。常见的图像压缩算法有JPEG和JPEG2000等。
05
离散傅里叶变换的局限性和改进方法
离散傅里叶变换的局限性
计算量大
离散傅里叶变换需要进行大量复杂的复数运算,对于大数据量信 号处理效率较低。
方式。
离散傅里叶变换的编程实现
01
编程语言如Python、C等提供了离散傅里叶变换的库函数,可 以直接调用进行计算。
02
编程实现时需要注意数据的输入输出、内存管理、异常处理等
问题,以保证程序的正确性和稳定性。
编程实现离散傅里叶变换时,可以根据实际需求选择不同的库
03
函数和算法,以达到最优的计算效果。
数字信号处理第三章补

在此频谱图中就分辨不出来。
v(n) 6
4
T=1 / fs
2
0
0 0
2 2T
4 4T
6 6T
8 8T t p =1 / F
10 10 T
12 12 T
14 14 T
16 16 T
18
n t
(a) |V(k )| 40 30 20 10 0 0 0 2 2F 4 4F 6 6F F=1 / tp
8 8F fs =1 / T
m 0
M 1
用DFT算法也就是用圆周卷积来代替这一线性卷积时,为了
不产生混叠,其必要条件是使x(n),h(n)都补零值点,补到至少
N=M+L-1, 即:
x(n) x(n) 0
0≤n≤L-1 L≤n≤N-1
h(n) 0≤n≤M-1 h(n ) 0 M≤n≤N-1
然后计算圆周卷积
y (n) x(n)
N
h( n )
这时,y(n)就能代表线性卷积的结果。 用FFT计算y(n)的步骤如下:
① 求N点X(k)=DFT[x(n)], N点;
② 求H(k)=DFT[h(n)], N点;
③ 计算Y(k)=X(k)H(k);
④ 求y(n)=IDFT[Y(k)],N点。
率(单位: Hz)。
由图可知:
t p NT fs 1 1 F N NT t p
在实际应用中, 要根据信号最高频率fh和频谱分辨率F的要求, 来确定T、tp和N的大小。 (1)首先,由采样定理,为保证采样信号不失真,fs≥2fh(fh为 信号频率的最高频率分量,也就是前置低通滤波器阻带的截止 频率), 即应使采样周期T满足
n
《数字信号处理》C3离散傅里叶变换及快速算法

j
n
x(n) z n
M 1 n 0
n x ( n ) z jn
X ( e ) DTFT [ x ( n )]
n
x ( n )e
M 1 n 0
jn ( ) x n e
2 j X ( e ) FT [ x N ( n )] N ( k ) DFS [ x N ( n )] X X ( k ) DFT [ x ( n )]N
n 0
N 1
n
1 n0 N
N 1
X (k )W
k 0
N 1
nk N
n z
1 N 1 N 1 nk n X (k ) WN z N k 0 n 0
N 1 1 N 1 k 1 n X (k ) WN z N k 0 n 0
(n) ak e x
k 0 N 1 j 2 kn N
2 2 T 0 0T NT N
为什么是有限项之和? 如何求系数?
( n )e x
n 0
N 1
j
2 mn N
2 2 j kn j mn ak e N e N n 0 k 0 N 1 N 1
N 1
ak ak lN
周期
3.1 周期序列的傅里叶级数
数字信号处理第三章8 用DFT对模拟信号作频谱分析
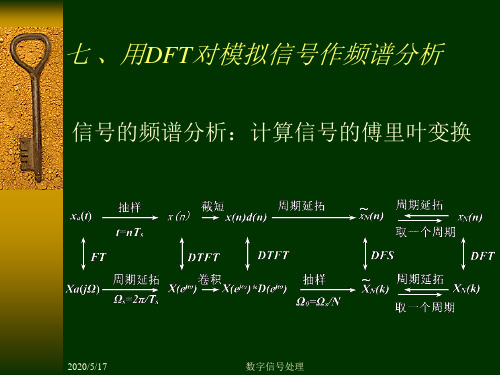
信号最高频率f h的确定
t0 Th / 2
1 1 fh Th 2t0
2013-8-8
数字信号处理
例:有一频谱分析用的FFT处理器,其抽样点数 必须是2的整数幂,假设没有采用任何的数据处理 措施,已给条件为:
1)频率分辨率 10 Hz 2)信号最高频率 4kHz
x(n)为周期序列,周期N 14
抽样点数至少为14点
或者因为频率分量分别为500、 、 600 700Hz
得 F0 100Hz
N f s / F0 1400/100 14
最小记录点数N 14
2013-8-8 数字信号处理
2013-8-8
数字信号处理
T 2 f / f s 2 k / N
2013-8-8
X ( j) T x (nT )e jnT
n 0
数字信号处理
3)频域抽样:一个周期分N段,采样间隔 F0 ,时域周期延拓,
周期为 T0 1/ F0
N-1 n 0 N 1
n 0
0 2 F0
X ( jk 0 ) T x (nT )e jk0nT
试确定以下参量: 1)最小记录长度T0 3)在一个记录中最少点数N
2)抽样点间的最大时间间隔T(即最小抽样频率)
2013-8-8
数字信号处理
解: 1)最小记录长度:
1 1 T0 0.1s F0 10
2)最大抽样间隔 (f s 2 f h
f s 1/ T)
1 1 T 0. ms 125 3 2 f h 2 4 10
2013-8-8 数字信号处理
f fs * k / N
数字信号处理课后第三章习题答案

1 e j 0 N
2 j(0 k ) N 1 e
k 0, 1, , N 1
(8) 解法一
直接计算:
1 j 0 n x8 (n) sin(0 n) RN (n) [e e j 0 n ] R N ( n ) 2j
X 8 (n)
n 0
N 1
kn x8 (n)WN
k 0, 1, , N 1
(4)
X (k ) WNkn
n 0
m1
π j ( m1) k 1 WNkm N e 1 WNk
π sin mk N R (k ) N π sin k N
第3章
离散傅里叶变换(DFT)及其快速算法 (FFT)
所以
DFT[ X (n)] X (n)W
n 0
N 1
N 1
kn N
N 1 mn kn x(m)WN WN n 0 m 0
N 1
n ( m k ) x(m)WN m 0 n 0
N 1
第3章
由于
离散傅里叶变换(DFT)及其快速算法 (FFT)
第3章
离散傅里叶变换(DFT)及其快速算法 (FFT)
(10) 解法一
X (k )
n 0
N 1
kn nWN
k 0, 1, , N 1
上式直接计算较难, 可根据循环移位性质来求解X(k)。 因为x(n)=nRN(n), 所
以
x(n)-x((n-1))NRN(n)+Nδ(n)=RN(n) 等式两边进行DFT, 得到
1 [e j0 n e j0 n ] e 2 j n 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.8.2 用DFT计算有限长序列与无限长序列 的线性卷积
用FFT计算有限长序列与无限长序列的线性卷积 问题: · h(n) 为某滤波器的单位脉冲响应,长度有限
· 输入信号 x(n)很长,h(n) 要补许多零再进行计算, 计算量有很大的浪费
解决方法:
重叠相加法 重叠保留法
重叠相加法: 将x(n)分段,每段长度为L,然后依次计算各段与h(n) 的卷积,再由各段的卷积结果得到y(n)。
3.8
DFT(FFT)应用举例
DFT因为具有快速算法FFT,应用非常广泛,限于篇幅,这里 仅介绍DFT在线性卷积和频谱分析两方面的应用。 本节主要论述:
3.8.1 用DFT(FFT)计算两个有限长序列的线性卷积 3.8.2 用DFT计算有限长序列与无限长序列的线性卷积
返回
3.8.1 用DFT(FFT)计算两个有限长序列的 线性卷积
比较截断前、后的幅度谱的差别: 泄露 定义:原来的离散谱线向两边展宽,这种将谱线展宽的现象称为频谱 泄漏。 约束因素:矩形窗的长度越长,展宽的宽度就越窄。 影响:泄漏会使频谱模糊,谱的分辨率降低。 谱间干扰 出现原因:频谱卷积以后存在着的旁瓣,引起不同频率分量干扰。旁 瓣淹没信号主谱线或者旁瓣误认为另一信号谱线。 影响:降低谱分辨率 泄漏和谱间干扰统称为信号的截断效应。 减轻截断效应的方法---提高谱分析的分辨率及精确性 。 1:增加窗时域的宽度,运算量及存贮量增大 2:其他缓变的窗,比如三角形窗等
例:设x1(n)和x2(n)都是N点的实数序列,试 用一次N点DFT运算来计算它们各自的DFT: DFT [ x1 (n)] X1 (k ) DFT [ x2 (n)] X 2 (k )
解:利用两序列构成一个复序列
w(n) x1 (n) jx2 (n)
则
W (k ) DFT [w(n)] DFT [ x1 (n) jx2 (n)] DFT [ x1 (n)] jDFT [ x2 (n)] X1 (k ) jX 2 (k )
F0 1/ T0 fs / N 提高采样频率不能提高频率分辨率 NT 提高了采样频率,虽然在相同的观察时长那的点数增多了,但与此同时 采样频率也变大了,点数增加几倍采样频率增加几倍,所以不改变观察 时长而仅仅提高采样频率并不能提高DFT谱的频率分辨率。 1
补零并不能提高频率分辨率 补零信号的谱,是通过截短信号的谱进行了推测(插值算法)得来的, 它并不能反映原信号的谱,所以虽然补零信号的谱线间隔变小了,但是 除了从截短信号的谱中取出来的谱线以外,其余的谱线都是无效的。去 掉这些无效的谱线,采样频率不变,有效的谱线数不变,所以其物理频 率分辨率自然没有改变。
公式推导及参数选择
模拟信号进行频谱分析时,有几个重要的参数要选择, 采样频率 Fs 频率分辨率F0 频谱分析范围 采样点N
信号的最高截止频率 能够分辨的两个频率分量最 小的间隔
Fs 2
与对信号的观测时间有关
T 时域采样间隔 f s 时域采样频率 T0 信号记录长度 F0 (频率分辨率)频域采样间隔 N 采样点数 f h 信号最高频率 f s 2 f h f s 1/ T
参数确定
1 (1)由采样定理, f s 2 f h , T 2 fh
(2)由频谱分辨率确定N
fs 1 N , 一般为2的整数次幂 F0 F0T
(3)确定最小记录长度
N 1 T0 =NT = f s F0
x(t ) 0.15sin(2 f1t ) sin(2 f 2t ) 0.1sin(2 f3t ) f1 1Hz, f 2 2 Hz, f3 3Hz; f s 32 Hz x(n) x(nT ) 0.15sin(2 / 32n) sin(2 / 32n) 0.1sin(2 / 32n) 32 64 point DFT F0 = 0.5Hz 64
f s NF0 T0 1/ F0
2 k k NT k fs fk k NT N
T0 NT
T0 f s N T F0
频率响应的混叠失真及参数的选择
时域抽样:f s 2 fh 频域抽样:F0 1/ T0
T0 f s N T F0
信号最高频率与频率分辨率之间的矛盾
由x1 (n) Re[w(n)]得
X1 (k ) DFT [ x1 (n)] DFT {Re[ w(n)]} Wep (k ) 1 [W ((k )) N W * (( N k )) N ]RN (k ) 2
由x2 (n) Im[w(n)]得
1 X 2 (k ) DFT [ x2 (n)] DFT {Im[ w(n)]} Wop (k ) j 1 [W ((k )) N W * (( N k )) N ]RN (k ) 2j
用DFT对模拟信号作频谱分析
信号的频谱分析:计算信号的傅里叶变换
a,b为任意常数 max( Rx , R y ) R z R min( Rx , R y )
a,b为任意常数 max( Rx , R y ) R z R min( Rx , R y )
3)最小记录点数
N fs 1 , 一般为2的整数次幂 F0 F0T
2 f h 2 4 103 N 800 F0 10
取N 2m 210 1024 800
例:有一调幅信号
xa t 1 cos 2 100t cos 2 600t
2)缓慢截短
截断效应 定义:对无限长的模拟信号进行截断而引起的误 差现象称为截断效应。 采样序列 x ( n ) ,对它用长为N的矩形窗进行截断: xN n x n RN n
矩形窗 R cos w0n , w0 4 加矩形窗前、后的幅度谱
用DFT做频谱分析,要求能分辨 xa t 的 所有频率分量,问 (1)抽样频率应为多少赫兹(Hz)? (2)抽样时间间隔应为多少秒(Sec)? (3)抽样点数应为多少点?
解:
xa t 1 cos 2 100t cos 2 600t
cos 2 600t 1 1 cos 2 700t cos 2 500t 2 2
y (n)
i i 0
yi ( n ) 的长度为N=L+M-1。用N点FFT和IFFT计算 yi ( n ) ,再按上式求和, yi (n) h(n) xi (n) 得到。
计算步骤: (1)计算H(k)=DFT[h(n)] ,N=L+M-1,i=0; (2)读入xi ( n ) 并计算 X i (k ) DFT[ xi (n)]N ; (3) Yi (k ) H (k ) X i (k ) ; (4)yi (n) IDFT[Yi (k )]N,n=0, 1, 2, …, N-1; (5) 将各段y (n)(包括重叠部分)相加,y(n)= y (n) i i
| X (k ) |
35
30
25
20
15
10
5
0
0
5
10
15
20
25
30
35
k
| X (k ) |
35
30
25
20
15
10
5
0
0
2
4
6
8
10
12
14
16
Hz
例:有一频谱分析用的FFT处理器,其抽样点数 必须是2的整数幂,假设没有采用任何的数据处理 措施,已给条件为:
1 )频率分辨率 10 Hz 2)信号最高频率 4kHz
试确定以下参量: 1 )最小记录长度T0 3)在一个记录中最少点数N
2)抽样点间的最大时间间隔T(即最小抽样频率)
解: 1)最小记录长度:
1 1 T0 0.1s F0 10
N 1 T0 =NT = f s F0
2)最大抽样间隔 (f s 2 fh
f s 1/ T)
1 1 T 0. ms 125 3 2 f h 2 4 10
(1)抽样频率应为
f s 2 700 1400Hz
(2)抽样时间间隔应为
1 1 T 0.00072Sec 0.72ms f s 1400
(3)因为频率分量分别为500、 、 600 700Hz
得 F0 100Hz
N f s / F0 1400 /100 14
最小记录点数N 14
用DFT(FFT)对周期信号进行谱分析的误差来源
1.频谱混叠 采样频率不满足采样定理 一般模拟信号的频谱函数并不是锐截止的 信号中总含有或多或少的干扰或噪声
f s 2.5 3.0 fh
2 频谱泄漏
对时域截短,使频谱变宽拖尾,称为泄漏
改善方法:
1)增加x(n)长度
3. 栅栏效应 定义:N点DFT(FFT)得到的只是N个采样点上的频谱值,两点之 间的频谱值是不知道的,就好像被栅栏遮住一样 应对策略: 增多DFT(FFT)的变换点数
在信号尾部加零的方法加大DFT(FFT)的变换点数。谱线更密。
频率分辨率
F0 1/ T0
提高频率分辨率方法: 增加信号实际记录长度
T0 f s N T F0
要增加信号最高频率f h 则f s 当N 给定 F0必 ,即分辨率
1 要提高频率分辨率,即F0 则T0 NT F0 当N 给定 则T f s 要不产生混叠,f h必
信号最高频率f h的确定
t0 Th / 2
1 1 fh Th 2t0
假设h(n)和x(n)是因果序列,对x(n)进行分段,每段长为L, 则x(n)可以表示为如下形式:
