电力电子建模与控制仿真作业
电力电子计算机仿真作业

电力电子计算机仿真作业电力电子计算机仿真作业是电力电子学科的重要部分,通过使用计算机仿真软件模拟电力电子系统,可以有效地研究和分析电力电子系统的性能及其控制策略。
下面,我们将通过一个具体的案例来介绍电力电子计算机仿真作业,以及其重要性和应用。
首先,让我们来考虑一个直流-直流变换器的仿真案例。
该案例涉及到一个电源控制器,将直流电源的电压转换为需要的电压。
通过对该系统进行仿真分析,我们可以得到变换器的性能指标和控制策略,进一步优化和改进变换器的设计。
仿真作业一般包括以下几个步骤:1.翻阅相关文献和资料,了解直流-直流变换器的工作原理和控制策略,指定需要仿真的系统结构和参数。
2.在计算机仿真软件中绘制直流-直流变换器的电路拓扑图,配置电路元件的参数和控制信号。
3.进行仿真运行,观察电路的响应特性,并记录关键的性能指标,如输出电压、电流波形、效率等。
4.分析仿真结果,识别系统中可能存在的问题或不足,并提出改进方案。
5.在仿真软件中实施改进方案,并再次进行仿真运行,观察改进后的性能指标。
通过上述步骤,我们可以利用电力电子计算机仿真作业来深入了解和研究直流-直流变换器的工作原理和性能特点,以及改进控制策略的方法。
此外,电力电子计算机仿真作业还可以应用于其他电力电子系统的设计和优化,如交流-直流变换器、交流-交流变换器等。
1.提高学生的实践能力:通过电力电子计算机仿真作业,学生可以深入理解电力电子系统的原理和性能,并掌握相关仿真软件的操作方法,提高了实践能力。
2.加深对电力电子系统的理解:通过仿真作业,学生可以观察和分析电力电子系统的运行情况,深入理解其工作原理和控制策略,加深对电力电子学科的理解。
3.探索优化和改进的途径:仿真作业可以帮助学生发现电力电子系统中可能存在的问题或不足,并通过改变参数或控制策略来优化和改进系统的性能,提高系统的效率和稳定性。
总结起来,电力电子计算机仿真作业是电力电子学科中不可或缺的一环。
电力电子系统建模与控制作业

电力电子系统建模与控制作业电力电子系统是指使用电力电子器件进行电能转换和控制的系统。
它广泛应用于电力传输、配电和电能控制等领域。
在电力电子系统的建模与控制方面,有很多不同的方法和技术可供选择,根据具体应用场景和系统要求来确定最合适的建模与控制方案。
电力电子系统的建模是指通过数学模型将实际电力电子系统转化为数学表达式,以便进行分析和控制。
建模的关键是确定系统的状态方程和输出方程,并利用这些方程进行仿真和分析。
建模的方法可以分为物理模型和简化模型两种。
物理模型是根据电力电子器件的物理特性和电路原理来建立的,通常使用较为复杂的微分方程或差分方程描述系统动态特性。
物理模型的优点是可以准确地描述电力电子器件和系统的行为,但缺点是复杂度高、计算量大,对计算机性能要求较高。
简化模型是在物理模型的基础上进行简化和近似处理得到的,通常使用等效电路或传递函数来描述系统的动态特性。
简化模型的优点是具有较低的复杂度和计算量,适合于系统级仿真和控制设计。
缺点是精度相对较低,无法准确地模拟所有的细节和非线性特性。
电力电子系统的控制是指通过调节控制器的输入信号,使系统输出达到所需的目标。
控制的目标可以是稳态操作、动态响应、输出品质等。
在控制设计中,需要根据建模结果选择合适的控制策略和算法,并进行系统参数的调整和优化。
常用的控制策略包括PID控制、模糊控制、神经网络控制、自适应控制等。
PID控制是最常用和经典的控制方法,通过比较系统输出与期望值之间的差异,通过调整控制器的三个参数(比例、积分、微分)来实现系统稳定和响应速度的控制。
模糊控制是一种基于模糊推理的控制方法,适用于复杂和非线性系统。
神经网络控制是利用神经网络的优良特性,进行系统建模和控制设计。
自适应控制是利用系统的自学习和自适应能力,通过不断调整自身参数来实现控制目标。
在实际应用中,根据具体的电力电子系统和控制要求,可以选择不同的建模与控制方案,并结合实时仿真和实验验证进行性能评估和参数调整。
(完整word版)电力电子电路建模与分析大作业

西安理工大学研究生课程论文/研究报告课程名称:电力电子系统建模与分析任课教师:完成日期: 2016 年 7 月 5 日专业:电力电子与电力传动学号:姓名:同组成员:成绩:题目要求某用户需要一直流电源,要求:直流输出24V/200W,输出电压波动及纹波均<1%。
用户有220V交流电网(±10%波动变化)可供使用:(1) 设计电源主电路及其参数;(2) 建立电路数学模型,获得开关变换器传函模型;(3) 设计控制器参数,给出控制补偿器前和补偿后开环传递函数波特图,分析系统的动态和稳态性能;(4)根据设计的控制补偿器参数进行电路仿真,实现电源要求;(5) 讨论建模中忽略或近似因素对数学模型的影响,得出适应性结论(量化性结论:如具体开关频率、具体允许扰动幅值及频率等)。
主要工作本次设计主要负责电源主电路及其参数的的设计,以及建立电路数学模型并获得开关变换器传函模型这两部分内容,具体如下:(1) 本次设计电源主电路及其参数,采用从后向前的逆向设计思想。
首先根据系统输出要求,设计了后级DC/DC型Buck电路的参数。
接着设计了前级不控整流电路以及工频变压器的参数.考虑到主电路启动运行时的安全性,在主电路中加入了软启动电路;(2) 本次DC/DC变换器的建模并没有采用传统的状态空间平均方法,而是采用更为简单、直观的平均开关建模方法,建立了Buck变换器小信号交流模型.最后,推到出了开关变换器的传递函数模型,并给出了Buck电路闭环控制框图。
1 设计主电路及其参数1.1主电路设计根据题目要求,系统为单相交流220V/50Hz 输入,直流24V/200W 输出。
对于小功率单相交流输入的场合,由于二极管不控整流电路简单,可靠性高,产生的高次谐波较少,广泛应用于不间断电源(UPS )、开关电源等场合。
所以初步确定本系统主电路拓扑为:前级AC-DC 电路为电源经变压器降压后的二极管不控整流,后级DC —DC 电路为Buck 斩波电路,其中Buck 电路工作在电感电流连续模式(CCM),前后级之间通过直流母线和直流电容连接在一起。
电力电子系统建模控制与仿真_参考教材参考实例

x&(t) = A1x(t) + B1u(t)
(1)
y(t) = C1x(t) + E1u (t)
(2)
其中:x(t)为状态向量;u(t)为输入向量;A1 和 B1 分别为状态矩阵与输入矩阵; y(t)为输出变量;C1 和 E1 分别为输出矩阵和传递矩阵。
(2)关闭状态,时间为[dTs,Ts]: 可以写出的状态方程为:
{ò ò } = 1 Ts
t +dTs
t +Ts
t [ A1á x(t )ñTs + B1áu(t )ñTs ]dt + t+dTs [ A2 á x(t )ñTs + B2 áu(t )ñTs ]dt
(12)
整理可以得到:
áx&(t)ñTs = [d (t) A1 + d ¢(t) A2 ]áx(t)ñTs + [d (t)B1 + d ¢(t)B2 ]áu(t)ñTs
(13)
这就是 CCM 模式下的平均变量状态方程一般公式,其中 d(t) + d¢(t) = 1 。
用同样的方法可以求得
á y(t)ñTs = [d (t)C1 + d ¢(t)C2 ]á x(t)ñTs + [d (t)E1 + d ¢(t)E2 ]áu(t)ñTs
(14)
分解平均变量为:
状态变量: áx(t)ñTs = X + xˆ(t)
=1 Ts
t+Ts x&(t )dt
t
(10)
将(1)(3)代入(10),可以得到:
ò ò áx&(t)ñTs
= 1( Ts
t+dTs x&(t )dt
电力系统建模仿真作业1

无穷大功率电源供电系统仿真假设无穷大功率电源供电系统,在0.02s时刻变压器低压母线发生三相短路故障,仿真其短路电流周期分量幅值和冲击电流的大小。
线路参数L=50km,x1=0.4Ω/km,r1=0.17Ω/km;变压器Sn=20MV·A,短路电压Us%=10.5,短路损耗ΔPs=135kw,空载损耗ΔP0=22kw,空载电流I0%=0.8,变比kT=110/11,高低压绕组均为Y行联接;并设供电点电压为110KV。
其对应的Simulink仿真模型如图1-1所示。
图1-1 无穷大功率电源供电系统的Simulink仿真图表1-1 图1-1仿真电路中各模块名称及提取路径模块名提取路径无穷大功率电源Three-Phase Source SimPowerSystems/Eletrical Sources三相并联RLC负荷模块5MW SimPowerSystems/Elements串联RLC支路Three-phaseParallelRLCBranch SimPowerSystems/Elements三相故障模块Three-phase-Fault SimPowerSystems/Elements三相电压电流测量模块V-I-M SimPowerSystems/Measurements示波器模块Scope Simulink/Sinks电力系统图形用户界面Poweigui SimPowerSystems双绕组变压器模块Three-PhaseTransformer SimPowerSystems/Elements图1-2 电源模块的参数设置变压器T 采用“Three-PhaseTransformer (Two Windings )”模型。
根据给定的数据,计算折算到110kv 侧的参数如下:变压器的电阻为2233221351101010 4.0820000s N T N PU R S ∆⨯=⨯=⨯Ω=Ω 变压器的电抗为22332%10.5110101063.5310010020000s N T N U U X S ⨯=⨯=⨯Ω=Ω⨯ 变压器的漏感:63.53/(2)0.2022 3.1450T T L X f H H π===⨯⨯变压器的励磁电阻为2233301101010 5.51022N m U R P =⨯=⨯Ω=⨯Ω∆ 变压器的励磁电抗为22330100100110101075625%0.820000N m N U X I S ⨯=⨯=⨯Ω=Ω⨯ 变压器的励磁电感为75625/(2)240.82 3.1450m m L X f H H π===⨯⨯变压器模块中的参数采用有名值则设置如图1-3所示图1-3采用有名值时变压器模块的参数设置如果要采用标幺值,则在Similink 的三相变压器模型中,一次、二次绕组漏感和电阻的标幺值以额定功率和一次、二次侧各自的额定线电压为基准值,励磁电阻和励磁电感以额定功率和一次额定线电压为基准值。
电力电子建模与仿真例题
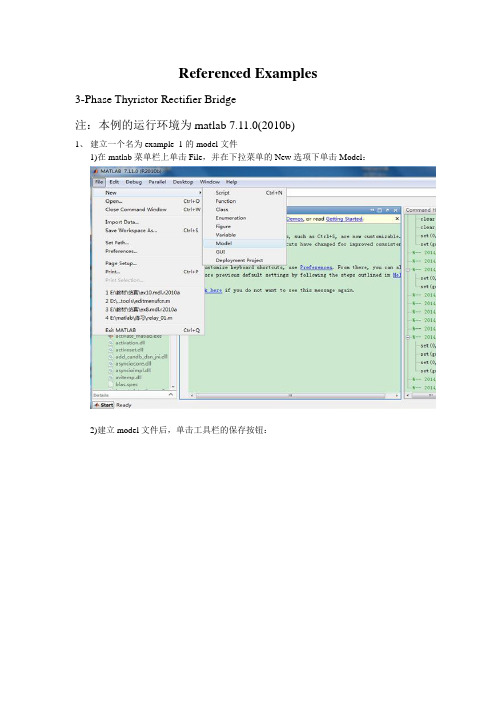
Referenced Examples3-Phase Thyristor Rectifier Bridge注:本例的运行环境为matlab 7.11.0(2010b)1、建立一个名为example_1的model文件1)在matlab菜单栏上单击File,并在下拉菜单的New选项下单击Model:2)建立model文件后,单击工具栏的保存按钮:3)将文件名保存为example_1这样就建立了一个名为example_1的model文件下一步就可以在这个界面上绘制例题上的电气原理图仿真了.用matlab对电路进行仿真通常经过以下几个步骤:(a)放置所需要的各种元器件(包括电源),设置各元器件的属性。
(b)用导线连接各个元器件,形成电路图。
(c)执行仿真。
(d)观看仿真波形,分析仿真结果。
2.绘制电气原理图:放置电路图中的电气元器件并分别设元器件属性置。
单击工具栏的Library Browser按钮添加元件功能模块,并找到他们所在的模块库。
a)三相电源SimPowerSystem/Electrical Sources/AC V oltage Source单击右键,选择Add to example_1,这样就在example_1中添加了一个交流电源,为了接下来绘图的方便,可采用ctrl+R使模型旋转水平放置。
三相电源即需要三个交流电源,可采用复制粘贴的办法。
下图为如何添加一个AC V oltage Source模型接下来就要对交流电源的模型参数进行设置双击a相的交流电源模型,弹出模块参数设置的对话框:相电压峰值大小根据题目要求线电压峰值为208V进行计算,a相相角为0,频率为60Hz,这样a相交流电源就设置完成。
B相,C相的参数设置类似,注意B相相角为240、C相为120。
最后添加一个SimPowerSystem/Elements/Ground.这样三相电源的部分全部添加完成。
b)电感(电阻)SimPowerSystem/Elements/Series RLC Branch双击模型在branch type里选择L:然后可以对电感的值进行设置,例如设为0.2mH:如果是电阻与电感串联即可以选择RL。
电力电子调制与控制仿真报告

电力电子调制与控制仿真报告电力电子调制与控制技术仿真报告基础篇一、电压型COT 控制与电压型CFT 控制Buck 变换器的稳态性 能和负载瞬态性能的比较A 、电压型COT 控制Buck 变换器的仿真采用电路元件建立PSIM 模型。
参数设置为:输入电压15=in V V ,电感H L μ200=,电容F C μ100=,固定负载Ω=5R ,瞬态加入负载Ω=20"R ,参考电压5=ref V V ,导通时间为s T ON μ5.2=。
根据COT 控制Buck 变换器发生脉冲簇现象的临界ESR 的值为Ω=⨯⨯⨯==--m C T RON ESRc5.12101002105.2266,为了不出现脉冲簇现象在本仿真中我们取Ω=m R ESR c 20仿真模型如图1所示。
仿真步长设为7101-⨯,仿真时间为0.2s ,在0.1s 的时候加入突变负载。
图1 电压型COT 控制Buck 变换器的PSIM 仿真模型仿真波形如下图:i的波形(1)、电感电流Li波形图2 电压型COT控制Buck变换器的电感电流LV的波形(2)、输出电压0.10.100050.10010.100150.1002Time (s)4.84.955.1Vo图3 电压型COT 控制Buck 变换器的输出电压0V 的波形(3)、控制电压C V 的波形图4 电压型COT 控制Buck 变换器的控制电压C V 的波形B 、电压型CFT 控制Buck 变换器的仿真采用电路元件建立PSIM 模型。
参数设置为:输入电压15=inV V ,电感H L μ200=,电容F C μ100=,固定负载Ω=5R ,瞬态加入负载Ω=20"R ,参考电压5=ref V V ,关断时间为s T OFF μ5.2=。
根据CFT 控制Buck 变换器发生脉冲簇现象的临界ESR 的值为Ω=⨯⨯⨯==--m C T ROFF ESRc5.12101002105.2266,为了不出现脉冲簇现象在本仿真中我们取Ω=m R ESR c 20仿真模型如图5所示。
电力电子、电机控制系统的建模及仿真(第1章)
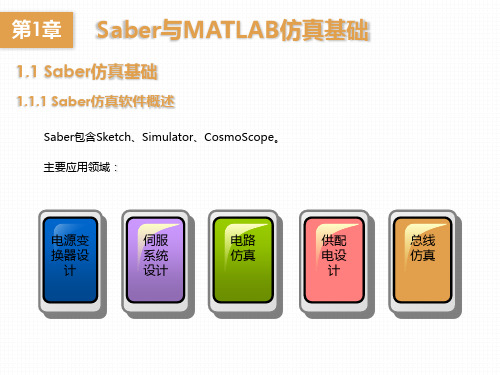
2. 保存目前空白的设计 (File>Save As …),在File Name字段输入名称VoltageRegulator,在保存文件的时候需要注 意,文件的保存路径必须为英文路径,否则在文件再次打开时会出现错误。
3. 放置元器件 按图1-2所示在原理框图上放置元器件。
(5) 将鼠标放置在窗口空白处并单击鼠标右键,通过图1-9中的选项可以改变主窗口背景颜色。 第一项为彩色黑背景;第二项为彩色白背景;第三项为黑色白背景。用户可根据自己的习惯进行 修改。
5. 连接原理图 在完成元件布局并设定属性后,可以将元件用导线连接在一起。在两个端口间连线的最简
单的方法如下: (1) 将光标放在第一端口上面(以V_dc符号的顶部开始); (2) 单击鼠标左键; (3) 将光标放在第二个端口上(lm317的左侧端口); (4) 再次单击鼠标左键。 重复步骤(1)-(4),从而将每个元件符号连至相关部件,如图1-10所示。
图1-31参数设置对话框
3. 在Saber中设置输入输出接口 启动Sketch并打开power_window_control.ai_sch 文件,文件位于:Synopsys\B
-2008.09-SP1\Saber\lib\tool_model\Simulink2SaberRTWexport_Matlab2008a\po wer_window,如图1-32所示。
主要功能: • 1. 数值计算功能 • 2. 符号计算功能 • 3. 数据分析和可视 化功能 • 4. 文字处理功能 • 5. SIMULINK动态仿真功能
主要特点: • 1. 功能强大
含有40多个应用于不同领域的工具箱.
• 2. 界面有好
其指令表达方式与习惯上的数学表达 式非常接近。 • 3. 扩展性强
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电力电子建模与控制
基于BUCK变换器反馈控制设计
专业:电气工程
姓名:________ 荏
学号:13S053072
BUCK 变换器反馈控制设计
第一部分:设计目标
图1 Buck 变换器系统
根据给定的条件,要求完成以下设计任务:
1•建立系统的传递函数TF ;
2. 给定参数:主电感 L 50 H ,R C 0.05 ,V g 30V15V ,R 5 C 100 F ,R 0 。
设计补偿网络Gc(s);
3. 画出补偿前后系统传递函数的bode 图;
4. 讨论补偿传递函数Gc(s)对于系统零点、极点、输出调节、输出阻抗及对 系统动态性能的影响。
第二部分:传递函数的建立与仿真
一、系统开环传递函数建立:
图2
统一电路模型
对于给定的buck 变换器电路,如图1所示
6
I 斗—lOw
1川
表1 BUCK 变换器统一电路模型参数
1. BUCK 变换器占空比至输出传递函数 G vd (s):
由以上模型和参数课求得占空比至输出的传递函数 G vd (s):
V (R sR RC)
R (L R c
RC) s LC (R R c
) s 2
2. 主拓扑参数选择:
本文控制系统中反馈电阻选择: R x 100k ,R y 100k ,即反馈系数 1
H(s);开关频率为f s 100kHz ,参考电压为5V ,锯齿波幅值3V
3. 工作方式:
根据BUCK 变换器电流连续与断续状态的临界电感公式为
二、补偿前系统传递函数bode 图
1•原始回路增益函数G °(s)
2.补偿前系统传递函数bode 图
利用Matlab 软件画出G °(s)的bode 图,如图3所示,从图中可以看出,系
统的幅值裕度无穷大,然而,相角裕度比价小,只有 Pm=15.7deg 不符合系统的
要求。
G vd (s)
(1)
I
crit
1 D?V g D 2T s
D ? 2L
(2)
代入给定的参数值,可知,电感电流 I I crit ,电路工作在连续CCM 模式
G)(s)
H(s)G m (s)G,d (s)
% 1 V g (R sRRC
& RV m 1 s(R RRC s 2
LC(R R)
(3)
G °(s) 100 1 30(5 2.5 10 5S)
100 100 3 5 7.5 10 5s 25.25 10 9s 2
5 2.5 10 5s
1 1.5 10 5s 5.05 109s 2
三、系统时域内实时仿真
利用 matlab/Simulink 中相关的模块,搭建开环实时仿真电路图,如图 4所示:
从仿真波形中可以看出,系统的动态特性较差,存在较大的输出超越量和较长的 调节时间,稳态时,输出结果并非精确的15V ,故存在较大的稳态误差。
通常选 择相位裕度在45度左右,增益裕度在10dB 左右,因此需要加入补偿网络G 』s ),
Bode Diujidrn
Gm=W Pm=157 deg 3.46e*04 radsi
图3补偿刖系统开环系统 bode 图
图4 BUCK 主电路实时仿真图 对
应的仿真波形图如图5所示:
□isaetG -r = le-D?号.
h ___________
pZIfeTLi
提高相位裕度和增益裕度。
图5开环系统(补偿前)实时仿真波形
图中黑色线条代表输出电压波形,紫红色代表流过电感的电流波形,黄色为矩形波发生器波形。
取其中一小段观察,如图6所示:
图6稳态时系统波形图
第三部分:补偿网络的设计
、补偿器传递函数
图1中所示的补偿器网络为一种有源超前--滞后补偿网络,其传递函数为
_
( 21 +屛R]十凡)G]
[拆二匚 + cj](i + J + G)
有源趙洲-滞后补偿网络二右两个零点、三个极点。
零点为:人=器=2爲2 C L 忆2 =器=2«( R, i Rj) C ;三C, 极点为:几V 7为威乩人厂器二晟可 2邈=r <CG
2n
CT7C ;
i _
2z/??C ;
二、补偿器设计方法
1.
采用推荐公式f g f s /5
即f g 20kHz ,f s 为BUCK 变换器的开关频率,一般说来,补偿后的回路函 数f g 越大,变换器的动态速度越快。
从bode 图中可以看出,原始回路函数G o (s)有两个相近的极点,极点的频率 为f p1,p 2 1/(2 JLC) 2.25 103
Hz ,可将补偿网络G c (s)两个零点设计为原始回
1
路函数G °(s)两个相近的极点频率的1/2,即f z1 f z2 - f p1,p2 1.2 103Hz 。
原 始回路函数G °(s)有一个零点,这是由于输出滤波电容的等效串联电阻 Rc 弓I 起 的,此时可用补偿网络的极点来补偿,令 G c (s)的极点f p2 f ZESR ,f p3 10f s 。
2. 零极点确定
1
两个零点:f z1
f z2 1
f p1,p2 1.2 103Hz ;
三个极点:f p1 0, f p2 f ZESR 32kHz ,f p3 10f p1 22.5kHz
3. 补偿网络G c (s)参数求取
这里R 3 R
1 ,
C
2
C 1。
"心)()// ( R* + 运 I
(1 1.3 104s)
2
ks(1 5 106
s)(1 7 106
s)
其中 k R i (C i C 2)。
原始回路函数G o (s)在f g 的增益为:
5 2.5 10 5
j2 f g
1 1.
2 10 5 j2 f g 5.05 10-9(j2 f g )2
补偿网络G c (s)在f g 的增益为:
1 G c (j
2 f g
) 1 13.3 9
|G °(j2 f g
)|
零点f z1、f z2处的增益为:
4.补偿网络G c (s)的bode 图
G c (s)的表达式为:
G c (s)
(5)
G o (j2 f g ) 0.075
AU R f
2
G c
(j2 f g
) f
上鴿
133
0.8
极点f p2的增益为:
AW R ¥G
c (j2f g ) 求取补偿网络电路各元件的参数: 假设R 2
10k ,可得
32
电 13-3 21.3
20 103
R 2 AV 2
470
1 2 f z1R 2
0.013 F
C
3
0.01 F
C
2
1
2 f
p3R
2
707pF
R 1
1
2 f
z2C
3
13.3k
1
5800 (1 1.3 104s)2
s(1 5 106s)(1 7 10 6s)
5800 1.58 s 9.8 105s2 s
1.2 10 5s2 3.5 10_11s3
第四部分:补偿后系统性能分析
一、补偿后系统的bode图
1•补偿后系统传递函数为
G(s) G c(s) G o(s)
图7补偿网络G c(s)的bode图
对应的bode图:
G c(s)
(6)
2•补偿后系统的bode图:
图8补偿后系统的bode图
此时从图中可以看出,系统的相位裕度为 50.3度,幅值裕度足够大,能很 好地满足系统的稳定性和快速响应性要求。
、补偿后系统实时仿真
1.补偿后时域内BUCK 变换器仿真图
Discrete,
Is ■ Lc -06 G
Pltk +
图10补偿后时域内BUCK 动态波形图
图10表明了系统的动态性能得到了改善,响应速度和稳态精度有很大程度 上的提高。
__________ J ..-m
u - 1_ T L
屮护£ ■
1 ||-
Mosfet
I
JOV 1
Lrs
图9补偿后时域内 BUCK 变换器仿真图
QI 沖R 林
0工T
二口
rStB-il
D-opla/l
2.补偿后时域内BUCK 动态波形图
3.局部图
选取0.0059s~0.0060s时间内局部波形图进行分析
图11局部图
纹波大约为0.06V左右,系统的稳态精度较好。
第五部分:总结
本文通过对BUCK变换器的建模与仿真,运用反馈补偿控制知识,最终完
成了一套控制补偿网络的设计,仿真结果也较好的验证了设计的正确性:由开环系统的响应时间长,稳态精度差,超调量过大等缺点,经过补偿环节的设计之后,较好地解决了这些问题。
当然补偿设计也不是唯一的,设计过程中运用过了相关经验公式,并简化了一些条件,最终形成的结果也肯定不是最佳的。
