DC-DC电感参数选择计算
DCDC变换器的设计方案

DC-DC变换器的设计方案一种模块化高效DC-DC变换器的开发与研制设计方案一、设计任务:设计一个将220VDC升高到600VDC 的DC-DC变换器。
在电阻负载下,要求如下:1、输入电压U=220VDC,输出电压u=600VDC。
2、输出额定电流|;:=2.5A,最大输出电流Iomax=3Ao3、当输入山在小范围内变化时,电压调整率SV W2%(在匕=2.5A时)。
4、当|<在小范围你变化时,负载调整率SI W5%(在||=220VDC时)。
5、要求该变换器的在满载时的效率n±90%o6、输出噪声纹波电压峰-峰值U t)pp<1V(在Ui=220VDC,u=600VDC,[(=2・5A条件下)。
7、要求该变换器具有过流保护功能,动作电流设定在3A o8、设计相关均流电路,实现多个模块之间的并联输出。
二、设计方案分析1、DC-DC升压变换器的整体设计方案主电路图1DC-DC变换器整体电路图如图1升压式DC-DC变换器整体电路所示,该DC/DC电压变换器由主电路、采样电路、控制电路、驱动电路组成;开关电源的主电路单元、样电路单元采、控制电路单元、驱动电路单元组成闭环控制系统,是相对输出电压的自动调整。
控制电路单元以SG3525为核心,精确控制驱动电路,改变驱动电路的驱动信号,达到稳压的目的。
2、DC-DC升压变换器主电路的工作原理DC-DC功率变换器的种类很多。
按照输入/输出电路是否隔离来分,可分为非隔离型和隔离型两大类。
非隔离型的DC-DC变换器又可分为DC600V降压式、升压式、极性反转式等几种;隔离型的DC-DC 变换器又可分为单端正激式、单端反激式、双端半桥、双端全桥等几种。
下面主要讨论非隔离型升压式DC-DC 变换器的工作原理。
图2(a )DC-DC变换器主电路图2(b )DC-DC 变换器主电路图2(a )是升压式DC-DC 变换器的主电路,它主要由开关变换电路、高频变压电路、整流电路、输出滤波电路四大部分组成;图1(b )是用matlab 模拟主电路 DC220V出的升压式DC-DC变换器的主电路图。
宽输入DC-DC Boost变换器电感参数设计

Boost变换器的拓扑结构电路。
根据电感电流的最小值是否为零,可将Boost 变换器工作模式分成电流连续模式(CCM)、电流临界连续模式(CRM)和电流断续模式(DCM)。CCM模式下Boost变换器电感电压和电流波形。
Boost变换器的CCM模式和DCM模式的临界电感LB为[4]:
(1)输入电压的变化范围12 V~36 V,得出占空比D的变化范围为0.25~0.75。
(2)由式(2)得出占空比在0.25和0.75时所对应的临界电感分别为67.5 H和22.5 H。
(3)由于1/3∈(0.25,0.75),临界电感在占空比1/3时取得最大值,则电感的最小值由式(8)得Lmin=71.1 H,此时所对应的输入电压为32 V。上述输入电压,占空比和临界电感对应关系如表1所示。
由表3可知,Boost变换器工作在CCM模式时,其最小电感等于临界电感的最大值。当最大占空比Dmax<1/3时,最小电感在Dmax处取得;当最小占空比Dmin>1/3时,最小电感在Dmin处取得;当1/3∈(Dmin,Dmax)时,最小电感在D=1/3处取得。
由此可见,仿真结果与理论分析一致,从而验证了理论分析的准确性。
3 仿真验证
为了验证上述理论分析,对Boost变换器进行仿真研究。其参数如下:输入电压UI为12 V~36 V,输出电压UO为48 V,负载电阻为48 ,输出滤波电容值为100 F,开关频率50 kHz。
将输入电压范围分12 V~24 V、12 V~36 V、33 V~36 V 3种情况进行讨论。首先分析输入电压12 V~36 V,其CCM模式电感的最小值确定方法如下:
对图4和表2进行分析,可得输入电压在12 V~36 V变化,电感值71.1 H能保证Boost变换器均工作在CCM模式,而它正好是D=1/3所对应的临界电感值。这说明当1/3∈(Dmin,Dmax)时,要使Boost变换器均工作在CCM模式,电感的最小值应为D=1/3所对应的临界电感值。
DC-DC电路中电感的意义及选择

ILP ILT
VD VOUT t OFF
L
(5)
Current flow in the coil L is almost the same as the output current; consequently,
ILP ILT 2 IOUT
From equations (3) and (6), ILP during Q1 ON-state is
(6)
ILP IOUT
VIN VSW
VOUT t ON 2L
(7)
Using equations (5) and (6), ILP can be calculated during the period when the switching element is OFF:
VIN fSW r IOUT
(17)
Then, solve (17) for L to calculate the inductance value:
VL( OFF ) VD VOUT
VD: VOUT: Forward Voltage Drop across D1 (V) Output Voltage (V)
(4)
Using equations (2) and (4), the current flowing through coil L when Q1 is OFF is as follows:
● Inductor Current Waveform Fig. 3 shows the inductor’s current waveform. IOUT is the average inductor current value. When switching element Q1 is ON, current flow is shown during ON period tON of Q1, and voltage VL(ON) of coil L can be calculated by the following equation:
buck电路参数计算

buck电路参数计算Buck电路是一种常见的DC-DC降压转换器,广泛应用于电子设备的电源管理中。
本文将详细介绍Buck电路的参数计算方法。
Buck电路的基本原理是通过切换开关管控制电感储能和输出电容放电,从而实现将输入电压降低到输出电压的转换。
在实际电路中,开关管通常采用MOSFET或BJT管。
Buck电路的主要参数包括输入电压Vin、输出电压Vout、输出电流Iout、开关频率f、开关管的导通电阻Rds(on)以及电感L和输出电容C等元器件参数。
其中,输入电压和输出电压是电路的基本需求,常由实际应用确定。
输出电流和开关频率则是根据实际负载和转换效率进行选择。
接下来,我们将分别介绍Buck电路中电感和输出电容的参数计算方法。
首先是电感L的计算。
电感是Buck电路中储能和滤波的重要元件,其大小直接影响电路的转换效率和输出波形。
电感的计算依据是输出电流Iout和开关频率f。
常用的计算公式为:L = (Vin - Vout) × D / (f × Iout)其中,D为开关管导通比,通常在0.4-0.8之间选择。
电感的选取应考虑其饱和电流和电流波形等因素,以保证电路的正常运行。
其次是输出电容C的计算。
输出电容是Buck电路中输出滤波的重要元件,其大小直接影响输出电压的稳定性和纹波水平。
输出电容的计算依据是输出电压Vout和开关频率f。
常用的计算公式为:C = Iout × (1 - D) / (f × ΔV)其中,ΔV为输出电压纹波的允许值,通常为输出电压的1%-10%。
输出电容的选取应考虑其漏电流和ESR等因素,以保证电路的正常运行。
我们需要考虑的是开关管的参数选择。
开关管的主要参数包括导通电阻Rds(on)和最大耗散功率Pmax。
导通电阻Rds(on)越小,开关管的损耗越小,但其价格也越高。
最大耗散功率Pmax应根据电路实际负载和工作环境进行选择,以保证开关管的正常工作和寿命。
TPS5450数控DC-DC电源

开关稳压电源(E题)摘要本系统以BUCK斩波电路为核心,以MSP430G2553单片机为主控制器,以TI 电源管理芯片TPS5450为核心DC-DC芯片,根据反馈信号对PWM信号做出调整,进行硬件闭环控制,单片机通过DA控制反馈段,从而实现可调稳压输出。
系统输出直流电压0V~20V 可调,可以通过键盘设定和步进调整,最大输出电流达到2A并实现2.2A过流保护,电压调整率和负载调整率小,DC-DC变换器的效率达到93.4%(10V 2A情况下测定)。
能对输出电压输出电流和输出功率进行测量和显示。
方案论证1.1D C-DC主回路拓扑方案一采用单片机产生PWM波控制MOS的开关,AD采样进行反馈,形成软件闭环控制系统,通过调整占空比稳压和调节输出电压。
方案二采用集成电源管理芯片,单片机控制DA经过电阻送至芯片反馈端,通过硬件欺骗的方法控制输出电压。
基于对电路结构和效率的考虑,我们选择方案二。
1.2系统总体框图图1-1 系统总体框图1.3 提高效率的方法及实现方案1)选择合适的开关电源控制芯片:集成开关电源芯片的MOS内阻对整机的效率有较大的影响,TI公司的TPS5450内部导通电阻110mΩ,工作频率500KHz,有较高的转换效率,并且带有使能端,输入最大电压36V,持续最大输出电流5A,适合本设计要求。
2)BUCK斩波电路中二极管的选取:本电路工作频率高,电压低,对二极管的开关速度要求高,对反向耐压要求不高。
与快速恢复二极管相比,肖特基二极管正向压降更小、恢复时间更短;反向耐压也已经满足要求。
故选择肖特基二极管。
本设计要求输出电流2A,可选用最大持续电流3A的1N5822二极管。
3)BUCK斩波电路中电感的选取:本设计电流较大,又由于开关频率较高,普通绕线电感会产生较大EMI,对输出电压有较大的影响,会产生较大的纹波,因次选用TDK屏蔽式额定电流4A的电感,能有效减少EMI 的产生并能满足设计的电流需求。
共模电容电感的选值

共模电容电感的选值共模电容(Common Mode Capacitance)和电感(Inductance)是电路中常见的两个参数。
它们分别用于描述电路中信号的共模和差模特性,对于电路的性能有着重要的影响。
本文将从基础概念、选值原则以及应用实例等方面对共模电容和电感进行详细介绍。
一、共模电容1.1 基础概念共模电容是指在共模模式下,电路中两个互不相干的信号引脚之间的容性耦合。
共模模式是指两个输入信号相同且同相时的模式。
在实际电路中,由于电路的布局导致的不均匀耦合、电路元件的失配以及电路板的共面等因素,会导致差分信号中的一部分信号以共模的形式出现在电路中的其他部分。
共模电容可以理解为差分信号之间和差分信号与地之间的电容。
它的存在会引发共模噪声,影响电路的性能。
1.2 选值原则选择合适的共模电容对于电路的正常工作以及抑制共模噪声有着重要的作用。
通常,选值共模电容的原则如下:(1)共模电容的容值越小越好,理想情况下应该为零。
因为容值越小,共模信号的干扰就越小。
(2)共模电容的参数应尽量匹配。
这是为了保证共模电容对差分信号的耦合效果较小。
(3)共模电容应具有较低的串扰电容,以提高电路的带宽和工作速度。
(4)共模电容的封装应具有良好的高频性能,以减小对差分信号的干扰。
1.3 应用实例共模电容的应用非常广泛,特别是在高速差分信号传输中。
以下是一些常见的应用实例:(1)数据通信中的高速差分信号传输。
共模电容用于抑制共模噪声,降低信号的误码率。
(2)USB接口中的共模电容。
USB接口通常需要满足较高的抗干扰能力,共模电容在USB接口中起到了重要的作用。
(3)音频和视频信号传输中的共模电容。
共模电容在音频和视频信号传输中用于抑制共模噪声,提高信号的质量。
二、电感2.1 基础概念电感是指通过绕线或其他方式将电流储存在磁场中的元件。
在直流电路中,电感是阻止电流突变的元件,它会储存电流并将其释放。
电感的单位用亨利(Henry)来表示,一亨利等于安培-秒/伏特。
DCDC-BUCK中电感的选型思考
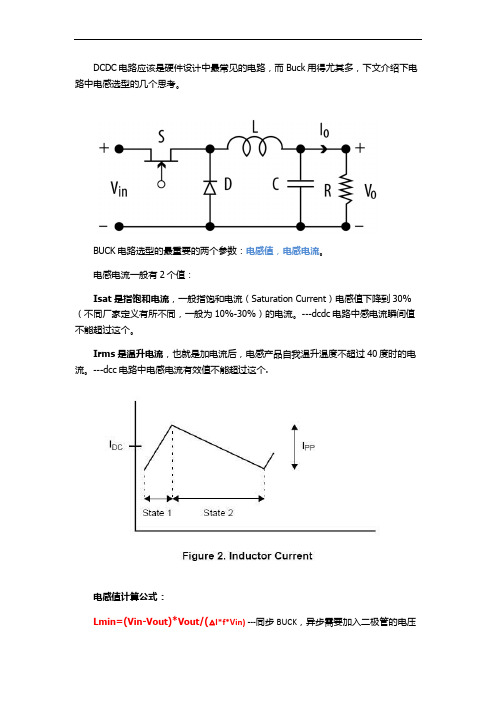
DCDC电路应该是硬件设计中最常见的电路,而Buck用得尤其多,下文介绍下电路中电感选型的几个思考。
BUCK电路选型的最重要的两个参数:电感值,电感电流。
电感电流一般有2个值:Isat是指饱和电流,一般指饱和电流(Saturation Current)电感值下降到30%(不同厂家定义有所不同,一般为10%-30%)的电流。
---dcdc电路中感电流瞬间值不能超过这个。
Irms是温升电流,也就是加电流后,电感产品自我温升温度不超过40度时的电流。
---dcc电路中电感电流有效值不能超过这个.电感值计算公式:Lmin=(Vin-Vout)*Vout/(△I*f*Vin) ---同步BUCK,异步需要加入二极管的电压步骤:(1)确认输出电流Iout(2)确认电感值Lmin=(Vin-Vout)*Vout/(△I*f*Vin)一般来说△I(上图的Ipp)取20%-30%的Iout(最大输出电流),f为DCDC开关频率(3)根据Lmin选取L,一般略取大一点(4)通过上面的公式计算△I,ImaxImax=Iout+1/2 △I,饱和电流要大于Imax(5)确认电感的饱和电流要大于Imax温升电流要大于Iout确认输出电流以上公式网上颇多,如果只写到这里,那么本文也没什么价值。
主要是有一个问题,上述的Iout到底取多少呢?是DCDC芯片的最大输出电流能力,还是实际工作过程中真正使用的最大电流呢?笔者认为应是DCDC芯片的最大输出电流能力,比如2A的DCDC芯片,那么这里Iout取2A。
理由如下:假设实际要用到2A电流,与芯片能力是一样的,那么不管取芯片电流能力还是实际使用电流,按照公式算得电感值是相同的,用这个电感可以设计出输出2A的DCDC电路。
这时如果用这个电路接入500mA的负载,即实际输出电流是500mA,难道就不能用了,显然是可以的。
由公式知道,L与输出电流成反比,如果按照实际电流计算,在接小负载时,比如200mA,那么算得的L值是2A时的10倍,电感值大,体积就大,这是我们不希望的。
buck电路参数计算实例

buck电路参数计算实例Buck电路是一种常见的降压型DC-DC转换器,广泛应用于电源管理系统中。
在设计和计算buck电路时,我们需要考虑各种参数和指标,以确保其正常工作和性能优越。
本文将以一个实际的buck 电路参数计算例子为基础,介绍如何进行参数计算和设计。
1. 输入电压(Vin)和输出电压(Vout):在这个例子中,我们假设输入电压为12V,输出电压为5V。
这是一个常见的应用场景,如手机充电器或电子设备的电源。
2. 输出电流(Iout):我们需要根据实际需求确定所需的输出电流。
假设在这个例子中,我们需要一个最大输出电流为2A的buck电路。
3. 电感(L):电感是buck电路中的重要元件,用于储存和释放能量。
根据设计要求和电路参数,我们可以计算出所需的电感值。
电感值的计算公式为L = (Vin - Vout) * (1 - D) / (f * ΔI),其中D为占空比,f为开关频率,ΔI为电感电流波动范围。
4. 电容(C):电容也是buck电路中的重要元件,用于平滑输出电压。
根据设计要求和电路参数,我们可以计算出所需的电容值。
电容值的计算公式为C = ΔI / (8 * f * Vr),其中ΔI为电感电流波动范围,f为开关频率,Vr为输出电压波动范围。
5. 开关频率(f):开关频率是buck电路的一个重要参数,它决定了电路的响应速度和效率。
通常,开关频率越高,电路越稳定,但也会增加开关器件的损耗。
在这个例子中,我们假设开关频率为100kHz。
6. 占空比(D):占空比是buck电路中的一个重要参数,它表示开关管导通时间与周期时间的比值。
占空比的计算公式为D = Vout / Vin。
在这个例子中,我们假设占空比为0.42。
7. 电感电流波动范围(ΔI):电感电流波动范围是buck电路中的一个重要参数,它表示电感电流的最大和最小值之间的差值。
根据设计要求和电路参数,我们可以计算出所需的电感电流波动范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DC-DC升压和降压电路电感参数选择
注:只有充分理解电感在DC-DC电路中发挥的作用,才能更优的设计DC-DC电路。
本文还包括对同步DC-DC及异步DC-DC概念的解释。
DC-DC电路电感的选择简介
在开关电源的设计中电感的设计为工程师带来的许多的挑战。
工程师不仅要选择电感值,还要考虑电感可承受的电流,绕线电阻,机械尺寸等等。
本文专注于解释:电感上的DC电流效应。
这也会为选择合适的电感提供必要的信息。
理解电感的功能
电感常常被理解为开关电源输出端中的LC滤波电路中的L(C是其中的输出电容)。
虽然这样理解是正确的,但是为了理解电感的设计就必须更深入的了解电感的行为。
在降压转换中(Fairchild典型的开关控制器),电感的一端是连接到DC输出电压。
另一端通过开关频率切换连接到输入电压或GND。
在状态1过程中,电感会通过(高边“high-side”)MOSFET连接到输入电压。
在状态2过程中,电感连接到GND。
由于使用了这类的控制器,可以采用两种方式实现电感接地:通过二极管接地或通过(低边“low-side”)MOSFET接地。
如果是后一种方式,转换器就称为“同步(synchronus)”方式。
现在再考虑一下在这两个状态下流过电感的电流是如果变化的。
在状态1过程中,电感的一端连接到输入电压,另一端连接到输出电压。
对于一个降压转换器,输入电压必须比输出电压高,因此会在电感上形成正向压降。
相反,在状态2过程中,原来连接到输入电压的电感一端被连接到地。
对于一个降压转换器,输出电压必然为正端,因此会在电感上形成负向的压降。
我们利用电感上电压计算公式:
V=L(dI/dt)
因此,当电感上的电压为正时(状态1),电感上的电流就会增加;当电感上的电压为负时(状态2),电感上的电流就会减小。
通过电感的电流如图2所示:
通过上图我们可以看到,流过电感的最大电流为DC电流加开关峰峰电流的一半。
上图也称为纹波电流。
根据上述的公式,我们可以计算出峰值电流:
其中,ton是状态1的时间,T是开关周期(开关频率的倒数),DC为状态1的占空比。
警告:上面的计算是假设各元器件(MOSFET上的导通压降,电感的导通压降或异步电路中肖特基二极管的正向压降)上的压降对比输入和输出电压是可以忽略的。
如果,器件的下降不可忽略,就要用下列公式作精确计算:
同步转换电路:
异步转换电路:
其中,Rs为感应电阻阻抗加电感绕线电阻的阻。
Vf是肖特基二极管的正向压降。
R是Rs加MOSFET导通电阻,R=Rs+Rm。
电感磁芯的饱和度
通过已经计算的电感峰值电流,我们可以发现电感上产生了什么。
很容易会知道,随着通过电感的电流增加,它的电感量会减小。
这是由于磁芯材料的物理特性决定的。
电感量会减少多少就很重要了:如果电感量减小很多,转换器就不会正常工作了。
当通过电感的电流大到电感实效的程度,此时的电流称为“饱和电流”。
这也是电感的基本参数。
实际上,转换电路中的开关功率电感总会有一个“软”饱和度。
要了解这个概念可以观察实际测量的电感VsDC电流的曲线:
当电流增加到一定程度后,电感量就不会急剧下降了,这就称为“软”饱和特性。
如果电流再增加,电感就会损坏了。
注意:电感量下降在很多类的电感中都会存在。
例如:toroids,gapped E-cores等。
但是,rodcore电感就不会有这种变化。
有了这个软饱和的特性,我们就可以知道在所有的转换器中为什么都会规定在DC输出电流下的最小电感量;而且由于纹波电流的变化也不会严重影响电感量。
在所有的应用中都希望纹波电流尽量的小,因为它会影响输出电压的纹波。
这也就是为什么大家总是很关心DC输出电流下的电感量,而会在Spec中忽略纹波电流下的电感量。
