杨氏双缝干涉
合集下载
杨氏双缝干涉

选用如图坐标来确定屏上的光强分布
y
S1
x
r1
r2
d 2 r1 = S1 P = ( x − ) + y 2 + D 2 P(x,y,D) 2
z
o
S2
d 2 r2 = S 2 P = ( x + ) + y 2 + D 2 2
由上面两式可求得
r22 − r12 = 2 xd 2 xd ∆ = r2 − r1 = r1 + r2
杨氏双缝干涉 托马斯·杨 Young) 托马斯 杨(Thomas Young) 英国物理学家、医生和考古学家, 英国物理学家、医生和考古学家, 光的波动说的奠基人之一 波动光学: 波动光学:杨氏双缝干涉实验 生理光学: 生理光学:三原色原理 材料力学: 材料力学:杨氏弹性模量 考古学: 考古学:破译古埃及石碑上的文字
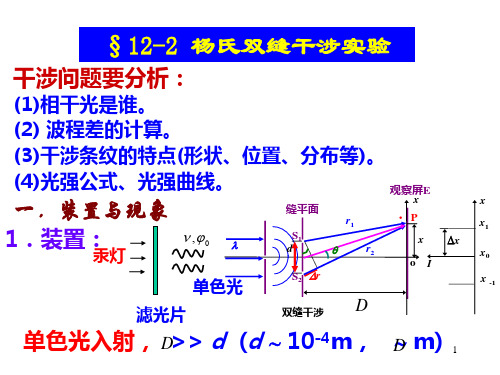
S线光源,G是一个遮光屏,其上有两条与S平行的狭缝S1、 线光源, 是一个遮光屏,其上有两条与S平行的狭缝S 且与S等距离,因此S 是相干光源,且相位相同; S2,且与S等距离,因此S1、S2 是相干光源,且相位相同;S1、 之间的距离是d 到屏的距离是D S2 之间的距离是d ,到屏的距离是D。
∆ = n(r2 − r1 ) = mλ (m = 0,±1,±2,L)
即光程差等于波长的整数倍时, 即光程差等于波长的整数倍时,P点有光强最大值
1 ∆ = n(r2 − r1 ) = (m + )λ (m = 0,±1,±2,L) 2 即光程差等于半波长的奇数倍时, 即光程差等于半波长的奇数倍时,P点的光强最小
I = I1 + I 2 + 2 I1 I 2 cos δ = 4 I 0 cos
波动光学实验系列之杨氏双缝干涉

波动光学实验系列之杨氏双缝干涉
一、引言
波动光学实验一直是光学领域中的重要研究方向,其中杨氏双缝干涉实验是一种经典的实验现象。
本文将介绍杨氏双缝干涉实验的原理、实验装置及其应用。
二、实验原理
杨氏双缝干涉实验是利用光的波动性质进行研究的实验。
在这个实验中,一束光线通过两个密接的缝隙后,形成交替明暗条纹的干涉图样。
这种干涉现象可以用光的波动理论来解释,根据叠加原理,两个波的相位差会决定光的干涉效应。
三、实验装置
杨氏双缝干涉实验的实验装置主要包括光源、双缝光栅、透镜和屏幕。
光源产生一束平行光,通过双缝光栅后,光线经过透镜成像在屏幕上,观察者可以看到干涉条纹的形成。
四、实验过程
在进行杨氏双缝干涉实验时,首先需要调整光源和双缝光栅的位置,使得光线通过双缝形成干涉条纹。
然后调整透镜的位置和焦距,使得干涉条纹清晰可见。
最后观察屏幕上的干涉条纹,并记录实验现象。
五、实验应用
杨氏双缝干涉实验不仅是一种经典的光学实验,还具有广泛的应用价值。
在现代科学研究中,杨氏双缝干涉实验常被用于测量光波的波长、验证光的波动性质,以及研究干涉现象对光学元件的影响等方面。
六、结论
通过对杨氏双缝干涉实验的介绍,我们可以更深入地了解光的波动性质和干涉现象。
这一实验不仅展示了光学的精彩世界,还为我们理解光的本质提供了重要的实验依据。
希望通过这篇文档,读者能够对光学实验有一个更加全面的认识。
以上是关于波动光学实验系列之杨氏双缝干涉的简要介绍,希望能为您带来有价值的信息。
杨氏双缝干涉
k 1,2,.....
2)、用波程差表示: k 0,1,2,3.....
d sin
2k .....加强(明).....
x2 d. {(2k 1) 减弱(暗).......(12.8)
D2
k——条纹级次
k 1,2,3.....
3
(2)干涉明纹和暗纹中心的位置: 1)明纹中心的位置:
x D k D ......(12 9) k 0,1,2,.....
d
d
2)暗纹中心的位置:
x D (2k 1) D ......(12 10) k 1,2,3,.....
d
d2
3)k=0时,x 0即在屏中央出现明纹—称为零级
明纹。
如D、不变,而d减小,某级条纹的位置如何
变化?
明纹: k (整数级)
暗纹:(2k-1)/2(半整数级) 5
观察屏
x
(4)相邻两明纹或相邻两暗纹间的距离:
亮纹位置:
xk
D d
k
xk 1
D d
(k
1)
暗纹 +2级
+1级
0级亮纹 -1级 -2级
相邻亮纹间距:
x
xk 1
xk
D d
相邻两明纹中心或相邻两暗纹中心间的距离:
x
D d
.........(12.11)
(2)、相位差: 2 ......(1)
——相干光的波长。
2
2、干涉明暗条纹的位置和条件:
· (1)、干涉明暗条纹的条件:
r1
Px x
1)、用相位差表示:
k 0,1,2,.....
d
r2
r
D
x o x0
杨氏双缝干涉实验

x k D 明纹中心
2a
k0,1,2,
x0 0 中央明纹
x1
D
2a
一级明纹
D
x2 a
二级明纹┄┄
2a
x D
(2k
1)
2
干涉减弱
x(2k1)D
4a
暗纹中心 k0 ,1 ,2 ,
x1
D
4a
一级暗纹
x2
3D
4aa
二级暗纹 ┄┄
2a x k 干涉加强
a
12
例4、
a
13
例5、
a
14
二、分波阵面干涉的其他实验
1.菲涅耳双面镜
M1
s1
d
s2
sL
o
M2
D
a
P
15
2.劳埃德镜
P'
P
s1
d
s2
ML
D
当P移动到P/时屏与反射镜M接触,由于半波损失,接触处为暗纹。
d x k 加强
D2
明纹x公 ( k式 -1) D
2d
a
16
总结杨氏双缝干涉
k = -2 k = -1 k =0
k =1
k =2
a
9
暗纹公式
d
x D
(2k 1)
2
x(2k1)D
2d
第五级暗纹 k 4
x 9D
2d
注意:当缝间距为d时
暗纹公式 x(2k1)D k =1,2,3…
2d
明纹公式 x k D
d
k =0,1,2,3…
条纹间距
a
x
D
d
10
a
11
杨氏双缝干涉

d' ( 2k 1) d 2
k 0,1,2,
暗纹
4
1、明、暗条纹的位置
x
p
d' x k 明纹 d
d' x ( 2k 1) 暗纹 d 2
x
d
d'
x
o
k 0,1,2,
2、相邻明(暗)条纹的间距
d' d' d' x xk 1 xk ( k 1) k d d d
11-2 杨氏双缝干涉实验 劳埃德镜
一 杨氏双缝干涉实验 (1801年)
光 源
s1
*
s2
1
一 杨氏双缝干涉实验
d
实 验 装 置
s1
r1
r2
d'
B
p
s
x
o
o
s2
r
波程差 r r2 r d sin 1
d ' d
x r d d'
2
实 s1 s 验 o 装 s 2 置 r 1 2
1、明、暗条纹的位置
p
d' x k 明纹 d
d' x ( 2k 1) 暗纹 d 2 k 0,1,2,
x
d
x
o
d'
2、相邻明(暗)条纹的间距
d' x d
19
例3 如图 离湖面 h=0.5m处有一电磁波接收器 位于 C ,当一射电星从地平面渐渐升起时, 接收器断续地检测到一系列极大值 . 已知射 电星所发射的电磁波的波长为20.0cm,求第一 次测到极大值时,射电星的方位与湖面所成 的角度.
杨氏双缝干涉
条纹位置
可直接利用Young 双缝干涉的结果。
8
三、洛埃境 半波损失
E/
S1
M S2
o E
装置:S: 线光源(或点光源)
M: 平玻璃片作反射镜
S发出的光一部分直接投射到屏上,一部分经 M反射后到屏
上,在重叠区干涉。
干涉的两部分光可以看作是一个实光源S1和一个虚光源 S2
发出的。
9
干涉图样 • 入射角很大,接近90o 。反射系数近于1,故反射很强。 • 两光的振幅几乎相等,可看成等幅干涉。 • 干涉条纹只出现在镜面上半部。 相位
一、杨氏双缝干涉
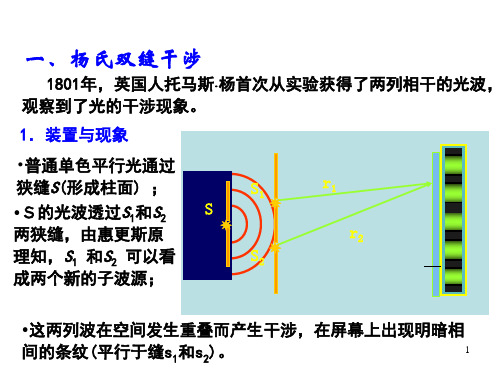
1801年,英国人托马斯杨首次从实验获得了两列相干的光波, 观察到了光的干涉现象。
1.装置与现象
•普通单色平行光通过
狭缝S(形成柱面) ;
•S的光波透过S1和S2
两狭缝,由惠更斯原
理知,S1 和S2 可以看
成两个新的子波源;
S1
S
S2
r1 r2
S1 S
S2
•这两列波在空间发生重叠而产生干涉,在屏幕上出现明暗相
五种波长的光在所给观察点最大限度地加强。 13
例12-3 在杨氏双缝实验中,欲使干涉条纹变宽,应作怎样 的调整: (A)增加双缝的间距, (B)增加入射光的波长, (C)减少双缝至光屏之间的距离, (D)干涉级k愈大时条纹愈宽。
解:由干涉条纹间距公式
x D
d 可知,应选(B)
14
例12-4 在空气中用波
6
二、菲涅尔双镜
S M1
S1
C S2
i
M2
P P0
E
7
装置
S点光源(或线光源,与两镜交线平行);M1和M2:镀银反射 镜,夹角很小; 两反射镜把 S 发出的光分成两部分,可以看 作是两个虚光源S1和S2发出的光。
杨氏双缝干涉

§4.2 分波阵面干预
一、杨氏双缝干预 二、其他分波阵面的干预
一、杨氏双缝干预
杨(T.Young)在1801年首先 发觉光的干预现象,并首次测 量了光波的波长。
杨氏双缝实验——第一个判 定光性质的关键性实验。
依据实验 观察的水波图 样,托马·杨 亲手绘制的双 缝干预现象。
§4.2 分波阵面干预
一、杨氏双缝干预
〔1〕假设A、B 两室内均为纯洁空气,O处为零级条纹。
〔2〕假设A室充满甲烷体积比为x 的井下气样:
n n x n0 (1 x)
纯甲烷气的折射率
纯洁空气的折射率
xk λ
(n n0 )L
一、杨氏双缝干预
§4.2 分波阵面干预
例:蓝绿光为杨氏干预实验的光源,波长范围
=100nm,中心波长 =490nm,估算第几级开始
x d
D (2k 1) λ —暗纹中心
d
2
二、其他分波阵面的干预
2、菲涅耳双面镜实验
s
M1
L
s1
d
s2
C
M2
D
方法:等效双缝〔略〕
§4.2 分波阵面干预
二、其他分波阵面的干预
3、洛埃镜实验
P’
§4.2 分波阵面干预
P
S●
d
s2
M
D
方法:等效双缝〔略〕
思考:在镜面最右端处是明纹还是暗纹?
小结
条纹变得无法识别?
解:
长波长:
1
2
,短波长: 1
2
长波长的k级亮条纹和短波长的k+1级亮条纹重合。
k长 (k 1)短
代入数值,解得:k 4.4
也就是说从第五级开始条纹变得不可分辩。
一、杨氏双缝干预 二、其他分波阵面的干预
一、杨氏双缝干预
杨(T.Young)在1801年首先 发觉光的干预现象,并首次测 量了光波的波长。
杨氏双缝实验——第一个判 定光性质的关键性实验。
依据实验 观察的水波图 样,托马·杨 亲手绘制的双 缝干预现象。
§4.2 分波阵面干预
一、杨氏双缝干预
〔1〕假设A、B 两室内均为纯洁空气,O处为零级条纹。
〔2〕假设A室充满甲烷体积比为x 的井下气样:
n n x n0 (1 x)
纯甲烷气的折射率
纯洁空气的折射率
xk λ
(n n0 )L
一、杨氏双缝干预
§4.2 分波阵面干预
例:蓝绿光为杨氏干预实验的光源,波长范围
=100nm,中心波长 =490nm,估算第几级开始
x d
D (2k 1) λ —暗纹中心
d
2
二、其他分波阵面的干预
2、菲涅耳双面镜实验
s
M1
L
s1
d
s2
C
M2
D
方法:等效双缝〔略〕
§4.2 分波阵面干预
二、其他分波阵面的干预
3、洛埃镜实验
P’
§4.2 分波阵面干预
P
S●
d
s2
M
D
方法:等效双缝〔略〕
思考:在镜面最右端处是明纹还是暗纹?
小结
条纹变得无法识别?
解:
长波长:
1
2
,短波长: 1
2
长波长的k级亮条纹和短波长的k+1级亮条纹重合。
k长 (k 1)短
代入数值,解得:k 4.4
也就是说从第五级开始条纹变得不可分辩。
杨氏双缝干涉

或 明条纹:r2-r1=xd/D=±mλ/n=±mλ’ m=0,1,2,… 暗条纹:r2-r1=xd/D=±(2m+1)λ/2n =±(2m+1)λ’ m=1,2,3,…
λ’为入射光在介质中旳波长 条纹间距为 Δx=Dλ/(nd)=Dλ’/d 干涉条纹变密。
杨氏双缝干涉旳应用
❖ 测量波长 ❖ 测量薄膜旳厚度和折射率 ❖ 长度旳测量微小变化量
S线光源,G是一种遮光屏,其上有两条与S平行旳狭缝S1、 S2,且与S等距离,所以S1、S2 是相干光源,且相位相同;S1、 S2 之间旳距离是d ,到屏旳距离是D。
P
r1
S1
x
Sd
r2
O
S2
D
I
光强分布 干涉条纹
同方向、同频率、有恒定初相差旳两个单色光源所发 出旳两列光波旳叠加。
考察屏上某点P处旳强度分布。因为S1、S2 对称设置,且大 小相等,以为由S1、S2 发出旳两光波在P点旳光强度相等, 即I1=I2=I0,则P点旳干涉条纹分布为
等于一种波长值。 m
(m 1)
2
上式中旳m为干涉条纹旳级次。
x mD
d
(m 0,1,2,)
亮纹
m=0,1,2,…依次称为零级、第一级、第二级亮纹等等。
零级亮纹(中央亮纹)在x=0处。
x (m 1) D
2d
(m 0,1,2,)
暗纹
m=0,1,2,…分别称为零级、第一级、第二级暗纹等等。
例1、求光波旳波长
在杨氏双缝干涉试验中,已知双缝间距为0.60mm,缝和屏相 距1.50m,测得条纹宽度为1.50mm,求入射光旳波长。 解:由杨氏双缝干涉条纹间距公式
e=Dλ/d
能够得到光波旳波长为
λ’为入射光在介质中旳波长 条纹间距为 Δx=Dλ/(nd)=Dλ’/d 干涉条纹变密。
杨氏双缝干涉旳应用
❖ 测量波长 ❖ 测量薄膜旳厚度和折射率 ❖ 长度旳测量微小变化量
S线光源,G是一种遮光屏,其上有两条与S平行旳狭缝S1、 S2,且与S等距离,所以S1、S2 是相干光源,且相位相同;S1、 S2 之间旳距离是d ,到屏旳距离是D。
P
r1
S1
x
Sd
r2
O
S2
D
I
光强分布 干涉条纹
同方向、同频率、有恒定初相差旳两个单色光源所发 出旳两列光波旳叠加。
考察屏上某点P处旳强度分布。因为S1、S2 对称设置,且大 小相等,以为由S1、S2 发出旳两光波在P点旳光强度相等, 即I1=I2=I0,则P点旳干涉条纹分布为
等于一种波长值。 m
(m 1)
2
上式中旳m为干涉条纹旳级次。
x mD
d
(m 0,1,2,)
亮纹
m=0,1,2,…依次称为零级、第一级、第二级亮纹等等。
零级亮纹(中央亮纹)在x=0处。
x (m 1) D
2d
(m 0,1,2,)
暗纹
m=0,1,2,…分别称为零级、第一级、第二级暗纹等等。
例1、求光波旳波长
在杨氏双缝干涉试验中,已知双缝间距为0.60mm,缝和屏相 距1.50m,测得条纹宽度为1.50mm,求入射光旳波长。 解:由杨氏双缝干涉条纹间距公式
e=Dλ/d
能够得到光波旳波长为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
提纲
1.了解光学的发展历史及光学分类 2.掌握光的相干条件及获得相干光的途径 3.掌握杨氏双缝干涉装置、条纹特点 4.掌握光程的概念
光学发展简史
1. 十七世纪两种学说的争论
(1)光的微粒说
可以解释:光的直线传播、 光的反射、折射
不能解释:光的双折射现象
(2)光的波动说
可以解释:光的干涉、衍射、光的直线 传播、反射、折射及双折射等现象。
一、相干光
2.光的相干叠加
若两束光的光矢量 E 满足相干条件,则它们是 相干光,对应的光源叫相干光源。
空间光强分布:
I I1 I22 I1I2cos
I
I1 = I2 = I0
4I0
2I0 I0
4 3 2 0 2 3 4
一、相干光
两个普通光源,在它们都能照到的区域, 能观察到明暗相间的条纹吗?为什么?
3.原子发光模型
原子或分子是物质发光的基元,它们通过
能级跃迁所发射的光是一个个有限长的光波列。
激发态
基态
由于普通光源中大量原子发 出波列具有独立、偶然、间歇 的特点,很难同时满足相干条 件,故不能构成相干光源.
一、相干光
4.如何获得相干光 ?
将普通光源的同一束光分割为两束或多束, 使之经不同路径后相遇而产生干涉现象。
光学发展简史
3. 光具有量子性
19世纪末20世纪初, Albert. Einstein 解释光电效应: 光具有量子性(光子) (具有崭新内涵的微粒说)
光具有波粒二像性(duality)
光学
研究各种光现象、光的本性、光与物质 相互作用的规律。
几何光学 以光的直线传播规律为基础,研究各种
光学仪器的理论。
“粒子”
波动光学 研究光的电磁性质和传播规律,特别是
光的干涉、衍射和偏振规律。“波”
量子光学 以近代量子理论为基础,研究光与物质
相互作用的规律。
“波粒二象”
照相机镜头前有无偏振片的效果对比
A
A
B
B
量子光学应用
一、相干光
•磁光场波a强是度一H种电磁: 波3,.94振动10的14 H是z电~场7.强5 度101E4和H;z
•
: 400 nm ~ 760 nm
其中能引起人眼视觉和底片感光的是
E,故
通常把 E叫做光矢量;
• 光的干涉和衍射是光波发生相干叠加的结果。
1.光波叠加原理
对于在真空中传播的光或在介质中传播的不 太强的光,当几列光波相遇时,其合成光波的光
矢量等于各分光波光矢量的矢量和。 E E1 E2 E3
光学发展简史
2. 波动说的崛起
(1)托马斯·杨的双缝干涉实验(1801) 为波动说提供了有力的证明。
“尽管我仰慕牛顿的大名,但我并不因此非得 认为他是百无一失的。我遗憾地看到他也会弄 错,而他的权威也许有时甚至阻碍了科学的进
(步。2)”菲涅耳采用波动说解释了偏振光的 相干性,并指出光是横波;
(3)19世纪中期,麦克斯韦由理论得到: 光是电磁波,光的传播无需介质。
基本方法:分波阵面法、 分振ห้องสมุดไป่ตู้法、
杨氏双缝干涉
薄膜干涉
1.了解光学的发展历史及光学分类 2.掌握光的相干条件及获得相干光的途径 3.掌握杨氏双缝干涉装置、条纹特点 4.掌握光程的概念
光学发展简史
1. 十七世纪两种学说的争论
(1)光的微粒说
可以解释:光的直线传播、 光的反射、折射
不能解释:光的双折射现象
(2)光的波动说
可以解释:光的干涉、衍射、光的直线 传播、反射、折射及双折射等现象。
一、相干光
2.光的相干叠加
若两束光的光矢量 E 满足相干条件,则它们是 相干光,对应的光源叫相干光源。
空间光强分布:
I I1 I22 I1I2cos
I
I1 = I2 = I0
4I0
2I0 I0
4 3 2 0 2 3 4
一、相干光
两个普通光源,在它们都能照到的区域, 能观察到明暗相间的条纹吗?为什么?
3.原子发光模型
原子或分子是物质发光的基元,它们通过
能级跃迁所发射的光是一个个有限长的光波列。
激发态
基态
由于普通光源中大量原子发 出波列具有独立、偶然、间歇 的特点,很难同时满足相干条 件,故不能构成相干光源.
一、相干光
4.如何获得相干光 ?
将普通光源的同一束光分割为两束或多束, 使之经不同路径后相遇而产生干涉现象。
光学发展简史
3. 光具有量子性
19世纪末20世纪初, Albert. Einstein 解释光电效应: 光具有量子性(光子) (具有崭新内涵的微粒说)
光具有波粒二像性(duality)
光学
研究各种光现象、光的本性、光与物质 相互作用的规律。
几何光学 以光的直线传播规律为基础,研究各种
光学仪器的理论。
“粒子”
波动光学 研究光的电磁性质和传播规律,特别是
光的干涉、衍射和偏振规律。“波”
量子光学 以近代量子理论为基础,研究光与物质
相互作用的规律。
“波粒二象”
照相机镜头前有无偏振片的效果对比
A
A
B
B
量子光学应用
一、相干光
•磁光场波a强是度一H种电磁: 波3,.94振动10的14 H是z电~场7.强5 度101E4和H;z
•
: 400 nm ~ 760 nm
其中能引起人眼视觉和底片感光的是
E,故
通常把 E叫做光矢量;
• 光的干涉和衍射是光波发生相干叠加的结果。
1.光波叠加原理
对于在真空中传播的光或在介质中传播的不 太强的光,当几列光波相遇时,其合成光波的光
矢量等于各分光波光矢量的矢量和。 E E1 E2 E3
光学发展简史
2. 波动说的崛起
(1)托马斯·杨的双缝干涉实验(1801) 为波动说提供了有力的证明。
“尽管我仰慕牛顿的大名,但我并不因此非得 认为他是百无一失的。我遗憾地看到他也会弄 错,而他的权威也许有时甚至阻碍了科学的进
(步。2)”菲涅耳采用波动说解释了偏振光的 相干性,并指出光是横波;
(3)19世纪中期,麦克斯韦由理论得到: 光是电磁波,光的传播无需介质。
基本方法:分波阵面法、 分振ห้องสมุดไป่ตู้法、
杨氏双缝干涉
薄膜干涉
