杨氏双缝干涉实验
杨氏双缝干涉实验步骤

杨氏双缝干涉实验步骤
杨氏双缝干涉实验是在两个狭缝上投射光线,观察穿过狭缝后形成的干涉图案的实验。
其步骤如下:
1. 准备实验装置:在一个黑暗的房间内,设置一块光屏,其中间打两个极细的狭缝(两缝之间的距离称为狭缝间距),可以使用细丝、刀片等制作。
在光屏后方放置一个光源,例如激光、单色光或者狭缝后有直线光源等。
2. 调整实验装置:调整光源和狭缝的位置和角度,使其能够发出平行光束并垂直照射在光屏上,确保两个狭缝之间的距离恰好在可观察范围内。
3. 观察干涉图案:在光屏的另一侧观察光的分布情况。
可以使用肉眼、放大镜或者干涉计等工具来观察光强的分布情况。
4. 分析干涉现象:观察到的干涉图案是由两个光波通过狭缝之后叠加形成的。
如果两个光波的相位差为整数倍的波长,那么干涉就是增强的;如果相位差为半整数倍的波长,干涉则是减弱的。
5. 记录和分析实验结果:观察干涉图案的特征,记录光强的分布情况。
使用干涉公式和波动理论等方法分析实验结果,确定两个狭缝间距、波长等参数。
杨氏双缝干涉实验是探究光的波动性质的重要实验,它可以验证光的波动理论,并提供了许多相关研究和应用的基础。
杨氏双缝实验实验报告

一、实验目的1. 通过杨氏双缝实验,观察光的干涉现象,验证光的波动性。
2. 理解光的干涉条件,包括相干光源的概念。
3. 掌握实验仪器的操作方法,包括光源、狭缝、透镜和屏幕等。
4. 学习如何测量光波的波长。
二、实验原理杨氏双缝实验是由英国物理学家托马斯·杨于1801年提出的,该实验通过观察光通过两个狭缝后在屏幕上形成的干涉条纹,验证了光的波动性。
实验原理基于以下两个假设:1. 光是一种波动现象。
2. 当两束相干光波相遇时,会发生干涉现象。
在杨氏双缝实验中,光通过两个狭缝后,在屏幕上形成一系列明暗相间的干涉条纹。
这些条纹的形成是由于两束光波相遇时发生干涉,即两束光波的振幅相加,导致某些区域光强增强(亮条纹),而另一些区域光强减弱(暗条纹)。
根据杨氏双缝实验的原理,可以推导出干涉条纹间距的公式:\[ \Delta x = \frac{\lambda L}{d} \]其中,\(\Delta x\) 是相邻两条亮条纹或暗条纹之间的距离,\(\lambda\) 是光波的波长,\(L\) 是屏幕到双缝的距离,\(d\) 是两个狭缝之间的距离。
三、实验仪器1. 激光器:提供单色光源。
2. 狭缝板:包含两个平行的狭缝。
3. 透镜:将激光束聚焦到狭缝板上。
4. 屏幕板:用于观察干涉条纹。
5. 支架:用于固定实验仪器。
四、实验步骤1. 将激光器、狭缝板、透镜和屏幕板按照实验要求放置在支架上。
2. 调整透镜,使激光束聚焦到狭缝板上。
3. 调整狭缝板,使两个狭缝平行且距离适中。
4. 调整屏幕板,使屏幕与狭缝板平行,并观察屏幕上的干涉条纹。
5. 记录屏幕上的干涉条纹间距,并计算光波的波长。
五、实验结果与分析1. 在实验过程中,成功观察到屏幕上的干涉条纹,验证了光的波动性。
2. 根据干涉条纹间距的测量结果,计算出光波的波长。
3. 通过实验结果,可以得出以下结论:- 光是一种波动现象。
- 干涉现象是光波的基本特性之一。
波动光学实验系列之杨氏双缝干涉

波动光学实验系列之杨氏双缝干涉
一、引言
波动光学实验一直是光学领域中的重要研究方向,其中杨氏双缝干涉实验是一种经典的实验现象。
本文将介绍杨氏双缝干涉实验的原理、实验装置及其应用。
二、实验原理
杨氏双缝干涉实验是利用光的波动性质进行研究的实验。
在这个实验中,一束光线通过两个密接的缝隙后,形成交替明暗条纹的干涉图样。
这种干涉现象可以用光的波动理论来解释,根据叠加原理,两个波的相位差会决定光的干涉效应。
三、实验装置
杨氏双缝干涉实验的实验装置主要包括光源、双缝光栅、透镜和屏幕。
光源产生一束平行光,通过双缝光栅后,光线经过透镜成像在屏幕上,观察者可以看到干涉条纹的形成。
四、实验过程
在进行杨氏双缝干涉实验时,首先需要调整光源和双缝光栅的位置,使得光线通过双缝形成干涉条纹。
然后调整透镜的位置和焦距,使得干涉条纹清晰可见。
最后观察屏幕上的干涉条纹,并记录实验现象。
五、实验应用
杨氏双缝干涉实验不仅是一种经典的光学实验,还具有广泛的应用价值。
在现代科学研究中,杨氏双缝干涉实验常被用于测量光波的波长、验证光的波动性质,以及研究干涉现象对光学元件的影响等方面。
六、结论
通过对杨氏双缝干涉实验的介绍,我们可以更深入地了解光的波动性质和干涉现象。
这一实验不仅展示了光学的精彩世界,还为我们理解光的本质提供了重要的实验依据。
希望通过这篇文档,读者能够对光学实验有一个更加全面的认识。
以上是关于波动光学实验系列之杨氏双缝干涉的简要介绍,希望能为您带来有价值的信息。
11-2杨氏双缝干涉实验 劳埃德镜

D
物理学
第五版
11-2 杨氏双缝干涉实验 劳埃德镜
例2 如图 离湖面 h = 0.5 m处有一电磁波接 收器位于 C ,当一射电星从地平面渐渐升 起时, 接收器断续地检测到一系列极大 值 . 已知射电星所发射的电磁波的波长为 20.0 cm,求第一次测到极大值时,射电星 的方位与湖面所成角度. 2
D 1 6 107 3 x 3 10 m 3m m 3 d 0.2 10
12
物理学
第五版
11-2 杨氏双缝干涉实验 劳埃德镜
[例题]用薄云母片(n=1.58)覆盖在杨氏双缝的其中一条 缝上,这时屏上的零级明纹移到原来的第七级明纹处。 如果入射光波长为5500Å,问云母片的厚度为多少?
[例题]杨氏双缝的间距为0.2mm,距离屏幕为1m。 (1)若第一到第四明纹距离为7.5mm,求入射光波长
(2)若入射光的波长为 6000 A 求相邻两明纹的间距。 解:
D x k d
x1, 4
k 0,1,2,
D x4 x1 k 4 k1 d
d x1,4 0.2 103 7.5 103 7 5 10 m 5000 A D k4 k1 1 4 1
2
物理德镜
剖面图
r1
r2 单 缝 双 缝
X I
屏
3
物理学
第五版
2)定量分析 S1 d S2
r1
X d 0.5mm 11-2 杨氏双缝干涉实验 劳埃德镜 P
C
r
r2
若:n=1 D
x
D d
在 r2 上截取 PC r1
r r 2 1 O d sin d tan
11-2杨氏双缝干涉实验 劳埃德镜

第 十一章 光学9Fra bibliotek4.* 强度及强度分布
I1 ≈ I 2 = I 0 (Q r1 ~ r2 )
S1
S
r1
θ
p
r2
d
S2
θ
x o
δ ≈ d sin θ
I p = I1 + I2 + 2 I1I2 cos ∆ϕ
0 0 0
d’ d << d '
∆φ = 2I + 2 I cos ∆φ = 4 I cos 2
第 十一章 光学
14
物理学
第五版
1111-2 杨氏双缝干涉实验 劳埃德镜
已知 d = 0.2 mm d ’ = 1 m 求 (1) ∆x14 = 7.5 mm λ = ? ) (2) λ = 600 nm ∆ x ’ = ? ) d’ 解 (1) xk = ± kλ , k = 0 , 1, 2,L ) d ’ d ∆x14 = x4 − x1 = (k 4 − k1 )λ d d ∆x14 λ= = 500 nm d ' (k 4 − k1 ) ’ 1d ’ λ = 1.5 mm (2) ∆x = ) 2d
洛埃镜的光程差
N
第 十一章 光学
18
物理学
第五版
1111-2 杨氏双缝干涉实验 劳埃德镜
例2 如图 离湖面 h = 0.5 m处有一电磁波接 收器位于 C ,当一射电星从地平面渐渐升 起时, 起时, 接收器断续地检测到一系列极大 值 . 已知射电星所发射的电磁波的波长为 求第一次测到极大值时, 20.0 cm,求第一次测到极大值时,射电星 的方位与湖面所成角度. 2
∆x ∝ λ
白光入射时, 级明纹中心为白色 白光入射时,0级明纹中心为白色 可用来定0级位置 级位置) (可用来定 级位置)
杨氏双缝干涉
k 1,2,.....
2)、用波程差表示: k 0,1,2,3.....
d sin
2k .....加强(明).....
x2 d. {(2k 1) 减弱(暗).......(12.8)
D2
k——条纹级次
k 1,2,3.....
3
(2)干涉明纹和暗纹中心的位置: 1)明纹中心的位置:
x D k D ......(12 9) k 0,1,2,.....
d
d
2)暗纹中心的位置:
x D (2k 1) D ......(12 10) k 1,2,3,.....
d
d2
3)k=0时,x 0即在屏中央出现明纹—称为零级
明纹。
如D、不变,而d减小,某级条纹的位置如何
变化?
明纹: k (整数级)
暗纹:(2k-1)/2(半整数级) 5
观察屏
x
(4)相邻两明纹或相邻两暗纹间的距离:
亮纹位置:
xk
D d
k
xk 1
D d
(k
1)
暗纹 +2级
+1级
0级亮纹 -1级 -2级
相邻亮纹间距:
x
xk 1
xk
D d
相邻两明纹中心或相邻两暗纹中心间的距离:
x
D d
.........(12.11)
(2)、相位差: 2 ......(1)
——相干光的波长。
2
2、干涉明暗条纹的位置和条件:
· (1)、干涉明暗条纹的条件:
r1
Px x
1)、用相位差表示:
k 0,1,2,.....
d
r2
r
D
x o x0
双缝干涉和杨氏实验

准备实验器材:激光器、单 缝、双缝、屏幕和测量工具
调整双缝,使光线能够通过 双缝形成干涉图样
观察屏幕上的干涉图样,并使 用测量工具测量干涉条纹间距
实验结果
观察到明显的干涉现象 证明了光的波动性 干涉条纹呈现明暗交替,间距相等 实验结果与理论预测相符
实验结论
双缝干涉和杨氏实验
汇报人:XX
目录
双缝干涉实验
杨氏实验
01
02
双缝干涉实验
实验原理
光源:单色光源,如激光 狭缝:两个相等的狭缝,平行且等距 观察屏:放置在狭缝后方的白色屏幕 干涉图样:明暗交替的干涉条纹
实验过程
准备实验器材:包括光源、双缝装 置、屏幕和测量工具
放置双缝装置:保持双缝平行,并 确保缝宽合适
添加标题
添加标题
添加标题
添加标题
调整光源:确保光源的稳定性和平 行性
观察干涉条纹:在屏幕上观察到明 暗交替的干涉条纹
实验结果
证明光具有波动性质
观察到明暗交替的干涉条纹
干涉条纹的分布与光程差有 关
实验结果支持光的波动理论
实验结论
观察到明显的干涉现象 证明了光的波动性 干涉条纹的分布与理论预测一致 通过实验数据可以杨氏实验采用了双缝干涉技术,通过将单色光投射到双缝上,产生干涉现象
干涉现象的产生是由于光波的相干性,导致光波在通过双缝后形成明暗相间的干涉条 纹
杨氏实验中,通过测量干涉条纹的宽度和间距,可以推导出光波的波长和双缝的间距
杨氏实验的结果证明了光的波动性,为光的本性的研究奠定了基础
实验过程
观察到干涉现象,证明了光的波动性 实验结果与理论预测相符,增强了波动说的可信度 杨氏实验是物理学史上的重要实验之一,为后续研究奠定了基础 实验结论对光的本质有了更深入的认识和理解
杨氏双缝实验

2 干涉减弱
明纹中心
x
D 2k 2a 2
D (2k 1) 2a 2
k 0,1,2,
暗纹中心
每一条纹都对应着一定的波程差(相位差), 如第三级明纹对应的波程差为3。
太原理工大学物理系
4 干涉条纹形状及间距 形状:明暗相间的直条纹(平行于缝) 间距:条纹均匀分布 相邻两条明纹或暗纹的距离: 观察屏 暗纹 +2级 +1级 0级亮纹 -1级 -2级
k红 k 1 紫 ( )
紫 4000 k 1 3 红 紫 7000 4000
未重叠的清晰光谱只有一级。 太原理工大学物理系
条纹形态: 平行于缝的等亮度、等间距、明暗相间条纹
条纹亮度:
I max 4I1
x D d
I min 0
条纹宽度:
条纹变化:
2
k
( n 1)e
太原理工大学物理系
7
缝光源垂直于轴上、下移动对干涉条纹的影响。
1 2
x
S’ S 单 缝
S1
o 0
S2 双缝
0
如图:光源 S 向上移动到 S 则干涉条纹怎么变化
,
屏
条纹将向下平移
太原理工大学物理系
例3 在双缝干涉实验中,单色光源 S 到两缝 S 和 S 1 2 的距离分别为 l1和l2,并且 l l 3 , 为入射
问:(1)中央明纹两测第十级明纹的距离
(2)第十条明纹的位置 (3)用厚度为 e 6.6 106 m ,折射率n=1.58 的玻璃片盖住一缝后,问零级明纹移动了第几 级明纹处? 太原理工大学物理系
D D D D 解: x10 ,10 10 ( 10 ) 20 20 2a 2a 2a d 2 5.5 107 20 1.1102 2 104
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D 解 (1)由双缝干涉明纹条件 x k ,可得 d
x15
D x5 x1 (k5 k1 ) d
杨氏双缝干涉实验
d x15 4 10 6 10 6.0 107 m(橙色) 11 D (k5 k1 ) 1 (5 1)
(2)当 4000 A时,相邻两明纹间距为
杨氏双缝干涉实验
D (1)d 、 一定时,若 变化, x 变化情况
4
杨氏双缝干涉实验
(2)、D 一定时,条纹间距 x 与 d 的关系
5
杨氏双缝干涉实验
二、其他分波阵面干涉装置
6
1.菲涅耳双面镜
装置 S点光源(或线光源,与两镜交线平行);M1和M2:镀 银反射镜,夹角很小; 两反射镜把S发出的光分成两 部分,可以看作缝干涉实验
相位分析
7
同一光源,分波面, 有固定的位相差。从两虚 光源看,位相差为
2 S1 p S 2 p
条纹位置 可直接利用Young双缝干涉的结果。
杨氏双缝干涉实验
2、洛埃镜 洛埃(H.Lloyd)镜的装置如图,它是一个平面镜.从狭缝
S1发出的光,一部分直接射向屏E,另一部分以近90° 的入射角掠射到镜面ML上,然后反射到屏幕E上.
(2k 1)
2
k 0,1, 2,
x
D (2k 1) d 2
D k d
k 0,1,2,
暗纹
杨氏双缝干涉实验
白光照射时,出现彩色条纹。
3
讨论
条纹间距
D x xk 1 xk d
d 、 一定时, D
条纹间距 与 的关系 ;
若 变化 , x 将怎样变化?
8
杨氏双缝干涉实验
发生半波损失的条件:
9
由光疏媒质入射,光密媒质反射;
正入射或掠入射。 半波损失,实际上是入射光在界面的位相与反 射光在界面的位相有的位相差,折合成波程差,就
好象反射波少走(或多走)了半个波长,即 的位相
差折算成波程差为2。
杨氏双缝干涉实验
例12.1 用单色光照射相距0.4mm的双缝,缝屏间距 10 为1m.(1)从第1级明纹到同侧第5级明纹的距离为6 mm,求此单色光的波长;(2)若入射的单色光波长为 4000Å的紫光,求相邻两明纹间的距离;(3)上述两种 波长的光同时照射时,求两种波长的明条纹第1次重 合在屏幕上的位置,以及这两种波长的光从双缝到该 位置的波程差.
4
3
D 1 4 107 x 1103 1.0mm d 4 104
(3)设两种波长的光的明条纹重合处离中央明纹的距 离为x,则有
D D x k1 1 k2 2 d d
k1 2 4000 2 k2 1 6000 3
杨氏双缝干涉实验
由此可见,波长为 4000 A 的紫光的第3级明条纹与波 12
杨氏双缝干涉实验
一、杨氏双缝干涉实验
1
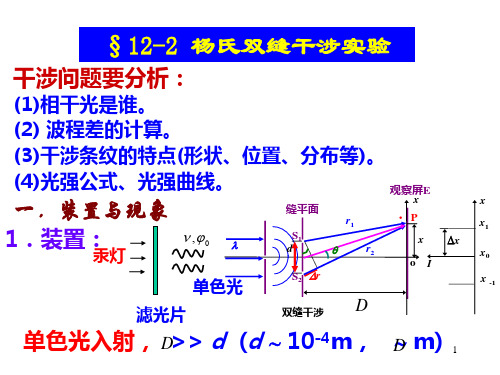
实 验 装 置
s
s1
dM
r1
P
r2
x
o
s2
D d
D
E
波程差
x r2 r1 d sin d tan d D
杨氏双缝干涉实验
s
s1
dM
r1
D
P
r2
x
2
s2
r2 r1
k
o
E
干涉加强 干涉减弱 明纹
长为 6000 A 的橙光的第2级明条纹第1次重合.重合的 位置为
D 2 1 6 10 3 x k1 1 3 10 m 3mm 4 d 4 10
双缝到重合处的波程差为
7
k11 k22 1.2 10 m
6
