§12-2 杨氏双缝干涉
杨氏双缝干涉实验原理

杨氏双缝干涉实验原理杨氏双缝干涉实验是物理学中经典的实验之一,它揭示了光的波动性质和干涉现象。
该实验由英国物理学家托马斯·杨于1801年设计并进行,成为光学领域的重要里程碑。
在这个实验中,通过狭缝中的光波的干涉现象,我们可以观察到光的波动性质和波动方程的应用。
首先,让我们来了解一下杨氏双缝干涉实验的基本原理。
实验装置通常由一束单色光源、两个狭缝和一个屏幕组成。
光源发出的单色光通过两个狭缝后,会形成一系列的光波。
这些光波在屏幕上叠加,形成了一系列明暗条纹,这就是干涉条纹。
这些条纹的分布规律能够揭示出光波的波动性质。
其次,我们来看一下这些干涉条纹是如何形成的。
当两个光波相遇时,它们会相互叠加,形成新的波的幅度。
如果两个波的幅度相同并且相位相同,它们就会相互加强,形成亮条纹;如果两个波的幅度相同但相位相反,它们就会相互抵消,形成暗条纹。
这种干涉现象是由光波的波动性质所决定的,它揭示了光波的波长和波速等重要特性。
在杨氏双缝干涉实验中,我们还可以通过改变狭缝之间的距离、光源的波长等参数,来观察干涉条纹的变化。
这些实验结果与理论计算相吻合,进一步验证了光的波动性质和波动方程的正确性。
通过这些实验,我们不仅可以认识到光的波动性质,还可以应用干涉原理来测量光的波长、研究光的相干性等重要问题。
总之,杨氏双缝干涉实验揭示了光的波动性质和干涉现象,成为了光学领域的重要实验之一。
通过这个实验,我们可以深入理解光的波动性质,探索光的波长、波速等重要特性。
这个实验不仅在理论上具有重要意义,还在实际应用中有着广泛的应用价值。
希望通过本文的介绍,读者对杨氏双缝干涉实验有了更深入的了解,对光的波动性质有了更清晰的认识。
杨氏双缝干涉概述

1.光的干涉现象 2.普通光源的发光机制 3.相干光的获得
1.光的干涉现象
满足一定条件 的两束光叠加时,在叠 加区域光的强度或明暗有一稳定的分布。 这种现象称作 光的干涉
两束光 不相干!
钠
光 灯A
钠 光
灯B
普通 光源(最基本发光单元是分子、原子)
E2
能级跃迁
E1
? ? ?E2 ? E1?/ h
?S
S1 ?
r1
d
?
r2
p x
o
?x
I
?
S2
D
? 波程差: ? r ? r
2
1
? d sin? ? d tg?
1
? d?x D
r2 ? r1 ? k?
干涉相长
r2
?
r1
?
? 2
?2k
? 1?干涉相消
明(暗)条纹的位置公式 ? ? d x
D
?明纹位置
(干涉相长 ? ? ? k? )
x? k
?
?k
D d
从一次发光的波面上取
出几部分再相遇。
S
S1
相 遇
S2
区
分束装置
菲涅耳双镜实验 劳埃德镜实验
分振幅法:
一支光线中分出 两部分再相遇。
薄膜干涉实验 劈尖
分束
薄膜
1 2
相遇
杨氏在杨氏双缝干涉
1801年首先用 实验的方法研 究了光的干涉 现象,为光的 波动理论确定 了实验基础。
光路图 D ?? d
x
(3)若用复色光源,则干涉条纹是彩色的。
(4) D,d 一定时,由条纹间距可算出单色光的波长。
杨氏双缝干涉

选用如图坐标来确定屏上的光强分布
y
S1
x
r1
r2
d 2 r1 = S1 P = ( x − ) + y 2 + D 2 P(x,y,D) 2
z
o
S2
d 2 r2 = S 2 P = ( x + ) + y 2 + D 2 2
由上面两式可求得
r22 − r12 = 2 xd 2 xd ∆ = r2 − r1 = r1 + r2
杨氏双缝干涉 托马斯·杨 Young) 托马斯 杨(Thomas Young) 英国物理学家、医生和考古学家, 英国物理学家、医生和考古学家, 光的波动说的奠基人之一 波动光学: 波动光学:杨氏双缝干涉实验 生理光学: 生理光学:三原色原理 材料力学: 材料力学:杨氏弹性模量 考古学: 考古学:破译古埃及石碑上的文字
S线光源,G是一个遮光屏,其上有两条与S平行的狭缝S1、 线光源, 是一个遮光屏,其上有两条与S平行的狭缝S 且与S等距离,因此S 是相干光源,且相位相同; S2,且与S等距离,因此S1、S2 是相干光源,且相位相同;S1、 之间的距离是d 到屏的距离是D S2 之间的距离是d ,到屏的距离是D。
∆ = n(r2 − r1 ) = mλ (m = 0,±1,±2,L)
即光程差等于波长的整数倍时, 即光程差等于波长的整数倍时,P点有光强最大值
1 ∆ = n(r2 − r1 ) = (m + )λ (m = 0,±1,±2,L) 2 即光程差等于半波长的奇数倍时, 即光程差等于半波长的奇数倍时,P点的光强最小
I = I1 + I 2 + 2 I1 I 2 cos δ = 4 I 0 cos
杨氏双缝干涉原理

杨氏双缝干涉原理
杨氏双缝干涉的原理:光波叠加原理
杨氏双缝干涉的原理是光波叠加原理,用光的波动性解释了干涉现象。
用强烈的单色光照射到开有小孔S的不透明的遮光扳上,后面置有另一块光阑,开有两个小孔S1和S2。
杨氏利用了惠更斯对光的传播所提出的次波假设解释了这个实验。
S1,S2为完全相同的线光源,P是屏幕上任意一点,它与S1,S2连线的中垂线交点S'相距x,与S1,S2相距为rl、r2,双缝间距离为d,双缝到屏幕的距离为L。
因双缝间距d远小于缝到屏的距离L,P点处的光程差:δ=r2-r1=dsinθ=dtgθ=dx/Lsinθ=tgθ,这是因为θ角度很小的时候,可以近似认为相等。
干涉明条纹的位置可由干涉极大条件d=kλ得:x=(L/d)kλ,干涉暗条纹位置可由干涉极小条件d=(k+1/2)λ得:x =(D/d)(k+1/2)λ明条纹之间、暗条纹之间距都是:Δx =λ(D/d)。
干涉条纹是等距离分布的,公式都有波长参数在里面,波长越长,相差越大。
条纹形状:为一组与狭缝平行、等间隔的直线(干涉条纹特点)菲涅尔双棱镜,菲涅尔双面镜、埃洛镜的干涉情况都与此类似。
光的干涉是指若干个光波相遇时产生的光强分布不等于由各个成员波单独造成的光强分布之和,而出现明暗相间的现象。
光的干涉现象的发现在历史上对于由光的微粒说到光的波动说的演进起了不可磨灭的作用。
1801年,托马斯·杨提出了干涉原理并首先做出了双狭缝干涉实验。
大学物理第12章2

(
k
0,1,2,
)
增透膜的最小厚度:d
4n
光学厚度: nd
4
2、增反膜:把低折射率的膜(MgF2)改成同样光学厚度的 高折射率的膜(ZnS)
—ZnS,折射率2.40
2nd
H
2
L
H
2
L
•多层高反射膜
—在玻璃上交替镀上光学厚度
均为/4的高折射率ZnS膜和低
牛顿环 装置简图
分束镜M
.S
显微镜
平凸透镜
o
平晶
R
r
d
A
干涉条纹
(2)光程差和明暗条纹条件
如果不是空 气劈尖,结 果又如何?
应用 ①测微小角度:
已知:λ、n。测出l。
l
2n
2nl
②测微小长度 已知 :λ、n。测出干涉条纹的总级数 K
d
d 2k 1 (明)d k (暗)
4n
2n
③测折射率:已知θ、λ,测l可得n
④ 检测物体表面的平整度
A
B 若干涉条纹是平行直线,说 明B 面是平的。
n11
n11
=
2 0
=
2 0
2n2d
n1
1
2
§12-5 薄膜干涉
薄膜干涉:光波经薄膜两表面反射后相互叠加所形成的 干涉现象。 薄膜干涉分为:等倾干涉与等厚干涉。
干涉光的获取方法:分振幅法。
一、等倾干涉条纹
1、产生条件
扩展光源发出的不同方向的光,入射到厚度均 匀的薄膜上。 同级干涉条纹对应的光线的入射角相 同,这种干涉称为等倾干涉。
《大学物理》第十二章 光学

h
结束 返回
解:
=a
acos2
+
2
=
2asin2
=
2
asin =h
sin =4h
a 2
h
结束 返回
12-5 一平面单色光波垂直照射在厚度 均匀的薄油膜上,油 膜 覆盖在玻璃板上, 所用 单色光的波长可以连续变化,观察到 500nm与700nm这两个波长的光在反射 中消失,油的折射率为 1.30,玻璃的折射 率为1.50。试求油膜的厚度 。
第二级明纹的宽度为
Δx
´=
Δx 2
=2.73 (mm)
结束 返回
12-15 一单色平行光束垂直照射在宽 为 1.0mm 的单缝上,在缝后放一焦距为 20m的会其透镜,已知位于透镜焦面处的 屏幕上的中央明条纹宽度为2.5mm。求入 射光波长。
结束 返回
解:
=
aΔx 2D
=
1.0×2.5 2×2.0×103
sinj
=
k (a+b)
sin =0.1786k-0.5000
在 -900 < j < 900 间,
对应的光强极大的角位置列表如下:
k
sinj j
k
sinj j
0
-0.500 -300
1
2
-0.3232 -0.1464
-18051’ -8025’
3
4
0.0304 0.2072
1045’ 11057’
结束 返回
12-22 一光栅,宽为2.0cm,共有
6000条缝。如用钠光(589.3nm)垂直入射,
中央明纹的位置? 共有几级?如钠光与光
杨氏双缝干涉实验全版.ppt

解 白光经蓝绿色滤光片后,只有蓝绿光。
波长范围21 100 nm
平均波长 1 2 490nm
2
1 440 nm 2 540 nm
2 1 100 2 1 980
条纹开始重叠时有 k2 ( k 1)1
k 1 1
0
2 1
k=4,从第五级开始无法分.辨.。...
例7 单色光照射到相距为0.2mm的双缝上,双缝与屏幕的垂直距离为1m。 求(1)从第一条明纹到同侧旁第四明纹间的距离为7.5mm,求单色光的波长;
(2)若入射光的波长为600nm,求相邻两明纹的距离。
解(1)根据双缝干涉明纹分布条件: x k D
d
明纹间距:
x1、4
x4
x1
D
d
(k4
k1)
k 0,1,2,
得: dx1、4
D(k4 k1)
将 d=0.2mm,x1,4 =7.5mm,D =1000mm 代入
上式
0.2 7.5
5104 mm 500nm
1、 杨氏双缝干涉实验装置
光程差
2a
x D
k
干涉加强
2、干涉条纹
明纹公式 x k D
2a
暗纹公式 x (2k 1) D
..。..
4a
k 0,1,2,
3 干涉条纹形状及间距
明纹条件 暗纹条件
x k D
x
2a (2k 1)
D
4a
k 0,1,2,
相邻两条明纹或暗纹的距离:
x
观察屏 暗纹 +2级 +1级 0级亮纹
1000 (4 1)
(2)由
x D
d
x D 1000 6104 3.0mm
杨氏双缝干涉
条纹位置
可直接利用Young 双缝干涉的结果。
8
三、洛埃境 半波损失
E/
S1
M S2
o E
装置:S: 线光源(或点光源)
M: 平玻璃片作反射镜
S发出的光一部分直接投射到屏上,一部分经 M反射后到屏
上,在重叠区干涉。
干涉的两部分光可以看作是一个实光源S1和一个虚光源 S2
发出的。
9
干涉图样 • 入射角很大,接近90o 。反射系数近于1,故反射很强。 • 两光的振幅几乎相等,可看成等幅干涉。 • 干涉条纹只出现在镜面上半部。 相位
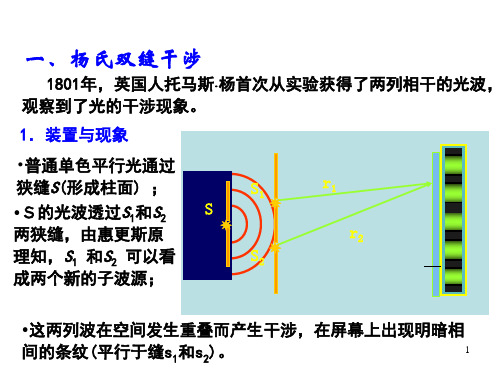
一、杨氏双缝干涉
1801年,英国人托马斯杨首次从实验获得了两列相干的光波, 观察到了光的干涉现象。
1.装置与现象
•普通单色平行光通过
狭缝S(形成柱面) ;
•S的光波透过S1和S2
两狭缝,由惠更斯原
理知,S1 和S2 可以看
成两个新的子波源;
S1
S
S2
r1 r2
S1 S
S2
•这两列波在空间发生重叠而产生干涉,在屏幕上出现明暗相
五种波长的光在所给观察点最大限度地加强。 13
例12-3 在杨氏双缝实验中,欲使干涉条纹变宽,应作怎样 的调整: (A)增加双缝的间距, (B)增加入射光的波长, (C)减少双缝至光屏之间的距离, (D)干涉级k愈大时条纹愈宽。
解:由干涉条纹间距公式
x D
d 可知,应选(B)
14
例12-4 在空气中用波
6
二、菲涅尔双镜
S M1
S1
C S2
i
M2
P P0
E
7
装置
S点光源(或线光源,与两镜交线平行);M1和M2:镀银反射 镜,夹角很小; 两反射镜把 S 发出的光分成两部分,可以看 作是两个虚光源S1和S2发出的光。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.装置与现象 装置: 1.装置:
汞灯
x 缝平面
x x1 ∆x I x0 x -1
ν , ϕ0
r1
·
r2
P x o
λ
S1 d S2 ∆ r
θ
单色光 滤光片
双缝干涉
D
D∼
单色光入射, D >> d 单色光入射,
(d ∼ 10-4m,
m)1
·x 波程差和位相差: 1、波程差和位相差: λ r θ d o x δ 波程差: (1)、波程差: D 在P处相遇叠加的两列相干光的波程差: 处相遇叠加的两列相干光的波程差: 波程差
λ1 = 600nm λ2 = 400nm k1 λ2 400 2 = = = k1 = 2 k2 = 3 即 k2 λ1 600 3 •由此可见,波长为400 由此可见, 400nm 的紫光的第3级明条纹与波长为 的紫光的第3 由此可见 波长为400
d
λ1 = k2
d
λ2
600nm 的橙光的第2级明条纹第1次重合.重合的位置为 的橙光的第2级明条纹第1次重合. 600
D ∆x = λ.........(12.11) d
——可由此测λ。 可由此测
∆l = Dλ .......(4) 2d
条纹的宽度—— ——相邻两明暗条纹中心之间的距离 (5)条纹的宽度——相邻两明暗条纹中心之间的距离:
∆l = xk暗 − xk明 D D 1 kλ = (k + )λ − d d 2
12
12-7)(1)由 ) 由
x明 =
D kλ d
知 6.0 × 10
−3
∴ λ = 0.6 × 10 −3 mm = 600 nm
1 = × 2λ −3 0.2 × 10
(2) ∆x = D λ =
d
1 × 0.6 × 10 −6 = 3 × 10 −3 m = 3mm 0.2 × 10 −3
13
δ 相位差: (2)、相位差: ∆ϕ = 2π ......(1) λ
相干光的波长。 相干光的波长 λ ——相干光的波长。
2
2、干涉明暗条纹的位置和条件: )、干涉明暗条纹的条件 (1)、干涉明暗条纹的条件:
λ
d
θ
r
∆
r
P
r
2
1
·x
x x x0
∆x
o
1)、用相位差表示: )、用相位差表示
∆ϕ =
2π
§12-2 杨氏双缝干涉实验 12干涉问题要分析: 干涉问题要分析:
(1)相干光是谁。 (1)相干光是谁。 相干光是谁 波程差的计算。 (2) 波程差的计算。 (3)干涉条纹的特点 形状、位置、分布等) 干涉条纹的特点( (3)干涉条纹的特点(形状、位置、分布等)。 (4)光强公式 光强曲线。 光强公式、 (4)光强公式、光强曲线。 观察屏E 观察屏
k = 0,1,2,.....
D
I
λ
δ ={
± 2 k π LLL .... 加强 ( 明 ) .......... .( 2 ) ± ( 2 k −1 ) π LL 减弱 ( 暗 ) .......... .( 3 )
k = 1,2,..... k = 0,1,2,3.....
± 2 k LLL.....加强 (明)..... 2
2)、用波程差表示: )、用波程差表示: 用波程差表示
x δ = d sin θ = d . = { λ D ± ( 2 k −1) 2 LL 减弱(暗).......(12.8)
k——条纹级次 条纹级次
k = 1,2,3.....
3
λ
干涉明纹和暗纹中心的位置: (2)干涉明纹和暗纹中心的位置: 1)明纹中心的位置: 明纹中心的位置: D D k = 0,1,2,..... x = δ = ± k λ......(12 − 9) d d 暗纹中心的位置: 2)暗纹中心的位置: D Dλ x = δ = ± (2k − 1) ......(12 − 10) k = 1,2,3,..... d d 2 k=0时 即在屏中央出现明纹—称为零 3)k=0时, x = 0 即在屏中央出现明纹 称为零 级明纹。 级明纹。 不变, 减小, 如D、λ不变,而d减小,某级条纹的位置如何 4 变化? 变化?
r
1
PxBiblioteka x∆x02
I
x δ = r2 − r1 ≈ d sinθ ≈ d tgθ = d ⋅ .......(12.7) D
d——S1,S2两缝之间的距离。 d∼ 10 -4m 两缝之间的距离。 x——两束光在屏上相遇的点P到屏中心的距离。 两束光在屏上相遇的点 到屏中心的距离。 D ——两缝的中心到观察屏中心的距离。 D ∼ m 两缝的中心到观察屏中心的距离 两缝的中心到观察屏中心的距离。
6
x
(6)*S向下移动, )*S向下移动, 向下移动
r1 S1 S S’ S2 d θ B O,
·
x
θ
C
r2 O
δ
d′
E
不变,O向上移到 向上移到O 为了保持光程差 δ = 0 不变 向上移到 ’处, 屏上各级条纹位置只有向上平移,条纹间距不变 条纹间距不变。 屏上各级条纹位置只有向上平移 条纹间距不变。
(2)分布: (2)分布:条纹等间距均匀分布 分布 级次:中间条纹级次最低。 (4) 级次:中间条纹级次最低。 某条纹级次k 某条纹级次 = 该条纹相应的r2 − r1 λ 明纹: 整数级) 明纹: ±k (整数级) 暗纹: 2(半整数级 暗纹:±(2k-1)/2(半整数级) 2(半整数级)
5
观察屏 暗纹 +2级
12. 用单色光照射相距0.4 mm的双缝 , 的双缝, 例 12.1,P142): 用单色光照射相距 的双缝 缝屏间距为1 缝屏间距为 m. (1) 从第 1 级明纹到同侧第 5 级明纹的距离为 6 mm, 1 从第1级明纹到同侧第5级明纹的距离为6 , 求此单色光的波长; 求此单色光的波长; 若入射的单色光波长为400 400nm 的紫光 , 求相 的紫光, (2) 若入射的单色光波长为 400 邻两明纹间的距离; 邻两明纹间的距离; 上述两种波长的光同时照射时, (3)上述两种波长的光同时照射时,求两种波长的明 条纹第1次重合在屏幕上的位置, 条纹第 1次重合在屏幕上的位置 , 以及这两种波长的 光从双缝到该位置的波程差. 光从双缝到该位置的波程差.
9
已知: 已知: d = 0.4mm D = 1m λ2 = 400nm D 解:(1)由双缝干涉明纹的位置 x = ± k λ d D ∆x1−5 = x5 − x1 = (k5 − k1 )λ 可得 d 已知 ∆x1−5 = 6mm 得
d ∆x1−5 0.4×10−3 6×10−3 λ1 = . = × m D (k5 − k1) 1 (5 −1) = 6×10−7 m = 600nm ——橙色 橙色
7
n空气 < n玻璃 , n——折射率 ——折射率 n小——光疏介质;n大——光密介质 ——光疏介质 光疏介质; ——光密介质
(3)、光的半波损失:当光从光疏介质( 较小) (3)、光的半波损失:当光从光疏介质(n较小)入射到光 密介质( 较大)而在界面上反射时,反射光会发生数值 密介质(n较大)而在界面上反射时,反射光会发生数值 的位相突变,相当于反射光多走了半个波长, 为 π 的位相突变,相当于反射光多走了半个波长,称反 射光有半波损失。 射光有半波损失。 有半波损失 发生半波损失的条件: 发生半波损失的条件: 1)、由光疏媒质入射,光密媒质反射; 1)、由光疏媒质入射,光密媒质反射; 2)、正入射或掠入射。 2)、正入射或掠入射。 半波损失, 半波损失,实际上是入射光在界面的位相与反射 光在界面的位相有π的位相差,折合成波程差, 光在界面的位相有π的位相差,折合成波程差,就 好象反射波少走(或多走)了半个波长, 好象反射波少走(或多走)了半个波长,即π 的位 8 相差折算成波程差为λ/ λ/2 相差折算成波程差为λ/2。
观察屏 暗纹 +2级
双缝干涉条纹特点: 3. 双缝干涉条纹特点 (1) 形状:单色光入射是一系列 形状:单色光入射是一系列
∆x
+1级
0级亮纹 -1级 -2级
平行于缝的明暗相间的直条纹。 平行于缝的明暗相间的直条纹。 屏中央( 屏中央(x=0)是零级明纹,两侧依次对称排列着各级 )是零级明纹, 暗条纹,中间级条纹次最低。 明、暗条纹,中间级条纹次最低。
D 1 x = k1 λ1 = 2. × 600×10−9 m = 3×10−3 m = 3mm d 0.4×10−3
双缝到重合处的波程差为
δ = k1λ1 = k2 λ2 = 1.2 × 10 m
−6
11
• 作业: 作业:
• 1、阅读:P97—P101 阅读: P • 2、ex: ex: • 习题:P162 习题: • 12-7) 12。
(2)当 λ2 = 400nm 时,相邻两明纹间距为 当
D 1 ∆x = λ2 = × 400×10−9 m = 1×10−3 m = 1mm d 0.4×10−3
10
(3)设两种波长的光的明条纹重合处离中央明纹的距 设两种波长的光的明条纹重合处离中央明纹的距 离为x, 离为 ,则有 D D
x = k1
∆x 相邻两明纹或相邻两暗纹间的距离: (4)相邻两明纹或相邻两暗纹间的距离: 亮纹位置: 亮纹位置:
xk = D kλ d xk +1 = D (k + 1)λ d
+1级
0级亮纹 -1级 -2级
相邻亮纹间距: 相邻亮纹间距:
∆x = xk +1 − xk =
D λ d
相邻两明纹中心或相邻两暗纹中心间的距离: 相邻两明纹中心或相邻两暗纹中心间的距离:
