用matlab实现杨氏双缝干涉的实验仿真
基于MATLAB的光学实验模拟
光学模拟计算实验报告班级：物理学122班姓名：学号：实验目的：利用MATLAB软件编程实现了用衍射积分的方法对单缝衍射、杨氏双缝干涉、黑白光栅衍射的计算机模拟；以及用傅立叶变换方法对简单孔径衍射、黑白光栅及正弦光栅夫琅和费衍射的模拟。
实验仪器及软件：MATLAB；衍射积分；傅立叶变换；计算机模拟实验原理：大学教学课程中引入计算机模拟技术正日益受到重视，与Basic、C和Fortran相比，用MA TLAB软件做光学试验的模拟，只需要用数学方式表达和描述，省去了大量繁琐的编程过程。
下面来介绍利用MATLAB进行光学模拟的两种方法。
（一）衍射积分方法：该方法首先是由衍射积分算出接收屏上的光强分布，然后根据该分布调制色彩作图，从而得到衍射图案。
1．单缝衍射。
把单缝看作是np个分立的相干光源，屏幕上任意一点复振幅为np个光源照射结果的合成，对每个光源，光程差Δ=ypsinΦ,sinΦ=ys/D,光强I=I0(Σcosα)2+(Σsinα)2，其中α=2Δ/λ=πypys/λD编写程序如下，得到图1lam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam;图1 单缝衍射的光强分布 sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2;endN=255;Br=(B/max(B))*N;subplot(1,2,1)image(ym,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys); 2． 杨氏双缝干涉两相干光源到接收屏上P 点距离r 1=(D 2+(y-a/2)2)1/2, r 2=(D 2+(y+a/2)2)1/2,相位差Φ=2π（r 2-r 1）/λ,光强I=4I 0cos 2（Φ/2） 编写程序如下，得到图2 clear lam=500e-9 a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n); for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2); r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); end N=255;Br=(B/4.0)*Nsubplot(1,2,1) image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys) 3． 光栅衍射公式：I=I 0（sin α/α）2（sin(λβ)/sin β）2α=(πa/λ)sin Φ β=(πd/λ)sin Φ编写程序如下：得到图3clearlam=500e-9;N=2; a=2e-4;D=5;d=5*a; ym=2*lam*D/a;xs=ym; n=1001;ys=linspace(-ym,ym,n); for i=1:nsinphi=ys(i)/D;alpha=pi*a*sinphi/lam; beta=pi*d*sinphi/lam;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2; B1=B/max(B);end图2 杨氏双缝干涉的光强分布 图3 黑白光栅衍射光强分布NC=255;Br=(B/max(B))*NC; subplot(1,2,1) image(xs,ys,Br); colormap(gray(NC)); subplot(1,2,2) plot(B1,ys);（二）傅立叶变换方法：在傅立叶变换光学中我们知道夫琅和费衍射场的强度分布就等于屏函数的功率谱。
基于MATLAB杨氏干涉仿真实验
基于MATLAB杨氏干涉仿真实验张防震 朱亚琼（河南财政税务高等专科学校 河南 郑州 450002）摘 要： 利用MATLAB 高性能的数值计算和可视化软件特点，对光学中的杨氏干涉实验进行仿真。
单色光双缝干涉的干涉图形是一组几乎是平行的直线条纹，且相邻两明条纹间间距相等，通过MATLABf仿真中可见相邻条纹间距，可知观察值与公式计算出的结果完全一致，故仿真结果正确。
使得学生对这一实验有更清楚的认识和了解。
关键词： 大学物理；激光技术；杨氏干涉；MATLAB中图分类号：O436.1 文献标识码：A 文章编号：1671－7597（2011）1020173－010 引言2 实验仿真波动光学实验（如光的干涉，菲涅耳衍射，夫琅和费衍射等）内容比以单色光模拟仿真杨氏双缝干涉，模拟时令D=1m ，d=1/100m ，根据公较抽象，如不借助实验，学生很难理解。
光学教材一般配有大量的图片式利用Matlab 编程，代码如下：（包括计算和实验获得的图片），来形象的说明光学中抽象难懂的理论。
D=1;波动光学实验一般需要稳定的环境，高精度的仪器，而教室条件有限，能d=1/100;做的光学实验极少，同时还要受到授课时间的限制。
为了让学生容易理解Lambda=500/1000000000;抽象的内容，克服光学实验对实验条件的限制，可采用计算机仿真光学实ymax=2*Lambda*D/d;验，特别是仿真光学演示实验，配合理论课的进行，把光学课程涉及的大ny=101;y=linspace(-ymax,ymax,ny);多数现象展示在学生面前。
如实验中液晶光阀的分辨率较低，很难得到清x=y;晰的相关峰，利用计算机仿真联合变换相关实验，可以得到清晰的相关for i=l:ny 峰；初学者不易理解光学菲涅耳衍射与夫琅和费衍射，通过光学仿真实for j=l:ny验，可以计算出它们之间的演化规律，清楚的说明二者之间的联系与区l1=squart((y(i)-d/2)^2+0*x(j)+D^2);别。
基于MATLAB的杨氏双缝干涉实验模拟
基于MATLAB的杨氏双缝干涉实验模拟基于MATLAB的杨氏双缝干涉实验模拟摘要：根据光的双缝干涉实验理论，利用MATLAB 编写程序对双缝干涉实验进行模拟，绘制出双缝干涉的图样和光强分布曲线，并且同步计算出相应的条纹间距和对比度，自观地展现了单色光的双缝干涉这一物理现象，实验结果与实际计算结果一致，为双缝干涉的理论与实验提供了有效的支持.关键词：MATLAB；双缝干涉；实验模拟0引言MATLAB既是一种直观、高效的计算机语言，同时又是一个科学计算平台.它为数据分析和数据可视化、算法和应用程序开发提供了最核心的数学和高级图形工具.双缝干涉实验是利用分波振面法获得相干光束，得到干涉图样.而利用MATLAB模拟实验可以形象、直观地演示实验现象，探究光的干涉问题，而且不受实验仪器和实验场所的限制，可以通过改变模拟参数获得不同的仿真结果，并在显示屏上直接显示出来，动态直观地展现各种物理量之间的关系，对于理解光学理论具有积极的作用.1 双缝干涉实验的理论分析杨氏双缝干涉实验是利用分波振面法获得相干光束的典型例了，如图1所示，在普通单色光光源后放一狭缝S,S后又放有与S平行且等距离的两平行狭缝S1,和S2.单色光通过两个狭缝S1,S2射向屏幕，相当于位置不同的两个同频率同相位光源向屏幕照射的叠合，由于到达屏幕各点的距离（光程）不同引起相位差，叠合的结果是在有的点加强，在有的点抵消，造成干涉现象。
d 为双缝的间隔,D 为屏幕到双狭缝平面的距离，y 为O 到P 的距离.考虑两个相干光源到屏幕上任意点P 的距离差为2212d r D y ⎛⎫=+- ⎪⎝⎭2222d r D y ⎛⎫=++ ⎪⎝⎭ 21r r r ∆=-引起的相位差为2rϕπλ∆= 设两束相干光在屏幕上P 点产生振幅相同，均为A 0，则夹角为λ的两个矢量A 0的合成矢量的幅度为()02cos 2A A ϕ=光强B 正比于振幅的平方，故P 点光强为 ()204cos 2B B ϕ= 下面我们从理论上加以推导，由上面的式（1-2）可得()()222121212r r r r r r dy -=+-=考虑到d,y 很小，()122r r D +≈结合（7）式有 21d r r y D -=这样就得点P 处于亮条纹中心的条件为 ,0,1,2,D y k k d λ==±±L（1） （2）（3） （4）（5） （6）（7）（8）（9）图1 双缝干涉示意图因此，亮条纹是等间距的.若采用红光，其波长λ=500 nm,屏幕到双狭缝平面的距离D=1 m ，双缝的间隔d=2mm ，则相邻条纹间距为94150010 2.5100.002D m m d λ--=⨯⨯=⨯2 双缝干涉实验的计算机模拟MATLAB 提供了十分强大的图形处理功能，应用MATLAB 可以实现各种二维图形和三维图形的绘制及控制与表现.对于双缝干涉实验模拟的基本过程是首先设置波长、屏幕到双狭缝平面的距离、双缝的间隔d,光屏的范围，再将仿真光屏的y 方向分成n 个点，然后调用循环语句，根据光强公式，即公式(6)对各采样点的光强进行计算，调用image 函数，绘制实验仿真图像，使用色谱函数colormap 着色，调用plot 函数，绘制光强分布曲线.这些函数都能根据数据自动选择精度、步长，进行颜色、光照及坐标轴等控制，代替用户完成大量底层工作，使用非常方便，根据上面的分析，编写程序Program1.m 文件如下，并运行程序程序得到干涉条纹如图2所示.图2 单色光的干涉条纹与光强变化曲线图2中左图是光屏上的干涉图条纹，右图是光屏上沿y 轴方向光强的变化曲线.从图2中也不难看出，干涉条纹是以点n 所对应的水平线为对称，沿上下两侧交替，等距离排列，从图2上可以看出相邻亮条纹中心间距为2.5x10-4 m.与式(10)计算结果相一致。
matlab演示杨氏双缝干涉实验
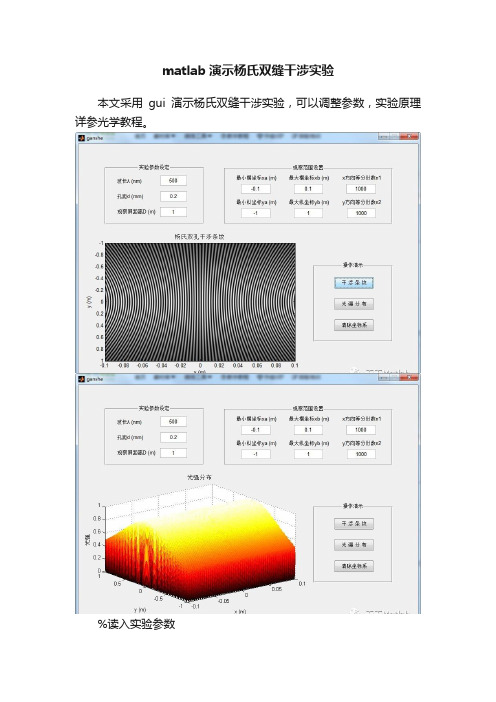
matlab演示杨氏双缝干涉实验本文采用gui演示杨氏双缝干涉实验，可以调整参数，实验原理详参光学教程。
%读入实验参数lambda=str2num(get(handles.edit1,'string'))*1e-9; %读入波长d=str2num(get(handles.edit2,'string'))*1e-3; %读入孔距D=str2num(get(handles.edit3,'string')); %读入观察屏距离%读入观察范围参数xa=str2num(get(handles.edit4,'string')); %最小的横坐标值xb=str2num(get(handles.edit5,'string')); %最大的横坐标值n1=str2num(get(handles.edit6,'string')); %x方向等分份数ya=str2num(get(handles.edit7,'string')); %最小的纵坐标值yb=str2num(get(handles.edit8,'string')); %最大的纵坐标值n2=str2num(get(handles.edit9,'string')); %y方向等分份数k=2*pi/lambda; %计算波数x=linspace(xa,xb,n1); %x坐标y=linspace(ya,yb,n2); %y坐标[x,y]=meshgrid(x,y);r1=sqrt((x-d/2).^2 y.^2 D^2);r2=sqrt((x d/2).^2 y.^2 D^2);I=(cos(k*r1)./r1 cos(k*r2)./r2).^2 (sin(k*r1)./r1 sin(k*r2)./r2).^2;I=I/(max(max(I)));I=I*255;axes(handles.axes1)x=linspace(xa,xb,n1);y=linspace(ya,yb,n2);image(x,y,I)colormap(gray(255))xlabel('x (m)')ylabel('y (m)')title('杨氏双孔干涉条纹')%读入实验参数lambda=str2num(get(handles.edit1,'string'))*1e-9; %读入波长d=str2num(get(handles.edit2,'string'))*1e-3; %读入孔距D=str2num(get(handles.edit3,'string')); %读入观察屏距离%读入观察范围参数xa=str2num(get(handles.edit4,'string')); %最小的横坐标值xb=str2num(get(handles.edit5,'string')); %最大的横坐标值n1=str2num(get(handles.edit6,'string')); %x方向等分份数ya=str2num(get(handles.edit7,'string')); %最小的纵坐标值yb=str2num(get(handles.edit8,'string')); %最大的纵坐标值n2=str2num(get(handles.edit9,'string')); %y方向等分份数k=2*pi/lambda; %计算波数x=linspace(xa,xb,n1); %x坐标y=linspace(ya,yb,n2); %y坐标[x,y]=meshgrid(x,y);r1=sqrt((x-d/2).^2 y.^2 D^2);r2=sqrt((x d/2).^2 y.^2 D^2);I=(cos(k*r1)./r1 cos(k*r2)./r2).^2 (sin(k*r1)./r1 sin(k*r2)./r2).^2;I=I/(max(max(I)));axes(handles.axes1)x=linspace(xa,xb,n1);y=linspace(ya,yb,n2);mesh(x,y,I)colormap(hot)xlabel('x (m)')ylabel('y (m)')zlabel('光强')title('光强分布')。
工程光学matlab仿真
工程光学仿真实验报告1、杨氏双缝干涉实验（1）杨氏干涉模型屏图, 0（1-8）21（2）仿真程序clear;Lambda=650; %设定波长,以Lambda表示波长Lambda=Lambda*1e-9;d=input('输入两个缝的间距 )'); %设定两缝之间的距离,以d表示两缝之间距离d=d*0.001;Z=0.5; %设定从缝到屏幕之间的距离,用Z表示yMax=5*Lambda*Z/d;xs=yMax; %设定y方向和x方向的范围Ny=101;ys=linspace(-yMax,yMax,Ny);%产生一个一维数组ys,Ny 是此次采样总点数%采样的范围从- ymax 到ymax,采样的数组命名为ys%此数组装的是屏幕上的采样点的纵坐标for i=1:Ny %对屏幕上的全部点进行循环计算,则要进行Ny 次计算L1=sqrt((ys(i)-d/2).^2+Z^2);L2=sqrt((ys(i)+d/2).^2+Z^2); %屏上没一点到双缝的距离L1和L2Phi=2*pi*(L2-L1)/Lambda; %计算相位差B(i,:)=4*cos(Phi/2).^2; %建立一个二维数组,用来装该点的光强的值end %结束循环NCLevels=255; %确定使用的灰度等级为255级Br=(B/4.0)*NCLevels; %定标:使最大光强(4. 0)对应于最大灰度级(白色) subplot(1,4,1),image(xs,ys,Br); %用subplot 创建和控制多坐标轴colormap(gray(NCLevels)); %用灰度级颜色图设置色图和明暗subplot(1,4,2),plot(B(:),ys); %把当前窗口对象分成2块矩形区域 %在第2块区域创建新的坐标轴%把这个坐标轴设定为当前坐标轴%然后绘制以( b (: ) , ys)为坐标相连的线title('杨氏双缝干涉');（3）仿真图样及分析a)双缝间距2mm b)双缝间距4mmc)双缝间距6mm d)双缝间距8mm图1.2改变双缝间距的条纹变化由上面四幅图可以看出，随着双缝之间的距离增大，条纹边缘坐标减小，也就是条纹间距减小，和理论公式d D e /λ=推导一致。
用matlab实现杨氏双缝干涉实验仿真
用MATLAB实现杨氏双缝干涉实验仿真摘要：实验室中，做普通光学实验，受到仪器和场所的限制；实验参数的改变引起干涉图样的改变不明显，难以体现实验的特征。
本文利用MATLAB仿真杨氏双缝干涉实验，创建用户界面，实现人机交互，输入不同实验参数，使干涉现象直观表现出来。
关键词：MATLAB；杨氏双缝干涉实验；用户界面设计；程序编写；仿真。
1. 引言：在计算机迅猛发展的今天，光学实验的仿真越来越多的受科研工作者和教育工作者关注。
其应用主要有两个方面：一是科学计算方面，利用仿真实验的结果指导实际实验，减少和避免贵重仪器的损害；二是在光学教学方面，将抽象难懂的光学概念和规律，由仿真实验过程直观的描述，使学生对学习感兴趣。
在科学计算方面，国外的光学实验仿真是模拟设计和优化光学系统的过程中发展起来的，在这方面美国走在最前，其中最具代表性的是劳伦斯利和弗莫尔实验光传输模拟计算机软件Prop92及大型总体优化设计软件CHAINOP和PROPSUITE；另外法国也开发完成其具有自身特点的光传输软件Miro。
在光学教学方面，国外已有相关的配有光盘演示光学实验的教材。
我国用于科学研究的光学实验计算机数值仿真软件随开发较晚，但也已经取得了显著成绩。
特别是1999年，神光——III原型装置TLL分系统集成实验的启动为高功率固体激光驱动器的计算机数值模拟的研究创造了条件。
目前已基本完成SG99光传输模拟计算软件的开发，推出的标准版本基本能稳定运行。
目前该软件已经应用于神光——III主机可行性论证的工作中。
计算机仿真具有观测方便，过程可控等优点，可以减少系统对外界条件对实验本身的限制，方便设置不同的参数，借助计算机的高数运算能力，可以反复改变输入的实验条件系统参数，大大提高实验效率。
MATLAB是MatlabWorks公司于1982年推出的一套高性能的数值计算和可视化软件。
具有可扩展性，易学易用性，高效性等优势。
通过对目前计算机仿真光学实验的现状和相关研究的分析，本文将用Matlab编程实现杨氏双缝干涉实验的仿真。
基于MATLAB的杨氏双缝干涉实验的研究
1杨氏双缝干涉如图1所示，设单缝光阑S 到狭缝S 1和S 2距离相等，狭缝S 1和S 2的宽度均为b ，双缝之间遮光部分的宽为a ，双缝间的距离为d （d =a +b ），光屏离双缝的距离为D 。
假设S 是单色光源，考察屏幕上某一点P ，从S 1和S 2发出的光波在该点叠加产生合振动的强度为：A 2p =A 21+A 22+2A 1A 2cos δ（1）式中δ为相位差，则δ=2πr 2-r 1λ（2）r 1=（x-d /2）2+y 2+D 2姨（3）r 2=（x+d /2）2+y 2+D 2姨（4）若实验装置中S 1和S 2狭缝宽度相等，有A 1=A 2=A '0，则A 2p =4A '20cos 2δ2（5）因为光波通过狭缝S 1和S 2必然发生衍射，为方便说明问题，在此引用夫琅禾费衍射的结果来说明。
此时（6）式中θ为衍射角，因为D>>d ，近似得到θ=yD （7）基于MATLAB 的杨氏双缝干涉实验的研究崔海瑛（大庆师范学院物理与电气信息工程系，黑龙江大庆163712）摘要：应用MATLAB 软件编程，模拟了杨氏双缝干涉实验光强分布图形，通过改变波长、缝宽等参数，研究了双缝干涉条纹的光强变化规律。
得到双缝的宽窄是造成杨氏双缝干涉实验条纹光强分布不均的主要因素，以及杨氏双缝干涉条纹宽度与波长反比等规律，这与光学理论相符合。
并且通过对该实验进行计算机模拟，可以直观地分析各参数对干涉结果的影响，对光学教学有重要的意义。
关键词：杨氏双缝干涉；光强分布；MATLAB ；模拟；衍射作者简介：崔海瑛（1983-），女，黑龙江大庆人，大庆师范学院物理与电气信息工程系教师，从事光学信息方向研究。
中图分类号：O436.1文献标识码：A 文章编号：1006-2165(2009)06-0095-03收稿日期：2009-04-15第29卷第6期2009年11月大庆师范学院学报JOURNAL OF DAQING NORMAL UNIVERSITYVol.29No.6November ，200995图1杨氏双缝干涉装置杨氏双缝干涉实验蕴含了干涉和衍射共同作用的结果，这时的双缝衍射的光强分布为（8）2杨氏双缝干涉条纹光强分布分析2.1双缝干涉与衍射的关系在杨氏双缝干涉实验中，在b<<λ的情况下，即两条缝宽度是任意窄的，也就是不考虑衍射的作用，此时它描述的是强度为A'20，相位差为δ的两束光干涉时的光强分布，光屏上任一点的光强为（5）式。
matlab的几个干涉实验模拟
基于matlab 的几个干涉实验模拟------------吴旭普摘要：根据干涉原理对牛顿环，杨氏双缝和迈克尔逊干涉仪原理进行分析得到各种参数的关系，采用计算机模拟方法并通过软件matlab 编程并运行得到干涉图样 关键词：干涉 matlab 牛顿环 杨氏干涉 迈克尔逊干涉仪 一．牛顿环干涉模拟 1.建模如图，牛顿环是一种分振幅法产生干涉的装置，由一光平玻璃和一曲率很大的平凸透镜构成，平玻璃和平凸透镜之间形成了一个空气劈尖，且其等厚轨迹是以接触点为圆心的一系列同心圆，所以干涉条纹的形状也是明暗相间的同心圆。
在编制程序之前，我们需要对决定干涉条纹特征的光程差、相位差与干涉条纹半径r ，光波波长和平凸透镜的曲率半径R 之间的曲率半径R 之间的关系。
对于形成牛顿环干涉处的空气层厚度e ，两相干光的光程差为: 22e λ∆=+由几何关系：因为R>>e ,所以略去故得:所以两相干光的相位差为：=两相干光的干涉光强为：其中分别是反射光1和反射光2的光强，为使问题简单化设平凸透镜和平板玻璃的反射率均为15%，并且设两反射光的光强近似相等，均设为最终牛顿环干涉的光强为2.程序编写Clear all %清除内存lamd=600e-9; %设定入射光波长 R=10; %设定牛顿环曲率 rm=1e-2; %设定干涉条纹区域 x=0:0.0001:rm; y=rm:-0.0001:0; [X,Y]=meshgrid(x,y); r2=X.^2+Y.^2;phi=2*pi*(r2/R+lamd/2)/lamd; %相位差I=4*cos(phi./2).^2; %第一象限干涉光强 N=255; %设定灰度等级Ir2=(I/4.0)*N; %最大光强为最大灰度Ir1=fliplr(Ir2); %矩阵对称操作Ir3=flipud(Ir1);Ir4=flipud(Ir2);Ir=[Ir1 Ir2;Ir3 Ir4]; %构造图像矩阵figureimage(Ir,'XData',[-0.02,0.02],'YData',[0.02,-0.02]); %画干涉条纹colormap(gray(N));axis squareTitle（“牛顿环干涉光强”）3．运行程序与结果分析如图2，模拟结果与实验一致，通过以上推倒可知牛顿环条纹与相位差有很大联系。
利用MATLABGUI模拟双缝干涉
［4］ 徐志东， 陈世涛． 大学物理实验 ［M］ ． 成都： 西南交通大学出版社， 2003． ［5］ 姚启钧． 光学教程 ［M］ ． 北京： 高等教育出版社， 1981．
The Simulation of Double-Slit Interference Based on M ATLAB GUI
Li Fangju
（Department of Physics and Electronic Engineering ，Weinan Teachers University，Wainan 714000，Shaanxi China ）
Abstract：According to the basic theory of optical interference and experimental device ， we set up a mathematical model of the interference experiment ， which can realize the simulation of Young’ s double slit interference experiment based on MATLAB GUI. The GUI （Graphical User Interfaces ）is beautiful and intuitive， the user can directly input the parameters on the GUI， also do not alter the primary procedure ， making the user able to analyze the par- ameters influencing the result． It makes it easy to teach optical theory and experiment ， and offers a new way to design the related CAI． Key words：MATLAB； graphical user interface； interference
基于MATLAB杨氏干涉仿真实验
基于MATLAB杨氏干涉仿真实验作者：张防震朱亚琼来源：《硅谷》2011年第20期摘要：利用MATLAB高性能的数值计算和可视化软件特点，对光学中的杨氏干涉实验进行仿真。
单色光双缝干涉的干涉图形是一组几乎是平行的直线条纹，且相邻两明条纹间间距相等，通过MATLABf仿真中可见相邻条纹间距，可知观察值与公式计算出的结果完全一致，故仿真结果正确。
使得学生对这一实验有更清楚的认识和了解。
关键词：大学物理；激光技术；杨氏干涉；MATLAB中图分类号：O436.1 文献标识码：A 文章编号：1671－7597（2011）1020173－010 引言波动光学实验（如光的干涉，菲涅耳衍射，夫琅和费衍射等）内容比较抽象，如不借助实验，学生很难理解。
光学教材一般配有大量的图片（包括计算和实验获得的图片），来形象的说明光学中抽象难懂的理论。
波动光学实验一般需要稳定的环境，高精度的仪器，而教室条件有限，能做的光学实验极少，同时还要受到授课时间的限制。
为了让学生容易理解抽象的内容，克服光学实验对实验条件的限制，可采用计算机仿真光学实验，特别是仿真光学演示实验，配合理论课的进行，把光学课程涉及的大多数现象展示在学生面前。
如实验中液晶光阀的分辨率较低，很难得到清晰的相关峰，利用计算机仿真联合变换相关实验，可以得到清晰的相关峰；初学者不易理解光学菲涅耳衍射与夫琅和费衍射，通过光学仿真实验，可以计算出它们之间的演化规律，清楚的说明二者之间的联系与区别。
学生们根据自己对光学原理和规律的理解，设置在仿真光学实验中的可控参数，探索和发现光学世界的奥秘，从而调动学习调动积极性。
1 杨氏干涉实验原理杨氏干涉实验是两点光源干涉实验的代表，无论从经典光学还是从现代光学的角度来看，杨氏实验都具有十分重要的意义。
杨氏干涉实验以极简单的装置和巧妙构思实现了普通光源干涉。
杨氏双缝实验的装置如图1所示，按照惠更斯-菲涅耳原理，线光源S上的点将作为次波源向前发射次波（球面波），形成交叠的波场。
基于MATLAB杨氏双缝干涉仿真实验的实现
基于MATLAB杨氏双缝干涉仿真实验的实现
王勤;谢仁权;施建南;王贤书;明雪梅
【期刊名称】《科技信息》
【年(卷),期】2013(000)025
【摘要】本文介绍MATLAB软件在物理实验教学中的应用,阐述杨氏双缝干涉实验的原理及怎样利用MATLAB编程技术实现了仿真.该仿真程序能够绘制单色光的杨氏双缝干涉图样和光强分布曲线,可以根据显示的杨氏双缝干涉模型更改实验参数,直观地分析各参数的变化对于干涉结果的影响,从而为光学理论和实验教学做了补充.
【总页数】2页(P56-57)
【作者】王勤;谢仁权;施建南;王贤书;明雪梅
【作者单位】贵阳中医学院,贵州贵阳550002;贵阳中医学院,贵州贵阳550002;贵阳中医学院,贵州贵阳550002;贵阳中医学院,贵州贵阳550002;贵阳中医学院,贵州贵阳550002
【正文语种】中文
【相关文献】
1.杨氏双缝干涉实验的MATLAB仿真 [J], 庄云飞;卞雅兰
2.杨氏双缝干涉实验的MATLAB仿真设计 [J], 陈燕;何松
3.基于MATLAB的杨氏双缝干涉实验仿真 [J], 毛欲民;洪家平
4.基于MATLAB的杨氏双缝干涉实验仿真 [J], 赵爽; 周哲海; 潘晗; 张亚男; 李文月
5.基于MATLAB GUI的杨氏双缝干涉仿真动画设计 [J], 张兴坊;刘凤收;闫昕;梁兰菊
因版权原因，仅展示原文概要，查看原文内容请购买。
matlab光学仿真
MATLAB光学仿真实验报告目录一、实验目的 (3)二、实验内容 (3)三、实验原理 (3)四.实验结果（各种干涉图样，） (4)1.平面波与球面波之间的相互干涉 (4)（1）平面波与平面波方向相对的干涉 (4)（2）球面波与球面波 (5)（3）球面波与平面波 (6)2.双缝干涉 (7)（1）经典杨氏双缝干涉 (7)（2）接收屏在侧面，且二者连线与干涉面垂直 (7)3.多孔干涉 (8)（1）三孔干涉 (8)（2）四个孔干涉 (9)4.多个不同方向的平面波 (10)5.牛顿环与电磁波传播 (10)（1）牛顿环 (10)（2）模拟电磁波动画 (11)五，实验总结与感想 (11)一、实验目的通过对光学现象的仿真，加深对各种光学现象本质的理解，同时，学会利用MATLAB，这种有效工具研究物理光学。
二、实验内容这次由于时间关系，只研究了光的干涉现象，不过干涉内容很多，按照老师给的实验的提示内容，我每个都做了。
并且自己还加了一些内容。
按先后顺序非别如下：1.平面波与球面波之间的相互干涉（1）平面波与平面波方向相对的干涉，并且调整角度，方向相对干涉。
（2）球面波与球面波，这个研究的比较多，我分别研究了两个光源，三个，四个以及六个光源在与之共面的平面上的干涉，得到许多精美的图案。
（3）球面波与平面波2.经典的杨氏双缝干涉由于杨氏干涉比较重要，所以研究的时间相对较长，这个我为了更好的调整参数，采用了先输入数据的方法，之后才运行得到结果，我还增加了研究非单色光的研究。
另外，我还研究了与两个点光源连线相垂直的屏上的干涉，虽然这个不属于杨氏干涉，但是原理其实差不多。
这部分其实原理差不多，只需要设置对参数。
这部分分别研究了三孔和四孔的干涉，并且干涉屏的位置也不一样，分为与孔面平行和与孔面平行，总共四中情况，从中自己也找到了规律。
这部分研究了三个不同方向的片面波与四个方向的平面波，从中得到一些图案，找到了规律。
5.模拟电磁波传播动画（代码借鉴一本参考书的）与牛顿环为了加深对电磁波传播的理解，做了个模拟电磁波传播的动画，另外，还做了个牛顿环干涉。
基于MATLAB的杨氏双缝干涉实验仿真
基于MATLAB 的杨氏双缝干涉实验仿真收稿日期：2018-11-06基金项目：校教学改革立项项目，信息化教学手段在《物理光学》教学中的应用探索（2018JGYB07）；北京市教育委员会科技计划项目，基于半导体激光列阵耦合的大功率板条激光器研究（KM201811232007）作者简介：赵爽（1974-），女（汉族），山东泰安人，副教授，博士，研究方向：大功率激光器件及平板显示器件。
一、引言物理光学研究的主要现象为光的干涉、光的衍射和光的偏振。
其中杨氏双缝干涉理论在光的干涉教学中占有很重要的地位。
由于物理光学从光的微观上来理解光的本质，因此比较抽象[1]。
如果不借助于实验现象，学生很难理解其原理。
这一直以来都是教学过程中的重点和难点。
但是由于实验条件的限制，学生很难在课堂上通过实验来观察光的干涉现象，因此也就无法获得直观的认识。
随着计算机技术的飞速发展，计算机辅助教学（CAI ）越来越受到人们的青睐，这为解决上述难题提供了途径。
Math Works 公司开发的Matlab （Matrix Laboratory ）软件是当今国际上公认的在数值计算和可视化图形、图像处理领域最为优秀的工程软件之一，广泛地应用于数学分析、系统仿真、信息光学、数字图像处理等领域[2]。
Matlab 强大的绘图和动画功能可以生动形象且准确地反映出连续变化的物理光学现象。
因此，将Matlab 与光学教学有机地结合起来[3-6]，有助于加深学生对基本概念和现象的理解以及认识，激发学生的学习热情，同时也能够使教学内容更加丰富，从而提高教学质量。
本文中，我们采用了计算机仿真技术对杨氏双缝实验进行仿真，课上学生可以形象直观地感受光的干涉现象。
可以让学生加深对所学光学内容的认知，把那些过于抽象的光学概念及解析公式简洁明了地呈现在学生面前。
二、杨氏干涉实验原理杨氏干涉实验根据干涉屏上光路要通过的形状不同分为双缝干涉和双孔干涉。
本文以杨氏双缝干涉为例，阐述其干涉原理[7]。
matlab光学仿真实验 13171019
光学仿真实验一．前言此次光学仿真实验，是基于matlab来进行的。
在这仿真的一系列过程中，对于光学现象出现的条件，以及干涉、衍射是光波叠加的本质都有了更深的认识。
还从中学习了matlab这一利器的知识，这两三个星期的学习是极其值得的。
二．正文1.杨氏双孔干涉学习的开端是从双孔干涉开始，在极其理想的情况下进行仿真，即忽略了孔的大小等影响因素，直接认为是俩球面波进行叠加干涉。
代码如下：clear;l=521*10.^(-9); %波长d=0.05; %俩孔的距离D=1; %孔到光屏的距离A1=1; %复振幅强度A2=1;x=linspace(-0.0001,0.0001,1000);y=linspace(-0.0001,0.0001,1000);[x,y]=meshgrid(x,y);r1=sqrt((x-d/2).^2+y.^2+D^2);r2=sqrt((x+d/2).^2+y.^2+D^2);E1=A1./r1.*exp(1i*r1*2*pi/l);E2=A2./r2.*exp(1i*r2*2*pi/l);E=E1+E2;I= abs(E).^2;pcolor(x,y,I);shading flat;colormap (gray);认为球面波位置在（d/2,0）和（-d/2,0）处，对于在光屏上任意（x,y）点计算距离，计算出每个球面波到其的复振幅，叠加求光强I。
所得图像：这是光屏很小的情况下正中心出条纹，近似于平行线。
现在来看一下大光屏下的条纹，即x，y最大都是0.1，黑白、彩色是这样的：复杂许多，与下文双缝对比明显！立体大屏下的图像为：现在讨论改变条件引起小屏条纹的变化趋势：ⅰ.波长变小为100nm，条纹变细，符合随波长增大，干涉条纹变粗，波长变小，干涉条纹变细的规律。
dⅱ.俩孔间距变大为0.1m，干涉条纹变细，符合孔间距与条纹宽度成反比的规律。
ⅲ.孔到光屏距离变大为2m，干涉条纹变粗，符合D与干涉条纹宽度成正比的规律。
Matlab在光学教学中的应用举例-4页word资料
Matlab在光学教学中的应用举例O1-4；G4341、引言近年来，随着教育的发展，学生规模不断扩大，使得高校的实验教学设施面临着严重的挑战；而另一方面，光学作为一门基础学科，如果只是推导理论公式，没有实验演示的话，难以引起学生的兴趣。
基于数值技术或虚拟仿真技术开发实验演示软件是扩大实验教学规模和提高教学质量、教学效率的有效途径，是目前高校教育现代化的发展趋势。
Matlab是美国MathWorks公司开发的一款商业数学软件。
Matlab具有友好的用户界面及接近数学表达式的自然化语言，因而相比C、Fortran 等语言，更方便与初学者入门。
在光学课程教学时，使用Matlab等软件编写实验仿真软件，将抽象的概念经仿真实验过程直观的展示出来，有助于提高学生的学习兴趣；并且利用计算机的高速运算能力，可以实现仿真实验参数的反复、快速的调整，大大提高实验效率。
杨氏双缝干涉是物理学中最重要最基本的实验之一，在物理光学以及原子物理中有着广泛的应用。
本文拟使用Matlab软件实现杨氏双缝干涉实验的仿真，使学生能够直观地学习双缝干涉现象及干涉理论。
2、杨氏双缝干涉相关基础理论杨氏双缝干涉实验的原理如图1（a）所示，图中双缝间距为d，双缝所在平面与观察屏平行，二者间距为D。
屏上O点到两个狭缝的距离相等。
当两个狭缝发出的光在屏上相遇时，会发生干涉现象，屏幕上可观测到干涉条纹。
双缝到达观察屏上P点的光程差满足由光程差导致的相位差为（2）。
假设两个光波在P点的振幅都等于A=1，则两列光干涉叠加后P点的光强为：（3）。
3.仿真过程及结果基于上述原理分析，主程序编写如下：lamda = 632.8e-9；d = 2e-3；D = 1； % 设置波长，双缝间距，双缝与屏的距离xm = 5*lamda*D/d； %设屏上观测点离中心最大距离x = linspace（-xm，xm，101）； % 屏上取101个预测点phi=2*pi*（d*x./D）/lamda； % 计算相位差I = 4*（cos（phi/2））.^2； % 根据相位差计算光强分布subplot（211）；plot（x*1000，I）；title（'干涉光强'）；axis （[-xm*1000 xm*1000 0 4]）；B = I*255/4； % 定?巳?255个级别，使I/4对应最亮subplot（212）；image（x*1000，xm*1000，B）；title（'干涉图样'）；%以图案表示干涉条纹图1（b）为双缝干涉的光强分布及干涉条纹的仿真结果，在平面波入射时可以观察到等间距的平行直条纹。
西邮MATLAB双光束干涉的仿真实验报告
phi=2*pi*(l2-l1)/lamd;
u(i,:)=4*cos(phi/2)^2; %干涉光强
end
colormap(gray)
subplot(1,4,1);
imagesc(x,y,u);%画单色光干涉条纹
title('单色光波干涉条纹')
subplot(1,4,2);
专业：
年级：
学号：
指导教师：
李晓莉
职称：
讲师
时间：
2013-11-18至2013-11-29
双光束干涉的仿真
一、实验目的
对双缝干涉进行计算，绘出1.单色光2.复色光的干涉条纹，总结双缝干涉的特点。
二、实验原理
杨氏双缝干涉实验是最早利用分波阵面法获得相干光，从而获得光波干涉现象的典型实验装置。
如图7.1.1所示，两狭缝间距为d，双缝所在平面与屏幕平行，两者之间的垂直距离为D，O为屏幕上的坐标原点且与两狭缝对称。两个狭缝光源满足振动方向相同、频率相同、相位差恒定的相干条件。故两列光在空间相遇，将产生干涉现象。屏幕上将出现明暗相间的干涉条纹。设OP=y，则由几何关系可知，两个相干光源到达屏幕上任意点P的距离分别为：
三、实验流程及程序
流程图：
N
Y
程序：
clear ;
lamd=5e-7; %设定入射波长
d=0.002; %缝间距
z=1; %屏缝间距
yzd=5*lamd*z/d; %设定屏幕范围
x=yzd;
y=linspace(-yzd,yzd,500);
for i=1:500
l1=sqrt((y(i)-d/2)^2+z^2);
基于matlab干涉系统仿真
成绩：《工程光学》综合性练习一题目：基于matlab的干涉系统仿真学院精密仪器与光电子工程学院专业测控技术与仪器年级 20*＊级班级 *班姓名 *＊学号20＊＊年*＊月综合练习大作业一一、要求3—4人组成小组，对下面给出的各题目利用Matlab等工具进行仿真。
二、仿真题目1、对于杨氏双缝干涉，改变双缝的缝宽和缝间距,观察干涉图样变化①原理图图中参数光线波长:lam=500纳米;双缝距离：d=0。
1毫米;（可调）双缝距接收屏距离：D=1米；接收屏范围：xs：-0.005～0.005ys：—0。
005~0。
005光源振幅:AI=A2=1;（单位振幅，可调)②matlab代码：clear;lam=500e-9；％设定波长lam(500纳米）d=0。
5e—3；％设定两缝之间距离d（0。
5毫米）D=1； %双缝到接收屏距离D（1米）A1=1; ％初始两光源均为单位振幅A2=1;xm=0.005；ym=xm；％接受屏的范围ym，xm(0.01＊0。
01矩形)n=1001；xs=linspace(—xm,xm,n）；％用线性采样法生成两个一位数组xs，ys％(n为总点数)ys=linspace(—ym,ym，n）;L1=sqrt(（xs-d/2).^2+ys。
^2+D^2）；%光屏上点(xs，ys）距光源1距离r1L2=sqrt（(xs+d/2）。
^2+ys。
^2+D^2)；%光屏上点（xs,ys)距光源2距离r2E1=A1。
/sqrt（L1)。
＊exp（1i＊L1＊2＊pi/lam)；%光源1在接受屏上复振幅E1E2=A2。
/sqrt(L2）。
*exp（1i*L2＊2＊pi/lam)；%光源2在接受屏上复振幅E2E=E1+E2; ％复振幅叠加为合成振幅EI=abs（E).^2；％和振幅光强nc=255； %灰度br=（I/4）*nc; ％灰度强度image（xs，ys，br）; ％生成干涉图样colormap(gray(nc)）；③初始干涉仿真图样④改变参数后的仿真图样（缝宽即光振幅A1、A2,缝间距d）A1=1。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
用MATLAB实现杨氏双缝干涉实验仿真摘要：实验室中，做普通光学实验，受到仪器和场所的限制；实验参数的改变引起干涉图样的改变不明显，难以体现实验的特征。
本文利用MATLAB仿真杨氏双缝干涉实验，创建用户界面，实现人机交互，输入不同实验参数，使干涉现象直观表现出来。
关键词：MATLAB；杨氏双缝干涉实验；用户界面设计；程序编写；仿真。
1. 引言：在计算机迅猛发展的今天，光学实验的仿真越来越多的受科研工作者和教育工作者关注。
其应用主要有两个方面：一是科学计算方面，利用仿真实验的结果指导实际实验，减少和避免贵重仪器的损害；二是在光学教学方面，将抽象难懂的光学概念和规律，由仿真实验过程直观的描述，使学生对学习感兴趣。
在科学计算方面，国外的光学实验仿真是模拟设计和优化光学系统的过程中发展起来的，在这方面美国走在最前，其中最具代表性的是劳伦斯利和弗莫尔实验光传输模拟计算机软件Prop92及大型总体优化设计软件CHAINOP和PROPSUITE；另外法国也开发完成其具有自身特点的光传输软件Miro。
在光学教学方面，国外已有相关的配有光盘演示光学实验的教材。
我国用于科学研究的光学实验计算机数值仿真软件随开发较晚，但也已经取得了显著成绩。
特别是1999年，神光——III原型装置TLL分系统集成实验的启动为高功率固体激光驱动器的计算机数值模拟的研究创造了条件。
目前已基本完成SG99光传输模拟计算软件的开发，推出的标准版本基本能稳定运行。
目前该软件已经应用于神光——III主机可行性论证的工作中。
计算机仿真具有观测方便，过程可控等优点，可以减少系统对外界条件对实验本身的限制，方便设置不同的参数，借助计算机的高数运算能力，可以反复改变输入的实验条件系统参数，大大提高实验效率。
MATLAB是MatlabWorks公司于1982年推出的一套高性能的数值计算和可视化软件。
具有可扩展性，易学易用性，高效性等优势。
通过对目前计算机仿真光学实验的现状和相关研究的分析，本文将用Matlab编程实现杨氏双缝干涉实验的仿真。
利用Matlab GUI建立用户界面，实现人机交互；通过自由输入不同实验参数，得到相应的干涉图样和光强分布曲线图，使双缝干涉现象直观化，便于比较不同实验参数对实验的影响。
本文由四部分构成：第一部分阐述杨氏双缝干涉相关理论知识；第二部分进行实现仿真主程序编写；第三部分创建用户界面，并编写回调函数，实现人机交互；第四部分将仿真的双缝干涉实验和传统双缝干涉实验进行比较。
2.杨氏双缝干涉实验．光波干涉的三个条件：第一、两列光波的频率必须相同。
（这一条件的必要性是显而易见的，两列不同频率的光波不可能叠加为简谐振动。
）第二、两列光波频率相同，在相遇点的振动方向必须相同，或者有振动方向相同的分量。
第三、两列光波在相遇的区域内，必须保持稳定的相位差。
. 杨氏双缝干涉实验的构想杨氏双缝干涉实验的装置如图1,所示：图1杨氏双缝干涉实验光路图S 是单色光源，1s 、2s 是不透明板上的两个小孔（后来托马斯·杨为了提高干涉条纹的亮度改为两条平行狭缝）V 是观察屏。
从S 发出的光波，其波面传到2s 、1s 以后形成两列频率相同，振动方向相同的光波，对空间某一点P ，从1s 、2s 到S干涉条纹 布P 点的距离是一定的，或者说光程是一定的，光程差也是一定的，那么从1s 、2s 发出的两列光波到达P 点时，在该点产生的相位差也是一点的，对于空间其他的点也是一样的，有类似的情况。
因此，在两列光波相遇的区域内可以得到稳定的相位差分布；这就满足了光的干涉条件中非常重要的第三个条件，即是这个古老的实验的构思巧妙之处。
2.3. 杨氏双缝干涉条纹的特点及计算S 发出的光波射到光屏上的两个小狭缝1s 和2s 上，1s 和2s 相距很近且道S 的距离相等，从1s 和2s 分别发散出的光波是由同一光波分出来的，所以是相干光，它们在相距为D 的观察屏V 上叠加，形成一定的干涉图样。
假设S 是单色点光源，在观察屏上某一点p ，P 到光屏中心O 点的距离为X ，1s 到P 得距离为1r ，2s 到P 得距离为2r 。
在P 点从1s 和2s 发出的光波在该点叠加产生的光强度为：12I I I =++δ （1）此实验中，令120I I I ==所以 ：204cos 2I I δ= （2） 在点P ，光波1、2的相位差应当是 2122r r r ππ-∆δ==λλ（3） 其中λ是光源的波长，r ∆是光波1、2到达点P 的光程差，在D 、d 、x 之间有D>>x>>d 的关系，因此和1r 和2r 可以看作是十分靠近而接近于平行的线段。
所以 'sin sin r d d d θθθ∆=≈≈ （4）而 2d x D θ-≈则 2()22d d d x dx r D D--∆== d 比x 小一到两个数量级，所以22d dx <<，则上式可以忽略22d ，因而得到dx r D≈∆ 所以 22*dx d x D D ππδ==λλ （P 点的相位差） （5） P 点式任意的，所以（5）式也是任意的。
在观察屏上不同的地方x 的值不同，代入的值就可以得到δ、r ∆。
实验中选定λ、d 、D 后，就可以得到稳定的干涉条纹。
如果观察屏上的某些点的x 值使得光程差满足 dx r m D==±∆λ （m=0、1、2,、3…..） （6） 那么相应的 22*2dx d x m D D πππδ===±λλ （m=0、1、2,、3…..） （7） 将（7）式代入（2）式可得到 ()22004cos 4cos 22I I I m πδ== （m=0、1、2,、3….） 即 04I I = （8）这说明。
在观察屏V 上满足r m =±∆λ的x ，光强最大，这些地方就是亮条纹的中心，此时的x 用x 亮来表示亮条纹中心。
即 =D x m d±亮λ （m=0、1、2,、3…..） （9） 如果观察屏V 上的某些x 的值是该处的光程差满足()'212r m =±+λ∆ （'m =0、1、2,、3…..） (10) 那么 ()'22*21dx d x m D D πππδ===±+λλ （'m =0、1、2,、3…..） （11） 光强为 ()22'004cos 4cos 21022I I I m πδ⎡⎤==+=⎢⎥⎣⎦ （12） 这就表明干涉的结果使这些地方的光强最小，这些地方最暗，这些地方就是观察屏上的暗条纹的中心。
()'=212D x m d ±+暗λ （'m =0、1、2、3…..） （13） 通过上面的推导，我们代入简单数值计算可以得出，相邻亮条纹和相邻暗条纹之间的距离是相等的，它们各自等于： ==D x x d亮暗∆∆λ （14） 通过上面的分析，可以得出杨氏双缝干涉条纹的特点：第一，这组明暗相间的条纹亮度的变化是逐渐的，从最亮慢慢地变弱，直到最暗；又从最暗慢慢加强，直到最亮。
第二，这组条纹是等间距的，即相邻的最暗条纹间的距离（或者说最亮条纹间的距离）是相等的。
3. 编写程序实验时以单色光入射，固定双缝到接收幕屏的距离，调整好双缝间距，双缝间距用d 表示，缝到屏幕的距离用D 表示。
根据上述理论分析，主程序编写如下，clearlam=500e-9;d=2e-3;D=1;ym=5*lam*D/d;xs=ym;n=101;ys=linspace(-ym,ym,n);for i=1:nr1=sqrt((ys(i)-d/2).^2+D^2);r2=sqrt((ys(i)+d/2).^2+D^2);phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2);endN=255;Br=(B/*Nsubplot(1,2,1)image(xs,ys,Br);colormap(gray(N));subplot(1,2,2)plot(B,ys);根据上述理论分析可得，相邻亮条纹和相邻暗条纹之间的距离是相等的，它们各自等于：==D x x d亮暗∆∆λ即条纹间距d D x λ=，用edit_lam 表示波长，单位是纳米；用edit_D 表示双缝到屏幕的距离，单位是米；用edit_d 表示双缝间距，单位是厘米；则可计算干涉条纹间距。
>>edit_interval=edit_lam*edit_D/(edit_d*10000);其中edit_interval 表示条纹间距，计算出来的单位是毫米。
回调函数编程为： num1=str2num(get,'string'));num2=str2num(get,'string'));num3=str2num(get,'string'));num4=num2str(num1*num2/(num3*10000));set,'string',num4);4. 用户界面设计为了实现人机交互，方便人们分析不同参数对实验的影响，我设计了图形用户界面，如图2， 自由输入参数，编写了相应的回调函数，可以实现人机交互；图2.用户界面当输入单色光光波波长，双峰间距，屏缝间距，然后点击演示，即可在图形框现实相应的干涉图样和光强分布图，如图3；图3干涉图样、光强分布曲线点击界面上的计算条纹间距，在interval数据框中可显示计算的条纹，如图4。
图4.计算条纹间距5.仿真实验与传统实验的比较传统实验，要受到实验环境、仪器设备的制约；除此之外，还要求操作者能熟练调节各个仪器，才能是实验顺利完成，在屏幕上才能看到清晰的干涉图样。
但是，当改变实验参数时，看到的干涉图样改变不是很明显，不易体现改变实验参数对实验的影响，不能完全体现实验的特征。
但它能锻炼学生的动手操作能了，熟悉实验步骤。
利用计算机仿真杨氏双缝干涉实验，不受实验环境、实验条件的影响，是难理解的干涉现象直观的呈现出来，通过输入不同实验参数，得到相应的干涉图样、光强分布曲线，便于观察和比较试验参数对地实验的影响。
但是，都使用仿真实验进行教学，不利于学生动手能力和创新能力的陪养。
6.结束语由上面的分析和讨论，可以看出，用计算机对光学实验进行仿真，给教学带来了很大便利，它可以不受实验场所、仪器的限制，使实验及时化、方便化，更使抽象难懂的光学概念形象化。
致谢：本论文是在老师悉心指导下完成的，在此，对任老师在我整个论文写作中提供的诸多帮助表示诚挚的感谢！参考文献：[1] 赵成美、丁兰英，《干涉与衍射》，科学出版社；[2] 胡守信、李柏年，《基于MATLAB的数学实验》，科学出版社。