传感器中的弹性敏感元件汇总
合集下载
传感器的敏感材料与敏感元件介绍
3.2.1 温度敏感陶瓷材料
❖ 陶瓷温度传感器是利用陶瓷材料的电阻、磁性、介电、半 导等物理性质随温度而变化的现象制成的，其中电阻随温度 变化显著的称为热敏电阻。对热敏电阻的基本特性要求包括 有：①电阻率；②温度系数的符号与大小；③稳定性。
❖ 按热敏电阻的温度特性可分为负温度系数热敏电阻 （NTC），正温度系数热敏电阻（PTC）和临界温度电阻 （CTR）3类。
❖ 根据被测参数的功能类型来划分敏感材料。例如温度敏 感材料、压力敏感材料、应变敏感材料、光照度敏感材 料等。
❖ 按照材料的结构类型进行分类。该分类方法包括半导体 敏感材料、陶瓷敏感材料、金属敏感材料、有机高分子 敏感材料、光纤敏感材料、磁性敏感词材料等等。
3.1 半导体敏感材料及元件
❖ 传感器对半导体敏感材料最基本要求是换能效率高，即可 将其他形式能量转换为电能，且易制成器件。
图3-8 TiO2含量对电阻的影响
❖ 3 钙钛矿型结构陶瓷湿度敏感材料
钙钛矿型结构的化学通式为ABO3 ，具有钙钛矿结构的纳米 级复合氧化物陶瓷材料的表面、界面性质优异，对环境湿气 度化非常敏感，是湿度敏感材料发展的新方向。 BaTiO3晶体是较早被人们认识的铁电材料之一。BaTiO3具 有很好的湿敏性质，随着BaTiO3颗粒尺寸的减小，湿敏特 性提高，响应加快。
积的空隙中。间隙较小的
是氧四面体中心，为A位置，
间隙较大的则是氧八面体
位置，为B位置。
图3-6 两种结构类型
❖ （2） 典型的尖晶石结构陶瓷湿度敏感材料 纯MgCr2O4为正尖晶石结构，是绝缘体，不宜用作感湿材料。 当加入适量杂质，如MgO、TiO2、SnO2等；或在高温煅 烧，瓷体中呈现过量的MgO时， MgCr2O4即形成半导体。 图3-7表示MgCr2O4中添加受主 杂质MgO时对电阻率的影响。
弹性敏感元件
x 2
1 O F
4、弹性后效
当载荷从某一数值变化到另一 数值时，弹性元件不是立即完成相 应的变形，而是在一定的时间间隔 中逐渐完成变形，这一现象称为弹 性后效。如图所示，当作用在弹性 敏感元件上的力由零增加至F0时， 弹性敏感元件先变形至x1，然后在 载荷未改变的情况下继续变形到x0 为止。反之，如果力由减至零，弹 性敏感元件变形至x2，然后继续减 小变形，直到恢复原状为止。
弹簧管
弹性敏感元件
一、应力与应变 二、弹性敏感元件的特性 三、弹性敏感元件的类型
一、应与应变： l.应力
截面积为S的物体受到外力F的作用并处于平 衡状态时，物体在单位面积上引起的内力称为应 力，记作σ，其值为 F
a)正向应力：物体两端受拉力或压力 作用时，物体处于拉伸或压缩状态。 拉为正，压为负； b)切向应力：物体一端固定，另一端 受平行于端面的力作用时，内部任 意截面上产生大小相等、方向相反 的应力；图示方向的应力为正值， 反之为负值。
河 南 工 业 职 业 技 术 学 院 电 气 工 程 系
第2章
结构型传感器
掌握结构型传感器的基本特
性和工作原理、典型测量电路
了解其典型应用
结构型传感器
它们以机械力或磁场力作用下产生的位移为基础，通 过弹性元件或构件本身的变换可构成力、压力、加速
度、转矩、液位、流量等传感器，基本上属于结构型
dF K dx
弹性元件特性曲线
K
dF tan dx
2、灵敏度 灵敏度是弹性敏感元件在单位力作用下产生变形的 大小，即为刚度的倒数 ，用k表示。
dx k dF
3、弹性滞后 弹性元件在加、卸载的正反行 程中变形曲线是不重合的，这种现 象称为弹性滞后现象，如图所示。 曲线1和2所包围的范围称为滞环。 弹性滞后现象会给测量带来误差。
传感器中的弹性敏感元件(特性)
Chapter3 传感器中的弹性敏感元 件
引言
变形：物体在外力作用下，形状或尺寸的改变。 弹性变形 弹性元件：具有弹性变形特性的物体。 弹性敏感元件作用：把力、力矩或压力变换成相应的应变 或位移; 然后由各种转换元件，将被测力、力矩或压力转换成电量 。
1
h
弹性特性
作用在弹性敏感元件上的外力与其引起的相应 变形〔应
2.应变
物体受外力作用时产生的相对变形
纵向应变εl
横向应变εr 切应变:切应力所产生的变形。
8
h
式中， x为力F使角点产生位移， L为固定端至力作用点之间的距离
3.虎克定律与弹性模量
σ=Eε τ=Gγ
式中，E为弹性模量或称杨氏模量，单位为N／m2； G为剪切模量或称刚性模量； τ为切应力。
9
h
11
h
弹性敏感元件的类型 1.变换力的弹性敏感元件
图3-1 变换力的弹性敏感元件 a)实心轴 b)空心轴 c、d)等截面圆环 e)变形的圆环
12 f)等截面悬梁 g)等强度悬臂梁 h)变形的悬臂梁 i)扭h转轴
2.变换压力的弹性元件
图3-2 变换压力的弹性敏感元件
1a3)弹簧管
b)波纹管
c)等截面薄板
5.0 9.5～10.5
2.用于一般传感器
2.7
h
21
d)膜盒
e)薄壁圆简
f)薄壁半球
h
1、根本拉压 ：材料受力变形的最根本形式是拉压变形， 由下式计算： E
式中：ε为应变，即单位长度的变形，
l l
因此它是一个
无量纲，习惯上将10-6称为一个微应变；Δl 是受力后发
生的变形，l为受载变形长度；E为材料的弹性模量，单位
引言
变形：物体在外力作用下，形状或尺寸的改变。 弹性变形 弹性元件：具有弹性变形特性的物体。 弹性敏感元件作用：把力、力矩或压力变换成相应的应变 或位移; 然后由各种转换元件，将被测力、力矩或压力转换成电量 。
1
h
弹性特性
作用在弹性敏感元件上的外力与其引起的相应 变形〔应
2.应变
物体受外力作用时产生的相对变形
纵向应变εl
横向应变εr 切应变:切应力所产生的变形。
8
h
式中， x为力F使角点产生位移， L为固定端至力作用点之间的距离
3.虎克定律与弹性模量
σ=Eε τ=Gγ
式中，E为弹性模量或称杨氏模量，单位为N／m2； G为剪切模量或称刚性模量； τ为切应力。
9
h
11
h
弹性敏感元件的类型 1.变换力的弹性敏感元件
图3-1 变换力的弹性敏感元件 a)实心轴 b)空心轴 c、d)等截面圆环 e)变形的圆环
12 f)等截面悬梁 g)等强度悬臂梁 h)变形的悬臂梁 i)扭h转轴
2.变换压力的弹性元件
图3-2 变换压力的弹性敏感元件
1a3)弹簧管
b)波纹管
c)等截面薄板
5.0 9.5～10.5
2.用于一般传感器
2.7
h
21
d)膜盒
e)薄壁圆简
f)薄壁半球
h
1、根本拉压 ：材料受力变形的最根本形式是拉压变形， 由下式计算： E
式中：ε为应变，即单位长度的变形，
l l
因此它是一个
无量纲，习惯上将10-6称为一个微应变；Δl 是受力后发
生的变形，l为受载变形长度；E为材料的弹性模量，单位
弹性敏感元件
敏感元件的输 出就是它的输 入，它把输入 转换成电路参 数量
上述电路 参数接入 转换电路， 便可转换 成电量输 出
1.4.2传感器的分类
根据传感器工作原理分类 其中传感器的工作可靠性、静 态精度和动态性能是最基本的 要求
分 类 方 法
分类根据传感器能量转换情况 根据传感器转换原理分类 按照传感器的使用分类
1.2
传感器及其基本特性
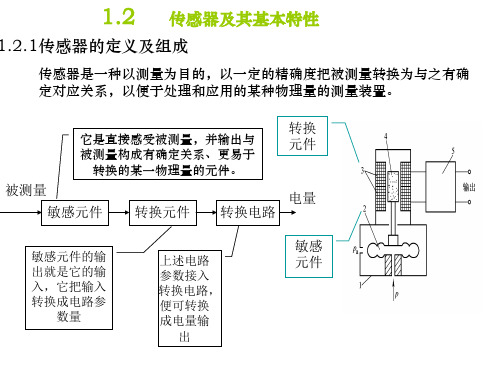
1.2.1传感器的定义及组成
传感器是一种以测量为目的，以一定的精确度把被测量转换为与之有确 定对应关系，以便于处理和应用的某种物理量的测量装置。
它是直接感受被测量，并输出与 被测量构成有确定关系、更易于 转换的某一物理量的元件。
转换 元件
被测量 电量 敏感元件 转换元件 转换电路 敏感 元件
1、刚度 、 刚度是弹性元件受外 力作用下变形大小的量度
刚度也可以从弹性特性曲线上 求得。如图1-11所示曲线1上A 点的刚度，可过A点作曲线1的 切线，该切线与水平夹角的正 切代表该弹性元件在A点处的 刚度, 即 k=tanθ =dF/dx
2 灵敏度
通常用刚度的倒数表示弹性元件的特性，称为弹 性元件的灵敏度
1.4.3传感器的基本特性
1.线性度 所谓的线性度也称非线 性误差，是指传感器实 际特性曲线与拟合直线 （也称理论直线）之间 的最大偏差与传感器满 量程输出的百分比
2.迟滞 迟滞 传感器在正（输入量增大）反（输入量减 小）行程中输出输入曲线不重合称为迟滞 必须指出，正反行程的特性曲线是不重合 的，且反行程特性曲线的终点与正行程特 性曲线的起点也不重合。迟滞会引起分辨 力变差，或造成测量盲区，故一般希望迟 滞越小越好。 3.重复性 重复性 重复性是指传感器在输入按同一方 向作全量程连续多次变动时所得特 性曲线不一致的程度
第三章 传感器中的弹性敏感元件
金属波纹膜片
锡青铜、铍青铜、不锈 钢金属波纹膜片：感受 压力从几百帕到几十兆 帕，材料厚度可从 0.03mm到1.6mm，直 径从十余毫米到250毫 米，其压力位移特性可 以是线性的、渐增的或 渐减的，精度可达千分 之五。
压力膜盒
铍青铜、锡青铜， 不锈钢压力膜盒： 其压力位移特性 可以是线性的， 渐增的或渐减的， 精度可达千分之 三。
灵敏度结构系数β
F
AE
应变大小决定于： •圆柱的灵敏结构系数 •横截面积 •材料性质 •圆柱所承受的力 与圆柱的长度无关。
弹性圆柱（实心、空心）
固有频率
EA
f0 0.159 2l ml
f0
0.249 l
E
结论：
为了提高应变量，应当选择弹性模量小的材料，此时 虽然相应的固有频率降低了，但固有频率降低的程度 比应变量的提高来得小，总的衡量还是有利的。
从弹性特性曲线求得 刚度的方法
做切线 找夹角 求正切
k tan dF
dx
如果弹性元件的弹性 特性是线性的，则其刚 度为常数
第二节 弹性敏感元件的基本特性
灵敏度
灵敏度就是单位力产生变形的大小。 灵敏度是刚度的倒数，一般用Sn表示。
Sn
dx dF
弹性元件并联时
1
Sn n 1
圆形膜片和膜盒（圆形平膜片）
中心扰度与压力关系
PR4
Eh4
16 y
31 2
h
2 23 9 21 1
y
3
h
非线性
小扰度：
ymax
3 1 2
16 E
第3章A传感器中的弹性敏感元件详解
其中，F —作用在弹性元件上的外力； x —弹性元件产生的变形。
刚度也可从弹性特性曲线求得，如下图 所示，曲线的斜率即为弹性元件这某一 点的刚度。 dF tan 代表了弹性元件在某点处的刚度。 dx 若弹性元件的弹性特性是线性的，如曲
线1所示，则其刚度为一常数。 b. 灵敏度(Sn)：弹性敏感元件的灵敏度为刚度的倒数。
圆形平膜片在均布载荷情况下应力分布如图所示。
在压力F作用下，中心最大挠度为：
y max
3 1 R 3 P 16 E h
2 2
（y max h）
P ——压力； R ——膜片的半径； h ——膜片的厚度； y ——膜片中心的最大挠度（位移）。
当
y max h 时,挠度与压力的关系具有下面的关系
F
A——圆柱的横截面积；——截面与轴线的夹角。
a. 在轴向(＝0)产生的应力、应变为
F F 2 2 (cos sin ) A A F F 2 2 (cos sin ) AE AE
b. 在横向(＝90o)产生的应力、应变为
F F 2 2 (cos sin ) A A F F 2 2 (cos sin ) AE AE
截面形状不同又可分为等截面梁和变截面(等强度粱)。
x
l
F
h
b
（1） 等截面梁 应变： x
6F (l x )
x
l
F
EAh
h
x ——距固定端为处的应变值
l ——梁的长度；
b
x ——某一位置到固定端的距离；
E ——梁的材料的弹性模量；
A——梁的截面积；h——梁的厚度。
刚度也可从弹性特性曲线求得，如下图 所示，曲线的斜率即为弹性元件这某一 点的刚度。 dF tan 代表了弹性元件在某点处的刚度。 dx 若弹性元件的弹性特性是线性的，如曲
线1所示，则其刚度为一常数。 b. 灵敏度(Sn)：弹性敏感元件的灵敏度为刚度的倒数。
圆形平膜片在均布载荷情况下应力分布如图所示。
在压力F作用下，中心最大挠度为：
y max
3 1 R 3 P 16 E h
2 2
（y max h）
P ——压力； R ——膜片的半径； h ——膜片的厚度； y ——膜片中心的最大挠度（位移）。
当
y max h 时,挠度与压力的关系具有下面的关系
F
A——圆柱的横截面积；——截面与轴线的夹角。
a. 在轴向(＝0)产生的应力、应变为
F F 2 2 (cos sin ) A A F F 2 2 (cos sin ) AE AE
b. 在横向(＝90o)产生的应力、应变为
F F 2 2 (cos sin ) A A F F 2 2 (cos sin ) AE AE
截面形状不同又可分为等截面梁和变截面(等强度粱)。
x
l
F
h
b
（1） 等截面梁 应变： x
6F (l x )
x
l
F
EAh
h
x ——距固定端为处的应变值
l ——梁的长度；
b
x ——某一位置到固定端的距离；
E ——梁的材料的弹性模量；
A——梁的截面积；h——梁的厚度。
5-1 弹性敏感元件
当膜片边缘固定,膜片的一面受力时,膜片产生弯曲变形,因而 产生径向和切向应变。在应变处贴上应变片,就可以测出应变量, 从而可测得作用力F的大小。也可以利用它变形产生的挠度组成 电容式或电感式力或压力传感器。
二、弹性敏感元件的分类
4.悬臂梁式弹性元件 悬臂梁式弹性元件是一个一端固定,一端自由的弹性元件。 它的结构简单,加工方便,应变和位移较大,适用于测量l～5kN的 力。 当悬臂梁式弹性元件的自由端加有作用力时,梁产生弯曲,梁 的上表面拉伸,下表面压缩。由于它的表面各部位的应变不同,因 此应变片要贴在合适的部位,否则将影响测量的精度。
第五章 力传感器
第一节 弹性敏感元件
¤ 了解弹性敏感元件的定义、特性及分类
介绍
力是物理基本量之一，因此各种动态、静态力的大小的 测量十分重要。
力的测量需要通过力传感器间接完成，力传感器是将各 种力学量转换为电信号的器件。
F 力敏感 元件
转换 元件
显示 设备
力传感器的测量Leabharlann 意图介绍弹性敏感元件：可以把力或压力转换成应变或位移，然 后再由传感器将应变或位移转换成电信号。(P72)
二、弹性敏感元件的分类
（2）波纹管 波纹管是由许多同心圆环状皱纹的薄壁圆管构成，如下图所 示。波纹管可以将压力转换成位移量，主要用做测量和控制压 力的弹性敏感元件，由于其灵敏度高，在小压力和压差测量中 使用较多。
二、弹性敏感元件的分类
（3）波纹膜片和膜盒 平膜片在压力或力的作用下位移量小，因而常把平膜片 加工制成具有环形同心波纹的圆形薄膜，这就是波纹膜片。 其波纹形状有正弦形、梯形和锯齿形。
薄壁圆筒弹性敏感元件的结构
2.变换流体压力的弹性敏感元件 （1）弹簧管 当被测压力p增大时，弹簧管撑直，通过齿条带动齿轮转 动，从而带动电位器的电刷产生角位移。
二、弹性敏感元件的分类
4.悬臂梁式弹性元件 悬臂梁式弹性元件是一个一端固定,一端自由的弹性元件。 它的结构简单,加工方便,应变和位移较大,适用于测量l～5kN的 力。 当悬臂梁式弹性元件的自由端加有作用力时,梁产生弯曲,梁 的上表面拉伸,下表面压缩。由于它的表面各部位的应变不同,因 此应变片要贴在合适的部位,否则将影响测量的精度。
第五章 力传感器
第一节 弹性敏感元件
¤ 了解弹性敏感元件的定义、特性及分类
介绍
力是物理基本量之一，因此各种动态、静态力的大小的 测量十分重要。
力的测量需要通过力传感器间接完成，力传感器是将各 种力学量转换为电信号的器件。
F 力敏感 元件
转换 元件
显示 设备
力传感器的测量Leabharlann 意图介绍弹性敏感元件：可以把力或压力转换成应变或位移，然 后再由传感器将应变或位移转换成电信号。(P72)
二、弹性敏感元件的分类
（2）波纹管 波纹管是由许多同心圆环状皱纹的薄壁圆管构成，如下图所 示。波纹管可以将压力转换成位移量，主要用做测量和控制压 力的弹性敏感元件，由于其灵敏度高，在小压力和压差测量中 使用较多。
二、弹性敏感元件的分类
（3）波纹膜片和膜盒 平膜片在压力或力的作用下位移量小，因而常把平膜片 加工制成具有环形同心波纹的圆形薄膜，这就是波纹膜片。 其波纹形状有正弦形、梯形和锯齿形。
薄壁圆筒弹性敏感元件的结构
2.变换流体压力的弹性敏感元件 （1）弹簧管 当被测压力p增大时，弹簧管撑直，通过齿条带动齿轮转 动，从而带动电位器的电刷产生角位移。
传感器中的弹性敏感元
悬臂梁称重传感器 型号：SQB
灵敏度结构系数 悬臂梁自由端的挠度(位移)
等截面悬臂梁的固有振动频率 J ——梁的横截面的惯性矩， ——梁的单位长度的质量。
4、结论
等截面梁的厚度的减小可以使灵敏度提高，固有振动频率降低。材料的特性参数(E，)对灵敏度和固有频率都有影响。
二、变截面梁(等强度粱)
薄壁圆筒的灵敏度结构系数 薄壁圆筒的固有振动频率为
——力矩； ——扭转棒圆半径； ——横截面对圆心的极惯性矩； ——扭转棒直径。 在力矩测量中常常用到扭转棒，当棒端承受力矩 时，在棒表面产生的最大剪切应力为 最大剪应力与作用的力矩成正比，而与其横截面的极惯性矩和半径之比成反比。
单位长度的扭转角
G为扭转棒材料的剪切弹性系数。
表明单位长度扭转角与扭矩 成正比，而与 抗扭刚度成反比。
——轴向集中作用力； ——工作的波纹数； ——波纹管内半径处的壁厚，即毛坏的厚度。 ——波纹管的外半径； ——波纹管的内半径； ——波纹管的圆弧半径。 ——波纹平面部分的斜角（又叫紧密角） ——相邻波纹的间隙。
波纹管的轴向位移与轴向作用力之间关系可表示为
——取决于K参数和m的系数。 计算K和m出后，可由图表查得 。
——抗扭刚度
扭转棒长度为l时的扭转角为
在与轴线成45o度角的方向上出现最大垂直应力 ，其数值与最大剪切应力 相等，即 这时最大应变为
3.4.4 圆形膜片和膜盒
圆形膜片分平面膜片和波纹膜片两种。在相同压力情况下，波纹膜片可产生较大的挠度。 一、圆形平膜片 圆形平膜片在均布载荷情况下应力分布如图所示。在压力F作用下，中心最大挠度为： ——压力； ——膜片的半径； ——膜片的厚度； ——膜片中心的最大挠度（位移）。
引言
灵敏度结构系数 悬臂梁自由端的挠度(位移)
等截面悬臂梁的固有振动频率 J ——梁的横截面的惯性矩， ——梁的单位长度的质量。
4、结论
等截面梁的厚度的减小可以使灵敏度提高，固有振动频率降低。材料的特性参数(E，)对灵敏度和固有频率都有影响。
二、变截面梁(等强度粱)
薄壁圆筒的灵敏度结构系数 薄壁圆筒的固有振动频率为
——力矩； ——扭转棒圆半径； ——横截面对圆心的极惯性矩； ——扭转棒直径。 在力矩测量中常常用到扭转棒，当棒端承受力矩 时，在棒表面产生的最大剪切应力为 最大剪应力与作用的力矩成正比，而与其横截面的极惯性矩和半径之比成反比。
单位长度的扭转角
G为扭转棒材料的剪切弹性系数。
表明单位长度扭转角与扭矩 成正比，而与 抗扭刚度成反比。
——轴向集中作用力； ——工作的波纹数； ——波纹管内半径处的壁厚，即毛坏的厚度。 ——波纹管的外半径； ——波纹管的内半径； ——波纹管的圆弧半径。 ——波纹平面部分的斜角（又叫紧密角） ——相邻波纹的间隙。
波纹管的轴向位移与轴向作用力之间关系可表示为
——取决于K参数和m的系数。 计算K和m出后，可由图表查得 。
——抗扭刚度
扭转棒长度为l时的扭转角为
在与轴线成45o度角的方向上出现最大垂直应力 ，其数值与最大剪切应力 相等，即 这时最大应变为
3.4.4 圆形膜片和膜盒
圆形膜片分平面膜片和波纹膜片两种。在相同压力情况下，波纹膜片可产生较大的挠度。 一、圆形平膜片 圆形平膜片在均布载荷情况下应力分布如图所示。在压力F作用下，中心最大挠度为： ——压力； ——膜片的半径； ——膜片的厚度； ——膜片中心的最大挠度（位移）。
引言
4.生物医学传感-电阻传感器汇总
8:56 PM
11
压力膜盒
圆形膜片
金属波纹膜片
8:56 PM
12
环行金属波 纹管
波纹管柔性联轴器
8:56 PM 13
弹簧管压力表
8:56 PM
14
电子秤
8:56 PM
15
电子地磅
8:56 PM
16
第四章
电阻式传感器
8:56 PM
17
工作原理
基本工作原理是将被测物理量的 变化转换成传感元件电阻值的变化， 再经转换电路变成电量输出。 包括电位器式、压阻式、热阻式、 应变式等。 学习要点: 1. 应变式传感器：应变效应、电桥测量电路 和温度补偿原理 2. 压阻式传感器：压阻效应、测量桥路及温 度补偿
– 弹性敏感元件 – 弹性支承
常用的弹性敏感元件有：波纹管、弹性梁、柱及 筒、膜片、膜盒、弹簧管等。
8:56 PM 3
二、基本特性
弹性特性： 弹性特性可用刚度或灵敏度来表征。 1. 刚度 弹性敏感元件在外力作用下变形大小的量度， 一般用k表示，它的数学表达式为：
F dF k lim x 0 dx x
8:56 PM
电阻丝电阻温度系数1 0
t温度变化量0 C
C
36
2) 电阻丝材料与受力件材料的线膨胀系数不同，使电 阻相对变化为：
m t c t
Rt K m c t R
式中 βm－受力件材料的线膨胀系数； βc－电阻丝材料的线膨胀系数； K－应变片
l
与n有关，n越大， 越小
l n 10 20 则 1.6 0.4%
l
8:56 PM
35
传感器的弹性敏感元件-第三章.
柱形弹性敏感元件的固有频率：
EA
f0 0.159 2l ml
l — 柱体元件的长度 ml — 柱体元件单位长度的质量
(3.7)
ml A
f0
0.249 l
E
(3.8)
ρ — 柱体元件的材料密度
圆柱形弹性敏感元件主要用于电阻应变式拉力 或压力传感器中。
§3 弹性敏感元件的特性参数计算
2、悬臂梁 结构简单，灵敏度高，多用于较小力的测
5、固有振动频率 固有频率决定其动态特性，一般来说，固
有频率越高，其动态特性越好。
1k
f
(Hz )
2 me
(3.5)
k — 弹性敏感元件的刚度
与灵敏度相矛盾
me — 弹性敏感元件的等效振动质量
§3 弹性敏感元件的特性参数计算
1、弹性圆柱(实心和空心) 结构简单，可承受很大载荷；但产生的位移
很小，所以往往以应变作为输出量。
§3 弹性敏感元件的特性参数计算
6、波纹管
图3.12 波纹管
压力(或轴向力)的变化与伸缩量成比例， 所以波纹管可以把压力(或轴向力)变成位移。
§3 弹性敏感元件的特性参数计算
轴向作用力下，与波纹管的轴向位移的关系：
1 2
n
yF
Eh0
A0
A1
2 A2
B0
h0 2 RH 2
(3.24)
F — 轴向集中作用力 n — 工作的波纹数
具有弹性变形特性的物体。
§1 概述
弹性敏感元件： 利用弹性变形实现将被测量由一种物
理状态变换为另一种相应物理状态的元件。
作用：直接测量被测量
常用的弹性敏感元件有波纹管、弹性梁、 柱及筒、膜片、膜盒、弹簧管等。
EA
f0 0.159 2l ml
l — 柱体元件的长度 ml — 柱体元件单位长度的质量
(3.7)
ml A
f0
0.249 l
E
(3.8)
ρ — 柱体元件的材料密度
圆柱形弹性敏感元件主要用于电阻应变式拉力 或压力传感器中。
§3 弹性敏感元件的特性参数计算
2、悬臂梁 结构简单，灵敏度高，多用于较小力的测
5、固有振动频率 固有频率决定其动态特性，一般来说，固
有频率越高，其动态特性越好。
1k
f
(Hz )
2 me
(3.5)
k — 弹性敏感元件的刚度
与灵敏度相矛盾
me — 弹性敏感元件的等效振动质量
§3 弹性敏感元件的特性参数计算
1、弹性圆柱(实心和空心) 结构简单，可承受很大载荷；但产生的位移
很小，所以往往以应变作为输出量。
§3 弹性敏感元件的特性参数计算
6、波纹管
图3.12 波纹管
压力(或轴向力)的变化与伸缩量成比例， 所以波纹管可以把压力(或轴向力)变成位移。
§3 弹性敏感元件的特性参数计算
轴向作用力下，与波纹管的轴向位移的关系：
1 2
n
yF
Eh0
A0
A1
2 A2
B0
h0 2 RH 2
(3.24)
F — 轴向集中作用力 n — 工作的波纹数
具有弹性变形特性的物体。
§1 概述
弹性敏感元件： 利用弹性变形实现将被测量由一种物
理状态变换为另一种相应物理状态的元件。
作用：直接测量被测量
常用的弹性敏感元件有波纹管、弹性梁、 柱及筒、膜片、膜盒、弹簧管等。
1-4传感器中的弹性敏感元件资料
常用弹性材料： 合金钢、碳钢、铜合金和铝合金；
等截面轴（实心、空心）
特点：
结构简单 能承受很大载荷
用途：
电阻应变式拉力 或压力传感器
图 弹性圆柱
悬臂梁
一端固定一端自由的弹性敏 感元件，以应变或自由端的 位移作为输出量
特点
结构简单，
灵敏度高，
适于较小力的测量
根据梁的截面形状不同又可分为 等截面梁和变截面梁
压力膜盒
铍青铜、锡青铜， 不锈钢压力膜盒。
薄壁圆筒
弹性元件的壁厚一般都小于圆筒直径的1/20， 内腔与被测压力相通时，内壁均匀受压，薄 壁无弯曲变形，只是均匀的向外扩张。所以， 筒壁的每一单元将在轴线方向和圆周方向产 生拉伸应力。
电子秤
电子秤系统基本原理
悬臂梁称重传感器
扭转轴
常用于力矩测量
自由端收到转矩的作用时，扭转轴表面会 产生拉伸或压缩应变
弹簧管
又称波登管，它是弯曲成各种形状的空心管 子，大多数是C型弹簧管。
一端固定，另一端自由。在压力作用下，自 由端将产生位移。
弹簧管
弹簧管的一端连在管接头上，压力通过 管接头导入弹簧管的内腔，管的另一端 （自由端）封闭，并与传感器的其他部 分相连。在压力作用下，管子的截面改 变了形状，截面的短轴伸长，长轴缩短， 截面形状的变化导致弹簧管趋向伸直， 一直伸到与压力的作用相平衡为止（虚 线所示 ）
当膜片的两面受到不同的压力（或力） 的作用时，膜片向压力低的一面应变 移动，使其中心产生与压力差成一定 关系的位移。膜片的 形式主要有平膜 片、垂链式膜片和波纹膜片三种。平 膜片又可按周边是否固定支撑、中心 是否开孔以及膜片区域受力分布状况 的不同等分为多种形式，其中最常用 的 是由周边固定的等截面圆形薄板构 成的平膜片。垂链式膜片由靠近边缘 处开槽的圆板构成，其弹性应变主要 发生在边缘环形槽处，常用这种膜片 压缩应变管或柱来达 到测压目的。垂 链式膜片的硬中心部分在受压移动时 接近平移，因此用于电容式传感器或 压电式传感器效果较好。波纹膜片压 有环状同心波纹。为了增加膜片中心 的 位移可把两个膜片焊在一起制成膜 盒或进一步把数个膜盒串接成膜盒组。
等截面轴（实心、空心）
特点：
结构简单 能承受很大载荷
用途：
电阻应变式拉力 或压力传感器
图 弹性圆柱
悬臂梁
一端固定一端自由的弹性敏 感元件，以应变或自由端的 位移作为输出量
特点
结构简单，
灵敏度高，
适于较小力的测量
根据梁的截面形状不同又可分为 等截面梁和变截面梁
压力膜盒
铍青铜、锡青铜， 不锈钢压力膜盒。
薄壁圆筒
弹性元件的壁厚一般都小于圆筒直径的1/20， 内腔与被测压力相通时，内壁均匀受压，薄 壁无弯曲变形，只是均匀的向外扩张。所以， 筒壁的每一单元将在轴线方向和圆周方向产 生拉伸应力。
电子秤
电子秤系统基本原理
悬臂梁称重传感器
扭转轴
常用于力矩测量
自由端收到转矩的作用时，扭转轴表面会 产生拉伸或压缩应变
弹簧管
又称波登管，它是弯曲成各种形状的空心管 子，大多数是C型弹簧管。
一端固定，另一端自由。在压力作用下，自 由端将产生位移。
弹簧管
弹簧管的一端连在管接头上，压力通过 管接头导入弹簧管的内腔，管的另一端 （自由端）封闭，并与传感器的其他部 分相连。在压力作用下，管子的截面改 变了形状，截面的短轴伸长，长轴缩短， 截面形状的变化导致弹簧管趋向伸直， 一直伸到与压力的作用相平衡为止（虚 线所示 ）
当膜片的两面受到不同的压力（或力） 的作用时，膜片向压力低的一面应变 移动，使其中心产生与压力差成一定 关系的位移。膜片的 形式主要有平膜 片、垂链式膜片和波纹膜片三种。平 膜片又可按周边是否固定支撑、中心 是否开孔以及膜片区域受力分布状况 的不同等分为多种形式，其中最常用 的 是由周边固定的等截面圆形薄板构 成的平膜片。垂链式膜片由靠近边缘 处开槽的圆板构成，其弹性应变主要 发生在边缘环形槽处，常用这种膜片 压缩应变管或柱来达 到测压目的。垂 链式膜片的硬中心部分在受压移动时 接近平移，因此用于电容式传感器或 压电式传感器效果较好。波纹膜片压 有环状同心波纹。为了增加膜片中心 的 位移可把两个膜片焊在一起制成膜 盒或进一步把数个膜盒串接成膜盒组。
2.1--弹性敏感元件PPT课件
14
2.1 弹性敏感元件
（3）波纹膜片和膜盒
图2.6 波纹膜片波纹的形状
-
平膜片在压力 或力作用下位移量 小，因而常把平膜 片加工制成具有环 状同心波纹的圆形 薄膜，这就是波纹 膜片。其波纹形状 有正弦形、梯形和 锯齿形。
15
2.1 弹性敏感元件
（4）薄壁圆筒
圆筒的壁厚一般小于圆 筒直径的1/20，当筒内腔受 流体压力时，筒壁均匀受力， 并均匀地向外扩张，所以在 筒壁的轴线方向产生拉伸力 和应变。
-
12
2.1 弹性敏感元件
2. 变换压力的弹性敏 感元件
这类弹性敏感元件 常见的有弹簧管、波 纹管、波纹膜片、膜 盒和薄壁圆筒等。它 可以把流体产生的压 力变换成位移量输出。
-
图2.4 弹簧管的结构
13
2.1 弹性敏感元件
（2）波纹管
图2..5波纹管的外形
-
波纹管的轴向在流体 压力作用下极易变形，有 较高的灵敏度。在形变允 许范围内，管内压力与波 纹管的伸缩力成正比，利 用这一特性，可以将压力 转换成位移量。
2.1.2 弹性敏感元件的结构形式 弹性敏感元件在形式上可分为两大类 （1）将力转换为应变或位移的变换力
的弹性敏感元件； （2）将压力转换为应变或位移的变换
压力的弹性敏感元件。
-
8
2.1 弹性敏感元件
1. 变换力的弹性敏感元件
图2.3一些变换力的弹性敏感元件形状
（a）实心柱形 （b）空心圆柱形 （c）等截面圆环形 （d）变截面圆环形
量度，一般用k表示
k dF dx
F——作用在弹性元件上的外力； X——弹性元件产生的变形。
-
3
K dx dF
2.1 弹性敏感元件
2.1 弹性敏感元件
（3）波纹膜片和膜盒
图2.6 波纹膜片波纹的形状
-
平膜片在压力 或力作用下位移量 小，因而常把平膜 片加工制成具有环 状同心波纹的圆形 薄膜，这就是波纹 膜片。其波纹形状 有正弦形、梯形和 锯齿形。
15
2.1 弹性敏感元件
（4）薄壁圆筒
圆筒的壁厚一般小于圆 筒直径的1/20，当筒内腔受 流体压力时，筒壁均匀受力， 并均匀地向外扩张，所以在 筒壁的轴线方向产生拉伸力 和应变。
-
12
2.1 弹性敏感元件
2. 变换压力的弹性敏 感元件
这类弹性敏感元件 常见的有弹簧管、波 纹管、波纹膜片、膜 盒和薄壁圆筒等。它 可以把流体产生的压 力变换成位移量输出。
-
图2.4 弹簧管的结构
13
2.1 弹性敏感元件
（2）波纹管
图2..5波纹管的外形
-
波纹管的轴向在流体 压力作用下极易变形，有 较高的灵敏度。在形变允 许范围内，管内压力与波 纹管的伸缩力成正比，利 用这一特性，可以将压力 转换成位移量。
2.1.2 弹性敏感元件的结构形式 弹性敏感元件在形式上可分为两大类 （1）将力转换为应变或位移的变换力
的弹性敏感元件； （2）将压力转换为应变或位移的变换
压力的弹性敏感元件。
-
8
2.1 弹性敏感元件
1. 变换力的弹性敏感元件
图2.3一些变换力的弹性敏感元件形状
（a）实心柱形 （b）空心圆柱形 （c）等截面圆环形 （d）变截面圆环形
量度，一般用k表示
k dF dx
F——作用在弹性元件上的外力； X——弹性元件产生的变形。
-
3
K dx dF
2.1 弹性敏感元件
传感器中的弹性元件(共7张PPT)
在横向（ α =90°）产生的应力、应变为：
σ =-μ F/A ； ε= -μ F/AE
柱形弹性元件的固有频率f0为：
f0 =(0.249/l) √E/ρ 3.4.2悬臂梁
(3-6)
一、等截面梁
x
F
x处的应变为：
εx=6F (l-x)/EAh (3-7)
悬臂梁自由端的挠度（位移）为：
l
h
y=4l³F/E bh³ (3-8)
第三章 传感器中的弹性敏感元件
3.1引言
弹性敏感元件：把被测参数由一种物理状态（如：力、力矩、 压力）变换为另一种所需要的相应物理状态（如：：应变、 位移）
3.2弹性敏感元件的基本特性 3.2.1弹性特性
指作用在弹性敏感元件上的外力与其引起的相应变形之间的关系， 可由刚度或灵敏度表示
一、刚度 弹性敏感元件在外力作用下抵抗变形的能力，即：
F h
l
在压力P的作用下，中心最大挠度为：
ymax=3(1-μ²)R²P/16Eh³ (3-12)
在半径为r处膜片的应变值：
εr=3(1-μ²) (R²-3r³)P/8Eh (3-13)
2F圆弹0 性形敏感平元件的膜基本片特性的固有振动频率：
εr=3(1-μ²) (R²-3r³)P/8Eh (3-13)
第一页，共7页。
k = dF /dx (3-1)
式中：F—作用在弹性元件上的外力；
x—弹性元件产生的变形；
二、灵敏度
F
Sn= dx / dF (3-2) 3.2.2弹性滞后
F
x
F
Δx
x
第二页，共7页。
3.2.3弹性后效
F
F0 3.2.4固有振动频率
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R4 Eh3
P
16
3(1 2 )
3(1 2 )16 NhomakorabeaR4 Eh3
P
3. 波纹膜片的选型依据 ：
（1）膜片所受的力；（2）允许的迟滞误差；（3）所需要的特 性；（4）非线性度等。
4. 膜片有效面积的计算 ：
对于平膜片（经验公式）：
Ax
4
(R
r)2
对于波纹膜片（近似公式）：Ax
3
(R2
Rr
r2)
最大应力；②所用材料的金相组织结构与化学成分；③弹性元件
的加工及热处理等。(分子间存在内摩擦)
解决弹性元件滞后和后效的方法主要有：①选取较大的安全
系数；②合理地选定机构和元件的连接方式，以减少应力集中；
③采用特殊合金，满足测量的要求等。
4. 有效面积Ax：
弹性元件把作用于其上的压力（压差）转化为集中力的能 力 5. 温。度Δ特P性(kg--/-c-m---2T)-越---大-F(,弹kg性) 模量降Ax低E=FPE0[1力 +B面 力t(t-积t0)] 面积
式中：R—膜片的工作半径；r —膜片的硬芯半径。
（二）波纹管 结构：波纹管是一种具有环形波纹的圆柱形薄壁管。
2. 工作原理及特点：
（1）工作原理：在轴向力的作用下波纹管将伸长或缩短；在横 向力的作用下波纹管将在轴向平面内弯曲。
（2）特点：波纹管在很大的变形范围内与压力具有线性关系， 有效面积比较稳定。波纹管的滞后误差较大，刚度较小。
量的比值在变形增量趋近于零时的极限称为弹性元件的刚度。
F
'
lim
0
F
dF
d
M
'
lim
0
M
dM
d
P'
lim
0
P
dP
d
当弹性元件具有线性特性（特性曲线上导数处处相等）时， 刚度即为一常数。这时，刚度就是弹性元件产生单位变形所需施 加的载荷量。因此，对线性弹性元件就有：
F' F
M' M
P' P
（2）灵敏度： 刚度的倒数称为灵敏度，也叫做柔度。
其总灵敏度为 :
n
j ji
i 1
如果把若干个刚度为Fi’ 的线性
弹性元件串联在一起使用，其
总刚度为 :
F'
1 n1
F i1 i
1
或：
n
1
F ' i1 F 'i
F
λ
λ1+λ2 λ1
3. 弹性滞后和弹性后效：
弹性滞后是指在弹性范围内， 弹性元件在加载与卸载时特 性曲线不重合的现象。
λ λ0
弹性后效是指载荷改变后，弹
jF
d
dF
jM
d
dM
jP
d
dP
同样，当弹性元件具有线性特性时灵敏度也为常数。其数值
等于单位载荷作用下弹性元件所产生的变形量。因此，对线性弹
性元件就有：
jF
F
jM
M
jP
P
弹性元件的刚度和灵敏度是两个完全等效的概念，可根据需
要和场合选用其一。
（3）组合线性弹性元件的刚度和灵敏度
① 并联线性弹性元件的刚度和灵敏度
（5）波纹膜片的特点：与平膜片相比，波纹膜片 的容许位移较大，即位移的线性区域较大； 灵敏度较高；工作更可靠。在外廓尺寸不大 时，可以得到较大的集中力——有效面积大； 适当选取波纹形状可以得到不同的输出特性。
（6）膜盒与膜盒组： 把两个膜片沿边缘焊接在一起制成膜盒。在输入 量相同的条件下，膜盒的输出位移比膜片增大近 一倍，提高了测量灵敏度。把几个膜盒首尾相连 构成膜盒组，相当于弹性元件的串联使用，同样 可使灵敏度大大提高。
j
1 F'
1
n
Fi '
i 1
1 n1 i1 ji
或：
1
n
1
j i1 ji
即并联线性弹性元件组成的系统总灵敏度 的倒数等于每个元
件灵敏度的倒数之和。
F
F
用并联线性弹性元件
的方法组成所需非线性
特性的弹性元件。
λ
② 串联线性弹性元件的刚度和灵敏度
如果把若干个灵敏度分别为ji的
F
线性弹性元件串联在一起使用，
第三章 传感器中的弹性敏感元件
一.弹性元件的基本特性
作用在弹性元件上的载荷（输入的力、力矩、压力、温度等） 与该载荷作用下弹性元件产生的变形之间的关系称为弹性元件的 基本特性。
1. 特性的表示方法：
位移
力
f (F)
转角 位移
f (M ) 力矩 f (P)
压力
2. 刚度和灵敏度：
（1）刚度： 作用在弹性元件上的载荷增量与弹性元件相应产生的变形增
l=l0[1+at(t-t0)] 热胀冷缩现象
6. 固有频率------提高灵敏度会降低固有频率,使动态特性变差
7. 机械品质因数
Q
Es Ec
每个振动周期存储的弹 每个振动周期由阻尼等
性应变能量 消耗的能量
f 1 k
2 m
二.几种常用弹性敏感元件介绍
（一）膜片、膜盒 1. 结构和用途：
（1）结构：膜片是一种周边固定的圆形弹性薄片；根据轴向截 面形状的不同分成平膜片和波纹膜片两种。为了便于膜片与输出 机构的其他零件相连，一般在膜片中心焊有硬芯。
2. 平膜片的计算公式 ：
结构：周边刚性固定、无硬芯的平膜片，在均匀压力P的作用下，
膜片中心位移量λ与压力P的关系式为：
PR 4 Eh4
16 3(1 2
)h
7 3(1 )
3
h3
式中：R—膜片的工作半径；h—膜片的厚度；E—膜片的弹性模
量；μ—膜片材料的泊松比，对于金属材料μ=0.3。
当λ<<h时，上式简化为：
输出位移与输入力的关系
如果把若干个刚度分
F
别为Fi’的线性弹性元
件并联在一起使用，
F1
F2
Fi
其总刚度为 ：
λ
Fn-1 Fn
F' F
n
式中 F Fi ； 1 2 i
n
i 1
所以：
F'
F
F i i 1
n i 1
Fi
i
n
Fi '
i 1
并联线性弹性元件组成的系统总刚度等于每个元件的刚度之和。
并联线性弹性元件组成的系统总灵敏度 j 等于：
性元件的输出变形不是立即完
成，而是在一定时间间隔内逐
渐完成的现象。
λ λ0 λ’0
0
F0 F
0
F0 F
λ 弹性滞后和弹性后效是同时发
生的，分别反映了弹性元件的
静态特性和动态特性，统称为 λ2 迟滞误差或滞后误差，用δch表 λ1
λmax
示：
ch
(1
2 )max m a x
100 %
0
F0
F
弹性元件产生滞后和后效的原因主要有：①弹性元件内部的
2004-10-25
传感器原理及应用 天津大学 李刚
11
λ
（2）用途： ① 测量压力、压差的弹性敏感元件；
② 用于隔离两种流体介质——隔离膜片。 （3）材料：分为金属和非金属两大类。
~ （4）测压范围及尺寸：从mmH2O 几百个大气压； ~ 直径从几个mm 几百个mm；
~ 金属膜片厚度为0.06mm 1.5mm； ~ 非金属膜片厚度为0. 1mm 5mm 。