大学高数期末考试题及答案

合集下载

大学高数期末试题及答案

大学高数期末试题及答案一、选择题（每题5分，共20分）1. 下列函数中，哪一个是奇函数？A. f(x) = x^2B. f(x) = x^3C. f(x) = xD. f(x) = sin(x)答案：C2. 函数f(x) = 2x + 1在x=2处的导数是：A. 3B. 4C. 5D. 6答案：B3. 曲线y = x^2 + 1在点(1, 2)处的切线斜率是：A. 0B. 1C. 2D. 3答案：C4. 定积分∫(0到1) x dx的值是：A. 0.5B. 1C. 2D. 3答案：A二、填空题（每题5分，共20分）1. 极限lim(x→0) (sin(x)/x)的值是______。

答案：12. 函数y = ln(x)的不定积分是______。

答案：xln(x) - x + C3. 微分方程dy/dx + y = e^(-x)的通解是______。

答案：y = -e^(-x) + Ce^(-x)4. 函数f(x) = x^3 - 6x^2 + 11x - 6的极值点是______。

答案：x = 1, x = 2三、解答题（每题15分，共30分）1. 求函数f(x) = x^2 - 4x + 3的极值。

答案：函数f(x)的导数为f'(x) = 2x - 4。

令f'(x) = 0，解得x = 2。

将x = 2代入原函数，得到f(2) = 3，这是函数的极小值。

2. 计算定积分∫(0到π) sin(x) dx。

答案：根据定积分的性质，∫(0到π) sin(x) dx = [-cos(x)](0到π) = -cos(π) + cos(0) = 2。

四、证明题（每题15分，共15分）1. 证明函数f(x) = x^3在R上是连续的。

答案：对于任意实数x，有f(x) = x^3。

因为多项式函数在其定义域内处处连续，所以f(x) = x^3在R上是连续的。

高数期末考试题大题及答案

高数期末考试题大题及答案一、极限题目1：求函数 $ f(x) = \frac{3x^2 - x}{x^2 + 2} $ 在 $ x \to \infty $ 时的极限。

解答：首先，我们可以通过分子分母同时除以 $ x^2 $ 来简化函数：\[ f(x) = \frac{3 - \frac{1}{x}}{1 + \frac{2}{x^2}} \]当 $ x \to \infty $ 时，$ \frac{1}{x} $ 和$ \frac{2}{x^2} $ 都趋向于 0，所以：\[ \lim_{x \to \infty} f(x) = \frac{3 - 0}{1 + 0} = 3 \]二、导数与微分题目2：求函数 $ g(x) = x^3 - 2x^2 + x $ 的导数。

解答：使用幂函数的导数规则，我们有：\[ g'(x) = 3x^2 - 4x + 1 \]三、积分题目3：计算定积分 $ \int_{0}^{1} x^2 dx $。

解答：首先，我们需要找到 $ x^2 $ 的原函数，即：\[ F(x) = \int x^2 dx = \frac{x^3}{3} + C \]然后，我们可以计算定积分：\[ \int_{0}^{1} x^2 dx = F(1) - F(0) = \frac{1^3}{3} -\frac{0^3}{3} = \frac{1}{3} \]四、无穷级数题目4：判断级数 $ \sum_{n=1}^{\infty} \frac{1}{n(n+1)} $ 的收敛性。

解答：该级数可以重写为：\[ \sum_{n=1}^{\infty} \left(\frac{1}{n} -\frac{1}{n+1}\right) \]这是一个交错级数，我们可以通过比较测试来判断其收敛性。

由于每一项都是正的且递减，我们可以得出结论，该级数是收敛的。

大一上学期(第一学期)高数期末考试题及答案

大一上学期(第一学期)高数期末考试题及答案高等数学I（大一第一学期期末考试题及答案）1.当 $\alpha x$ 和 $\beta x$ 都是无穷小时，$\alpha(x)+\beta(x)$ 不一定是无穷小。

2.极限 $\lim\limits_{x\to a}\dfrac{\sin x+e^{2ax}-1}{x}$ 的值是 $2a$。

3.如果 $f(x)=\begin{cases}\dfrac{\ln(x+a)-\ln a}{x},& x\neq 0\\ \quad\quad 1,& x=0\end{cases}$ 在 $x=a$ 处连续，则$a=e^{-1}$。

4.如果 $f(x)$ 在 $x=a$ 处可导，则$f'(a)=\dfrac{1}{3}(f(a+2h)-f(a-h))$。

5.极限 $\lim\limits_{x\to a}\dfrac{\ln(x+a)-\ln a}{x}$ 的值是 $1/a$。

6.确定函数 $y(x)$，使得 $y(x)$ 的导函数为$y'(x)=\dfrac{y}{2\sin(2x)}+\dfrac{y e^{xy}}{x}-\dfrac{x}{y\ln x}$，则 $y(x)=\dfrac{1}{\ln x}$。

7.过点 $M(1,2,3)$ 且与平面 $x+2y-z=0$ 和 $2x-3y+5z=6$ 平行的直线 $l$ 的方程为 $\dfrac{x-1}{-1}=\dfrac{y-2}{-1}=\dfrac{z-3}{2}$。

8.函数 $y=2x-\ln(4x)$ 的单调递增区间为 $(-\infty,0)\cup(1,+\infty)$。

9.计算极限 $\lim\limits_{x\to 0}\dfrac{(1+x)^{-e^x}-e}{x}$，结果为 $-1/2$。

10.设 $f(x)$ 在 $[a,b]$ 上连续，则 $F(x)=\int_a^x(x-t)f(t)dt$ 的二阶导数为 $F''(x)=f(x)$。

青岛大学高等数学期末考试试卷(含答案)

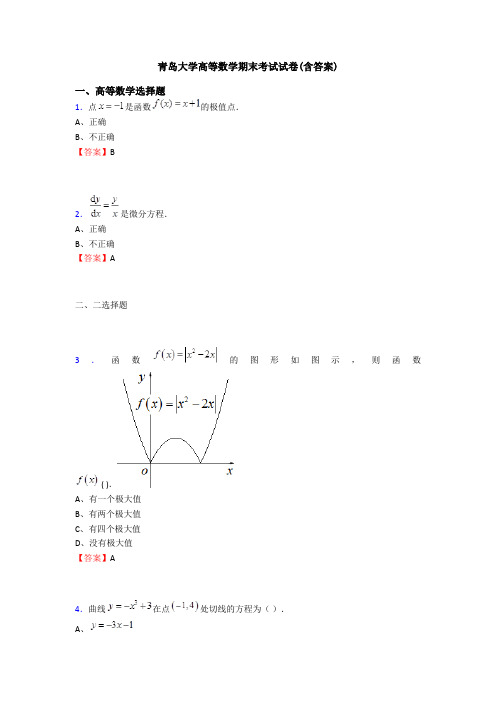
青岛大学高等数学期末考试试卷(含答案)
一、高等数学选择题
1．点是函数的极值点．
A、正确
B、不正确
【答案】B
2．是微分方程．
A、正确
B、不正确
【答案】A
二、二选择题
3．函数的图形如图示，则函数
( )．
A、有一个极大值
B、有两个极大值
C、有四个极大值
D、没有极大值
【答案】A
4．曲线在点处切线的方程为（）．
A、
B、
C、
D、
【答案】C
5．设，不定积分（1）
（2）（3）则上述解法中（）．
A、第（1）步开始出错
B、第（2）步开始出错
C、第（3）步出错
D、全部正确
【答案】A
6．设为上的连续函数，且，则定积分（）．A、
B、
C、
D、
【答案】D
一、一选择题
7．.
A、正确
B、不正确
【答案】A
8．（）．
A、
B、
C、
D、
【答案】B
9．曲线在点处切线的方程为（）．A、
B、
C、
D、
【答案】D
10．函数在点处连续．
A、正确
B、不正确
【答案】A
11．定积分．
A、正确
B、不正确
【答案】B
12．设函数，则（）．
A、
B、
C、
D、
【答案】B
13．设，则=（）．A、
B、
C、
D、
【答案】D
14．设，则．
A、正确
B、不正确
【答案】B
15．是偶函数．
A、正确
B、不正确
【答案】A。

高数b2期末考试试题及答案

高数b2期末考试试题及答案一、选择题（每题5分，共30分）1. 设函数f(x)=x^3-3x+1，求f'(x)的值。

A. 3x^2 - 3B. x^2 - 3xC. 3x^2 - 3xD. x^3 - 3x^2答案：A2. 计算定积分∫(0,1) x^2 dx。

A. 1/3B. 1/2C. 2/3D. 1/4答案：B3. 求极限lim(x→0) (sin x) / x。

A. 1B. 0C. 2D. ∞答案：A4. 判断下列级数是否收敛。

∑(1/n^2)，n从1到∞。

A. 收敛B. 发散答案：A5. 判断函数f(x)=e^x在实数域R上的连续性。

A. 连续B. 不连续答案：A6. 求二阶偏导数f''(x,y)，其中f(x,y)=x^2y+y^2。

A. 2xyB. 2xC. 2yD. 2答案：B二、填空题（每题5分，共20分）1. 设函数f(x)=ln(x+1)，求f'(x)=______。

答案：1/(x+1)2. 计算定积分∫(0,2π) sin(x) dx=______。

答案：03. 求极限lim(x→∞) (1+1/x)^x=______。

答案：e4. 判断级数∑(1/n)，n从1到∞是否收敛，答案是______。

答案：发散三、解答题（每题10分，共50分）1. 求函数f(x)=x^3-6x^2+11x-6的极值点。

答案：首先求导数f'(x)=3x^2-12x+11，令f'(x)=0，解得x=1,x=11/3。

经检验，x=1为极大值点，x=11/3为极小值点。

2. 计算定积分∫(0,1) e^x dx。

答案：∫(0,1) e^x dx = [e^x](0,1) = e^1 - e^0 = e - 1。

3. 求极限lim(x→0) (e^x - 1) / x。

答案：根据洛必达法则，lim(x→0) (e^x - 1) / x = lim(x→0) e^x = 1。

大学高数期末考试题与答案

第一学期高等数学期末考试试卷答案一．计算题（本题满分 35 分，共有 5 道小题，每道小题 7 分），1．求极限lim1 cos x x2 x．3 x 0 si n x解：1 cosx x x x2 1 1 c o xs 1cosx x 2x21 2lim lim lim si n 3 x x 3 x 3 x 0 x 0 x 0x ln 1 cosx x ln 1 c oxs 1 cosx ln 1 cosxe 2 1 e 2 1 xln 2 2 lim lim limlimx 3 1 cosx x 3 x 2x 0 x 0 x 0 x 0xln 2l i m s inx 1 ．x 0 1 c o sx 2x 4与 x 2 3x2．设 x 0 时，fx 是等价无穷小， f t dt 与 Ax k等价无穷小，求常数 k 与 A ．2 0 解：3 x3 x f t dt由于当 x 0 时， f t dt 与 Ax k等价无穷小，所以 lim 0 k 1 ．而0 x 0 Ax3 x21 x 31f t dt f 3 x 2 23 3 x 2f 3 x 2 3 3 x 2x 3 x 31lim 0 lim li m li mlimAx kxx 0 Akx k 1 x 0 2Akx k 1 x 0 6Akx k 1 x 0 6Akx k 1x 32所以， lim11．因此， k 1, A 1． x 0 6 Akx k 163 x 2ax b dx 中不含有对数函数，求常数 a 与b应满足的条件．2 ．如果不定积分x 1 1x 2解：x 2ax b 化为部分分式，有将2 1 x 2x 1x 2ax bA B CxD ，x 1 2 1 x 2x 1 x 1 21 x 2因此不定积分x 2ax bdx 中不含有对数函数的充分必要条件是上式中的待定系数x 1 2 x 21A C 0 ．即x 2ax bB D B 1 x 2D x 1 22 22 2 ．1 x 2x 1 1 x 2x 1 x 1 1 x所以，有x 2ax b B 1 x 2 D x 1 2 B D x 2 2DxB D ．比较上式两端的系数，有 1 B D , a 2D , b B D ．所以，得 b 1．525．计算定积分 min 1, x 2 dx ． 0解：m i n1, x 2 x 2x 2 11 x2 1 1 x 12 x 1 x 2x 2 2 x ．31x35521 2 2 13 所以， min 1, x 2 dx 1dx 2 x dx x 2 dx ．0 0 1 2 85．设曲线 C 的极坐标方程为 r a sin 3，求曲线 C 的全长． 3解：曲线 r a sin 3一周的定义域为 0 3 ，即 03 ．因此曲线 C 的全长为 3 3 2 2 3 3 3 s r r d 2 6 a 24 2 2aa s i n s i n c o s d a s i n d ．0 0 3 3 3 0 3 2二．（本题满分 45 分，共有 5 道小题，每道小题 9 分），6．求出函数f x sin x lim 2n 的所有间断点，并指出这些间断点的类型． n 1 2 x解：sin x x1 21sin x x 1 2 2f x lim 2n．1 1 n12 x x 2 20 x 1 2因此 x 1 1 1 是函数 f x与 x 2 2 的间断点． 2l i m f x l i m 0 0 ， lim f x lim si nx 1 ，因此 x 1x 的第一类可是函数 f 1 x 1 x 1 1 2x 2 2 x2 2去型间断点．li mf x lim s i n x1 ，limf x lim 0 0 1 是函数 f x 的第一类可去型，因此 x 1 x 1x 1 x 1 2 x2 2 2 2 间断点．7．设是函数 f x arcsin x 在区间 0, b 上使用 Lagrange （拉格朗日）中值定理中的 “中值 ”，求极限 lim ．b 0 b 解：f x ar c s ixn 在区间0, b 上应用 Lagrange 中值定理，知存在 0, b ，使得arcsinb arcsin0 1 b 0 ．1 2b 2所以， 21．因此，arcsinbb 22 12 2arcsinblim lim a r c s bin bb 2 2 lim2b 0 b 0 bb 0 b 2a r c sbin令t arcsinb，则有2lim t 2 2limt2 2lim sin t s i n tb 0b 2t 0t2 sin 2tt0 t 4lim 2t sin 2t lim 22cos2t 1 lim 1 cos2t1 lim2 s in2t 1 t 0 4t 3t 0 12t 26 t 0 t 2 6 t 0 2t 3所以， lim 1 ．b 0 b31 x 18．设 fx e y 2 y dy ，求f x dx ．0 0解：111f x dx xf xf x dxx 00 01 x在方程f x e y 2ydy 中，令x 1 ，得1 1 0f 1 e y 2 y dy e y 2 y dy 0 ．0 0再在方程1 因此，1 xf xe1 x2f x e y 2y dy 两端对 x 求导，得，011 1f x dx xfx xf x dx xf x dx 00 0 01 11 11 x 2x 2e x2xe dx e xe dx e0 0 2 0 1e 1 ．29．研究方程 e x a x2 a 0 在区间, 内实根的个数．解：设函数f x ax2 e x1， f x 2axe x ax2e x ax 2 x e x．令f x 0 ，得函数 f x 的驻点 x10, x2 2 ．由于 a 0 ，所以lim fx lim ax2e x 1 ，x xlim f x lim 2ex1 a limx21 a lim2x1 a lim21 1．axe xexexx x x x x因此，得函数 f x 的性态x , 0 0 0, 2 2 2,f x 0 0f x 1 4ae 21 1⑴若 4ae 2 1 0，即 a e2时，函数f x ax2 e x1在, 0、0, 2、2, 内4各有一个零点，即方程e x a x2在, 内有 3 个实根．⑵若 4ae 2 1 0 ，即 a e2时，函数f x ax2 e x1在, 0、0, 内各有一个零4点，即方程 e x a x2在, 内有 2 个实根．⑶若 4ae 2 1 0 ，即 a e2时，函数f x ax 2e x 1 在, 0 有一个零点，即方程4e xa x 2在, 内有 1 个实根．10．设函数 f x 可导，且满足f x x f x 1 ， f 0 0 ．试求函数 f x 的极值．解：在方程 f x xf x 1 中令 tx ，得f t t f t 1 ，即f x x f x 1 ．f x xf x x 中消去f x ，得在方程组xf x f x xf x x x2．1 x2x t 2积分，注意 f 0 0 ，得 f x f 0 t 0 1t 2 dt ．即x t t 2 1 ln 1 x 2f x 2 dt x arctan x ．0 1t 2由 f x x x 2f x 的驻点 x10, x21 ．而f 1 2 x x 21 x 2得函数 x 1 x 22 ．所以，f 0 1 0 ， f1 1 0 ．21ln 2所以， f0 0 是函数f x 极小值； f 1 1 是函数 f x 极大值．2 4三．应用题与证明题（本题满分20 分，共有 2 道小题，每道小题 10 分），11．求曲线 y x 的一条切线，使得该曲线与切线 l 及直线 x 0 和 x 2 所围成的图形绕 x 轴旋转的旋转体的体积为最小．解：设切点坐标为 t, t 1 ，可知曲线 y x 在 t , t 处的切线方程为，由 y 2 t yt11x t ．x t ，或 y2 t2 t因此所求旋转体的体积为 2V1 2 82x tx dx 4 2t2 t4 3t所以， dV8 2 0 ．得驻点 t2 ，舍去 t2 ．由于 dt 4 3t 233d 2V16 0 ，因而函数 V 在 t 2 dt 24 3t 2 处达到极小值，而且也是最小值．因此所求切 t 2 t 3233 线方程为 y 3 x 1 ．4 212．设函数 f x 在闭区间0， 1 上连续，在开区间0， 1 内可导，且2e f xarctan xdx 1， f 1 0 ．2 证明：至少存在一点 0， 1 ，使得 f1．1 2arctan 解：因为 f x 在闭区间 0, 1 上连续，所以由积分中值定理，知存在20,，使得2e fx arctanxdx 2 e f arctan ．0 2由于 e fx arctan xdx 1，所以， 2 e farctan 1 ．再由 f 1 0 ，得 022e farctan e f1 arctan 1．4作函数 g xe f x arctan x ，则函数在区间 , 1 0, 1 上连续，在区间 , 1 内可导．所以由 Rolle 中值定理，存在, 1 0, 1 ，使得 g 0 ．而 g x e fx f e fx 2 ．x a r c t axnx1所以存在, 10, 1 ，使得e ff a r c t a ne f20 ．1由于 e f0 ，所以 farctan 1 2 0，即 f11．12 arctan一个处处像别人表明自己优秀的，恰恰证明了他（她）并不优秀，或者说缺什么，便炫耀什么。

高数期末考试题及答案选择

高数期末考试题及答案选择一、选择题（每题2分，共20分）1. 函数 $ f(x) = x^2 $ 在 $ x = 0 $ 处的导数是：A. 0B. 1C. 2D. 4答案： A2. 定积分 $ \int_{0}^{1} x^2 dx $ 的值是：A. $ \frac{1}{3} $B. $ \frac{1}{2} $C. $ \frac{2}{3} $D. $ \frac{3}{4} $答案： A3. 若 $ \lim_{x \to 0} \frac{f(x)}{g(x)} $ 存在，则$ \lim_{x \to 0} f(x) $ 与 $ \lim_{x \to 0} g(x) $ 必须：A. 都存在B. 都不存在C. 至少有一个存在D. 至少有一个不存在答案： D4. 函数 $ y = \sin(x) $ 的周期是：A. $ 2\pi $B. $ \pi $C. $ \frac{\pi}{2} $D. $ \frac{1}{2} $答案： A5. 根据泰勒公式，函数 $ e^x $ 在 $ x = 0 $ 处的泰勒展开式为：A. $ 1 + x $B. $ 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots $C. $ 1 - x + \frac{x^2}{2!} - \frac{x^3}{3!} + \cdots $D. $ 1 + x - \frac{x^2}{2!} + \frac{x^3}{3!} - \cdots $答案： B6. 级数 $ \sum_{n=1}^{\infty} \frac{1}{n^2} $ 收敛于：A. $ \frac{1}{2} $B. $ \frac{\pi^2}{6} $C. $ \frac{e}{2} $D. $ \frac{1}{e} $答案： B7. 若 $ \lim_{x \to \infty} f(x) = L $，则函数 $ f(x) $ 必须：A. 在 $ x $ 足够大时，值接近 $ L $B. 在 $ x $ 足够大时，值等于 $ L $C. 在 $ x $ 足够大时，值小于 $ L $D. 在 $ x $ 足够大时，值大于 $ L $答案： A8. 函数 $ y = x^3 - 3x^2 + 2x $ 的拐点是：A. $ x = 0 $B. $ x = 1 $C. $ x = 2 $D. $ x = 3 $答案： B9. 若 $ f(x) $ 在区间 $ I $ 上连续，则 $ \int_{a}^{b}f(x) dx $ 存在，其中 $ a, b $ 是区间 $ I $ 上的任意两点：A. 正确B. 错误答案： A10. 函数 $ y = \ln(x) $ 的定义域是：A. $ x > 0 $B. $ x < 0 $C. $ x \geq 0 $D. $ x \leq 0 $答案： A二、填空题（每题2分，共20分）11. 函数 $ f(x) = \frac{1}{x} $ 在 $ x = 1 $ 处的导数是_______。

高数下册期末考试题及答案

高数下册期末考试题及答案一、选择题（每题2分，共10分）1. 函数 $ f(x) = \ln(x^2 + 1) $ 的导数是：A. $ 2x/(x^2 + 1) $B. $ 2x/x^2 + 1 $C. $ 2x/(x^2 - 1) $D. $ 2x/(x^2 + 1)^2 $答案：A2. 已知 $ e^x $ 的泰勒展开式为 $ 1 + x + x^2/2! + x^3/3! + \cdots $，那么 $ e^{-x} $ 的泰勒展开式是：A. $ 1 - x + x^2/2! - x^3/3! + \cdots $B. $ 1 + x - x^2/2! + x^3/3! - \cdots $C. $ 1 - x - x^2/2! + x^3/3! - \cdots $D. $ 1 + x + x^2/2! - x^3/3! + \cdots $答案：A3. 若 $ \int_0^1 x^2 dx = \frac{1}{3} $，则 $ \int_0^1 x^3 dx $ 的值是：A. $ \frac{1}{4} $B. $ \frac{1}{5} $C. $ \frac{1}{6} $D. $ \frac{1}{7} $答案：A4. 曲线 $ y = x^3 - 3x^2 + 2x $ 在 $ x = 2 $ 处的切线斜率是：A. 0B. 1C. 2D. -1答案：B5. 若 $ \lim_{x \to 0} \frac{\sin x}{x} = 1 $，则$ \lim_{x \to 0} \frac{\sin 2x}{x} $ 等于：A. 1B. 2C. 4D. 8答案：B二、填空题（每题3分，共15分）6. 若 $ f(x) = x^3 - 2x^2 + x $，则 $ f'(x) = $ ________。

大学高数期末考试题与答案

因为懂得，人生的风景，最终是回归到心灵的本源。和谐共生，平等友爱，才是对生命的尊重和对自己的珍视。
解：
设切点坐标为 t,
t ，由 y 1 ，可知曲线 y 2t
x 在 t , t 处的切线方程为
y t 1 x t ，或 y 1 x t ．
2t
2t
因此所求旋转体的体积为
2
2
V
1 xt
0 2t
2
x dx
8 4 2t
4 3t
dV
所以，
dt 4
8 3t 2
2
0 ．得驻点 t
2 ，舍去 t
3
2
．由于
3
d 2V
10．设函数 f x 可导，且满足
f x x f x 1 ， f 0 0．
试求函数 f x 的极值．
解：
在方程 f x x f x 1 中令 t x ，得 f t
t f t 1 ，即
f x x f x 1．
f x xf x x
在方程组
中消去 f
xf x f x x
x ，得
x x2 f x 1 x2 ．
dt 2 t 2
3
16
4 3t 2 t 2
3
0 ，因而函数 V 在 t
2
处达到极小值，而且也是最小值．因此所求切
3
线方程为 y
31 x．
42
12．设函数 f x 在闭区间 0， 1 上连续，在开区间 0， 1 内可导，且
证明：至少存在一点解：
2
e f x arctan xdx 1 ， f 1 0 ．
f
ef
ef
arct an
2 0．
1
由于 e f

(完整版)大一高等数学期末考试试卷及答案详解

（二）
一、填空题（每小题3分，共18分）
1．设函数，则是的第类间断点.
2．函数，则 .
3． .
4．曲线在点处的切线方程为.
5．函数在上的最大值，最小值.
6． .
二、单项选择题（每小题4分，共20分）
1．数列有界是它收敛的（）.
必要但非充分条件；充分但非必要条件；
充分必要条件；无关条件.
二．选择题（每小题4分，4题共16分）：
1．设常数，则函数在内零点的个数为（B）.
(A)3个;(B)2个;(C)1个;(D)0个.
2．微分方程的特解形式为（C）
（A）；（B）；
（C）；（D）
3．下列结论不一定成立的是（A）
(A)(A)若 ,则必有 ;
(B)(B)若在上可积,则 ;
(C)(C)若是周期为的连续函数,则对任意常数都有 ;
2．下列各式正确的是（）.
；；
； .
3．设在上，且，则曲线在上.
沿轴正向上升且为凹的；沿轴正向下降且为凹的；
沿轴正向上升且为凸的；沿轴正向下降且为凸的.
4．设，则在处的导数（）.
等于；等于；
等于；不存在.
5．已知，以下结论正确的是（）.
函数在处有定义且；函数在处的某去心邻域内有定义；
大一高等数学期末考试试卷
（一）
一、选择题（共12分）
1. （3分）若为连续函数,则的值为( ).
(A)1 (B)2 (C)3 (D)-1
2. （3分）已知则的值为（）.
(A)1 (B)3 (C)-1 (D)
3. （3分）定积分的值为（）.

大一第二学期高数期末考试题(含答案)

大一第二学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分)1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小；（B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小；（D ）()x β是比()x α高阶的无穷小.3.若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（）.（A ）函数()F x 必在0x =处取得极大值；（B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点；（D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x （B ）222x +（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分）5. =+→xx x sin 2)31(lim .6. ,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则.7.lim(cos cos cos )→∞-+++=22221L n n nnn n ππππ .8.=-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）9. 设函数=()y y x 由方程sin()1x ye xy ++=确定，求'()y x 以及'(0)y . 10. .d )1(177x x x x ⎰+-求11. ．　求，，设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12.设函数)(x f 连续，=⎰1()()g x f xt dt，且→=0()lim x f x A x ，A 为常数. 求'()g x并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、解答题（本大题10分）14. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程. 五、解答题（本大题10分）15. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V . 六、证明题（本大题有2小题，每小题4分，共8分）16. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰q f x d x q f x dx.17. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题（本大题有4小题，每小题4分，共16分）5.6e . 6.cx x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导(1)cos()()0x y e y xy xy y +''+++= cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==，(0)1y '=- 10. 解：767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11.解：10330()x f x dx xe dx ---=+⎰⎰⎰3()x xd e --=-+⎰⎰00232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰　令3214e π=--12. 解：由(0)0f =，知(0)0g =。

大一(第一学期)高数期末考试题及答案

大一上学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小；（B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小；（D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（）.（A ）函数()F x 必在0x =处取得极大值；（B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点；（D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

（A ）22x （B ）222x +（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分） 4.=+→xx x sin 2)31(lim .5. ,)(cos 的一个原函数是已知x f x x =⋅⎰x x x x f d cos )(则 .6.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ .7. =-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）8. 设函数=()y y x 由方程sin()1x ye xy ++=确定，求'()y x 以及'(0)y . 9.设函数)(x f 连续，=⎰1()()g x f xt dt，且→=0()limx f x A x ，A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.10. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、解答题（本大题10分）11. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程.五、解答题（本大题10分）12. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题（本大题有2小题，每小题4分，共8分）13. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰qf x d x q f x dx.14. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，0cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分)1、D2、A3、C4、C二、填空题（本大题有4小题，每小题4分，共16分）5. 6e . 6.c x x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导0,0x y ==，(0)1y '=-10. 解：767u x x dx du == 11. 解：101233()2xf x dx xe dx x x dx---=+-⎰⎰⎰12. 解：由(0)0f =，知(0)0g =。

高数期末考试题及答案

高数期末考试题及答案【高数期末考试题及答案】一、选择题1. 高数的完整名称是什么？A. 高等数学B. 高级数学C. 高纯度数学D. 高度数学答案：A2. 常用的微积分法则中，“乘法法则”是指什么？A. 两个函数相乘的导数等于它们的导数相加B. 两个函数相乘的导数等于它们的导数相减C. 两个函数相乘的导数等于它们的导数相乘D. 两个函数相乘的导数等于它们的导数相除答案：C3. 下面哪个是高数中常用的极限符号？A. $lim$B. $lag$C. $limt$D. $sum$答案：A4. 函数$f(x)=\frac{x}{x-1}$的定义域是什么？A. $[-\infty, 0)\cup(0, +\infty)$B. $(-\infty, 0)\cup(0, +\infty)$C. $(-\infty, 1)\cup(1, +\infty)$D. $[-\infty, 1)\cup(1, +\infty)$答案：D二、计算题1. 求函数$f(x)=3x^2-2x+1$的导函数。

解答：将函数$f(x)$按导数的定义求导，得到：$f'(x)=\lim_{\Delta x \to 0}\frac{f(x+\Delta x) - f(x)}{\Delta x}$代入函数$f(x)$的表达式，化简得到：$f'(x)=\lim_{\Delta x \to 0}\frac{3(x+\Delta x)^2-2(x+\Delta x)+1-(3x^2-2x+1)}{\Delta x}$展开并化简得到：$f'(x)=\lim_{\Delta x \to 0}\frac{3x^2+6x \Delta x+3(\Delta x)^2-2x-2 \Delta x+1-3x^2+2x-1}{\Delta x}$合并同类项并约去，得到：$f'(x)=\lim_{\Delta x \to 0}6x+3 \Delta x-2$由于$\Delta x$趋近于0时，$3 \Delta x$和2趋近于0，所以最后的结果为：$f'(x)=6x-2$答案：$f'(x)=6x-2$2. 求函数$F(x)=\int_0^x\frac{1}{1+t^3}dt$的原函数。

高数下册期末a卷考试题及答案

高数下册期末a卷考试题及答案一、选择题（每题5分，共30分）1. 以下哪个函数不是周期函数？A. $ \sin(x) $B. $ \cos(x) $C. $ e^x $D. $ \tan(x) $答案：C2. 函数 $ f(x) = x^2 $ 在 $ x=1 $ 处的导数是：A. 0B. 1C. 2D. 3答案：C3. 以下哪个选项是 $ \int_0^1 x^2 dx $ 的正确计算结果？A. $ \frac{1}{3} $B. $ \frac{1}{2} $C. $ 1 $D. $ 2 $答案：A4. 以下哪个选项是 $ \lim_{x \to 0} \frac{\sin x}{x} $ 的值？A. 0B. 1C. 2D. 3答案：B5. 以下哪个选项是 $ \int \frac{1}{x} dx $ 的原函数？A. $ \ln|x| + C $B. $ x + C $C. $ e^x + C $D. $ \sin x + C $答案：A6. 以下哪个选项是 $ \int e^x \cos x \, dx $ 的正确积分结果？A. $ \frac{1}{2} e^x (\cos x + \sin x) + C $B. $ \frac{1}{2} e^x (\cos x - \sin x) + C $C. $ \frac{1}{2} e^x (\cos x + \sin x) - C $D. $ \frac{1}{2} e^x (\cos x - \sin x) - C $答案：B二、填空题（每题5分，共20分）1. 函数 $ f(x) = \ln(x) $ 的定义域是 $ ______ $。

答案：$ (0, +\infty) $2. 函数 $ f(x) = \sqrt{x} $ 的导数是 $ ______ $。

大一高等数学期末考试试卷及答案详解

大一高等数学期末考试试卷及答案详解大一高等数学期末考试试卷一、选择题（共12分）2ex,x0,1. （3分）若f(x)为连续函数,则a的值为( ).a x,x0(A)1 (B)2 (C)3 (D)-12. （3分）已知f(3)2,则limh0f(3h)f(3)的值为（）. 2h(A)1 (B)3 (C)-1 (D)1 23. （3分）定积分2的值为（）. 2(A)0 (B)-2 (C)1 (D)24. （3分）若f(x)在x x0处不连续,则f(x)在该点处( ).(A)必不可导 (B)一定可导(C)可能可导 (D)必无极限二、填空题（共12分）1．（3分）平面上过点(0,1)，且在任意一点(x,y)处的切线斜率为3x2的曲线方程为 .2. （3分）(x2x4sinx)dx . 113. （3分） limx2sinx01= . x4. （3分） y2x33x2的极大值为三、计算题（共42分）1. （6分）求limx0xln(15x). sin3x22. （6分）设y求y. 3. （6分）求不定积分xln(1x2)dx.4. （6分）求 30x,x1, f(x1)dx,其中f(x)1cosx ex1,x 1.5. （6分）设函数y f(x)由方程edt costdt0所确定,求dy. 00ytx6. （6分）设f(x)dx sinx2C,求f(2x3)dx.37. （6分）求极限lim1. n2n四、解答题（共28分）1. （7分）设f(lnx)1x,且f(0)1,求f(x). n2. （7分）求由曲线y cosx x与x轴所围成图形绕着x轴旋转一周2 2所得旋转体的体积.3. （7分）求曲线y x33x224x19在拐点处的切线方程.4. （7分）求函数y x[5,1]上的最小值和最大值.五、证明题(6分)设f(x)在区间[a,b]上连续,证明baf(x)dx b a1b[f(a)f(b)](x a)(x b)f(x)dx. 22a 标准答案一、 1 B; 2 C; 3 D; 4 A.二、 1 y x1; 2 32; 3 0; 4 0. 3三、 1 解原式limx5x 5分 x03x25 1分 32分 2 x lxn2(解lny l2x1212x[2] 4分y2x12x 13 解原式1ln(1x2)d(1x2) 3分 212x[(1x2)ln(1x2)(1x2)dx2分 221x1[(1x2)ln(1x2)x2] C 1分 24 解令x1t,则 2分03f(x)dx1f(t)dt 1分122t11(et1)dt 1分 1cost2 1分0[et t]1e2e 1 1分5 两边求导得ey y cosx0, 2分ycosx 1分 ye cosx 1分 sinx 1cosx dy dx 2分 sinx 16 解f(2x3)dx 12f(2x3)d(2x 2分1sin(2x3)2 C 4分 27 3lim1解原式=n2n322n332 4分 =e 2分四、1 解令lnx t,则x et,f(t)1et, 3分f(t)(1et)dt=t et C. 2分f(0)1,C0, 2分f(x)x ex. 1分2 解 Vx22cosxdx 3分 2202cos2xdx 2分3 解22. 2分6x 6 1分 y3x26x24,y 令y0,得x 1. 1分当x1时,y0; 当1x时,y0, 2分(1,3)为拐点, 1分该点处的切线为y321(x1). 2分 4 解y1 2分令y0,得x3. 1分435y(5)5 2.55,y,y(1)1, 2分4 435y(5)5y最大值为. 分最小值为4 4五、证明ba(x a)(x b)f(x)(x a)(x b)df(x)分 ab[(x a)(x b)f(x)]a af(x)[2x(a b)dx分a[2x(a b)df(x)分 bbb[2x(a b)]f(x)a2af(x)dx分(b a)[f(a)f(b)]2af(x)dx,分移项即得所证分 bbb。

(完整版)大一高等数学期末考试试卷及答案详解

大一高等数学期末考试一试卷一、选择题（共12 分）1.（ 3 分）若 f ( x)2e x , x 0,为连续函数 , 则a的值为 ().a x, x0(A)1 (B)2 (C)3 (D)-12.（ 3 分）已知f(3) 2, 则lim f (3 h) f (3) 的值为（）.h02h(A)1 (B)3 (C)-1(D)1 23.（ 3 分）定积分212xdx 的值为（）.cos2(A)0 (B)-2 (C)1(D)24.（3分）若f (x)在x x0处不连续,则 f ( x) 在该点处().(A)必不行导 (B) 必定可导 (C) 可能可导 (D) 必无极限二、填空题（共 12 分）1．（3 分）平面上过点(0,1) ，且在任意一点 ( x, y) 处的切线斜率为 3x2的曲线方程为.2.（ 31x4 sin x) dx.分）( x213.（ 3分） lim x2 sin1=.x0x4.（ 3分） y2x33x2的极大值为.三、计算题（共42 分）1.（ 6x ln(15x).分）求 limsin 3x2x02.（6 分）设ye xx2, 求 y .13.（ 6分）求不定积分x ln(1 x2 )dx.x 4.（ 63f ( x 1)dx, 此中f (x) 1, x 1,分）求cosxe x1,x 1.5. （ 6 分）设函数 yy x f ( x) 由方程e t dtcostdt 0 所确立 , 求 dy.6. （ 6 分）设 f ( x)dxsin x 2 C, 求 f (2 x 3)dx.3 n7. （ 6 分）求极限 lim 1 .2nn四、解答题（共 28 分）1. （ 7 分）设 f (ln x) 1 x, 且 f (0)1, 求 f ( x). 2. （ 7 分）求由曲线 ycos x2x与 x 轴所围成图形绕着 x 轴旋转一周2所得旋转体的体积 .3. （ 7 分）求曲线 y x 3 3x 2 24x 19 在拐点处的切线方程 .4. （ 7 分）求函数 yx1 x 在 [ 5,1] 上的最小值和最大值 .五、证明题 (6 分)设 f ( x) 在区间 [ a, b] 上连续 , 证明b b a1 bf (x)dx[ f (a) f (b)]( x a)( x b) f ( x) dx.a22 a标准答案一、 1 B;2C; 3D; 4 A.二、 1y x31;22 ;3 0;40.3三、 1解原式limx5x 5 分x 03x 251 分32 解Q ln y lne x x ln( x 2 1),2 分x 2 12y e x[12x] 4 分x 21 2x 2 13 解原式1ln(1 x 2 ) d (1 x 2 )3 分21[(12)ln(12 (12) 12xdx]2xx )xx 22 分1[(1 x 2 )ln(1 x 2 )x 2 ] C1 分24解令 x1 t, 则2 分320 f ( x)dx1 f (t )dt1t2 t11 costdt1 (e 1)dt0 [ e tt ]12e 2 e 15两边求导得 eyy cosx 0,cosxQ ye ycosxsin x 1dycosx dxsin x 16 解f (2 x 3) dx1 f (2 x2 1sin(2 x 3)2 C21 分1 分1 分 1 分2 分1 分1 分2 分3)d(2 x 2)2 分4 分32 n 37 解原式 = lim3 24 分1n2n3= e22 分四、 1 解令 ln xt, 则 xe t ,f (t) 1 e t ,3 分f (t )(1 e t )dt = t e tC.2 分Q f (0)1, C 0,2 分f (x) xe x .1 分2 解V x2 23 分cos xdx222cos 2 xdx2 分2.2 分23 解 y3x 2 6x 24, y6x 6,1 分令 y 0, 得 x 1.1 分当x 1时 , y0; 当 1 x时 , y0,2 分(1,3) 为拐点 ,1 分该点处的切线为 y 3 21(x 1).2 分4 解 y 11x2 1 x 1, 2 分2 12 1 x令 y0, 得 x3 . 1 分4y( 5)56,2.55,y3 5, y(1) 1,2 分44最小值为 y(5)56, 最大值为 y35 . 2 分44五、证明ba)( x b) f(x) ba)( x b) df ( x)1 分(x( xaabb[( x a)( x b) f (x)] aaf ( x)[2 x ( a b)dx1分ba [2 x (a b)df ( x)1分[2 x (a b)] f ( x)(b a)[ f ( a) f (b)]移项即得所证 .b ba2 a f ( x)dx1分b2 a f ( x)dx,1分1分。

大学高等数学期末考试试题与答案

大学高等数学期末考试试题与答案下列哪个公式不是牛顿-莱布尼茨公式的应用？B) (4x3 + 5x2 + 6x + 7)′D) (e2x + 3y)′答案：D) (e2x + 3y)′填空题(每题3分，共18分)略解答题(每题10分，共60分)略综合题(每题15分，共30分)略当谈论数学时，大家可能会想到那些复杂的公式和令人头疼的问题。

然而，数学在我们的日常生活中无处不在，它不仅是一门学科，更是一种思维方式。

在吉林大学，高等数学课程一直受到高度重视。

本文将通过学生们的期末试题来展示数学的魅力和应用。

试题是数学学习的重要组成部分。

通过做题，学生不仅可以巩固所学知识，还可以培养解决问题的能力和举一反三的思维方式。

以下是一道吉林大学高等数学的期末试题：求函数 y=x^3-3x^2+2在区间 [0,4]上的最大值和最小值。

这道题目的答案是：最大值为28，最小值为-16。

要解决这个问题，我们需要对函数进行求导，并确定函数的极值点。

然后，我们可以在给定的区间内找到函数的最大值和最小值。

除了在高等数学中学习数学基础知识，我们还可以将这些知识应用到实际生活中。

例如，在经济学的课程中，学生们可以使用数学模型来分析股票市场的波动；在工程学中，可以使用数学方法来设计桥梁和建筑的结构等。

数学是人类文化的重要组成部分，它为我们的日常生活提供了很多帮助。

通过学习高等数学，我们可以更好地理解数学的应用价值，提高我们的思维能力和解决问题的能力。

在未来的学习和工作中，这些能力将是我们不可或缺的竞争优势。

吉林大学高等数学期末试题不仅考察了学生的数学知识，还体现了数学在生活中的应用价值。

通过学习数学，我们可以培养举一反三的思维方式，提高解决问题的能力和竞争力。

让我们一起感受数学的魅力吧！下列哪个选项是高等数学中“极限”的概念？ ( )下列哪个选项是高等数学中“导数”的概念？( )下列哪个选项是高等数学中“积分”的概念？( )积分在高等数学中是一个非常广泛的概念，它涉及到面积、体积、平均值等多个方面，但不能简单地说积分就是求面积或体积或平均值。

首都医科大学高等数学期末考试试卷(含答案)

首都医科大学高等数学期末考试试卷(含答案) 一、高等数学选择题
1．点是函数的间断点.
A、正确
B、不正确
【答案】A
2．设函数，则（）．
A、
B、
C、
D、
【答案】C
3．不定积分，其中为任意常数．
A、正确
B、不正确
【答案】B
4．设函数，，则函数．
A、正确
B、不正确
【答案】A
5．．
A、正确
B、不正确
【答案】A
6．设函数，则．
A、正确
B、不正确
【答案】B
二、二选择题
7．不定积分（）．
A、
B、
C、
D、
【答案】D
8．设，则微分．
A、正确
B、不正确
【答案】B
二、二选择题
9．函数的图形如图示，则是函数的
( )．
A、极小值点也是最小值点
B、极小值点但非最小值点
C、最大值点
D、极大值点
【答案】A
10．微分方程的通解是（）．A、
B、
C、
D、
【答案】A
一、一选择题
11．设，则．
A、正确
B、不正确
【答案】B
二、二选择题
12．函数在点处连续．
A、正确
B、不正确
【答案】A
13．是微分方程．
A、正确
B、不正确
【答案】A
14． ( )．
A、
B、
C、
D、
【答案】B
15．不定积分．A、
B、
C、
D、
【答案】B。