高斯定理习题课共20页文档
合集下载
高斯定理
喷泉形成的流速场—— 源 正电荷 —— 喷泉形成的流速场 有洞水池中的流速场——汇 汇 负电荷 —— 有洞水池中的流速场
静电力是有心力，但高斯定理只给出了源和 静电力是有心力， 通量的关系， 通量的关系，并没有反映静电场是有心力场 这一特性， 这一特性，它只反映静电场性质的一个侧面 下一节还要讲另一个定理——环路定理） 环路定理） （下一节还要讲另一个定理 环路定理
S S S
+ ∫∫ E k +1 ⋅ d S + L + ∫∫ E n ⋅ d S =
S S
1
ε0
∑q
S内
i
=0
讨论： 讨论： Gauss 定理说明
闭合面内的电荷决定通过闭合面的电通量, 闭合面内的电荷决定通过闭合面的电通量,只要 S 则通量不为零——有源 内电荷不为零 ，则通量不为零 则通量不为零 有源 闭合面外的电荷虽然对通量没有贡献 闭合面外的电荷虽然对通量没有贡献，但并不意 面外的电荷虽然对通量没有贡献， 味着不影响闭合面上的电场， 味着不影响闭合面上的电场，高斯面上的场强是 空间所有带电体所产生的. 空间所有带电体所产生的. 高斯定理是静电场的一条重要的定理， 高斯定理是静电场的一条重要的定理，反映场和 源的关系,有其重要的理论地位 有其重要的理论地位， 源的关系 有其重要的理论地位，是静电场基本方 它是由库仑定律导出的， 程之一 ，它是由库仑定律导出的， 反映了电力 如果电力平方反比律不满足， 平方反比律 ，如果电力平方反比律不满足，则高 斯定理也不成立。 斯定理也不成立。
结论： 结论：均匀带电的无限大平面板产生的场强大 小与场点到平面的距离无关 图示c板间场强为何 板间场强为何？ 图示 板间场强为何？
讨论：
以上三例电荷分布分别具有球对称性、轴对称性、 以上三例电荷分布分别具有球对称性、轴对称性、 面对称性，电荷分布的对称性决定了场的对称性。 面对称性，电荷分布的对称性决定了场的对称性。 Gauss定理可以计算具有强对称性场的场强 用 Gauss定理可以计算具有强对称性场的场强 Gauss定理可以和场强叠加原理结合起来运用， Gauss定理可以和场强叠加原理结合起来运用， 定理可以和场强叠加原理结合起来运用 计算各种球对称性、轴对称性、面对称性的场。 计算各种球对称性、轴对称性、面对称性的场。
静电力是有心力，但高斯定理只给出了源和 静电力是有心力， 通量的关系， 通量的关系，并没有反映静电场是有心力场 这一特性， 这一特性，它只反映静电场性质的一个侧面 下一节还要讲另一个定理——环路定理） 环路定理） （下一节还要讲另一个定理 环路定理
S S S
+ ∫∫ E k +1 ⋅ d S + L + ∫∫ E n ⋅ d S =
S S
1
ε0
∑q
S内
i
=0
讨论： 讨论： Gauss 定理说明
闭合面内的电荷决定通过闭合面的电通量, 闭合面内的电荷决定通过闭合面的电通量,只要 S 则通量不为零——有源 内电荷不为零 ，则通量不为零 则通量不为零 有源 闭合面外的电荷虽然对通量没有贡献 闭合面外的电荷虽然对通量没有贡献，但并不意 面外的电荷虽然对通量没有贡献， 味着不影响闭合面上的电场， 味着不影响闭合面上的电场，高斯面上的场强是 空间所有带电体所产生的. 空间所有带电体所产生的. 高斯定理是静电场的一条重要的定理， 高斯定理是静电场的一条重要的定理，反映场和 源的关系,有其重要的理论地位 有其重要的理论地位， 源的关系 有其重要的理论地位，是静电场基本方 它是由库仑定律导出的， 程之一 ，它是由库仑定律导出的， 反映了电力 如果电力平方反比律不满足， 平方反比律 ，如果电力平方反比律不满足，则高 斯定理也不成立。 斯定理也不成立。
结论： 结论：均匀带电的无限大平面板产生的场强大 小与场点到平面的距离无关 图示c板间场强为何 板间场强为何？ 图示 板间场强为何？
讨论：
以上三例电荷分布分别具有球对称性、轴对称性、 以上三例电荷分布分别具有球对称性、轴对称性、 面对称性，电荷分布的对称性决定了场的对称性。 面对称性，电荷分布的对称性决定了场的对称性。 Gauss定理可以计算具有强对称性场的场强 用 Gauss定理可以计算具有强对称性场的场强 Gauss定理可以和场强叠加原理结合起来运用， Gauss定理可以和场强叠加原理结合起来运用， 定理可以和场强叠加原理结合起来运用 计算各种球对称性、轴对称性、面对称性的场。 计算各种球对称性、轴对称性、面对称性的场。
1.3高斯定理
S，两底面到带电平面距离相同。
E dS E dS E dS E dS 2ES
s
左底
右底
側
圆柱形高斯面内电荷 q S
由高斯定理得
E
S
E
2ES S / 0
E 2 0
σ
33
E 20
0 场强方向指离平面; / 20 / 20
§1.3 高斯定理
/ 2 0 / 2 0
§1.3 高斯定理
ห้องสมุดไป่ตู้
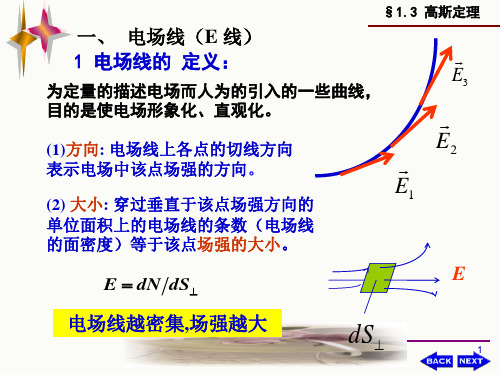
一、 电场线（E 线）
1 电场线的 定义：
为定量的描述电场而人为的引入的一些曲线，
E3
目的是使电场形象化、直观化。
(1)方向: 电场线上各点的切线方向 表示电场中该点场强的方向。
E2
(2) 大小: 穿过垂直于该点场强方向的
E1
单位面积上的电场线的条数（电场线
的面密度）等于该点场强的大小。
E dN dS
E
电场线越密集,场强越大
dS
1
2. 电场线示例
几
+
种
电
荷
分
布
的
+
电
场
线
+
图
§1.3 高斯定理
-
+
-
2
3. 电场线的性质：
§1.3 高斯定理
1）电场线起于正电荷，终止于负电 荷；电荷是电场线的“源”和“尾闾 ”2）电场线不会在无电荷的地方中断；
3）电场线不会在无电荷的地方相交； q
（2）半径为R的均匀带电体密度为ρ
的长圆柱体。
R2
E
2 0 r
r
2 0
(r R) (r R)
《高斯定理例》课件
磁场计算
在计算磁场分布时，高斯定理也发挥了重要 作用。它可以用来确定磁场线穿过任意封闭 曲面的通量，进而推导出磁场分布。
在工程学科中的应用
电力工程
在电力工程中，高斯定理被广泛应用于电磁 场分析和计算。例如，在输电线路和变压器 设计中，需要利用高斯定理来评估电磁场对 周围环境的影响。
电子工程
在电子工程领域，高斯定理用于分析集成电 路和电子元件中的电磁场。通过高斯定理， 工程师可以更好地理解电子元件的工作原理
要点二
量子计算
随着新型材料科学的发展，高斯定理在研究材料电磁性质 、导电性能等方面将发挥更大的作用。
量子计算领域的发展为高斯定理提供了新的应用场景，有 助于更深入地理解量子力学中的相关概念。
高斯定理在数学领域的发展趋势
数学物理
随着数学物理的不断发展，高斯定理在数学物理中的地 位将更加重要，有助于推动数学物理理论的发展。
总结词
均匀带电圆环产生的电场分布可以通过高斯定理求解。
详细描述
首先，我们需要将均匀带电圆环分割成许多小的带电圆环，然后利用高斯定理计算每个小圆环产生的 电场强度。最后，将所有小圆环的电场强度进行叠加，得到均匀带电圆环的总电场分布。
例题三：求无限长均匀带电直线的电场分布
总结词
无限长均匀带电直线产生的电场分布也 可以通过高斯定理求解。
《高斯定理例》ppt课件
目录
• 高斯定理简介 • 高斯定理的数学推导 • 高斯定理的例题解析 • 高斯定理的实践应用 • 高斯定理的未来发展
01
高斯定理简介
高斯定理的定义
总结词
高斯定理是描述闭合曲面电场分 布的定理。
详细描述
高斯定理表述为通过任意闭合曲 面的电场通量等于该闭合曲面所 包围的电量的代数和除以真空中 的介电常数。
2020年高中物理竞赛(电磁学)稳恒磁场和电磁场的相对性(含真题)磁场中的高斯定理(共27张PPT)
1. 求均匀磁场中 半球面的磁通量
B S1
R
O S2
S1 S2 0 S1 ( BR2 ) 0 S1 BR2
课 2. 在均匀磁场B 3i 2 j
堂 中，过YOZ平面内
练 习
面积为S的磁通量。
Y
S
n
B
O
X
Z
m
B
•S
( 3i 2 j )• Si
3S
五 、毕奥---沙伐尔定律
1)
dB
P
X
B
0I 4a
(cos1
cos2 )
无限长载流直导线
1 0 2
B 0I 2a
半无限长载流直导线 1 2
2
B 0I 4a
B
直导线延长线上 B ?
dB
0 4
Idl sin
r2
I
0 dB 0 B 0
2. 圆型电流轴线上的磁场
已知: R、I，求轴线上P
点的磁感应强度。
r
L r3
2、运动电荷的磁场
电流 电荷定向运动
电流元 Idl
dB
0 4
Idl r2
r0
其中
I
q v
S
dl
I qnvS
载流子
总数 dN nSdl
电荷 密度 速率 截面积
B
dB dN
0 4
qv sin( v , r0
r2
)
运动电荷产生的磁场
B
0 4
qv
r
r3
若q 0, B与v r同向
csc2
B
2(
1
0
2
nI
sin )d
0
习题09 电场线 电通量 真空中的高斯定理
一、选择题1．关于高斯定理的理解有下面几种说法，其中正确的是（ ）。
（A ）如果高斯面上E处处为零，则该面内必无电荷。
（B ）如果高斯面内无电荷，则高斯面上E 处处为零。
（C ）如果高斯面上E 处处不为零，则高斯面内必有电荷。
（D ）如果高斯面内有净电荷，则通过高斯面的电通量必不为零。
2．如右图所示，闭合面S 内有一点电荷q ，P 点为S 面上一点，在S 面外A 点处有一点电荷q ′，若将q ′移至B 点，则（ ）。
（A ）S 面的总电通量改变，P 点的场强不变。
（B ）S 面的总电通量不变，P 点的场强改变。
（C ）S 面的总电通量和P 点的场强都不改变（D ）S 面的总电通量和P 点的场强都改变3．如右图所示，半径为R 1的均匀带电球面1，带电量为Q 1，其外有一同心的半径为R 2的均匀带电球面2，带电量为Q 2，则离球心为r （R 1< r <R 2）处的某点P 的场强为（ ）。
（A ）r r Q E 2014πε= （B ）r rQ Q E 20214πε+= （C ）r r Q E 3014πε= （D ）r r Q Q E 30214πε+= 二、填空题1．如右图所示，三个平行的“无限大”均匀带电平面，其电荷面密度都是+σ，则A 、B 、C 、D 四个区域的电场强度分别为：A E = ，B E = ，C E = ，DE = ，（设方向向右为正）。
2．带电量分别为1q 和2q 的两个点电荷单独在空间各点建立的静电场分别为1E 和2E ，空间各点总场强为21E E E +=。
现在作一封闭曲面S ，如下图所示，则以下两式可分别求出通过S 的电通量：3．（1）点电荷q 位于一个边长为a 的立方体中心，试求在该点电荷电场中穿过立方体一面的电通量是 。
（2）如果将该场源点电荷移到立方体的的一个角上，这时通过立方体各面的电通量是 ； 。
一 D B C二 1. 032A E σε=-，02B E σε=-02C E σε=032D E σε= 2.10q ε，20q ε 3，06q ε，024q ε，0三 计算题1．解：薄板可近似为带电面分析知，场强分布是面对称的，因而建立如图所示的关于薄板面对称的柱形高斯面，两个底面分别为S 1和S 2。
大学物理高斯定理课堂PPT
由高斯定理知 E
q
2 0lr
（1）当r<R 时， q0
E0
.
25
高斯定理的应用
（2）当r>R 时，
ql
E
2 0r
均匀带电圆柱面的电场分布
r
l
E Er 关系曲线
2 0 R
r1
0
R
r
.
26
高斯简介 高斯（Carl Friedrich Gauss 1777~1855）
高斯长期从事于数学并将数学应用于物理学、天 文学和大地测量学等领域的研究，主要成就：
6-3 电场线 高斯定理
一、电场线
1、定义
在电场中画一组带箭头的曲线, 这些曲线与电场强度 E 之间具有
E
以下关系:
①电场线上任一点的切线方向给出了该点电场 强度的方向；
②某点处电场线密度与该点电场强度的大小 相等。
.
1
电场线密度:经过电场中任一点， 作一面积元dS，并使它与该点的 场强垂直，若通过dS面的电场线 条数为dN，则电场线密度
由电场线的连续性可知，穿 过 S的电场线都穿过同心球 面 S ，故两者的电通量相等， 均为 q ε 0 。
结论说明，单个点电荷包围 在任意闭合曲面内时，穿过 该闭曲面的电通量与该点电 荷在闭曲面内的位置无关。
.S
S
q •
S
电场线
S'
q+
r
10
③不包围点电荷q的任意闭合曲面S的电通量恒为零．
由于电场线的连续性可知，穿 入与穿出任一闭合曲面的电通 量应该相等。所以当闭合曲面 无电荷时，电通量为零。
斯定律。然而每一个带电平面的场强先可用高斯定
律求出，然后再用叠加原理求两个带电平面产生的
1-3章习题课
+q
S
−q
12
(1271)如图所示，在电量为q的点电荷的静 如图所示，在电量为 的点电荷的静 如图所示 电场中， 电场中，与点电荷相距分别为 ra 和rb 的 a,b两点之间的电势差 U a－U b ＝ 两点之间的电势差 _________ q 1 1 ( − ) 4πε0 ra rb
ra
q
a
r a
解：选坐标原点在带电平面所在处，x轴垂直于平面。 选坐标原点在带电平面所在处， 轴垂直于平面。 轴垂直于平面 由高斯定理可得场强分布为： 由高斯定理可得场强分布为：
E = ±σ (2ε0 )
（式中“＋”对x>0区域，“－”对x<0区域）。平面外 区域， 区域）。 式中“ 区域 区域）。平面外 任意点x处电势 处电势： 任意点 处电势： 在 x ≤ 0 区域 0 0 −σ σx U = ∫ E dx = ∫ dx = x x 2ε 2ε 0 0 在 x ≥ 0 区域 0 0 σ −σ x U = ∫ Edx = ∫ dx = x x 2ε 2ε 0 0 17
(1407) 一半径为 的均匀带电圆盘，电荷面 一半径为R的均匀带电圆盘 的均匀带电圆盘， 设无穷远处为电势零点， 密度为 σ ，设无穷远处为电势零点，则圆 盘中心O点的电势 盘中心 点的电势 U 0 ＝_____.
σ
P
x
r → r + dr 处圆环在 点产生的电势为： 处圆环在P点产生的电势为 点产生的电势为：
(B)
r
p
9
（1567）一半径为 的“无限长”均匀带电圆 ）一半径为R的 无限长” 柱面， 该圆柱面内、 柱面，其电荷面密度为σ．该圆柱面内、外场 强分布为( 表示在垂直于圆柱面的平面上， 表示在垂直于圆柱面的平面上， 强分布为 r 从轴线处引出的矢径)： 从轴线处引出的矢径 ： 0 E(r ) ＝______________________(r<R )，
S
−q
12
(1271)如图所示，在电量为q的点电荷的静 如图所示，在电量为 的点电荷的静 如图所示 电场中， 电场中，与点电荷相距分别为 ra 和rb 的 a,b两点之间的电势差 U a－U b ＝ 两点之间的电势差 _________ q 1 1 ( − ) 4πε0 ra rb
ra
q
a
r a
解：选坐标原点在带电平面所在处，x轴垂直于平面。 选坐标原点在带电平面所在处， 轴垂直于平面。 轴垂直于平面 由高斯定理可得场强分布为： 由高斯定理可得场强分布为：
E = ±σ (2ε0 )
（式中“＋”对x>0区域，“－”对x<0区域）。平面外 区域， 区域）。 式中“ 区域 区域）。平面外 任意点x处电势 处电势： 任意点 处电势： 在 x ≤ 0 区域 0 0 −σ σx U = ∫ E dx = ∫ dx = x x 2ε 2ε 0 0 在 x ≥ 0 区域 0 0 σ −σ x U = ∫ Edx = ∫ dx = x x 2ε 2ε 0 0 17
(1407) 一半径为 的均匀带电圆盘，电荷面 一半径为R的均匀带电圆盘 的均匀带电圆盘， 设无穷远处为电势零点， 密度为 σ ，设无穷远处为电势零点，则圆 盘中心O点的电势 盘中心 点的电势 U 0 ＝_____.
σ
P
x
r → r + dr 处圆环在 点产生的电势为： 处圆环在P点产生的电势为 点产生的电势为：
(B)
r
p
9
（1567）一半径为 的“无限长”均匀带电圆 ）一半径为R的 无限长” 柱面， 该圆柱面内、 柱面，其电荷面密度为σ．该圆柱面内、外场 强分布为( 表示在垂直于圆柱面的平面上， 表示在垂直于圆柱面的平面上， 强分布为 r 从轴线处引出的矢径)： 从轴线处引出的矢径 ： 0 E(r ) ＝______________________(r<R )，
高二物理竞赛高斯定理课件
只有在场强分布具有一定的对称性时，才能比较方便应用高斯定理求出场强。 (3) 根据高斯定理求电场强度。
则 在空腔处补上球体（ ρ 、r）后，
是所有电荷产生的， e 只与内部电荷有关。
n E [补偿法] 距直线r 处一点P 的电场强度
n 一均匀带电球体，半径为R，电荷密度为ρ，现在球内挖去一半径为r(r <R)的球体。
n S S S 0 取过场点 P 的同心球面为高斯面
德国数学家、天文学家和物理学家，有“数学王子”美称，他与韦伯制成了第一台有线电报机和建立了地磁观测台，高斯还创立了电
磁量的绝对单位制.
1
在电场中穿过任意曲面S 的电场线条数称为穿过
1
2
电场线是非闭合曲线，不相交。
R 电场线是非闭合曲线，不相交。
挖去的球体空腔可等效成是 带等量异种电荷的球体在该
处的叠加。
O•R O• r
设 球体带正电,电荷密度为+ρ,
则 在空腔处补上球体（ ρ 、r）后， E p E R E r
E R 3 0 r ,
Er
3 0
r
19
r •P
+ρ
•
OR
•
Or
r
-ρ
E p 3 0 (r r )
a
3 0
Ep E R Er
例已知“无限大”均匀带电平面上电荷面密度为
求 电场强度分布
解电场强度分布具有面对称性 E
n E
选取一个圆柱形高斯面
eSEdS
n
n
侧 E d S 左 E 底 d S 右 E 底 d S
0 E E S 2 E S S Ex
根据高斯定理有
2ES 1 S 0
E 2 0
则 在空腔处补上球体（ ρ 、r）后，
是所有电荷产生的， e 只与内部电荷有关。
n E [补偿法] 距直线r 处一点P 的电场强度
n 一均匀带电球体，半径为R，电荷密度为ρ，现在球内挖去一半径为r(r <R)的球体。
n S S S 0 取过场点 P 的同心球面为高斯面
德国数学家、天文学家和物理学家，有“数学王子”美称，他与韦伯制成了第一台有线电报机和建立了地磁观测台，高斯还创立了电
磁量的绝对单位制.
1
在电场中穿过任意曲面S 的电场线条数称为穿过
1
2
电场线是非闭合曲线，不相交。
R 电场线是非闭合曲线，不相交。
挖去的球体空腔可等效成是 带等量异种电荷的球体在该
处的叠加。
O•R O• r
设 球体带正电,电荷密度为+ρ,
则 在空腔处补上球体（ ρ 、r）后， E p E R E r
E R 3 0 r ,
Er
3 0
r
19
r •P
+ρ
•
OR
•
Or
r
-ρ
E p 3 0 (r r )
a
3 0
Ep E R Er
例已知“无限大”均匀带电平面上电荷面密度为
求 电场强度分布
解电场强度分布具有面对称性 E
n E
选取一个圆柱形高斯面
eSEdS
n
n
侧 E d S 左 E 底 d S 右 E 底 d S
0 E E S 2 E S S Ex
根据高斯定理有
2ES 1 S 0
E 2 0