1.5 二值逻辑变量与基本逻辑运算
康华光《电子技术基础-数字部分》(第5版)笔记和课后习题(含考研真题)详解

第1章 数字逻辑概论1.1 复习笔记一、模拟信号与数字信号 1.模拟信号和数字信号 (1)模拟信号在时间上连续变化,幅值上也连续取值的物理量称为模拟量,表示模拟量的信号称为模拟信号,处理模拟信号的电子电路称为模拟电路。
(2)数字信号 与模拟量相对应,在一系列离散的时刻取值,取值的大小和每次的增减都是量化单位的整数倍,即时间离散、数值也离散的信号。
表示数字量的信号称为数字信号,工作于数字信号下的电子电路称为数字电路。
(3)模拟量的数字表示①对模拟信号取样,通过取样电路后变成时间离散、幅值连续的取样信号; ②对取样信号进行量化即数字化;③对得到的数字量进行编码,生成用0和1表示的数字信号。
2.数字信号的描述方法(1)二值数字逻辑和逻辑电平在数字电路中,可以用0和1组成的二进制数表示数量的大小,也可以用0和1表示两种不同的逻辑状态。
在电路中,当信号电压在3.5~5 V 范围内表示高电平;在0~1.5 V 范围内表示低电平。
以高、低电平分别表示逻辑1和0两种状态。
(2)数字波形①数字波形的两种类型非归零码:在一个时间拍内用高电平代表1,低电平代表0。
归零码:在一个时间拍内有脉冲代表1,无脉冲代表0。
②周期性和非周期性周期性数字波形常用周期T 和频率f 来描述。
脉冲波形的脉冲宽度用W t 表示,所以占空比100%t q T=⨯W③实际数字信号波形在实际的数字系统中,数字信号并不理想。
当从低电平跳变到高电平,或从高电平跳到低电平时,边沿没有那么陡峭,而要经历一个过渡过程。
图1-1为非理想脉冲波形。
图1-1 非理想脉冲波形④时序图:表示各信号之间时序关系的波形图称为时序图。
二、数制 1.十进制以10为基数的计数体制称为十进制,其计数规律为“逢十进一”。
任意十进制可表示为:()10iDii N K ∞=-∞=⨯∑式中,i K 可以是0~9中任何一个数字。
如果将上式中的10用字母R 代替,则可以得到任意进制数的表达式:()iR ii N K R ∞=-∞=⨯∑2.二进制(1)二进制的表示方法以2为基数的计数体制称为二进制,其只有0和1两个数码,计数规律为“逢二进一”。
逻辑变量与基本运算图文

3
卡诺图还可以用于检测逻辑错误和优化 逻辑电路设计。通过观察卡诺图,可以 快速发现输入与输出之间的不正确关系 ,从而及时纠正错误。
逻辑函数表达式与真值表的关系
逻辑函数表达式是描述输入与输出之间逻辑关系的数 学表达式。真值表则是一种表格形式,列出输入变量
逻辑变量与基本运算图文
目录
• 逻辑变量的概念与表示 • 基本逻辑运算 • 逻辑运算的复合与扩展 • 逻辑运算的应用 • 逻辑运算的图形表示
01
逻辑变量的概念与表示
逻辑变量的定义
逻辑变量是用于表示逻辑值的符号或 标记,通常用于逻辑运算和逻辑推理 中。
逻辑变量可以是任何符号,如字母、 数字或特定的符号,只要它们能够表 示逻辑值即可。
算法设计
算法设计是数字系统设计的核心,需要根据系统 需求设计合适的算法,以满足性能、精度和稳定 性等方面的要求。
硬件平台选择
数字系统设计需要考虑硬件平台的选择,包括处 理器、存储器、输入输出接口等硬件资源的配置 和优化。
05
逻辑运算的图形表示
卡诺图(Karnaugh Map)
1
卡诺图是一种用于表示逻辑函数输入与 输出之间关系的图形表示方法。它通过 将输入变量和输出变量的所有可能组合 表示为小方格,并使用特定的符号来表 示逻辑函数的值。
(land) 表示逻辑与运算。
3
在逻辑或-与复合运算中,首先进行括号内的逻辑与运算
(B land C),然后再与 (A) 进行逻辑或运算。
4
逻辑或-与复合运算的运算优先级高于单纯的逻辑或和
逻辑与运算。
多重逻辑运算的扩展
电子技术基础数字部分第六版康华光

模拟信号 3V
模数转换器
00000011 数字输出
1.1.4 数字信号的描述方法
1、二值数字逻辑和逻辑电平 二值数字逻辑
0、1数码---表示数量时称二进制数
表示方式
---表示事物状态时称二值逻辑
a 、在电路中用低、高电平表示0、1两种逻辑状态
逻辑电平与电压值的关系(正逻辑)
电压(V) 二值逻辑
3、数字电路的分析、设计与测试
(1)数字电路的分析方法 数字电路的分析:根据电路确定电路输出与输入之间的逻辑关系。 分析工具:逻辑代数。 电路逻辑功能主要用真值表、功能表、逻辑表达式和波形图。
(2) 数字电路的设计方法 数字电路的设计:从给定的逻辑功能要求出发,选择适当的 逻辑器件,设计出符合要求的逻辑电路。 设计方式:分为传统的设计方式和基于EDA软件的设计方式。
1.8万个电子管
保存80个字节
晶体管时代
器件
电流控制器件 —半导体技术
半导体二极管、三极管
半导体集成电路
电路设计方法伴随器件变化从传统走向现代
a)传统的设计方法: 采用自下而上的设计方法;由人工组装,经反复调试、验证、 修改完成。所用的元器件较多,电路可靠性差,设计周期长。
b)现代的设计方法: 现代EDA技术实现硬件设计软件化。采用从上到下设计方 法,电路设计、 分析、仿真 、修订 全通过计算机完成。
--数字电路可分为TTL 和 CMOS电路
从集成度不同 --数字集成电路可分为小规模、中规模、大规模、超
大规模和甚大规模五类。
集成度:每一芯片所包含的门个数
分类
小规模 中规模 大规模 超大规模
甚大规模
门的个数
典型集成电路
电子技术基础(数字部分)_数电_(第五版)康华光主编[1]
![电子技术基础(数字部分)_数电_(第五版)康华光主编[1]](https://img.taocdn.com/s3/m/66203cec551810a6f5248631.png)
3、)书写简洁。
1.3 二进制的算术运算(自学)
1.3.1 无符号二进制的数算术运算
1.3.2 有符号二进制的数算术运算
1.3 二进制的算术运算(自学) 1.3.1 无符号数算术运算
1.2
数制
1.2.1十进制 1.2.2 二进制 1.2.3 二-十进制之间的转换 1.2.4十六进制和八进制
1.2 数制
数制:多位数码中的每一位数的构成及低位向高位进位的规则
1.2.1十进制
十进制采用0, 1, 2, 3, 4, 5, 6, 7, 8, 9十个数码,其进位的规则是
“逢十进一”。
4587.29=4103+5102+8101+7100+2101+9102
3、模拟信号的数字表示
由于数字信号便于存储、分析和传输,通常都将模拟信号转换为数字信号.
模数转换的实现
3 V
模拟信号
模数转换器 00000011 数字输出
1.1.4 数字信号的描述方法
1、二值数字逻辑和逻辑电平 二值数字逻辑 0、1数码---表示数量时称二进制数
---表示事物状态时称二值逻辑 表示方式 a 、在电路中用低、高电平表示0、1两种逻辑状态
表示一位八进制数。 例 (10110.011)B = (26.3)O
将每位八进制数展开成三位二进制数,排列顺序不变即可。 例 (752.1)O= (111 101 010.001)B
5.十六进制的优点 :
1、)与二进制之间的转换容易;
2、)计数容量较其它进制都大。假如同样采用四位数码, 二进制最多可计至( 1111)B =( 15)D; 八进制可计至 (7777)O = (2800)D; 十进制可计至 (9999)D; 十六进制可计至 (FFFF)H = (65535)D,即64K。其容量最大。
基本逻辑运算
3 3.6V
2T 3 截止
3 主要参数
(1)TTL与非门提高工作速度的原理
a.采用多发射极三极管加快了存储电荷的消散过程。
iB1
Rb1
4kΩ
+VCC Rc 2 1.6kΩ
3.6V
A B C
1
1V 1.4V
31
T1 β iB1
0.7V
0.3V
3
2T2
1
Re2 1kΩ
Vo
3
2T 3
b.采用了推拉式输出级,输出阻抗比较小,可迅速给负载电容充放电。
应的输入电压。即输入高电压的3最.5 小值。在产B(品0.6V手,3.6V册) 中常
称为输入高电平电压,用VIHV(OH(mmiinn))23.5.0表2示.4V 。产C 品规C(1定.3V,V2.4I8HV() min)
=2V。(1.4-1.8V)
D(1.4V, 0.3V)
2.0
1.5
E(3.6V, 0.3V)
表2 -5 电位关系与正、 负逻辑
同样的方法可得到正与等于负或, 正异或等于负同或。
2.3 集 成 逻 辑 门
集成门电路的分类 1.按内部有源器件的不同分为:
双极型晶体管集成门电路:LSTTL、ECL、I2L 单极型MOS集成门电路:CMOS、NMOS、 PMOS、LDMOS、VDMOS…… 晶体管和MOS管集成门电路:BiCMOS
B
NP
A
C
NP
B C
1
+VCC ( +5V) Rb1
3
T1
1. 电路基本结构
Rb1 4kΩ
Rc 2 1.6kΩ
Vc 2
1
+VCC( +5V) Rc4 130Ω
数电02(逻辑概论)

通电
灭
3.
非运算
非逻辑真值表
A 0 1 L 1 0
非逻辑举例状态表 A 不通电 通电 非逻辑符号
A
1
灯 亮
灭 表示反相
L A
L
逻辑表达式
L=A
4. 几种常用复合逻辑运算 1)与非运算
与非逻辑符号
与非逻辑真值表
A 0 0 1 1 B 0 1 0 1 L 1 1 1 0
A
B
有 0 出 1 全 1 出 0
逻辑真值表
A 0 0 B 0 1 L 0 0
1
1
0
1
0
1
与逻辑符号 A B 逻辑表达式 L A B 与逻辑: &
L
L = A · = AB B
2、或运算
只要在决定某一事件的各种条件中,有一个或几个条件具 备时,这一事件就会发生。这种因果关系称为或逻辑关系。 或逻辑举例
S1 S2 开关S1 断 电路状态表 开关S2 断 合 断 合 灯 灭 亮 亮 亮
1、逻辑函数的表示方法
◆
逻辑图法
采用规定的图形符号,构成的逻辑运算关系的网 络图形。
◆ 卡诺图法 一种几何图形,是由美国工程师卡诺首先提出的,
可以用来表示和简化逻辑函数表达式。
◆ 波形图(时序图)法 输入端在不同逻辑信号作用下,对应的输出信号的 波形图。是一种表示输入、输出信号动态变化的图形,反 映了函数值随时间变化的规律。 几种表示方法可以互相转换。
1.数字逻辑概论 2.逻辑代数与硬件描述语言概述 3.逻辑门电路 4.组合逻辑电路 5.锁存器与触发器 6.时序逻辑电路 7.存储器、复杂可编程器件和 现场可编程门阵列 8.脉冲波形的变换与产生 9.模数与数模转换器
三种基本的逻辑运算

以上为最基本的三种逻辑运算,除此之外,还 有下面的由基本逻辑运算组合出来的逻辑运算
4. 与非(NAND)逻辑运算 与非运算是先与运算后非运算 的组合。以二变量为例,布尔 代数表达式为:
Y ( AB)
其真值表如表2.2.4所示
表2.2.4 与非逻辑真值表Fra bibliotek输入 输出A
BY
0
01
0
11
1
01
1
10
其逻辑规律服从“有0出1, 全1才出0”
注意:
1. 逻辑代数和普通数学代数的运算相似,如有交换 律、结合律、分配律,而且逻辑代数中也用字母表 示变量,叫逻辑变量。
2. 逻辑代数和普通数学代数有本质区别,普通数学 代数中的变量取值可以是正数、负数、有理数和无 理数,是进行十进制(0~9)数值运算。而逻辑代 数中变量的取值只有两个:“0”和“1”。并且“0” 和“1”没有数值意义,它只是表示事物的两种逻辑 状态。
2.1 概述
2.1.1 二值逻辑和逻辑运算 在数字电路中,1位二进制数码“0”和“1”不仅
可以表示数量的大小,也可以表示事物的两种不同 的逻辑状态,如电平的高低、开关的闭合和断开、 电机的起动和停止、电灯的亮和灭等。
当二进制数码“0”和“1”表示二值逻辑,并按
某种因果关系进行运算时,称为
,最基本
的三种逻辑运算为“与”、“或”、“非”,它与
Y
图2.2.4 或门逻辑符号
若有n个逻辑变量做或运算,其逻辑式可表示为
Y A1 A2 An
3. 非逻辑运算
条件具备时,事件不发生;条件不具备时,事 件发生,这种因果关系叫做逻辑非,也称逻辑求反
如图2.2.5所示电路,一个开关 控制一盏灯就是非逻辑事例, 当开关A闭合时灯就会不亮。
《电子技术基础数字部分》考研康华光版2021考研复习笔记

《电子技术基础数字部分》考研康华光版2021考研复习笔记第1章数字逻辑概论1.1 复习笔记本章是《电子技术基础数字部分》的开篇,主要讲述了模拟信号和数字信号以及数字信号的描述方法,进而讨论了数制、二进制的算术运算、二进制代码和数字逻辑的基本运算,是整本教材的学习基础。
笔记所列内容,读者应力求理解和熟练运用。
一、模拟信号与数字信号1模拟信号和数字信号(见表1-1-1)表1-1-1 模拟信号和数字信号2数字信号的描述方法(见表1-1-2)表1-1-2 数字信号的描述方法3数字波形详细特征(1)数字波形的两种类型见表1-1-3表1-1-3 数字波形的类型(2)周期性和非周期性与模拟信号波形相同,数字波形亦有周期型和非周期性之分。
周期性数字波形常用周期T和频率f来描述。
脉冲波形的脉冲宽度用表示,所以占空比(3)实际数字信号波形在实际的数字系统中,数字信号并不理想。
当从低电平跳变到高电平,或从高电平跳到低电平时,边沿没有那么陡峭,而要经历一个过渡过程。
图1-1-1为非理想脉冲波形。
图1-1-1 非理想脉冲波形(4)波形图、时序图或定时图波形图、时序图或定时图概述见表1-1-4。
表1-1-4 波形图、时序图或定时图概述时序图和定时图区别与特征见表1-1-5。
表1-1-5 时序图、定时图特征二、数制1几种常用的进制(见表1-1-6)表1-1-6 几种常用的进制2进制之间的转换(1)其他进制转十进制任意一个其他进制数转化成十进制可用如下表达式表示:其中R表示进制,Ki表示相应位的值。
例如(二进制转十进制):(1011.01)2=1×23+0×22+1×21+1×20+0×2-1+1×2-2=(11.25)10。
(2)十进制转二进制①整数部分的转换:将十进制数除以2,取所余数为k0;将其商再除以2,取其余数为k1,……以此类推,直到所得商等于0为止,余数k n…k1k0(从下往上排)即为二进制数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电路状态表 开关S 开关 2 断 合 断 合 灯 灭 灭 灭 亮
重庆工学院
《数字电子技术》 数字电子技术》
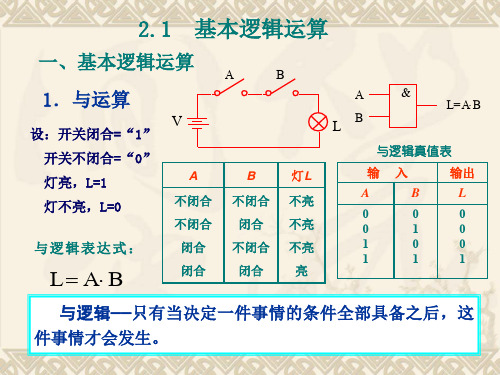
1.与运算
与逻辑举例状态表
开关S1 开关S 断 断 合 合 开关S2 开关S 断 合 断 合 灯 灭 灭 灭 亮
逻辑真值表 A 0 0 1 1 B 0 1 0 1 L 0 0 0 1
与逻辑符号 A B 逻辑表达式 L A B & L
S1 S2 电源 灯 开关S 开关 1 断 断 合 合 电路状态表 开关S 开关 2 断 合 断 合 灯 灭 亮 亮 亮
重庆工学院
《数字电子技术》 数字电子技术》
2、或运算
或辑举例状态表
开关S 开关S1 断 断 合 合 开关S 开关S2 断 合 断 合 灯 灭 灭 灭 亮
逻辑真值表 A 0 0 1 1 B 0 1 0 1 L 0 1 1 1
重庆工学院
《数字电子技术》 数字电子技术》
1.与运算
(1) 与逻辑:只有当决定某一事件的条件全部具备时, 与逻辑 只有当决定某一事件的条件全部具备时, 只有当决定某一事件的条件全部具备时
这一事件才会发生。这种因果关系称为与逻辑关系。 这一事件才会发生。这种因果关系称为与逻辑关系。
与逻辑举例 S1 电源 S2 灯 开关S 开关 1 断 断 合 合
或逻辑符号
A B
≥1
L
A B
L
逻辑表达式
或逻辑: 或逻辑: L = A +B
重庆工学院
《数字电子技术》 数字电子技术》
3.
非运算
事件发生的条件具备时,事件不会发生; 事件发生的条件具备时 , 事件不会发生 ; 事件发生的条件 不具备时,事件发生。这种因果关系称为非逻辑关系。 不具备时,事件发生。这种因果关系称为非逻辑关系。
L
L= A ⊕ B
重庆工学院
《数字电子技术》 数字电子技术》
4 )
同或运算
若两个输入变量的值相同,输出为1 否则为0 若两个输入变量的值相同,输出为1,否则为0。 同或逻辑真值表 A 0 0 1 1 B 0 1 0 1 L 1 0 0 1 同或逻辑逻辑符号
A B A B L = L
同或逻辑表达式 L=AB+ AB =A B
重庆工学院
或非逻辑符号 A B A B
≥1
L
L
《数字电子技术》 数字电子技术》
3)
异或逻辑
若两个输入变量的值相异,输出为1,否则为0。 若两个输入变量的值相异,输出为 ,否则为 。 异或逻辑真值表 A 0 0 1 1 B 0 1 0 1 L 0 1 1 0 异或逻辑符号 A B A B 异或逻辑表达式 L =1
《数字电子技术》 数字电子技术》
1.5 二值逻辑变量与基本逻辑运算
表示逻辑状态时 *逻辑运算:当0和1表示逻辑状态时,两个二进制数码按照某种 逻辑运算: 和 表示逻辑状态时, 特定的因果关系进行的运算。 特定的因果关系进行的运算。 逻辑运算使用的数学工具是逻辑代数。 逻辑运算使用的数学工具是逻辑代数。 * 逻辑代数与普通代数:与普通代数不同 逻辑代数中的变量只有 逻辑代数与普通代数:与普通代数不同,逻辑代数中的变量只有 逻辑代数中的变量只有0 两个可取值, 和1两个可取值,它们分别用来表示完全两个对立的逻辑状态。 两个可取值 它们分别用来表示完全两个对立的逻辑状态。 在逻辑代数中,有与、 在逻辑代数中,有与、或、非三种基本的逻辑运算。 非三种基本的逻辑运算。 逻辑运算的描述方式:逻辑代数表达式、真值表、逻辑图、 逻辑运算的描述方式:逻辑代数表达式、真值表、逻辑图、 卡诺图、波形图和硬件描述语言( 卡诺图、波形图和硬件描述语言(HDL) 等。
重庆工学院
与逻辑: 与逻辑: L = A ·B= AB
重庆工学院
《数字电子技术》 数字电子技术》
2、或运算
只要在决定某一事件的各种条件中, 只要在决定某一事件的各种条件中 , 有一个或几个条件具 备时,这一事件就会发生。这种因果关系称为或逻辑关系。 备时,这一事件就会发生。这种因果关系称为或逻辑关系。 或逻辑举例
1) 与非运算 两输入变量与非 逻辑真值表 A 0 0 1 1 B 0 1 0 1 L 1 1 1 0 与非逻辑符号 A B A B & L
L
与非逻辑表达式
L= A·B
重庆工学院
《数字电子技术》 数字电子技术》
2) 或非运算 两输入变量或非 逻辑真值表 A 0 0 1 1 B 0 1 0 1 L 1 0 0 0 或非逻辑表达式: 或非逻辑表达式: L = A+B
非逻辑举例 A NC V
非逻辑举例状态表 A 不通电 通电 灯 亮 灭
重庆工学院
《数字电子技术》 数字电子技术》
3.
非运算
非逻辑真值表 A 0 1 L 1 0
非逻辑举例状态表 A 不通电 通电 非逻辑符号
A
1
灯 亮 灭
L
A
L
逻辑表达式
L=A
重庆工学院
《数字电子技术》 数字电子技术》
4. 几种常用复合逻辑运算
