(完整版)诱导公式练习题
02三角函数诱导公式(含经典例题+答案)
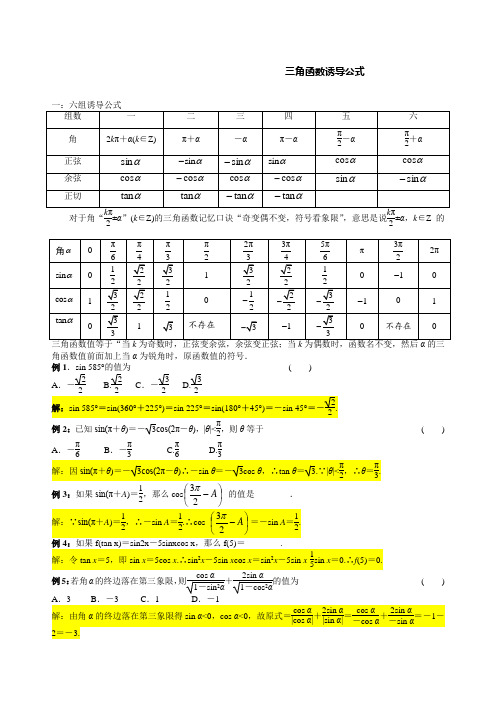
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说k π2±α,k ∈Z 的角函数值前面加上当α为锐角时,原函数值的符号.例1.sin 585°的值为 ( )A .-2 B.2 C .-3 D.3例2:已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于 ( )A .-πB .-π C.π D.π例3:如果sin(π+A )=12,那么cos ⎪⎫⎛-A 3 的值是________. 例5:若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 ( )例6:已知α∈(-π,0),tan(3π+α)=31,则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B .-1010 C.31010 D .-31010解:tan α=13,cos ⎪⎭⎫⎝⎛+απ23=sin α.∵α∈(-π,0),∴sin α=-1010. A .-32 B.32 C.3-12 D.3+12解:sin 600°+tan 240°=sin(720°-120°)+tan(180°+60°)=-sin 120°+tan 60°=-32+3=32. ( ) A .3 B .5 C .1 D .不能确定解:f(2 011)=asin(2 011π+α)+bcos(2 011π+β)+4=asin(π+α)+bcos(π+β)+4=-asin α-bcos β+4 =5.∴asin α+bcos β=-1.∴f(2 012)=asin(2 012π+α)+bcos(2 012π+β)+4=asin α+bcos β+4 =-1+4=3.1.诱导公式在三角形中经常应用,常用的变形结论有:A +B =π-C ; 2A +2B +2C =2π;A 2+B 2+C 2=π2.2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.例9:△ABC 中,cos A =13,则sin(B +C )=________.解:∵△ABC 中,A +B +C =π,∴sin(B +C )=sin(π-A )=sin A =1-cos 2A =223.例10:在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角. 解:由已知得⎩⎨⎧sin A =2sin B ①3cos A =2cos B ②①2+②2得2cos 2A =1,即cos A =22或cos A =-22.(1)当cos A =22时,cos B =32,又A 、B 是三角形的内角,∴A =π4,B =π6,∴C =π-(A +B )=712π. A .B .C .D .2.cos (﹣30°)的值是( ) A .B .C .D .3.下列能与sin20°的值相等的是( ) A .cos20° B .sin (﹣20°) C .sin70° D .sin160°4.已知,则下列各式中值为的是( )A .B .sin (π+α)C .D .sin (2π﹣α)换元法与诱导公式例11:已知41)3sin(=+απ,则=-)6cos(απ 。
诱导公式练习题含答案

诱导公式练习题含答案学校:__________ 班级:__________ 姓名:__________ 考号:__________1. 已知tan(x+π2)=5,则1sin x cos x=()A.265B.−265C.±265D.−5262. cos390∘=( )A.1 2B.√32C.−12D.−√323. cos23π6=()A.1 2B.−12C.√32D.−√324. 已知sin(α2−π4)=√210,则sinα=()A.−1225B.1225C.−2425D.24255. 已知tanα=3,则2sin a+cosα2cos a−3sinα的值是()A.5 3B.1C.−1D.−536. 已知sin(α−π4)=13,则cos(α+π4)的值等于()A.−13B.13C.−2√23D.2√237. 若cosα=−45,且α是第三象限角,则tanα=()A.−34B.34C.43D.−438. 若tanα=√3,且α为第三象限角,则cosα−sinα的值为( )A.−1+√32B.√3−12C.1−√32D.1+√329. 已知f(α)=sin (π−α)cos (2π−α)cos (3π2−α)cos (π2−α)sin (−π−α).(1)化简f(α);(2)若α是第三象限角,且sin (α−π)=15,求f(α)的值.10. 在△ABC 中,∠A,∠C 均为锐角,且|12−sin A|+(cos C −√22)2=0,求∠B 的度数.11. 已知sin (30∘+α)=35,60∘<α<150∘,求cos α的值.12. 已知f(x)=sin (π2+x)−2cos (π+x)sin (π−x)+cos (−x).(1)求f (π4)的值;(2)若f(α)=2,α是第三象限角,求tan α及sin α的值.13. 已知f (α)=sin (α−π)cos (3π2+α)cos (−α−π)sin (5π+α)sin (α−2π).(1)化简f (α);(2)若sin (α+π2)=−25√6,求f (α+π)的值;(3)若α=2021π3,求f (α)的值.14. 已知f(α)=sin (α−π2)cos (3π2−α)tan (π+α)cos (π2+α)sin (2π−α)tan (−α−π)sin (−α−π).(1)化简f(α);(2)若α是第三象限角,且cos(α−3π2)=15,求f(α)的值.15. 已知sin(x+π3)=13,求sin(4π3+x)+cos2(−x+5π3)的值.16. 已知函数f(x)=2cos x(sin x+cos x)−1.(Ⅰ)求f(x)的最小正周期;(Ⅱ)求f(x)在[0, π]上的单调递增区间.参考答案与试题解析诱导公式练习题含答案一、选择题(本题共计 8 小题,每题 5 分,共计40分)1.【答案】B【考点】同角三角函数间的基本关系【解析】本题考查同角三角函数间的基本关系.【解答】解:因为tan(x+π2)=sin(x+π2)cos(x+π2)=cos x−sin x =−1tan x=5,所以tan x=−15,所以1sin x cos x =sin2x+cos2xsin x cos x=tan2x+1tan x =−265.故选B.2.【答案】B【考点】运用诱导公式化简求值【解析】利用诱导公式化简即可得解.【解答】解:cos390∘=cos(360∘+30∘)=cos30∘=√32.故选B.3.【答案】C【考点】运用诱导公式化简求值【解析】由题意,直接利用诱导公式和特殊角的三角函数值进行化简求值即可. 【解答】解:已知cos23π6=cos(23π6−4π)=cos(−π6)=cosπ6=√32.故选C.4.【考点】两角和与差的三角函数【解析】两边同时平方,然后结合二倍角正弦公式即可求解.【解答】∵sin(α2−π4)=√210,∴√22(sin12α−cos12α)=√210,即sin12α−cos12α=15,两边同时平方可得,1+2sin12αcos12α=125,则sinα=−2425.5.【答案】C【考点】运用诱导公式化简求值【解析】此题暂无解析【解答】此题暂无解答6.【答案】A【考点】运用诱导公式化简求值【解析】运用诱导公式即可化简求值.【解答】解:∵sin(α−π4)=13,∴cos(α+π4)=sin[π2−(π4+α)]=sin(π4−α)=−sin(α−π4 )=−13.故选A.7.【考点】同角三角函数间的基本关系 【解析】由cos α的值,及α为第三象限角,利用同角三角函数间的基本关系求出sin α的值,即可确定出tan α的值即可. 【解答】解:∵ cos α=−45,且α是第三象限角, ∴ sin α=−√1−cos 2α=−35, 则tan α=sin αcos α=34. 故选B . 8.【答案】 B【考点】同角三角函数基本关系的运用 运用诱导公式化简求值 【解析】由tan α=2,即sin αcos α=2,sin 2α+cos 2α=1,且α是第三象限角,即可求解sin α,cos α.从而求解cos α−sin α的值. 【解答】解:∵ tan α=√3,α为第三象限角, ∴ sin α=√3cos α,sin α<0,cos α<0, 由sin 2α+cos 2α=1, 则(√3cos α)2+cos 2α=1, 解得cos α=−12,sin α=−√32. 则cos α−sin α=−12−(−√32) =−12+√32=√3−12. 故选B .二、 解答题 (本题共计 8 小题 ,每题 5 分 ,共计40分 ) 9.【答案】f(α)=sin (π−α)cos (2π−α)cos (3π2−α)cos (π2−α)sin (−π−α) =sin αcos α(−sin α)sin αsin α=−cos α.∵ α是第三象限角,且sin (α−π)=15,∴ sin α=−15,∴ cos α=−√1−sin 2α=−√1−125=−2√65, ∴ f(α)=−cos α=2√65. 【考点】运用诱导公式化简求值 【解析】(1)利用诱导公式化简即可得到结果;(2)由α是第三象限角及sin α的值,利用同角三角函数间的基本关系求出cos α的值,所求式子利用诱导公式化简后,代入计算即可求出值; 【解答】f(α)=sin (π−α)cos (2π−α)cos (3π2−α)cos (π2−α)sin (−π−α)=sin αcos α(−sin α)sin αsin α=−cos α. ∵ α是第三象限角,且sin (α−π)=15,∴ sin α=−15,∴ cos α=−√1−sin 2α=−√1−125=−2√65, ∴ f(α)=−cos α=2√65. 10. 【答案】解:因为|12−sin A|+(cos C −√22)2=0,所以12−sin A =0,cos C −√22=0,所以sin A =12,cos C =√22. 因为∠A,∠C 均为锐角,所以∠A =30∘,∠C =45∘,所以∠B =180∘−30∘−45∘=105∘. 【考点】运用诱导公式化简求值 【解析】 此题暂无解析 【解答】解:因为|12−sin A|+(cos C −√22)2=0,所以12−sin A =0,cos C −√22=0,所以sin A =12,cos C =√22. 因为∠A,∠C 均为锐角,所以∠A =30∘,∠C =45∘,所以∠B =180∘−30∘−45∘=105∘. 11. 【答案】已知sin (30∘+α)=35,60∘<α<150∘, 所以90∘<30∘+α<180∘ 所以cos (30+α)=−45,则:cos α=cos [(30∘+α)−30∘]=cos (30∘+α)cos 30∘+sin (30∘+α)sin 30∘=−45×√32+35×12=3−4√310. 【考点】两角和与差的三角函数 【解析】直接利用三角函数关系式的应用求出结果. 【解答】已知sin (30∘+α)=35,60∘<α<150∘, 所以90∘<30∘+α<180∘ 所以cos (30+α)=−45,则:cos α=cos [(30∘+α)−30∘]=cos (30∘+α)cos 30∘+sin (30∘+α)sin 30∘=−45×√32+35×12=3−4√310. 12. 【答案】 解:(1)∵ f(x)=sin (π2+x)−2cos (π+x)sin (π−x)+cos (−x)=cos x +2cos xsin x +cos x=3tan x+1,∴ f (π4)=3tan π4+1=31+1=32.(2)∵ 已知f(α)=3tan α+1=2, ∴ tan α=sin αcos α=12,又sin2α+cos2α=1,α是第三象限角,∴ 解得:sinα=−√55.【考点】运用诱导公式化简求值同角三角函数间的基本关系【解析】此题暂无解析【解答】解:(1)∵f(x)=sin(π2+x)−2cos(π+x) sin(π−x)+cos(−x)=cos x+2cos x sin x+cos x=3tan x+1,∴f(π4)=3tanπ4+1=31+1=32.(2)∵已知f(α)=3tanα+1=2, ∴tanα=sinαcosα=12,又sin2α+cos2α=1,α是第三象限角,∴ 解得:sinα=−√55.13.【答案】解:(1)f(α)=−sinαsinα(−cosα)−sinαsinα=−cosα(α≠kπ,k∈Z).(2)∵sin(α+π2)=cosα=−2√65,∴ f(α+π)=−cos(α+π)=cosα=−2√65.(3)∵ α=2021π3=674π−π3,∴ f(α)=−cosα=−cos(674π−π3 )=−cosπ3=−12.【考点】运用诱导公式化简求值【解析】(1)由条件利用诱导公式化简所给式子的值,可得f(α)的解析式.(2)由条件利用诱导公式化简可得cosα=−2√65,从而求得f(α)=−cosα的值;(3)α=2021π3=674π−π3,利用诱导公式求得f(α)的值.【解答】解:(1)f(α)=−sinαsinα(−cosα)−sinαsinα=−cosα(α≠kπ,k∈Z).(2)∵sin(α+π2)=cosα=−2√65,∴ f(α+π)=−cos(α+π)=cosα=−2√65.(3)∵ α=2021π3=674π−π3,∴ f(α)=−cosα=−cos(674π−π3 )=−cosπ3=−12.14.【答案】解:(1)由题意知f(α)=−sin(π2−α)(−sinα)tanα(−sinα) sin(−α)(−tanα)[−sin(π+α)]=−cosα(−sinα)tanα(−sinα)−sinα(−tanα)sinα=−cosα.(2)∵cos(α−3π2)=cos(3π2−α)=−sinα=15,∴sinα=−15,又α为第三象限角,∴cosα=−√1−sin2α=−2√65, ∴ f(α)=−cosα=2√65. 【考点】运用诱导公式化简求值【解析】此题暂无解析【解答】解:(1)由题意知f(α)=−sin(π2−α)(−sinα)tanα(−sinα) sin(−α)(−tanα)[−sin(π+α)]=−cosα(−sinα)tanα(−sinα)−sinα(−tanα)sinα=−cosα.(2)∵ cos (α−3π2)=cos (3π2−α)=−sin α=15, ∴ sin α=−15,又α为第三象限角,∴ cos α=−√1−sin 2α=−2√65, ∴ f(α)=−cos α=2√65. 15.【答案】解:∵ sin 2(x +π3)+cos 2(x +π3)=1, 又sin (x +π3)=13,∴ cos 2(x +π3)=1−sin 2(x +π3)=89, ∴ 原式=sin (π+π3+x)+cos 2[2π−(x +π3)]=−sin (π3+x)+cos 2(x +π3) =−13+89=59. 【考点】运用诱导公式化简求值【解析】直接利用诱导公式化简即可.【解答】解:∵ sin 2(x +π3)+cos 2(x +π3)=1, 又sin (x +π3)=13, ∴ cos 2(x +π3)=1−sin 2(x +π3)=89, ∴ 原式=sin (π+π3+x)+cos 2[2π−(x +π3)]=−sin (π3+x)+cos 2(x +π3) =−13+89=59.16.【答案】(Ⅰ)f(x)=2sin x cos x+2cos2x−1=sin2x+cos2x=√2sin(2x+π4).∴f(x)的最小正周期为T=2π2=π;(Ⅱ)由−π2+2kπ≤2x+π4≤π2+2kπ(k∈Z),得−3π8+kπ≤x≤π8+kπ(k∈Z).当x∈[0, π]时,单调递增区间为[0,π8brack和[5π8,πbrack.【考点】运用诱导公式化简求值【解析】(Ⅰ)利用倍角公式降幂,再由辅助角公式化积,由周期公式求周期;(Ⅱ)利用复合函数的单调性求出增区间,进一步得到f(x)在[0, π]上的单调递增区间.【解答】(Ⅰ)f(x)=2sin x cos x+2cos2x−1=sin2x+cos2x=√2sin(2x+π4).∴f(x)的最小正周期为T=2π2=π;(Ⅱ)由−π2+2kπ≤2x+π4≤π2+2kπ(k∈Z),得−3π8+kπ≤x≤π8+kπ(k∈Z).当x∈[0, π]时,单调递增区间为[0,π8brack和[5π8,πbrack.。
诱导公式基础练习题(含详细答案)

数学诱导公式作业1.3,2παπ⎛⎫∈ ⎪⎝⎭,sin 10α=-,tan α=______. 2.已知点()1,2P -为角θ终边上一点,则2sin cos sin cos θθθθ-=+______. 3.已知1sin cos 3αα+=,则sin cos αα的值为________. 4.若3sin cos 0αα+=,则21cos sin 2αα+的值为_ 5.已知02πα-<<,且5cos 13α=.则2cos()3sin()4cos()sin(2)παπααπα--+-+-的值为_____. 6.已知1tan()2πα-=-,则cos()+22cos sin cos παααα+-的值是______. 7.已知3sin 25πα⎛⎫-= ⎪⎝⎭,则cos()πα+的值为________. 8.sin 315=________.9.计算:1125sin tan 33ππ⎛⎫+-= ⎪⎝⎭________ 10.sin 30︒=__________,11cos4π=_________.11.已知角α终边上有一点()1,P y,且sin α=(1)求tan α的值; (2)求()()sin sin 2sin cos 2ππαααπα⎛⎫-++ ⎪⎝⎭--的值.12.已知()()()π3π=cos cos 2πsin 223πsin πsin 2f a ααααα⎛⎫⎛⎫+⋅-⋅-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫--⋅+ ⎪⎝⎭. (1)化简()f a ;(2)若α 是第三象限角,且31cos 25πα⎛⎫-= ⎪⎝⎭,求()f a 的值.13.已知02πα<<,且513sin α=. ()1求tan α的值;()2求()222222sin sin sin cos sin απααπαα--⎛⎫++ ⎪⎝⎭的值.14.化简或求值: (1)sin()cos()sin()cos()222cos()sin()πππααπααπαπα+--++++; (2)6sin(90)3sin08sin 27012cos180-+-+.15.已知角α的终边与单位圆交于点P(45,35).(1)写出sin αααtan ,cos ,值; (2)求)cos(2)2sin(2)sin(απαπαπ--++的值.16.已知角α的终边经过点P (m ,4),且35cos α=-, (1)求m 的值; (2)求()()()2sin sin cos sin παπααπα⎛⎫-++ ⎪⎝⎭-+-的值. 17.已知sin α=α是第一象限角. (1)求cos α的值. (2)求()()3sin 2tan cos πααππα⎛⎫- ⎪⎝⎭++-的值. 18.已知sin 1sin cos ααα=-- (1)求tan α的值,(2)求222sin 2sin cos 3sin cos ααααα++的值.参考答案1.13【解析】【分析】先计算cos α=,再根据sin tan cos ααα=计算得到答案. 【详解】3,2παπ⎛⎫∈ ⎪⎝⎭,sin 1sin cos tan cos 3ααααα==== 故答案为:13【点睛】 本题考查了同角三角函数关系,意在考查学生的计算能力.2.5【解析】【分析】首先求tan θ,再化简2sin cos 2tan 1sin cos tan 1θθθθθθ--=++,求值. 【详解】 由题意可知2tan 21θ==-- 2sin cos 2tan 15sin cos tan 1θθθθθθ--==++ . 故答案为:5【点睛】本题考查三角函数的定义和关于sin ,cos θθ的齐次分式求值,意在考查基本化简和计算. 3.49- 【解析】 ∵1sin cos 3αα+=, ∴2221(sin cos )sin cos 2sin cos 12sin cos 9αααααααα+=++=+=,解得4sin cos 9αα=-。
(完整版)诱导公式练习题

诱导公式练习题一、选择题 1. sin11π6的值是( ) A 。
21 B 。
-21 C 。
23 D.-232.已知的值为( )A.B. C.D.3.已知tan ,是关于x 的方程x 2-kx+k 2—3=0的两个实根,且3π<<,则cos +sin= ( )A.B 。
C 。
-D 。
-4.已知tan =2,,则3sin 2—cos sin +1= ( ) A.3 B.—3 C 。
4 D 。
-45.在△ABC 中,若sinA ,cosA 是关于x 的方程3x 2-2x+m=0的两个根,则△ABC 是 ( ) A.钝角三角形 B 。
直角三角形 C 。
锐角三角形 D 。
不能确定6.若1sin()33πα-=,则5cos()6πα-的值为()A .13 B.13- C.223 D 。
223-7.已知3cos()sin()22()cos()tan()f ππ+α-αα=-π-απ-α,则25()3f -π的值为( )A .12 B .-12C .32D . -328.定义某种运算a S b =⊗,运算原理如上图所示,则式子131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π的值为( )A .4B .8C .11D .139.若76πα=,则计算21sin(2)sin()2cos ()αππαα+-⋅+--所得的结果为( )A 。
34- B. 14- C. 0 D. 5410.已知sin()0,cos()0θπθπ+<->,则θ是第( )象限角。
A .一 B .二 C .三 D .四11.已知sinx=2cosx ,则sin 2x+1=( ) (A) (B) (C) (D )12.设02x π≤≤sin cos x x =-,则( ) A.0x π≤≤ B.744x ππ≤≤C 。
544x ππ≤≤ D.322x ππ≤≤ 二、填空题13.已知。
角α(0)πα-<<的终边与单位圆交点的横坐标是13,则cos()2πα+的值是___.14.化简:___________)cos()3sin()sin()23cos()3cos()2sin(=---+--+-πααπαπαπαπαπ15.已知32cos =a ,且02<<-a π,求)tan()cos()2sin()tan(a a a a +-+--πππ的值。
诱导公式练习题答案

诱导公式练习题答案诱导公式是三角函数中常用的公式,主要用于将正弦、余弦等三角函数的角转换为锐角,从而简化计算。
以下是一些诱导公式的练习题及其答案。
# 练习题1:求 \(\sin(90^\circ - x)\) 的值。
答案:根据诱导公式,我们知道 \(\sin(90^\circ - x) = \cos(x)\)。
# 练习题2:计算 \(\cos(180^\circ - x)\)。
答案:根据诱导公式,\(\cos(180^\circ - x) = -\cos(x)\)。
# 练习题3:给出 \(\tan(270^\circ - x)\) 的表达式。
答案:\(\tan(270^\circ - x) = -\cot(x)\)。
# 练习题4:求 \(\sin(360^\circ - x)\) 的值。
答案:\(\sin(360^\circ - x) = -\sin(x)\)。
# 练习题5:计算 \(\cos(90^\circ + x)\)。
答案:\(\cos(90^\circ + x) = -\sin(x)\)。
# 练习题6:给出 \(\tan(180^\circ + x)\) 的表达式。
答案:\(\tan(180^\circ + x) = \tan(x)\)。
# 练习题7:求 \(\sin(270^\circ + x)\) 的值。
答案:\(\sin(270^\circ + x) = -\cos(x)\)。
# 练习题8:计算 \(\cos(360^\circ + x)\)。
答案:\(\cos(360^\circ + x) = \cos(x)\)。
这些练习题涵盖了诱导公式的基本应用,通过这些练习,学生可以更好地理解和掌握诱导公式,提高解决三角函数问题的能力。
诱导公式练习

《诱导公式》练习一、选择题一、以下各式不正确的选项是 ( B )A . s in (α+180°)=-sin αB .cos (-α+β)=-cos (α-β)C . sin (-α-360°)=-sin αD .cos (-α-β)=cos (α+β) 二、假设sin (π+α)+sin (-α)=-m ,则sin (3π+α)+2sin (2π-α)等于( ) A .-23 m B .-32 m C .23 m D .32 m3、⎪⎭⎫⎝⎛-π619sin 的值等于( ) A .21B . 21-C .23 D . 23-4、若是).cos(|cos |π+-=x x 则x 的取值范围是( C )A .)(]22,22[Z k k k ∈++-ππππB .)()223,22(Z k k k ∈++ππππC .)(]223,22[Z k k k ∈++ππππD .)()2,2(Z k k k ∈++-ππππ5.已知函数1tan sin )(++=x b x a x f ,知足.7)5(=f 则)5(-f 的值为 ( )A .5B .-5C .6D .-6六、sin34π·cos 625π·tan 45π的值是A .-43B .43C .-43D .437.设,1234tan a =︒那么)206cos()206sin(︒-+︒-的值为 ( )A .211aa ++ B .-211aa ++ C .211aa +-D .211aa +-8.假设)cos()2sin(απαπ-=+,那么α的取值集合为( )A .}42|{Z k k ∈+=ππαα B .}42|{Z k k ∈-=ππααC .}|{Z k k ∈=πααD .}2|{Z k k ∈+=ππαα二、填空题一、求值:sin160°cos160°(tan340°+cot340°)= .二、假设sin (125°-α)=1213,那么sin (α+55°)= .3、cos π7 +cos 2π7 +cos 3π7 +cos 4π7 +cos 5π7 +cos 6π7 = .4、已知,1)sin(=+βα则=+++)32sin()2sin(βαβα .三、解答题一、已知 3)tan(=+απ, 求)2sin()cos(4)sin(3)cos(2a a a a -+-+--πππ的值.二、若cos α=23,α是第四象限角,求sin(2)sin(3)cos(3)cos()cos()cos(4)απαπαππαπααπ-+--------的值.3、设sin ,(0)()(1)1,(0)x x f x f x x π<⎧=⎨-+≥⎩和1cos ,()2()1(1)1,()2x x g x g x x π⎧<⎪⎪=⎨⎪-+≥⎪⎩求)43()65()31()41(f g f g +++的值.4.设)(x f 知足)2|(|cos sin 4)(sin 3)sin (π≤⋅=+-x xx x f x f ,(1) 求)(x f 的表达式;(2)求)(x f 的最大值.《诱导公式》参考答案一、选择题ABAC BABC二、填空题一、1.2、1312.3、0.4、0三、解答题一、7.2、25.3、22)41(=g ,512()1,()sin()1,6233g f π=+=-+ 1)4sin()43(+-=πf , 故原式=3.4、解析:(1)由已知等式(sin )3(sin )4sin cos f x f x x x -+=⋅ ①得x x x f x f cos sin 4)sin (3)(sin -=-+ ② 由3⨯①-②,得8x x x f cos sin 16)(sin ⋅=,故212)(x x x f -=.(2)对01x ≤≤,将函数212)(x x x f -=的解析式变形,得()f x ==当2x =时,max 1.f =。
诱导公式练习题

三角函数的诱导公式1.设α为任意角,则π.2.诱导公式(1)公式一:sin(α+2k π)=__________,cos(α+2k π)=________,tan(α+2k π)=________,其中k ∈Z .(2)公式二:sin(π+α)=______,cos(π+α)=________,tan(π+α)=________.(3)公式三:sin(-α)=________,cos(-α)=________,tan(-α)=________.(4)公式四:sin(π-α)=________,cos(π-α)=________,tan(π-α)=________.3.诱导公式五~六(1)公式五:sin ⎝ ⎛⎭⎪⎫π2-α=________;cos ⎝ ⎛⎭⎪⎫π2-α=________. 以-α替代公式五中的α,可得公式六.(2)公式六:sin ⎝ ⎛⎭⎪⎫π2+α=________;cos ⎝ ⎛⎭⎪⎫π2+α=________. 4.诱导公式记忆记忆口诀为“奇变偶不变,符号看象限”.一、选择题1.sin 585°的值为( )A .-22 B.22 C .-32 D.322.若n 为整数,则代数式sin n π+α cos n π+α的化简结果是( ) A .±tan α B .-tan αC .tan α D.12tan α 3.若cos(π+α)=-12,32π<α<2π,则sin(2π+α)等于( ) A.12 B .±32 C.32 D .-324.tan(5π+α)=m ,则sin α-3π +cos π-α sin -α -cos π+α的值为( ) A.m +1m -1 B.m -1m +1C .-1D .1 5.记cos(-80°)=k ,那么tan 100°等于( )A.1-k 2k B .-1-k 2k C.k 1-k 2 D .-k 1-k2 6.若sin(3π+α)=-12,则cos ⎝ ⎛⎭⎪⎫72π-α等于( )A .-12 B.12 C.32 D .-327.已知sin ⎝ ⎛⎭⎪⎫α-π4=13,则cos ⎝ ⎛⎭⎪⎫π4+α的值等于( ) A .-13 B.13 C.-223 D.2238.若sin(π+α)+cos ⎝ ⎛⎭⎪⎫π2+α=-m ,则cos ⎝ ⎛⎭⎪⎫32π-α+2sin(2π-α)的值为( ) A .-2m 3 B.2m 3 C .-3m 2 D.3m 29.已知cos(75°+α)=13,则sin(α-15°)+cos(105°-α)的值是( ) A.13 B.23 C .-13 D .-23二、填空题10.已知cos(π6+θ)=33,则cos(5π6-θ)=________. 11.若sin ⎝ ⎛⎭⎪⎫α+π12=13,则cos ⎝⎛⎭⎪⎫α+7π12=________. 12.代数式sin 2(A +45°)+sin 2(A -45°)的化简结果是______.附加题:1.已知f (sin x )=cos 3x ,则f (cos 10°)的值为( )A .-12 B.12 C .-32 D.322.代数式1+2sin 290°cos 430°sin 250°+cos 790°的化简结果是______. 3.设f (x )=a sin(πx +α)+b cos(πx +β)+2,其中a 、b 、α、β为非零常数.若f (2 009)=1,则f (2 010)=____.4.sin 21°+sin 22°+…+sin 288°+sin 289°=________.。
诱导公式练习题 (职业培训)

诱导公式练习题 (职业培训)
简介
本文档旨在为职业培训提供一些诱导公式练题。
通过这些练题,学员可以加深对诱导公式的理解,并通过实践巩固所学的知识。
练题
1. 电路中的诱导公式
已知一个电路中的电感器$L$和电$C$,电感器$L$的自感系数
为$M$,电$C$的电容量为$Q$,电流$I$随时间变化的方程为:
I = M * d^2(q)/d(t)^2
其中,$q$为电$C$上的电荷量。
请问,当电流$I$为定值时,
如何表示电荷量$q$随时间变化的方程?
2. 法拉第电磁感应定律
根据法拉第电磁感应定律,磁通量的变化速率是导致感应电动
势产生的根本原因。
已知一个线圈的磁通量$\Phi$,磁通量的变化
速率随时间$t$的方程为:
d(Phi)/d(t) = B * A * cos(theta)
其中,$B$为磁感应强度,$A$为线圈的面积,$\theta$为磁场与线圈的夹角。
请问,根据法拉第电磁感应定律,感应电动势
$E$随时间$t$变化的方程是怎样的?
3. 围绕导线的磁场
在距离一根长直导线的距离$r$处,磁场的大小随距离$r$的变化方程为:
B = (mu0 * I) / (2 * pi * r)
其中,$\mu0$为真空中的磁导率,$I$为电流。
请问,在距离为$r$处围绕导线一圈的圆形轨道上行驶的电荷$q$的旋转周期
$T$是多少?
总结
通过以上练习题的实践,学员可以进一步巩固对诱导公式的应用理解。
这些练习题覆盖了电路中的诱导公式、法拉第电磁感应定律以及围绕导线的磁场等方面的知识点,对于职业培训的学习和提高具有一定的帮助作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
诱导公式练习题一、选择题 1. sin11π6的值是( ) A.21 B.-21 C.23 D.-232.已知的值为( )A.B. C.D.3.已知tan ,是关于x 的方程x 2-kx+k 2-3=0的两个实根,且3π<<,则cos +sin= ( )A.B.C. -D. -4.已知tan =2,,则3sin 2-cos sin +1= ( ) A.3 B.-3 C.4 D.-45.在△ABC 中,若sinA,cosA 是关于x 的方程3x 2-2x+m=0的两个根,则△ABC 是 ( ) A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定 6.若1sin()33πα-=,则5cos()6πα-的值为() A .13 B.13- C.223 D.223-7.已知3cos()sin()22()cos()tan()f ππ+α-αα=-π-απ-α,则25()3f -π的值为( ) A .12 B .-12C .32D . -328.定义某种运算a S b =⊗,运算原理如上图所示,则式子131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π的值为( )A .4B .8C .11D .139.若76πα=,则计算21sin(2)sin()2cos ()αππαα+-⋅+--所得的结果为( ) A. 34- B. 14- C. 0 D. 5410.已知sin()0,cos()0θπθπ+<->,则θ是第( )象限角. A .一 B .二 C .三 D .四11.已知sinx=2cosx,则sin 2x+1=( ) (A) (B) (C) (D)12.设02x π≤≤,sin cos x x =-,则( ) A.0x π≤≤ B.744x ππ≤≤C.544x ππ≤≤D.322x ππ≤≤ 二、填空题13.已知.角α(0)πα-<<的终边与单位圆交点的横坐标是13,则cos()2πα+的值是___. 14.化简:___________)cos()3sin()sin()23cos()3cos()2sin(=---+--+-πααπαπαπαπαπ15.已知32cos =a ,且02<<-a π,求)tan()cos()2sin()tan(a a a a +-+--πππ的值。
16.已知tan θ=2,则()22sin cos sin sin πθπθπθπθ⎛⎫⎪⎝⎭⎛⎫⎪⎝⎭+--+-(-)=__________. 三、解答题17. (1)化简()f α=)23cos()2cos(3)sin()2sin(απαπαπαπ-++--+-; (2)若tan 2α=,求()f α的值.18.已知31)4sin(-=-x π,且20π<<x ,求)4sin(x +π的值。
19.化简:cos()tan()sin()2ππθπθθ-++-.20.已知在△ABC 中,sinA +cosA =15. (1)求sinA·cosA;(2)判断△ABC 是锐角三角形还是钝角三角形;(3)求tanA 的值.21.已知0<x<π,sinx +cosx =15. (1)求sinx -cosx 的值; (2)求tanx 的值.参考答案1.B 试题分析:111sinsin(2)sin()sin 66662πππππ=-=-=-=-. 考点:诱导公式,特殊角的三角函数值. 2.A,选A.3.C ∵tan ·=k 2-3=1 ∴k=±2, 而3π<<,∴tan>0,即tan+=k=2,解之得tan α=1,所以sin =cos =∴cos +sin =- 4.A 3sin2-cos sin+1=4sin 2-cossin +cos2==35.A ∵sinA,cosA 是关于x 的方程3x 2-2x+m=0的两个根 ∴sinA+cosA=∴(sinA+cosA)2=1+2sinAcosA=即sinAcosA=-∵0o <A<180o ,∴sinA>0,所以cosA<0,即90o <A<180o 故知△ABC 是钝角三角形 6.B5cos()cos(())sin()6233ππππααα-=+-=-,51cos()63πα∴-=. 考点:三角函数的诱导公式.7.A()()()sin cos cos cos tan f αααααα--==--,25()3f -π=25cos 3π⎛⎫- ⎪⎝⎭=25cos 3π=cos 83ππ⎛⎫+ ⎪⎝⎭=cos 3π=12.考点:诱导公式.8.D 试题分析:∵5tantan()tan 1444ππππ=+==,2lg100lg102lg102===,ln 1e =,11()33-=,∴151(2tan )ln lg100()212343e π-⊗+⊗=⊗+⊗2(11)3(21)13=⨯++⨯+=.考点:1.程序框图;2.三角函数值;3.对数的运算.9.A 先根据诱导公式化简,原式=αααα22cos )(cos 2)sin (sin 1-=---⋅+,再将67πα=代入即得答案为A. 考点:诱导公式. 10.B 由sin()sin 0sin 0θπθθ+=-<⇒>,cos()cos 0cos 0θπθθ-=->⇒<,由sin 0cos 0θθ>⎧⎨<⎩可知θ是第二象限角,选B.考点:诱导公式及三角函数在各个象限的符号. 11.B 【解析】【思路点拨】由sinx=2cosx 可得tanx,将所求式子弦化切代入求解. 解:由sinx=2cosx 得tanx=2, 而sin 2x+1=2sin 2x+cos 2x= ===.12.C()x x x x x x x cos sin cos sin cos sin 2sin -12-=-=-=,x x cos sin >∴,π20≤≤x ,ππ454<<∴x ,故选C. 考点:1.二倍角公式;2.三角函数的化简;3.解三角不等式. 13.22 由角α(0)πα-<<的终边与单位圆交点的横坐标是13,即122cos ,sin 3αα==由于cos()2πα+sin α=-.所以cos()2πα+22=考点:1.三角函数的定义.2.三角函数的诱导公式.14.1-根据诱导公式:奇变偶不变,符号看象限进行化简.1)cos )(sin()sin ()sin )(cos )(sin -()cos()3sin()sin()23cos()3cos()2sin(-=----=---+--+-ααααααπααπαπαπαπαπ考点:诱导公式 15.25-试题分析:根据诱导公式进行化简 试题解析:原式=αααααtan tan cos sin tan --=⋅⋅,又因为32cos =α,02-<<απ,根据⎪⎩⎪⎨⎧==+αααααtan cos sin 1cos sin 22解得25tan =α,∴)tan()cos()2sin()tan(a a a a +-+--πππ=25-=. 考点:诱导公式化简 16.-2()22sin cos sin sin πθπθπθπθ⎛⎫⎪⎝⎭⎛⎫ ⎪⎝⎭+--+-(-)=(222112cos cos cos cos sin cos sin tan θθθθθθθθ--)===----=-2. 17.(1) cos sin ()3cos sin f ααααα+=-;(2)12()332f α+==-.试题分析:(1)由诱导公式化简可得,牢记诱导公式“奇变偶不变,符号看象限”;(2)将正余弦转化为正切的形式,可得. 试题解析:解:(1)cos sin ()3cos sin f ααααα+=- , 8分(每个公式2分,即符号1分,化对1分)(2)cos sin 1tan ()3cos sin 3tan f ααααααα++==--, 12分(每化对1个得1分) 若tan 2α=,则12()332f α+==-, 14分(说明:用其他方法做的同样酌情给分)考点:诱导公式,同角间的基本关系式. 18.232 试题分析:根据诱导公式⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛+x x x 4cos 42sin 4sin ππππ,由已知得⎪⎭⎫⎝⎛-∈∴0,4-4ππx ,确定正负数,在根据1cos sin 22=+αα公式求解. ⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛+x x x 4cos 42sin 4sin ππππ314sin -=⎪⎭⎫⎝⎛-x π ,⎪⎭⎫ ⎝⎛-∈∴⎪⎭⎫ ⎝⎛∈4,4-42,0ππππx x ,又因为314sin -=⎪⎭⎫ ⎝⎛-x π ,⎪⎭⎫⎝⎛-∈∴0,4-4ππx ,那么2323114cos 2=⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛-x π.即232)4sin(=+x π考点:1.诱导公式;2.三角函数的化简. 194πθ⎛⎫-⎪⎝⎭. 试题分析:本小题主要考查三角函数的诱导公式、同角三角函数的基本关系式及辅助角公式,属于容易题.根据诱导公式cos()cos ,tan()tan ,sin()cos 2ππθθπθθθθ-=+=-=及同角三角函数的商数关系:sin tan cos θθθ=进行展开运算得到sin cos θθ-,再运用辅助角公式sin cos )a b θθθα++(其中tan baα=)或运用两角和差公式进行化简即可.试题解析:cos()tan()sin()2ππθπθθ-++-cos tan cos θθθ=-+⋅ 4分=sin cos )cos cos sin )44ππθθθθθθ-==- 8分4πθ⎛⎫=- ⎪⎝⎭ 10分.考点:1.诱导公式;2.同角三角函数的基本关系式;3.辅助角公式(两角和差公式);4.三角恒等变换.20.(1)-1225(2)钝角三角形.(3)-43 (1)因为sinA +cosA =15①,两边平方得1+2sinAcosA =125,所以sinA·cosA=-1225.(2)由(1)sinAcosA =-1225<0,且0<A<π,可知cosA<0,所以A 为钝角,所以△ABC 是钝角三角形. (3)(sinA -cosA)2=1-2sinAcosA =1+2425=4925. 又sinA>0,cosA<0,sinA -cosA>0,所以sinA -cosA =75②, 所以由①,②可得sinA =45,cosA =-35,则tanA =sinAcosA =4535-=-43.21.(1)75(2)-43(1)∵sinx +cosx =15,∴1+2sinxcosx =125,∴2sinxcosx =-2425,又∵0<x<π,∴sinx>0,2sinxcosx =-2425<0,∴cosx<0,∴sinx -cosx>0,∴sinx -cosx =75=.(2) 111717sinx cosx tanx sinx cosx tanx ++=,=--,tanx =-43.。
