钢结构毕业设计牛腿设计
钢结构牛腿设计毕业设计

钢结构牛腿设计毕业设计钢结构牛腿设计毕业设计引言在现代建筑设计中,钢结构被广泛应用于各种建筑物中,其优越的强度和耐久性使其成为许多工程项目的首选材料。
本篇文章将探讨钢结构牛腿设计的毕业设计项目,旨在展示钢结构在建筑设计中的应用和创新。
第一部分:钢结构的优势钢结构作为一种重要的建筑材料,具有许多优势。
首先,钢材具有出色的强度和刚性,可以承受较大的荷载。
其次,钢材具有较高的耐腐蚀性,能够抵御恶劣环境的侵蚀。
此外,钢结构的施工速度快,能够节省时间和成本。
最后,钢结构还具有可塑性,可以实现各种复杂的形状和结构。
第二部分:钢结构牛腿设计的意义钢结构牛腿设计是一项具有挑战性和创新性的毕业设计项目。
牛腿是建筑中的重要支撑结构,其设计需要考虑到荷载分布、结构强度和稳定性等因素。
钢结构的应用使得牛腿设计更加灵活和可行,为建筑师提供了更多的设计空间。
第三部分:设计过程钢结构牛腿设计的过程包括以下几个步骤。
首先,需要进行荷载计算,确定牛腿所承受的荷载大小和分布情况。
其次,根据荷载计算结果,进行结构设计,确定牛腿的形状、尺寸和材料。
然后,进行结构分析,验证设计的合理性和稳定性。
最后,进行施工图设计,详细说明牛腿的构造和连接方式。
第四部分:案例分析为了更好地理解钢结构牛腿设计的实际应用,我们可以分析一个具体的案例。
以一座大型体育馆为例,设计师需要设计一组牛腿来支撑屋顶结构。
通过荷载计算和结构分析,设计师确定了牛腿的形状为倒梯形,材料为高强度钢。
在施工图设计中,设计师详细说明了牛腿的连接方式和支撑结构。
最终,这组钢结构牛腿成功地支撑起了整个体育馆的屋顶。
结论钢结构牛腿设计是一项具有挑战性和创新性的毕业设计项目。
通过合理的荷载计算、结构设计和施工图设计,钢结构牛腿能够有效地支撑建筑物的结构,并为建筑师提供更多的设计空间。
未来,随着科技的进步和建筑设计的发展,钢结构牛腿设计将继续发挥重要作用,为建筑师创造更多的可能性。
5 计算书牛腿的设计计算
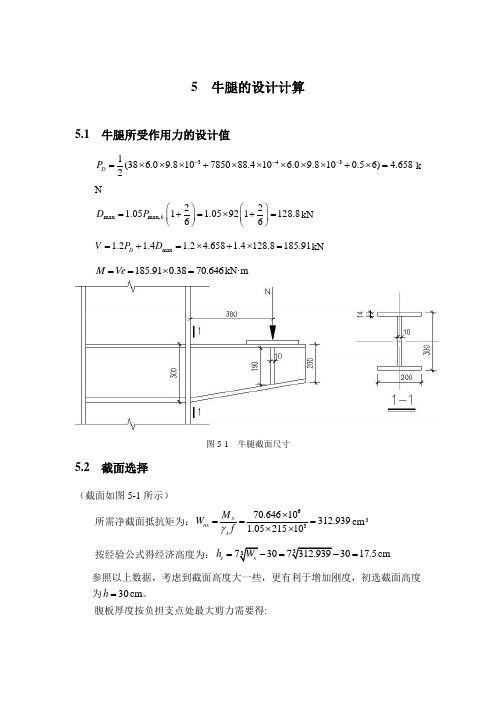
5 牛腿的设计计算5.1 牛腿所受作用力的设计值3431(38 6.09.810785088.410 6.09.8100.56) 4.6582D P ---=⨯⨯⨯+⨯⨯⨯⨯⨯+⨯=k Nmax max,221.051 1.05921128.866k D P ⎛⎫⎛⎫=+=⨯+= ⎪ ⎪⎝⎭⎝⎭kN max 1.2 1.4 1.2 4.658 1.4128.8185.91D V P D =+=⨯+⨯=kN185.910.3870.646M Ve ==⨯=kN·m图5-1 牛腿截面尺寸5.2 截面选择(截面如图5-1所示) 所需净截面抵抗矩为:6370.64610312.9391.0521510x nx x M W f γ⨯===⨯⨯cm 3 按经验公式得经济高度为:337307312.9393017.5e x h W =-=-=cm参照以上数据,考虑到截面高度大一些,更有利于增加刚度,初选截面高度为30h =cm 。
腹板厚度按负担支点处最大剪力需要得:31.5 1.5185.91107.44300125w w v V t h f ⨯⨯===⨯mm 按经验公式估算: 30 1.651111ww h t ===cm 选用腹板厚度为:10w t =mm依近似公式计算所需翼缘板面积:312.939 1.030 5.436306x w w w W t h bt h ⨯=-=-=cm 2 试选翼缘板厚度为:14t =mm ,翼缘板宽度为200mm ,翼缘得外伸宽度为: ()120010952b -==mm ,952356.1131314yf =<= 所以翼缘板得局部稳定可以保证。
使用变截面牛腿,端部截面高度为:200h =mm 。
5.3 强度验算20 1.42(30 1.42) 1.083.2A =⨯⨯+-⨯⨯=cm 2()()3311203020 1.030 1.4213137.55731212x I =⨯⨯-⨯-⨯-⨯=cm 4 13137.5573875.83715x x I W h ===cm 3 ,492.880S =cm 3` 正应力为:6370.6461076.821.05875.83710x x x M W σγ⨯===⨯⨯N/mm 2<215f =N/mm 2 剪应力为:64185.91492.8801069.7513137.55731010x w VS I t τ⨯⨯===⨯⨯N/mm 2<125v f =N/mm 2 强度满足要求。
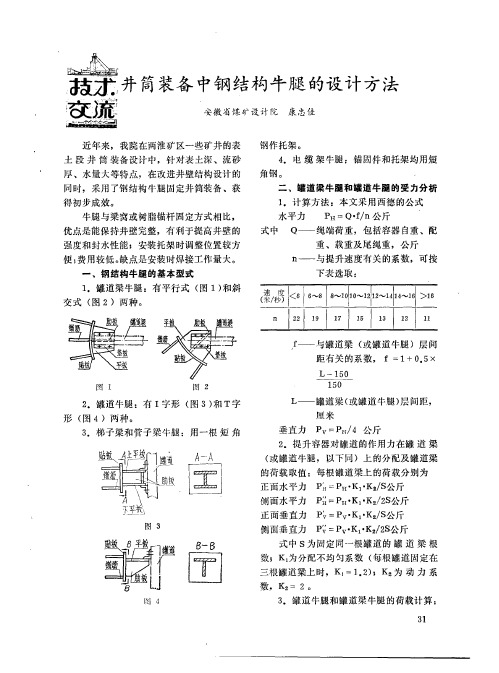
井筒装备中钢结构牛腿的设计方法
f
=
1
十
。 s
x
150
15 0 2
.
罐 道 牛腿
4
:
有
I
字形 ( 图
:
3 )和 T
字
L
形 (图
3
.
) 两种
。
—
罐 道梁 ( 或罐 道牛腿 ) 层 间距
厘米
P
v 二
,
梯 子 梁 和 管子 梁 牛 腿
、
用一 根 短 角
垂 直力
2
.
P
。
/
4
公斤
提 升 容器对 罐 道 的 作 用力 在罐 道 梁
,
衬
图 3
,
承受 一 侧 两 根 罐 道 的 正 面 水 平 力 和 另 一 侧 两
根罐 道 指 向 同 一 端 (
用时 (图
8 )
。
最 不 利 受 力状 态
分 别 计 算受 水平 荷 载 作 用
,
B
端 ) 的 侧 面 水平力 作
和受 垂 直 荷载 作用 时
v
罐 道 梁牛腿 在 纵 横 竖
: x
、
三 个方 向 ( 图 5 m b ) 的最 大 荷 载 N a
;
可 不 考 虑梁
式中
为 每 根罐 道 的 重 量
。
公斤
S
为 固定
的 扭 转 问题 )
。
同 一 根 罐道 的 牛 腿 个 数
.a
( 1 ) 纵 向最 大 荷 载发 生 在 罐 道 梁 同 时
奴 罐道 梁 牛 腿(
承 受 四根 罐道 指 向 同 一 端 ( B 端 ) 的 侧 面 水
牛 腿( 雄道
钢结构计算表格-钢牛腿设计

截面腹板上 端抵抗矩W’
n3
W’n3=In/(y-tf)=
3602064.516 mm3
腹板下端的正 应力σ1
σ=M/ Wn2=
70.95 N/mm2<120 N/mm2 ,满足要求
腹板上缘的正应力σ和切应力τ σ=M*(y-tf)/I=
τ=V*S/(I*n*tw)=
42.02589913 N/mm2<120 N/mm2 24.10 N/mm2<120 N/mm2
组合应力
三、 牛腿与 柱的连接焊 缝计算:
2 3 2
= 59.23455569
N/mm2<120 N/mm2
由于牛腿翼缘竖向刚度较差,一般不考虑承担剪力,因此计算时通常假定腹板焊缝承受所有剪力, 矩则由全部焊缝承受。
焊缝截面的型心y坐标 y=(b*t*(-0.5t)+b*t*(0.5t+tf)+(h-t)*t*n*2*(0.5(h-t)+t+tf))/(2*b*t+2*n*
和柱的连接
采用角焊缝
连接。 二、牛腿强度的计算
F*e= 151.38 kN.m
V= 504.6 kN
牛腿根部的
净截面积An
An=b*tf+tw*h*n=
24000 mm2
上翼缘板上
边缘至截面
形心轴处的
距离y
y=(b*tf*0.5*tf+n*h*tw*(tf+0.5*h))/An=
669984000 mm4
,满足要求 ,满足要求 ,满足要求
假定腹板焊缝承受所有剪力,而弯 .5(h-t)+t+tf))/(2*b*t+2*n*(h-t)*t) +
钢牛腿设计及工程实例

f
tw * hw * f v 59.79<f wf 160 N / mm2 ,满足抗剪承载力要求。 4*0.7* h f *(hw 20)
3. 结语
本工程牛腿上部钢梁承担有 31.8m 钢桁架栈桥支座, 大跨度栈桥为其下的道 路提供了通行便利,自 2009 年竣工后使用效果很好。设计中优先选择了抗弯能 力显著的“工”形作为牛腿端部截面,实现了截面的优化设计。而且通过文中的 对比不难发现,当柱外竖向荷载偏心较小,即牛腿端部弯矩很小时,可考虑采用 抗剪能力突出的“π ”形截面。 钢牛腿在工业建筑中应用普遍,但是计算过程较为繁琐,因此目前多采用经 验设计。如果将本文中的计算步骤转化为 excel 表格辅助计算,则可以极大提高 计算速度,同时有助于比较得出优化方案,减少钢材浪费。
1 Wn1 42.2<215N / mm2 ,上翼缘抗弯满足。
下翼缘外边缘的正应力 σ2
2 Wn 2 51.07<215N / mm2 ,下翼缘抗弯满足。
截面形心轴处的剪应力 τ
= VS / Itw 72.95< 120 N / mm2 ,截面抗剪满足。
腹板下端的剪应力τ
1
1 VS1 / Itw 57.68N / mm2
腹板下端的折算应力
(12 312 ) 111.24< 1.1*215N / mm2 ,满足承载力要求。
2.3 焊缝连接验算 考虑牛腿端部内力向柱传递时,原则上端部弯矩全部由牛腿翼缘承担,端部 剪力全部由腹板承担。牛腿腹板与柱的连接,除对端部剪力进行验算外,尚应以 腹板净截面面积的抗剪承载力设计值的 1/2 来确定。 基于以上假定,牛腿的上、下翼缘与柱连接采用完全焊透的对接焊缝,当焊 缝质量等级为一、二级时,焊缝与钢材为等强连接,焊缝强度可不必验算;当质 量等级为三级时,对接焊缝抗拉强度设计值低于钢材本身,尚需验算焊缝的抗拉 强度。 本工程按三级对接焊缝验算抗拉。牛腿腹板与柱连接采用通长双面贴角焊 缝,焊脚尺寸 hf=12mm。
钢牛腿设计施工图 TD-T07-02
钢牛腿设计

钢牛腿设计
一、钢结构部分设计软件(工字型截面和钢牛腿受力计算)
二、牛腿荷载值计算(竖向压力计算值KN)
1、吊车(大车自重)/2=t
2、吊车(小车自重)x1=t
3、吊车最大起重量x1= t
4、吊车梁及梁上附件:
每延长m重量x最大榀间距=t
5、轨道重量:
每延长m重量x最大榀间距=t
以上5项相加之和x1.4系数/0.098t = (竖向压力值)KN
三、牛腿几何尺寸确定原则:
1、牛腿翼缘板,宽度和厚度:
取相邻两钢柱的翼缘板较小的宽度和厚度数值。
2、牛腿腹板厚度:
取相邻两钢柱的腹板较小的厚度数值。
3、牛腿竖向劲板和柱横向加劲板的厚度和宽度:
厚度取牛腿翼缘板厚,宽度取(牛腿宽-牛腿腹板厚度)/2
四、钢牛腿受力计算界面
1、牛腿信息输入:写入翼缘板宽度,厚度
腹板宽度,厚度
腹板高度可以假定一个数值。
2、荷载:
1)填入计算好的竖向压力设计值()KN
20.65m.
3、
出现判断情况界面
4、调整腹板高度达到经济,安全合理的数值。
钢结构钢牛腿设计计算表格

钢牛腿设计一、计算资料牛腿尺寸(单位:mm)荷载竖向压力设计值F=80kN柱边与竖向压力距离e=0.5m 材料钢材为Q345-B焊条为E50焊接形式手工焊焊缝质量三级角焊缝焊角尺寸hf(mm)=6牛腿翼缘和柱的连接采用对接焊缝(坡口焊)连接,腹板和柱的连接采用角焊缝连接。
二、牛腿强度的计算作用于牛腿根部的弯炬M和剪力VM=F*e=40.00kN.mV=F=80kN牛腿根部的净截面积AnAn=bf1*t1+bf2*t2+tw*hw=6208mm2上翼缘板中心至截面形心轴处的距离yy=(tw*hw*0.5*(hw+t1)+bf2*tf2*(hw+0.5*t1+0.5*t2))/An=143.00mm 形心轴以上面积对形心轴的面积矩SS=(y-0.5*t1)*tw*0.5*(y-0.5*t1)+t1*bf1*y=362176mm3净截面的惯性矩In腹板中心距与y的距离a=(0.5*hw+0.5*t1-y)=0mmIn=(bf1*t1^3)/12+t1*bf1*y^2+(bf2*t2^3)/12+t2*bf2*(hw+0.5*t1+0.5*t2)^2+(tw*hw^3)/12+tw*hw*a^2=95845717.33mm4净截面的上、下抵抗矩Wn1、Wn2Wn1=In/(y+0.5*t1)=647606.1982mm3Wn2=In/(hw+0.5*t1-y+t2)=647606.1982mm3上翼缘外边的正应力σσ=M/ Wn1=61.77N/mm2<310N/mm2,满足要求下翼缘外边的正应力σσ=M/ Wn2=61.77N/mm2<310N/mm2,满足要求截面形心轴处的剪应力ττ=V*S/(I*tw)=37.79N/mm2<310N/mm2,满足要求截面腹板下端抵抗矩W’n2W'n2=In/(hw+0.5*t1-y)=694534.1836mm3下翼缘对形心轴的面积矩S1S1=t2*bf2*(hw+0.5*t1+0.5*t2-y)=286000mm3腹板下端的正应力σ1σ1= M/W'n2=57.59 N/mm2腹板下端的剪应力τ1τ=V*S1/(I*t w)=29.84 N/mm2腹板下端的折算应力√(σ12+3τ12)=77.38N/mm2<1.1*310 N/mm2,满足要求腿与柱的连接焊缝计算:由于牛腿翼缘竖向刚度较差,一般不考虑承担剪力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 牛腿设计
5.1 荷载计算
根据吊车梁的设计,吊车梁截面面积22125.4410A mm =⨯, Q235钢的密度为
37850/kg m ,吊车梁自重为4785010125.4410984.704/N m -⨯⨯⨯=,轨道自重为
430/N m 由吊车最大轮压引起的支座反力标准值为: .max 139(10.453)201.967k D kN =⨯+=
牛腿根部支座反力影响线示意图
则牛腿根部承受的剪力:
3.max 1.2(98
4.704430)107.5 1.429
5.486k V D kN -=⨯+⨯⨯+=
5.2 截面选择
牛腿选用600500400810BH -⨯⨯⨯ 偏心距为450e mm =外伸长度为200d mm =,截面高度600h mm =, 截面宽度400b mm = ,翼缘板厚度 10f t mm =,腹板厚度8w t mm =,力作用点处截面为537400810BH ⨯⨯⨯。
牛腿
牛腿节点示意图
则:295.4860.45132.97M V e kN m =⋅=⨯=⋅
5.3截面特性
牛腿根部截面示意图
牛腿根部截面:2230010(600210)810640A mm =⨯⨯+-⨯⨯= 33244
11600108(600210)23001030010()1212265227.4710x I mm -⎡⎤=⨯⨯-⨯+⨯⨯⨯+⨯⨯⎢⎥⎣⎦=⨯
4
3365227.471021742.49106002
x x I W mm y ⨯===⨯ 2
33600101600103001081233.1010222S mm --⎛⎫⎛⎫=⨯⨯+⨯⨯=⨯ ⎪ ⎪⎝⎭⎝⎭ 3316001030010885102S mm -⎛⎫=⨯⨯=⨯ ⎪⎝⎭ 5.4 强度验算
5.4.1抗弯强度
6
223132.9710 5.82/215/1.0521742.4910
x nx M N mm f N mm W σγ⨯===<=⨯⨯ 5.4.2抗剪强度
3224295.486101233.1069.83/125/65227.47108
v x w VS N mm f N mm I t τ⨯⨯===<=⨯⨯ 5.4.3 腹板计算高度边缘处折算应力
6214132.971060021059.12/65227.47102
nx M y N mm I σ⨯-⨯=⋅=⨯=⨯ 32295.4861088550.11/65227.478
x w VS N mm I t τ⨯⨯===⨯ σ和τ的最不利组合出现在腹板边缘,因此验算公式为: 2222
22359.12350.11105.2/215/N mm f N mm στ+=+⨯=<=
∴满足要求。
5.5 焊缝验算。
