Tobit模型、泊松模型
Tobit模型

Tobit模型估计方法与应用(一)周华林李雪松2012-10-25 10:01:28 来源:《经济学动态》(京)2012年5期第105~119页内容提要:Tobit模型从最初的结构式模型扩展到时间序列模型、面板数据模型以及非参数模型等形式,无论Tobit模型的结构形式如何变化,现有的估计方法基本上都是在Heckman(1976)两步法的基础上扩展的。
本文结合一些经典文献,介绍了不同类型的Tobit 模型的结构形式、估计方法、估计结果的性质等,为做实证分析的研究者们提供一个分析此类问题的基本方法。
关键词:Tobit模型 Heckman两步法面板Tobit模型 Tobit GARCH ARCH模型作者简介:周华林,中国社会科学院研究生院,电子邮箱:zhimadexin009@16一、引言自从Tobin(1958)研究了被解释变量有上限、下限或者存在极值等问题以来,这类研究受到学者们的广泛关注。
人们为了纪念Tobin对这类模型的贡献,把被解释变量取值有限制、存在选择行为的这类模型称之为Tobit模型。
这类模型实际上包含两种方程,一种是反映选择问题的离散数据模型;一种是受限制的连续变量模型。
第二种模型往往是文献中人们更感兴趣的部分。
Tobit模型不同于离散选择模型和一般的连续变量选择模型,它的特点在于因变量是受限变量,模型实际上由两类方程组成,主要研究在某些选择行为下,连续变量如何变化的问题。
当前,这种模型已经引入了更复杂的形式,面板数据、半参数等形式的Tobit模型在研究中广泛应用。
国外这种模型已经陆续在各领域内广泛使用,国内也有一些实证分析的论文用到了这种模型。
但是人们在应用这些模型分析问题时还存在一些误区,如误认为离散选择模型就是Tobit模型,无法解释样本选择性偏差的经济含义,不区分所建立的模型是否是联立方程,对估计结果的性质不进行检验等。
本文所介绍的经典文献,概括了Tobit模型的起源、结构形式、估计方法、适用的研究问题、自身缺陷等方面,这些经典文献中提到的一些细节问题在实证分析中很重要,然而现在已有的教材或者引文并没有摘录出来,可能导致一些作者在实证分析中对该模型有种种误解。
tobit模型公式(一)

tobit模型公式(一)Tobit模型公式Tobit模型是一种常用的统计模型,用于处理有截断取值的数据。
在该模型中,有些观测值可能无法被观测到,只能观测到其上限或下限。
下面列举了Tobit模型的相关公式,并通过示例进行解释说明。
Tobit模型Tobit模型是由Tobin于1958年提出的,用于处理存在自我选择(指对于某些观测值可能不可观测)的取值。
在Tobit模型中,存在两个阶段的生成过程:一个线性回归方程用于预测变量取值的期望,以及一个二项分布模型来描述观测值的可能取值范围。
Tobit模型公式Tobit模型可以表示为以下公式:1.观测方程: [观测方程]( [观测方程](其中,[观测方程](2.似然函数: [似然函数](其中,[似然函数](3.最大似然估计:最大似然估计的目标是最大化似然函数,从而找到最优的回归系数和误差项方差。
示例解释假设我们想研究商品房的售价与面积之间的关系,但房价数据存在下限(价格为0),无法观测到低于该下限的房价。
我们可以使用Tobit模型来估计房价与面积之间的线性关系。
首先,我们根据样本数据拟合Tobit模型,得到回归系数和误差项方差的最大似然估计。
然后,我们可以根据估计的回归系数,计算面积对房价的影响。
最后,我们可以使用模型进行预测,根据不同的面积值估计对应的房价。
通过Tobit模型,我们可以得出结论,面积与房价呈正相关关系,面积越大,房价越高。
这可以帮助我们了解房价的形成机制,并为房地产市场的决策提供参考。
总结Tobit模型是一种用于处理有截断取值的数据的统计模型。
通过估计回归系数和误差项方差,Tobit模型可以帮助我们理解变量之间的关系,并进行预测。
在实际应用中,Tobit模型在经济学、金融学等领域被广泛使用。
tobit模型

2 yi 0
2
yi 0
4.Tobit模型的最大似然估计(基本模型)
ln L
1 2
yi
0
2(
yi xi
2
)
xi
1
yi 01 ( xi
)
f
( xi
) xi
yi 0
yi
Байду номын сангаас
xi
2
xi
yi 01
1
( xi
)
f
(
xi
)
xi
0
5.Tobit模型的应用
5.Tobit模型的应用
yi* xi i
i ~ N (0, 2 )
yi
yi*
0
if yi* 0
if yi* 0
2.Tobit模型
2.2第二类Tobit模型
y1*i x1i 1 1i
y2*i x2i2 2i
y 2i
y2*i 0
if if
y1*i 0 y1*i 0
i 1,2,....,n
2.Tobit模型
y1*i x1i 1 1i
y y2*i
2i
0
y2*i x2i 2 2i
if y1*i 0 if y1*i 0
y y3*i
3i
0
if y1*i 0
if
y1*i 0
y3*i x3i 3 3i
i 1,2,....,n
3.Tobit模型变量的概率分布(基本模型)
P( yi
0)
5.Tobit模型的应用
研究中遇到的很多问题实际上都是受限因变量问题, 如工资的问题、受教育问题、提供对外援助的问题、用电 消耗量问题、香烟消费问题、工厂选址问题、保险消费问 题等等都是这类问题。
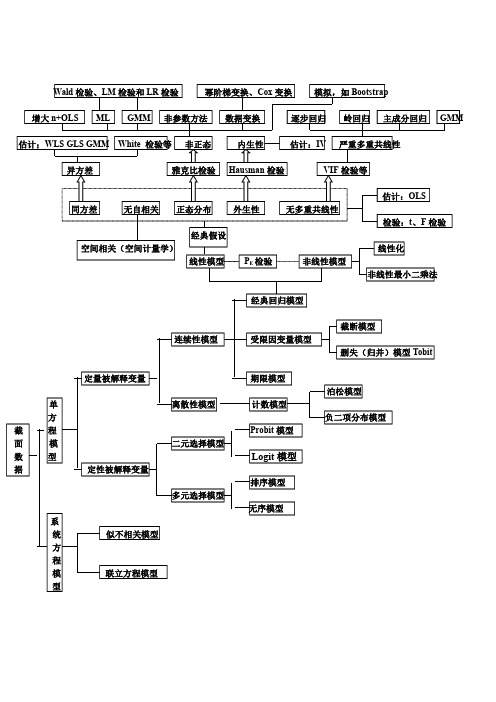
(超全)计量经济学框架图
面
模
二元选择模型
数
型
Logit 模型
据
定性被解释变量
排序模型
多元选择模型
无序模型
系
统
似不相关模型
方
程
模
联立方程模型
型
泊松模型 负二项分布模型
平稳序列 ARMA 模型
单变量序列
非平稳序列
ARIMA 模型 SARMA 模型
单方程模型
平稳序列 建模方法同截面数据
多变量序列 单位根检验
时
协整(同阶单整)
间
Wald 检验、LM 检验和 LR 检验
幂阶梯变换、Cox 变换 模拟,如 Bootstrap
增大 n+OLS ML GMM 非参数方法 数据变换
逐步回归 岭回归 主成分回归 GMM
估计;WLS GLS GMM White 检验等 非正态
内生性
估计:IV 严重多重共线性
异方差
雅克比检验 Hausman 检验
VIF 检验等
同方差
无自相关 正态分布 外生性
无多重共线性
空间相关(空间计量学)
经典假设 线性模型
PE 检验
非线性模型
估计:OLS 检验:t、F 检验 线性化 非线性最小二乘法
经典回归模型
连续性模型
受限因变量模型
截断模型 删失(归并)模型 Tobit
定量被解释变量
期限模型
单
离散性模型
计数模型
方
截
程
Probit 模型
随机效应模型
面
时间效应模型
板
数
据
PVAR
类似时间序列数据的方法
面板单位根
二元选择模型

二元选择摸型如果回归模型的解释变量中含有定性变量,则可以用虚拟变量处理之。
在实际经济问题中,被解释变量也可能是定性变量。
如通过一系列解释变量的观测值观察人们对某项动议的态度,某件事情的成功和失败等。
当被解释变量为定性变量时怎样建立模型呢?这就是要介绍的二元选择模型或多元选择模型,统称离散选择模型。
这里主要介绍Tobit (线性概率)模型,Probit (概率单位)模型和Logit 模型。
1.Tobit (线性概率)模型 Tobit 模型的形式如下,y i = α + β x i + u i (1) 其中u i 为随机误差项,x i 为定量解释变量。
y i 为二元选择变量。
此模型由James Tobin 1958年提出,因此得名。
如利息税、机动车的费改税问题等。
设 1 (若是第一种选择) y i =0 (若是第二种选择)-0.20.00.20.40.60.81.01.2330340350360370380XY对y i 取期望,E(y i ) = α + β x i (2) 下面研究y i 的分布。
因为y i 只能取两个值,0和1,所以y i 服从两点分布。
把y i 的分布记为, P ( y i = 1) = p i P ( y i = 0) = 1 - p i 则E(y i ) = 1 (p i ) + 0 (1 - p i ) = p i (3) 由(2)和(3)式有p i = α + β x i (y i 的样本值是0或1,而预测值是概率。
) (4)以p i = - 0.2 + 0.05 x i 为例,说明x i 每增加一个单位,则采用第一种选择的概率增加0.05。
现在分析Tobit 模型误差的分布。
由Tobit 模型(1)有,u i = y i - α - β x i =⎩⎨⎧=--=--0,1,1i i i i y x y x βαβαE(u i ) = (1- α - β x i ) p i + (- α - β x i ) (1 - p i ) = p i - α - β x i 由(4)式,有E(u i ) = p i - α - β x i = 0因为y i 只能取0, 1两个值,所以,E(u i 2) = (1- α - β x i )2 p i + (- α - β x i )2 (1 - p i )= (1- α - β x i )2 (α + β x i ) + (α +β x i )2 (1 - α - β x i ), (依据(4)式) = (1- α - β x i ) (α + β x i ) = p i (1 - p i ) , (依据(4)式) = E(y i ) [1- E(y i ) ]上两式说明,误差项的期望为零,方差具有异方差。
Tobit模型估计方法与应用

Tobit模型估计方法与应用一、本文概述本文旨在全面探讨Tobit模型估计方法及其应用。
Tobit模型,也称为截取回归模型或受限因变量模型,是一种广泛应用于经济学、社会学、生物医学等领域的统计模型。
该模型主要处理因变量在某一范围内被截取或受限的情况,例如,当因变量只能取正值或只能在某一特定区间内变动时。
本文首先将对Tobit模型的基本理论进行阐述,包括模型的设定、参数的估计方法以及模型的检验等方面。
随后,文章将详细介绍Tobit模型在各个领域中的应用案例,包括工资水平、耐用消费品需求、医疗支出等方面的研究。
通过这些案例,我们将展示Tobit模型在处理受限因变量问题时的独特优势和应用价值。
文章还将对Tobit模型的发展趋势和前景进行展望,以期为相关领域的研究提供有益的参考和启示。
二、Tobit模型的基本原理Tobit模型,也称为受限因变量模型或截取回归模型,是一种广泛应用于经济学、社会学、生物医学等领域的统计模型。
该模型主要处理因变量受到某种限制或截取的情况,例如因变量只能取正值、只能在某个区间内取值等。
Tobit模型的基本原理基于最大似然估计法,通过构建似然函数来估计模型的参数。
截取机制:在Tobit模型中,因变量的取值受到某种截取机制的限制。
这种截取机制可以是左截取、右截取或双侧截取。
左截取意味着因变量只能取大于某个阈值的值,右截取则意味着因变量只能取小于某个阈值的值,而双侧截取则限制了因变量的取值范围在两个阈值之间。
潜在变量:在Tobit模型中,通常假设存在一个潜在变量(latent variable),它是没有受到截取限制的因变量。
潜在变量与观察到的因变量之间的关系由截取机制决定。
潜在变量通常假设服从某种分布,如正态分布。
最大似然估计:在给定截取机制和潜在变量分布的假设下,可以通过构建似然函数来估计Tobit模型的参数。
似然函数反映了观察到的数据与模型参数之间的匹配程度。
通过最大化似然函数,可以得到模型参数的估计值。
泊松扩散模型基本思路
泊松扩散模型基本思路泊松扩散模型是一种常用的数学模型,用于描述随机过程中的粒子扩散行为。
它由法国数学家西蒙·泊松于19世纪中叶提出,被广泛应用于物理、化学、生物、金融等领域的研究中。
本文将从泊松扩散模型的基本思路入手,介绍该模型的原理和应用。
泊松扩散模型的基本思路是将扩散的粒子视为泊松过程,即粒子在时间和空间上的分布服从泊松分布。
泊松分布是一种概率分布,描述了在一个固定时间或空间区间内,事件发生的次数的概率。
在泊松扩散模型中,将粒子的扩散视为一系列独立的随机事件,每个事件表示粒子从一个位置跳到另一个位置的概率。
这些跳跃事件之间的时间间隔服从指数分布,描述了粒子在不同位置之间扩散的速率。
泊松扩散模型的数学表达是通过偏微分方程来描述的。
该方程称为扩散方程,形式上是一个二阶偏导数方程,描述了粒子浓度随时间和空间变化的规律。
扩散方程的解可以通过数值方法或解析方法求得,从而得到粒子的扩散行为。
泊松扩散模型的应用十分广泛。
在物理学中,它被用于描述热传导、电子扩散等过程。
在化学反应动力学中,泊松扩散模型可以用于描述反应物在溶液中的扩散行为。
在生物学中,它被应用于描述细胞内物质的扩散和传输。
在金融学中,泊松扩散模型可以用于描述股票价格的随机波动。
泊松扩散模型的优点是简单易用,适用于描述一些简单的扩散过程。
它可以通过调整模型参数来适应实际情况,从而得到更准确的结果。
然而,泊松扩散模型也有一些局限性。
它假设粒子之间的相互作用是弱的,忽略了粒子之间的相互作用对扩散行为的影响。
对于复杂的扩散过程,泊松扩散模型可能无法给出准确的结果。
泊松扩散模型是一种常用的数学模型,可以描述随机过程中的粒子扩散行为。
它的基本思路是将扩散的粒子视为泊松过程,通过偏微分方程来描述粒子的扩散行为。
泊松扩散模型具有简单易用、适应性强的优点,被广泛应用于物理、化学、生物、金融等领域的研究中。
然而,它也存在一些局限性,对于复杂的扩散过程可能无法给出准确的结果。
古扎拉蒂《计量经济学基础》第15章
问题的提出: LPM的局限:
P 1
(1)ui非正态 (2)ui异方差 (3)Yˆi在[0,1]之外 (4)R 2一般比较小
0
X
从几何图形看,希望模型像右图所示:
1.Logit模型
a.Logit模型中条件概率的表达式
Pi
P(Yi
1|
Xi)
E(Yi
|
Xi)
1
1 e ( 1
2
Xi
)
(1)
比较LPM : Pi P(Yi 1 | X i ) E(Yi | X i ) 1 2 X i
的概率增加0.1021或10.21%。 3.Yˆi的估计值中有12个小于0或大于1。
4. W L S 估 计
Yi 1.2456 1 0.1196 X i
Wi
Wi
Wi
(0.1206)
(0.0069)
t
(10.332)
(1 7 .4 5 4 )
R 2 0.9214
五、对数单位模型(Logit Model)
区间;可以将小于0的值改为0;大于1的值 改为1。 (2)在 log it模型和probit模型中, 可以保证条件期望的值域区间在[0,1]。
4.拟和优度 通常情况下,拟和优度不会太高,在0.2至 0.6之间。
Yˆ
LPM
……….无约束
1
Yˆ
………. 受约束
1
LPM
……….
……….
0
X
X
0
(a)
5.对于这些现象该如何建模:比如每年看 病的次数、给定年份中一个厂商获得专利的个 数、一年中大学教授所发表论文的篇数、五分 钟内接到电话的次数或者五分钟内通过某个收 费站的汽车数量?这些被称为计数数据(count data)或者稀有事件(rare event)数据的现 象都是泊松(概率)过程的例子。
第十讲 受限因变量模型(Tobit)
[95% Conf. .187246 -.2533721 -.2407998 -2.142552 -8.626323 -.9080753 -.0000152 -.7821601 -5.545201
Interval] 1.318625 -0.0209686 0.4514313 8.102282 -1.600061 0.5065954 0.0001876 0.1433702 8.039255
E ( yi | y > 0) = E ( yi | ε i > − xi β )
*
= E ( xi β + ε i | ε i > − xi β ) = xi β + E (ε i | ε i > − xi β ) ≠ xi β
∵
E(ε i | ε i > − xi β ) ≠ 0
f(εi)
-50
2)和3)的关系
∂E[ yi | x] ∂E[ yi | yi > 0, x] ∂F ( z ) = F ( z) * + E[ yi | yi > 0, x] * ( ) ∂x j ∂x j ∂x j = Fi ⋅ β j
Tobit模型的应用 模型的应用
调用数据库: 调用数据库:dairy data
5. 边际效应
Marginal Effects: Latent Variable variable scaler303100 agehh eduhh labper offlab pculti passet roaddistant _cons dF/dx Std. Err. z 2.62 -2.32 0.60 1.14 -2.86 -0.56 1.67 -1.36 0.36 P>z X_at [ 95% C.I. ]
课件:微观面板数据模型 - logitprobit模型Tobit模型
Yit* i X it it
(8.1) E(Yit | X it ) pit P(Yit 1| X it )
1, Yit 0,
Yit* (0 表示已购买住房) Yit* (0 表示未购买住房)
家庭选择购房(Yit 1)的概率,
1 F (i X it ) Yit E(Yit | X it ) it
财大 面板数据与非参数计量
右删失模型
Yit* i Xit it
Yit
Yit* , cu ,
当Yit* cu时 当Yit* cu时
• 在cu处右归并(删失)
财大 面板数据与非参数计量
左右删失模型
Yit* i Xit it
Yit Ycit*l ,
cu
当Yit* cl时 当cl Yit* cu时
财大 面板数据与非参数计量
Ch8 微观面板数据模型
• Ch8.1 微观面板数据模型及估计 • Ch8.2 模型设定检验 • Ch8.3 案例分析
财大 面板数据与非参数计量
Ch8.3 案例分析
① 面板二元离散选择模型 ② 面板Tobit模型
财大 面板数据与非参数计量
面板二元离散选择模型
财大 面板数据与非参数计量
家庭选择不购房(Yit 0)的概率,
P(Yit 0 | X it , ,i ) P(Yit* 0 | X it , ,i )
P(it i X it | X it , ,i )
F (i X it )
1 F (i X it )
P(Yit 0 | Xit ) 1 P(Yit 1| Xit )
当Yit* cu时
• 在cl处左归并(删失)、cu处右归并
财大 面板数据与非参数计量
