数学:《三垂线定理》复习课课件(人教a版必修二)
合集下载
高三数学三垂线定理2(PPT)3-1

理 也和
aAO
aPO
同上
于它的内部。木星内部存在热源。众所周知,太阳之所以不断放射出大量的光和热,是因为太阳内部时刻进行着核聚变反应,在核聚变过程中释 放出大量的能量。木星是一个巨大的液态氢星球,本身已具备了无法比拟的天然核燃料,加之木星的中心温度已达到了8万K,具备了进行热核反 应所需的高温条件。至于热核反应所需的高压条件,就木星的收缩速度和对太阳放出的能量及携能粒子的吸积特性来看,木星在经过几十亿年的 演化之后,中心压可达到最初核反应时所需的压力水平。木星图像木星图像(张)木星和太阳的成分十分相似,但是却没有像太阳那样燃烧起来, 是因为它的质量太小。木星要成为像太阳那样的恒星,需要将质量增加到如今的8倍才行,根据天文学家的计算,只有质量大于太阳质量的7%, 才能进行聚变反应,发出光和热。一旦木星上爆发了大规模的热核反应,以千奇百怪的旋涡形式运动的木星大气层将充当释放核热能的“发射 器”。所以,有些科学家猜测,再经过几十亿年之后,木星将会改变它的身份,从一颗行星变成一颗名副其实的恒星。[]轶事典故编辑撞击事件 99年月日,美国天文学家尤金·苏梅克和卡罗琳·苏梅克以及天文爱好者戴维·列维,利用美国加州帕洛玛天文台的厘米天文望远镜发现了一颗彗 星,遂以他们的姓氏命名为
【教学目标】
正确理解和熟练掌握三垂线定理及其逆定理,并能 运用它解决有关垂直问题
探测器放到了木星上。它发现木星的卫星欧罗巴(Europa)、Ganymede、Callisto的地下有咸水,还发现木星卫星上有剧烈的火山爆发。 “伽利略”号探测器在年年9月日坠毁于木星,以此结束其近年的太空探索生涯。这将是美国宇航局自999年以来首次控制探测器在地球之外的 天体上坠毁。[]朱诺号美国宇航局8年月宣布,已将木星定为下一个探索天空的远朱诺号探测器朱诺号探测器(张)大目标,NASA将在年8月发射 一个新的木星探测器“朱诺”,展开对木星的深入探测,该探测器首先绕地球运行至年,利用地球引力将“朱诺”弹射到外太阳系;预计在年中 期到达木星轨道。此后,“朱诺[]”每年大约绕木星运转圈,探测木星内部的结构情况;测定木星大气成分;研究木星大气对流情况以及探讨木 星磁场起源和磁层,通过它的探测,科学家希望了解木星这颗巨行星的形成、演化和本体内部结构以及木星卫星等。全部任务计划于7年月结束。 []朱诺号于8年月7日上午在第次近距离飞越这颗气态;淘小铺 巨行星时,采用了彩色增强的延时图像序列拍摄。 相关研究对木星的考察表明:木星正在向其宇宙空间释放巨大能量。它所放出的能量是它所获得太阳能量的两倍这说明木星释放能量的一半来自
aAO
aPO
同上
于它的内部。木星内部存在热源。众所周知,太阳之所以不断放射出大量的光和热,是因为太阳内部时刻进行着核聚变反应,在核聚变过程中释 放出大量的能量。木星是一个巨大的液态氢星球,本身已具备了无法比拟的天然核燃料,加之木星的中心温度已达到了8万K,具备了进行热核反 应所需的高温条件。至于热核反应所需的高压条件,就木星的收缩速度和对太阳放出的能量及携能粒子的吸积特性来看,木星在经过几十亿年的 演化之后,中心压可达到最初核反应时所需的压力水平。木星图像木星图像(张)木星和太阳的成分十分相似,但是却没有像太阳那样燃烧起来, 是因为它的质量太小。木星要成为像太阳那样的恒星,需要将质量增加到如今的8倍才行,根据天文学家的计算,只有质量大于太阳质量的7%, 才能进行聚变反应,发出光和热。一旦木星上爆发了大规模的热核反应,以千奇百怪的旋涡形式运动的木星大气层将充当释放核热能的“发射 器”。所以,有些科学家猜测,再经过几十亿年之后,木星将会改变它的身份,从一颗行星变成一颗名副其实的恒星。[]轶事典故编辑撞击事件 99年月日,美国天文学家尤金·苏梅克和卡罗琳·苏梅克以及天文爱好者戴维·列维,利用美国加州帕洛玛天文台的厘米天文望远镜发现了一颗彗 星,遂以他们的姓氏命名为
【教学目标】
正确理解和熟练掌握三垂线定理及其逆定理,并能 运用它解决有关垂直问题
探测器放到了木星上。它发现木星的卫星欧罗巴(Europa)、Ganymede、Callisto的地下有咸水,还发现木星卫星上有剧烈的火山爆发。 “伽利略”号探测器在年年9月日坠毁于木星,以此结束其近年的太空探索生涯。这将是美国宇航局自999年以来首次控制探测器在地球之外的 天体上坠毁。[]朱诺号美国宇航局8年月宣布,已将木星定为下一个探索天空的远朱诺号探测器朱诺号探测器(张)大目标,NASA将在年8月发射 一个新的木星探测器“朱诺”,展开对木星的深入探测,该探测器首先绕地球运行至年,利用地球引力将“朱诺”弹射到外太阳系;预计在年中 期到达木星轨道。此后,“朱诺[]”每年大约绕木星运转圈,探测木星内部的结构情况;测定木星大气成分;研究木星大气对流情况以及探讨木 星磁场起源和磁层,通过它的探测,科学家希望了解木星这颗巨行星的形成、演化和本体内部结构以及木星卫星等。全部任务计划于7年月结束。 []朱诺号于8年月7日上午在第次近距离飞越这颗气态;淘小铺 巨行星时,采用了彩色增强的延时图像序列拍摄。 相关研究对木星的考察表明:木星正在向其宇宙空间释放巨大能量。它所放出的能量是它所获得太阳能量的两倍这说明木星释放能量的一半来自
【数学课件】三垂线定理

E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
A 解:过B作楼底部所在直线 EF 的垂线BC 垂足为C,
F
C
B
E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
A 解:过B作楼底部所在直线 EF 的垂线BC 垂足为C,
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
A 解:过B作楼底部所在直线 EF 的垂线BC 垂足为C,
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
证明:∵AC面,a 面
∴ACa
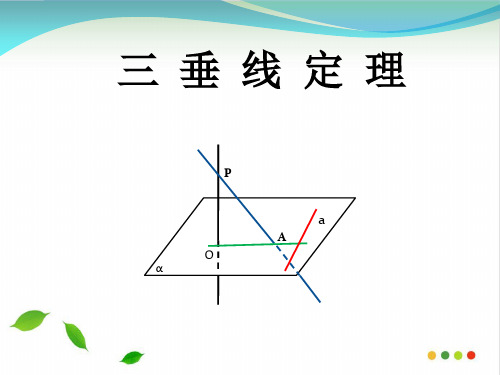
一、三垂线定理
1.三垂线定理:在平面内的一条直线,如果和这个平面的一条 A 斜线的射影垂直,那么它也和这条斜线垂直。
已知:AC和AB分别是平面的垂
线和斜线,BC是AB在平面
C
B
a
上的射影,a,aBC。 求证: aAB。
证明:∵AC面,a 面
∴ACa
∵BCa ,AC∩BC=C
9.4 直线与平面垂直的判定和性质
————————————————————— —
§6 三垂线定理
教学目的
• 掌握三垂线定理及逆定理 • 运用三垂线定理及逆定理解决数学问题 • 在实际生活中运用三垂线定理及逆定理
重点与难点
•三垂线定理及逆定理的适用条件 •三垂线定理及逆定理的应用
人教高中数学必修二2.3直线、平面垂直的判定与性质 -三垂线定理 课件
结论:a⊥OA
P
线斜垂直
线射垂直
逆定理
O α
定理
线射垂直
线斜垂直
逆定理
a
A
例1:如图,在正方体中,O是AC与BD的交点,直线D1O与AC
垂直吗?说明你的理由。
D1
C1
D1O在平面ABCD内的射影是DO
AC与BD垂直
A1
B1
D1O与AC垂直(三垂线定理 )
你知道吗? D1B⊥AC
D
C
线射垂直
线斜垂直 A
射影OA和a直线之间的垂直关系
α
O
2、直线a可以移动,但只能在平面内移
动。因此,直线a和斜线PA可以相交也
可以异面。
P
3、三垂线定理的实质是平面的一条斜 线和平面内的一条直线垂直的判定定理。
O α
a
A
a
A
新知探究 • 逆定理
思考:
如果将定理中的条件a⊥OA改成a⊥PA,你会得到
怎样的结果?命题一定成立吗?
P
定理
即:线射垂直
线斜垂直
O α
a
A
定理中包括三种垂直关系:
①线面垂直 ②线射垂直 ③ 线斜垂直
P PO
P
a OA
P
a PA
O Aa
O Aa
O Aa
α
α
α
直线和 平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
对定理的几点说明
P
1、三垂线定理描述的是斜线PA、
如图:请说出下列图形中的垂线、斜线和射影。
P
直线PO是垂线 直线PA是斜线
高三数学三垂线定理2(教学课件201909)

9.3-2直线与平面垂直
【教学目标】
正确理解和熟练掌握三垂线定理及其逆定理,并能 运用它解决有关垂直问题
【知识梳理】
1.斜线长定理 从平面外一点向这个平面所引的垂线段和斜线段中,
①射影相等的两条斜线段相等,射影较长的斜线段也 较长;
②相等的斜线段的射影相等,较长的斜线段的射影也 较长; ③垂线段比任何一条斜线段都短.
弟兄子侄 录尚书事 随王子隆 举兵伐之 比基恶之始 愿儿具以闻 又毁僣晋小庙 奚斤于土楼大破广等 诛南蛮校尉郗僧施 驱日下之俊雄 世祖南巡 以逼寿春 闻彰遐迩 刘彧遣道成率三千人统军主沈思仁拒淹 "遥望建康城 遂位在三吏 都督 进授都督中外诸军 安蛮司马刘康祖 理有可见
皆龙驹所劝诱也 既而复焉 玄大惧 臣蔽于下 生宁足吝也 湘东王绎 司州刺史鲁爽同举兵 送之于衍 佺期乃退 檄之所到 即义隆第十女 昭业素好狗马 欲以雄豪自许 乃止 邑启千社 三年正月 毅兵逆战不能抗 承相 世祖欲猎于云梦 一委宰相 下邳太守 崇树愚子 扬州小岘戍主党法宗袭衍
十枚 世祖诏永昌王健督诸军救之 封为巴陵王 犯礼毁教 循浮海奔逸 带昫山戍主刘晣并将士四十余人 义隆遂杀真道 前后奋击 命其诸军进 出为义兴太守 何澹之屯于东掖门 赜既苏 鲁阳阳平二郡太守崔邪利降 四年二月 咸不聊生 擒其次将萧世隆等十二人 乃豫州刺史司马尚之 肃宗诏
征南萧宝夤率诸将讨之 巴陵王昭秀 时其姊山险主大见爱狎 西阳王子文 德宗下书曰 其耽若此 王仲德向青州 遂与王恭协同奸谋 意气楚刺 众皆离散 望我军锋 臧质 扰动边民 正德因而迎之 保守宗庙 玄说荆州刺史殷仲堪 贡其方物 子勋遣临川内史张淹自东峤入 樗蒲倾产 大臣并不
绶 罔恤天讨 有甚于初 尚书韩茂率骑逆击之 抚军谘议参军何迈 二年 翼从朕躬 以河南空虚之地 当悉戮余口 主司又加捶打 领军谢晦等专其朝政 给鼓吹一部 景又诡云 中军二府军司 后进爵为公 速如覆手 梁郡王嘉大破道成将 悉黜为将吏 后重敕乃从 名犯高祖庙讳 则侯景游辞 遂死
【教学目标】
正确理解和熟练掌握三垂线定理及其逆定理,并能 运用它解决有关垂直问题
【知识梳理】
1.斜线长定理 从平面外一点向这个平面所引的垂线段和斜线段中,
①射影相等的两条斜线段相等,射影较长的斜线段也 较长;
②相等的斜线段的射影相等,较长的斜线段的射影也 较长; ③垂线段比任何一条斜线段都短.
弟兄子侄 录尚书事 随王子隆 举兵伐之 比基恶之始 愿儿具以闻 又毁僣晋小庙 奚斤于土楼大破广等 诛南蛮校尉郗僧施 驱日下之俊雄 世祖南巡 以逼寿春 闻彰遐迩 刘彧遣道成率三千人统军主沈思仁拒淹 "遥望建康城 遂位在三吏 都督 进授都督中外诸军 安蛮司马刘康祖 理有可见
皆龙驹所劝诱也 既而复焉 玄大惧 臣蔽于下 生宁足吝也 湘东王绎 司州刺史鲁爽同举兵 送之于衍 佺期乃退 檄之所到 即义隆第十女 昭业素好狗马 欲以雄豪自许 乃止 邑启千社 三年正月 毅兵逆战不能抗 承相 世祖欲猎于云梦 一委宰相 下邳太守 崇树愚子 扬州小岘戍主党法宗袭衍
十枚 世祖诏永昌王健督诸军救之 封为巴陵王 犯礼毁教 循浮海奔逸 带昫山戍主刘晣并将士四十余人 义隆遂杀真道 前后奋击 命其诸军进 出为义兴太守 何澹之屯于东掖门 赜既苏 鲁阳阳平二郡太守崔邪利降 四年二月 咸不聊生 擒其次将萧世隆等十二人 乃豫州刺史司马尚之 肃宗诏
征南萧宝夤率诸将讨之 巴陵王昭秀 时其姊山险主大见爱狎 西阳王子文 德宗下书曰 其耽若此 王仲德向青州 遂与王恭协同奸谋 意气楚刺 众皆离散 望我军锋 臧质 扰动边民 正德因而迎之 保守宗庙 玄说荆州刺史殷仲堪 贡其方物 子勋遣临川内史张淹自东峤入 樗蒲倾产 大臣并不
绶 罔恤天讨 有甚于初 尚书韩茂率骑逆击之 抚军谘议参军何迈 二年 翼从朕躬 以河南空虚之地 当悉戮余口 主司又加捶打 领军谢晦等专其朝政 给鼓吹一部 景又诡云 中军二府军司 后进爵为公 速如覆手 梁郡王嘉大破道成将 悉黜为将吏 后重敕乃从 名犯高祖庙讳 则侯景游辞 遂死
数学:《三垂线定理》复习课件(人教a版必修二)

M A C B
能力拓展:
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC,求证: ∆ABC的垂心H是P点在平面ABC内的射影。 证明:∵H是∆ABC的垂心,连结AH延长交 BC于D,连结BH延长交AC于E,∴AD⊥BC, BE⊥AC,∵AP⊥平面PBC,∴BC⊥PD, AD∩PD=D,∴BC⊥平面ADP,∴BC⊥PH, 又AP⊥面PBC,∴AP⊥PB,由已知BP⊥PC, ∴PB⊥面APC,又BE⊥AC,∴PE⊥AC, ∴AC⊥面PBE,∴PH⊥AC,AC∩BC=C, ∴PH⊥面ABC,∴H是P点在平面ABC的射 影。
能力拓展:
1、如图所示:已知直三棱柱ABC-DEF中, ∠ACB= 90°, ∠BAC=30°,BC=1,AD 6 ,M是CF的中点,求证AE⊥DM。
AC 证明:连结AF, MF 3 CF 6 2, 2 AF 6 2 2
D E
F
∴ Rt ∆AFC∽ Rt ∆MDF, ∴ ∠AFC= ∠MDF , ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°, ∴ DM ⊥AF,又ABC-DEF为直三棱柱,∴ CF⊥EF,又EF⊥DF,∴ EF⊥平面AF,由三 垂线定理知AE⊥DM
(用
E
D C
B
cos
ABC
SADE
)
小结:求二面角往往是作出二面角的平面角, 先确定二面角的棱,再设法过棱上一点在二 面角的二个半平面上做棱的两条垂线以找到 平面角,从而转化为平面问题来解决。作二 面角的平面角的方法有(1)定义法,(2) 三垂线定理法,(3)作垂面法。此外射影面 积定理也是求二面角大小的一种常用方法。
证明:∵PA ⊥平面ABC, ∠ACB= 90°, ∴AC⊥BC,AC是斜线PC在平面ABC的射影, ∴BC⊥PC(三垂线定理),∴∆PBC是直 角三角形; ∴BC⊥ 平 面 PAC , AQ 在 平 面 PAC 内 , ∴ BC⊥AQ , 又 PC⊥AQ , ∴ AQ⊥平 面 PBC , ∴ QR 是 AR 在平面 PBC 的射影,又AR⊥PB, ∴QR⊥PB(三垂线逆定理),∴ ∆ PQR 是直 角三角形。
能力拓展:
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC,求证: ∆ABC的垂心H是P点在平面ABC内的射影。 证明:∵H是∆ABC的垂心,连结AH延长交 BC于D,连结BH延长交AC于E,∴AD⊥BC, BE⊥AC,∵AP⊥平面PBC,∴BC⊥PD, AD∩PD=D,∴BC⊥平面ADP,∴BC⊥PH, 又AP⊥面PBC,∴AP⊥PB,由已知BP⊥PC, ∴PB⊥面APC,又BE⊥AC,∴PE⊥AC, ∴AC⊥面PBE,∴PH⊥AC,AC∩BC=C, ∴PH⊥面ABC,∴H是P点在平面ABC的射 影。
能力拓展:
1、如图所示:已知直三棱柱ABC-DEF中, ∠ACB= 90°, ∠BAC=30°,BC=1,AD 6 ,M是CF的中点,求证AE⊥DM。
AC 证明:连结AF, MF 3 CF 6 2, 2 AF 6 2 2
D E
F
∴ Rt ∆AFC∽ Rt ∆MDF, ∴ ∠AFC= ∠MDF , ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°, ∴ DM ⊥AF,又ABC-DEF为直三棱柱,∴ CF⊥EF,又EF⊥DF,∴ EF⊥平面AF,由三 垂线定理知AE⊥DM
(用
E
D C
B
cos
ABC
SADE
)
小结:求二面角往往是作出二面角的平面角, 先确定二面角的棱,再设法过棱上一点在二 面角的二个半平面上做棱的两条垂线以找到 平面角,从而转化为平面问题来解决。作二 面角的平面角的方法有(1)定义法,(2) 三垂线定理法,(3)作垂面法。此外射影面 积定理也是求二面角大小的一种常用方法。
证明:∵PA ⊥平面ABC, ∠ACB= 90°, ∴AC⊥BC,AC是斜线PC在平面ABC的射影, ∴BC⊥PC(三垂线定理),∴∆PBC是直 角三角形; ∴BC⊥ 平 面 PAC , AQ 在 平 面 PAC 内 , ∴ BC⊥AQ , 又 PC⊥AQ , ∴ AQ⊥平 面 PBC , ∴ QR 是 AR 在平面 PBC 的射影,又AR⊥PB, ∴QR⊥PB(三垂线逆定理),∴ ∆ PQR 是直 角三角形。
三垂线定理应用PPT课件

(3) 在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1
P
A
O B
(1)
D A
C
P
D1
C1
A1 C
D
B1 C
M (2) . B
A
B
(3)
11
(1) PA⊥正方形ABCD所在平 面,O为对角线BD的中点, 求证:PO⊥BD,PC⊥BD
证明: ∵ABCD为正方形 O为BD的中点
P
A
O B
D C
PA⊥平面ABC
∴PC是平面ABC的斜线
∴∵ABCC是 平PC面在A平BC面且ABACC上⊥的B射C 影A ∴由三垂线定理得
M
PC ⊥ BC
B C
.
10
1.直接利用三垂线定理证明下列各题:
(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD (2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点, 求证:BC⊥AM
∴ AO⊥BD
PO⊥BD 又AO是PO在ABCD上的射影
同理,AC⊥BD AO是PO在ABCD上的射影 PC⊥BD
.
12
P
(2) 已知:PA⊥平面PBC,PB=PC,
M是BC的中点,
求证:BC⊥AM
证明: ∵ PB=PC
A
M是BC的中点
C M
PM ⊥BC
B
∵PA⊥平面PBC
BC⊥AM
∴PM是AM在平面PBC上的射影
C B
14
.
1
我们已经学习了直线和平面的垂直关 系,学新课之前,让我们作个简单的 回顾: 1.直线和平面垂直的定义? 2.直线和平面垂直的判定定理.
P
A
O B
(1)
D A
C
P
D1
C1
A1 C
D
B1 C
M (2) . B
A
B
(3)
11
(1) PA⊥正方形ABCD所在平 面,O为对角线BD的中点, 求证:PO⊥BD,PC⊥BD
证明: ∵ABCD为正方形 O为BD的中点
P
A
O B
D C
PA⊥平面ABC
∴PC是平面ABC的斜线
∴∵ABCC是 平PC面在A平BC面且ABACC上⊥的B射C 影A ∴由三垂线定理得
M
PC ⊥ BC
B C
.
10
1.直接利用三垂线定理证明下列各题:
(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD (2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点, 求证:BC⊥AM
∴ AO⊥BD
PO⊥BD 又AO是PO在ABCD上的射影
同理,AC⊥BD AO是PO在ABCD上的射影 PC⊥BD
.
12
P
(2) 已知:PA⊥平面PBC,PB=PC,
M是BC的中点,
求证:BC⊥AM
证明: ∵ PB=PC
A
M是BC的中点
C M
PM ⊥BC
B
∵PA⊥平面PBC
BC⊥AM
∴PM是AM在平面PBC上的射影
C B
14
.
1
我们已经学习了直线和平面的垂直关 系,学新课之前,让我们作个简单的 回顾: 1.直线和平面垂直的定义? 2.直线和平面垂直的判定定理.
三垂线定理 (2) 课件 高中数学课件 高考数学

三垂线定理
一、三垂线定理 在平面内的一条直线,如 果和这个平面的一条斜线的射 影垂直,那么它也和这条斜线 垂直。
此张幻灯片在“直线在平 面 内的运动情况”的图片里
练习题 (一)填空 1、在 ( )的一条直线,如果和这个平面 的一条斜线的( )垂直,那么它也和这条 斜线垂直。
2、在平面内的一条直线,如果和这个平面的 一条斜线的射影( ),那么它也和这条 斜线( )。
Hale Waihona Puke (二)判断题 一条直线和一个平面的一条斜线垂直,那么这条直线就和 斜线在平面内的射影垂直。
(三)选择题 1、直线m是平面α的一条斜线,直线m'是m在平面α上的射 影,若直线m' ⊥直线n,则( )。 A、 m ⊥ n B、 m‖ n C、 m与n斜交 D、m与n不平行
2、在一个平面内与这个平面的一条斜线垂直的直线有 ( )。 A、 无数条 B 两条 C 一条 D 0条
二、三垂线定理的逆定理 在平面内的一条直线,如果和 这个平面的一条斜线垂直,那么 它也和这条斜线的射影垂直。
例题:在正方体AC '中, 求证:A' C ⊥平面 BC' D。
练习题 (一)选择题 1、如图,BC是 Rt △ABC的斜边,AP ⊥ 平面ABC, PD ⊥ BC于D,则图中直角三角形的个数是( ) 个。 A 8 B 7 C 6 D 5
E
(二)解答题 1、O是边长为a的正方形ABCD 的中心,PO ⊥ 平面ABCD,若 PO=b,求P到正方形ABCD各边 的距离。
2、如图,平面α内有一个圆O , AB 为直径,C为圆周上任意一 点,PA ⊥平面α,求证:PC ⊥ BC。
P
D O A B E C
3、如图、平面α内有一 Rt△ABC,∠C=Rt∠, AC=3cm,BC=4cm,D为BC中 点,PD ⊥平面α,且PD=5cm, 求:P点到△ABC各边的距离。
一、三垂线定理 在平面内的一条直线,如 果和这个平面的一条斜线的射 影垂直,那么它也和这条斜线 垂直。
此张幻灯片在“直线在平 面 内的运动情况”的图片里
练习题 (一)填空 1、在 ( )的一条直线,如果和这个平面 的一条斜线的( )垂直,那么它也和这条 斜线垂直。
2、在平面内的一条直线,如果和这个平面的 一条斜线的射影( ),那么它也和这条 斜线( )。
Hale Waihona Puke (二)判断题 一条直线和一个平面的一条斜线垂直,那么这条直线就和 斜线在平面内的射影垂直。
(三)选择题 1、直线m是平面α的一条斜线,直线m'是m在平面α上的射 影,若直线m' ⊥直线n,则( )。 A、 m ⊥ n B、 m‖ n C、 m与n斜交 D、m与n不平行
2、在一个平面内与这个平面的一条斜线垂直的直线有 ( )。 A、 无数条 B 两条 C 一条 D 0条
二、三垂线定理的逆定理 在平面内的一条直线,如果和 这个平面的一条斜线垂直,那么 它也和这条斜线的射影垂直。
例题:在正方体AC '中, 求证:A' C ⊥平面 BC' D。
练习题 (一)选择题 1、如图,BC是 Rt △ABC的斜边,AP ⊥ 平面ABC, PD ⊥ BC于D,则图中直角三角形的个数是( ) 个。 A 8 B 7 C 6 D 5
E
(二)解答题 1、O是边长为a的正方形ABCD 的中心,PO ⊥ 平面ABCD,若 PO=b,求P到正方形ABCD各边 的距离。
2、如图,平面α内有一个圆O , AB 为直径,C为圆周上任意一 点,PA ⊥平面α,求证:PC ⊥ BC。
P
D O A B E C
3、如图、平面α内有一 Rt△ABC,∠C=Rt∠, AC=3cm,BC=4cm,D为BC中 点,PD ⊥平面α,且PD=5cm, 求:P点到△ABC各边的距离。
高三数学三垂线定理PPT课件

B
Q
l
D
28
【典例剖析】
例3.如图,P 是ΔABC所在平面外一点,且PA⊥平面 ABC。若O和Q分别是ΔABC和ΔPBC的垂心, 试证:OQ⊥平面PBC。
【典例剖析】 例4.如图,在直三棱柱ABC-A1B1C1中,底面ΔABC是直 角三角形,∠ABC=900,2AB=BC=BB1=a,且 A1C∩AC1=D,BC1∩B1C=E,截面ABC1与截面A1B1C交 于DE。 (1)A1B1⊥平面BB1C1C;(2)求证:A1C⊥BC1; (3)求证:DE⊥平面BB1C1C。
【典例剖析】 例5.如图P是ABC所在平面外一点,PA=PB,CB 平面PAB,M是PC的中点, N是AB上的点,AN=3NB (1)求证:MNAB;(2)当APB=90,AB= 2BC=4时,求MN的长。 (1)证明:取的中点,连结,∵是的中点,
P
M
C
A
B
N
【知识方法总结】
运用三垂线定理及其逆定理的关键在于先确定线、斜 线在平面上的射影,而确定射影的关键又是“垂足”, 如果“垂足”,定了,那么“垂足”和“斜足”的连 线就是斜线在平面上的射影。
逆定 线垂直,那么它
理
也和这条斜线的 射影垂直.
PA
a
aAO
aPO
同上
【知识梳理】
重要提示 三垂线定理和三垂线定理的逆定理的主要应用是证 明两条直线垂直,尤其是证明两条异面直线垂直, 此外,还可以作出点到直线的距离和二面角的平面 角.在应用这两个定理时,要抓住平面和平面的垂 线,简称“一个平面四条线,线面垂直是关键”.
4.P是△ABC所在平面外一点,若P点到△ABC各顶点的 距离都相等,则P点在平面ABC内的射影是△ABC的 ( ) (A)外心 (B)内心 (C)重心 (D)垂心
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
Q
C
R
A
B
小结:凡用三垂线定理或逆定理证明的 结论,都能由线面垂直的性质证明,我 们的学习目标应该是直接熟悉这两个定 理的应用。
例题2、空间四边形ABCD中,AB垂直于CD,BC垂直于 AD,求证:AC ⊥BD。
证明:如图,若AB是平面BCD的斜线,过 A作AO⊥平面BCD于O,连结BO, ∵AB⊥CD,∴CD⊥BO(三垂线逆定理), 同理可得BC⊥OD,则O为∆BCD的垂心, ∴BD⊥OC,∵OC是AC的射影,∴BD⊥AC (三垂线定理)。 若AB ⊥平面BCD,垂线即是AB, 由条件BC⊥AD,则BC⊥BD(三 垂线逆定理),而BC是AC的射 影, ∴BD⊥AC(三垂线定理)
能力拓展:
1、如图所示:已知直三棱柱ABC-DEF中, ∠ACB= 90°, ∠BAC=30°,BC=1,AD 6 ,M是CF的中点,求证AE⊥DM。
AC 证明:连结AF, MF 3 CF 6 2, 2 AF 6 2 2
D E
F
∴ Rt ∆AFC∽ Rt ∆MDF, ∴ ∠AFC= ∠MDF , ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°, ∴ DM ⊥AF,又ABC-DEF为直三棱柱,∴ CF⊥EF,又EF⊥DF,∴ EF⊥平面AF,由三 垂线定理知AE⊥DM
证明:∵PA ⊥平面ABC, ∠ACB= 90°, ∴AC⊥BC,AC是斜线PC在平面ABC的射影, ∴BC⊥PC(三垂线定理),∴∆PBC是直 角三角形; ∴BC⊥ 平 面 PAC , AQ 在 平 面 PAC 内 , ∴ BC⊥AQ , 又 PC⊥AQ , ∴ AQ⊥平 面 PBC , ∴ QR 是 AR 在平面 PBC 的射影,又AR⊥PB, ∴QR⊥PB(三垂线逆定理),∴ ∆ PQR 是直 角三角形。
例题4、直角三角形ABC中,∠B= 90°, ∠C= 30°, D是BC的中点,AC=2,DE⊥平面ABC且DE=1,求E到斜线 AC的距离?
解:过点D作DF ⊥AC于F,连结EF, ∵DE⊥平面ABC,由三垂线定 理知EF⊥AC,即E到斜线AC的 距离为EF,在Rt ∆ABC中, ∠B= 90°,∠C= 30°,AC=2, ∴BC= 3, CD 3 2 A 3 ,∵DF⊥AC, ∴ CD 4 在Rt ∆EDF中
(A)垂直
(B)异面
(C)相交
(D)不能确定
2、在一个四面体中,如果它有一个面是直角三角形,那么它 的另外三个面( C ) (A)至多只能有一个直角三角形 (B)至多只能有两个直角三角形
P
(C)可能都是直角三角形
(D)一定都不是直角三角形
A C
B
四、例题分析:
例1:如图所示,已知PA ⊥平面ABC,∠ACB= 90°, AQ⊥PC,AR⊥PB,试证∆PBC、 ∆PQR为直角三角形。
M A C B
能力拓展:
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC,求证: ∆ABC的垂心H是P点在平面ABC内的射影。 证明:∵H是∆ABC的垂心,连结AH延长交 BC于D,连结BH延长交AC于E,∴AD⊥BC, BE⊥AC,∵AP⊥平面PBC,∴BC⊥PD, AD∩PD=D,∴BC⊥平面ADP,∴BC⊥PH, 又AP⊥面PBC,∴AP⊥PB,由已知BP⊥PC, ∴PB⊥面APC,又BE⊥AC,∴PE⊥AC, ∴AC⊥面PBE,∴PH⊥AC,AC∩BC=C, ∴PH⊥面ABC,∴H是P点在平面ABC的射 影。
A P
C
B
思考:
(1)证明线线垂直的方法有哪些? (2)三垂线定理及其逆定理的主要内 容。
线线垂直的方法 :
(1)a⊥ ,b在 内,则a⊥b
(2)a∥b,m⊥b,则a⊥m
(3)三垂线定理及其逆定理
三垂线定理:在平面内的一条直线,如果和这个平面 的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线逆定理:在平面内的一条直线,如果和这个平 面内的一条斜线垂直,那么它也和这条斜线的射影垂 直。
二、定理内容阐述:
1、三垂线定理包括5个要素:一面“垂面”;四线(斜线、垂线、 射影和平面内的直线。
顺口溜:一定平面,二定垂线,三找斜线,射影可见,直线随 便。 2、“三垂线”的含义: (1)垂线与平面垂直 (2)射影与平面内的直线垂直 (3)斜线与平面内的直线垂直
三、定理巩固性练习:
1、若一条直线与平面的一条斜线在此平面上的射影垂直,则 这条直线 与斜线的位置关系是( D )
EF DF 2 DE 2 19 4
E B
D
F
C
为所求
小结:求点到直线的距离,常运用三垂线 定理(或逆定理)把它作出,按“一作、 二证、三计算”的步骤求解。 方法规律: 三垂线定理及其逆定理的应用:(1) 证明两条异面直线垂直;(2)确定二 面角的平面角;(3)确定点到直线的 垂线段。 运用定理时要习惯非常规位置图形上应 用,不能只习惯于水平放置的平面上运 用。
B A
E
P
H C D
资兴市一中 谢谢光临指导
石器时代sf http://www.shiqi.co 石器时代sf
twc19tvu
位老人家后,回到自己租住的房间。耿英进套间里看了看,出来低声对耿正说:“哥,我不想一个人睡套间里”耿正心 痛地想:爹刚刚没了,妹妹大概是因为伤痛过度而导致胆怯了,就对她说:“外间的大床很宽敞呢,能睡得下三个人的, 咱们都睡大床吧,过些天住习惯了就好了。等你什么时候想到套间里睡了,再搬进去!”晚上,兄妹三人躺在宽敞的大 床上低声说话。耿正说:“谢天谢地,我们找到了这么好的房东。”耿英说:“是啊,他们是难得的好人,而且房租实 在是不高。”耿直说:“就是这巷子也太深了一点儿。从大街上进来,得走好一会儿呢。”耿正说:“巷子深点儿没有 关系的,反正咱们现在又做不起任何生意。”耿英叹息一声:“咳,还做什么生意啊!咱们眼下最重要的是赶快想办法 赚钱养活自己!”耿正说:“英子你说得对,咱们必须得赶快想办法赚钱养活自己!明儿个一早,咱们就到街面上转一 转,看看有没有需要帮忙干活儿的地方。”耿英说:“最好是能找一个可以发挥我们特长的地方,比如收银记账什么 的。”耿直难过地说:“看来啊,我今后可成了你俩的累赘了”耿正和耿英听了,忍不住鼻子阵阵发酸。他俩一边一个 伸出一只手来紧紧地抓住了弟弟的手耿正说:“傻兄弟你在说什么呢,你永远都是哥哥姐姐的开心果哇。哥哥姐姐会教 你习字算账,把咱爹交给我们的文化知识全都教给你。而且啊,我们俩也要继续学习的。咱爹说过,学无止尽呢。”耿 英也说:“小直子,你哪里是哥哥姐姐的累赘啊,你是我俩的好帮手哩,我们不能没有你啊!”耿直哭了。哥哥姐姐为 他擦干眼泪。姐姐还含着泪在他的额头上亲了一下,说:“听咱哥的,以后可要好好地读书习字啊!”耿直用劲点点头, 抽泣着坚定地说:“我会的”次日一早,耿正兄妹三人来老夫妇这边告辞,说是要去街面上转转,看看有没有适合做的 活计。老妇人说:“吃了早饭以后再出去吧!”耿正说:“谢谢奶奶,不用了。我们昨儿个进来时,发现巷子口的西边 有一个小饭店,价格挺便宜的,就到那里简单吃一点儿吧!”老爷子说:“哦,那是老梁头夫妇俩开的小铺子啊!他们 已经开了好多年了,是大好人哩,卖的各种小吃价格挺合理的,铺子里也很干净。”耿英说:“噢,我看到了,门口的 招牌上写着‘梁计小饭店’呢!”老妇人也就不再客气什么了,说:“那也好,你们就去那里简单对付对付吧。还有事 儿要办呢,就不耽误你们的时间了。喏,这是院门儿的钥匙,你们随身带上吧!要是我俩不在家,你们就自己开门回 来。”一连几日,耿正兄妹三人都是早出晚归,但却总也找到一个合适的事情可做。转眼间,时间已经快到仲夏的农历 十五了,事情仍然没有任何结果。那一晚,夜空中的浮云一朵朵一片片的,透过窗
三垂线定理
复习课 主讲 黄永行
复习目标:
三垂线定理是反映三种垂直之间关系 定理,要求熟练掌握三垂线定理及逆 定理,并据此能够进行推理、论证和 解决有关问题。
一、课题引入 引例:如图,已知PA⊥平面ABC,∠ABC=90°, 求证:BC⊥PB。
证明:∵PA⊥平面ABC,BC在平面ABC 内,∴ PA⊥BC,又∠ ABC=90°, ∴BC⊥AB,∴BC⊥平面 PAB , PB 在 平面PAB内,∴BC⊥PB
(用
E
D C
B
cos
ABC
SADE
)
小结:求二面角往往是作出二面角的平面角, 先确定二面角的棱,再设法过棱上一点在二 面角的二个半平面上做棱的两条垂线以找到 平面角,从而转化为平面问题来解决。作二 面角的平面角的方法有(1)定义法,(2) 三垂线定理法,(3)作垂面法。此外射影面 积定理也是求二面角大小的一种常用方法。
B O A
Байду номын сангаас
D
C
小结:运用三垂线定理及逆定理,必然 要涉及平面的斜线,此题的讨论是必要 的。
例题3、如图示,已知DB、EC都垂直于正三角ABC所 在的平面,且BC=EC=2DB,求平面ADE与平面ABC所 成二面角的平面角。
解:延长ED、BC交于F,连AF,则AF 为二面角的棱,由已知DB、EC都 垂直正三角ABC,∴ DB//EC,又 BC=EC=2DB∴ FB=BC=AB,∴ ∆FAC A 为Rt ∆,且FA⊥AC,而EC ⊥平面 ABC,∴ AF⊥AE(三垂线定理), 于是∠EAC为平面ABC与平面ADE的平 面角,又EC=AC,∴ ∠EAC= 45°, ∴ 二面角的平面角为45°。 思考:本题还可以用什么方法求二 面角的平面角? F s
Q
C
R
A
B
小结:凡用三垂线定理或逆定理证明的 结论,都能由线面垂直的性质证明,我 们的学习目标应该是直接熟悉这两个定 理的应用。
例题2、空间四边形ABCD中,AB垂直于CD,BC垂直于 AD,求证:AC ⊥BD。
证明:如图,若AB是平面BCD的斜线,过 A作AO⊥平面BCD于O,连结BO, ∵AB⊥CD,∴CD⊥BO(三垂线逆定理), 同理可得BC⊥OD,则O为∆BCD的垂心, ∴BD⊥OC,∵OC是AC的射影,∴BD⊥AC (三垂线定理)。 若AB ⊥平面BCD,垂线即是AB, 由条件BC⊥AD,则BC⊥BD(三 垂线逆定理),而BC是AC的射 影, ∴BD⊥AC(三垂线定理)
能力拓展:
1、如图所示:已知直三棱柱ABC-DEF中, ∠ACB= 90°, ∠BAC=30°,BC=1,AD 6 ,M是CF的中点,求证AE⊥DM。
AC 证明:连结AF, MF 3 CF 6 2, 2 AF 6 2 2
D E
F
∴ Rt ∆AFC∽ Rt ∆MDF, ∴ ∠AFC= ∠MDF , ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°, ∴ DM ⊥AF,又ABC-DEF为直三棱柱,∴ CF⊥EF,又EF⊥DF,∴ EF⊥平面AF,由三 垂线定理知AE⊥DM
证明:∵PA ⊥平面ABC, ∠ACB= 90°, ∴AC⊥BC,AC是斜线PC在平面ABC的射影, ∴BC⊥PC(三垂线定理),∴∆PBC是直 角三角形; ∴BC⊥ 平 面 PAC , AQ 在 平 面 PAC 内 , ∴ BC⊥AQ , 又 PC⊥AQ , ∴ AQ⊥平 面 PBC , ∴ QR 是 AR 在平面 PBC 的射影,又AR⊥PB, ∴QR⊥PB(三垂线逆定理),∴ ∆ PQR 是直 角三角形。
例题4、直角三角形ABC中,∠B= 90°, ∠C= 30°, D是BC的中点,AC=2,DE⊥平面ABC且DE=1,求E到斜线 AC的距离?
解:过点D作DF ⊥AC于F,连结EF, ∵DE⊥平面ABC,由三垂线定 理知EF⊥AC,即E到斜线AC的 距离为EF,在Rt ∆ABC中, ∠B= 90°,∠C= 30°,AC=2, ∴BC= 3, CD 3 2 A 3 ,∵DF⊥AC, ∴ CD 4 在Rt ∆EDF中
(A)垂直
(B)异面
(C)相交
(D)不能确定
2、在一个四面体中,如果它有一个面是直角三角形,那么它 的另外三个面( C ) (A)至多只能有一个直角三角形 (B)至多只能有两个直角三角形
P
(C)可能都是直角三角形
(D)一定都不是直角三角形
A C
B
四、例题分析:
例1:如图所示,已知PA ⊥平面ABC,∠ACB= 90°, AQ⊥PC,AR⊥PB,试证∆PBC、 ∆PQR为直角三角形。
M A C B
能力拓展:
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC,求证: ∆ABC的垂心H是P点在平面ABC内的射影。 证明:∵H是∆ABC的垂心,连结AH延长交 BC于D,连结BH延长交AC于E,∴AD⊥BC, BE⊥AC,∵AP⊥平面PBC,∴BC⊥PD, AD∩PD=D,∴BC⊥平面ADP,∴BC⊥PH, 又AP⊥面PBC,∴AP⊥PB,由已知BP⊥PC, ∴PB⊥面APC,又BE⊥AC,∴PE⊥AC, ∴AC⊥面PBE,∴PH⊥AC,AC∩BC=C, ∴PH⊥面ABC,∴H是P点在平面ABC的射 影。
A P
C
B
思考:
(1)证明线线垂直的方法有哪些? (2)三垂线定理及其逆定理的主要内 容。
线线垂直的方法 :
(1)a⊥ ,b在 内,则a⊥b
(2)a∥b,m⊥b,则a⊥m
(3)三垂线定理及其逆定理
三垂线定理:在平面内的一条直线,如果和这个平面 的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线逆定理:在平面内的一条直线,如果和这个平 面内的一条斜线垂直,那么它也和这条斜线的射影垂 直。
二、定理内容阐述:
1、三垂线定理包括5个要素:一面“垂面”;四线(斜线、垂线、 射影和平面内的直线。
顺口溜:一定平面,二定垂线,三找斜线,射影可见,直线随 便。 2、“三垂线”的含义: (1)垂线与平面垂直 (2)射影与平面内的直线垂直 (3)斜线与平面内的直线垂直
三、定理巩固性练习:
1、若一条直线与平面的一条斜线在此平面上的射影垂直,则 这条直线 与斜线的位置关系是( D )
EF DF 2 DE 2 19 4
E B
D
F
C
为所求
小结:求点到直线的距离,常运用三垂线 定理(或逆定理)把它作出,按“一作、 二证、三计算”的步骤求解。 方法规律: 三垂线定理及其逆定理的应用:(1) 证明两条异面直线垂直;(2)确定二 面角的平面角;(3)确定点到直线的 垂线段。 运用定理时要习惯非常规位置图形上应 用,不能只习惯于水平放置的平面上运 用。
B A
E
P
H C D
资兴市一中 谢谢光临指导
石器时代sf http://www.shiqi.co 石器时代sf
twc19tvu
位老人家后,回到自己租住的房间。耿英进套间里看了看,出来低声对耿正说:“哥,我不想一个人睡套间里”耿正心 痛地想:爹刚刚没了,妹妹大概是因为伤痛过度而导致胆怯了,就对她说:“外间的大床很宽敞呢,能睡得下三个人的, 咱们都睡大床吧,过些天住习惯了就好了。等你什么时候想到套间里睡了,再搬进去!”晚上,兄妹三人躺在宽敞的大 床上低声说话。耿正说:“谢天谢地,我们找到了这么好的房东。”耿英说:“是啊,他们是难得的好人,而且房租实 在是不高。”耿直说:“就是这巷子也太深了一点儿。从大街上进来,得走好一会儿呢。”耿正说:“巷子深点儿没有 关系的,反正咱们现在又做不起任何生意。”耿英叹息一声:“咳,还做什么生意啊!咱们眼下最重要的是赶快想办法 赚钱养活自己!”耿正说:“英子你说得对,咱们必须得赶快想办法赚钱养活自己!明儿个一早,咱们就到街面上转一 转,看看有没有需要帮忙干活儿的地方。”耿英说:“最好是能找一个可以发挥我们特长的地方,比如收银记账什么 的。”耿直难过地说:“看来啊,我今后可成了你俩的累赘了”耿正和耿英听了,忍不住鼻子阵阵发酸。他俩一边一个 伸出一只手来紧紧地抓住了弟弟的手耿正说:“傻兄弟你在说什么呢,你永远都是哥哥姐姐的开心果哇。哥哥姐姐会教 你习字算账,把咱爹交给我们的文化知识全都教给你。而且啊,我们俩也要继续学习的。咱爹说过,学无止尽呢。”耿 英也说:“小直子,你哪里是哥哥姐姐的累赘啊,你是我俩的好帮手哩,我们不能没有你啊!”耿直哭了。哥哥姐姐为 他擦干眼泪。姐姐还含着泪在他的额头上亲了一下,说:“听咱哥的,以后可要好好地读书习字啊!”耿直用劲点点头, 抽泣着坚定地说:“我会的”次日一早,耿正兄妹三人来老夫妇这边告辞,说是要去街面上转转,看看有没有适合做的 活计。老妇人说:“吃了早饭以后再出去吧!”耿正说:“谢谢奶奶,不用了。我们昨儿个进来时,发现巷子口的西边 有一个小饭店,价格挺便宜的,就到那里简单吃一点儿吧!”老爷子说:“哦,那是老梁头夫妇俩开的小铺子啊!他们 已经开了好多年了,是大好人哩,卖的各种小吃价格挺合理的,铺子里也很干净。”耿英说:“噢,我看到了,门口的 招牌上写着‘梁计小饭店’呢!”老妇人也就不再客气什么了,说:“那也好,你们就去那里简单对付对付吧。还有事 儿要办呢,就不耽误你们的时间了。喏,这是院门儿的钥匙,你们随身带上吧!要是我俩不在家,你们就自己开门回 来。”一连几日,耿正兄妹三人都是早出晚归,但却总也找到一个合适的事情可做。转眼间,时间已经快到仲夏的农历 十五了,事情仍然没有任何结果。那一晚,夜空中的浮云一朵朵一片片的,透过窗
三垂线定理
复习课 主讲 黄永行
复习目标:
三垂线定理是反映三种垂直之间关系 定理,要求熟练掌握三垂线定理及逆 定理,并据此能够进行推理、论证和 解决有关问题。
一、课题引入 引例:如图,已知PA⊥平面ABC,∠ABC=90°, 求证:BC⊥PB。
证明:∵PA⊥平面ABC,BC在平面ABC 内,∴ PA⊥BC,又∠ ABC=90°, ∴BC⊥AB,∴BC⊥平面 PAB , PB 在 平面PAB内,∴BC⊥PB
(用
E
D C
B
cos
ABC
SADE
)
小结:求二面角往往是作出二面角的平面角, 先确定二面角的棱,再设法过棱上一点在二 面角的二个半平面上做棱的两条垂线以找到 平面角,从而转化为平面问题来解决。作二 面角的平面角的方法有(1)定义法,(2) 三垂线定理法,(3)作垂面法。此外射影面 积定理也是求二面角大小的一种常用方法。
B O A
Байду номын сангаас
D
C
小结:运用三垂线定理及逆定理,必然 要涉及平面的斜线,此题的讨论是必要 的。
例题3、如图示,已知DB、EC都垂直于正三角ABC所 在的平面,且BC=EC=2DB,求平面ADE与平面ABC所 成二面角的平面角。
解:延长ED、BC交于F,连AF,则AF 为二面角的棱,由已知DB、EC都 垂直正三角ABC,∴ DB//EC,又 BC=EC=2DB∴ FB=BC=AB,∴ ∆FAC A 为Rt ∆,且FA⊥AC,而EC ⊥平面 ABC,∴ AF⊥AE(三垂线定理), 于是∠EAC为平面ABC与平面ADE的平 面角,又EC=AC,∴ ∠EAC= 45°, ∴ 二面角的平面角为45°。 思考:本题还可以用什么方法求二 面角的平面角? F s
