概率与数理统计PPT2、3章测试题
概率论与数理统计 张天德版 第2章 课件 例题

例1 从1~10这10个数字中随机取出5个数字, X 表示取出的5个数字中的最大值. 试求X 的 分布列
解: X 的取值为5,6,7,8,9,10. 并且
P
X k
C4 k 1
C150
k 5, 6, , 10
即 X 的分布列为
X 5 6 7 8 9 10
X0
1
2
3
4
5
P1 3 1 4 3 4
16 16 16 16 16 16
则
P X 2 P X 0 P X 1 P X 2
1 31 16 16 16
5 16
例3(续)
P X 3 P X 4 P X 5
34 16 16
7 16
P 0.5 X 3 P X 1 P X 2
X
a1 a2 an
pk
1 1 1 nn n
其中 (ai a j ), (i j) ,则称 X 服从等可能分布.
实例 抛掷骰子并记出现的点数为随机变量 X,
则有 X 1 2 3 4 5 6
pk
1 1 11 6 6 66
11 66
3. 几何分布
若随机变量 X 的分布律为
X 12 k pk p qp q k1 p
一、离散型随机变量的分布律 定义1
若随机变量 X 所有可能的取值为有限个或可 列无穷多个,则称X为离散型随机变量。否则称 为非离散型随机变量。
注: 为了描述随机变量 X ,我们不仅需要 知道随机变量X的取值,而且还应知道X取每个 值的概率.
例
从中任取3 个球
取到的白球数X是一个随机变量
X可能取的值是0,1,2
X
1, 0,
《概率论与数理统计》课件-第2章随机变量及其分布 (1)

HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次 数,公共汽车车站候车的乘客数,售票窗口买票的人数, 原子放射的粒子数,保险公司在一定时期内被索赔的次 数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
二、随机变量的概念
定义: 设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在 上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)
概率论与数理统计图文课件最新版-第2章-随机变量及其分布
函数 f ( x),使得对于任意实数 x 有:
x
F ( x) f (t)dt ( P( X x))
则称 X 为连续型变量,f ( x)为 X 的概率密度函数 注 ▲ 连续型随机变量与离散型随机变量的区别
离散型: P( X xk ) 0 连续型:P( X xk ) 0
机
多,而且还不能一 一列
变 连续型随机变量 量
举,而是充满一个区间
例如,“电视机的寿命”,实际中
常 遇到的“测量误差”等等.
概率统计
第二章知识结构图
随机变量
离散型随 机变量
连续型随 机变量
分布律
分布 函数
函数的 分布
概率 密度
分布 函数
函数的 分布
定义 常用分布
概率统计
定义 常用分布
第四节 连续型随机变量及其概率密度
0 x 0
则称 X 为服从参数 的指数分布.
概率统计
二 . 连续型随机变量的分布函数
定义: 若定义在 (, )上的可积函数 f ( x)
满足: (1). f ( x) 0
(2). f ( x)dx 1
f (x)确定了 分布函数F(x),
则称 F ( x)
x
f ( x)dx
f (x)是F(x)的 导函数, F(x)是f (x)的一
(2) 某段时间内候车室的旅客数目为 X , 则它也是一个随机变量,它可以取 0 及一切 自然数。X 是定义在样本空间,则:
S e {人数 人数 0}
X X (e)的值域RX [0, )
概率统计
二. 随机变量的分类 离散型随机变量
概率论与数理统计--第二章PPT课件
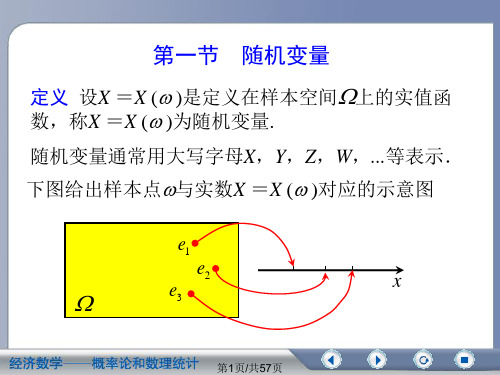
F(x) pk xk x
分布函数F(x)在x xk , 其跳跃值为pk P{X
对k 所1,有2,满足处x有k 跳 x跃的,k求和。
xk }
第26页/共57页
第四节 连续型随机变量及其概率密度
定义 对于随机变量X的分布函数F(x),如果存在非 负函数f (x),使对于任意实数有
售量服从参数为 10的泊松分布.为了以95%以上的
概率保证该商品不脱销,问商店在月底至少应进该商 品多少件? 解 设商店每月销售该种商品X件,月底的进货量为n件,
按题意要求为 PX n 0.95
由X服附从录的泊1松0的分泊布松表分知布k,140 1则k0!k有e1k0n01k00!k.9e1160 6
可以用泊松分布作近似,即
n
k
pk
1
p
nk
np k
k!
enp , k
0,1, 2,
.
例 4 为保证设备正常工作,需要配备一些维修工.如果各台设备
发生故障是相互独立的,且每台设备发生故障的概率都是 0.01.
试求在以下情况下,求设备发生故障而不能及时修理的概率.
(1) 一名维修工负责 20 台设备.
于是PX I P(B) Pw X (w) I.
随机变量的取值随试验的结果而定,而试验的各个 结果出现有一定的概率,因而随机变量的取值有一 定的概率.
按照随机变量可能取值的情况,可以把它们分为两 类:离散型随机变量和非离散型随机变量,而非离 散型随机变量中最重要的是连续型随机变量.因此, 本章主要研究离散型及连续型随机变量.
x
x
4. F(x 0) F(x) 即F(x)是右连续的
第23页/共57页
概率论与数理统计ppt课件(完整版)

( 1)
n 1
例4. 设P(A)=p, P(B)=q, P(AB)=r, 用p, q, r表示下列 事件的概率:
(1) P ( A B ); (2) P ( A B); (3) P ( A B); (4)P( A B ).
28
§5. 条件概率
(一)条件概率: 设试验E的样本空间为S, A, B是事件, 要考虑 在A已经发生的条件下B发生的概率, 这就是条件概 率问题.
概率论与数理统计
第一章 概率论的基本概念 前 言
1. 确定性现象和不确定性现象.
2. 随机现象: 在个别试验中其结果呈现出不确定性, 在 大量重复试验中其结果又具有统计规律性. 3. 概率与数理统计的广泛应用.
2
§1.随机试验
我们将对自然现象的一次观察或进行一次科学试验 称为试验。
举例:
E1: 抛一枚硬币,观察正(H)反(T) 面 的情 况.
B A 类似地, 事件 S 为可列个事件A1, A2, ...的积事件.
k 1 K
(2) A B A B
S
(3)A B
9
4.差事件:
事件A-B={x|xA且xB} 称为A与B的差. 当且仅当 A发生, B不发生时事件A-B发生. 即:
A - B A AB
显然: A-A=, A- =A, A-S=
(一) 频率 1. 在相同的条件下, 共进行了n次试验,事件A发生的次 数nA, 称为A的频数, nA/n称为事件A发生的频率, 记为 fn(A).
2. 频率的基本性质: (1) 0 f( 1; (非负性) n A) (2) f n ( S ) 1; (规范性) (3)若A1,A 2, , Ak 两两互不相容 ,则 f n ( A1 A2 Ak ) f n ( A1 ) f n ( A2 ) f n ( Ak ).(有限可加性)
六年级下册数学总复习课件-统计与概率 检测卷-通用版(共14张PPT).pptx

一、填空。(每空 3 分,共 33 分) 1.一个布袋里装有 13 个红球,2 个黄球,7 个花球,任意 摸出一个球,摸到( 红 )球的可能性最大,摸到( 黄 )球的可 能性最小。 2.把 1、2、3、…、20 这 20 个自然数分别写在 20 张同样 的卡片上,打乱后反扣在桌上,从中任意抽一张,抽到奇数的 可能性比抽到质数的可能性( 大 ),抽到偶数的可能性比抽到 合数的可能性( 小 )。
4.下面的游戏规则公平的是( B )。 A.乐乐说:“用 3、4、5 三张数字卡片摆三位数,如果 摆出的是奇数,算我赢,否则算你赢。” B.奇奇说:“抛两枚硬币,如果朝上的面相同,我获胜, 否则你获胜。” C.皮皮说:“掷一枚骰子,点数大于 3 我赢,点数小于 3 你赢。”
5.星期天晚饭后,阳阳从 家里出去散步,右图描述了他散 步过程中离家的距离与散步所 用时间之间的关系。根据右图判 断,下面描述符合阳阳散步情景 的是( B )。
。2020年6月18日星期四上午9时39分28秒09:39:2820.6.18
• •
T H E E N D 15、会当凌绝顶,一览众山小。2020年6月上午9时39分20.6.1809:39June 18, 2020
16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2020年6月18日星期四9时39分28秒09:39:2818 June 2020
• 13、志不立,天下无可成之事。20.6.1820.6.1809:39:2809:39:28June 18, 2020
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
概率论与数理统计第二章
1 ,max= 2
4. 渐近线 以X轴为渐进线
5. 曲线的变化规律
设X~ N ( , ) ,
2
X的分布函数是
1 F ( x) 2
x
(t ) 2 22Fra bibliotekedt , x
标准正态分布
0, 1 的正态分布称为标准正态分布.
若随机变量X的概率分布为: P(X=1)=p,0<p<1 P(X=0)=1-p=q 则称X服从参数为p的两点分布.
二项分布
例4 设射手每一次击中目标的概率为p,现连续 射击n次,求恰好击中次数X 的概率分布.
若随机变量X的概率分布为
Pn (k ) P( X k)C p (1 p)
k n k
3. F(x+0)=F(x)
例1:设随机变量X的分布函数为
a be x , x 0 F ( x) x0 0 ,
求常数a, b及概率 P( X 2)
2.2
离散型随机变量的概率分布
定义1 :设xk(k=1,2, …)是离散型随机变量X 所取的一切可能值,pk是X取 xk值的概率,称
0
1 8
1
a
2
2a
Pk
(1)求常数a ; (2) P( X 1), P(2 X 0), P( X 2)
例2 在五件产品中有两件次品,从中任取出两 件。用随机变量X表示其中的次品数,求X的分 布律和分布函数.
X
P
0
0.3
1
0.6
2
0.1
1.0 0.9
0 0.3 F ( x) 0.9 1.0
均匀分布
概率论与数理统计-第二章-随机变量及其分布函数ppt课件
表格: X
x1 x2
pk
p1 p2
概率分布图:
1P
xn
pn
0.5
x4 x3
x1
x2
X
.
由概率的性质易知离散型随机变量的分布列
pk
满足下列特征性质:
k 1
① pk 0(k 1,2,) [非负性]
②
pk 1 [规范性]用于确定待定参数
k 1
③ F( x) P( X x) P(X xi ). xi x
1. 2
.
【例2】设随机变量X的分布函数为
aex b, x 0
F(x)
0,
x0
解: 因为 F(x) 在 x=0 点右连续
求: 常数 a 和 b。
所以 lim F ( x) lim (ae x b) a b 0
x0
x0
又因为 F () lim (ae x b) b 1 x
1、两点分布 或(0 - 1)分布
two-point distribution
定义1 设离散型随机变量X的分布列为
X0 1 pk 1 p p
其中 0<p<1
则称 X 服从(0 - 1)分布,记作 X ~(0 - 1)分布
F(x)
(0 - 1)分布的分布函数
0 , x0 F ( x) 1 p, 0 x 1
X = “三次试验中 A 发生的次数”,
{ X 2} A1A2 A3 A1A2 A3 A1A2 A3 P{X 2} P(A1A2 A3 A1A2 A3 A1A2 A3 )
P(A1A2 A3 ) P(A1A2 A3 ) P(A1A2A3 ) P(A1)P(A2)P(A3) P(A1)P(A2)P(A3) P(A1)P(A2 )P(A3 ) C32 p2(1 p)32
概率论与数理统计第2章课件例题
oa
连续型随机变量的一个重要特点:
连续型r.v取任一指定实数值a 的概率均为0. 即
PX a 0 .
这是因为
0 PX a Pa x X a F a F a x
当 x 0 时, 得到 P X a 0 .
由此得,1) 对连续型 r.v X,有
P(a X b) P(a X b) P(a X b)
f ( x )x 在连续型 r .v 理论中所起的作用与 P ( X xk ) pk 在离散型 r .v 理论中所起的作用 相类似.
注意 连续型随机变量密度函数的性质与离散型随机变 量分布律的性质非常相似,但是,密度函数不是
概率! 我 们 不 能 认 为 : PX a f a !
即密度函数 f (x)在某点处a的高度,并不反映X取值 的概率. 但是,这个高度越大,则X取a附近的值的概 率 f (a)就x 越大. 也可以说,在某点密度曲线的高 度反映了概率集中在该点附近的程度.
1
f
(
x)
c x2
,
0,
x 1000 其他
c = 1000
(2) P( X 1700 1500 X 2000)
P ( X 1700 , 1500 X 2000) P (1500 X 2000)
P (1500 X 1700) P (1500 X 2000)
1700 1000 1500 x2 d x
F '( x) lim F ( x x) F ( x) lim Px X x x f ( x)
x0
x
x0
x
故 X的密度 f(x) 在 x 这一点的值,恰好是X 落在
区间 ( x, x x ]上的概率与区间长度 x之比的极限.
概率论与数理统计第3章随机变量的数字特征2-5节精品文档
1
D(X ) 21002
1
7002 21002
1 (1)2 3
8. 9
即P(5200X9400)8. 9
2019/10/16
n
n
D( CiXi) Ci2D(Xi).
i1
i1
(4) 对于任意实数C∈R,有 (书P93. 8题)
E ( X-C )2≥D( X )
当且仅当C = E(X)时, E ( X-C )2取得最小值D(X).
2019/10/16
19
求证
E ( X-C )2≥D( X )
证: E(XC)2 E {X [E]X [E X C )]2}
证: D(C)E{C [E(X)2 ]}E{C [ C]2} 0.
(2 )若 D (X )存则 在 D (C) , X C 2D (X )C ,为; 常
证: D(CX) E{C [ X E(C)X2]}
E{C [ X C(E X)2]} E{C2[XE(X)2 ]}
C2E{X [E(X)2]}C2D(X).
复习: 数学期望
它反映随机变量取值的平均水平,是随机变量的 一个重要的数字特征.
EX xk pk, k1
X离散型
E X xf(x )d x,
X 连 续 型
EYE[g(X)]
g(xk)pk,
k1
X离散型
g(x)f(x)dx, X连续型
2019/10/16
0
E(X 2)
函数有下列结论:
(1 ) (1 ) ();
(2Γ()n1 )n!;
tx
1
2
t2etdt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二、三章小测
1.若函数!1)(k c k f =,
,2,1=k ,是某一离散型随机变量X 的分布律,则c 应取何值?
2.设一汽车在开往目的地的道路上需经过四
盏信号灯,每盏信号灯以21
的概率允许或禁止汽车通过.以X 表示汽车首次停下来时,它已通过的信号灯的盏数(设各信号灯的工作是相互独立的),求X 的分布律.
3.一份考卷中有10道选择题,每题有4个可能答案,其中只有一个答案是正确的
(1)某学生随机猜测,问他至少能答对2题的概率及答对题数的分布律.
(2)若一人答对6题,则推测他是猜对的还是有答题能力的
4.某一交通道口每天有大量汽车通过,设每辆汽车在每天某段时间内发生事故的概率是0.0001,今在该段路口的某个时间段内有若干辆汽车通过,求(1)若有1500辆汽车通过,不发生事故及发生事故次数小于2的概率;(2)若有20000辆汽车通过,则至少发生一次事故的概率.
5.设每颗子弹打中飞机的概率为0.01,问在500发子弹中打中飞机的最大可能次数是多少?并求其相应的概率.
6.保险事业是最早使用概率论的部门之一.保险公司为了估计企业的利润,需要计算各种各样的概率,下面是典型的问题之一.
设在保险公司里有2500名同一年龄和同社会阶层的人参加了人寿保险.在一年里每个
人死亡的概率为0.002,每个参加保险的人在每年一月一日付12元保险费,而在死亡时其家属可到保险公司领取2000元赔偿金.求:(1)一年内保险公司亏本的概率是多少?(2)一年内保险公司获利不少于10000元的概率是多少?
7.一本300页的书,每页出现错别字的概率等可能地为0.001,求在给定的一页上至少有两个错别字的概率.
8.设随机变量X 的分布律为
求随机变量X 的分布函数并求}21{≤X P ,
}2523{≤<X P ,}32{≤≤X P .
9.随机变量X的分布律如下表
求
)
(
),
1
1
(
),
(2
X
E
X
E
X
E
.D(X)
10.某人的一串钥匙上有n 把钥匙,其中只有一把能打开自己的家门,他随意地试用这串钥匙中的某一把去开门. 若每把钥匙试开一次后除去,求打开门时试开次数的数学期望.
请分别写出0-1分布、二项分布、泊松分布的分布律、期望与方差。
