《平行线分线段成比例》课件1(人教A版选修4-1)
合集下载
高中数学《平行线分线段成比例》课件1 新人教A选修41

本文详细阐述了平行线分线段成比例定理,这是高中数学中的重要内容。首先通过复习提问引出新知识,观察图形并推导出结论,进而引入平行线分线段成比例定理。该定理指出,三条平行线截两条直线所得的对应线段成比例。在理解定理的基础上,通过例题解析进一步加深对定理的应用。例如,在已知平行线和部ቤተ መጻሕፍቲ ባይዱ线段长度的情况下,利用定理求解未知线段的长度。此外,还通过巩固练习来加强学生对定理的掌握和运用。本文不仅证明了平行线分线段成比例是高中数学的重要内容,还提供了详细的教学和解题过程,有助于学生全面理解和掌握该知识点。
高中数学1.2平行线分线段成比例定理课件新人教A版选修4-1

=
������������ . ������������
= =
������������ ������������ ,即 ������������ ������������ ������������ ,即 ������������
KO =KE· KF.
探究一
探究二
探究三
探究四
特别提醒利用平行线来转移比例是常用的证题技巧,当题
������������ ������������
=
������������ ������������ , ������������ ������������
=
������������ 等. ������������
(3)当截得的对应线段成比例,且比值为 1 时,则截得的线段相等,因此平 行线分线段成比例定理是平行线等分线段定理的扩充,而平行线等分线段 定理是平行线分线段成比例定理的特例;平行线等分线段定理是证明线段 相等的依据,而平行线分线段成比例定理是证明线段成比例的途径.
a∥b∥c,直线 m 分别与 a,b,c 相交于点 A, B,C,直线 n 分别与 a,b,c 相交于 点 D,E, F,则
AB BC
=
DE EF
总结(1)定理的条件与平行线等分线段定理的条件相同,它需要
a,b,c 互相平行,构成一组平行线,m 与 n 可以平行,也可以相交,但它们必须与 已知的平行线 a, b,c 相交,即被平行线 a, b,c 所截.平行线的条数还可以更多. (2)定理的结论还有
探究一
探究二
探究三
探究四
思路分析:KO,KE,KF 在一条直线上,要证明 KO2=KE· KF,即要证
������������ ������������
人教A版高中数学选修4-1课件:1.2.平行线分线段成比例定理
A D
L1
E A
D
L2 L1
E
L2 C L3 B
B
C L3
A B C
l
l D E F
l1 l2
l3
除此之外,还有其它对应线段成比例吗?
反比
合比
合比
反比
?Hale Waihona Puke 合比三、定理的运用
例1(一、基础题) 1、已知:L1∥L2∥L3则:
A B
D
E
L1 L2
AB BC AB DE
DE () ()EF BC () EF ()
已知:如图,DE//BC分别交AB、AC于点D、 E.求证:
A
(图形语言)
法2:为了证明,需用平行 线分线段成比例定理.故作 CG//AB,且与DE的延长线交 于点G.
D B
E C
G
证明:过点C作CG//AB,且与DE的延长线交于点G. ∵DE//BC,∴AD:AB=AE:AC ∵CG//AB,∴DE:DG=AE:AC ∵四边形DEFB为平行四边形,∴DG=BC.
l1 a1
A B
D E
L1
A (D) B E
L1 L2 2 L3
L2
F 1 L3
C
C
F
D
A
L1 L2
D B (E)
A
L1 L2 4 L3
B
C
E
F
L3
3
C
F
平行线分线段成比例定理
三条平行线截两条直线,所得的对应线段成比例.
若将下图中的直线L2看成是平行于△ABC的边 BC的直线,那么可得: 推论:平行于三角形一边的直线截其他两边( 或两边的延长线)所得的对应线段成比例.
数学人教A版选修4-1课件:1.2 平行线分线段成比例定理

)
解析:∵a∥b∥c,
∴
������1 ������1 ������������ 2 = = . ������1 ������1 ������������ 3
答案:B
-5-
二 平行线分线段 成比例定理
1 2
M 目标导航
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
������ ������
������ ������
-9-
二 平行线分线段 成比例定理
M 目标导航
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
(4)比例的性质: ①基本性质:a∶b=c∶d⇔ad=bc.
������ ②合比性质:如果 ������ ������ ③等比性质:如果 ������ ������+������+…+������ ������ = . ������+������+…+������ ������
= 17.5.
-8-
二 平行线分线段 成比例定理
M 目标导航
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
比例的有关概念及性质 剖析:(1)线段的比:用同一个长度单位去量两条线段,所得的长度 比叫做这两条线段的比. (2)比例线段:在四条线段中,如果其中两条线段的比等于另外两 条线段的比,那么这四条线段叫做成比例线段,简称比例线段.
平行线分线段成比例定理-课件(人教A选修4-1)

[证明] 作 EH∥AB 交 AC 于点 H, 则AAHC=BBEC,∴BACC=ABHE. 同理:AAHF=DDFE,∴DAFF=ADHE. ∵△BDC 为直角三角形, 且 E 为 BC 边中点, ∴BE=CE=DE. ∴ABHE=ADHE.∴ABCC=DAFF.
证明比例式成立,往往会将比例式中各线段放到 一组平行线中进行研究.有时图形中没有平行线,要 添加辅助线,构造相关图形,创造可以形成比例式的 条件,达到证明的目的.
5.如图,梯形 ABCD 中,AD∥BC, 点 E,F 分别在 AB,CD 上,且 EF∥ BC,若AEEB=23,AD=8 cm,BC= 18 cm,求 EF 长.
解:作 AG∥DC 分别交 BC,EF 于 G,H, ∴AD=HF=GC=8 cm. BG=18-8=10(cm). ∵EABE=23,∴AAEB=25. ∴EBHG=AAEB=25. ∴EH=25×BG=25×10=4(cm). ∴EF=EH+HF=4+8=12(cm).
证明:在正方形 ABCD 中,AB∥CD, ∴AFBC=EAFE. ∵FG∥AD,∴FAGD=EAFE. ∴AFBC=FAGD. ∵AB=AD. ∴FC=FG.
4.如图,在▱ABCD 中,E 是 AB 延长线上一点,DE 交 AC 于 G,交 BC 于 F. 求证:(1)DG2=GE·GF; (2)CCBF=AAEB.
2.平行线分线段成比例定理的推论 (1)文字语言:平行于三角形一边的直线截其他两边 (或两边的延长线)所得的 对应线段 成比例. (2)图形语言:如图l1∥l2∥l3,
则有:AADB=
AACE,ADDB=
EACE,DABB=
CE AC .
3.平行线分线段成比例定理的作用 平行线分线段成比例定理及推论是研究相似三角形 的理论基础,它可以判定线段成比例.另外,当不能直 接证明要证的比例成立时,常用该定理借助“中间比”转 化成另两条线段的比,来得出正确结论.合理添加平行 线,运用定理及推论列比例式,再经过线段间的转换可 以求线段的比值或证明线段间倍数关系.
高二数学人教A版选修4-1课件:1.2 平行线分线段成比例定理

(3)比例的有关概念:已知四条线段
a,b,c,d,如果ba
=
c或
d
a∶ b=c∶ d,
那么线段 a,d 叫做比例外项,线段 b,c 叫做比例内项,线段 d 叫做线段
a,b,c
的第四比例项.若ba
=
b或
c
b2=ac,那么线段
b
叫做线段
a,c
的比例
中项.
(4)比例的性质:①基本性质:a∶ b=c∶ d⇔ad=bc. ②合比性质:如果ba = dc,那么a+b b = c+dd. ③等比性质:如果ba = dc=…=mn (b+d+…+n≠0),那么ab++cd++… …++mn = ba.
题型四 计算线段长度的比值 【例题 4】如图,M 是▱ ABCD 的边 AB 的中点,直线 l 过 M 分别交 AD,AC 于 E,F,交 CB 的延长线于 N,若 AE=2,AD=6.求 AF∶ AC 的值.
分析:AD∥BC,AM=MB⇒ AE=BN⇒ AF∶ AC 的值
解:∵AD∥BC,∴AFCF = NAEC,
BC=
.
解析:如图,取 AB,CD 的中点 G,H,连接 GH,
则 GH 为梯形 ABCD 的中位线,EF 为梯形 AGHD 的中位线, 故 GH=2EF-AD=2×4-3=5,BC=2GH-AD=2×5-3=7. 答案:7
2.如图,DE∥BC,EF∥DC,求证:AD2=AF·AB. 分析:要证 AD2=AF·AB,只要证AADF = AADB,由于 AF,AD,AB 在同一直线 上,需借助中间量AAEC进行转化. 证明:∵DE∥BC,∴AADB = AAEC.
人教A版高中数学选修4-1课件:1.2.平行线分线段成比例定理

由这组平行线截得的线段.
故作EF//AB.
已知:如图,DE//BC分别交AB、AC于点D、 E.求证:
A
(图形语言)
D 法2:为了证明,需用平行 线分线段成比例定理.故作 B CG//AB,且与DE的延长线交 于点G.
E
G
C
证明:过点C作CG//AB,且与DE的延长线交于点G. ∵DE//BC,∴AD:AB=AE:AC ∵CG//AB,∴DE:DG=AE:AC ∵四边形DEFB为平行四边形,∴DG=BC.
3、如图:△ABC中,DE∥BC, DF∥AC,AE=4,EC=2,BC=8, 求线段BF,CF之长.
F
D
E
B
C
A
D
E
BF
C
例2:三角形内角平分线分对边成两线段,这
两线段和相邻的两边成比例.
已知:AD是△ABC中∠A的平
分线,
A
4 E 求证:
F 12
3
证明:作CE//DA交BA的延长线于E.
B
D
C
高中数学课件
(金戈铁骑 整理制作)
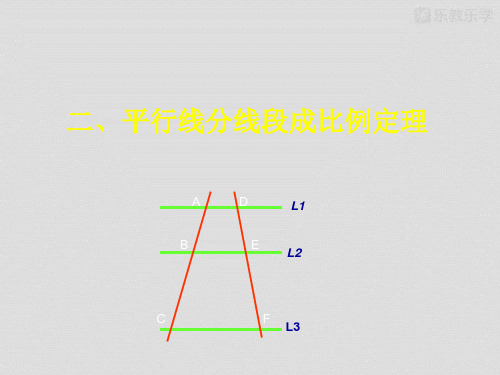
二、平行线分线段成比例定理
A
D
L1
B
E L2
C
F L3
一、复习导入
如图:,
且AP=PB=BQ=QR=RC. (1)你能推出怎样的结论? 为什么?
由平行线等分线段定理可知. (注意其前提条件是:等距)
A P B Q R C
D
L1
S
L2
E L3
T L4
G L5
F L6
A
L1
B (E) L2
C
F
4
L3
平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段成比例.
高二数学之数学人教A版选修4-1课件:1.2 平行线分线段成比例定理

12
名师点拨1.定理的条件与平行线等分线段定理的条件相同,它需 要a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它 们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.平行线的条 数还可以更多.
2.定理的结论还有
������������ ������������
=
������������ ������������
HISHI SHHHIUSIHLSIHI SI HSHUULILI HONGNAN JVJHHIAOOONNGGNNAANNJJVVJJIIAAONOLI TOUXI IIAANNLLUIITTITOOAUUNXXGIIYANLIAN
比例的有关概念及性质
剖析:(1)线段的比:用同一个长度单位去量两条线段,所得的长度
题型一 题型二 题型三 题型四
题型一
证明线段成比例
【例1】 如图,AD为△ABC的中线,在AB上取点E,AC上取点F,使
AE=AF.
求证:
������������ ������������
=
������������������������.
分析:这道题目要证的比例中的线段都没有直接的联系,可以考 虑把比例转移,过点C作CM∥EF,交AB于点M,交AD于点N,且BC的 中点为D,可以考虑补出一个平行四边形来证明.
12
2.推论
文字 平行于三角形一边的直线截其他两边(或两边的延长线)所 语言 得的对应线段成比例
符号 直线 DE 分别与△ABC 的两边 AB,AC 所在直线交于点பைடு நூலகம்D,E,
语言
且
DE∥BC,则
AD DB
=
AE EC
图形 语言
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线分线段成比例定理
一、复习提问
1、说出平行线等分线段定理 2、观察图(1)已知L1∥L2 ∥ L3 ∥ L4 , AB=BC=CD A (1)你能推出怎样的结论? B ∵ L1∥L2 ∥ L3 ∥ L4 C
AB=BC=CD
∴EF=FG=GH
E F G H
L1 L2 L3 L4
D (1)
(2).计算下面各比的值,并填空
D、
AC CE BD DF
1、解: L1∥L2∥L3 ∵
∴ 即
AB DE BC EF
(平行线分线段成比例定理) ∴ DE=
2、证明:
∴
AB DE BC EF
a DE b c
ac b
∵ L1∥L2∥L3 (平行线分线段成比例定理)
AB BC AB DE EF DE
AB BC ∴ ∴ DE EF AB BC AC ∴ DE EF DF
返回
四、小结:
1、本节课介绍了平行线分线段成比例定理 及应用;
2、在运用平行线分线段成比例定理时要 注意弄清三条平行线截两条直线,所得 哪条线段与哪条线段是对应线段,同时 要根据需要写出正确的比例式。
五、布置作业
课外作业: 如图7,已知L1∥L2 ∥ L3 ∥ L4,求X,Y的值
L1
3 5 3.5 y 4 L3 L4 x L2
BD FH 左下 右下 ( ) AB EF 左上 右上
H L4 (2)
练一练:如图(3) L1∥L2 ∥ L3 ,试根据图形写出 b a 成比例线段。 D A
AB DE BC EF BC EF AB DE AB DE AC DF
L1
L2
E B
AC DF AB DE
BC EF AC DF
H (2)
由此可得到:
1、平行线分线段成比例定理:三条平行线截两条直线所
得的对应线段成比例。
说明: ①定理的条件是“三条平行线截两条直线” ②是“对应线段成比例”,注意“对应”两字。
a b A E L1 F L2 B
强化“对应“两字理解和记忆如图(2) D
AB EF 左上 右上 ( ) BD FH 左下 右下
E B
AB m , DE AB AB 由 BC n DF AC AB BC AB m 由比例性质发现
AB BC mn
(图5) (平行线分 线段成比 例定理)
证明:
∵ L1∥L2∥L3
EF n , ∴ DE m
∴
DE AB m EF BC n
EF DE n m DE m
AC DF BC EF
F
C (3)
L3
注:“对应线段”是指一条直线 被两条平行线截得的线段与另 一条直线被这两条平行线截得 的线段成对应线段。而“对应线 段成比例”是指同一条直线上的 两条线段的比等于与他们 对应 的另一条直线上的两条线段的比
例题解析:
例1、 已知:如图L1∥L2∥L3,AB=3,DE=2, EF=4,求BC A 分析:图形已具备什么定理的基本 图形? 平行线分线段成比例定理 那么如何求线段BC的长呢? (建立比例) C 解: ∵ L1∥L2∥L3 ∴
AB BC
1 , = __
2 _, =__ =___,
1/2
EF FG EG GH
EF 1 可得 __=__ FG =___
AB BC
AC CD
2 可得 __=__ =___
AC CD
EG GH
BC BD
FG FH
1/2 =___
BC 可得 BD
__=__
FG FH
二、新知识:平行线分线段成比例定理
即
DF m n DE m
∴
DE m DF m n
(三)巩固练习:
1、课本P21 3 ,练习1、2
2、如图(6)AB∥CD∥EF,则在图中下列关系式 一定成立的是( D ) A AC DF A、 B、 AC DF C
CE BD
BD CE
B D
E
F
(6)
中的直线L3擦掉得到图(2),仍
使L1∥L2 ∥ L4 不变,你能否发现在两直线a,b上截得 b 的线段有什么关系? a E A 通过计算可以得到:
AB EF BD FH
AB EF AD EH
BD FH AD EH
B
D
F
L1 L2 L4
AD EH 等等 BD FH
AB DE BC EF
D E F
L1
B
L2
L3
(平行线分线段成比例定理)
3 2 即 BC 4
∴2BC=3×4 BC=6
AB m 例2:已知:如图(5),L1∥L2∥L3, BC n
求证:
DE m DF m n
D
A
F
L1 L2 C L3
分析:图形是平行线分线段成比例定理
的一个变式图形,由已知条件可以出现
一、复习提问
1、说出平行线等分线段定理 2、观察图(1)已知L1∥L2 ∥ L3 ∥ L4 , AB=BC=CD A (1)你能推出怎样的结论? B ∵ L1∥L2 ∥ L3 ∥ L4 C
AB=BC=CD
∴EF=FG=GH
E F G H
L1 L2 L3 L4
D (1)
(2).计算下面各比的值,并填空
D、
AC CE BD DF
1、解: L1∥L2∥L3 ∵
∴ 即
AB DE BC EF
(平行线分线段成比例定理) ∴ DE=
2、证明:
∴
AB DE BC EF
a DE b c
ac b
∵ L1∥L2∥L3 (平行线分线段成比例定理)
AB BC AB DE EF DE
AB BC ∴ ∴ DE EF AB BC AC ∴ DE EF DF
返回
四、小结:
1、本节课介绍了平行线分线段成比例定理 及应用;
2、在运用平行线分线段成比例定理时要 注意弄清三条平行线截两条直线,所得 哪条线段与哪条线段是对应线段,同时 要根据需要写出正确的比例式。
五、布置作业
课外作业: 如图7,已知L1∥L2 ∥ L3 ∥ L4,求X,Y的值
L1
3 5 3.5 y 4 L3 L4 x L2
BD FH 左下 右下 ( ) AB EF 左上 右上
H L4 (2)
练一练:如图(3) L1∥L2 ∥ L3 ,试根据图形写出 b a 成比例线段。 D A
AB DE BC EF BC EF AB DE AB DE AC DF
L1
L2
E B
AC DF AB DE
BC EF AC DF
H (2)
由此可得到:
1、平行线分线段成比例定理:三条平行线截两条直线所
得的对应线段成比例。
说明: ①定理的条件是“三条平行线截两条直线” ②是“对应线段成比例”,注意“对应”两字。
a b A E L1 F L2 B
强化“对应“两字理解和记忆如图(2) D
AB EF 左上 右上 ( ) BD FH 左下 右下
E B
AB m , DE AB AB 由 BC n DF AC AB BC AB m 由比例性质发现
AB BC mn
(图5) (平行线分 线段成比 例定理)
证明:
∵ L1∥L2∥L3
EF n , ∴ DE m
∴
DE AB m EF BC n
EF DE n m DE m
AC DF BC EF
F
C (3)
L3
注:“对应线段”是指一条直线 被两条平行线截得的线段与另 一条直线被这两条平行线截得 的线段成对应线段。而“对应线 段成比例”是指同一条直线上的 两条线段的比等于与他们 对应 的另一条直线上的两条线段的比
例题解析:
例1、 已知:如图L1∥L2∥L3,AB=3,DE=2, EF=4,求BC A 分析:图形已具备什么定理的基本 图形? 平行线分线段成比例定理 那么如何求线段BC的长呢? (建立比例) C 解: ∵ L1∥L2∥L3 ∴
AB BC
1 , = __
2 _, =__ =___,
1/2
EF FG EG GH
EF 1 可得 __=__ FG =___
AB BC
AC CD
2 可得 __=__ =___
AC CD
EG GH
BC BD
FG FH
1/2 =___
BC 可得 BD
__=__
FG FH
二、新知识:平行线分线段成比例定理
即
DF m n DE m
∴
DE m DF m n
(三)巩固练习:
1、课本P21 3 ,练习1、2
2、如图(6)AB∥CD∥EF,则在图中下列关系式 一定成立的是( D ) A AC DF A、 B、 AC DF C
CE BD
BD CE
B D
E
F
(6)
中的直线L3擦掉得到图(2),仍
使L1∥L2 ∥ L4 不变,你能否发现在两直线a,b上截得 b 的线段有什么关系? a E A 通过计算可以得到:
AB EF BD FH
AB EF AD EH
BD FH AD EH
B
D
F
L1 L2 L4
AD EH 等等 BD FH
AB DE BC EF
D E F
L1
B
L2
L3
(平行线分线段成比例定理)
3 2 即 BC 4
∴2BC=3×4 BC=6
AB m 例2:已知:如图(5),L1∥L2∥L3, BC n
求证:
DE m DF m n
D
A
F
L1 L2 C L3
分析:图形是平行线分线段成比例定理
的一个变式图形,由已知条件可以出现
