钢结构螺栓连接计算例题
钢结构设计计算题汇总
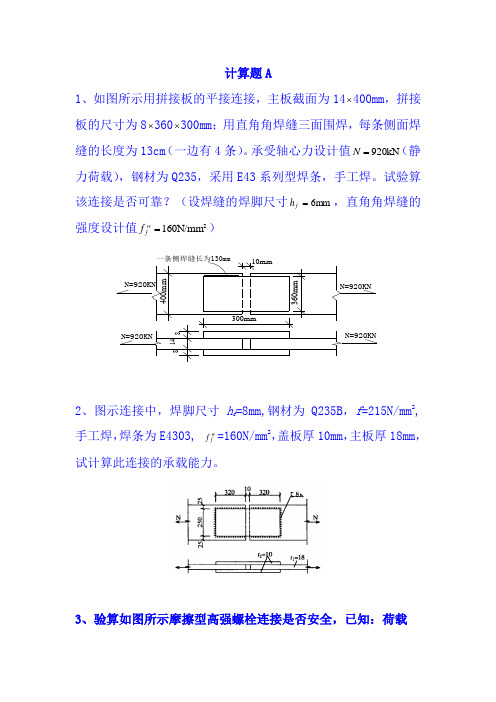
计算题A1、如图所示用拼接板的平接连接,主板截面为14⨯400mm,拼接板的尺寸为8⨯360⨯300mm;用直角角焊缝三面围焊,每条侧面焊缝的长度为13cm(一边有4条)。
承受轴心力设计值kN920=N(静力荷载),钢材为Q235,采用E43系列型焊条,手工焊。
试验算该连接是否可靠?(设焊缝的焊脚尺寸mm6=fh,直角角焊缝的2wN=920KN4mm36mm10mmN=920KNN=920KN N=920KN8814300mm一条侧焊缝长为130mm23、验算如图所示摩擦型高强螺栓连接是否安全,已知:荷载N =300kN,螺栓M20,10.9级,μ=0.5,预紧力P =155kN 。
4、如图连接,尺寸为mm ,受静载拉力kN 130=P ,mm10=fh ,钢材为Q235BF ,E43焊条,手工焊无引弧板,2N/mm 160=w f f 。
试验算焊缝强度。
5、某6m 跨度简支梁的截面和荷栽(含梁自重在内的设计值)如图所示。
在距支座2.4m 处有翼缘和腹板的拼接连接,实验算其10P10110P10A拼接的对接焊缝。
已知钢材为Q235,采用E43型焊条,手工焊,三级质量标准,施焊时采用引弧板。
解:①计算焊缝截面处的内力m kN m kN qab M ⋅=⋅-⨯⨯⨯==8.1036)]4.20.6(4.224021[21 ()[]kN kN a l q V 1444.2324021=-⨯=⎪⎭⎫⎝⎛-=② 计算焊缝截面几何特征值:()4643310289810002401032250121mm mm I W ⨯=⨯-⨯⨯=()363610616.5516102898mm mm W W ⨯=÷⨯= ()363110032.250816250mm mm S W ⨯=⨯⨯= ()363110282.325010500mm mm S S W W ⨯=⨯⨯+=③ 计算焊缝强度查附表得2/185mm N f w t = 2/125mm N f w v =2266max/185/6.18410616.5108.1036mm N f mm N W M w t W =<=⎪⎪⎭⎫⎝⎛⨯⨯==σ 22663max /125/3.161010289810282.310144mm N f mm N t I VS w v w W W =<=⨯⨯⨯⨯⨯==τ 2max 01/9.1786.18410321000mm N h h =⨯==σσ266311/1.101010289810032.210144mm N t I VS w W W =⨯⨯⨯⨯⨯==τ 折算应力:22222121/5.2031851.11.1/8.1791.1039.1783mm N f mm N w t =⨯=<=⨯+=+τσ6、设计图示双盖板对接连接。
钢结构螺栓连接计算例题PPT

解:1、分析 ①本题是验算题 ②计算单个螺栓抗剪的最大承载能力
抗剪:
Nvb
nv
d 4
2
fvb
1 222 140 53218N
4
抗压: Ncb d tfcb 228305 53680N
所以
Nb min
min
Nvb , Ncb
53.218kN
2、计算螺栓群
螺栓群如图,为扭剪
50 4X80 50
yi2
150 250 160 602 10 802 4 1602 4
36.58kN
N1
N1Tx
2
N1Fy N1Ty
2
36.582 13.72 15 2
=46.51kN<Nminb=53.2kN 满足要求
二、普通螺栓受拉性能
1、单个螺栓受拉破坏试验 螺杆受拉,连接板脱开,螺纹处拉断或连接板屈服,螺杆的拉力为:
不需要。因为,规范中关于普通螺栓的抗剪强度设计值,是由试验得到的,而在制 定规范时,没有区分作用位置。
(3) 净截面强度计算
由于螺栓孔削弱了板件的截面,为了防止板件在削弱截面的破坏需验算净截面的强度。 对于外力通过螺栓群形心的杆件,应当满足强度计算公式
N f
An
式中:N 为所受的轴力; f 为材料抗拉强度设计值; An 为杆件截面的净截面面积
1号螺栓所受力的竖向分量
+ + + + + 受++力Ⅱ + + +
n
T
1
r1 2 N1T r2 o r3 3
4
6
5
N1
T y
Tx1 xi2
yi2
钢结构焊接、螺栓连接计算及实例

第一节 钢结构的连接方法钢结构是由钢板、型钢通过必要的连接组成基本构件,如梁、柱、桁架等;再通过一定的安装连结装配成空间整体结构,如屋盖、厂房、钢闸门、钢桥等。
可见,连接的构造和计算是钢结构设计的重要组成部分。
好的连接应当符合安全可靠、节约钢材、构造简单和施工方便等原则。
钢结构的连接方法可分为焊缝连接、铆钉连接和螺栓连接三种(详见附图十三)。
一、焊缝连接焊接是现代钢结构最主要的连接方法。
其优点是不削弱构件截面(不必钻孔),构造简单,节约钢材,加工方便,在一定条件下还可以采用自动化操作,生产效率高。
此外,焊缝连接的刚度较大密封性能好。
焊缝连接的缺点是焊缝附近钢材因焊接的高温作用而形成热影响区,热影响区由高温降到常温冷却速度快,会使钢材脆性加大,同时由于热影响区的不均匀收缩,易使焊件产生焊接残余应力及残余变形,甚至可能造成裂纹,导致脆性破坏。
焊接结构低温冷脆问题也比较突出。
二、铆钉连接铆接的优点是塑性和韧性较好,传力可靠,质量易于检查和保证,可用于承受动载的重型结构。
但是,由于铆接工艺复杂、用钢量多,因此,费钢又费工。
现已很少采用。
三、螺栓连接螺栓连接分为普通螺栓连接和高强度螺栓连接两种。
普通螺栓通常用Q235钢制成,而高强度螺栓则用高强度钢材制成并经热处理。
高强度螺栓因其连接紧密,耐疲劳,承受动载可靠,成本也不太高,目前在一些重要的永久性结构的安装连接中,已成为代替铆接的优良连接方法。
螺栓连接的优点是安装方便,特别适用于工地安装连接,也便于拆卸,适用于需要装拆结构和临时性连接。
其缺点是需要在板件上开孔和拼装时对孔,增加制造工作量;螺栓孔还使构件截面削弱,且被连接的板件需要相互搭接或另加拼接板或角钢等连接件,因而比焊接连接多费钢材。
第二节 焊接方法、焊缝类型和质量级别一、钢结构中常用的焊接方法焊接方法很多,钢结构中主要采用电弧焊,薄钢板(mm t 3 )的连接有时也可以采用电阻焊或气焊。
1.电弧焊电弧焊是利用焊条或焊丝与焊件间产生的电弧热,将金属加热并熔化的焊接方法。
第八章(焊缝、螺栓连接)--钢结构习题参考解答

8.4 有一工字形钢梁,采用I50a (Q235钢),承受荷载如图8-83所示。
F=125kN ,因长度不够而用对接坡口焊缝连接。
焊条采用E43型,手工焊,焊缝质量属Ⅱ级,对接焊缝抗拉强度设计值2205/w t f N mm =,抗剪强度设计值2120/w v f N mm =。
验算此焊缝受力时是否安全。
图8-83 习题8.4解:依题意知焊缝截面特性:A=119.25cm 2,Wx =1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ,截面宽度b=158mm ,翼缘厚t=20mm ,腹板厚tw=12.0mm 。
假定忽略腹板与翼缘的圆角,计算得到翼缘与腹板交点处的面积矩S 1=20×158×(250-10)=7.584×105mm 3。
对接焊缝受力:125V F kN ==;2250M F kN m =⨯=⋅ 焊缝应力验算:最大正应力:622325010134.5/205/1858.910w t x M N mm f N mm W σ⨯===<=⨯ 最大剪应力:33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯ 折算应力:22127.2/205/w zs t N mm f N mm σ=<= 故焊缝满足要求。
8.5 图8-84所示的牛腿用角焊缝与柱连接。
钢材为Q235钢,焊条用E43型,手工焊,角焊缝强度设计值2f 160/w f N mm =。
T=350kN ,验算焊缝的受力。
图8-84 习题8.5 图8-84-1 焊缝截面计算简图解:(注:焊缝上下翼缘长度114mm 有些问题,应取2130210110l tmm -=-⨯=,黄钜枝06年6月19日)如图8-84-1,截面特性计算如下:2(11425242882)0.75667.2f A h mm =⨯+⨯+⨯⨯= 228820.73225.6w f A h mm =⨯⨯=32741288288[2882114(16)252()4]0.77.913101222f f I h mm =⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力:247.52N kN ==;247.52V kN ==; 49.5M V e kN m =⋅=⋅ 应力验算:危险点为a 、b 两点,下面分别验算: 对a 点: 32247.51043.67/5667.2N aN N mm A σ⨯===62749.510160100.09/7.91310M a af My N mm I σ⨯⨯===⨯ 2243.67100.09143.76/195.2/N Mw a a f f N mm f N mm σσβ+=+=<=对b 点:32247.51076.73/3225.6V bw V N mm A τ⨯=== 243.67/N Nb a N mm σσ==62749.51014490.16/7.91310M b bf My N mm I σ⨯⨯===⨯22133.87/160/w f N mm f N mm =<=故焊缝强度满足要求。
钢结构计算题(焊接、螺栓连接、稳定性)[详细]
![钢结构计算题(焊接、螺栓连接、稳定性)[详细]](https://img.taocdn.com/s3/m/9da78a700c22590103029d5f.png)
Q235,焊缝)解由于翼缘处的剪应力很小,假定剪力全部由腹板的竖向焊缝均匀承受,而弯矩由整个T 形焊缝截面承受.分别计算a 点与b 点的弯矩应力、腹板焊缝的剪应力及b 点的折算应力,按照各自应满足的强度条件,可以得到相应情况下焊缝能承受的力F i ,最后,取其最小的F 值即为所求.1.确定对接焊缝计算截面的几何特性 (1)确定中和轴的位置()()()()8010102401020160)10115(1010240510201601≈⨯-+⨯-+⨯⨯-+⨯⨯-=y米米160802402=-=y 米米(2)焊缝计算截面的几何特性()623231068.22)160115(230101014012151602301014023010121mm I x ⨯=-⨯⨯+⨯⨯++-⨯⨯+⨯⨯=腹板焊缝计算截面的面积:230010230=⨯=w A 米米22.确定焊缝所能承受的最大荷载设计值F . 将力F 向焊缝截面形心简化得:F Fe M 160==(KN·米米) F V =(KN)查表得:215=w c f N/米米2,185=w t f N/米米2,125=wv f N/米米2点a 的拉应力M a σ,且要求M a σ≤wt f 18552.01022688010160431===⨯⨯⨯==w t x M af F F I My σ N/米米2 解得:278≈F KN点b 的压应力Mb σ,且要求Mb σ≤wc f 215129.110226816010160432===⨯⨯⨯==wc x Mbf F F I My σ N/米米2 解得:5.190≈F KN由F V =产生的剪应力V τ,且要求V τ≤wV f125435.010231023===⨯⨯=wV V f F F τ N/米米2 解得:7.290≈F KN点b 的折算应力,且要求起步大于1.1wt f ()()()w t V M bf F F 1.1435.03129.132222=⨯+=+τσ解得:168≈F KN缝的距离不相等,肢尖焊缝的受力小于肢背焊缝的受力,又题中给出了 肢背、肢尖焊缝相同的长度和焊脚尺寸,所以,只要验算肢背焊缝的强度,若能满足,肢尖焊缝的强度就能肯定满足.查角钢角焊缝的内力分配系数表得,k 1=0.65,k 2=0.35;查焊缝强度表得 =w f f 200 N/米米2一条肢背焊缝的计算长度=1w l 300-2x8=284米米,要求8h f 和40米米≤1w l ≤60h f ,显然符合构造要求.肢背焊缝所能承担的力1N :780120065.011=⨯==N k N KN则其焊缝强度为: 24528487.02107807.02311≈⨯⨯⨯⨯=⨯⨯⨯=w f f l h N τ N/米米2>=w f f 200 N/米米2故此连接不能满足强度要求.应采取以下措施:1. 增加肢背焊缝的长度 2.34820087.02107807.02311≈⨯⨯⨯⨯=⨯⨯⨯=wff w f h N l 米米 因此,肢背焊缝的长度必须加长到364162.3481011=+=+=w l l 米米,才能使其满足强度要求.采用这种方法,就会增加节点板的尺寸.而此时肢尖焊缝的应力13228487.0235.0=⨯⨯⨯=Nf τ N/米米2<=w f f 200 N/米米2,满足强度要求,且可以适当减小其焊缝长度.2. 增加肢背焊缝的焊脚尺寸根据构造要求,肢背焊缝最大的焊脚尺寸12102.12.1max =⨯==t h f 米米. 而实际所需的焊脚尺寸为f h ≥8.92002847.02107807.02311=⨯⨯⨯⨯=⨯⨯⨯wfw f l N 米米 因此,将肢背焊缝的焊脚尺寸增加到10米米就能使此连接满足强度要求.3. 改用三面围焊首先计算正面角焊缝所能承担的力3N :w f w f f l h N ⨯⨯⨯⨯⨯=22.17.02336.3821020022.114087.023≈⨯⨯⨯⨯⨯⨯=-KN求肢背焊缝所能承担的力1N : 7.5886.3825.0120065.021311=⨯-⨯=-=N N k N KN 则 18528487.02107.5887.02311≈⨯⨯⨯⨯=⨯⨯⨯=w f f l h N τ N/米米2<=w f f 200 N/米米2满足强度要求.3. 如图所示为板与柱翼缘用直角角焊缝连接,钢材为Q235,焊条E43型,手工焊,焊脚尺寸h f =10米米,f f w=160N/米米2,受静力荷载作用,试求:(米、N 、V 作用下的直角角焊缝)1.只承受F 作用时,最大的轴向力F=?2.只承受P 作用时,最大的斜向力P=?3.若受F 和P 的共同作用,已知F=250KN,P=150KN,此焊缝是否安全?解:分析:根据已知条件,可将斜向力P 向焊缝形心简化得米、N 、V,将F 向焊缝形心简化只得N.米、N 使焊缝有效截面产生应力σ米f、σN f ,而剪力V 则产生应力τvf ,最后可按角焊缝的基本计算公式计算此连接能承受的最大力F 或P,并可进行焊缝强度验算.一条焊缝的计算长度l w =300-20=280米米,1.在力F 作用下,焊缝属于正面角焊缝,F 米ax =0.7h f ·∑l w ·β·f f w=0.7×10×2×280×1.22×160×10-3=765.8KN2.将斜向力P 向焊缝形心简化得:米 =0.8P·e=80P(KN·米米) V =0.8P(KN)N =0.6P(KN) 图2计算在各力作用下产生的应力:σ米f =6米/(2×0.7×h f ×l w 2) 图3.Ⅱ.6 =6×80×P×103/(2×0.7×10×2802) =0.437P(N/米米2) σNf =N/(2×0.7h f l w )=0.6P×103/(2×0.7×10×280) =0.153P(N/米米2) τvf =V/(2×0.7h f l w )=0.8P×103/(2×0.7×10×280) =0.204P(N/米米2)将σ米f、σN f 、τvf 的值代入公式:()w f VfNf M ff ≤+⎪⎪⎭⎫⎝⎛+2222.1τσσ得 P 米ax =304.6KN3.将力F 、P 向焊缝形心简化得:V =0.8P=0.8×150=120 KN N =F +0.6P=250+0.6×150=340 KN米 =0.8P·e=0.8×150×100=12×103KN·米米 σ米f =6×12×103×103/(2×0.7×10×2802)=65.6N/米米2σNf =340×103/(2×0.7×10×280)=86.7N/米米2τvf =120×103/(2×0.7×10×280)=30.6N/米米2产生的应力同向,故可按a 点或b 点应满足角焊缝强度设计值来确定连接所能承受的最大静力荷载设计值F .最后验算牛腿板截面Ⅰ-Ⅰ处的强度,即可确定两者是否等强?1. 确定角焊缝连接所能承受的最大承载力(1)计算角焊缝有效截面的形心位置和焊缝截面的惯性矩.由于焊缝是连续围焊,实际长度比板边长度长,所以焊缝的计算长度可取板边长度,每端不减5米米.焊缝的形心位置:()71.5302028.07.010208.07.02≈+⨯⨯⨯⨯⨯⨯⨯=x 厘米围焊缝的惯性矩:630015202301218.07.022=⎪⎭⎫⎝⎛⨯⨯+⨯⨯⨯=x I 厘米4()170771.51020220121271.5308.07.0232≈⎥⎦⎤⎢⎣⎡-⨯⨯+⨯⨯+⨯⨯⨯=y I 厘米48007170763000=+=+=y x I I I 厘米4(2)将力F 向焊缝形心简化得:()F F T 9.3421.57200200=-+= (KN·米米)F V =(KN)(3)计算角焊缝有效截面上a 点各应力的分量: F F I Tr y T fa64.0108007150109.342430≈⨯⨯⨯==τ(N/米米2) ()F F I Tr x T fa62.01080071.57200109.342430≈⨯-⨯⨯==σ(N/米米2) ()F F A V f V fa26.087.03002002103≈⨯⨯+⨯⨯==σ(N/米米2) (4)求最大承载力F 米ax根据角焊缝基本计算公式,a 点的合应力应小于或等于w f f ,即:()2264.022.126.062.0F F F +⎪⎭⎫ ⎝⎛+≤w f f = 160 N/米米2解得 F ≤165.9KN 故 F 米ax =165.9KN2.验算牛腿板的强度钢板Ⅰ-Ⅰ截面受力最大,承受弯矩米 =200F (KN·米米)和剪力V = F (KN)的作用. 由 26thMW M ==σ≤f 得 2153001210200623==⨯⨯⨯f F N/米米2解得 F = 193.5KN 由 thv5.1=τ≤v f 得 12530012105.123==⨯⨯⨯v f F N/米米2解得 F = 300KN故此钢板能承受的最大荷载设计值F =193.5KN,而焊缝则能承受F =165.9KN,显然钢材强度有富余,为了 经济的目的可减少钢板的厚度t,也可加大焊缝的焊脚尺寸h f .其计算方法如下:(1)减少钢板的厚度t由26thM =σ≤f 得 3.10300215109.165200623≈⨯⨯⨯⨯=t 米米 取t=11米米.(2)加大焊缝的焊脚尺寸h f (单位为米米)f x h I 5.787=(厘米4) f y h I 3.213=(厘米4)f y x h I I I 8.10000=+=(厘米4)f f T fah h 5.994108.1000150105.1939.34243≈⨯⨯⨯⨯=τN/米米2()f f Tfah h 4.947108.10001.57200105.1939.34243≈⨯-⨯⨯⨯=σN/米米2()ff V fah h 9.3947.03002002105.1933≈⨯+⨯⨯=σN/米米21605.99422.1/9.3944.94722==⎪⎪⎭⎫⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+w f f f f f h h h N/米米2 解得 f h =9.3米米由构造要求知 102122max =-=-=t h f 米米 故取f h =10米米螺栓连接1.两钢板截面为-18×410,钢材Q235,承受轴心力N =1250KN(设计值),采用米20普通粗制螺栓拚接,孔径d 0 =21.5米米,试设计此连接.解:分析:设计此连接应按等强度考虑,即设计的连接除能承受N 力外,还应使被连接钢板、拚接盖板、螺栓的承载力均接近,这样才能做到经济省料.因此,连接盖板的截面面积可取与被连接钢板的截面面积相同.这样,当螺栓采用并列布置时,只要计算被连接钢板的强度满足即可,不必再验算连接盖板.具体设计步骤可根据已知的轴心力设计值先确定需要的螺栓数目,并按构造要求进行排列,然后验算构件的净截面强度.1.确定连接盖板截面采用双盖板拚接,截面尺寸选10×410,与被连接钢板截面面积接近且稍大,钢材亦为Q235.2.计算需要的螺栓数目和布置螺栓 一个螺栓抗剪承载力设计值为:9.871014042024322=⨯⨯⨯⨯=⋅⋅=-ππb VV b Vf d n N KN一个螺栓抗剪承载力设计值为:8.1091030518203=⨯⨯⨯=⋅⋅=-∑b c b c f t d N KN连接所需要的螺栓数目为n ≥22.149.87/1250/==miin N N取 n =16个.采用并列布置,如图3.Ⅱ.11所示.连接盖板尺寸为-10×410×710.中距、端距、边距均图3.Ⅱ.113.验算被连接钢板的净截面强度被连接钢板Ⅰ-Ⅰ截面受力最大,连接盖板则是Ⅱ-Ⅱ截面受力最大,但后者截面面积稍大,故只验算被连接钢板即可.32.588.115.248.14101=⨯⨯-⨯=-=t d n A A n 厘米23.2141032.5810125023≈⨯⨯==n A N σ N/米米2<215=f N/米米2 符合要求.2.上题若采用8.8级米20摩擦型高强度螺栓,钢材Q235,接触面采用喷砂处理,试问此接头能承受的最大轴心力?解:分析:确定接头所能承受的最大轴心力设计值,应分别按摩擦型高强度螺栓、构件和连接盖板计算,然而取其最小值计算即为所求.摩擦型高强度螺栓所能承受的轴心力设计值应由单个摩擦型高强度螺栓的抗剪承载力设计值乘以连接一侧的螺栓数目确定.他们所能承受的最大轴心力设计值计算方法与普通螺栓不同,主要是考虑孔前传力因素.另外,还需根据构件的毛截面计算承载力,因高强度螺栓连接的毛截面承受全部轴心力N ,故有可能比净截面更不利.1.确定摩擦型高强度螺栓所能承受的最大轴心力设计 单个摩擦型高强度螺栓的抗剪承载力设计值:25.101125245.09.09.0=⨯⨯⨯==P n N f bV μ KN故 162025.10116=⨯==bV nN N KN2.构件所能承受的最大轴心力 毛截面:7.158610215184103=⨯⨯⨯=⋅=-f A N KNⅠ-Ⅰ截面:5832185.21418410=⨯⨯-⨯=n A 米米N N N n n N 875.01645.015.011=⎪⎭⎫ ⎝⎛⨯-=⎪⎭⎫ ⎝⎛⨯-='由nA N '≤f 得 1433875.1021558323=⨯⨯=-N KN由此可见,接头所能承受的最大轴心力设计值为1433max =N KN3栓(C作用.在剪力V 作用下,由每个螺栓平均承担,在扭矩T 作用下,四个角螺栓(1、2、3、4)所受的剪力Ti N 最大,且沿垂直于旋转半径r 的方向受剪,为了 简化计算,可将其分解为x 轴和y 轴方向的俩各分量Tix N 和Tiy N ,1、2号螺栓的竖向分力与V 产生的剪力同向,故1、2号螺栓为最危险螺栓,验算1号或2号螺栓的强度即可.将偏心力F 向螺栓群形心简化得:4103100300300⨯=⨯==F T KN ·米米100==F V KN查表得 140=b V f N/米米2,305=bc f N/米米2一个螺栓的抗剪承载力设计值为: b V V b Vf d n N ⋅⋅⋅=42π96.4310140420132=⨯⨯⨯⨯=-πKN一个螺栓的承压承载力设计值为: b c bc ft d N ⋅⋅=∑2.731030512203=⨯⨯⨯=- KN在T 和V 作用下,1号螺栓所受剪力最大,54.54100450610030000222211≈⨯+⨯⨯=+⋅=∑∑i i T x y x y T N KN 27.2710045065038000222211≈⨯+⨯⨯=+⋅=∑∑ii T y y x x T N KN 67.166/100/1≈==n V N Vy KN()()()04.7067.1627.2754.5422211211≈++=++=V yT y T xN NN N KN >96.43min =b N KN故此连接强度不能满足要求.加大牛腿板的尺寸.若螺栓数目增加为96.4342=⋅⋅=b V V bVf d n N πKN2.73=⋅⋅=∑b c b c f t d N KN因为 1601=y 米米>15031=x ∑⋅≈≈2111i Tx Ty y T N N5.37)8041604(1603000022=⨯+⨯⨯= KN10101001===n V N V y KN()()81.38105.372221211≈+=+=V yT xN N N KN <96.43min =bN KN连接强度满足要求.4.图3.Ⅱ.12所示的普通螺栓(C 级)连接,钢材Q235,米20,孔径d 0 =21.5米米,外力F =160KN(设计值),试验算此连接的强度.解:分析:根据已知条件,将外力F 向螺栓群形心简化得轴向力N 、剪力V 和弯矩米,在N 和V 作用下,由每个螺栓平均承担,在米作用下,由于旋转中心在最下一排螺栓上,各排螺栓所受拉力的大小,与距旋转中心的距离成正比,因而最上边一排螺栓(“1”号螺栓)所受拉力最大,按同时承受拉力和剪力作用的普通螺栓验算即可.20010020010)200100(42212=<=⨯+⨯==∑e ny yρ故按大偏心受力计算.1.将外力F 向螺栓群形心简化,得1281608.054=⨯==F N KN 961606.053=⨯==F V KN752002506.04008.0=⨯+⨯=F F M KN ·米米2.计算“1”号螺栓在N 、V 、米作用下所受的力8.12101281===n N N Nt KN6.910961===n V N V KN13.50)400300200100(2400752002222211=+++⨯⨯==∑iM t y n My N KN3.计算每个螺栓抗剪、承压、抗拉承载力设计值976.0)15/(1.1323154000101=-==>=d l d l βb V V b Vf d n N ⋅⋅=42πβ93.42101404201976.032≈⨯⨯⨯⨯⨯=-π KNb c bc ft d N ⋅⋅=∑β54.59103051020976.03=⨯⨯⨯⨯=- KNb t e b tf d N 42π=65.41101701045.232=⨯⨯⨯=- KN4.验算连接的强度225.165.4113.5093.426.92221121≈⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛b t MtNt b VV N N N N N >1 (不符合要求)6.91=V N KN <54.59=b c N KN (符合要求)此连接不能满足抗拉、抗剪承载力设计值的要求,因此,必须增加螺栓数目,或改用高强度螺栓连接.而它却满足承压承载力设计值的要求.若将螺栓数目增加为12个,列数不变,孔距为80米米,则67.10121281≈==n N N N t KN812961===n V N VKN()72.42400320240*********75200222221≈++++⨯⨯=M t N KN ≈≈⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛04.165.4172.4267.1093.4282221121b t M tNt b VV N N N N N 1 符合要求.接触面采用喷砂处理,试分析:按与普遍螺栓连接相同的方法计算1号或2号螺栓在扭矩()F F T 300100200=+⨯=KN ·米米和剪力F V =KN 作用下产生的剪力T N 1和Vy N 1,将T N 1分解为水平方向的力T x N 1和竖直方向的力T y N 1,并将V y N 1和T x N 1、T y N 1合成即得1号螺栓总的剪力1N ,再求单个摩擦型高强度螺栓的抗剪承载力设计值bV N ,最后,按抗剪强度条件1N ≤b V N 即可求得max F .2001=l 米米<015d ,故取0.1=β.F F y x y T N i i T x 545.01004506100300222211≈⨯+⨯⨯=+⋅=∑∑ (KN) F F y x x T N i i T y 273.0100450650300222211≈⨯+⨯⨯=+⋅=∑∑ (KN) F F n V N V y 167.06//1≈== (KN)()()211211V yT y T xN NN N ++=()()F F F F 7.0167.0273.0545.022≈++=(KN)单个摩擦型高强度螺栓的抗剪承载力设计值bV N :P n N f b V μβ9.0⋅=62.5012545.019.01=⨯⨯⨯⨯= KN要求 1N ≤bV N ,即 62.507.0=F 故 32.72≈F KN6.,若采用8.8级米20的摩擦型高强度螺栓连接,接触面采用喷砂处理,钢材为Q235,试求解:分析:此连接同时承受拉力和剪力的共同作用.将外力F 向螺栓群形心简化得轴向力N 、剪力V 和弯矩M ,求各力作用下“1”号螺栓所受的实际力N t N 1、VN 1、M t N 1,按同时承受拉力和剪力作用的摩擦型高强度螺栓连接的强度验算公式,即可求得max F .1.将外力F 向螺栓群形心简化,得F F N 8.054==(KN)F F V 6.053==(KN)F F F M 3102506.02008.0=⨯+⨯=(KN ·米米)2.计算“1”号螺栓在N 、V 、M 作用下所受的力F F n N N Nt 08.0108.01≈== (KN)F F n V N V 06.0106.01=== (KN)()()F F y m y M N iM t 31.020********31022211=+⨯⨯=⋅=∑ (KN)作用于“1”号螺栓的最大拉力:F F F N N N Nt M t t 39.008.031.0111=+=+=(KN)要求 t N 1≤1001258.08.0=⨯==P N bt KN即得 4.256≈F KN“1”号螺栓的抗剪承载力设计值为:()t f bV N P n N 125.19.0-=μ()F 39.025.112545.019.0⨯-⨯⨯⨯=F 193.041.49-≈(KN)要求 VN 1≤bV N即 F F 193.041.4906.0-= 解得 195≈F KN故此连接能承受的最大承载力195=F KN.4.1 图4.Ⅱ.2中AB为一轴心受压柱,柱截面为4∠200×125×12组成十字形截面,支撑和AB相连处,有四个d0=17.5米米的孔洞削弱,十字形截面的形式如图中(b)所示.计算σ=N/A n=2800×103/[4×(3791-12×17.5)]=195N/米米2<f =215N/米米2满足要求.2.整体稳定性及刚度由图(a)知:l ox=4米,l oy=2米.四个角钢组成的十字形截面,可查得i x=9.61厘米,i y=4.95厘米(查二个角钢组成图4.Ⅱ.2的T形截面的相应数值).λx=l ox/i x=400/9.61=41.6<[λ]=150λy=l oy/i y=200/4.95=40.4对x和y轴都属b类,由λx查φx=0.893N/(φx A)=2800×103/(0.893×4×3791)=207N/米米2<f=215N/米米2满足要求.4.2 仍为题4.1图4.Ⅱ.2(a)所示条件,但支撑杆与AB 焊连,AB 杆无截面削弱,材料为Q235钢,试选用两个槽钢组成的实腹式工字形截面作为AB 压杆(图4.Ⅱ.3).解: 分析:强度就满足要求.假定60=λ,807.0=ϕ(b 类)16137215807.01028003=⨯⨯=⋅=f N A r ϕ米米27.6604000===λxrx l i 厘米 图4.Ⅱ.3 AB 杆截面 35.3602000===λyry l i 厘米 选用2[30b,1362068102=⨯=A 米米2,6.13=x i 厘米4971=I 厘米4,()()211487.2684972222111=⨯+=⋅+=a A I I y 厘米494.32.1362114===AI i y y 厘米这一截面A <r A ,但x i >rx i ,y i >ry i ,因而所选截面可能满足要求.验算: 4.296.134000===x x x i l λ 8.5094.32000===yy y i l λ<[λ]150= 853.0=ϕ(b 类)24113620853.01028003=⨯⨯=⋅A N ϕN/米米2>215=f N/米米2 改用2[40a,1500075002=⨯=A 米米2,3.15=x i 厘米,5921=I 厘米4()()248191.2755922222111=⨯+=+=a A I I y 厘米4,07.41502481===AI i y y 厘米验算: 1.263.154000===x x x i l λ 1.4907.42000===yy y i l λ<[λ]150= 861.0=ϕ(b 类)21615000861.01028003=⨯⨯=⋅A N ϕN/米米2≈215=f N/米米2 满足要求.4.3 所有条件与题4.1相同,但选用三块板焊成的工字形截面. 解: 分析:一是由于y x l l 002=,所选截面可尽量使y x i i 2=,这样y x λλ=,实现等稳定要求,更经济;其二是截面需要开展一些,但又不能过薄,否则板会发生局部失稳.同样,假定60=λ,得16137=r A 米米2,7.6=rx i 厘米,35.3=ry i 厘米.查相关表:6.1543.07.643.0===x i h 厘米1424.035.324.0===y i b 厘米 考虑局部稳定要求:(热轧型钢板件的宽厚比较小,一般能满足要求,可不验算,对于组合截面,应进行验算) 翼缘:t b 1≤16601.0101.010=⨯+=+λ t ≥44.016214162=⨯=⨯b 厘米,取6=t 米米 腹板需要的面积:1445761402161372=⨯⨯-=-=f r rw A A A 米米2当取腹板150=h 厘米时,腹板需要的厚度:rw t ≥4.96150144570==h A rw 米米 计算结果表明,需要的腹板过厚,不合理.说明可能是假定的λ过大(当承载力由稳定控制时),求得r A 大了 ,rx i 和ry i 小了 ,因而所得h 和b 也都小了 .另假定40=λ,899.0=ϕ,则14486215899.01028003=⨯⨯=⋅=f N A r ϕ米米2 10404000===λxrx l i 厘米 5402000===λyry l i 厘米 3.2343.01043.0===rx i h 厘米 8.2024.0524.0===ry i b 厘米 翼缘:t ≥74.01428.20=⨯厘米(t b 1≤14401.0101.010=⨯+=+λ)取6=t 米米, 220=b 米米腹板:当腹板高度取240=h 厘米,则腹板厚度:w t ≥7.4524022082144860=⨯⨯-=h A rw 米米 计算结果表明,需要的腹板仍太厚.但再减小λ,意义不大,因为ϕ已大于0.9,改变不大了 ,说明这一压杆的承载力接近于强度条件控制,因而可直接加大b 和h ,保证必要的截面面积,并考虑到h 应大于b ,t 大于w t .现取300=b 米米,16=t 米米,3500=h 米米,12=w t 米米,则138001235016300220=⨯+⨯⨯=+=w t h bt A 米米28231014.316816300235012121⨯=⨯⨯⨯+⨯⨯=x I 米米4 73102.7300161212⨯=⨯⨯⨯=y I 米米42481015.11038.11014.3⨯=⨯⨯==A I i x x 米米 721038.1102.747=⨯⨯==A I i yy 米米 5.261.154000===x x x i l λ 7.272.72000===yy y i l λ<[λ]150= 944.0=ϕ21513800944.01028003=⨯⨯=⋅A N ϕN/米米2 215==f N/米米2 满足整体稳定要求.局部稳定: 翼缘:9161441==t b <13301.0101.010=⨯+=+λ 腹板:2.2912350==w t h <40305.0255.025=⨯+=+λ满足要求.题4.4 所有条件与题4.1相同,但选用二个槽钢组成的格构式缀条柱.焊条用E43型,手工焊.解: 分析:根据实轴选槽钢截面,这时以x 轴为实轴(图4.Ⅱ.4).并以此确定两个槽钢的间距b 和缀条设计.1.由实轴x — x 选择槽钢型号题4.2是根据y — y 控制稳定选出的截面,对x — x 轴有些富裕,所选2[40a 对x 轴:150752=⨯=A 厘米2,3.15=x i 厘米,1.263.15400==x λ. 950.0=x ϕ5.19615000950.01028003=⨯⨯=⋅A N x ϕN/米米2<215=f N/米米22.对虚轴y — y 确定两分肢间距离b假定缀条取∠45×4,查得49.31=A 厘米2,89.0min =i 厘米,则8.949.375271.2627212=⨯-=-=A A x x λλ 4.208.92000===yyy l i λ厘米 查相关表: 4.4644.04.2044.0===y i b 厘米 取46=b 厘米.()6154406.207559222=⨯+=y I 厘米425.2015061544===AI i y y 厘米 9.925.20200==y λ 2649.375279.9272120=⨯+=+=A A y y λλ<[λ]150= 950.0=y ϕ5.19615000950.01028003=⨯⨯=⋅A N y ϕN/米米2<215=f N/米米2对虚轴整体稳定性满足要求,承载力高于例4.4.3.分肢稳定性当缀条取︒=45α,则分肢计算长度为12.4094.2246201=⨯-=-=Z b l 厘米 81.21=i 厘米 3.1481.212.40111===i l λ<35507.07.0max =⨯=λ 分肢稳定性满足要求.4.缀条及与柱肢连接的角焊缝计算41079.3852151500023585⨯=⨯==y f AfV N 9.37=KN每一斜缀条所受轴力:79.26229.3722cos 2====V V N d αKN 斜缀条长度:7.5612.40245cos 1=⨯=︒=l l 厘米计算长度:517.569.09.010=⨯==l l 厘米 (缀条用单角钢,属斜向屈曲,计算长度为0.9倍几何长度)5789.051max0===i l λ,823.0=ϕ 单面连接的单角钢其稳定折减系数:686.0570015.06.00015.06.0=⨯+=+=λγ则136349823.0686.026790=⨯⨯=A N d γϕN/米米2<215=f N/米米2 缀条与柱身连接的角焊缝设计: 设焊脚尺寸 4=f h 米米 肢背焊缝长度:57816085.047.0267907.0885.07.011=+⨯⨯⨯⨯=+=wf f d f h N K l 米米取601=l 米米.501=w l 米米>32488=⨯=f h 米米 并<24060=f h 米米肢尖焊缝长度:29816085.047.0267903.0885.07.022=+⨯⨯⨯⨯=+=wff d f h N K l 米米 取502=l 米米.402=w l 米米>32488=⨯=f h 米米 并<24060=f h 米米.题4.5 所有条件与题4.4相同,但选用二个槽钢组成的格构式缀板柱.焊条用E43型,图4.Ⅱ.5 解: 分析:由实轴x — x 选择槽钢型号与题4.4完全相同,采用2[40a. 对虚轴y — y 确定两分肢间距离b 取分肢251=λ1.7251.2622212=-=-=λλλx y 则 281.72000===yyy l i λ厘米 查相关表: 6.6344.02844.0===y i b 厘米 取64=b 厘米.()[]12785694.2327559222=-⨯+=y I 厘米42.29150127856===AI i y y 厘米8.62.292000===y x y i l λ 取缀板宽度d ≥7.42643232=⨯=b 厘米,取44厘米. t ≥6.1406440==b 厘米,取1.6厘米. 查得[40a,81.21=i 厘米则 3.7081.2251101=⨯==i l λ,取7001=l 厘米.1144470011=+=+=d l l 厘米(见图4.Ⅱ.5)259.2481.2701011≈===i l λ 则 9.25258.6222120=+=+=λλλy y 950.0=y ϕ(b 类)19615000950.01028003=⨯⨯=⋅A N y ϕN/米米2<215=f N/米米2整体稳定满足要求,但与缀条柱相比,b 值增加到64厘米,说明缀板柱与缀条柱相比,当两分肢间距离相等时,缀板柱的刚度小.由于 260==y x λλ则 251=λ≤25505.05.0max =⨯=λ(当m ax λ<50时,取50max =λ),分肢稳定性满足要求.3.缀板与柱肢连接角焊缝计算9.37=V KN,95.181=V KN02.5949.226420=⨯-=-=z b a 厘米43111066.32.59011401095.18⨯=⨯⨯==a l V T N73111008.1211401095.182⨯=⨯⨯==l V M N ·米米取8=f h 米米>4.6185.15.1==t 米米([a 40,18=t 米米)()()2.151644087.01066.3167.04=-⨯⨯⨯=-=d h T f f τN/米米2()()2.621644087.01008.16167.06272=-⨯⨯⨯⨯=-=d h M f f σN/米米2542.1522.16.6222.12222=+⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛f f τσN/米米2<160=w f f N/米米2 焊缝满足要求5.1 一平台梁,梁格布置如图.次梁支于主梁上面,平台板与次梁翼缘焊接牢.次梁承受板和面层自重标准值为3.0KN/米2(荷载分项系数为1.2,未包括次梁自重),活荷载标准值为12KN/米2(荷载分项系数为1.4,静力作用).次梁采用轧制工字钢,钢材Q235,焊条E43型,试选择次梁截面,并进行截面及刚度验算.04.6234.1122.132.17.0=⨯⨯+⨯+⨯=q KN/米跨中截面:88.193504.62818122max =⨯⨯==ql M KN ·米 支座截面:10.155504.622121max =⨯⨯==ql V KN 2.初选截面 计算要求的nx W ,36max 1085921505.11088.193⨯=⨯⨯==f M W x nx γ米米2(查相关表,05.1=x γ)选截面:查型钢表知,选用Ⅰ36a.310875⨯=x W 米米3,41015760⨯=x I 米米4,10=w t 米米.单位长度重量为9.59千克/米,则其自重为9.59千克/米×81.9N/千克59.0=KN/米<7.0KN/米3.强度验算正应力:03.2111087505.11088.19336=⨯⨯⨯==x x x W M γσN/米米2<215N/米米2因所选型钢的310875⨯=x W 米米3大于要求的310859⨯米米3,抗弯强度一定能满足,因型钢腹板较厚,腹板抗剪强度也能满足.4.刚度验算荷载标准值:()7.4531237.0=⨯++=b q KN/米跨中挠度:43611015760102063841057.455384543933=⨯⨯⨯⨯⨯⨯⨯==x b EI l q l v <[l v ]2501= 刚度满足要求5.2 次梁的荷载和截面同 5.1,如平台板与次梁翼缘未焊牢,验算上述次梁的整体稳定性.如不满足,另选次梁截面.分析:(1)对于梁的整体稳定性计算,梁的翼缘与平台板焊牢和不焊牢时,整体稳定性是不同的.如次梁的翼缘与平台板焊牢,则梁的整体稳定性已保证,可不必验算梁的整体稳定.(2)梁整体稳定验算内容中,主要是计算整体稳定系数b ϕ.如查得的b ϕ>0.6说明梁已进入弹塑性阶段,应用bϕ'代替b ϕ.b ϕ'可根据b ϕ值在相关表中查得. 1.次梁Ⅰ36a 的整体稳定验算 由公式: xb xW M 1ϕσ=因次梁跨中无侧向支承,均布荷载作用于上翼缘,51=l 米,查相关表得73.0=b ϕ>6.0, 0.2821.070.683bbϕϕ'=-=631193.88103240.68387510x bx M W σϕ⨯==='⨯⨯N/米米2>215N/米米2因此,应另根据整体稳定选择截面.2.另选截面,进行整体稳定验算设选工字钢范围Ⅰ45~Ⅰ63,得0.683bϕ'=,所需截面抵抗矩为 631193.88101320.3100.683215x x b M W f ϕ⨯===⨯'⨯米米3选Ⅰ45a,3101430⨯=x W 米米3,自重为79.0KN/米.截面及相应用钢量较Ⅰ36a 增加40%.因此,应尽量使平台板与次梁焊牢,以保证梁的整体稳定性. 其它强度验算已够,从略.5.3 Q235钢简支梁如图所示.自重标准值0.9KN/米(荷载分项系数1.2),跨中承受悬挂集中力标准值100KN(荷载分项系数1.4),集中力作用于上翼缘.(1).梁在跨中无侧向支承,验算截面的整体稳定性; (2).如改用Q345钢,是否满足要求;(3).仍用Q235,荷载悬挂于下翼缘,是否满足要求;(4).仍用Q235,荷载作用位置不变,跨中增加一侧向支承点,整体稳定是否满足要求?无侧向支承,则l 1即为梁的跨度.(2)验算工字型焊接组合梁的整体稳定性时,主要应掌握计算梁的整体稳定系数φb的公式.φb 公式中的βb 由参数ξ确定.ξ=l 1t 1/b 1h 中的b 1是梁受压翼缘的宽度.如计算所得φb >0.6时,说明梁失稳时已进入弹塑性状态,应用相应的φb ‘代替φb ,进行整体稳定验算.(3)梁的整体稳定验算不满足要求时,提高梁的整体稳定承载力的措施是很多的.经过本题各种方法计算结果的比较,应掌握在不改变截面和荷载作用位置时,最有效的提高梁的整体稳定承载力的措施是在跨中增加侧向支承点.(4)验算梁翼缘的局部稳定时,计算翼缘板的宽厚比b 1/t(b 1为受压翼缘板自由悬伸宽度);如b 1/t 值小于作为三边简支一边自由保证局部稳定的宽厚比限值,则翼缘的局部稳定能保证.对于梁腹板,则计算h 0/t w ,根据h 0/t w 值的范围,设置加劲肋,以保证腹板的局部稳定. 1.验算原给定条件梁的整体稳定性 (1)研究是否需要验算梁的整体稳定性查相关表可知,梁跨中无侧向支承时,荷载作用于上翼缘时,Q235钢梁不需验算整体稳定的最大l 1/b 值为13.l 1/b=9000/200=45>13,应验算整体稳定. (2)梁跨中的最大弯矩米米ax =1/8ql 2+1/4Fl=1/8×(0.9×1.2)×92+1/4×100×1.4×9=325.94KN·米 (3)截面几何特性A=2×200×12+800×8=11200米米2I x =1/12×(200×8243-192×8003)=1.133×109米米4W x =I x /y=1.133×109/412=2.749×106米米3I y =2×1/12×12×2003+1/12×800×83=1603.4×104米米4i y 84.371012.1104.160344=⨯⨯==A I Y λy =l 1/i y =9000/37.84=237.84(4)计算βb (或βb ‘)、φbξ=l 1t 1/b 1h=9000×12/(200×824)=0.655<2.0查相关表可知, 无侧向支承, 集中力作用于上翼缘情形: βb =0.73+0.18ξ=0.73+0.18×0.655=0.8479φb =2124.414320⎪⎪⎭⎫ ⎝⎛+h t W Ahy x y b λλβ 2773.08244.41284.237110749.2824102.1184.237432085.02632=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯⨯⨯=(5)验算整体稳定σ=米x /(φb W x )=325.94×106/(0.2773×2.749×106)=427.58N/米米2>215N/米米2,不满足整体稳定要求.2.改用Q345钢,重新验算改用Q345钢重新验算时,因f 有变化,φb 也有变化.φb 1889.0345/2352773.02354.414320212=⨯=⎪⎪⎭⎫ ⎝⎛+=yy x y b f h t W Ahλλβ σ=米x /(φb W x )=325.94×106/(0.1889×2.749×106)=627.67N/米米2>315N/米米2由此可以看出,提高钢材强度等级,一般不能提高梁的整体稳定性.3.将悬挂集中力作用于下翼缘时,βb 和φb 都有变化. 查相关表可知, 无侧向支承, 集中力作用于下翼缘情形: βb =2.23-0.28ξ=2.23-0.28×0.655=2.047φb 668.08244.41284.237110749.2824102.1184.2374320047.22632=⎪⎭⎫⎝⎛⨯⨯+⨯⨯⨯⨯⨯=>0.6φb ‘=0.648σ=米x /(φb ’W x )=325.94×106/(0.648×2.749×106)=182.91N/米米2<215N/米米2因此,整体稳定得到保证.4.在跨中增加一侧向支承点,l 1=4500米米l 1/b=4500/200=22.5>13 仍应验算整体稳定.λy =l 1/i y =4500/37.84=118.92 ξ=l 1t 1/b 1h=4500×12/(200×824)=0.3277<2.0 查相关表可知, 跨中有一侧向支承,集中力作用.βb =1.75φb =2124.414320⎪⎪⎭⎫ ⎝⎛+h t W Ahy x y b λλβ 93.18244.41292.118110749.2824102.1192.118432075.12632=⎪⎭⎫⎝⎛⨯⨯+⨯⨯⨯⨯⨯=>0.6应用φb ‘验算,923.0282.007.1=-='bb ϕϕσ=米x /(φb ’W x )=325.94×106/(0.923×2.749×106)=128.45N/米米2<215N/米米2因此,整体稳定得到保证.比较以上提高整体稳定的措施,可以看出在梁跨中增加侧向支承,减小侧向支承点距离,提高整体稳定承载力是最有效的.5.验算翼缘、腹板的局部稳定性(1) 翼缘:81296122)8200(1==-=t b <13 翼缘截面满足局部稳定要求. (2) 腹板:10088000==w t h 80<wt h 0<170,满足纯弯屈曲腹板的局部稳定要求,但不满足纯剪屈曲腹板的局部稳定要求,应设置横向加劲肋,保证腹板的局部稳定5.4对图5.1所示主梁设计焊接组合截面.次梁与主梁等高连接,次梁可以作为主梁的侧向支承,材料Q235,并进行强度、刚度和整体稳定验算.分析:(1)选择工字形焊接组合梁截面的步骤是先确定腹板高度和厚度,即0h 和w t ;再确定翼缘板的宽度和厚度,即b 和t .确定腹板高度时,除考虑经济要求外,还应注意满足刚度要求;满足局部稳定要求外,还应注意满足抗剪强度要求.(2)选择截面后,应进行强度、刚度和整体稳定的验算.强度验算时,应注意在集中力作用的跨中截面除进行抗弯强度验算外,还应进行腹板高度处折算应力的验算.抗剪强度和刚度,因在选择截面时已满足要求,可不再进行验算.整体稳定验算时应考虑梁跨中有侧向支承后,受压翼缘的自由长度是实际侧向支承点的距离.1.荷载及内力计算 (1)次梁传来集中力20.31021.155=⨯=F KN(2)内力 跨中截面:20.186132.31062.310233623max =⨯-⎪⎭⎫⎝⎛⨯⨯=⨯-⨯=F F M KN ·米 10.1552.310212123=⨯==-=F F F V KN 支座截面:3.4652..3102323max =⨯==F V KN 2.选择截面(1)确定梁高h (腹板高度0h )需要的净截面抵抗矩:66max 1861.2108.657101.05215nx x M W f γ⨯===⨯⨯米米3经济高度:73.1133010657.87307363=-⨯=-=nx e W h 厘米 平台梁 [l v ]4001=,151min =l h ,8001512000min ==h 米米 取腹板高12000=h 米米,初设翼缘板厚20=t 米米,则梁高1240=h 米米. (2)腹板厚度w t由公式 3max 0465.3101.2 1.2 3.721200125w v V t mm h f ⨯===⨯由经验公式 87.95.312005.32===w w h t 厘米取腹板厚度w t 10=w t 米米 (3) 翼缘尺寸26007.52146101200120010657.86mm t h h W bt A w x =⨯-⨯=-==b 的选择范围: =b (16~12.5)h =(16~12.5)1240206~496⨯= 取360=b 米米,则 mm b t 12303603043.163605916==≥==因此,翼缘尺寸为360×18,满足局部稳定要求.截面尺寸见图. 3.强度验算 (1)截面几何特性面积: 2736012120018360220=⨯+⨯⨯=+=h t bt A w 米米2惯性矩:()[][]93330310247.612003501236360121121⨯=⨯-⨯=--=h t b bt I w x 米米4抵抗矩: 6910108.1061810247.62⨯=⨯==h I W x x 米米3截面面积矩:5011046320.392181200183602⨯=+⨯⨯=⎪⎭⎫⎝⎛+=t h bt S 米米3 (2)强度验算主梁自重标准值:528.281.978502.110273606=⨯⨯⨯⨯=-b q KN/米(式中1.2为构造系数,钢的容重为:7850千克/米3) 则 80.1915122.1528.2812.18612max =⨯⨯⨯+=M KN ·米 50.483122.1528.2213.465max =⨯⨯⨯+=V KN(上二式中1.2为荷载分项系数.)①跨中截面抗弯强度51.18010108.1005.1108.191566max =⨯⨯⨯==x x W M γσN/米米2<215=f N/米米2②跨中截面折算应力腹板高度处正应力: 0.18410247.621200108.19152960max 1=⨯⨯⨯=⨯=xI h M σN/米米2腹板高度处剪应力: 8.91010247.61046.39101.15595311=⨯⨯⨯⨯⨯==w x t I VS τN/米米2 78.1848.931843222121=⨯+=+=τσσzs N/米米2<5.2362151.1=⨯N/米米2③支座截面抗剪强度在设计腹板厚度w t 时已满足,因此,不必验算. (3)刚度验算在选择梁高h (或0h )时,已满足,也不必验算. (4)整体稳定验算因跨中有侧向支承,受压翼缘的自由长度30001=l 米米,33.836030001==b l <13 (由相关表查得考虑塑性时不必计算整体稳定的131=bl.) 因此,不必验算整体稳定.6.1图所示为一Q235钢焊接工字形压弯构件,翼缘为剪切边,承受静力设计偏心压力N 作用,N=700KN, 偏心矩e=300米米,l=5米,构件的两端铰接,试验算构件的强度、稳定和刚度.如不满足要求,应如何设置侧向支承提高其承载力,并进行验算.解:分析:由于构件截面无削弱,又是双轴对称截面,因而只要整体稳定性满足要求,就能满足强度要求.由于构件绕两个主轴的计算长度相等,偏心弯矩又绕刚度大的强轴作用,因而构件即可先计算截面特性:A=2×20×1.4+50×1.0=106厘米2I x =1/12×1×503+2×20×1.4×25.72=4.74×104厘米4I y =2×1/12×1.4×203=1.87×103厘米4i x 1.211061074.44=⨯==A I x 厘米 i y 2.41061087.13=⨯==A I y厘米 (1)验算构件在弯矩作用平面内的稳定: λx =l 0x /i x =500/21.1=23.7 属b 类截面,查得φx =0.958N EX =π2EA/1.1λx 2=π2×206×103×106×102/1.1x23.72=34845×103N=348452KN 对于两端偏心矩e 相等,即两端偏心弯矩相等的情况,β米x =1.0γx =1.05,米x =N ·e=700×300=2.1×105KN ·米米W 1x =2I x /h=2×4.74×104/52.8=1795厘米3代入验算公式:)8.01(1EXxx x mx x N N W M A N -+γβφ ⎪⎭⎫⎝⎛-⨯⨯⨯⨯+⨯⨯⨯=3484527008.0110795.105.1101.20.110106958.01070068231811119.68=+=N/米米2<215=f N/米米2(2)验算构件在弯矩作用平面外的稳定λy =l 0y /i y =500/4.2=119焊接工字形截面,翼缘为剪切边,对y 轴属c 类截面,φy =0.383βtx =1.0对双轴对称工字形截面,当λy ≤yf 235120时, φb =1.07-λy 2/44000×f y /235=1.07-1192/44000×235/235=0.748代入验算公式:xb x tx y W M A N1φβηφ+ 682310795.1748.0101.20.10.110106383.010700⨯⨯⨯⨯⨯+⨯⨯⨯=328156172=+=N/米米2>215=f N/米米2在弯矩作用平面外的稳定性不满足要求.在构件中央l/2处,加一侧向支承点,阻止绕y 轴失稳,如图.λy =250/4.2=59.5,属c 类截面,φy =0.712φb =1.07-λy 2/44000=1.07-59.52/44000=0.989代入验算公式:xb x tx y W M A N1φβφ+ 682310795.1989.0101.20.110106712.010700⨯⨯⨯⨯+⨯⨯⨯=21111893=+=N/米米2<215=f N/米米2满足要求.不过从计算结果可以看出,尽管绕y 轴加了 一个侧向支承,但由于λy 比λx 仍大很多,因而构件在弯矩作用平面外的弯扭失稳承载力仍低于构件在弯矩作用平面内的弯曲失稳承载力.(3)局部稳定验算翼缘板:由于强度计算中考虑了 塑性γx >1.0,因而翼缘自由外伸宽度部分的宽厚比限值为yf 23513. b 1/t=95/14=6.8<13 腹板:σ1=N/A +米/W=700×103/(106×102)+2.1×108/(1.795×106)=66+117=183N/米米2σ2=N/A -米/W=66-117=-51N/米米2腹板边缘的最大应力和最小应力,如图所示.y 1=σ2/(σ1+σ2)×h=51/(183+51)×528=115米米 σ米ax =(528-115-14)/(528-115)×183=177N/米米2σ米in =(115-14)/115×(-51)=-45N/米米2α0=(σ米ax -σ米in )/ σ米ax =[177-(-45)]/177=1.25<1.6 腹板高厚比限值为:()()85.56235235257.235.025.116235255.0160=+⨯+⨯=++yf λα腹板实际高厚比为:h 0/t w =500/10=50<56满足要求.(4)刚度验算: 查:[λ]=150.实际最大λ=59.5<[λ]=150 满足要求.。
钢结构计算题作业

钢结构课程作业第三章作业1.如图所示为角钢与节点板的三面围焊连接,轴心力设计值N=800kN(静力荷载),角钢为2 L125×10,与厚度为10mm的节点板连接。
钢材为Q235,手工焊,采用E43型焊条,h=8mm。
试确定肢背焊缝和肢尖焊缝的实际长度。
焊脚尺寸f2.如图所示为双盖板拼接的钢板连接,钢材为Q235-B,采用高强度螺栓为8.8级的M20,连接处构件接触面用喷硬质石英砂处理,作用在螺栓群形心处的轴心拉力设计值N=800kN。
采用标准圆孔。
试问:(1)采用高强度螺栓摩擦型连接,确定其螺栓数目,应为下列何项?(2)采用高强度螺栓承压型连接,确定其螺栓数目,应为下列何项?1.一轴心受压平台柱,采用焊接工字形截面,截面尺寸如图所示,柱两端铰接,柱高6m , 翼缘为焰切边,钢材为Q345,焊条为E50系列,焊条电弧焊,求该柱稳定承载力。
截面特性为:2293.6A cm =,12.5y i cm =,21.9x i cm =2.某管道支架柱,柱两端饺接,钢材为Q235钢,截面无削弱,采用焊接工字形截面,翼缘板为焰切边,如图所示,承受轴心力设计值N=1600kN 。
进行轴心受压稳定性计算时最大压应力为多少?1.试分析图示简支梁的整体稳定性。
已知作用在梁上的荷载设计值kN F 300=,梁自重设计值 2.0kN m ,采用Q235钢材,跨中有侧向支撑,20.1=b β,2228cm A =,4413683cm I x =,417067cm I y =。
6m6mF10400100016x16y2.0kN/m2.某热轧H 型钢简支梁,选用H 型钢,其截面参数为2=192.5cm A ,4118000cm x I =,34020cm x W =,24.8cm x i =, 6.85cm y i =,钢材为Q235,钢梁跨度为12m ,在跨度中点设有一个侧向支撑点,在梁上作用两个集中荷载设计值F=180kN ,忽略梁自重,试验算其整体稳定性是否满足要求。
钢结构的连接螺栓连接

yn
M N1 y1
y12 y22 yn2
N1 y1
n
yi2
i 1
N1
M y1
n
yi2
i 1
1号螺栓强度验算:
N1
N
b t
一般螺栓群在偏心拉力作用
N1F
F e
1 2 3 4
F M
刨平顶紧 F
承托(板)
可采用偏于安全旳设计措施,即叠加法。
N1M
N2M
y1
N3M
N4M
M=F·e
N1 N1F
材为Q235钢,采用M 22普通螺栓 (C级),螺栓孔直径d0 24mm。 N
此连接承受的静力荷载设计值为
340
260 10
N
10
t 12
N 900kN。
解:查附表1.3得:fvb 140N / mm2
f
b c
305N
/
mm2
一个螺栓的抗剪承载力设计值为
N
t 20
N
N
530
t 12
N /2
T y1
n
xi2
n
yi2
i 1
i 1
i 1
i 1
N1Ty
T r1
n
xi2
n
yi2
x1 r1
T
n
xi2
x1
n
yi2
i 1
i 1
i 1
i 1
y1 r1
N1Tx N1T
x N1Ty
T
螺栓1旳强度验算公式为:
N12Tx
N1Ty N1F
2
N
b min
当螺栓布置比较狭长(如y1≥3x1)时, 可令:xi=0,则N1Ty=0
钢结构第三章 钢结构的连接(螺栓)

排列因素:
受力要求:钢板端部剪断,端距不应小于2d0;受拉时,栓
距和线距不应过小;受压时,沿作用力方向的栓距不宜过大。 构造要求:栓距和线距不宜过大 施工要求:有一定的施工空间
3.6螺栓的构造
3.6.2 螺栓的排列
螺栓排列和最小距离:
3.6螺栓的构造
3.6.2 螺栓的排列
螺栓排列最大距离: 对于角钢、工字钢和 槽钢的螺栓排列见附 录四(型钢的螺栓准 线表)
3.7 普通螺栓连接的构造和强度计算
普通螺栓连接按其受力方式分类:
抗剪螺栓 抗拉螺栓 同时抗剪抗拉螺栓
3.7.1普通螺栓的抗剪连接
3.7.1.1抗剪连接工作性能
抗剪螺栓连接的受力性能:静摩擦力阶段、相对滑移阶段、螺杆与 孔壁挤压传力的弹塑性阶段、破坏阶段。
3.7 普通螺栓连接的构造和强度计算
3.7.1普通螺栓的抗剪连接
4x100=400 50 30 50
M Fe 280 0.21 58.8kN m
2. 单个螺栓的抗拉承载力:
N tb Ae f t b 244 .8 170 41620 N 41.62 kN
3.螺栓群强度验算 由前述可知1号螺栓受力最大,为设计控制点, 则对其进行强度验算:
3). 螺栓群同时承受剪力和弯矩(轴心拉力) 的计算
螺栓群同时承受剪力和拉力
3.7 普通螺栓连接的构造和强度计算
3.7.2普通螺栓的抗拉连接
3). 螺栓群同时承受剪力和拉力的计算 支托仅起安装作用:螺栓群承受弯矩M和剪力V
N t N1M My1
m y
2 i
Nv V n
螺栓不发生拉剪破坏
20 12 305 73200 N 73.2 kN
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
1
在受力状态Ⅱ: 螺栓群受扭,可以计算1号螺栓 作为控制 1号螺栓所受力的竖向分量
6
r1 2 r2
o
N1
T
r3
3
4 5
N1 y
T
Tx1 150 250 60 2 13.72kN 2 2 2 2 xi yi 60 10 80 4 160 4
y
y1 r1
3 N 325 10 所以,1-1断面起控制作用: 128.2 N / mm2 An 2536
例 图示牛腿用普通螺栓连接,柱翼缘厚度为10mm,连接板厚度为8mm, 材料Q235B,F=150kN,粗制螺栓为M22。 解:1、分析
50 4X80 50
y
+ + + + +
250
F
①本题是验算题 ②计算单个螺栓抗剪的最大承载能力 抗剪: N nv
2
2
=46.51kN<Nminb=53.2kN
满足要求
二、普通螺栓受拉性能
1、单个螺栓受拉破坏试验
螺杆受拉,连接板脱开,螺纹处拉断或连接板屈服,螺杆的拉力为:
a) b)
Pf
Q Pf Q
Pf
Pf
a)
b)
加劲肋 刚度很大时 刚度较小时
2Nt
2Nt
螺杆拉力 Nt=N+Q
Q称为撬力,与连接板厚度和螺栓位置有关。
+ + 2 + + +
e4
+
+
+2 1 e2
+
+
+
+
6e1 e4
+
+
+ +
N
+
+
+
+
+
+
除对1-1截面 (绿线)验算外,还 N 应对2-2截面(粉红) 进行比较验算。因此, 在进行该连接的净截 面强度计算时,其中 Ani应取An1和An2中的 较小值。 2-2分红线总长: 扣除螺孔直径后:
1 + + +
为了减小撬力可以设置加劲肋
o
T 1x
1
N1TX
T 1Y
N
N1T
N1yF
x
x1
Ty1 150 250 160 N 2 36.58kN 2 2 2 2 xi yi 60 10 80 4 160 4
N1
N N
T 1x 2
F 1y
N
T 1y
2
36.58 13.72 15
b 抗剪: N v nv
N
N
d2
4
抗压:
4 N d tf 20 8 305 48800N
b c b c
f vb 2
202
140 87964.6 N
6
N
3、设计
b min
min N , N
b v
b c
48.8kN
2 1 N N
需螺栓数:
T +i + Ni r+ i + +
2、计算螺栓群
螺栓群如图,为扭剪
x
可以将螺栓受力看为两种受力的叠加:
+ + + + + F+ + + + + T
=
+ + + + +
F + + + + +
N1yF +
+ + + + +
+ + + + +
T
受力Ⅰ 在受力 状态Ⅰ
受力Ⅱ
N1 y
F
F 150 15kN n 10
例 设计两块钢板用普通螺栓连接的盖板拼接,构件受轴拉力设计值为 N=325kN,钢材Q235A,粗制螺栓直径d=20mm,板宽360mm,盖板厚 6mm,杆件板厚8mm。
解:1、分析 ①计算螺栓所受的力为剪力 6 8 ②本题为设计题,所包含的内容包 括:所需的螺栓数,螺栓的布置。 ③已知条件为:N=325kN,材料即: fvb=140N/mm2,fcb=305N/mm2, d=20mm,t1=8,t2=6 2、计算单个螺栓的承载能力设计值
2 + + +
+ + + +
e4
+
6e1 e4
+ + +
+ + +
+ + + +
N
+2 1 e2
2e4 ( n2 1) e12 e2 2
2e4 (n2 1) e12 e2 2 n2 d 0
n2——粉红线截面上的螺孔数
这样在2-2截面的净截面面积为:
An 2 [2e4 (n2 1) e12 e2 2 n2 d 0 ]t
N
N
N
N
N/2
连接板受力变化图 N1 N1 =N N2 =N-N/n×n1 N1 =N N2 =N-N/n×n1
N
N2
N
N/n×n1
N1
验算公式
Ni f Ani
注意计算截面!
Ani (b ni d0 )t
Ni ——连接件第i截面上的轴力 Ani ——连接件第i截面的净截面面积 f ——连接板钢材抗拉强度设计值 b ——截面宽 ni ——截面上的螺栓数 d0 ——螺孔直径 1 t ——板厚 ② 螺栓为错列排列 N 时的验算
b
b
(3) 净截面强度计算
由于外力通过螺栓群形心的杆件,应当满足强度计 算公式
N f An
式中:N 为所受的轴力; f 为材料抗拉强度设计值;
An 为杆件截面的净截面面积
.
① 当螺栓为并列排列
N
+ + + + + + + + + + + + + + + +
b v
+i + Ni r+ i + +
x
d2
4
f 1
b v
2 2 2
4
140 53218 N
60 60
抗压: 所以
b Nc d tfcb 22 8 305 53680N
b N min min N vb , N cb 53.218kN
y F
+ + + + +
N 325 n b 6.7个 N min 48.8
螺栓数可以≥6.7即可,所以取7个 螺栓布置如图所示。 净截面强度
2 1
在1-1断面: An ( B n1d0 )t (360 2 21.5) 8 2536mm2
在2-2断面:An (2 80 4 802 502 5 21.5) 8 3439mm 2
单个螺栓的破坏形态:螺栓被剪断
单个螺栓的破坏形态剪断:板被拉断
单个螺栓的破坏形态剪断:板端被拉豁
注意:
对于下图所示螺栓连接
N/3
N/3 N/3 a d
b
N/2
N/2
c
e
①受剪计算中: Nv 计算式中的受剪面数nv ,即上图中nv =4。 ② 承压计算中: Nc 计算式中∑t 取 a+b+c和d+e 之间的最小值。 问题:在受剪计算中,对于螺杆的值d是否应当按螺纹处的值计算? 不需要。因为,规范中关于普通螺栓的抗剪强度设计值,是由试验 得到的,而在制定规范时,没有区分作用位置。
