形式语言与自动机理论试题答案解析
《形式语言与自动机》(王柏、杨娟编著)课后习题答案-推荐下载

P2
9.对应图(a)(b)的状态转换图写出正则式。(图略) (1) 由图可知 q0=aq0+bq1+a+ε
q1=aq2+bq1 q0=aq0+bq1+a =>q1=abq1+bq1+aaq0+aa =(b+ab) q1+aaq0+aa =(b+ab) *( aaq0+aa)
=>q0=aq0+b(b+ab) *( aaq0+aa ) +a+ε
(2) 由生成式得:
S=aA+B ①
A=bB+cC ② B=a+bB ③ C=D+abB ④ D=dB ⑤ 由③得 B=b*a ⑥ 将⑤⑥代入④ C=d+abb*a=d+ab+a ⑦ 将⑥⑦代入② A=b+a+c(d+b+a) ⑧ 将⑥⑧代入① S=a(b+a+c(d+ab+a))+b*a
=ab+a+acd+acab+a+b*a
4.对下列文法的生成式,找出其正则式 (1) G=({S,A,B,C,D},{a,b,c,d},P,S),生成式 P 如下:
S→aA S→B
A→abS A→bB
B→b B→cC
C→D D→bB
D→d
(2) G=({S,A,B,C,D},{a,b,c,d},P,S),生成式 P 如下:
S→aA S→B
P: S→aS S→bS S→ε
(2) 右线性文法 G=({S},{a,b},P,S)
P: S→aS S→bS S→abb
形式语言与自动机Chapter7练习参考解答

Chapter 7 练习参考解答Exercise 7.1.3 从以下文法出发:S → 0A0 | 1B1 | BBA → CB → S | AC → S | εa) 有没有无用符号?如果有的话去除它们。
b) 去除ε-产生式。
c) 去除单位产生式。
d) 把该文发转化为乔姆斯基范式。
参考解答:a)没有无用符.b) 所有符号S,A,B,C都是可致空的,消去ε-产生式后得到新的一组产生式:S → 0A0 | 1B1 | BB | B | 00 | 11A → CB → S | AC → Sc) 单元偶对包括:(A,A),(B,B),(C,C),(S,S),(A,C),(A,S),(A,B),(B,A),(B,C),(B,S),(C,A),(C,B),(C,S),(S,A),(S,B),(S,C),消去单元产生式后得到新的一组产生式S → 0A0 | 1B1 | BB | B | 00 | 11A → CB → S | AC → SS → 0A0 | 1B1 | BB | 00 | 11A → 0A0 | 1B1 | BB | 00 | 11B → 0A0 | 1B1 | BB | 00 | 11C → 0A0 | 1B1 | BB | 00 | 11d)先消去无用符号C,得到新的一组产生式:S → 0A0 | 1B1 | BB | 00 | 11A → 0A0 | 1B1 | BB | 00 | 11B → 0A0 | 1B1 | BB | 00 | 11引入非终结符C,D,增加产生式C → 0和D → 1,得到新的一组产生式:S → CAC | DBD | BB | CC | DDA → CAC | DBD | BB | CC | DDB → CAC | DBD | BB | CC | DDC → 0D → 1引入非终结符E,F,增加产生式E → CA和F → DB,得到满足Chomsky范式的一组产生式:S → EC | FD | BB | CC | DDA → EC | FD | BB | CC | DDB → EC | FD | BB | CC | DDE → CAF → DBC → 0D → 1Exercise 7.2.1(b)用CFL泵引理来证明下面的语言都不是上下文无关的:b) {a n b n c i | i ≤n}。
形式语言与自动机理论试题
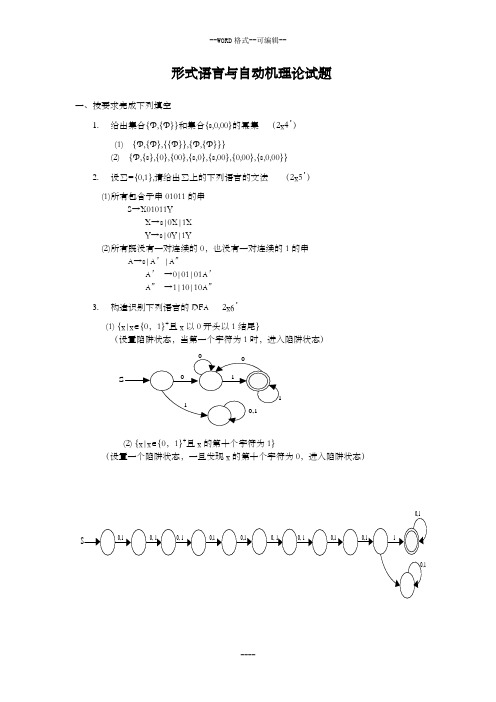
形式语言与自动机理论试题一、按要求完成下列填空1.给出集合{Φ,{Φ}}和集合{ε,0,00}的幂集 (2x4')(1) {Φ,{Φ},{{Φ}},{Φ,{Φ}}}(2) {Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}2.设∑={0,1},请给出∑上的下列语言的文法 (2x5')(1)所有包含子串01011的串 S →X01011YX →ε|0X|1X Y →ε|0Y|1Y(2)所有既没有一对连续的0,也没有一对连续的1的串 A →ε|A ’|A ”A’ →0|01|01A ’ A ” →1|10|10A ”3.构造识别下列语言的DFA 2x6'(1) {x|x ∈{0,1}+且x 以0开头以1结尾}(设置陷阱状态,当第一个字符为1时,进入陷阱状态)1S110,10 (2) {x|x ∈{0,1}+且x 的第十个字符为1}(设置一个陷阱状态,一旦发现x 的第十个字符为0,进入陷阱状态)1S0,10,10,10,10,110,0,10,10,10,10,1二、判断(正确的写T ,错误的写F ) 5x2'1.设1R 和2R 是集合{a,b,c,d,e}上的二元关系,则3231321)(R R R R R R R ⊆( T )任取(x.,y),其中x,y },,,,{e d c b a ∈,使得321)(),(R R R y x ∈。
)),(),((321R y z R R z x z ∈∧∈∃⇒ },,,,{e d c b a z ∈ )),(),(),((321R y z R z x R z x z ∈∧∈∧∈∃⇒)),(),(()),(),((3231R y z R z x z R y z R z x z ∈∧∈∃∧∈∧∈∃⇒ 3231),(),(R R y x R R y x ∈∧∈⇒ 3231),(R R R R y x ∈⇒2.对于任一非空集合A ,Φ⊆A2 ( T ) 3.文法G :S A|AS A a|b|c|d|e|f|g 是RG ( F ) 4.3型语言2型语言1型语言0型语言 ( T )5.s (rs+s )*r=rr *s (rr *s )* ( F )不成立,假设r,s 分别是表示语言R ,S 的正则表达式,例如当R={0},S={1}, L(s(rs+s)*r)是以1开头的字符串,而L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) ≠ L(rr*s(rr*s)*) 所以s(rs+s)*r ≠ rr*s(rr*s)*,结论不成立三、设文法G 的产生式集如下,试给出句子aaabbbccc 的至少两个不同的推导(12分)。
形式语言与自动机理论试题
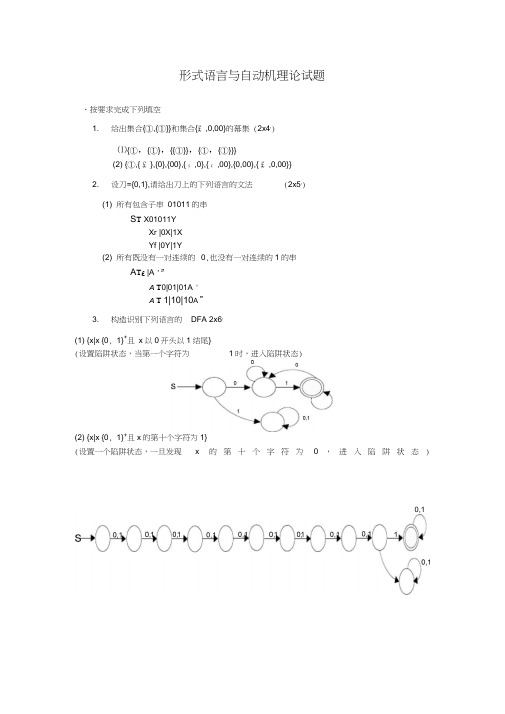
形式语言与自动机理论试题、按要求完成下列填空1. 给出集合{①,{①}}和集合{£ ,0,00}的幕集 (2x4')⑴{①,{①},{{①}},{①,{①}}}(2) {①,{ £ },{0},{00},{ £,0},{ £,00},{0,00},{ £ ,0,00}}2. 设刀={0,1},请给出刀上的下列语言的文法(2x5')(1) 所有包含子串01011的串S T X01011YXr |0X|1XYf |0Y|1Y(2) 所有既没有一对连续的0,也没有一对连续的1的串A T£ |A ' ”A T0|01|01A 'A T 1|10|10A ”3. 构造识别下列语言的DFA 2x6'(1) {x|x {0, 1}+且x以0开头以1结尾}(设置陷阱状态,当第一个字符为1时,进入陷阱状态)(2) {x|x {0, 1}+且x的第十个字符为1}(设置一个陷阱状态,一旦发现x的第十个字符为0,进入陷阱状态)0,1、判断(正确的写 T ,错误的写F ) 5x21•设R 和R 2是集合{a,b,c,d,e}上的二元关系,则(R只2)民RR 只只(T )任取(x.,y),其中 x,y {a,b,c,d,e},使得(x,y) (RR 2)FR 。
不成立,假设r,s 分别是表示语言 R, S 的正则表达式,例如当R={0}, S={1}, L(s(rs+s)*r)是以1开头的字符串,而 L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) L(rr*s(rr*s)*) 所以s(rs+s)*r rr*s(rr*s)*,结论不成立 、设文法G 的产生式集如下,试给出句子aaabbbccc 的至少两个不同的推导(12分)。
S aBC|aSBC aB abbB T bbCB T BC bC T bcC C T cc 推导一:S=>aSBC =>aaSBCBC =>aaaBCBCBC =>aaabCBCBC =>aaabBCCBC =>aaabbCCBC =>aaabbCBCCz((x, z) R R 2(z, y) R 3) z {a,b,c,d,e}z((x, z)R 1 (x, z )R 2(z, y) R 3)z((x,z)R 1 (z,y) R a )z((x,z)R 2 (z, y)(x,y)R 1 R 3(x, y) R 2R 3(x, y)R 1 R 3 R 2 R 32.对于任 •非空集合A , ①2A(T ) 3.文法G : S f A|AS A —► a|b|c|d|e|f|g 是 RG(F) 型语言2型语言1型语言0型语言(T )*(rs+s ) * *r=rr s (rr s ) *(F )R a )=>aaabbBCCC=>aaabbbCCC=>aaabbbcCC=>aaabbbccC=>aaabbbccc推导二:S=>aSBC =>aaSBCBC =>aaaBCBCBC =>aaaBBCCBC =>aaaBBCBCC=>aaabBCBCC =>aaabbCBCC =>aaabbBCCC =>aaabbbCCC =>aaabbbcCC=>aaabbbccC =>aaabbbccc四、判断语言{O n1n O n|n>=1}是否为RL如果是,请构造出它的有穷描述(FA,RG或者RL); 如果不是,请证明你的结论(12分)解:设L={O n1n O n|n>=1}。
形式语言与自动机理论试题答案解析
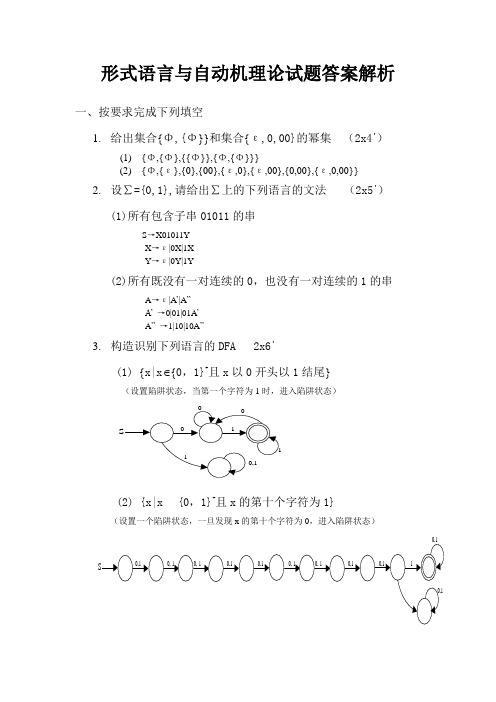
形式语言与自动机理论试题答案解析一、按要求完成下列填空1. 给出集合{Φ,{Φ}}和集合{ε,0,00}的幂集 (2x4')(1) {Φ,{Φ},{{Φ}},{Φ,{Φ}}}(2) {Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}2. 设∑={0,1},请给出∑上的下列语言的文法 (2x5') (1)所有包含子串01011的串 S →X01011YX →ε|0X|1X Y →ε|0Y|1Y(2)所有既没有一对连续的0,也没有一对连续的1的串 A →ε|A ’|A ”A’ →0|01|01A ’ A ” →1|10|10A ”3. 构造识别下列语言的DFA 2x6'(1) {x|x {0,1}+且x 以0开头以1结尾} (设置陷阱状态,当第一个字符为1时,进入陷阱状态)1S110,10(2) {x|x{0,1}+且x 的第十个字符为1}(设置一个陷阱状态,一旦发现x 的第十个字符为0,进入陷阱状态)1S0,10,10,10,10,110,0,10,10,10,10,1二、判断(正确的写T ,错误的写F ) 5x2'1R 和2R 是集合{a,b,c,d,e}上的二元关系,则3231321)(R R R R R R R ⊆( T )任取(x.,y),其中x,y },,,,{e d c b a ∈,使得321)(),(R R R y x ∈。
)),(),((321R y z R R z x z ∈∧∈∃⇒ },,,,{e d c b a z ∈ )),(),(),((321R y z R z x R z x z ∈∧∈∧∈∃⇒)),(),(()),(),((3231R y z R z x z R y z R z x z ∈∧∈∃∧∈∧∈∃⇒ 3231),(),(R R y x R R y x ∈∧∈⇒ 3231),(R R R R y x ∈⇒2.对于任一非空集合A ,Φ⊆A2 ( T ) 3.文法G :S A|AS A a|b|c|d|e|f|g 是RG ( F )2型语言1型语言0型语言 ( F )5.s (rs+s )*r=rr *s (rr *s )* ( F )不成立,假设r,s 分别是表示语言R ,S 的正则表达式,例如当R={0},S={1}, L(s(rs+s)*r)是以1开头的字符串,而L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) ≠ L(rr*s(rr*s)*) 所以s(rs+s)*r ≠ rr*s(rr*s)*,结论不成立三、设文法G 的产生式集如下,试给出句子aaabbbccc 的至少两个不同的推导(12分)。
形式语言与自动机Chapter5练习参考解答

Chapter 5 练习参考解答Exercise 5.1.2 (c) 下面的文法产生了正则表达式0*1(0+1)*的语言:εε|1|0|01B B B A A BA S →→→试给出下列串的最左推导和最右推导:c) 00011。
参考解答:一个最左推导:S ⇒lm A1B ⇒lm 0A1B ⇒lm 00A1B ⇒lm 000A1B ⇒lm 0001B ⇒lm 00011B ⇒lm 00011一个最右推导:S ⇒rm A1B ⇒rm A11B ⇒rm A11 ⇒rm 0A11⇒rm 00A11⇒rm 000A11 ⇒rm 00011! Exercise 5.1.3 证明任何正则语言都是上下文无关语言。
提示:通过对正则表达式中的运算符的数目进行归纳的方法来构造CFG 。
参考解答:对于任何正规表达式R ,归纳于R 中算符的数目n 构造如下产生式集合P(R),相应的开始符号为S(R):基础:n=0.(1)R 为ε,则任选非终结符A ,令P(R)只包含A →ε,以及S(R)为A ;(2)R 为φ,令P(R) 为空集;(3)R 为a ,则任选非终结符A ,令P(R)只包含A →a ,以及S(R)为A ; 基础:n>0.(1)R为R1+R2,则适修改非终结符的名字,使得P(R1)与P(R2)中的所有非终结符没有重名,任选不出现在P(R1)⋃P(R2)中的非终结符A,令P(R)= P(R1) ⋃P(R2)⋃{ A→ S(R1), A→ S(R2) },并且,令S(R)为A;(2)R为R1R2,则适修改非终结符的名字,使得P(R1)与P(R2)中的所有非终结符没有重名,任选不出现在P(R1)⋃P(R2)中的非终结符A,令P(R)= P(R1) ⋃P(R2)⋃{ A→ S(R1)S(R2) };并且,令S(R)为A;(3)R为R1*,任选不出现在P(R1) 中的非终结符A,令P(R)= P(R1) ⋃{ A→ AS(R1) , A→ε };并且,令S(R)为A.设L为正规语言,R为正规表达式,且有L=L(R). 令上下文无关文法G 的产生式集合为上述归纳过程所得到的P(R),以及G的开始符号为S(R). 可以归纳证明L(G)=L(R)=L.! Exercise 5.1.4 (选做)如果一个CFG的每个产生式的体都最多只有一个变元,并且该变元总在最右端,那么该CFG称做右线性的。
形式语言与自动机Chapter3练习参考解答
Chapter 3 练习参考解答Exercise 3.1.1 写出下列语言的正规表达式:c) The set of strings of 0' s and1' s with at most one pair of consecutive 1' s.c)最多包含两个相继的 1 的所有0, 1 字符串的集合.参考解答:该题的翻译有二义性(Sorry ).1)按原题意的解法对不包含相继的 1 的所有0, 1 字符串的集合,正规表达式可以为:1*(0+01)* 或(0+10 )*1*;包含最多一对相继的1,正规表达式可以为:(0+10)*11(0+01)*;所以,结果正规表达式可以为:1*(0+01)* + (0+10 )*11(0+01)2)若理解为11 可以出现多次的解法正规表达式可以为:1*(0+01+011 )* 或(0+10+110)*1*;等等Exercise 3.1.2 写出下列语言的正规表达式:b) 0 的个数能够被 5 整除的所有0, 1 字符串的集合. 参考解答:该题问题不多.正规表达式可以为:(1*01*01*01*01*01* )*Exercise 3.2.1(2)c)给出所有正规表达式R(i2j), 并尽可能简化之.d)给出该自动机的语言的一个正规表达式.参考解答:该题问题反映较多的是关于正规表达式的简化. 本科程较侧重原理,技术方面不够细致,因此对于“最简“的正规表达式没有作明确的规定,也没有类似于命题演算中有关”范式“的讨论.同学们在做题时除了应用有关定律外, 还可以自己总结出一些规律,比如一个表达式的语言 R 是另一个表达式S 所代 表语言的一个子集,则对于 R+S 就可以消去R ,例如 +1*可以简化为1*.再 如,在已做过的习题中出现的公式,例如Exercise3.4.1(g)我们可以验证(汁R)*= R*,因此 (+1)*可以简化为1*.综合已阅过的作业,推荐以下结果:C) R (121)= 1*+1*0 ( +11*0)*11* = 1*+1*0(11*0)*11*R (1 2 = 1*0+1*0 ( ;+11*0)* ( ;+11*0) = 1*0(11*0)*R (123)= * +1*0 2+11*0)*0 = 1*0(11*0)*0R (221)= 11* + ( +11*0) ( +11*0)*11* = (11*0)*11* R (222)= +11*0 + ( +11*0) ( ;+11*0)* ( ;+11*0) = (11*0)*R (223)= 0 + ( +11*0) ( +11*0)*0 = (11*0)*0R (321) = * + 1 (<+11*0)*11* =1(11*0)*11*R (322)= 1 + 1 ( +11*0)* ( ;+11*0) =1(11*0)*R (323)= ; + 0 + 1 ( +11*0)* 0 = ; + 0 + 1(11*0)*0d)该自动机的语言的一个正规表达式为R (133) =1*0(11*0)*0 +1*0(11*0)*0 ( ; + 0 + 1(11*0)*0)* ( ; + 0 + 1(11*0)*0)=1*0(11*0)*0 (0 + 1(11*0)*0)*Exercise 3.2.3 使用状态消去技术,将如下 DFA 转化为一个正规表达式.参考解答:该题问题不多,状态消去的次序不同,结果形式上可能有所不同,但 相互之间是等价的.以下是一个解法:/1+0(01+10*11)*(00+10*10) Start 5结果正规表达式可以为:(1+0(01+10*11)*(00+10*10))* 原状态图:消去状态r :消去状态s :1Start 0Exercise 324 将下列正规表达式转化为带 &转移的NFA.b) (0+1)01 c) 00(0+1)*参考解答:若严格按照所介绍的算法构造,则结 果如下:b)Exercise 3.4.1验证下列包含正规表达式的等式 c) (RS) T = R (ST) .g)(+R)* = R* . 参考解答:c)将两个表达式具体化,将R 替换为a ,将S 替换为b.(RS)T 具体化为(ab)a ,R(ST)具体化为 a(ba),而 L((ab)a)=L(a(ba))={abc}, 所以原等式成立;g)将两个表达式具体化,将R 替换为a.(+R)* 具体化为(;+a)*,R*具体化为 a*,而 L(( +a)*)=L(a*)={ ,a ,aa,aaa,…, (注:严格证明L(( ;+a)*)=L(a*),可以在归纳证明:对任意k>=0,{;,a}k ={a}k 的基础上进行),所以原等式成立;Exercise 342证明或否证下列关于正规表达式的命题 b) (RS+R)*R = R (SR+R)*.d) (R+S)*S = (R*S)* .Start参考解答:b)将两个表达式具体化,将R替换为a,将S替换为b.(RS+R)*R 具体化为(ab+a)*a,R (SR+R)*具体化为a(ba+a)*,可以证明L((ab+a)*a)=L(a(ba+a)*) (注:同上,可以先归纳证明:对任意k>=0,{ab,a}k{a}={a}{ba ,a}k,而由连接运算对-运算的分配律,—k —k 可知L((ab+a)*a)= *0,1,2, -({ab,a} {a}), L(a(ba+a)*)= k=o,1,2, ・({a}{ba,a}),由此证得L((ab+a)*a)=L(a(ba+a)*)),所以原等式成立;g)将两个表达式具体化,将R替换为a,将S替换为b.(R+S)*S 具体化为(a+b)*b,(R*S)* 具体化为(a*b)*,由于〉L((a*b)*),而>■' L((a*b)*),所以原等式不成立。
形式语言与自动机Chapter6练习参考解答
Chapter 6 练习参考解答Exercise 6.2.1 设计PDA 使它接受下列语言,你可以使用以终结状态方式接受或者以空栈方式接受中方便的一个。
b) 所有由0,1 构成的,并且任何前缀中 1 的个数都不比0 的个数多的串的集合。
c) 所有0,1 个数相同的0,1 串的集合。
参考解答:b)构造以终态方式接受的PDA P = (Q,艺,r , S , q o, Z o, F),其中Q={q o};状态q o表示当前扫描过的输入串的任何前缀中1的个数不比0的个数多;工={0 , 1};r ={ Z o, X};下推栈中,X的个数表示当前扫描过的输入串中o的个数比1 的个数多多少;F={q o};S (q o,o, Z o)={( q o,X Z o)}, S (q o,o, X)={( q o,X X)}, S (q o,1, X)={( qo, )}.c)构造以空栈方式接受的PDA P = (Q, 2 , r , S , q o, Z o),其中Q={q o, q i };状态q o表示当前扫描过的输入串的任何前缀中o的个数不少于1 的个数,状态q1 表示当前扫描过的输入串的任何前缀中 1 的个数不少于o 的个数;2 ={o, 1};r ={ Z o, X };下推栈中,X的个数表示当前扫描过的输入串中o的个数比i 的个数或 1 的个数比o 的个数多多少;S(q o,o, Z o)={( q o,X Z o)}, S(q o,1, Z o)={( q1,X Z o)};S (q i,O, Z o)={( q o,X Z o)}, S (q i,1, Z o)={( q i,X Z o)};S (q o,O, X)={( q o,X X)}, S (q o,1, X)={( q o, )};S(q1,o, X)={( q 1, )},S(q1,1, X)={( q 1, X X)} ;S(q o, , Z o)={( q o, )},S(q1, , Z o)={( q1, )}.Exercise 6.3.2 把下面的文法S aAAA aS | bS | a转换成以空栈方式接受同样语言的PDA 。
形式语言与自动机蒋宗礼答案
形式语言与自动机蒋宗礼答案形式语言与自动机蒋宗礼答案【篇一:形式语言第四章参考答案(蒋宗礼)】p> 解:所求正则表达式为:(0+1)*。
+⑵ {0, 1}。
解:所求正则表达式为:(0+1)+。
⑶ { x│x∈{0,1}且x中不含形如00的子串 }。
解:根据第三章构造的fa,可得所求正则表达式为:1*(01+)*(01+0+1)。
⑷ { x│x∈{0,1}*且x中不含形如00的子串 }。
++ +q1为终态时的正则表达式:0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式:0*11*0((10)*(111*11*0)*(00*11*0)*)*q3为终态时的正则表达式:0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式:0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)* 将以上5个正则表达式用“+”号相连,就得到所要求的正则表达式。
⑺ { x│x∈{0,1}且当把x看成二进制数时,x模5与3同余和x为0时,│x│=1且x≠0时,x的首字符为1}。
解:先画出状态转移图,设置5个状态q0、q1、q2、q3、q4,分别表示除5的余数是0、1、2、3、4的情形。
另外,设置一个开始状态q.由于要求x模5和3同余,而3模5余3,故只有q3可以作为终态。
由题设,x=0时,│x│=1,模5是1,不符合条件,所以不必增加关于它的状态。
下面对每一个状态考虑输入0和1时的状态转移。
q: 输入1,模5是1,进入q1。
+q0: 设x=5n。
输入0,x=5n*2=10n,模5是0,故进入q0输入1,x=5n*2+1=10n+1,模5是1,故进入q1q1:设x=5n+1。
输入0,x=(5n+1)*2=10n+2,模5是2,故进入q2输入1,x=(5n+1)*2+1=10n+3,模5是3,故进入q3 q2:设x=5n+2。
形式语言与自动机答案蒋宗礼
形式语言与自动机答案蒋宗礼【篇一:形式语言第四章参考答案(蒋宗礼)】p> 解:所求正则表达式为:(0+1)*。
+⑵ {0, 1}。
解:所求正则表达式为:(0+1)+。
⑶ { x│x∈{0,1}且x中不含形如00的子串 }。
解:根据第三章构造的fa,可得所求正则表达式为:1*(01+)*(01+0+1)。
⑷ { x│x∈{0,1}*且x中不含形如00的子串 }。
++ +q1为终态时的正则表达式:0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式:0*11*0((10)*(111*11*0)*(00*11*0)*)*q3为终态时的正则表达式:0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式:0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)*将以上5个正则表达式用“+”号相连,就得到所要求的正则表达式。
⑺ { x│x∈{0,1}且当把x看成二进制数时,x模5与3同余和x为0时,│x│=1且x≠0时,x的首字符为1}。
解:先画出状态转移图,设置5个状态q0、q1、q2、q3、q4,分别表示除5的余数是0、1、2、3、4的情形。
另外,设置一个开始状态q.由于要求x模5和3同余,而3模5余3,故只有q3可以作为终态。
由题设,x=0时,│x│=1,模5是1,不符合条件,所以不必增加关于它的状态。
下面对每一个状态考虑输入0和1时的状态转移。
q: 输入1,模5是1,进入q1。
+q0: 设x=5n。
输入0,x=5n*2=10n,模5是0,故进入q0输入1,x=5n*2+1=10n+1,模5是1,故进入q1q1:设x=5n+1。
输入0,x=(5n+1)*2=10n+2,模5是2,故进入q2输入1,x=(5n+1)*2+1=10n+3,模5是3,故进入q3 q2:设x=5n+2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形式语言与自动机理论试题答案解析
一、按要求完成下列填空
1.给出集合{Φ,{Φ}}和集合{ε,0,00}的幂集(2x4')
(1) {Φ,{Φ},{{Φ}},{Φ,{Φ}}}
(2) {Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}
2.设∑={0,1},请给出∑上的下列语言的文法(2x5')
(1)所有包含子串01011的串
S→X01011Y
X→ε|0X|1X
Y→ε|0Y|1Y
(2)所有既没有一对连续的0,也没有一对连续的1的串
A→ε|A’|A”
A’→0|01|01A’
A”→1|10|10A”
3.构造识别下列语言的DFA 2x6'
(1) {x|x∈{0,1}+且x以0开头以1结尾}
(设置陷阱状态,当第一个字符为1时,进入陷阱状态)
(2) {x|x∈{0,1}+且x的第十个字符为1}
(设置一个陷阱状态,一旦发现x的第十个字符为0,进入陷阱状态)
二、判断(正确的写T ,错误的写F ) 5x2'
1.设1R 和2R 是集合{a,b,c,d,e}上的二元关系,则
3231321)(R R R R R R R ⊆ ( T )
任取(x.,y),其中x,y },,,,{e d c b a ∈,使得321)(),(R R R y x ∈。
)),(),((321R y z R R z x z ∈∧∈∃⇒ },,,,{e d c b a z ∈ )),(),(),((321R y z R z x R z x z ∈∧∈∧∈∃⇒
)),(),(()),(),((3231R y z R z x z R y z R z x z ∈∧∈∃∧∈∧∈∃⇒ 3231),(),(R R y x R R y x ∈∧∈⇒ 3231),(R R R R y x ∈⇒
2.对于任一非空集合A ,Φ⊆A
2 ( T ) 3.文法G :S A|AS A a|b|c|d|e|f|g 是RG ( F ) 4.3型语言
2型语言
1型语言
0型语言 ( F )
5.s (rs+s )*r=rr *s (rr *s )* ( F )
不成立,假设r,s 分别是表示语言R ,S 的正则表达式,例如当R={0},S={1}, L(s(rs+s)*r)是以1开头的字符串,而L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) ≠ L(rr*s(rr*s)*) 所以s(rs+s)*r ≠ rr*s(rr*s)*,结论不成立
三、设文法G 的产生式集如下,试给出句子aaabbbccc 的至少两个不同的推导(12分)。
aSBC
aBC S |→
ab aB bB →bb CB →BC bC →bc cC →cc
推导一:
S=>aSBC
=>aaSBCBC =>aaaBCBCBC =>aaabCBCBC =>aaabBCCBC =>aaabbCCBC =>aaabbCBCC =>aaabbBCCC =>aaabbbCCC =>aaabbbcCC =>aaabbbccC =>aaabbbccc
推导二:
S=>aSBC
=>aaSBCBC =>aaaBCBCBC
=>aaaBBCCBC =>aaaBBCBCC
=>aaabBCBCC
=>aaabbCBCC
=>aaabbBCCC =>aaabbbCCC =>aaabbbcCC
=>aaabbbccC =>aaabbbccc
四、判断语言{n n n 010|n>=1}是否为RL ,如果是,请构造出它的有穷描述(FA,RG 或者RL );如果不是,请证明你的结论(12分)
解:设L={n n n 010|n>=1}。
假设L 是RL ,则它满足泵引理。
不妨设N 是泵引理所指的仅依赖于 L 的正整数,取Z=N N N 010 显然,Z ∈L 。
按照泵引理所述,必存在u ,v ,w 。
由于|uv|<=N,并且|v|>=1,所以v 只可能是由0组成的非空串。
不妨设v=k 0,k>=1 此时有u=j k N --0 ,w=N N j 010 从而有uv i w=N N j i k j k N 010)0(0-- 当i=2时,有uv 2w=N N k N 010+ 又因为k>=1,
所以 N+k>N 这就是说N N k N 010+不属于L , 这与泵引理矛盾。
所以,L 不是RL 。
五、构造等价于下图所示DFA 的正则表达式。
(12分)
答案(之一):(
01+(1+00)((1+00*1)0)*((1+00*1)1)
)*
(ε+(1+00)((1+00*1)0)*00*)
3
Y
S
30
去掉q 3:
去掉q 1
去掉q 2:
Y
Y
01+(1+00)((1+00*1)0)*((1+00*1)1)
去掉q 0:
六、设M=({210,,q q q },{0,1},{0,1,B},{δ},0q ,B,{2q }),其中δ的定义如下:
δ(0q ,0)=(0q ,0,R ) δ(0q ,1)=(1q ,1,R ) δ(1q ,0)=(1q ,0,R ) δ(1q ,B )=(2q ,B ,R )
请根据此定义,给出M 处理字符串00001000,10000的过程中ID 的变化。
(10分)
解:处理输入串00001000的过程中经历的ID 变化序列如下:
0q 00001000
00q 0001000
000q 001000
0000q 01000
00000q 10000
000011q 0000 0000101q 00
00001001q 0
000010001q
00001000B 2q
处理输入串10000的过程中经历的ID 变化序列如下:
0q 10000
11q 00000 101q 000 1001q 00 10001q 0 100001q
10000B 2q
X
Y
(01+(1+00)((1+00*1)0)*((1+00*1)1))* ( +(1+00)((1+00*1)0)*00*)
七、根据给定的NFA,构造与之等价的DFA。
(14分)NFA M的状态转移函数如下表
解答:。
