弯曲与扭转的组合变形
材料力学第八章组合变形

A截面
C3
C1
C4
C3
C1
C2
C4
T
C1
C2
三、强度分析
1.主应力计算
1 2 2 1 2 ( ) 4 2 3 2 2 2 2
C1
2 0
2.相当应力计算 第三强度理论,计算相当力
r 3 1 3 4
拉
z0 z
y
z1
F F
350 n n 150
50
50 150
F
n
n
FN My
由弯矩 My产生的最大弯曲正应力为
tmax
max c
M y z0 425 7.5F MPa ( ) Iy 5310 M y z1 425 12.5 F MPa ( ) Iy 5310
杆件将发生拉伸 (压缩 )与弯曲组合变形 示例1 F1 产生弯曲变形 F2 产生拉伸变形 示例2 F2 F1 F2
Fy 产生弯曲变形
Fx 产生拉伸变形
Fy
F
Fx
三、内力分析
横截面上内力 FS Mz
O
z x
FN
1.拉(压) :轴力 FN
2.弯曲
剪力F
弯矩 Mz
s
y
因为引起的切应力较小,故一般不考虑.
2 z 2 y
My Qy T
Mz Qz
T H1 r 510 Nm
l
强度校核
按第四强度理论
r4
1 W
M 0.75T 111 MPa [ ]
2 2
工程力学弯扭组合
Fy
Fz
A 1 B 100 300
Fy F'y
d
C
F'y Fz
1
D 300 2
2 F'z
F'z
D1 D2
上海应用技术学院
Fy Fz
A 1 B 100 300
Fy F'y
d
C
F'y
Fz
1 2
11
2 F'z
300
D
F'z
Fy M1 Fz
A
y M2
B
F'y
C
D1 D2
D
z 解:1. 外力分析
x
32 M 0.75 T 2 πd 3
2
O
x
32 1.0642 106 0.75 1 106 99.4MPa [σ ] 3 π 0.052
∴ 轴满足强度要求。
上海应用技术学院
例4 已知一单级直齿圆柱齿轮减速器输出轴,齿轮轮齿受力:14 Ft= 4053 N,Fr=1475.2 N,输出转矩T= 664669 N· mm,支 承间跨距 l=180mm,齿轮对称布置,轴的材料为 45钢,许 用应力[s ]=100 MPa。 试按第三强度理论确定该轴危险截面处的直径 d。
上海应用技术学院
㊀
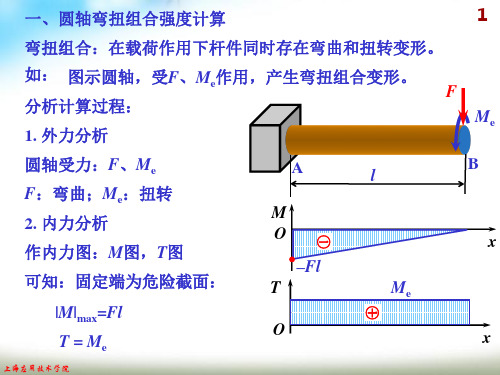
x Me
–Fl
O
x
3. 应力分析 由危险截面上的s、t 分布可知: a、b点为危险点: 取单元体: a b A M O T
㊉
F
2 MesMa来自lBsM
M σM W T T sM τT Wp 2W
tT tT
b
组合变形

M y 187 N m
T 1020 N m
合弯矩:
2 M M y M z2 4402 187 2
478N m
第四强度理论:
W
r4
1 W
M 2 0.75T 2
603 109
32
21.2110 6 m3
危险截面: B 截面
T 21.7 N m M 26.7 N m
第三强度理论:
r3
W
1 W
M 2 T 2
T图
21.7 N m
353 109
32
2
4.2110 6 m3
2
r3
8.18MPa
26.7 21.7 4.21106
第四强度理论:
式中: T
r4
危险截面上的扭矩 危险截面上的合弯矩
M
M
实心轴 W
2 2 My Mz
D3
32 D3 空心轴 W 1 4 32
,
例题 8-5 45钢的传动轴AB的直径为35mm,许用应力为 85MPa。电动机功率P = 2.2kW,由带轮C 传入。带轮C转速为 966r/min,带轮的直径为 D = 132mm,带拉力为F+F’ = 600N。齿轮E的 d 节圆直径为: 1 50mm 。
Fz Fz F sin 240 F sin 300 257 N
二、作出轴的弯矩图 和扭矩图
T图
21.7 N m
My 图
7.43N m 20.4 N m 11.4 N m 24.1N m
Mz 图
工程力学弯扭组合精选全文

为弯扭组合。
上海应用技术学院
2. 内力分析 作 T 图: 作M 图:
危险截面为E 截面:
M 1kN m T 1kN m
3. 确定轴的直径 d
M1
A
z T
y
F
M2
E C
1kN·m
9
x
B
由第四强度理论:
O
x
σr4
M
M 2 0.75T 2 32 W
M 2 0.75T 2 πd 3
[σ]
O
1kN·m
用应力[s ]=100 MPa。
试按第三强度理论确定该轴危险截面处的直径 d。
上海应用技术学院
解: 计算简图: 1. 外力分析 约束力: FBy = FDy = Fr/2= 737.6 N FBz = FDz = Ft/2= 2026.5 N 2. 内力分析 作垂直面弯矩图: 作水平面弯矩图:
上海应用技术学院
径D= 300mm,材料的许用应力[s ]=160MPa。
试按第四强度理论确定轴AB的直径。
上海应用技术学院
8
y
F
M1
M2
A
E
C
z
x
B
解:1. 外力分析
由 SMx=0
M1
(FN
FN
)
D 2
得:F'N= 6.67kN FN= 13.33kN
将FN,F'N向轴线平移: F = F'N+FN= 20.1kN M2=1kN·m
M1
A
B
150
200
F2y = F2z tan10º=70.5N
上海应用技术学院
C 100 D z
F2y y M2
弯扭组合变形实验报告数据

实验名称:弯扭组合变形实验一、实验目的:1. 通过实验,了解和掌握材料在弯扭组合变形下的力学性能。
2. 熟悉和掌握弯扭组合变形的测量方法和数据处理技巧。
3. 通过实验,验证理论知识和计算方法的正确性。
二、实验设备:1. 材料试验机2. 弯曲和扭转加载装置3. 千分尺4. 数据记录仪三、实验材料:1. 实验材料为Q235钢,其化学成分和力学性能如下:-碳(C)含量:0.12%-锰(Mn)含量:0.3%-硅(Si)含量:0.3%-磷(P)含量:0.035%-硫(S)含量:0.035%-屈服强度:235MPa-抗拉强度:375MPa-伸长率:26%四、实验步骤:1. 将试样安装在试验机上,确保试样与加载装置之间的接触良好。
2. 设置试验机的弯曲和扭转加载参数,包括加载速度、加载时间等。
3. 开始加载,同时记录试样的弯曲和扭转角度以及载荷大小。
4. 当试样发生断裂时,停止加载,记录断裂载荷和断裂角度。
5. 清理实验现场,整理实验数据。
五、实验数据:1. 试样尺寸:长度100mm,宽度10mm,厚度2mm。
2. 弯曲加载参数:加载速度1mm/min,加载时间1min。
3. 扭转加载参数:加载速度1r/min,加载时间1min。
4. 实验数据记录如下:-弯曲角度:0°,15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°,180°。
-扭转角度:0°,15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°,180°。
-弯曲载荷:0N,2.5N,5N,7.5N,10N,12.5N,15N,17.5N,20N,22.5N,25N,27.5N,30N。
悬臂梁弯扭组合变形设计案例

悬臂梁弯扭组合变形设计案例咱们来聊一个悬臂梁弯扭组合变形的设计案例,就像搭积木一样,但这个积木可是有大学问的。
想象一下,有一个机械手臂,它就像是一个悬臂梁。
这个机械手臂在工作的时候啊,可不光是受到一种力的作用,而是弯扭组合的变形情况。
一、项目背景。
这个机械手臂呢,要在一个自动化生产线上工作。
它需要伸出去抓取零件,然后再把零件放到指定的位置。
在这个过程中,手臂一端固定在机器上(这就是悬臂梁的固定端啦),另一端自由活动。
由于抓取的零件重量不一样,而且手臂运动的速度和方向也会变化,所以就产生了弯曲和扭转这两种变形情况。
二、受力分析。
1. 弯曲力。
当手臂伸出去抓取零件的时候,零件的重量就像一个小坏蛋,使劲儿地把手臂往下拽,这就产生了弯曲力。
比如说,我们抓取一个5千克的零件,假设手臂长度是1米,这个零件的重力就会在手臂上产生一个弯矩。
根据弯矩的计算公式M = FL(这里F就是零件的重力,L就是手臂的长度),那这个弯矩就是M = 5×9.8×1 = 49牛·米(这里g = 9.8米/秒²)。
这个弯矩就会让手臂像被掰弯的小树枝一样,有弯曲变形的趋势。
2. 扭转力。
然后呢,当手臂转动把零件送到指定位置的时候,这个转动就产生了扭转力。
比如说,手臂要以一定的角速度转动,就像拧麻花一样,在手臂的轴线上就会产生扭矩。
假设手臂的转动惯量是I,角加速度是α,根据扭矩的计算公式T=Iα。
如果手臂快速地转动,这个扭矩可就不小了,它会让手臂产生扭转变形。
三、材料选择。
考虑到这种弯扭组合变形的情况,我们得找个厉害的材料来做这个悬臂梁(也就是机械手臂)。
经过一番挑选,我们选择了高强度合金钢。
为啥呢?这种材料就像钢铁侠的盔甲一样,又硬又结实。
它的屈服强度高,能够承受较大的弯曲和扭转应力。
比如说,它的屈服强度可以达到800兆帕,这就意味着在这么大的压力下,材料才会开始变形得很厉害。
而且它的韧性也不错,不会轻易断裂,就像一个坚强又有弹性的战士,能够在复杂的受力情况下保持稳定。
9.组合变形

2 y
2 z
设挠度 的方向与Y轴间的夹角 ,则:
z Iz tg tg y Iy
讨论:由上式可看出:要使得 必须:I z I y 即,只 有在 I z I y 的条件下,才是平面弯曲, 否则是斜弯 曲。
思考题
正方形,圆形,当外力作用线通过截面形心时,为平面弯曲还 是斜弯曲?
总目录
本章要点
(1)斜弯曲 (2)偏心压缩 (3)弯扭组合变形
重要概念
组合变形、斜弯曲、偏心压缩、弯扭组合
§9-1 概述
*工程中几种常见的组合变形:
斜弯曲 —————斜屋架上的檩条 拉弯组合 ————冻结管 偏心压缩 ————设有吊车的厂房柱子 弯扭组合变形——机床中靠齿轮传递的轴
由于组合变形是几种基本变形相互组合的结果, 因此,在进行组合变形下的强度和刚度计算时,只 需分别计算形成这种组合变形的几种基本变形下的 应力和变形,然后进行叠加即可得到组合变形下的 应力和变形。 计算组合变形强度问题的步骤如下:
可得中性轴的方程式为:
yP y z P z 1 2 2 0 iz iy
根据该方程式可知中性轴是不过形心的直线。
现令:应力零线N-N,它在y、z轴上的截距分别为 a y a z 分别将 a y ,0 0, az 代入 k 表达式得:
iZ 2 ay yP
aZ
2 1 2 2 1 2 2 3 3 1 2
将C式代入上式,简化整理后可得:
W 3
2
2 n
代入<a><b>式即可得:
1 W
M W 0.75Tn2
材料力学_ 组合变形_:扭转与弯曲的组合_

M2 T2 W
M 2 0.75T 2 W
式中W为杆的抗弯截面系数.M,T分别为危险截面的弯矩和扭 矩. 以上两式只适用于弯扭组合变形下的圆截面杆.
例题4 空心圆杆AB和CD杆焊接成整体结构,受力如图.AB杆的外
径 D=140mm,内外径之比α= d/D=0.8,材料的许用应力[] =
160MPa.试用第三强度理论校核AB杆的强度
A
C
D
F1
F2
解:将F2向AB杆的轴线简化得
400
ቤተ መጻሕፍቲ ባይዱ
400
F2 1kN Me 0.4kN m
AB为弯扭组合变形
B
A
C
D
F1
固定端截面是危险截面 F2
Mmax 0.8F1 0.4F2 0.8kN m
Tmax 0.4kN m
400
400
r3
Mm2 ax Tm2ax
W
d 38.5mm
W πd 3
32
d 44.83mm
MeC F=3F2
T=1kN·m + 1kN·m
+
例题6 F1=0.5kN,F2=1kN,[]=160MPa.
(1)用第三强度理论计算 AB 的直径 (2)若AB杆的直径 d = 40mm,并在B端加一水平力
F3 = 20kN,校核AB杆的强度.
400
400
B
对于许用拉压应力相等的塑性材
料制成的杆,这两点的危险程度是相同 的.可取任意点C1 来研究.
C1 点处于平面应力状态, 点的单元体如图示
该
C1
A截面
C3
C4
C2
C1
C3
T
C4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
按第三强度理论
eq3 1 3
代入已求的主应力得:
按第四强度理论
eq4
1 2
1
2
2
2
3
2
3
1 2
代入已求的主应力得:
eq3 2 4t 2
eq4 2 3t 2
eq3 2 4t 2 (A)
eq3
1 W
M 2 T 2
(B)
W
D1
tn
公式的使用条件
(A)(C)式适用 于形如D1点应力状 态的强度校核;
eq4 2 3t 2 (C)
eq4
1 W
M 2 0.75T 2 (D)
1 3
2
2 0
2
2
t
2
校核危险点的强度
对于脆性材料,由于拉大压小,应采用第一强度理论。
eq1 1
代入已求的主应力得:
eq1
2
2
2
t 2
T
校核危险点的强度 对于塑性材料,应采用第三强度理论或第四强度理论。
试比较采用哪个强度理论偏于保守(安全)?
二、弯曲--扭转组合变形
问题
A
z
y
T
MZ
PYL MY
校核AB杆的强度
内力分析
找危险截面
PY PZ
B
x Me
xy平面:MZ max PY L xz平面:MY max PZ L
? A截面危险! 圆截面双向平面弯曲 如何处理弯矩的问题
Me
My
最大拉应力σT
y
400
500
600
A
2t2
t1
C
D
x
B
z
t2
2t1
y
2t2
y
t1
45o c z t2
G2
Dz
G1
2t1
y
400
500
600
1.外力简化
A
2t2
t1
C
D
x
B
M0
9550
PK n
MC MD M0
z
3t2
t2
y
2t2
2t1
y
t1
t1
MD R1
t2
MC R2
pcy 3t2 cos 45o G2 PCZ 3t2 sin 45o
一、拉(压)--扭转组合变形
A
z
y
B
P Me
•画内力 图
N
校核AB杆的强度 x
•内力分析:拉-扭组合变形
•找危险截 面
任意截面
T
应力分析
D1
t
找危险点
在D1点截取原始单元体
D1
t
t D1
D2 危险点应力状态分析
D1
N
A
t T
原 始 单 元
WT 体
D1点是二向应力状态,根据 主应力公式求得主应力:
(B)(D)式适用 于塑性材料的圆截 面或空心圆截面轴 发生弯扭组合变形 的强度校核。
思考:如果危险截面是拉伸-弯曲-扭转组合变 形,应当怎么样校核强度?
y
PY
A
Px
x
PZ
Me
z
思考:曲拐受力如图,危险截面在哪里?应当 怎么样校核强度?
y q
A
z
l
2 ql 3 C
P
B a
例题:皮带轮传动轴如图示。已知D轮为主动轮,半径R1=30cm,
皮带轮自重G1=250N,皮带方向与Z轴平行;C轮为被动轮,皮带轮
自重G2=150N,半径R2=20cm,皮带方向与Z轴夹45度角。电动机的
功 率 PK=14.65 千 瓦 , 轴 的 转 速 n=240 转 / 分 , 轴 材 料 的 许 应 力
[σ]=80MPa 。 试用第三强度理论设计轴的直径d。
对于塑性材料,应采用第三强度理论或第四强度理论。
按第三强度理论
按第四强度理论
eq3 1 3
eq4
1 2
1
2
2
2
3
2
3
1 2
代入已求的主应力得:
代入已求的主应力得:
eq3 2 4t 2
eq4 2 3t 2
代入原始单元体应力元素, 并注意到圆截面WT=2W得:
eq3
1 W
M 2 T 2
Hale Waihona Puke 代入原始单元体应力元素, 并注意到圆截面WT=2W得:
eq4
1 W
M 2 0.75T 2
研究结果的讨论 对于危险点应力状态的强度条件
YB ZB
外力值的计算
M0
9550 PK n
955014.65 240
583 Nm
YA 4.39kN
t1
MD R1
583 30 102
1.79kN
t2
MC R2
583 20 103
2.69kN
ZA 6.33kN YB 1.71kN ZB 4.74kN
M
z
Mz
最大压应力σC
PZL
中性轴
y
应力分析
D1
t
找危险点
在D1点截取原始单元体
D1
t
t D1
D2 危险点应力状态分析
D1
M
W
t T
原 始 单 元
WT 体
D1点是二向应力状态,根据 主应力公式求得主应力:
1 3
2
2 0
2
2
t
2
校核危险点的强度
§8–4 弯曲与扭转的组合变 形
•问题的特点:在横截面上既有正应力又有切应力。
•分析问题的方法:由于正应力和切应力不能直接 相叠加,因此,必须根据不同的材料,采用适当 的强度理论进行强度分析。
•分析问题的步骤:根据内力图,确定危险截面, 在危险截面上画出应力分布,确定最大(拉、压) 应力(即:危险点),采用强度理论进行强度校核。
pcy 3t2 cos 45o G2 5.85kN
PCZ 3t2 sin 45o 5.7kN
PDy G1 0.25kN
PDz 3t1 5.37kN
y ZAA
FAY y
A y
MC
C
z PCY
PCZ
MC
C
z
MD
D PDZ
PDY
MD D
A
FAY y
C
z PCY
Z AA
C
z
PCZ
D
PDY
D
PDZ
Bx
YB ZB 2.内力计算
B x 圆轴
扭转
弯
B x Xy面的
扭 组 合
YB
平面弯曲
变
形
Xz面的
B x 平面弯曲
ZB
y
ZAA FAY
MC
C
z PCY
PCZ
T kNm
M Z kNm 1.756
M Y kNm 2.532
MD
D PDZ
PDY
0.538
1.026 2.844
45o c z
t2
MD
y G2
MC
ZA
3t1 Dz
M D G1
2t1
MD
PDy G1 PDz 3t1 YA,ZA,YB , ZB可由 平衡方程求得。
B x 轴上的外力
A FAY
C
z PCY
PCZ
D PDZ
PDY
YB ZB 可全部确定
y
ZA
A
FAY
MC
C
z PCY
PCZ
MD
D PDZ
PDY
Bx
