弯曲与扭转组合变形的强度计算.
12组合变形的强度计算.

例 一桥墩如图示。承受的荷载为:上部结构传递给桥墩的压力F0= 1920kN,桥墩墩帽及墩身的自重F1=330kN,基础自重F2=1450kN, 车辆经梁部传下的水平制动力FT=300kN。试绘出基础底部AB面上的 正应力分布图。已知基础底面积为b×h=8m×3.6m的矩形。
3700kN 1740kNm
例
FB
FAx
FBy
FAy
FBx
F
49.7kN
30kNm
B左截面压应力最大
max
FN M z A Wz
3
Mz Wz
Wz 187.5cm3
查表并考虑轴力的影响:
20a Wz 237cm
A 35.5cm
2
max
49.7 103 30 106 140.6MPa 2 3 35.5 10 237 10
bh 2 a b 1.786mm 12 F
12.1 弯扭组合变形的强度计算
一、弯扭组合变形的应力分析F
MBy B Iz M max max Wz
a
L
F Fa
T IP T max WP
2
B
x x 2 13 x 2 2
B
FL
1 3
2 4 2
1 1 2 2 2 3 2 3 1 2 2
Fa
2 3 2
二、弯扭组合变形的强度计算
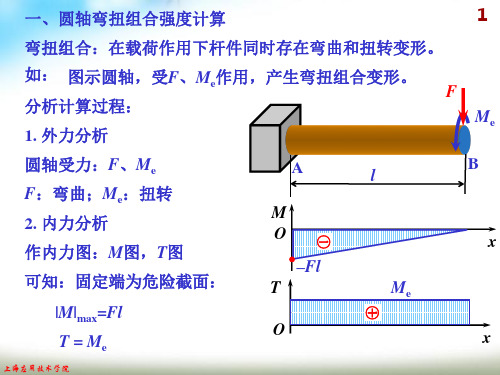
图示圆轴.已知,F=8kN,M=3kNm,[σ]=100MPa,试用第 三强度理论求轴的最小直径. T 3kNm M max FL 4kNm F
工程力学弯扭组合
Fy
Fz
A 1 B 100 300
Fy F'y
d
C
F'y Fz
1
D 300 2
2 F'z
F'z
D1 D2
上海应用技术学院
Fy Fz
A 1 B 100 300
Fy F'y
d
C
F'y
Fz
1 2
11
2 F'z
300
D
F'z
Fy M1 Fz
A
y M2
B
F'y
C
D1 D2
D
z 解:1. 外力分析
x
32 M 0.75 T 2 πd 3
2
O
x
32 1.0642 106 0.75 1 106 99.4MPa [σ ] 3 π 0.052
∴ 轴满足强度要求。
上海应用技术学院
例4 已知一单级直齿圆柱齿轮减速器输出轴,齿轮轮齿受力:14 Ft= 4053 N,Fr=1475.2 N,输出转矩T= 664669 N· mm,支 承间跨距 l=180mm,齿轮对称布置,轴的材料为 45钢,许 用应力[s ]=100 MPa。 试按第三强度理论确定该轴危险截面处的直径 d。
上海应用技术学院
㊀
x Me
–Fl
O
x
3. 应力分析 由危险截面上的s、t 分布可知: a、b点为危险点: 取单元体: a b A M O T
㊉
F
2 MesMa来自lBsM
M σM W T T sM τT Wp 2W
tT tT
b
工程力学弯扭组合精选全文

为弯扭组合。
上海应用技术学院
2. 内力分析 作 T 图: 作M 图:
危险截面为E 截面:
M 1kN m T 1kN m
3. 确定轴的直径 d
M1
A
z T
y
F
M2
E C
1kN·m
9
x
B
由第四强度理论:
O
x
σr4
M
M 2 0.75T 2 32 W
M 2 0.75T 2 πd 3
[σ]
O
1kN·m
用应力[s ]=100 MPa。
试按第三强度理论确定该轴危险截面处的直径 d。
上海应用技术学院
解: 计算简图: 1. 外力分析 约束力: FBy = FDy = Fr/2= 737.6 N FBz = FDz = Ft/2= 2026.5 N 2. 内力分析 作垂直面弯矩图: 作水平面弯矩图:
上海应用技术学院
径D= 300mm,材料的许用应力[s ]=160MPa。
试按第四强度理论确定轴AB的直径。
上海应用技术学院
8
y
F
M1
M2
A
E
C
z
x
B
解:1. 外力分析
由 SMx=0
M1
(FN
FN
)
D 2
得:F'N= 6.67kN FN= 13.33kN
将FN,F'N向轴线平移: F = F'N+FN= 20.1kN M2=1kN·m
M1
A
B
150
200
F2y = F2z tan10º=70.5N
上海应用技术学院
C 100 D z
F2y y M2
组合变形的强度计算

组合变形的强度计算 组合变形的概念拉伸与弯曲的组合一.组合变形的概念1.组合变形:在外力的作用下,构件若同时产生两种或两种以上基本变形的情况在小变形和线弹性的前提下,可以采用叠加原理研究组合变形问题所谓叠加原理是指若干个力作用下总的变形等于各个力单独作用下变形的总和(叠加)在复杂外载作用下,构件的变形会包含几种简单变形PRzxyPP2、组合变形的研究方法——叠加原理叠加原理应用的基本步骤:①外力分析:将载荷进行分解,得到与原载荷等效的几组载荷,使构件在每一组载荷的作用下,只产生一种基本变形.②内力分析:分析每种载荷的内力,确定危险截面.③应力分析:分别计算构件在每种基本变形情况下的危险将各基本变形情况下的应力叠加,确定最④强度计算:二.弯曲与拉伸(的组合杆件在外力作用下同时产生弯曲和拉伸(压缩)变形称为弯曲与拉伸(压缩)的组合偏心拉伸:弯曲与拉伸的组合变形链环受力立柱受力拉伸与弯曲组合的应力分析ϕϕsin p p cos p p y x ==A P x ='σy I M x l P M zy =''-=σ)(作用下:z T W M A N max max +=σzC W M A N max max -=σ危险截面处的弯矩抗弯截面模量y I M A N z +=''+'=σσσ根据叠加原理,可得x 横截面上的总应力为[]T z max max T W M A N σσ≤+=[]c zmax max C W M A N σσ≤-=强度条件为例:悬臂吊车,横梁由25 a 号工字钢制成,l =4m ,电葫芦重Q 1=4kN ,起重量Q2=20kN , α=30º, [σ]=100MPa,试校核强度。
取横梁AB为研究对象,受力如图b所示。
梁上载荷为P =Q1+Q2= 24kN,斜杆的拉力S 可分解为X B和Y B(1)外力计算横梁在横向力P和Y A、Y B作用下产生弯曲;同时在X A和X B作用下产生轴向压缩。
第八章组合变形时的强度计算
Iy
IY
由 mz 产生的正应力
s"' MZ .y Fyp y
IZ
IZ
假设C 点在第一象限内,根据杆件的变形可知, s ',s '',s ''' 均为拉应
力,由叠加原理,即得 C点处的正应力为:
σ σ' σ'' σ'''
任意横截面 n-n上的 C点的正应力为
c
σ F F zP z F yP y
与y轴的夹角θ为:
tgθ z0 Mz Iy Iy tgφ y0 My Iz Iz
公式中角度 是横截面上合成弯矩 M 的矢量与 y 轴的夹角 . 横截面上合成弯矩 M 为:
M
M
2 y
M
2 z
tgθ Iy tgφ Iz
讨论:
(1) 一般情况下,截面的 IzIy ,故中性轴与合成弯矩 M 所在平面不垂直,此为斜弯曲的受力特征。导致挠曲线与外 力(合成弯矩)所在面不共面,此为斜弯曲的变பைடு நூலகம்特征。
s s ' s '' My z - Mz y
Iy
Iz
式中,Iy和Iz分别为横截面对于两对称轴y和z的惯性矩; M y和Mz分别是截面上位于水平和铅垂对称平面内的弯矩,且 其力矩矢量分别与y轴和z轴的正向相一致。在具体计算中,
也可以先不考虑弯矩M y、Mz和坐标y、z的正负号,以它们的 绝对值代入,然后根据梁在P1和P2分别作用下的变形情况, 来判断上式右边两项的正负号。
FN A
Mz Wz
158 MPa
s
所以强度是安全
【例8-4】矩形截面柱如图所示。P1的作用线与杆轴线重合, P2作用在 y 轴上。已知, P1= P2=80kN,b=24cm , h=30cm。 如要使柱的m—m截面只出现压应力,求P2的偏心距e。
弯扭组合应力实验报告

弯扭组合应力实验报告一、实验目的:1.了解弯扭组合应力的概念和特性;2.掌握弯扭应力下构件应变性能的变化规律;3.探究弯扭组合应力对材料疲劳寿命的影响。
二、实验原理:1. 弯曲应力在支撑不良时,构件横截面的形状和尺寸不再恒定,会引起截面内部应力和应变。
当弯曲应力作用于构件时,构件截面内部产生剪应力和正应力。
当弯曲跨度为l,力F作用在构件的中心处时,构件的弯曲应力σb可根据公式计算:σb = (M × y) / I2. 扭转应力当扭矩作用于杆件的端部时,杆件沿轴线方向的每一截面都要扭转。
因此,当扭矩t作用在截面上时,将产生切应力τ,它的大小可以使用公式计算:τ = (t × R) / I其中,R表示截面的半径,I表示扭转惯性矩。
3. 弯扭组合应力弯扭组合应力是指同时在构件上施加弯曲和扭转载荷时的应力。
具体而言,施加在构件上的载荷的平面与构件的长轴和横轴不平行,这会引起构件的剪辑应力。
弯扭组合应力的计算有许多方法,比较常用的一种方法是所谓的最大剪应力理论。
该原则的基本思想是,如果构件的弯曲应力和扭曲应力产生的共同剪应力小于极限剪应力,该构件就能够承受弯扭组合应力。
三、实验步骤:1. 准备实验设备,包括万能试验机,弯曲夹具和扭转夹具。
2.准备试样(直径为5mm的低合金钢棒)。
3.将试样安装在试验机的弯曲夹具和扭转夹具上。
4.施加不同的弯曲载荷和扭转载荷,并在此过程中记录试样在不同载荷下的弯曲度和扭转度。
5.根据试样的弯曲度和扭曲度计算出弯扭组合应力下试样的弯曲应力、扭曲应力以及最大剪应力。
6.比较不同载荷下试样的最大剪应力,计算出疲劳寿命。
四、实验结果分析:1.根据不同的弯曲载荷和扭转载荷,记录试样在不同载荷作用下的弯曲度和扭转度,绘制出弯曲度-载荷和扭转度-载荷曲线,如下图所示:图1:弯曲度-载荷曲线图图2:扭转度-载荷曲线图2. 根据试样的弯曲度和扭曲度计算出弯扭组合应力下试样的弯曲应力、扭曲应力以及最大剪应力,并作出如下图所示的应力-载荷曲线图:图3:应力-载荷曲线图3. 比较不同载荷下试样的最大剪应力,并计算出疲劳寿命,如下表所示:载荷(N)最大剪应力(MPa)疲劳寿命(次)100 42.31 1000200 82.4 2000300 118.6 3000五、实验结论:1.在弯曲载荷和扭转载荷的联合作用下,试样的变形强度和变形模式发生了明显变化,特别是当载荷超过一定阈值后。
弯曲与扭转组合变形的强度计算_工程力学_[共6页]
![弯曲与扭转组合变形的强度计算_工程力学_[共6页]](https://img.taocdn.com/s3/m/6ab7e43c6294dd88d1d26b3e.png)
σ1
σ+ 2
σ 2
2
+τ
2
,,
σ2
=
0
σ3
=
σ 2
−
σ 2
2
+τ2
对于塑性材料,通常选第三或第四强度理论,强度条件分别为
σ r3 = σ 2 + 4τ 2 ≤≤[σ≤] , σ r4 σ 2 + 3τ 2 [σ ]
(10.6)
将式(a)代入式(10.6)并注意到 Wp=2Wz,得到圆杆弯扭组合变形以内力表示的强度条件
= σ eq3
M 2 + = MT2 Wz
7.62 + 62 × 106 =
50.5 MPa <= [σ ]
80 MPa
π × 1253
32
计算结果表明轴 OA 的强度是足够的。
162
− 1125 × 103 1003 / 6
=6.99 MPa < [σ ]
故梁是安全的。
10.2 弯曲与扭转组合变形的强度计算
弯曲与扭转组合变形在机械工程中是很常见的,例如皮带轮传动轴、齿轮轴、曲柄轴等轴
类构件,在传递扭矩的同时往往还发生弯曲变形。
如图 10-5(a)所示水平直角曲拐,AB 段为圆杆,受集中力 F 作用。将 F 向 AB 杆的 B 端
σr3
= 1 M 2 + M Wz
2 n
≤≤[σ
]
,
σr4
= 1 M 2 + 0.75 Wz
M
2 n
[σ ]
(10.7)
工程中除了弯扭组合的杆件外,还有拉(压)与扭转的组合,或者拉压、弯曲与扭转的组 合变形,运用相同的分析方法,仍可用式(10.6)进行强度计算。
弯扭组合变形

作业:8-12 8-16
[σ]=180MPa, 用第三强度理论校核
F2 y
解: F2 z
M e1
=
F1y D1 2
= 95.8 N·m
轴的强度。 y
x B
A
z
Me2
=
F2 y D2 2
= 95.8 N·m
F1 y
M1e
F M 2e 2 y B
F1 z
C
F2 z
E
T/kN
95.8
x
T = 95.8 N·m
x
Mc =
M
2 z
+
M
2 y
=
152.32 + 37.52 =156.8 N·m
(M E =113N·m)
M 2 + T 2 32 156.82 + 95.82
r3 =
W
=
×223
Mz/N· m
=175.8 MPa<[ ] =180 MPa ∴此轴安全。
MyN·m
F1 y F2 y
152.3 112.9 x
F1z F2 z
=
M Amax W
≤ [σ]
σmt ax
= σe
=
M Amax W
≤ [σt ]
D3
W= 32
σmc ax
= σd
=
M Amax W
≤ [σc ]
例6. 梁表面A、B两点的纵向正应变为εA=2.1×10-4,
εB=3.2×10-4,l 试求b载荷Fl=及40其0m方m位,角b=β2。0mE=m2,00hG=P5a0。mm。
r4 = 2 + 3 2 =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
外力偶矩的大小为
10 M C M D 9550 N m 360 .38N m 265
则
Ft1
2M D
Fr1 Ft1 tan 1820 N tan20 662N
Fr 2 Ft 2 tan 4290 N tan20 1561 N
MC =(FT+Ft)D/2
FT+Fd=(8+4)kN=12kN M=(FT-Fd)D/2
c)
T=(FT-Ft)D/2
=(8-4)×0.5/2kN· m=1kN· m
FT+Fd与A、B处的约束力使轴产生
弯曲变形,附加力偶M与联轴器上的 外力偶使轴产生扭转变形,因此,轴
d) 图8-4
AB发生弯扭组合变形。
(2)作内力图 如图所示,轴在两相互垂直的平面内同时受到力的作用, 所以在两个平面内都会发生弯曲变形,同时也可以作出两个相
D2
2 360.38103 N 1820 N 396
2M D 2 360.38103 Ft 2 N 4290 N D2 168
Myz Mxy
133N· m
M max Mn max 和 max Wz Wn
式中,Mmax为危险截面上的弯矩;Mn为危险截面上的扭矩;Wz 为抗弯截面系数;Wn为抗扭截面系数。 第三、第四强度理论的强度条件分别为
xd 3 2 4 2 [ ]
xd 4 2 3 2 [ ]
第二节 弯曲与扭转组合变形的强度计算
一、弯曲与扭转组合变形的概念
Y A
C
F
Z
B x
a)
Y
A MA F Z
l
B
b)
x
c)
MB=Fl
图8-3
Mn=FR
d)
二、应力分析与强度计算 圆轴在力F和力偶MA的作用下,横截面上存在着变矩与扭
矩,作出圆轴的弯矩图(图8-3c)和扭矩图(图8-3d)。危险点
的正应力和切应力的值分别为
2 2 M D M Dyz M Dxy 263 2 1312 N m 293 .82N m
(3) 按第四强度理论
xd 4
2 MD 0.75T 2 Wz
32 3 2 3 2 ( 297 . 94 10 ) 0 . 75 ( 360 . 38 10 ) MPa 3 50
式中бxd3为第三强度理论的相当应力;бxd4为第四强度理论 的相当应力。
圆轴弯扭组合变形时第三、第四强度理论的强度条件分别
为
M max M n2 xd 3 [ ] Wz
2
(8-3)
xd 4
2 M max 0.75M n2 [ ] Wz
(8-4)
例8-3 图8-4a所示的直轴AB,在轴右端的联轴器上作用有 外力偶M。已知带轮直径D=0.5m,带拉力FT=8kN,Ft=4kN,轴 的直径d=90mm,间距a=500mm,若轴的许用应力[б]=50MPa。
2 M max M n2 (3 10 6 ) 2 (110 6 ) 2 xd 3 MPa 3 Wz 0.1 90
43.4MPa <[б]
所以轴的强度满足要求。
例8-4 某减速器齿轮箱中的第Ⅱ轴如图8-5所示,该轴转 速为n=265r/min;输入功率Pc=10kw;C、D两轮的节圆直径分 别为D1=396mm;D2=168mm;轴径d=50mm;齿轮压力角α=20°; 若轴的许用应力[б]=100MPa,试按第四强度理论校核轴的强 度。
试按第三强度理论校核轴的强度。
a A D C a B
联轴器
解 (1)外力分析
a)
dቤተ መጻሕፍቲ ባይዱ
将带的拉力平移到轴线,画直 轴的力学模型,如图8-4b所
FT
A FA
Ft
B F T+F t
示,作用于轴上的载荷有C点
b)
垂直向下的(FT+Ft)和作用面垂 直于轴线的附加力偶矩
FB
图8-4
(FT-Ft) D/2。其值分别为
263N· m
互垂直平面内的弯矩图,如
y y
c)
图8-5c、d所示。由失量合成 法可以将两俱方向的弯矩合 成,合成后的弯矩称为合成 弯矩,各截面上合成弯矩的大
140N· m
131N· m
T
d)
y
360.38N· m
2 2 M xy 小可用式 M M yz 进
e)
行计算。
图8-5
由yz平面和xy平面两弯矩图(图8-5c、d)可见,轴的D截面 是最大合成弯矩所在的截面,即是轴的危险截面,其最大合成 弯矩为
34.9MPa<[б]
所以,轴的强度满足要求。
讨论与思考:若将D轮的啮合点改为前边缘点 ( 图中之E
点),则Ft1与Fr2及Fr1与Ft2互成反向,这可使截面内的弯矩大幅 度减小,使轴更加安全或可承受更大的载荷。
(2) 内力分析 作轴的弯矩图和扭矩图,如图8-4c、d所示,由图可知,
轴的C截面为危险截面,该截面上的弯矩和扭矩分别为
Mc=(FT+Fd)a/2=(8+2)×0.5/2kN· m=3kN· m Mn = M = 1kN· m
(3) 校核强度 由以上分析可知,C截面的上、下边缘点是轴的危险点, 按第三强度理论,其最大相当应力为
y A Fr1 α F t1
图8-5
F1
C
Ft2 E D .
α
F2
Fr2B x
80
解 (1)外力分析
将齿轮啮合力正交分解
Ft1=F1cosα Fr1=F1sinα Ft2=F2cosα
z
80
130
a) 图8-5
Fr2=F2sinα
MC Fr1
FAx FAz Ft1
b) 图8-5
MD Ft2 Fr2 FBx FBz
