正弦表和余弦表
完整三角函数公式表

完整三角函数公式表三角函数公式表是数学中常用的一个工具,用于计算三角函数的数值。
它包含了各种三角函数的定义和性质,能够帮助我们在解决三角函数相关问题时,快速找到所需的公式和计算方法。
以下是一个完整的三角函数公式表,包含了常见的正弦、余弦、正切、余切、正割和余割函数的公式:1. 正弦函数(sin):- 定义:在单位圆上,从原点到圆上一点与x轴的正角对应的y坐标。
- 基本关系:sin θ = y/r,其中θ是角度,y是对应的y坐标,r是单位圆的半径(常为1)。
- 周期性:sin (θ + 2π) = sin θ。
- 奇偶性:sin (-θ) = -sin θ。
2. 余弦函数(cos):- 定义:在单位圆上,从原点到圆上一点与x轴的正角对应的x坐标。
- 基本关系:cos θ = x/r,其中θ是角度,x是对应的x坐标,r是单位圆的半径(常为1)。
- 周期性:cos (θ + 2π) = cos θ。
- 奇偶性:cos (-θ) = cos θ。
3. 正切函数(tan):- 定义:tan θ = sin θ / cos θ。
- 周期性:tan (θ + π) = tanθ。
- 奇偶性:tan (-θ) = -tan θ。
4. 余切函数(cot):- 定义:cot θ = 1 / tan θ = cos θ / sin θ。
- 周期性:cot (θ + π) = cot θ。
- 奇偶性:cot (-θ) = -cot θ。
5. 正割函数(sec):- 定义:sec θ = 1 / cos θ。
- 周期性:sec (θ + 2π) = sec θ。
- 奇偶性:sec (-θ) = sec θ。
6. 余割函数(csc):- 定义:csc θ = 1 / sin θ。
- 周期性:csc (θ + 2π) = csc θ。
- 奇偶性:csc (-θ) = -csc θ。
此外,三角函数还有一些重要的性质:1. 三角函数的范围:sin、cos、csc、sec的值在[-1, 1]之间,tan、cot的值在整个实数范围内。
正余弦函数值表

正余弦函数值表正余弦函数值表是数学中常见的表格,用来表示正弦函数和余弦函数在不同角度上的函数值。
正余弦函数是三角函数中最基本的两个函数,它们在数学、物理、工程等领域中有广泛的应用。
正弦函数和余弦函数是周期函数,它们的函数值随着角度的增加而变化。
在一个周期内,正弦函数和余弦函数的函数值会在一定的区间内波动。
正弦函数的函数值在-1到1之间变化,余弦函数的函数值也在-1到1之间变化。
下面是一个正余弦函数值表,展示了正弦函数和余弦函数在不同角度上的函数值:角度(度) 正弦函数值余弦函数值0 0 130 0.5 0.86645 0.707 0.70760 0.866 0.590 1 0120 0.866 -0.5135 0.707 -0.707150 0.5 -0.866180 0 -1210 -0.5 -0.866225 -0.707 -0.707240 -0.866 -0.5270 -1 0300 -0.866 0.5315 -0.707 0.707330 -0.5 0.866360 0 1从上表可以看出,正弦函数和余弦函数的函数值在不同角度上有不同的变化规律。
当角度为0度时,正弦函数的函数值为0,余弦函数的函数值为1;当角度为90度时,正弦函数的函数值为1,余弦函数的函数值为0;当角度为180度时,正弦函数的函数值为0,余弦函数的函数值为-1;当角度为270度时,正弦函数的函数值为-1,余弦函数的函数值为0。
正弦函数和余弦函数在不同角度上的函数值可以通过计算机或计算器来得到。
在实际应用中,我们经常使用这些函数值来进行各种数学计算和问题求解。
正余弦函数值表是学习和应用正弦函数和余弦函数的重要工具,对于理解和掌握这两个函数的性质和特点非常有帮助。
总之,正余弦函数值表是用来表示正弦函数和余弦函数在不同角度上的函数值的表格。
它对于学习和应用正弦函数和余弦函数具有重要的意义,是数学中常用的工具之一。
余弦正弦值角度对照表

余弦正弦值角度对照表正弦余弦角度对照表:1、Sin θ = 0.0对应的角度θ:θ = 0°2、Sin θ = 0.25对应的角度θ:θ = 15°3、Sin θ = 0.5对应的角度θ:θ = 30°4、Sin θ = 0.75对应的角度θ:θ = 45°5、Sin θ = 1.0对应的角度θ:θ = 60°6、Sin θ = -0.5对应的角度θ:θ = -30°7、Sin θ = -1.0对应的角度θ:θ = -60°正弦余弦角度对照表是计算几何学上常见的对照表,通过正弦值和角度之间的关系,求出正弦值和余弦值根据角度的正弦值可知正弦值与角度之间关系:1、当角度θ=0°时,正弦值Sinθ= 0;2、当角度θ=15°时,正弦值Sinθ= 0.25;3、当角度θ=30°时,正弦值Sinθ= 0.5;4、当角度θ=45°时,正弦值Sinθ= 0.75;5、当角度θ=60°时,正弦值Sinθ= 1;6、当角度θ=-30°时,正弦值Sinθ=-0.5;7、当角度θ=-60°时,正弦值Sinθ=-1;余弦值的角度和正弦值的角度相反,由余弦定理可知:知道θ的余弦值Cosθ可求出相应的角度,即:1、当角度θ=0°时,余弦值Cosθ=1;2、当角度θ=15°时,余弦值Cosθ=0.9659;3、当角度θ=30°时,余弦值Cosθ=0.8660;4、当角度θ=45°时,余弦值Cosθ=0.7071;5、当角度θ=60°时,余弦值Cosθ=0.5;6、当角度θ=-30°时,余弦值Cosθ=-0.8660;7、当角度θ=-60°时,余弦值Cosθ=-0.5;因为正弦值、余弦值和角度是属于数学运算,非常容易进行计算。
tan三角函数值表

tan三角函数值表《正弦、余弦、正切的三角函数值表》是数学中最基本的函数表之一,在学习图形学、三角学和微积分学等学科中,它们都是有用的参考。
三角函数表示在三角形中各角度对应的正弦值、余弦值和正切值,并通过角度的变化,反映出三角函数之间的关系。
在三角函数中,正弦函数表示为 y=sin x,它可用来表示任意一个角度的正弦值。
余弦函数表示为 y=cos x,它可用来表示任意一角度的余弦值。
正切函数表示为 y=tan x,它可用来表示任意一角度的正切值。
下面是各角度的正弦、余弦和正切函数值表:角度(度)t0t30t45t60t90正弦值t0t0.5t0.707t0.866t1余弦值t1t0.866t0.707t0.5t0正切值t0t0.577t1t1.73t无穷角度(度)t120t135t150t180t270正弦值t-0.866t-0.707t-0.5t-0t-1余弦值t0.5t0.707t0.866t1t0正切值t-1.73t-1t-0.577t0t无穷此外,也可以看出,正弦、余弦和正切三角函数之间存在着一定的关系,即 sin2x+cos2x=1;tan2x+1=sec2x;cot2x+1=csc2x。
这些关系的存在使得计算更加轻松方便。
值得一提的是,除了上面介绍的正弦、余弦与正切三角函数,还有其他几个函数,如余割函数cscx,反余弦函数arccos x,反正切函数arctan x,反正弦函数arcsin x等,它们也是三角函数的重要组成部分,它们拥有各种角度值对应的函数值,可以实现图形几何等多种应用。
最后,我们还要提到,三角函数值表拥有极大的价值,它可以帮助我们更好地理解三角函数的特性,以及它们的应用,它总结了三角函数的角度值与函数值的对应关系,是学习图形学、三角学和微积分学的重要参考书。
三角函数正弦余弦表

三角函数正弦余弦表
正弦和余弦是三角函数中最基本的两个函数,它们在数学、物理、工程等领域都有广泛的应用。
下面是正弦和余弦表:一、正弦表角度0°30°45°60°90°
sinθ0 1/2 √2/2√3/2 1二、余弦表角度 0° 30°45° 60° 90°
cosθ 1 √3/2 √2/2 1/2 0
从上述表格可以看出,当角度为0时,正弦值为0,余弦值为1;当角度为30时,正弦值为1/2,余弦值为√3/2;当角度为45时,正弦值和余弦值均为√( ) / ( ) ,即根号二分之一;当角度为60时,正弦值和余弧值分别是√( ) / ( ) 和半径的一半;而当角底等于90时,则正弧值等于半径长(即单位圆的直径),而其餘则无定义。
需要注意的是,在三维空间中存在着双曲线函数tanh(x)与双曲线反函数arctanh(x),这些也被称作“超越函数”,但它们并不属于三角函数的范畴。
三角函数度数表
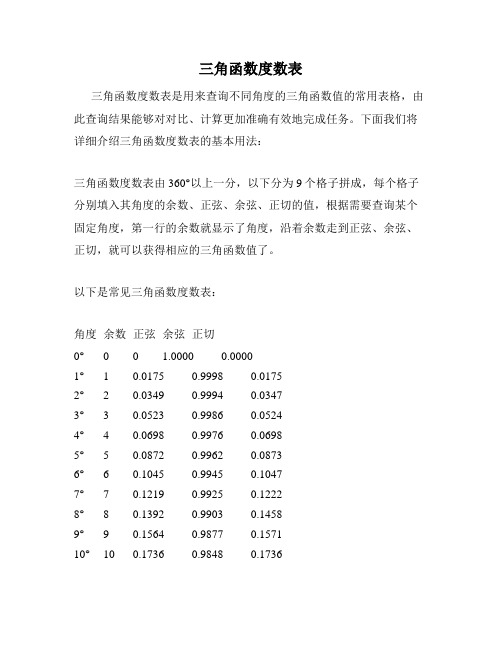
三角函数度数表三角函数度数表是用来查询不同角度的三角函数值的常用表格,由此查询结果能够对对比、计算更加准确有效地完成任务。
下面我们将详细介绍三角函数度数表的基本用法:三角函数度数表由360°以上一分,以下分为9个格子拼成,每个格子分别填入其角度的余数、正弦、余弦、正切的值,根据需要查询某个固定角度,第一行的余数就显示了角度,沿着余数走到正弦、余弦、正切,就可以获得相应的三角函数值了。
以下是常见三角函数度数表:角度余数正弦余弦正切0°0 0 1.0000 0.00001° 1 0.0175 0.9998 0.01752° 2 0.0349 0.9994 0.03473° 3 0.0523 0.9986 0.05244° 4 0.0698 0.9976 0.06985° 5 0.0872 0.9962 0.08736° 6 0.1045 0.9945 0.10477°7 0.1219 0.9925 0.12228°8 0.1392 0.9903 0.14589°9 0.1564 0.9877 0.157110°10 0.1736 0.9848 0.1736以此类推,以90度为一个角度区间,360度整体循环直到余数为0,就是整个三角函数度数表,利用这个三角函数度数表,就可以准确快速地计算出某角度的三角函数值,有效提高工作效率。
此外,三角函数度数表虽然只是一本参考书,但仍有很多用处。
许多数学计算都会应用到三角函数,而有了三角函数度数表,就可以更准确快捷地找到三角函数值,不仅在数学计算上有用,还可以在科学、工程、天文、物理等各个领域极大地提高工作效率。
三角函数表

1
0
-1
0
cos
1
0.966
0.866
0.707
0.5
0.259
0
-1
0
1
Tg
0
0.268
0.577
1
1.732
3.73
-∞
0
-∞
0
ctg
∞
3.732
1.732
1
0.577
0.268
0
-∞
0
+∞
三.cosΦ与tg的对应值表:
COSΦ
tgΦ
COSΦ
tgΦ
COSΦ
tgΦ
COSΦ
tgΦ
1
0
0.86
正弦sin
余切ctg
正切tg
角度
正弦SinA=a/c=对边/斜边=cosB余弦cosA=b/c=邻边/斜边=sinB
正切tgA=a/b=对边/邻边=ctgB余切ctgA=b/a=邻边/对边=tgB
二.特殊角度函数值:
角度
0
15
30
45
60
75
90
180
270
360
Sin
0
0.259
0.5
0.707
0.866
0.74
0.9089
0.60
1.334
0.30
3.180
0.87
0.5668
0.73
0.9362
0.59
1.638
0.25
3.867
四.公式:A的对边是y,A的邻边是x,A的另一边(斜边)是r
1.α角的正弦=α角的对边/斜边。(塞因)sinα=y/r
常见三角函数及图像表格

三角函数是数学中非常有用的函数,它们与角有关。
三角函数经常应用于几何图形,
特别是三角形的计算,也能用来计算复杂函数的结果。
常见的三角函数有正弦函数、余弦函数和正切函数。
正弦函数的图像是一个曲线,当
角度逐渐增加时,曲线的高低也会变化。
余弦函数的图像是一个曲线,当角度逐渐增加时,曲线的高低也会变化。
正切函数的图像是一个线段,当角度增加时,线段的长度也会变化。
下表是常见三角函数的图像表格:
角度(°)正弦函数余弦函数正切函数
0 0 1 0
30 0.5 0.866 0.577
45 0.707 0.707 1
60 0.866 0.5 1.73
90 1 0 无穷
正弦函数、余弦函数和正切函数是数学中非常有用的函数,它们与角度有关,因此可
以通过图像表格来表示它们的变化。
三角函数在数学中被广泛应用,是解决几何图形和复杂函数的重要工具。
