(完整)二年级图形的个数
二年级专题第四讲:数几何图形的个数

⼆年级专题第四讲:数⼏何图形的个数第四讲:数⼏何图形的个数“数⼏何图形的个数”是趣味图形问题的⼀种。
数图形虽然很简单,但重复计数和遗漏是经常出现的错误,在细⼼的同时还要掌握⽅法和技巧。
⼀、数线段1. 数出下列每条线段上线段的总条数。
分析与解:数线段的时候⼀定按⼀定的顺序数,否则就会出现重复或遗漏。
数时可以先数最基本的⼩线段,再数两条基本线段组成的线段,再数三条基本线段组成的线段,……,最后把各种“线段”条数相加起来。
法⼀:照下⾯的⽅法数(以第2⼩题为例):3+2+1=6(条)法⼆:(规律) 线段总条数都是从1开始的⼏个连续⾃然数的和,⽽且最后⼀个加数正好和最基本线段数相同。
(1)(条)(2)(条)(3)(条)⼆、数⾓2. 数出右图中总共有多少个⾓.分析与解:在∠AOB内有三条⾓分线OC1、OC2、OC3,∠AOB被这三条⾓分线分成4个基本⾓,那么∠AOB内总共有多少个⾓呢?⾸先有这4个基本⾓,其次是包含有2个基本⾓组成的⾓有3个(即∠AOC2、∠C1OC3、∠C2OB),然后是包含有3个基本⾓组成的⾓有2个(即∠AOC3、∠C1OB),最后是包含有4个基本⾓组成的⾓有1个(即∠AOB),所以∠AOB内总共有⾓:4+3+2+1=10(个).令狐⽼师注:数⾓的⽅法可以采⽤例1数线段的⽅法来数,就是⾓的总数等于从1开始的⼏个连续⾃然数的和,这个和⾥⾯的最⼤的加数是⾓分线的条数加1,也就是基本⾓的个数. 【巩固】数⼀数右图中总共有多少个⾓?分析与解:因为∠AOB内⾓分线OC1、OC2…OC9共有9条,即9+1=10个基本⾓.所以总共有⾓:10+9+8+…+4+3+2+1=55(个).三、数三⾓形3. 如右图中,各个图形内各有多少个三⾓形?分析与解:⽅法⼀:(1)先数图中包含⼀个⼩三⾓形个数:△ABD、△ADE、△AEF、△AFC 共4个三⾓形.(2)再数由两个⼩三⾓形组合在⼀起的三⾓形个数:△ABE、△ADF、△AEC 共3个三⾓形,(3)以三个⼩三⾓形组合在⼀起的三⾓形:△ABF、△ADC 共2个三⾓形,(4)最后数以四个⼩三⾓形组合在⼀起的只有△ABC⼀个.所以图中三⾓形的个数总共有:4+3+2+1=10(个).⽅法⼆:我们就可以把数三⾓形问题转化为数线段问题了。
二年级数三角形的题目

二年级数三角形的题目一、基础题型(单个图形中的三角形计数)1. 数一数,下面这个图形中有几个三角形?- △.- 解析:这个图形就是1个三角形,直接数出即可。
2. 观察下面的图形,数出三角形的个数。
- △.- △.- 解析:这里有2个独立的三角形,所以三角形个数为2。
3. 数出这个图形中的三角形个数。
- △.- △.- △.- 解析:图中有3个独立的三角形,三角形个数为3。
二、组合图形中的三角形计数(简单组合)4. 数一数下面图形中有多少个三角形?- △.- △△.- 解析:这里有3个三角形。
上面1个单独的三角形,下面由2个小三角形组成1个大三角形,总共1 + 2=3个。
5. 数出该图形中的三角形数量。
- △.- △△.- △.- 解析:图中共有5个三角形。
上面2个单独的三角形,下面2个单独的三角形,再加上由下面2个小三角形组成的1个大三角形,即2+2 + 1=5个。
6. 求下面图形中三角形的个数。
- △△.- △△.- 解析:这个图形中有6个三角形。
可以先数单个的小三角形有4个,然后由2个小三角形组成的大三角形有2个,4+2 = 6个。
三、较复杂组合图形中的三角形计数。
7. 数出下面图形里三角形的个数。
- △.- △△.- △△△.- 解析:单个小三角形有6个,由2个小三角形组成的三角形有3个(上面2个、中间2个、下面2个),由3个小三角形组成的大三角形有1个,总共6+3+1 = 10个。
8. 数一数这个图形中的三角形数量。
- △.- △△.- △△△.- △.- 解析:单个小三角形有7个,由2个小三角形组成的三角形有3个(左边2个、中间2个、右边2个),由3个小三角形组成的三角形有1个,总共7+3+1 = 11个。
9. 求下面图形中三角形的个数。
- △△.- △△△.- △△△△.- 解析:单个小三角形有10个,由2个小三角形组成的三角形有6个(上排相邻2个有3组,下排相邻2个有3组),由3个小三角形组成的三角形有3个(上排3个、中间3个、下排3个),由4个小三角形组成的大三角形有1个,总共10+6 + 3+1=20个。
完整)二年级图形的个数

完整)二年级图形的个数第6讲图形个数一、知识要点为了正确地数出线段、角、三角形、长方形等图形的个数,我们需要有条理、有次序地进行计数,并从中发现规律。
首先,我们需要从基本图形入手,弄清楚图形中包含的基本图形有哪些,数量是多少。
然后,我们再数出由基本图形组成的新图形,并求出它们的和。
二、精讲精练例题1】数出下图中有多少条线段?A-----BD。
C思路导航】方法一:以线段左端点为分类依据。
以A点为左端点的线段有:AB、AC、AD 3条;以B点为左端点的线段有:BC、BD 2条;以C点为左端点的线段有:CD 1条。
因此,图中共有线段3+2+1=6条。
方法二:把图中线段AB、BC、CD看做基本线段来数。
由1条基本线段构成的线段有:AB、BC、CD 3条;由2条基本线段构成的线段有:AC、BD 2条;由3条基本线段构成的线段有:AD 1条。
因此,图中共有线段3+2+1=6条。
练1:1)数出下图中有多少条线段?A-----BD。
CE2)数出下图中有几个长方形?A-----BE-----D例题2】数出图中有几个角?BC。
OD思路导航】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA为一边的角有:∠AOB、∠AOC、∠AOD 3个;以OB为一边的角还有:∠BOC、∠BOD 2个;以OC为一边的角还有:∠COD 1个。
因此,图中共有角3+2+1=6个。
方法二:把图中∠AOB、∠BOC、∠COD看做基本角来数。
由1个基本角构成的角有:∠AOB、∠BOC、∠COD 3个;由2个基本角构成的角有:∠AOC、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。
因此,图中共有角3+2+1=6个。
练2:数出图中有几个角?A。
BC-----O-----DE。
F例题3】数出右图中共有多少个三角形?A-----BD。
C思路导航】由三条线段构成的三角形有:ABC、ABD、ACD、BCD4个;由两条线段构成的三角形有:ABD、ABC、ACD、BCD 4个;由一条线段构成的三角形有:ABD、ABC、ACD、BCD 4个。
强烈推荐 二年级思维训练 图形的计数

图形的计数例1 数出下图中各条线上线段的总条数。
图中的线段有:()条。
图中的线段有:()条。
例2 数一数,下面的各个图形内,各有多少个角?
一共有()个角。
一共有()个角。
一共有()个角。
一共有()个角。
例3 数一数,下面的各个图形内,各有多少个三角形?
三角形有()个。
三角形有()个。
三角形有()个。
三角形有()个。
C
B
A D
A B C
A B C D E
三角形有()个。
三角形有()个。
三角形有()个。
三角形有()个。
4数出下面图形中有多少个三角形?
三角形有()个三角形有()个
5 数出下面图形中有多少个长方形?
长方形有()个。
长方形有()个。
带☆的长方形有()个。
二年级奥数:巧数图形

二年级奥数:巧数图形体系所属体系板块:第三级上能力培养:分类思考、数形结合思想体系对接:第一级下《有趣的平面图形》第三级下《飞速图形计数》预热知识一、分类法1、打枪法2、恰含法3、分大小【例】下图你能数出多少条线段?【例】下图共有多少个长方形?【解析】分类法(打枪法)【解析】分类数(恰含法)总:4+3+2+1=10(个)总:3+2+1=6(个)答:共10个。
答:共6个。
【例】下图你能数出多少个正方形?【解析】分类数(大小)1个小正方形:4个4个小正方形:1个总:4+1=5(个)答:共5个。
二、巧数图形(分层数)1、总数=每层个数相加每层个数=上层个数+看得见【例】下图中的小方块有几个?【解析】巧数图形(分层数)总:1+4+5=10(个)答:有10个。
课前思考1、正方形如何计数呢?2、小方块如何计数呢?3、如何利用学过的乘法来进行计数?4、一年级秋季要求背的1-10的三角形数还记得吗?数数中的枚举知识点精讲知识点总结一、数字:0、1、2、3、4、5、6、7、8、9(共10个)数:由数字组成的(无数个)二、组数(最高位不为0)1.确定几位数2.确定从哪位开始写注:①“比”后为目标②“相差”:2种情况3.确定顺序(从小到大/从大到小)4.有无特殊要求反序数下降数(上升数)例题精讲1.根据条件组数——有序的排列(例2)你能根据下面的要求,写出所有符合条件的两位数吗?(1)十位上的数字比个位上的数字大2;(2)十位上的数字与个位上的数字相差2。
解析:(1)先确定要题目要求我们写的是两位数,再确定从哪一位开始写——通过比较,发现先写出“比”字后面的,再写前面的思考起来更容易,所以一般我们把“比”字后面的当做是目标。
在这里也就是“个位上的数字”为目标,先写出来个位可能是几,再寻找十位上比个位上大2的数字即可组成我们需要的两位数。
个位上可能是:0、1、2、3、4、5、6、7、8、9。
而十位上最大是9,十位上的数字比个位上的数字大2,所以个位上最大是7。
(完整)二年级角、数图形练习题

(完整)二年级角、数图形练习题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN角的初步认识数图形练习一、1.下面图形, 哪些是角哪些不是角画出√或×.2.下面哪几个图形是直角?是的画√, 不是画×.二二、1. 把序号填写在相应的圆圈内。
长方形正方形平行四边形2.数一数()个正方形()个长方形()个平行四边形3.一张长16厘米,宽12厘米的长方形卡纸。
如果要剪出一个最大的正方形,正方形的边长是多少厘米?4. 画一画(1)在下面的方格纸上画出一个含有12个方格的长方形,你有多少种不同的画法?请试一试。
(2)你能在下面的方格纸上画出一个含有9个方格的正方形吗?在下面4个点中,连结每两个点画一条线段,共可以画多少条线段?A●B●C●()条线段D●一、数一数,下图中共有多少条线段?(1)A B C D E F G H( )条线段A B C D E F( )条线段(2)一条直线上共有11个点,可以数出( )条线段( )个三角形 ( )个三角形( )个三角形 ( )个三角形( )个长方形 ( )个正方形( )条线段 ( )条线段()个角()个角()个三角形()个三角形()个正方形()个正方形二、应用1、小红在纸上画了一条线段,小亮又拿起笔,在小红画的线段上点了5个点,然后问小红:“你知道现在一共有多少条线段吗”小红一会儿就说出了答案。
聪明的小朋友,你知道小红说的是几吗2、小明过生日,他邀请了10个小朋友来吃晚饭,席间,小明提议每两个人都要握一次手,他们两两握手,全部握完,共要握多少次手?。
《数图形》(教案)二年级上册数学青岛版

《数图形》(教案)二年级上册数学青岛版在今天的数学课上,我们将一起探索《数图形》这个主题。
我们将使用青岛版二年级上册的数学教材。
一、教学内容我们将会学习第五章《数图形》的内容。
这部分包括:认识长方形、正方形,了解它们的特征;学会通过数图形的方法来认识它们;能够用语言描述图形的特征。
二、教学目标通过本节课的学习,我希望孩子们能够:1. 认识长方形和正方形,理解它们的特征;2. 学会通过数图形的方法来认识长方形和正方形;3. 能够用语言描述长方形和正方形的特征。
三、教学难点与重点重点:认识长方形和正方形,理解它们的特征。
难点:学会通过数图形的方法来认识长方形和正方形,能够用语言描述长方形和正方形的特征。
四、教具与学具准备教具:长方形和正方形的卡片,数图形的工具。
学具:每组一张长方形和正方形的卡片,数图形的工具。
五、教学过程1. 引入:我会通过展示长方形和正方形的实物卡片,让孩子们观察并说出它们的特征。
2. 讲解:我会用数图形的工具,展示如何通过数图形的方法来认识长方形和正方形。
3. 练习:孩子们将会用学具,尝试自己数图形,并描述长方形和正方形的特征。
六、板书设计板书设计将会包括长方形和正方形的特征,以及数图形的方法。
七、作业设计作业题目:请孩子们用数图形的方法,找出生活中的长方形和正方形,并描述它们的特征。
答案:孩子们需要找出生活中的长方形和正方形,并描述它们的特征。
八、课后反思及拓展延伸课后,我会反思孩子们在课堂上的表现,以及他们对长方形和正方形的理解程度。
对于那些还没有完全掌握的孩子,我会考虑如何在课后给予他们更多的帮助。
同时,我也会鼓励孩子们在生活中多观察长方形和正方形,加深他们对这些图形的理解。
通过本节课的学习,我希望孩子们能够掌握长方形和正方形的特征,学会用数图形的方法来认识它们,并能够用语言描述它们的特征。
重点和难点解析在今天的数学课上,我们将一起探索《数图形》这个主题。
我们将使用青岛版二年级上册的数学教材。
二年级奥数:《飞速图形计数》
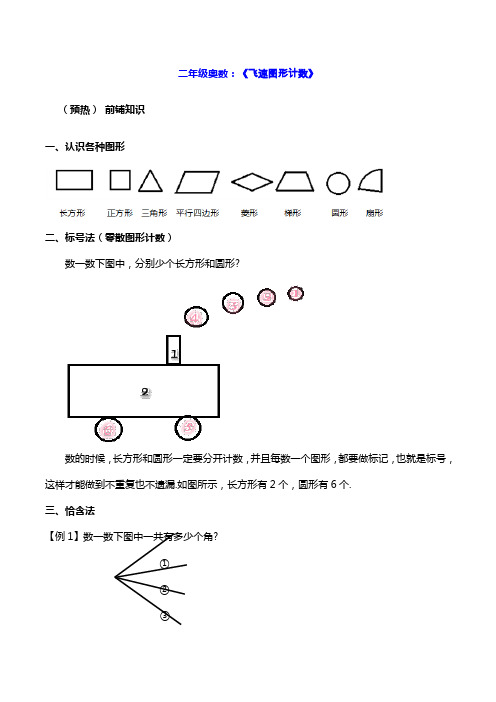
二年级奥数:《飞速图形计数》(预热)前铺知识一、认识各种图形二、标号法(零散图形计数)数一数下图中,分别少个长方形和圆形?数的时候,长方形和圆形一定要分开计数,并且每数一个图形,都要做标记,也就是标号,这样才能做到不重复也不遗漏.如图所示,长方形有2个,圆形有6个.三、恰含法【例1】数一数下图中一共有多少个角?①②③恰含1个角的:①、②、③,共3个;恰含2个角的:①+②、②+③,共2个;恰含3个角的:①+②+③,共1个.一共:3+2+1=6(个)答:一共有6个角.【例2】数一数下图有多少个长方形?①⑤②③④恰含1个长方形的:①、②、③、④、⑤,共5个;恰含2个长方形的:①+②、②+③、③+④、④+⑤,共4个;恰含3个长方形的:②+③+④,共1个.一共:5+4+1=10(个)答:一共有10个长方形.四、其他分类方法1、按大小分类有4个小正方形,3个大正方形.2、按位置分类中间有2个圆,周围有3个圆.如何预习?为了保护孩子课前的好奇心和学习兴趣,以及保证课堂效果,家长在给孩子预习的时候,一定要把握好度.预习,切忌给孩子讲解书本上的例题和知识点,因为孩子容易先入为主,如果家长选取的方式方法不当,那么孩子很难转换思路了;另外,家长给孩子讲过例题后,孩子可能会觉得自己已经学会了,上课的时候就不愿意认真听了.我们预习的目的是回顾这一讲课前的铺垫知识,以及引起孩子的思考,因此家长可以把我们的这份预习资料打印出来,让孩子自己看一看,如果孩子有不明白的,您可以适当点拨.《飞速图形计数》知识点精讲【知识点总结】复习1、枚举法(标号法)2、恰含法(通用)新知识一、简单规整图形(肩并肩、手拉手排成一排)开火车大法总数=火车头(基本图形数)依次加到1二、多层规整图形分层数(相合不能忘)三、不规整图形分类法:①分部分②分大小(恰含法)③分方向注:常见的【简单规整图形】(特别:数正方形不能用开火车大法)线段角【例1】数一数下面一共有多少条线段?①②③④方法1:恰含1条:4条恰含2条:①②、②③、③④3条恰含3条:①②③、②③④2条恰含4条:①②③④1条总数:4+3+2+1=10(条)方法2:基本线段有4条,所以从4开始依次加到14+3+2+1=10(条)答:一共有10条线段.【例2】数一数图中有多少个三角形?每层个数:4+3+2+1=10(个)层数:3层总数:10×3=30(个)答:一共有30个三角形.【例3】数一数右侧图形中一共有多少个三角形?左边:3+2+1=6(个)右边:3+2+1=6(个)合起来:3个总数:6+6+3=15(个)答:一共有15个三角形.【例4】数一数右侧图形中一共有多少个三角形?恰含1个:①、②、③、④、⑤、⑥6个Array恰含2个:①②、③④、⑤⑥3个恰含3个:①②③、②③④、③④⑤、④⑤⑥、⑤⑥①、⑥①②6个恰含6个:①②③④⑤⑥1个6+3+6+1=16(个)答:一共有16个三角形.【例5】数一数下面图形中一共有多少个正方形?方法:先按照正的和斜的这两个不同方向,把图形拆分出来.正的:按大小分类数,斜的:一个田字格,有5个正方形最小:4个中等大小:5个最大:1个共4+5+1=10(个)总数:10+5=15(个)答:一共有15个正方形.【学习建议】本讲讲的是数图形的方法,根据不同类型的图形有不同的巧妙方法,同学们要仔细辨认图形的种类,像是简单规整图形和多层规整图形都是有巧妙方法的;如果是不规则图形,那么一定要注意分类,分类的依据是什么,数的时候思路要清楚,这样才不会数错.《飞速图形计数》补充题1.数一数下面两幅图中分别有多少条线段?2. 在一条直线上有10个端点,那么在这条直线上可以数出多少条线段?3. 下图中有多少个三角形?4、数一数,下面有多少个长方形?5、数一数图中有多少个正方形?6、数一数下面一共有几个正方形.7、数一数,下图中包含有苹果的三角形有几个?8、数一数下图中一共有多少个平行四边形?答案解析1、(1)5+4+3+2+1=15(条)答:这幅图中有15条线段.(2)(3+2+1)+(2+1)=9(条)答:这幅图中有9条线段.2、基本线段数:10-1=9(条)总线段数:9+8+7+6+5+4+3+2+1=45(条)答:这条直线上有45条线段.3、每层个数:5+4+3+2+1=15(个)层数:3层总数:15×3=45(个)答:图中共有45个三角形.4、长边线段数:3+2+1=6(条)宽边线段数:4+3+2+1=10(条)长方形总个数:10×6=60(个)答:图中共有60个长方形.5、恰含1个:5×3=15(个)恰含4个:8个恰含9个:3个正方形总个数:15+8+3=26(个)答:图中共有26个正方形.6、按照正的和斜的两个方向,先把原图形拆分成如下两个图形.恰含1个:4×4=16(个)一个田字格有5个正方形恰含4个:3×3=9(个)恰含9个:2×2=4(个)恰含16个:1×1=1(个)共:16+9+4+1=30(个)所以一共有:30+5=35(个)正方形答:一共有35个长方形.7、按照三角形从小到大的顺序,且时刻注意题目要求,要包含苹果.恰含1个:2个恰含4个:6个恰含9个:5个恰含16个:3个最大的:1个共:2+6+5+3+1=17(个)答:含有苹果的三角形一共有17个.8、是简单规整图形,肩并肩、手拉手,可以用开火车大法.6+5+4+3+2+1=21(个)答:一共有21个平行四边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6讲 图形个数
一、知识要点 同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
二、精讲精练
【例题1】数出下图中有多少条线段?
【思路导航】方法一:我们可以采用以线段左端点分类数的方法。
以A 点为左端点的线段有:AB 、AC 、AD 3条;以B 点为左端点的线段有:BC 、BD 2条;以C 点为左端点的线段有:CD 1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段 AB 、BC 、CD 看做基本线段来数,那么,由1条基本线段构成的线段有:AB 、BC 、CD 3条;由2条基本线段构成的线段有:AC 、BD 2条;由3条基本线段构成的线段有:AD 1条。
所以,图中一共有3+2+1=6(条)线段。
练习1:
(1)数出下图中有多少条线段?
(2)数出下图中有几个长方形?
E A B C D D A B
C
【例题2】数出图中有几个角?
【思路导航】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA 为一边的角有:∠AOB 、∠AOC 、∠AOD 3个;以OB 为一边的角还有:
∠BOC 、∠BOD 2个;以OC 为一边的角还有:∠COD 1个。
所以,图中共有角3+2+1=6(个)。
方法二:把图中∠AOB 、∠BOC 、∠COD 看做基本角来数,那么,由1个基本角构成的角有:∠AOB 、∠BOC 、∠COD 3个;由2个基本角构成的角有: ∠AOC 、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。
所以,图中一共有3+2+1=6(个)角。
练习2:数出图中有几个角?
【例题3】数出右图中共有多少个三角形? 【思路导航】方法一:我们可以采用按边分类数的方法。
以PA 为边的三角形有:△PAB 、△PAC 、△PAD 、3个;以PB 为边的三角形还有:△PBC 、△PBD 2个;以PC 为边的三角形还有:△PCD 1个。
所以,图中共有三角形3+2+1=6(个)。
方法二:把图中三角形 △PAB 、△PBC 、△PCD 看做基本三角形来数,那么,由1个基本三角形构成的三角形有:△PAB 、△PBC 、△PCD 3个;由2个基本三角形构成的三角形有: △PAC 、△PBD 2个;由3个基本三角形构成的三角形有:△PAD 1个。
所以,图中一共有3+2+1=6(个)三角形。
方法三:我们发现,要数出图中三角形的个数,只需数出线段 AD 中包含几条线段就可以了,即3+2+1=6(个)。
所以图中共有6个三角形。
O
D
C B
A
O
C B
A E D
O C B A P
D C
B A
练习3:数出图中共有多少个三角形?
(1) (2)
【例题4】数出下图中有多少个长方形?
【思路导航】数图中有多少个长方形和数三角形的方法一样,长方形是由长、宽两对线段围成,线段 CD 上有3+2+1=6(条)线段,其中每一条与AC 中一条线段对应,分别作为长方形的长和宽,这里共有6×1=6(个)长方形,而AC 上共有2+1=3(条)线段也就有6×3=18(个)长方形。
它的计算公式为:
长方形的总数=长边线段的总数×宽边线段的总数
(3+2+1)×(2+1)=18(个) 答:图中共有18个长方形。
练习4:
(1)数出下图中有多少个长方形?
(2)(2)数出下图中有多少个正方形?
A
K
G I H G D
C B A
D C
B
A D C
B A
【例题5】有5个同学,每两个人握手一次,一共要握手多少次?
【思路导航】这道题可以用数线段的方法来解答。
根据题意,画出线段图,每一个端点代表一个同学。
从图上可以看出,第1个同学要与其余4个同学握手共握手4次;第2个同学还要与其余3个同学握手共握手3次,第3个同学要与其余2个同学握手共握手2次;第4个同学还要与最后1个同学握手共握手1次。
所以,一共要握手4+3+2+1=10(次)
练习5:
(1)银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?
(2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个不同的两位数?
543
21
家庭作业:
1、
A B C D E
图中的线段有:_____________条。
2、
一共有____________个角。
一共有________________个角。
3、
三角形有_______个。
三角形有_______个。
三角形有_______个。
4、
正方形有________________个。
正方形有__________________个。
5、周末奥数班一共有8位同学,老师为了让全班新同学互相认识,请这8位同学彼此握手为礼,并同时彼此介绍自己。
在一阵喧哗后,同学完成工作。
老师提出一个问题:“谁知道,刚才全班同学总共握手几次?”。
