推荐-浙江省2018年五校联考试数学参考答案 精品
浙江省衢州市五校联盟2024-2025学年高一上学期期中联考数学试题
B． m = 2
C． m = 1或 m = 2
D． m 不存在
4．函数 y =
4 - x2 的定义域是（ x
）
A． [ -2,2]
B． (-2, 2)
C．[-2,0) U (0, 2] D．[-4,0) È (0, 4]
5．设函数
f
(x)
=
æ çè
1 2
öx(x-a) 在区间 (0,1)
÷ø
a 上单调递增，则
x x2 + x -12 £ 0
，B
=
ìíx î
x
3 +1
£
1üý þ
．
(1)判断 2 是否为集合 B 中的元素，并说明理由；
(2)若全集U = R ，求 A Ç B ， A È (ðU B) ．
16．已知函数 f ( x) = x2 - 2ax - 3 ．
(1)若 f ( f (-1)) = -3 ，求 a 的值；
C．{Æ,{0},{1}}
D．{Æ,{0},{1},{0,1}}
2．设 x Î R ，则“ x < 1”是“ x2 < 1 ”的（ ）
A．充分不必要条件 C．充要条件
B．必要不充分条件 D．既不充分也不必要条件
3．已知幂函数 f (x) = (m2 - 3m + 3)x m-1 为偶函数，则（ ）
A． m = 1
的取值范围是（
）
A． [ -2, 0)
B．(-¥, 0]
C． (0, 2]
D．[2, +¥)
6．若
x
£
2
，则函数
f
(x)
=
1 2x +
1
2018-2019学年浙江省台州市温岭市五校联考八年级(上)期中数学试卷
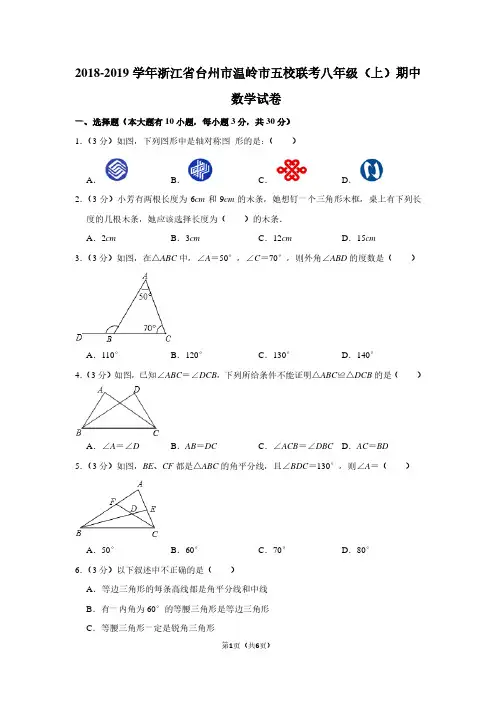
2018-2019学年浙江省台州市温岭市五校联考八年级（上）期中数学试卷一、选择题（本大题有10小题，每小题3分，共30分）1．（3分）如图，下列图形中是轴对称图形的是：（）A．B．C．D．2．（3分）小芳有两根长度为6cm和9cm的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为（）的木条．A．2cm B．3cm C．12cm D．15cm3．（3分）如图，在△ABC中，∠A＝50°，∠C＝70°，则外角∠ABD的度数是（）A．110°B．120°C．130°D．140°4．（3分）如图，已知∠ABC＝∠DCB，下列所给条件不能证明△ABC≌△DCB的是（）A．∠A＝∠D B．AB＝DC C．∠ACB＝∠DBC D．AC＝BD5．（3分）如图，BE、CF都是△ABC的角平分线，且∠BDC＝130°，则∠A＝（）A．50°B．60°C．70°D．80°6．（3分）以下叙述中不正确的是（）A．等边三角形的每条高线都是角平分线和中线B．有一内角为60°的等腰三角形是等边三角形C．等腰三角形一定是锐角三角形D．在一个三角形中，如果两条边不相等，那么它们所对的角也不相等；反之，如果两个角不相等，那么它们所对的边也不相等7．（3分）等腰三角形一腰上的高与另一腰的夹角为60°，则顶角的度数为（）A．30°B．30°或150°C．60°或150°D．60°或120°8．（3分）在平面直角坐标系中，点A的坐标为（4，0），使△OAB是等腰三角形，此时，点B的坐标不可能是（）A．（0，4）B．（2，4）C．（4，4）D．（4，2）9．（3分）如图，在△ABE中，∠A＝105°，AE的垂直平分线MN交BE于点C，且AB+BC ＝BE，则∠B的度数是（）A．45°B．60°C．50°D．55°10．（3分）如图，点I为△ABC角平分线交点，AB＝8，AC＝6，BC＝4，将∠ACB平移使其顶点C与I重合，则图中阴影部分的周长为（）A．9B．8C．6D．4二、填空题（本大题6小题，每小题3分，共18分）11．（3分）已知在△ABC中，∠C＝∠A+∠B，则△ABC的形状是．12．（3分）若正多边形的一个内角等于120°，则这个正多边形的边数是．13．（3分）若点P（a+2，3）与点Q（﹣1，b+1）关于y轴对称，则a+b＝．14．（3分）如图，DE是△ABC边AC的垂直平分线，若BC＝18cm，AB＝10cm，则△ABD 的周长为．15．（3分）如图，在第1个△A1BC中，∠B＝30°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E，…按此做法继续下去，第2018个三角形的底角度数是．16．（3分）有依次排列的3个数：3，9，8，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，﹣1，8，这称为第一次操作；做第二次同样的操作后也产生一个新数串：3，3，6，3，9，﹣10，﹣1，9，8，相继依次操作下，则从数串：3，9，8开始操作第100次时所产生的那个新数串的所有数之和是．三、解答题（本大题共8小题，17-19小题每小题6分，20-22小题每小题6分，23-24小题10分，共52分）17．（6分）已知：如图，A、C、F、D在同一直线上，AF＝DC，AB＝DE，BC＝EF，求证：△ABC≌△DEF．18．（6分）a，b分别代表铁路和公路，点M、N分别代表蔬菜和杂货批发市场．现要建中转站O点，使O点到铁路、公路距离相等，且到两市场距离相等．请用尺规画出O点位置（不写作法，保留作图痕迹）．19．（6分）如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处．求∠1+∠2的度数．20．（6分）如图，在四边形ABCD中，AB＝CD，AD＝BC，点O为BD上任意一点，过点O的直线分别交AD，BC于M，N两点．求证：∠1＝∠2．21．（7分）小王准备用一段长30m的篱笆围成一个三角形形状的场地，用于饲养家兔，已知第一条边长为am，由于受地势限制，第二条边长只能是第一条边长的2倍多2m．（1）请用a表示第三条边长．（2）问第一条边长可以为7m吗？请说明理由．22．（7分）如图，已知在△ABC中，∠BAC为直角，AB＝AC，D为AC上一点，CE⊥BD 于E，交BA的延长线于F．（1）求证：△ABD≌△ACF；（2）若BD平分∠ABC，求证：CE＝BD；（3）若D为AC上一动点，∠AED如何变化，若变化，求它的变化范围；若不变，直接写出它的度数．23．（7分）问题情境：如图1，在直角三角形ABC中，∠BAC＝90°，AD⊥BC于点D，可知：∠BAD＝∠C（不需要证明）；（1）特例探究：如图2，∠MAN＝90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB＝AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；（2）归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB＝AC，∠1＝∠2＝∠BAC．求证：△ABE≌△CAF；（3）拓展应用：如图4，在△ABC中，AB＝AC，AB＞BC．点D在边BC上，CD＝2BD，点E、F在线段AD上，∠1＝∠2＝∠BAC．若△ABC的面积为3，则△ACF与△BDE的面积之和为．24．（7分）已知△ABC在平面直角坐标系中的位置如图所示，直线l过点M（3，0）且平行于y轴．（1）作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标．（2）如果点P的坐标是（﹣a，0），其中a＞0，点P关于y轴的对称点是P1，点P1关于直线l的对称点是P2，求P1P2的长．（用含a的代数式表示）（3）通过计算加以判断，PP2的长会不会随点P位置的变化而变化．2018-2019学年浙江省台州市温岭市五校联考八年级（上）期中数学试卷参考答案一、选择题（本大题有10小题，每小题3分，共30分）1．C；2．C；3．B；4．D；5．D；6．C；7．B；8．D；9．C；10．B；二、填空题（本大题6小题，每小题3分，共18分）11．直角三角形；12．6；13．1；14．28cm；15．（）2017×75°；16．520；三、解答题（本大题共8小题，17-19小题每小题6分，20-22小题每小题6分，23-24小题10分，共52分）17．；18．；19．；20．；21．；22．；23．1；24．；。
2025届浙江省杭州市五校联盟高三第二次联考数学试卷含解析
2025届浙江省杭州市五校联盟高三第二次联考数学试卷注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．运行如图所示的程序框图，若输出的值为300，则判断框中可以填（ ）A ．30i >?B ．40i >?C ．50i >?D ．60i >?2．已知x ，y R ∈，则“x y <”是“1xy <”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件3．若不等式22ln x x x ax -+对[1,)x ∈+∞恒成立，则实数a 的取值范围是（ ）A ．(,0)-∞B ．(,1]-∞C ．(0,)+∞D ．[1,)+∞4．等比数列{}n a 的各项均为正数，且384718a a a a +=，则3132310log log log a a a +++=() A ．12 B ．10 C ．8 D ．32log 5+5．已知集合{}22|A x y x ==-，2{|}10B x x x =-+≤，则A B =( )A ．[12]-，B ．[2]-，C ．(2]-，D ．2,2⎡-⎣6．给出下列三个命题：①“2000,210x x x ∃∈-+≤R ”的否定；②在ABC 中，“30B ︒>”是“3cos 2B <”的充要条件； ③将函数2cos2y x =的图象向左平移6π个单位长度，得到函数π2cos 26y x ⎛⎫=+ ⎪⎝⎭的图象． 其中假命题的个数是（ ）A ．0B ．1C ．2D ．37．将函数()sin(2)3f x x π=-()x R ∈的图象分别向右平移3π个单位长度与向左平移n (n >0)个单位长度，若所得到的两个图象重合，则n 的最小值为( )A ．3πB ．23πC ．2πD ．π8．已知函数()ln ln(3)f x x x =+-，则（ ）A ．函数()f x 在()0,3上单调递增B ．函数()f x 在()0,3上单调递减C ．函数()f x 图像关于32x =对称D ．函数()f x 图像关于3,02⎛⎫ ⎪⎝⎭对称 9．已知,x y 满足001x y x y x -⎧⎪+⎨⎪⎩，则32y x --的取值范围为（ ） A ．3,42⎡⎤⎢⎥⎣⎦ B ．(1,2] C ．(,0][2,)-∞+∞ D ．(,1)[2,)-∞⋃+∞10．已知等差数列{}n a 中，若5732a a =，则此数列中一定为0的是（ ）A ．1aB ．3aC ．8aD ．10a11．如图，在平面四边形ABCD 中，满足,AB BC CD AD ==，且10,8AB AD BD +==，沿着BD 把ABD 折起，使点A 到达点P 的位置，且使2PC =，则三棱锥P BCD -体积的最大值为（ ）A ．12B ．122C ．23D ．16312．函数||1()e sin 28x f x x =的部分图象大致是（ ） A ． B ．C ．D ．二、填空题：本题共4小题，每小题5分，共20分。
推荐-浙江省2018年五校联考理数学参考答案 精品
浙江省2018年五校联考试题数学(理工类)答案11.()⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫ ⎝⎛<-⎪⎭⎫ ⎝⎛≥-21121122x x x 12. (]9,∞- 13.1- 14.()2,0 三、解答题：本大题共6小题，每小题14分，共84分。
解答应写出文字说明，证明过程或演算步骤。
15．解：设()11,y x =，()22,y x =………………………………………………（2分） 则023211=+-=y x c a ；423222-=+-=y x c b ；………………………………………………（6分） 82121=+=y x ；42222=+=y x ．………………………………………………（10分）解得⎩⎨⎧==6211y x ，或⎩⎨⎧-=-=6211y x ，对应的b 分别为⎩⎨⎧-==2022y x ，或⎩⎨⎧==1322y x ，分别代入()2,32-=+=n m ，解得6,4±=-=m n ……………（14分）16．解：()()cos 1sin sin 4f x a x x b x a b π⎛⎫=+++=+++ ⎪⎝⎭……………（2分）（Ⅰ）当1a =时，()14f x x b π⎛⎫==+++ ⎪⎝⎭∴当()22242k x k k Z πππππ-≤+≤+∈时，()f x 是增函数，∴函数()f x 的单调增区间为()32,244k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦……………（8分） （Ⅱ）由0x π≤≤得5444x πππ≤+≤∴sin 14x π⎛⎫≤+≤ ⎪⎝⎭………………………………………………（10分）∵0a <∴当sin 14x π⎛⎫+= ⎪⎝⎭时，()f x 取最小值33a b ++=……………（※）当sin 4x π⎛⎫+= ⎪⎝⎭时， ()f x 取最大值4，即4b =将4b =代入（※）式得1a =5a b +=（14分） 17．解：1）3P =31………………………………………………（4分） 2）由于第n 次到顶点A 是从D C B ,,三个顶点爬行而来，从其中任何一个顶点到达A 的概率都是31，而第1-n 次在顶点A 与小虫在D C B ,,是对立事件． 因此，第n 次到顶点A 的概率为()1131--=n n P P ………………（8分）即⎪⎭⎫⎝⎛--=--4131411n n P P ………………………………………（11分） ⎭⎬⎫⎩⎨⎧-∴=41,11n P P 是以43411=-P为首项，公比为31-的等比数列， ()N n n P n n ∈≥+⎪⎭⎫⎝⎛-=∴-,2 4131431………………………………（14分） 18．（Ⅰ）取1CC 的中点G ，则DG 为AE 在面1DC 内的射影，11D F DG AE D F ⊥∴⊥ 又1AD AE A D F ⋂=∴⊥面ADE ………………………………（5分） （Ⅱ）不成立………………………………（7分） 设1CC 、F D 1与平面ADE 的交点分别为G 、H, 在菱形11C CDD 中，可得DG DD ⊥1 又 平面⊥ABCD 平面11C CDD ，且平面⋂ABCD 平面11C CDD =CD ，CD AD ⊥1DD AD ⊥∴，因此AED DD 平面⊥1所以1DHD ∠为直线ADE F D 与平面1所成的角………………………………（10分） 在菱形11C CDD 内，因为CD C 1∠=060，所以01120=∠DE D可求得a F D 271=，所以1475arccos1=∠F D D ， 在H DD Rt 1∆中，211π=∠+∠HD D H DD ，∴1DHD ∠=1475arcsin所以直线ADE F D 与平面1所成的角为1475arcsin．………………………（14分） 19．解：（1）设(0,),(,0)P b M a ，则,PF PM bk b k a=-=-201PF PM PM PF k k a b ⋅=∴⋅=-∴=-2(,0)M b ∴-，又PM PN =，即P 为MN 的中点，2(,2)N b b ∴因此，N 的轨迹方程为：24y x =，其轨迹为以(1,0)F 为焦点的抛物线………………………………………………（6分）（2）设:l y kx b =+，与24y x =联立得：20(*)4k y y b -+= 设1122(,),(,)A x y B x y ，则12y y 、是（*）式的两根，且124b y y k=由4OA OB ⋅=-得：12124x x y y +=-，即221212124,844y y y y y y ⋅+=-∴=-482bb k k∴=-∴=-………………………（10分） 因此，直线方程可写为：2(2)y kx k k x =-=- （*）式可化为：21212420,84k y y k y y y y k--=∴+==-而AB ⎡=⎣ 即：22116(1)(2)30k k ≤++≤ 令211x k =+，解得211125141122x k k k ≤≤∴≤≤∴-≤≤-≤≤或 ………………………（14分） 20．证明：（1） 0)1()1(==-f f ，v u v f u f -≤-)()( ∴()()()x x f x f x f -=-≤-=111由此可得：()x x f x -≤≤-11………………………（5分） （2）若01≤<≤-v u ，则由v u v f u f -≤-)()(，得1)()(≤-≤-u v v f u f ，同理，若10≤<≤v u ，则由v u v f u f -≤-)()(， 得1)()(≤-≤-u v v f u f ………………………………（9分）若101<≤<≤-v u ，则()()()()11)()(f v f f u f v f u f +---=- ()()()()()1111-+--≤-+--≤v u f v f f u f =()u v v u --=-++21110≤<≤v u ，1≥-∴u v ，因此()12≤--u v()()1≤-∴v f u f综上所述，对任意的]1,1[,-∈v u ，都有1)()(≤-v f u f ………（14分）。
浙江省2018年五校联考数学试题最终稿学参考答案
1 5
13． 26 2 34 ,
125 2 3
17． 4 33
三、解答题：本大题共 5 小题，共 74 分．解答应写出文字说明、证明过程或演算步骤． 18． （本题满分 14 分） 解：（Ⅰ）由 (b c) a (2
2 2
2)bc得
b 2 c 2 a 2 2bc,
km 1 x ，解得 xQ 1 k2 k
…………………………9 分
由 PB : y kx m 联立 OQ : y
∴ PQ 1 k
2
km 4k 1 k2 m
∴ S OPQ
PQ OQ 2
m 1 km 4k 1 k2 …………………………12 分 2 2 1 k 1 k2 m
EG EF sin
o
…………………15 分
方法（体积法）作，则由面面可得面 2 PE BF PBF , 由解得点到面距离从而 VP ACD VD PAC , D PAC h
ABCD, 3 , 2
PE
ABCD
sin
h 3 AD 4
20． （本小题满分 15 分）
xx 1 ' g x x ln x , 可得： f x 0 x 1 解: （Ⅰ）设 x 2x x 所以是增函数，得即欲证成立 g x g x .g 1 0, （5分） L L
2
x 1 ln x x 1 x ' x （Ⅱ）① f x ln x 0 x 1 2 2 2 2 x x 1 ln x x 1 ln x
当 k 1 时取等号
浙江省五校联考2018年高考模拟数学理科试卷及答案解析
浙江省五校联考2018年高考模拟数学理科试卷（总分：150分 时间：120分钟）一、选择题：本题共12小题，每小题5分，共60分． 1. 已知集合(){},|1A x y y x ==-，(){},|1B x y y x ==-+，则A B =I( )A.∅B.{}1C.{}0,1D.(){}1,02.已知复数z= 201821i i++（i 为虚数单位），则复数z 的共轭复数．．．．在复平面内对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩（单位：分），已知甲组数据的中位数为17，乙组数据的平均数为17.4，则x 、y 的 值分别为（ ）A. 7、8B. 5、7C. 8、5D. 7、74. 设向量a ，b 满足，()3-=g a a b ，则a 与b 的夹角为5若123)(23++-=x x a x x f 在区间⎪⎭⎫⎝⎛3,21上有极值点,则实数的取值范围是( )A. B. C. D.6. 执行如图所示的程序框图，若输出的57S =，则判断框内应填入的条件是（ ） A ．4k > B ．5k > C.6k > D ．7k >7. 已知ABCD 为正方形，其内切圆I 与各边分别切于E ，F ，G ，H ，连接EF ，FG ，GH ，HE ．现向正方形ABCD 内随机抛掷一枚豆子，记事件A ：豆子落在圆I 内，事件B ：豆子落在四边形EFGH 外，则(|)P B A =（ ）A ．14π-B ．4π C ．21π-D ．2π8. 已知函数⎪⎩⎪⎨⎧≥<≤=1,4sin 10,2)(x x x x f x π，则=-+)7log 3()2(2f fA ．87 B ． 227 C ．158 D ． 1579.我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中，有5架“歼— 15”飞机准备着舰，如果乙机不能最先着舰，而丙机必须在甲机之前着舰（不一定相邻），那么不同的着舰方法种数为（ ） A. 24 B. 36 C.48 D. 9610．已知抛物线C ：24y x =的焦点为F ，直线24y x =-与C 交于A ，B 两点．则cos AFB ∠=( )A ．45B ．35C ．35-D ．45-11. 中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖b i e．如图为一个阳马与一个鳖臑的组合体，已知三棱锥P ADE -为鳖臑,且PA ⊥平面ABCE ，2AB AD ==，1ED =，该鳖臑．．的外接球的表面积为9π，则阳马．．的外接球的体积为A． B． C． D．12．已知函数()(1)(2)e e xf x m x x =----，若关于x 的不等式0)(>x f 有且只有一个正整数解，则实数m 的最大值为A ．3e e 2+B ．2e e 2+C ．3e e 2-D ．2e e2-第Ⅱ卷（非选择题，共90分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答．作图题可先用2B 铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚，在试题卷上作答无效． 二、填空题：本大题共4个小题，每小题5分，共20分．13. 已知平面向量(==m ,n ，则m 在n 上的投影=_______.14. 已知6260126(2)(1)(1)...(1)x a a x a x a x +=+++++++，则3a = ．（结果用数值表示）．15．在ABC △中，AB BC =，7cos 18B =-．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．16．对1x R ∀∈，[]23,4x ∃∈，使得不等式2211221223x x x x x mx ++≥++成立，则实数m 的取值范围是 ．三、解答题：共70分．解答应写出文字说明、证明过程和演算步骤．第17～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答． 17. （本小题满分12分）已知数列{a n }满足a l =﹣2，a n+1=2a n +4． （I ）证明数列{a n +4}是等比数列；（Ⅱ）求数列{|a n |}的前n 项和S n ．18. （本小题满分12分）如图，已知长方形ABCD 中，22AB =，2AD =，M 为DC 的中点.将∆ADM 沿AM 折起，使得平面ADM ⊥平面ABCM.（1）求证：AD BM ⊥；（2若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为519. （本小题满分12分）四川省阆中中学某部根据运动场地的影响，但为尽大可能让学生都参与到运动会中来，在2018春季运动会中设置了五个项目，其中属于跑步类的两项，分别是200米和400米，另外三项分别为跳绳、跳远、跳高．学校要求每位学生必须参加，且只参加其中一项，学校780名同学参加各运动项目人数统计如下条形图：其中参加跑步类的人数所占频率为713，为了了解学生身体健康与参加运动项目之间的关系，用分层抽样的方法从这780名学生中抽取．．13．．人进行分析．．．．．．．（Ⅰ）求条形图中m 和n 的值以及抽取的13人中参加200米的学生人数；（Ⅱ）现从抽取的参加400米和跳绳两个项目中随机抽取4人，记其中参加400米跑的学生人数为X ，求离散型随机变量X 的分布列与数学期望．20.（本小题满分12分）已知椭圆C ：22221x y a b+=（0a b >>）的左右焦点分别为1F ，2F ，离心率为12，点A 在椭圆C 上，1||2AF =，1260F AF ∠=︒，过2F 与坐标轴不垂直的直线l 与椭圆C 交于P ，Q 两点．（Ⅰ）求椭圆C 的方程；（Ⅱ）若P ，Q 的中点为N ，在线段2OF 上是否存在点(,0)M m ，使得MN PQ ⊥？若存在，求实数m 的取值范围；若不存在，说明理由． 21.（本小题满分12分）已知函数()()R a a x x a x x x f ∈+--=22ln 在其定义域内有两个不同的极值点. （1）求a 的取值范围；（2）记两极值点分别为.,,2121x x x x <且已知0>λ，若不等式112e x x λλ+<⋅恒成立，求λ的范围.请考生在第22,23,三题中任选一题作答，如果多做，则按所做的第一题给分.作答时请写清题号22. （本小题满分10分）已知曲线C ： 21sin ρθ=-，直线cos :sin x t l y t αα=⎧⎨=⎩（t 为参数，0απ≤<）. （Ⅰ）求曲线C 的直角坐标方程；（Ⅱ）设直线 与曲线C 交于A 、B 两点（A 在第一象限），当30OA OB +=时，求α的值. 23. （本小题满分10分）已知函数f （x ）=﹣x 2+ax+4，g （x ）=|x+1|+|x ﹣1|． （1）当a=1时，求不等式f （x ）≥g （x ）的解集；（2）若不等式f （x ）≥g （x ）的解集包含[﹣1，1]，求a 的取值范围．理科数学答案一、选择题（每小题5分，共计60分）二．填空题（每小题5分，共计20分）13． -1 14． 20 15． 3816．(],3-∞ 三、解答题17.（I ）证明：∵数列{a n }满足a l =﹣2，a n+1=2a n +4，∴a n+1+4=2（a n +4）..................3分 ∴数列{a n +4}是等比数列，公比与首项为2．...............................................................6分 （II ）解：由（I ）可得：a n +4=2n ， ∴a n =2n ﹣4，...............................................8分∴当n=1时，a 1=﹣2；n≥2时，a n ≥0，..........................................................................9分 ∴n≥2时，S n =﹣a 1+a 2+a 3+…+a n =2+（22﹣4）+（23﹣4）+…+（2n ﹣4） =﹣4（n ﹣1）=2n+1﹣4n+2．n=1时也成立．............................................11分∴S n =2n+1﹣4n+2．n ∈N * ．.............................................................................................12分 18. 【答案】（1）解：证明：∵长方形ABCD 中，AB=，AD=，M 为DC 的中点，∴AM=BM=2，∴BM ⊥AM.....................................3分∵平面ADM ⊥平面ABCM ，平面ADM∩平面ABCM=AM ，BM ⊂平面ABCM ∴BM ⊥平面ADM ∵AD ⊂平面ADM∴AD ⊥BM.......................................................5分 （2）解：建立如图所示的直角坐标系设，则平面AMD 的一个法向量 ，...................................7分，设平面AME 的一个法向量 则 取y=1，得所以，............................................10分因为 ，求得 ，所以E 为BD 的中点 .......................11分19..（Ⅱ）由题意，得抽取的13人中参加400米的学生人数有240134780⨯=，参加跳绳的学生人数有3人，所以X 的所有可能取值为1、2、3、4，………………6分()134347C C 41C 35P X ===，()224347C C 182C 35P X ===，()314347C C 123C 35P X ===，()4447C 14C 35P X ===，………………9分所以离散型随机变量X 的分布列为：……………………………………………………………………………11分 所以41812116()1234353535357E X =⨯+⨯+⨯+⨯=．………………12分 20．解：（Ⅰ）由12e =得2a c =，1||2AF =，2||22AF a =-， 由余弦定理得，222121212||||2||||cos ||AF AF AF AF A F F +-⋅=，解得1c =，2a =，2223b a c =-=，所以椭圆C 的方程为22143x y +=． (5)分（Ⅱ）存在这样的点M 符合题意. 设11(,)P x y ，22(,)Q x y ，00(,)N x y ， 由2(1,0)F ，设直线PQ 的方程为(1)y k x =-，由221,43(1),x y y k x ⎧+=⎪⎨⎪=-⎩得2222(43)84120k x k x k +-+-=，…………………7分 由韦达定理得2122843k x x k +=+，故212024243x x k x k +==+， 又点N 在直线PQ 上，02343k y k -=+，所以22243(,)4343k kN k k -++. …………………9分 因为MN PQ ⊥，所以22230143443MNk k k k k m k --+==--+，整理得22211(0,)34344k m k k==∈++， 所以存在实数m ，且m 的取值范围为1(0,)4．...12分21.I 依题意得函数)(x f 得定义域为(0,+∞)，所以方程0)('=x f 在(0,+∞)有两个不同的根， 即方程0ln =-ax x 在(0,+∞)有两个不同的根. 问题转化为函数xx x g ln )(=与ay =的图象(0,+∞)有两个不同的交点. 又,ln 1)('2xxx g -=即当e x <<0时，0)('>x g ；当e x >时，0)('<x g ， 所以)(x g 在),0(e 上单调递增，在),(+∞e 上单调递减.从而ee g x g 1)()(==极大值 ………………3分 又)(x g 有且只有一个零点是1，且当0→x 时，-∞→)(x g ；当+∞→x 时，0)(→x g . 所以，要想函数xxx g ln )(=与函数a y =的图象(0,+∞)有两个不同的交点， 只需e a 10<<.…6分 (II )因为λλ+⋅<211x x e 等价于21ln ln 1x x λ+<λ+，由(I )知21,x x 是方程0ln =-ax x 的两个根，即2211ln ,ln ax x ax x ==，所以原式等价于)(ln ln 12121x x a x x λ+=λ+<λ+，因为2100x x <<>λ，，所以原式等价于211x x a λ+λ+>. …………8分又由2211ln ,ln ax x ax x ==作差得)(ln2121x x a x x -=，即2121ln x x x x a -=.所以原式等价于2121211lnx x x x x x λ+λ+>-，因为210x x <<时，原式恒成立，即212121)()1(ln x x x x x x λλ+-+〈恒成立. 令)1,0(,21∈=t x x t ，则不等式)1()1(ln -++<t t t λλ在)1,0(∈t 上恒成立. 令λλ+-+-=t t t t h )1()(1ln )(，又2222)()()1()()(11)('λ+λ--=λ+λ+-=t t t t t t t h ，当12≥λ时，可见)(0,1∈t 时，0)('>t h ，所以)(0,1)(∈t t h 在上单调递增, 又)(0,10)(,0)(1∈<=t t h h 在上恒成立，符合题意. …………10分当12<λ时，可见当)(0,2λ∈t 时，0)('>t h ，当)1(2，λ∈t 时，0)('<t h 所以)(0,)(2λ∈t t h 在上单调递增, 在),1(2λ∈t 上单调递减，又)(0,10)(,0)(1∈<=t t h h 在上不恒成立，不符合题意，舍去.综上所述，若不等式λλ+⋅<211x x e 恒成立，只需12≥λ，又0>λ，所以1≥λ…………12分22解：（Ⅰ）由 ，得 ，................................................................2分 所以曲线C 的直角坐标方程为 ................................................................................5分（Ⅱ）将直线l 的参数方程代入，得 ，.......7分设A ，B 两点对应的参数分别为 ，由韦达定理及 得 ，故 (10)分23.（1）解：（1）当a=1时，f （x ）=﹣x 2+x+4，是开口向下，对称轴为x=的二次函数，g （x ）=|x+1|+|x ﹣1|= ，................................................................................2分当x ∈（1，+∞）时，令﹣x 2+x+4=2x ，解得x=，g （x ）在（1，+∞）上单调递增，f （x ）在（1，+∞）上单调递减，∴此时f （x ）≥g （x ）的解集为（1，]； (3)分当x ∈[﹣1，1]时，g （x ）=2，f （x ）≥f （﹣1）=2．当x ∈（﹣∞，﹣1）时，g （x ）单调递减，f （x ）单调递增，且g （﹣1）=f （﹣1）=2． 综上所述，f （x ）≥g （x ）的解集为[﹣1，]；...........................................................5分（2）依题意得：﹣x 2+ax+4≥2在[﹣1，1]恒成立，即x 2﹣ax ﹣2≤0在[﹣1，1]恒成立，则只需，解得﹣1≤a≤1，故a 的取值范围是[﹣1，1]． ...............................................................................................10分。
浙江省宁波市五校联盟2023-2024学年高一下学期4月期中联考数学试题(含答案)
第二学期宁波五校联盟期中联考高一年级数学学科 试题考生须知：1．本卷共4页满分150分，考试时间120分钟。
2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。
3．所有答案必须写在答题纸上，写在试卷上无效。
4．考试结束后，只需上交答题纸。
选择题部分一、单选题：本题共8小题，每小题5分，共40分。
在每小题给出的选项中，只有一项是符合题目要求的。
1．已知复数()i 1i z =-，则z =（ ）A ．2B ．3C D2．如图，用斜二测画法得到ABC △的直观图为等腰直角三角形A B C '''，其中A B ''=，则ABC △的面积为（）A ．B ．C ．2D ．13．设{}12,e e是平面内的一个基底，则下面的四组向量不能构成基底的是（ ）A ．122e e + 和12e e -B ．123e e - 和2126e e -C ．123e e + 和213e e + D ．1e 和12e e + 4．在ABC △中，a x =，2b =，60B =︒，若三角形有两解，则x 的取值范围是（ ）A ．2x <<B ．2x <<C 2x <<D ．2x <<5．,a b 为不重合的直线，,αβ为互不相同的平面，下列说法正确的是（ ）A ．若αβ∥，a α⊂，b β⊂，则a b ∥B ．若a b ∥，a α∥，b β∥，则αβ∥C ．若a b ∥，b α∥，则a α∥D ．若a α∥，b α⊂，则a b ∥或a 与b 异面6．已知向量(1,a = ，1b = ，且()()223a b a b -⋅+=．则2a b + 在a 方向上的投影向量的坐标是（ ）A．32⎛⎝B．12⎛⎝C．12⎛- ⎝D．32⎛ ⎝．7．点O 在ABC △的内部，且满足：1255AO AB AC =+，则ABC △的面积与AOB △的面积之比是（ ）A ．72B ．3C ．52D ．28．已知,,a b e是平面向量，e 是单位向量，若非零向量a 与e 的夹角为π4，向量b 满足2680b b e -⋅+= ，则a b -的最小值是（ ）A1-B1+C1+D．2二、多选题：本题共3小题，共18分。
浙江省届高三下学期五校联考试题数学Word版含
2018学年浙江省高三“五校联考”考试数学试题卷命题学校：绍兴一中说明：本试题卷分选择题和非选择题两部分．全卷共4页，满分150分，考试时间 120分钟．请考生按规定用笔将全部试题的答案涂、写在答题纸上．参照公式柱体的体公式：V=Sh ，此中S 表示柱体的底面,h 表示柱体的高；体的体公式：V=1Sh ，此中S 表示体的底面,h 表示体的高；3台体的体公式：V1 (S 1 S1S2S2)h ，此中S 1,S2分表示台体的上、下底面,h 表示台体的高；3球的表面公式： 2 ，球的体公式：V=4 3S=4πR πR ，此中R 表示球的半径；3若事件A,B 互斥, P(A+B)=P(A)+P(B)；若事件A,B 互相独立, P(A·B)=P(A)·P (B)；k若事件A 在一次中生的概率是p,n 次独立重复中事件A 恰巧生k 次的概率Pn(k)=Cn kpn-kn)⋯．, (1－p)(k=0,1,2,选择题部分（共一、选择题：本大题共 10目要求的.40分）小题，每题4分，共40分，在每题给出的四个选项中，只有一项为哪一项切合题1.已知会合U 1,1,3,5,7,9，A{1,5}，B1,5,7，则C U (AB) （▲）A.3,9B.1,5,7C.1,1,3,9D. 1,1,3,7,9 2.如图，网格纸上的小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（▲ ）A.426B.46C.422D.423.已知数列{a },知足 an 1 3an,且aa a69，则n2 4log 3a 5log 3a 7log 3a 9 （▲）（第2）A.5B.6C.8D.114.已知xy0 ，则“x”是“2|x|x 22|y|y 2”的（▲）A.充足不用要条件B. 必需不充足条件C.充足必需条件D. 既不充足也不用要条件5.函数y1x e x的大概图象为（▲）1 xCy1,6.已知实数x,y知足y2x10,假如目标函数z x y的最小值为－1，则实数m等于（▲）x y m0,A．7B．5C．4D．37.已知M tan sin cos，N tan(tan82)，则M和N的关系是（▲）28A.M NB.M NC.M ND.M和N没关8.已知函数f(x)|log2x|,x0,|2f(x)m|1，且mZ，若函数g(x)存在5个零1x,x，函数g(x)0.点，则m的值为（▲）9.设a,b,c为平面向量，|a||b|2，若(2c a)(c b)0，则cb的最大值为（▲）A.2B.9C.17D.5 4410.如图，在三棱锥S ABC中，SC AC,SCB,ACB,二面角S BC A的平面角为，则（▲）A. B.SCA C.SBA D.SBA非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分. 11．已知复数z知足1+2iz2i，则z=▲，|z|=▲.12．f(x)(x2x1)(2x1)5的睁开式中各项系数的和为▲，该睁开式中的常数项为▲. x13．已知函数f(x)cos(x)(0,||)象中两相的最高点和最低点分(,1),72121)，函数f(x)的增区▲，将函数f(x)的象起码平移▲个位度后对于直(,12x称.414．一个正四周体的四个面上分有1，2，3，4，将正四周体抛两次，向下一面的数字和偶数的概率▲，两个数字和的数学希望▲.15．已知双曲x2y21(a0,b0)中，A1,A2是左、右点，F是右焦点，B是虚的上端点．若在a2b2段BF上（不含端点）存在不一样的两点P i(i1,2)，使得PA i1PA i20，双曲离心率的取范是▲.16．从0,1,2,⋯,8九个数字中取五个不一样的数成五位偶数，且奇数数字不可以放在偶数位（从万位到个位分是第一位，第二位⋯⋯），有▲个不一样的数.（用数字作答）17．已知数x,y[1,1]a,a b,，max{a,b}b.b,amax{x2y21,|x2y|}的最小▲.三、解答：本大共5小，共74分，解答写出文字明、明程或演算步. 18．（安分14分）已知ABC中，角A,B,C所的分a,b,c，且cos AsinA2.222(Ⅰ)求角A的大小；(Ⅱ)当a7,sin(A C)21，求c的. 1419．（安分15分）如，已知ABC中，ABBC7,AC1，点A平面，点B,C在平面的同，且B,C在平面上的射影分E,D，BE2CD2.(Ⅰ)求：平面ABE平面BCDE；(Ⅱ)若M是AD中点，求平面BMC与平面所成二面角的余弦.20．（此题满分15分）已知正项数列a n的前n项和为S n，知足2S n12a n2a n(nN).(Ⅰ)（i）求数列a n的通项公式；（ii）已知对于n 1111M的最小值；N，不等式S2S3M恒建立，务实数S1S n(Ⅱ)数列b n的前n项和为T n，知足42a n1T n2(n N)，能否存在非零实数，使得数列b n为等比数列？并说明原因.21．（此题满分15分）x2y21，抛物线x22y的准线与椭圆交于A,B两点，过线段AB上的动点P作斜率已知椭圆4为正的直线l与抛物线相切，且交椭圆于M,N两点.(Ⅰ)求线段AB的长及直线l斜率的取值范围；1MNQ面积的最大值.(Ⅱ)若Q（0，），求422．（此题满分15分）已知函数f(x) e x ax (Ⅰ)若f(x)0恒建立，求b.(此中e为自然对数的底数ab的最大值；)(Ⅱ)设g(x)lnx1，若F(x)g(x)f(x)存在独一的零点，且对知足条件的a,b不等式m（ae1)b恒建立，务实数m的取值会合.。
浙江省宁波市五校联盟2023-2024学年高一上学期期中联考数学试题含解析
2023学年第一学期宁波五校联盟期中联考高一年级数学学科试题（答案在最后）考生须知：1．本卷共5页满分150分，考试时间120分钟．2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字．3．所有答案必须写在答题纸上，写在试卷上无效．4．考试结束后，只需上交答题纸．选择题部分一、单项选择题（本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.设集合{}{}{}1,2,3,4,5,6,1,3,5,3,4,5U A B ===，则()U A B ⋃=ð（）A.{}2,6 B.{}3,5 C.{}1,3,4,5 D.{}1,2,4,6【答案】A 【解析】【分析】先求A B ⋃，再求补集可得答案.【详解】集合{}{}{}1,3,53,4,51,3,4,5== A B ，则(){}2,6U A B ⋃=ð.故选：A.2.=是“22=”的（）A .充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】利用充分必要条件的判断方法判断即可.=1,1a b =-=-，22=不成立，则充分性不成立；当22=时，0a b =≥，则220a b =≥，=综上：=是“22=”的必要不充分条件.故选：B.3.已知命题p ：“R x ∃∈，210x ax -+<”为假命题，则实数a 的取值范围为（）.A.(],2-∞ B.()2,2-C.()(),22,∞∞--⋃+ D.[]22-,【答案】D 【解析】【分析】由命题p ⌝为真命题，则0∆≤，解不等式得出实数a 的取值范围即可．【详解】命题2:,10p x R x ax ∃∈++<为假命题，所以2:,10p x R x ax ⌝∀∈++≥为真命题，则240a ∆=-≤，解得[]2,2a ∈-故选：D4.已知0x >，0y >，且21x y +=，下列结论中错误的是（）A.xy 的最大值是18B.24x y +的最小值是2C.12x y+的最小值是9 D.224x y +的最小值是12【答案】B 【解析】【分析】根据基本不等式判断各选项即可.【详解】对于A ，由0x >，0y >，且21x y +=，由2x y +≥，当且仅当122x y ==时，等号成立，所以1≤，解得18xy ≤，即xy 的最大值为18，故A 正确；对于B ，由22224x y x y =+≥=+=当且仅当122x y ==时，等号成立，所以24x y +最小值为B 错误；对于C ，()1212222559y x x y x y x y x y ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当22y x x y =，即13x y ==时，等号成立，所以12x y +的最小值是9，故C 正确；对于D ，由()2222224212224x y x yx y +++⎛⎫=≥= ⎪⎝⎭，当且仅当122x y ==时，等号成立，所以224x y +的最小值是12，故D 正确.故选：B.5.设(,)a -∞是函数245y x x =-+的一个减区间，则实数a 的取值范围为（）A.2a ≤- B.2a ≥- C.2a ≥ D.2a ≤【答案】A 【解析】【分析】根据图象的翻折变换作出函数图象，观察图象可得.【详解】函数224545y x x x x =-+=-+，先作函数245y x x =-+的图象，如图：根据函数图象的翻折变换可得245y x x =-+的图象如图：由图可知，当2a ≤-时，(,)a -∞是函数245y x x =-+的一个减区间，所以，实数a 的取值范围为(,)a -∞.故选：A6.已知函数()f x 是偶函数，()g x 是奇函数，满足2()()2f x g x x x +=+-，则(2)f =（）A.1B.2C.3D.4【答案】B 【解析】【分析】根据奇偶性求得函数()f x ，然后再代入计算函数值．【详解】2()()2f x g x x x +=+-，则2()()2f x g x x x +-=---，又函数()f x 是偶函数，()g x 是奇函数，则2()()2f x g x x x =---，所以()()()()()()22222222x x x x f x g x f x g x f x x +-+--⎡⎤⎡⎤++-⎣⎦⎣⎦===-，2(2)222f =-=，故选：B ．7.已知2535a ⎛⎫= ⎪⎝⎭，3525b ⎛⎫= ⎪⎝⎭，2525c ⎛⎫= ⎪⎝⎭，则a ，b ，c 的大小关系为（）A.a b c <<B.c b a <<C.b<c<aD.c<a<b【答案】C 【解析】【分析】根据指数函数和幂函数的单调性即可比较.【详解】25y x= 在()0,+¥为增函数，22553255⎛⎫⎛⎫∴> ⎪ ⎪⎝⎭⎝⎭，即a c >，25xy ⎛⎫= ⎪⎝⎭为减函数，32552255⎛⎫⎛⎫∴< ⎪ ⎪⎝⎭⎝⎭，即b c <，a c b ∴>>，故选：C.【点睛】本题考查了指数函数和幂函数的单调性，属于基础题.8.已知幂函数f （x ）=x a 的图象经过点（2），则函数f （x ）为（）A.奇函数且在()0,+∞上单调递增B.偶函数且在()0,+∞上单调递减C.非奇非偶函数且在()0,+∞上单调递增D.非奇非偶函数且在()0,+∞上单调递减【答案】C 【解析】【分析】根据已知求出a=12，从而函数f（x）=12x ，由此得到函数f（x）是非奇非偶函数且在（0，+∞）上单调递增．【详解】∵幂函数f（x）=x a），∴2a，解得a=12，∴函数f（x）=12x ，∴函数f（x）是非奇非偶函数且在（0，+∞）上单调递增．故选C．【点睛】本题考查命题真假的判断，考查幂函数的性质等基础知识，考查运算求解能力，是基础题．二、多项选择题（本大题共4个小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求全部选对得5分，选对但不全的得3分，有选错的得0分）9.下列各组函数中是同一函数的是（）A.()f x =()g x =B.()f x =，()g x =C.()||f x x =，()g t =D.()1f x x =+，()1g t t =-【答案】BC 【解析】【分析】逐一判断定义域和对应关系即可.【详解】A 选项：由1010x x +≥⎧⎨-≥⎩得()f x 的定义域为[)1,+∞，由()()110x x +-≥解得()g x 的定义域为(][),11,-∞-⋃+∞，A 错误；B 选项：由1010x x +≥⎧⎨-≥⎩得()f x 的定义域为[]1,1-，由()()110x x +-≥解得()g x 的定义域为[]1,1-，且()f x ==，故B 正确；C 选项：()f x 和()g x 的定义域都是R ，()g t t ==，对应关系相同，故C 正确；D 选项：对应关系不同，故D 错误.故选：BC10.已知关于x 的不等式20ax bx c ++>的解集为{|2x x <-或}3x >，则下列说法正确的是（）A.0a >B.不等式0bx c +>的解集是{}6x x <C.0a b c ++<D.不等式20cx bx a -+<的解集是{1|3x x <-或12x ⎫>⎬⎭【答案】ACD 【解析】【分析】由不等式20ax bx c ++>与方程20ax bx c ++=之间的关系及题设条件得到,,a b c 之间的关系，然后逐项分析即可得出正确选项.【详解】由题意不等式20ax bx c ++>的解集为{|2x x <-或}3x >，则可知0a >，即A 正确；易知，2-和3是方程20ax bx c ++=的两个实数根，由韦达定理可得2323b ac a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，则,6b a c a =-=-；所以不等式0bx c +>即为60ax a -->，解得6x <-，所以B 错误；易知60a b c a ++=-<，所以C 正确；不等式20cx bx a -+<即为260ax ax a -++<，也即2610x x -->，解得{1|3x x <-或12x ⎫>⎬⎭，所以D 正确.故选：ACD11.如果函数()f x 在[],a b 上是增函数，对于任意的[]()1212,,x x a b x x ∈≠，则下列结论中正确的是（）A.()()1212f x f x x x ->- B.()()()12120x x f x f x -->⎡⎤⎣⎦C.()()()()12f a f x f x f b ≤<≤ D.()()12f x f x >【答案】AB 【解析】【分析】根据函数单调性的等价条件进行判断即可．【详解】由函数单调性的定义可知，若函数()f x 在给定的区间上是增函数，则12x x -与()()12f x f x -同号，由此可知，选项A ，B 正确；对于选项C ，D ，因为12,x x 的大小关系无法判断，则()()12,f x f x 的大小关系确定也无法判断，故C ，D 不正确.故选：AB【点睛】结论点睛：若函数()f x 在[],a b 上是增函数，对于任意的[]()1212,,x x a b x x ∈≠，则有()()12120f x f x x x ->-（或者()()()12120x x f x f x -->⎡⎤⎣⎦）；若函数()f x 在[],a b 上是减函数，对于任意的[]()1212,,x x a b x x ∈≠，则有()()12120f x f x x x -<-（或者()()()12120x x f x f x --<⎡⎤⎣⎦）；12.形如()()0af x x a x=+>的函数，我们称之为“对勾函数”.“对勾函数”具有如下性质：该函数在(上单调递减，在)+∞上单调递增.已知函数()()0af x x a x=+>在[]2,4上的最大值比最小值大1，则a 的值可以是（）A.4B.12C.6-D.6+【答案】AD 【解析】2≤、4≥、24<<三种情况讨论，分别求出函数的最值，即可得到方程，解得即可.【详解】依题意可得()()0af x x a x=+>在(上单调递减，在)+∞上单调递增，2≤，即04a <≤时()f x 在[]2,4上单调递增，所以()()max 444a f x f ==+，()()min 222a f x f ==+，所以()()max min 4221424a a af x f x ⎛⎫-=+-+=-= ⎪⎝⎭，解得4a =；4≥，即16a ≥时()f x 在[]2,4上单调递减，所以()()min 444af x f ==+，()()max 222a f x f ==+，所以()()max min 2421244a a af x f x ⎛⎫-=+-+=-= ⎪⎝⎭，解得12a =（舍去）；当24<<，即416a <<时()f x 在⎡⎣上单调递减，在4⎤⎦上单调递增，所以()min f x f ==，()()(){}max max 2,4f x f f =，若4242a a +>+且416a <<，即48a <<，()()max 444af x f ==+，所以()()max min 414af x f x -=+-=，解得4a =或36a =（舍去）；若4242a a +≤+且416a <<，即816a ≤<，()()max 222a f x f ==+，所以()()max min 212af x f x -=+-=，解得6a =+或6a =-（舍去）；综上可得6a =+或4a =.故选：AD非选择题部分三、填空题（本大题共4个小题，每小题5分，共20分）13.221302182********--⎛⎫⎛⎫+--= ⎪ ⎪⎝⎭⎝⎭______．【答案】54-【解析】【分析】根据幂的运算法则计算．【详解】222133()03218295202316144()1227344--⨯-⎛⎫⎛⎫+--=+--=-=- ⎪ ⎪⎝⎭⎝⎭，故答案为：54-．14.集合{}Z |23A x x =∈-≤<的子集个数是______．【答案】32【解析】【分析】确定出集合A 中元素个数，由子集的概念可得．【详解】由已知{2,1,0,1,2}A =--，A 有5个元素，它的子集个数为5232=．故答案为：32.15.若函数()f x x x a =-在区间(0,2]上既有最小值又有最大值，那么实数a 的取值范围是______．【答案】(0,2]【解析】【分析】当a<0，0a =讨论函数单调性，当0a >时，利用函数图象分析可得.【详解】当a<0时，在(0,2]上2()f x x ax =-，对称轴为2ax =，所以，函数()f x 在(0,2]上单调递增，所以()f x 有最大值，无最小值；当0a =时，在(0,2]上2()f x x =，在(0,2]上单调递增，所以()f x 有最大值，无最小值；当0a >时，22,(),x ax x af x ax x x a ⎧-≥=⎨-<⎩，函数图象如图所示，()f x 在0,2a ⎛⎫ ⎪⎝⎭和(),a +∞上单调递增，在,2a a ⎛⎫⎪⎝⎭上单调递减，要使()f x 在(0,2]上既有最小值又有最大值，则02a <≤，即实数a 的取值范围为(0,2].故答案为：(0,2]16.设()f x 是定义在R 上的奇函数，且当0x ≥时，2()f x x =，若对任意的[,1]x t t ∈+，不等式()2()f x t f x +≥恒成立，则实数t 的最小值是______．【答案】2【解析】【分析】由奇偶性求得()f x 的解析式，从而可得2())f x f =，然后由函数的单调性求解不等式．【详解】由已知0x <时，22()()()f x f x x x =--=--=-，即22,0(),0x x f x x x ⎧≥=⎨-<⎩，所以()f x 在R 上是增函数，且2())f x f =，不等式()2()f x t f x +≥化为())f x t f +≥，所以x t +≥，1)x t -≤，所以1)x t ≤，在[,1]x t t ∈+时恒成立，1)(1)t t -+≤，2t ≥，所以t 的最小值是2，故答案为：2．四、解答题（共6小题，共70分．解答题应写出文字说明，证明过程或演算步骤）17.已知集合A x y ⎧⎫⎪==⎨⎪⎩，{|123}B x m x m =-≤≤+．（1）当0m =时，求A B ⋂，A B ⋃；（2）若B A ⊆时，求实数m 的取值范围．【答案】（1）[1,2)A B ⋂=，(1,3]A B =- .（2）1,2⎛⎫-∞-⎪⎝⎭.【解析】【分析】（1）先解一元二次不等式得集合A ，然后由集合的运算可得；（2）根据集合的包含关系可解.【小问1详解】由220-++>x x 解得(1,2)A =-，当0m =时，[1,3]B =，故[1,2)A B ⋂=，(1,3]A B =- .【小问2详解】由题知B A ⊆，（ⅰ）当123m m ->+，即23m <-时，B =∅符合题意；（ⅱ）当123m m -≤+，即23m ≥-时，B ≠∅，因为B A ⊆，所以11232m m -<-⎧⎨+<⎩，解得12m <-，所以2132m -≤<-．综上所述，实数m 的取值范围为12∞⎛⎫--⎪⎝⎭.18.已知命题2:23,0p x x a ∀≤≤-≥，命题2:R,220q x x ax a ∃∈++=.（1）若命题p ⌝为假命题，求实数a 的取值范围；（2）若命题p 和q ⌝均为真命题，求实数a 的取值范围.【答案】（1）(],4∞-（2）()0,2【解析】【分析】（1）根据题意，由条件可得命题p 为真命题，列出不等式，即可得到结果；（2）根据题意，先求得当命题q 为真命题时a 的范围，即可得到q ⌝为真命题时a 的范围，再结合（1）中的结论，即可得到结果.【小问1详解】若命题p ⌝为假命题，则命题p 为真命题，即2a x ≤在[]2,3x ∈恒成立，所以()2min 4a x≤=，即实数a 的取值范围是(],4∞-.【小问2详解】当命题q 为真命题时，因为2R,220x x ax a ∃∈++=，所以2480a a ∆=-≥，解得0a ≤或2a ≥，因为q ⌝为真命题，则02a <<，又由（1）可知，命题p 为真命题时4a ≤，所以4a ≤且02a <<，即实数a 的取值范围是()0,2.19.已知二次函数2()(24)3(15)f x x a x a x =--++≤≤．（1）记()f x 的最小值为()g a ，求()g a 的解析式；（2）记()f x 的最大值为()h a ，求()h a 的解析式．【答案】（1）28,3()51,37489,7a a g a a a a a a -<⎧⎪=-+-≤≤⎨⎪->⎩（2）489,5()8,5a a h a a a -<⎧=⎨-≥⎩【解析】【分析】（1）结合二次函数()f x 的图像和性质，分类讨论单调性和最小值，求出()g a ，最后写成分段函数的形式即可；（2）结合二次函数()f x 的图像和性质，分类讨论函数最大值，求出()h a ，最后写成分段函数的形式即可．【小问1详解】二次函数()f x 的图像抛物线开口向上，对称轴为直线2=-x a ，（ⅰ）当21a -≤，即3a ≤时，此时()f x 在区间[1,5]上单调递增，所以()f x 的最小值()(1)8g a f a ==-；（ⅱ）当25a -≥，即7a ≥时，此时()f x 在区间[1,5]上单调递减，所以()f x 的最小值()(5)489g a f a ==-；（ⅲ）当125a <-<，即37a <<时，函数()f x 在[]1,2a -上单调递减，在(]25a -,上单调递增，此时()f x 的最小值2()(2)51g a f a a a =-=-+-；综上所述，()28,351,37489,7a a g a a a a a a -≤⎧⎪=-+-<<⎨⎪-≥⎩.【小问2详解】二次函数()f x 的图像抛物线开口向上，对称轴为直线2=-x a ，（ⅰ）当23a -<，即5a <时，右端点5x =距离对称性较远，此时()f x 的最大值()(5)489h a f a ==-；（ⅱ）当23a -≥，即5a ≥时，左端点1x =距离对称轴较远，此时()f x 的最大值()(1)8h a f a ==-；综上所述，489,5()8,5a a h a a a -<⎧=⎨-≥⎩.20.（1）已知正数,a b 满足121a b+=，求8a b +的最小值；（2）已知正数,a b 满足21a b +=，求11a ab+的最小值．【答案】（1）25；（2）5+.【解析】【分析】（1）（2）妙用“1”求解即可.【详解】（1）因为121a b+=，所以128(8)a b a b a b ⎛⎫+=++⎪⎝⎭281161717825a b b a =+++≥+=+=，当且仅当28121a b b a a b⎧=⎪⎪⎨⎪+=⎪⎩，即552a b =⎧⎪⎨=⎪⎩时，取得最小值，最小值为25.（2）因为21a b +=，所以111231a b a ab a ab a b++=+=+316(2)32552b a a b a b a b ⎛⎫=++=+++≥++ ⎪⎝⎭，当且仅当621b a a b a b ⎧=⎪⎨⎪+=⎩，即312a b ⎧=-⎪⎨=-⎪⎩时，取得最小值，最小值为5+.21.“绿色低碳、节能减排”是习近平总书记指示下的新时代发展方针.某市一企业积极响应习总书记的号召，采用某项新工艺，把企业生产中排放的二氧化碳转化为一种可利用的化工产品，以达到减排效果.已知该企业每月的二氧化碳处理量最少为300吨，最多为600吨，月处理成本y （元）与月处理量x （吨）之间的函数关系式可近似地表示为213001250002y x x =-+，且每处理一吨二氧化碳得到可利用的化工产品价值为100元.（1）该企业每月处理量为多少吨时，才能使其每吨的平均处理成本最低？（2）该市政府也积极支持该企业的减排措施，试问该企业在该减排措施下每月能否获利？如果获利，请求出最大利润；如果不获利，则该市政府至少需要补贴多少元才能使该企业在该措施下不亏损？【答案】（1）500（2）不能获利，该市政府需要补贴45000元【解析】【分析】（1）由题意列出每吨二氧化碳的平均处理成本的表达式，进而结合基本不等式求解即可；（2）由题意列出该企业每月的利润的函数表达式，进而结合二次函数的性质求解即可.【小问1详解】由题意，()213001250003006002y x x x =-+≤≤，所以每吨二氧化碳的平均处理成本为11250003003002002y x x x =-+≥=元，当且仅当11250002x x=，即500x =时，等号成立，所以该企业每月处理量为500吨时，才能使其每吨的平均处理成本最低.【小问2详解】设该企业每月的利润为()P x ，则()()22211130012500040012500040045000022210x P x x x x x x -++-=⎛⎫=-=- -⎪⎝⎭--，因为300600x ≤≤，所以当400x =时，函数()P x 取得最大值，即()()max 40045000P x P ==-，所以该企业每月不能获利，该市政府至少需要补贴45000元才能使该企业在该措施下不亏损.22.已知函数21()x f x ax b+=+是定义域上的奇函数，且(1)2f -=-．（1）判断并用定义证明函数()f x 在(0,)+∞上的单调性；（2）设函数()()g x f x m =-，若()g x 在(0,)+∞上有两个零点，求实数m 的取值范围；（3）设函数221()2()(0)h x x t f x t x =+-⋅<，若对121,,22x x ⎡⎤∀∈⎢⎥⎣⎦，都有()()12154h x h x -≤，求实数t 的取值范围．【答案】（1）()f x 在(0,1)上单调递减，在(1,)+∞上单调递增，证明见解析（2）m>2（3）3,02⎡⎫-⎪⎢⎣⎭【解析】【分析】（1）根据奇函数性质和已知列方程求出a ，b ，然后按照定义法证明单调性的步骤取值、作差、化简、定号、下结论即可；（2）利用一元二次方程根的分布列不等式组求解可得；（3）令1z x x =+换元得222y z tz =--，将问题转化为求最值问题，然后由()()max min 154h z h z -≤求解可得.【小问1详解】由(1)2f -=-，且()f x 是奇函数，得(1)2f =，于是2222a b a b ⎧=-⎪⎪-+⎨⎪=⎪+⎩，解得10a b =⎧⎨=⎩，即1()f x x x =+．经检验，()f x 是奇函数，满足题意.函数()f x 在(0,1)上单调递减，在(1,)+∞上单调递增，证明如下：任取12,(0,)x x ∈+∞，且12x x <，则()()()()121212121212121211111x x f x f x x x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫--=+-+=--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，当12,(0,1)x x ∈，且12x x <，则120x x -<，1201x x <<，∴1210x x -<，∴12())0(f x f x ->，即()()12f x f x >，所以，函数()f x 在(0,1)上单调递减．当()12,1,x x ∈+∞，且12x x <，则120x x -<，121x x >，∴1210x x ->，∴12())0(f x f x -<，即()()12f x f x <所以，函数()f x 在(1,)+∞上单调递增．【小问2详解】函数()g x 在(0,)+∞上有两个零点，即方程10x m x+-=在(0,)+∞上有两个不相等的实数根，所以210x mx -+=在(0,)+∞上有两个不相等的实数根，则21212Δ400210m m x x x x ⎧=->⎪⎪+=>⎨⎪=>⎪⎩，解得m>2．【小问3详解】由题意知2221111()222h x x t x x t x x x x x ⎛⎫⎛⎫⎛⎫=+-+=+-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，令1z x x=+，则222y z tz =--，由（1）可知函数1z x x =+在1,12⎡⎤⎢⎥⎣⎦上单调递减，在[1,2]上单调递增，∴52,2z ⎡⎤∈⎢⎥⎣⎦，因为函数222y z tz =--的对称轴方程为0z t =<，∴函数222y z tz =--在52,2⎡⎤⎢⎥⎣⎦上单调递增，当2z =时，222y z tz =--取得最小值，min 42y t =-+；当52z =时，222y z tz =--取得最大值，max 1754y t =-+．所以min ()42h x t =-+，max 17()54h x t =-+，又因为对任意的1x ∀，21,22x ⎡⎤∈⎢⎥⎣⎦都有()()12154h x h x -≤恒成立，∴max min 15()()4h x h x -≤，即17155(42)44t t -+--+≤，解得32t ≥-，。
2018~2019学年浙江省5月高三模拟考五校联考数学试卷 word版 含参考答案
2018学年浙江省高三“五校联考”考试数学试题卷命题学校：绍兴一中说明：本试题卷分选择题和非选择题两部分．全卷共4页，满分150分，考试时间120分钟．请考生按规定用笔将所有试题的答案涂、写在答题纸上． 参考公式选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合{}1,1,3,5,7,9U =-，{1,5}A =，{}7,5,1-=B ，则()U C A B =（ ▲ ）A.{}3,9B.{}1,5,7C.{}9,3,1,1-D.{}1,1,3,7,9-2. 如图，网格纸上的小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（ ▲ ） A. 624+ B. 64+C. 224+D. 24+3. 已知数列}{n a ,满足n n a a 31=+,且9642=a a a ，则 =++937353log log log a a a （ ▲ ） A.5 B. 6 C. 8 D. 114. 已知0>+y x ，则“0>x ”是“2||2||22y x y x +>+”的 （ ▲ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件（第2题图）5. 函数1e 1xx y x--=+的大致图象为（ ▲ ）6. 已知实数y x ,满足1,210,0,y y x x y m ≥⎧⎪-+≤⎨⎪+-≤⎩如果目标函数y x z -=的最小值为－1，则实数m 等于（ ▲ ）A ．7B ．5C ．4D ．3 7. 已知αααcos sin 2tan+=M ，)28(tan8tan+=ππN ，则M 和N 的关系是（ ▲ ）A.N M >B.N M <C.N M =D. M 和N 无关 8. 已知函数2|log |,0,()1,0.x x f x x x >⎧=⎨-≤⎩，函数1|)(2|)(--=m x f x g ，且Z m ∈，若函数)(x g 存在5个零点，则m 的值为（ ▲ ）A. 5B. 3C. 2D. 19. 设,,为平面向量，2||||==，若0)()2(=-⋅-，则⋅的最大值为（ ▲ ） A. 2 B.49C. 174D. 5 10. 如图，在三棱锥ABC S -中，AC SC =,θ=∠SCB ,θπ-=∠ACB ,二面角A BC S --的平面角为α，则 （ ▲ ）A.θα≥B.α≥∠SCAC.α≤∠SBAD.SBA α∠≥非选择题部分（共110分）二、填空题：本大题共7小题，多空题每小题6分，单空题每小题4分，共36分. 11．已知复数z 满足()1+22i z i =+，则z = ▲ ，|z |= ▲ .12． 251()(1)(2)f x x x x x=++-的展开式中各项系数的和为 ▲ ，该展开式中的常数项为 ▲ .B （第 10题图）SACB13．已知函数()cos()(0,||)2f x x πωϕωϕ=+><图象中两相邻的最高点和最低点分别为(,1),12π7(,1)12π-，则函数()f x 的单调递增区间为 ▲ ，将函数()f x 的图象至少平移 ▲ 个单位长度后关于直线4x π=-对称.14．一个正四面体的四个面上分别标有1，2，3，4，将该正四面体抛掷两次，则向下一面的数字和为偶数的概率为 ▲ ，这两个数字和的数学期望为 ▲ .15．已知双曲线22221(0,0)x y a b a b-=>>中，12,A A 是左、右顶点，F 是右焦点，B 是虚轴的上端点．若在线段BF 上（不含端点）存在不同的两点(1,2)i P i =，使得120i i PA PA ⋅=，则双曲线离心率的取值范围是 ▲ .16．从0,1,2,…,8这九个数字中取五个不同的数组成五位偶数，且奇数数字不能放在偶数位（从万位到个位分别是第一位，第二 位……），有 ▲ 个不同的数.（用数字作答） 17．已知实数,[1,1]x y ∈-，,,max{,},.a a b a b b a b ≥⎧=⎨<⎩则22max{1,|2|}x y x y -+-的最小值为 ▲ .三、解答题：本大题共5小题，共74分，解答应写出文字说明、证明过程或演算步骤.18．（本题满分14分） 已知ABC ∆中，角,,A B C 所对的边分别为,,a b c，且cos sin 22A A -= (Ⅰ)求角A 的大小； (Ⅱ)当)14a A C =+=，求c 的值.19．（本题满分15分）如图，已知ABC ∆中，AB BC AC ===，点A ∈平面α，点,B C 在平面α的同侧，且,B C 在平面α上的射影分别为,E D ，22BE CD ==. (Ⅰ)求证：平面ABE ⊥平面BCDE ；(Ⅱ)若M 是AD 中点，求平面BMC 与平面α所成锐二面角的余弦值.AE.BCDMα（第19题图）20．（本题满分15分）已知正项数列{}n a 的前n 项和为n S ，满足2212(N )n n n S a a n *+=+∈.(Ⅰ)（i ）求数列{}n a 的通项公式； （ii ）已知对于N n *∈，不等式1231111nM S S S S ++++<恒成立，求实数M 的最小值； (Ⅱ) 数列{}n b 的前n 项和为n T ，满足2142(N )n a n T n λ-*=-∈，是否存在非零实数λ，使得数列{}n b为等比数列？ 并说明理由. 21．（本题满分15分）已知椭圆2214x y +=，抛物线22x y =的准线与椭圆交于,A B 两点，过线段AB 上的动点P 作斜率 为正的直线l 与抛物线相切，且交椭圆于,M N 两点. (Ⅰ)求线段AB 的长及直线l 斜率的取值范围； (Ⅱ)若104Q （，），求MNQ ∆面积的最大值.22．（本题满分15分）已知函数()e xf x ax b =--.(其中e 为自然对数的底数)(Ⅰ)若()0f x ≥恒成立，求ab 的最大值；(Ⅱ)设()ln 1g x x =+，若()()()F x g x f x =-存在唯一的零点，且对满足条件的,a b 不等式e 1)-+≥（m a b 恒成立，求实数m的取值集合.2019 五校联考参考答案一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题11．4355i-，1； 12． 3，-40 ； 13．5[,]()1212k k k Zππππ-+∈，6π； 14．12,5；15e<<； 16．1680； 17．32．三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.18. 解：(Ⅰ)由得21)2sin2(cos2=-AA,即212cos2sin21=-AA21sin=A，-------------------3分又π<<A0，02sin2cos>-AA,2sin)22sin(2cosAAA>-=π,2,222ππ<>-AAA所以6π=A-------------------7分(Ⅱ)由1421)sin(=+AC,得1421sin=B由正弦定理：BbAasinsin=,得3=b-------------------10分由余弦定理：Abccba cos2222-+=，得cc3372-+=，4=c或1-=c（舍去）所以4=c-------------------14分19. (Ⅰ)证明：由条件，ADEBE平面⊥,AEBE⊥∴,由计算得3,6,3===ADEDAE,222ADEDAE=+∴,AEED⊥又EBEED=⋂,BCDEAE平面⊥∴,而ABEAE平面⊂∴BCDEABE平面平面⊥------------------6分(Ⅱ)以E为坐标原点，直线EA,ED,EB为x,y,z轴建立空间直角坐标系，)1,6,0(),0,6,0(),2,0,0(),,0,3(CDBA,则)0,26,23(M,3(,2)22BM=-, 1)BC=-,平面α的法向量为(0,0,1)m=-------------------8分设平面MBC的法向量),,(zyxn=，由{n BCn BM⋅=⋅=20zz-=-=⇒取1,(32,1,y n==------------------11分设平面BMC 与平面α所成锐二面角为θ，则6cos ||5||||m n m n θ⋅==⋅所以平面BMC 与平面α所成锐二面角的余弦值为5. -------------------15分20. 解：(Ⅰ) （i ）1，所以0又,212,时111211=>+=+=a a a a a n n ，…………………….1分 当,时2≥n )(2122∙∈+=+N n a a S n n n )(2121-21-1-∙∈+=+N n a a S n n n作差整理得： ,因为 ,所以，故数列{}n a 为等差数列，. ……………………………………………………..4分 （ii ）由（i ）知，4)3(+=n n S n ，所以)311(34)3(41+-=+=n n n n S n，从而=++++nS S S S 1111321)311()2111()1121()6131()5121()411((34+-++--++--++-+-+-n n n n n n )31211131211(34+-+-+-+++=n n n 922)312111611(34<+-+-+-+=n n n ， 所以922≥M ，故实数的最小值为922…………………………………….8分 (Ⅱ)由)(2412∙-∈-=N n T n a n λ知λλλ241,24+=-=n n n n T T …………………………..9分当λ6,时11==b n ，……………………………………………………10分当λλλλ241241,时211--+=-=≥--n n n n n T T b n143-=n λ所以)2(4431≥==+n b b n n n λ，…………………………………………………….12分若数列{}n b 是等比数列，则有124b b =而λ122=b ，所以212=b b 与b 2=4b 1矛盾。
2018年浙江省“五校联考”高考数学二模试卷(解析版)
2018年浙江省“五校联考”高考数学二模试卷一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（4分）设集合A＝{x||x﹣1|≤1}，B＝{x|log2x≤2}，则B∩∁R A＝（）A．[2，4]B．（2，4]C．[0，4]D．（2，4]∪（﹣∞，0）2．（4分）若复数z满足z（1+i）＝|1﹣i|+i（其中i为虚数单位），则z的虚部为（）A．B．C．D．3．（4分）已知随机变量X～B（4，p），若，则P（X＝2）＝（）A．B．C．D．4．（4分）设a，b是两条直线，α，β是两个平面，则a⊥b的一个充分条件是（）A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β5．（4分）如图，设A、B是半径为2的圆O上的两个动点，点C为AO中点，则的取值范围是（）A．[﹣1，3]B．[1，3]C．[﹣3，﹣1]D．[﹣3，1]6．（4分）（1﹣）6（1+）4的展开式中x的系数是（）A．﹣4B．﹣3C．3D．47．（4分）点D是△ABC的边AB的中点，∠ABC＝120°，，若以A、B为焦点的双曲线恰好经过点C，则该双曲线的离心率为（）A．B．C．D．8．（4分）若，则α∈（）A．B．C．D．9．（4分）已知△ABC的三边长分别为a、b、c，有以下四个命题：（1）以，，为边长的三角形一定存在；（2）以2a，2b，2c为边长的三角形一定存在；（3）以a3，b3，c3为边长的三角形一定存在；（4）以|a﹣b|+c，|b﹣c|+a，|c﹣a|+b为边长的三角形一定存在，其中正确命题的个数为（）A．1个B．2个C．3个D．4个10．（4分）已知函数的最小值为2a﹣1，则实数a的取值范围是（）A．a＝±1B．0≤a≤1C．a≤0或a＝1D．a≤0或a≥1二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．11．（4分）已知2log6x＝1﹣log63，则x的值是．12．（6分）若实数x，y满足，则x+y的最大值为，x2+y2的取值范围为．13．（6分）一个三棱锥的三视图如图所示，则其表面积为，其外接球的体积是．14．（6分）点G是△ABC的重心，过G作直线与AB、AC两边分别交于M、N两点，且，．若，则y＝，若，则x+y＝．15．（6分）已知正项等比数列{a n}的前n项和为S n，若﹣1，S5，S10成等差数列，则S10﹣2S5＝，S15﹣S10的最小值为．16．（4分）将一个4×4正方形棋盘中的8个小正方形方格染成红色，使得每行、每列都恰有两个红色方格，则有种不同的染色方法．17．（4分）棱长为36的正四面体A﹣BCD的内切球球面上有一动点M，则的最小值为．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18．（14分）在△ABC中，角A、B、C的对边分别为a、b、c，且，．（Ⅰ）求角A和角B的大小；（Ⅱ）已知当x∈R时，函数f（x）＝sin x（cos x+a sin x）的最大值为，求a的值．19．（15分）如图，四棱锥P﹣ABCD的底面是梯形．BC∥AD，AB＝BC＝CD＝1，AD＝2，，（Ⅰ）证明；AC⊥BP；（Ⅱ）求直线AD与平面APC所成角的正弦值．20．（15分）（Ⅰ）求证：；（Ⅱ）设函数（ⅰ）求证：f（x）是减函数；（ⅱ）若不等式对任意n∈N*恒成立（e是自然对数的底数），求实数a的取值范围．21．（15分）如图，已知椭圆离心率为，焦距为2．（Ⅰ）求椭圆C的方程；（Ⅱ）直线l与椭圆切于点P，OQ⊥l，垂足为Q，其中O为坐标原点．求△OPQ面积的最大值．22．（15分）已知正项数列{a n}满足a1＝4，，n∈N*．（Ⅰ）求证：a n≥4n；（Ⅱ）求证：2018年浙江省“五校联考”高考数学二模试卷参考答案与试题解析一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（4分）设集合A＝{x||x﹣1|≤1}，B＝{x|log2x≤2}，则B∩∁R A＝（）A．[2，4]B．（2，4]C．[0，4]D．（2，4]∪（﹣∞，0）【解答】解：集合A＝{x||x﹣1|≤1}＝{x|﹣1≤x﹣1≤1}＝{x|0≤x≤2}＝[0，2]，B＝{x|log2x≤2}＝{x|0＜x≤4}＝（0，4]，∴∁R A＝（﹣∞，0）∪（2，+∞），∴B∩∁R A＝（2，4]．故选：B．2．（4分）若复数z满足z（1+i）＝|1﹣i|+i（其中i为虚数单位），则z的虚部为（）A．B．C．D．【解答】解：设z＝a+bi，∵复数z满足z（1+i）＝|1﹣i|+i（其中i为虚数单位），∴（a+bi）（1+i）＝+i，∴a+bi+ai+bi2＝a﹣b+（b+a）i＝+i，∴，解得a＝，b＝．∴z的虚部为．故选：A．3．（4分）已知随机变量X～B（4，p），若，则P（X＝2）＝（）A．B．C．D．【解答】解：由随机变量X～B（4，p），且，即np＝4p＝，解得p＝；∴P（X＝2）＝••＝．故选：B．4．（4分）设a，b是两条直线，α，β是两个平面，则a⊥b的一个充分条件是（）A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β【解答】解：A、B、D的反例如图．故选：C．5．（4分）如图，设A、B是半径为2的圆O上的两个动点，点C为AO中点，则的取值范围是（）A．[﹣1，3]B．[1，3]C．[﹣3，﹣1]D．[﹣3，1]【解答】解：如图所示，可得O（0，0），A（﹣2，0），C（﹣1，0），设B（2cosθ，2sinθ）．θ∈[0，2π）．＝（1，0）•（2cosθ+1，2sinθ）＝2cosθ+1∈[﹣1，3]．故选：A．6．（4分）（1﹣）6（1+）4的展开式中x的系数是（）A．﹣4B．﹣3C．3D．4【解答】解：的展开式的通项为∴展开式中常数项为C60，含x的项的系数为C62，含的项的系数为﹣C61的展开式的通项为∴的展开式中的x的系数为C42，常数项为C40，含的项的系数为C41故的展开式中x的系数是C60C42+C62C40﹣C61C41＝6+15﹣24＝﹣3故选：B．7．（4分）点D是△ABC的边AB的中点，∠ABC＝120°，，若以A、B为焦点的双曲线恰好经过点C，则该双曲线的离心率为（）A．B．C．D．【解答】解：不妨设AB＝2，则CD＝，BD＝AB＝1，在△BCD中，由余弦定理可得：cos∠ABC＝＝﹣，解得BC＝1，在△ABC中，由余弦定理得AC＝＝，不妨设以AB为焦点的双曲线方程为＝1，则2a＝AC﹣BC＝﹣1，2c＝AB＝2，∴离心率e＝＝＝．故选：A．8．（4分）若，则α∈（）A．B．C．D．【解答】解：cosα+sinα＝，当0＜α＜时，＜＜，则∈（1，]⊂（1，），∴tanα∈（1，）．得α∈（）．故选：C．9．（4分）已知△ABC的三边长分别为a、b、c，有以下四个命题：（1）以，，为边长的三角形一定存在；（2）以2a，2b，2c为边长的三角形一定存在；（3）以a3，b3，c3为边长的三角形一定存在；（4）以|a﹣b|+c，|b﹣c|+a，|c﹣a|+b为边长的三角形一定存在，其中正确命题的个数为（）A．1个B．2个C．3个D．4个【解答】解：三角形ABC的三边长分别为a，b，c，不妨设a≥b≥c，则b+c＞a．（1）∵（）2﹣（）2＝b+c﹣a+2＞0，∴+＞，∴以，，为边长的三角形一定存在；（2）当b＝3，c＝2，a＝4时，22+23＞24不成立，因此以2a，2b，2c为边长的三角形不一定存在；（3）当b＝3，c＝2，a＝4时，a3＞b3+c3不成立，因此以a3，b3，c3为边长的三角形不一定存在；（4）∵|a﹣b|+c+|b﹣c|+a≥|a﹣c|+c+a＞|c﹣a|+b，∴以|a﹣b|+c，|b﹣c|+a，|c﹣a|+b为边长的三角形一定存在；其中正确命题的个数为2个．故选：B．10．（4分）已知函数的最小值为2a﹣1，则实数a的取值范围是（）A．a＝±1B．0≤a≤1C．a≤0或a＝1D．a≤0或a≥1【解答】解：若a＝0，则f（x）＝，可得x＜0时，f（x）＞﹣1；x≥0时，f（x）≥0，可得f（x）的值域为（﹣1，+∞），无最小值；当a＝1时，f（x）＝，当x＜0时，f（x）＝|x﹣1|+1＞2，当x≥0时，f（x）＝|（x﹣1）2﹣1|+1≥1，当x＝0时，取得最小值1，则f（x）的最小值为1，满足题意，当a＝﹣1时，f（x）＝，当x＜0时，f（x）≥﹣3；当x≥0时，f（x）＝x2+2x﹣1的值域为[﹣1，+∞），可得f（x）的最小值为﹣1．故排除B，C，D，故选：A．二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．11．（4分）已知2log6x＝1﹣log63，则x的值是．【解答】解：原式等价于log6x2＝log66﹣log63＝log62，所以x2＝2，又x＞0，∴x＝，故答案为：．12．（6分）若实数x，y满足，则x+y的最大值为5，x2+y2的取值范围为[，13]．【解答】解：不等式组可化为或，在同一坐标系中画出两个不等式组表示的平面区域，如图所示；则由图形知，目标函数z＝x+y过点C时，z取得最大值，由，解得C（2，3），∴x+y的最大值为5；又z＝x2+y2表示区域内的点到原点的距离的平方，由图形知，x2+y2的最小值为，最大值为22+32＝13，∴x2+y2的取值范围是[，13]．故答案为：5，[，13]．13．（6分）一个三棱锥的三视图如图所示，则其表面积为26+2，其外接球的体积是．【解答】解：如图：P A⊥平面ABC，AB⊥BC，P A＝5，AB＝3，BC＝4，三棱锥的表面积为：＝26+2三棱锥的外接球就是长方体三度为：5，4，3的外接球，所以外接球的半径为：＝．外接球的体积为：＝．故答案为：26+2；．14．（6分）点G是△ABC的重心，过G作直线与AB、AC两边分别交于M、N两点，且，．若，则y＝1，若，则x+y＝2．【解答】解：根据条件：＝，＝；又＝+；∴＝+；又M，G，N三点共线；∴+＝1；∵x＝，∴y＝1；∵，∴＝＝xy＝，又＝3，即＝3，∴x+y＝2．故答案为：1，2．15．（6分）已知正项等比数列{a n}的前n项和为S n，若﹣1，S5，S10成等差数列，则S10﹣2S5＝1，S15﹣S10的最小值为4．【解答】解：∵﹣1，S5，S10成等差数列，∴2S5＝S10﹣1，∴S10﹣2S5＝1，又由等比数列的性质可得S5，S10﹣S5，S15﹣S10为等比数列，∴S5（S15﹣S10）＝（S10﹣S5）2，∴S15﹣S10＝＝＝S5++2≥2+2＝4，当且仅当S5＝即S5＝1时取等号，∴S15﹣S10的最小值为4，故答案为：1；4．16．（4分）将一个4×4正方形棋盘中的8个小正方形方格染成红色，使得每行、每列都恰有两个红色方格，则有90种不同的染色方法．【解答】解：第一行染2个红色方格有C42种染法；第一行染好后，有如下三种情况：①第二行的红色方格均与第一行的红色方格同列，这时其余行都只有1种染法；②第二行染的红色方格与第一行的红色方格均不同列，这时第三行有C42种染法，第四行的染法随之确定；③第二行染的红色方格恰有一个与第一行的红色方格同列，而第一、第二这两行染好后，第三行的红色方格必然有一个与上面的红色方格均不同列，这时第三行的染法有2种，第四行染法随之确定．因此，共有染法为：6×（1+6+4×2）＝90（种）．故答案为：9017．（4分）棱长为36的正四面体A﹣BCD的内切球球面上有一动点M，则的最小值为4．【解答】解：由阿波罗尼斯球得内切球球心O是线段CH上以C，E为定点，空间中满足＝λ（λ≠1）的点P的集合，连结CO并延长交平面ABD于H，交内切球上方的点设为K，过M作ME⊥CH，交CH于E，连结BM，CM，设OE＝x，由已知得CO＝9，OH＝3，＝，∴＝，解得x＝，∴λ＝＝＝3，∴，∴，∴MB+＝MB+ME≥BE，在△BOE中，BO＝CO＝9，OE＝，cos∠BOE＝﹣cos∠BOH＝﹣，∴BE＝＝4．∴的最小值为4．故答案为：4．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18．（14分）在△ABC中，角A、B、C的对边分别为a、b、c，且，．（Ⅰ）求角A和角B的大小；（Ⅱ）已知当x∈R时，函数f（x）＝sin x（cos x+a sin x）的最大值为，求a的值．【解答】解：（Ⅰ）由，可得：b2+c2﹣a2＝bc，所以cos A＝＝＝，又0＜A＜π，可得：A＝，由sin A sin B＝cos2，可得：sin B＝，sin B＝1+cos C，∴B+C＝，则sin（﹣C）＝1+cos C，∴可得：sin C＝1，解得C＝，∴B＝．…（6分）（Ⅱ）f（x）＝sin x（cos x+a sin x）＝sin2x+（1﹣cos2x）＝+sin（2x﹣θ），tanθ＝a，∵函数f（x）＝sin x（cos x+a sin x）的最大值为，∴+＝，∴解得a＝．．…（6分）19．（15分）如图，四棱锥P﹣ABCD的底面是梯形．BC∥AD，AB＝BC＝CD＝1，AD＝2，，（Ⅰ）证明；AC⊥BP；（Ⅱ）求直线AD与平面APC所成角的正弦值．【解答】（I）证明：取AC的中点M，连接PM，BM，∵AB＝BC，P A＝PC，∴AC⊥BM，AC⊥PM，又BM∩PM＝M，∴AC⊥平面PBM，∵BP⊂平面PBM，∴AC⊥BP．（II）解：∵底面ABCD是梯形．BC∥AD，AB＝BC＝CD＝1，AD＝2，∴∠ABC＝120°，∵AB＝BC＝1，∴AC＝，BM＝，∴AC⊥CD，又AC⊥BM，∴BM∥CD．∵P A＝PC＝，CM＝＝，∴PM＝，∵PB＝，∴cos∠BMP＝＝﹣，∴∠PMB＝120°，以M为原点，以MB，MC的方向为x轴，y轴的正方向，以平面ABCD在M处的垂线为z轴建立坐标系M﹣xyz，如图所示：则A（0，﹣，0），C（0，，0），P（﹣，0，），D（﹣1，，0），∴＝（﹣1，，0），＝（0，，0），＝（﹣，，），设平面ACP的法向量为＝（x，y，z），则，即，令x＝得＝（，0，1），∴cos＜，＞＝＝﹣，∴直线AD与平面APC所成角的正弦值为|cos＜，＞|＝．20．（15分）（Ⅰ）求证：；（Ⅱ）设函数（ⅰ）求证：f（x）是减函数；（ⅱ）若不等式对任意n∈N*恒成立（e是自然对数的底数），求实数a的取值范围．【解答】（I）证明：令g（x）＝lnx﹣（x＞1），则g′（x）＝﹣＝＝＝﹣＜0，∴g（x）在（1，+∞）上单调递减，∴g（x）＜g（1）＝0，即lnx﹣＜0．∴lnx＜（x＞1）．（II）证明：（i）f′（x）＝﹣+＝，由（I）可知lnx＜，∴（lnx）2＜，∴x（lnx）2＜（x﹣1）2，∴f′（x）＜0，∴f（x）＝﹣（x＞1）是减函数．（ii）由得（n+a）ln（1+）＜1，∵ln（1+）＞ln1＝0，∴n+a＜，即a＜﹣n，令1+＝t，则n＝（1＜t≤2）．∴a＜﹣＝f（t），由（i）可知f（t）在（1，2]上单调递减，∴f（t）的最小值为f（2）＝．∴a＜．21．（15分）如图，已知椭圆离心率为，焦距为2．（Ⅰ）求椭圆C的方程；（Ⅱ）直线l与椭圆切于点P，OQ⊥l，垂足为Q，其中O为坐标原点．求△OPQ面积的最大值．【解答】解：（Ⅰ）由椭圆的离心率e＝＝，则2c＝2，c＝1，则a＝2，b＝＝3，∴椭圆C的方程：；（Ⅱ）方法一：设P（x0，y0），（x0≠0，y0≠0）由椭圆在P的切线方程：，即3x0x+4y0y﹣12＝0，则直线OQ的方程：y＝x，即3x0y﹣4y0x＝0，则|OQ|＝，|PQ|＝＝，则△OPQ面积S△OPQ＝×|OQ|×|PQ|＝××＝≤＝，当且仅当9x02＝16y02，即x02＝，y02＝时取等号，△OPQ面积的最大值．方法二：设切线方程：y＝kx+m，（k≠0）切点P（x0，y0），（x0≠0，y0≠0），O到切线的距离：|OQ|＝，联立，整理得：（3+4k2）x2+8kmx+4m2﹣12＝0，△＝（8km）2﹣4×（3+4k2）（4m2﹣12）＝0，整理得：m2＝3+4k2，代入解得：x0＝﹣，y0＝k0x+m＝，直线OQ的方程：y＝﹣x，即ky+x＝0，则|PQ|＝＝，则则△OPQ面积S△OPQ＝×|OQ|×|PQ|＝×|PQ|•|OQ|＝ו＝×≤×＝，当且仅当k2＝1时，即x02＝，y02＝时取等号，△OPQ面积的最大值．22．（15分）已知正项数列{a n}满足a1＝4，，n∈N*．（Ⅰ）求证：a n≥4n；（Ⅱ）求证：【解答】证明：（Ⅰ）首先利用lnx≤x﹣1，可得，即，以下用数学归纳法证明a n≥4n，①当n＝1时显然成立；②假设当n＝k时，不等式成立，即a k≥4k，则当n＝k+1时，由函数的单调性可得，，也就是说，当n＝k+1时，不等式也成立；由①②可知，a n≥4n对任意的n∈N*成立；（Ⅱ）易知，由≥3a n+4，则a n+1+2≥3（a n+2），所以，，则，因此，＝，所以，．。
浙江省宁波市五校2017-2018学年高三下学期适应性联考数学(文)试卷 Word版含解析
浙江省宁波市五校联考2017-2018学年高考数学适应性试卷（文科）一、选择题（本大题共8小题，每小题5分，共40分.在每个小题给出的四个选项中只有一项是符合题目要求的）1．已知p：∀x∈R，x2﹣2x﹣4≤0，则￢p为( )A．∀x∈R，x2﹣2x﹣4≥0 B．∃x0∈R，x02﹣2x0﹣4＞0C．∀x∉R，x2﹣2x+4≤0 D．∃x0∈R，x02﹣2x0﹣4＞02．已知x，y∈R，则“x＞y”是“|x|＞|y|”的( )A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件3．已知α∈（π，2π），且cosα+sinα=，则tanα=( )A．B．﹣C．D．﹣4．已知直线m，n及平面α，β，下列中正确的是( )A．若m⊥α，n∥β，且m∥n，则α∥βB．若m∥α，n∥β，且m∥n，则α∥βC．若m⊥α，n∥β，且m⊥n，则α⊥βD．若m⊥α，n⊥β，且m⊥n，则α⊥β5．一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的体积是( )A．B．C．D．6．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）单调递增．若实数a满足f （log2a）+f（log a）≤2f（1），则a的取值范围是( )A．[1，2]B．C．D．（0，2]7．已知数列{a n}中满足a1=15，=2，则的最小值为( )A．10 B．2﹣1 C．9 D．8．设双曲线=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A，B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若（λ，μ∈R），λ•μ=，则双曲线的离心率为( )A．B．C．D．二、填空题（本大题共7小题，9～12小题每题6分，其它小题每题4分，共36分）9．已知全集U=R，集合A={x||x|＜1}，B={x|x＞﹣}，则A∪B=__________，A∩B=__________，（∁U B）∩A=__________．10．已知直线l1：ax+y﹣1=0，直线l2：x﹣y﹣3=0，若直线l1的倾斜角为，则a=__________；若l1⊥l2，则a=__________；若l1∥l2，则两平行直线间的距离为__________．11．函数y=3sin（4x+）﹣3的最小正周期为__________，单调递减区间为__________．12．设x、y满足约束条件目标函数z=2x+y的最大值是__________，若目标函数z=ax+by（a＞0，b＞0）的最大值为10，则+的最小值为__________．13．已知两圆C1：（x+1）2+y2=1与C2：（x﹣1）2+y2=25，动圆M与这两个圆都内切，则动圆的圆心M的轨迹方程为__________．14．若直线l：xcosθ+ysinθ﹣1=0与圆（x﹣cosθ）2+（y﹣1）2=相切，且θ为锐角，则直线l的斜率是__________．15．设非零向量与的夹角是，且||=|+|，则的最小值是__________．三、解答题（共5小题，共74分．解答时应写出必要的文字说明、证明过程或演算步骤）16．设△ABC的内角A、B、C所对的边分别为a、b、c，已知a=1，b=2，cosC=（Ⅰ）求△ABC的周长；（Ⅱ）求cos（A﹣C）的值．17．已知公差不为0的等差数列{a n}的前n项和为S n，满足a2，a3，a5成等比数列，S6=45．（Ⅰ）求数列{a n}的通项公式及前n项和S n；（Ⅱ）令p n=+，是否存在正整数M，使不等式p1+p2+…+p n﹣2n≤M 恒成立，若存在，求出M的最小值；若不存在，说明理由．18．如图，四边形ABCD为平行四边形，AB=5，AD=4，BD=3，将△BCD沿着BD翻折到平面BC1D处，E，F分别为边AB，C1D的中点．（Ⅰ）求证：EF∥平面BCC1；（Ⅱ）若异面直线EF，BC1所成的角为30°，求直线C1D与平面ABCD所成角的正弦值．19．如图，已知抛物线y2=4x的焦点为F，过F的直线交抛物线于M、N两点，其准线l与x轴交于K点．（1）求证：KF平分∠MKN；（2）O为坐标原点，直线MO、NO分别交准线于点P、Q，求|PQ|+|MN|的最小值．20．已知二次函数f（x）=x2+bx+c，其中常数b，c∈R．（Ⅰ）若任意的x∈[﹣1，1]，f（x）≥0，f（2+x）≤0，试求实数c的取值范围；（Ⅱ）若对任意的x1，x2∈[﹣1，1]，有|f（x1）﹣f（x2）|≤4，试求实数b的取值范围．浙江省宁波市五校联考2015届高考数学适应性试卷（文科）一、选择题（本大题共8小题，每小题5分，共40分.在每个小题给出的四个选项中只有一项是符合题目要求的）1．已知p：∀x∈R，x2﹣2x﹣4≤0，则￢p为( )A．∀x∈R，x2﹣2x﹣4≥0 B．∃x0∈R，x02﹣2x0﹣4＞0C．∀x∉R，x2﹣2x+4≤0 D．∃x0∈R，x02﹣2x0﹣4＞0考点：的否定；特称．专题：简易逻辑．分析：直接利用全称的否定是特称写出结果即可．解答：解：因为全称的否定是特称，所以，p：∀x∈R，x2﹣2x﹣4≤0，则￢p为：∃x0∈R，x02﹣2x0﹣4＞0．故选：B．点评：本题考查的否定，特称与全称的否定关系，基本知识的考查．2．已知x，y∈R，则“x＞y”是“|x|＞|y|”的( )A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件考点：充要条件．专题：简易逻辑．分析：举例，结合结合充分条件和必要条件的定义即可得到结论．解答：解：若x＞y，如x=1，y=﹣1，则|x|＞|y|不成立，故：“x＞y”⇒“|x|＞|y|”为假；若|x|＞|y|成立，如x=﹣2，y=1则x＞y不成立，故：“|x|＞|y|”⇒“x＞y”为假；故x＞y”是“|x|＞|y|”的既不充分也不必要条件．故选：D．点评：本题考查的知识点是充要条件的定义，我们先判断p⇒q与q⇒p的真假，再根据充要条件的定义给出结论是解答本题的关键．3．已知α∈（π，2π），且cosα+sinα=，则tanα=( )A．B．﹣C．D．﹣考点：同角三角函数基本关系的运用．专题：三角函数的求值．分析：已知等式两边平方，利用完全平方公式及同角三角函数间基本关系化简，整理求出cosα﹣sinα的值，与已知等式联立求出cosα与sinα的值，即可求出tanα的值．解答：解：∵α∈（π，2π），且cosα+sinα=①，∴两边平方得：1+2sinαcosα=，即2sinαcosα=﹣，∴α∈（，2π），即sinα＜0，cosα＞0，∴cosα﹣sinα＞0，∴（cosα﹣sinα）2=1﹣2sinαcosα=，即cosα﹣sinα=②，联立①②解得：sinα=﹣，cosα=，则tanα=﹣，故选：B．点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．4．已知直线m，n及平面α，β，下列中正确的是( )A．若m⊥α，n∥β，且m∥n，则α∥βB．若m∥α，n∥β，且m∥n，则α∥βC．若m⊥α，n∥β，且m⊥n，则α⊥βD．若m⊥α，n⊥β，且m⊥n，则α⊥β考点：平面与平面之间的位置关系．专题：空间位置关系与距离．分析：根据直线与平面平行，垂直的性质定理，判断定理，灵活判断，可以正确推导，也可以举反例说明．解答：解：（1）∵若m⊥α，n∥β，且m∥n，∴n⊥α，n∥β，∴α⊥β故A不正确；（2）若m∥α，n∥β，且m∥n，则α∥β．不正确，如两个面相交，两个相交的墙面，直线m，n都平行于交线，也满足，m∥α，n∥β，所以B不正确；（3）若m⊥α，n∥β，且m⊥n，则有可能α∥β，不一定α⊥β，所以C不正确；（4）若m⊥α，n⊥β，且m⊥n可以判断α⊥β是正确的，因为可以设两个平面的，，可得数量积为零，⊥，所以可判断α⊥β是正确的，故D 正确，故选：D点评：本题考察了直线与平面的位置关系，熟练掌握好平行，垂直的定理即可判断．5．一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的体积是( )A．B．C．D．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：由已知中的三视图，可知该几何体是一个以俯视图为底面的三棱锥，求出底面面积，代入锥体体积公式，可得答案．解答：解：由已知中的三视图，可知该几何体是一个以俯视图为底面的三棱锥，其底面面积S=×1×（1+1）=1，高h=，故体积V==，故选：A点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．6．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）单调递增．若实数a满足f （log2a）+f（log a）≤2f（1），则a的取值范围是( )A．[1，2]B．C．D．（0，2]考点：奇偶性与单调性的综合．专题：函数的性质及应用．分析：根据偶函数的定义将所给的式子化为：f（|log2a|）≤f（1），再利用偶函数的单调性列出关于a的不等式求解．解答：解：∵f（x）是定义在R上的偶函数，∴，∴可变为f（log2a）≤f（1），即f（|log2a|）≤f（1），又∵在区间[0，+∞）上单调递增，且f（x）是定义在R上的偶函数，∴，即，解得≤a≤2，故选：C．点评：本题考查了函数的奇偶性和单调性的综合应用，易错处是忽略定义域内的单调性不同，即对称区间单调性相反，注意自变量的取值范围，考查了学生的转化能力．7．已知数列{a n}中满足a1=15，=2，则的最小值为( )A．10 B．2﹣1 C．9 D．考点：数列递推式．专题：等差数列与等比数列．分析：由已知得a n+1﹣a n=2n，从而a n=a1+（a2﹣a1）+（a3﹣a2）+…+（a n﹣a n﹣1）=n2﹣n+15，进而=n+﹣1，由此能求出当且仅当n=，即n=4时，取最小值4+=．解答：解：∵数列{a n}中满足a1=15，=2，∴a n+1﹣a n=2n，∴a n=a1+（a2﹣a1）+（a3﹣a2）+…+（a n﹣a n﹣1）=15+2+4+6+8+…+2（n﹣1）=15+=n2﹣n+15，∴=n+﹣1≥2﹣1，∴当且仅当n=，即n=4时，取最小值4+=．故选：D．点评：本题考查的最小值的求法，是中档题，解题时要注意累加法和均值定理的合理运用．8．设双曲线=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A，B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若（λ，μ∈R），λ•μ=，则双曲线的离心率为( )A．B．C．D．考点：双曲线的简单性质．专题：平面向量及应用；直线与圆；圆锥曲线的定义、性质与方程．分析：由方程可得渐近线，可得A，B，P的坐标，由共线向量式可得λ+μ=1，λ﹣μ=，解之可得λμ的值，由λ•μ=可得a，c的关系，由离心率的定义可得．解答：解：双曲线的渐近线为：y=±x，设焦点F（c，0），则A（c，），B（c，﹣），P（c，），因为=λ+μ，所以（c，）=（（λ+μ）c，（λ﹣μ）），所以λ+μ=1，λ﹣μ=，解得：λ=，μ=，又由λμ=，得：=，解得：=，所以，e==．故选：A．点评：本题考查双曲线的简单性质，涉及双曲线的离心率的求解，属于中档题．二、填空题（本大题共7小题，9～12小题每题6分，其它小题每题4分，共36分）9．已知全集U=R，集合A={x||x|＜1}，B={x|x＞﹣}，则A∪B={x|x＞﹣1}，A∩B={x|﹣＜x＜1}，（∁U B）∩A={x|x|﹣1＜x≤﹣}．考点：交、并、补集的混合运算．专题：集合．分析：根据集合的基本运算进行计算即可．解答：解：A={x||x|＜1}={x|﹣1＜x＜1}，∁U B={x|x≤﹣}，则A∪B={x|x＞﹣1}，A∩B={x|﹣＜x＜1}，（∁U B）∩A={x|﹣1＜x≤﹣}；故答案为：{x|x＞1}，{x|﹣＜x＜1}，{x|x|﹣1＜x≤﹣}；点评：本题主要考查集合的基本运算，比较基础．10．已知直线l1：ax+y﹣1=0，直线l2：x﹣y﹣3=0，若直线l1的倾斜角为，则a=﹣1；若l1⊥l2，则a=1；若l1∥l2，则两平行直线间的距离为2．考点：两条平行直线间的距离；直线的倾斜角．专题：直线与圆．分析：求出直线的斜率即可求解a，利用直线的垂直，斜率乘积为﹣1，求解a；通过直线的平行求解a，然后求解平行线之间的距离．解答：解：直线l1：ax+y﹣1=0，直线l2：x﹣y﹣3=0，若直线l1的倾斜角为，k=1，即﹣a=1，则a=﹣1：若l1⊥l2，则﹣a×1=﹣1，解得a=1；若l1∥l2，所以a=﹣1，则两平行直线间的距离为：=．故答案为：﹣1；1；．点评：本题考查直线的垂直，平行，平行线之间的距离求法，考查计算能力．11．函数y=3sin（4x+）﹣3的最小正周期为，单调递减区间为[+，+]，k∈z．考点：正弦函数的图象．专题：三角函数的图像与性质．分析：由题意根据正弦函数的周期性求得它的最小正周期，再根据正弦函数的单调性求得它的减区间．解答：解：对于函数y=3sin（4x+）﹣3，它的最小正周期为=，令2kπ+≤4x+≤2kπ+，求得+≤x≤+，k∈z，故函数的减区间为[+，+]，k∈z，故答案为：；[+，+]，k∈z．点评：本题主要考查正弦函数的周期性和单调性，属于基础题．12．设x、y满足约束条件目标函数z=2x+y的最大值是14，若目标函数z=ax+by（a＞0，b＞0）的最大值为10，则+的最小值为5．考点：简单线性规划．专题：不等式的解法及应用．分析：①作出不等式对应的平面区域，①由z=2x+y得：y=﹣2x+z，显然y=﹣2x+z过A 点时，z最大，将A（4，6）代入求出即可；②利用线性规划的知识先求出a，b的关系，然后利用基本不等式的性质求出+的最小值即可．解答：解：由z=ax+by（a＞0，b＞0）得y=﹣x+，作出可行域如图：①由z=2x+y得：y=﹣2x+z，显然y=﹣2x+z过A点时，z最大，由，解得，即A（4，6），∴z最大值=2×4+6=14，②∵a＞0，b＞0，∴直线y=﹣x+的斜率为负，且截距最大时，z也最大．平移直线y=﹣x+，由图象可知当y=﹣x+经过点A时，直线的截距最大，此时z也最大．此时z=4a+6b=10，即2a+3b﹣5=0，即+=1，则+=（+）（+）=+++≥+2=+=5，当且仅当=，即a=b=1时，取等号，故+的最小值为5，故答案为：14，5．点评：本题主要考查线性规划的应用以及基本不等式的应用，利用数形结合是解决线性规划题目的常用方法．13．已知两圆C1：（x+1）2+y2=1与C2：（x﹣1）2+y2=25，动圆M与这两个圆都内切，则动圆的圆心M的轨迹方程为．考点：轨迹方程．专题：计算题；直线与圆；圆锥曲线的定义、性质与方程．分析：设圆（x+1）2+y2=1的圆心O1（﹣1，0），半径r1=1；圆（x﹣1）2+y2=25的圆心O2（1，0），半径r2=5．设动圆C的圆心C（x，y），半径R．由于动圆C与圆（x+1）2+y2=1及圆（x﹣1）2+y2=25都内切，可得|O1C|=R﹣1，|O2C|=5﹣R．于是|O1C|+|O2C|=5﹣1=4＞|O1O2|=2，利用椭圆的定义可知：动点C的轨迹是椭圆．求出即可．解答：解：设圆（x+1）2+y2=1的圆心O1（﹣1，0），半径r1=1；圆（x﹣1）2+y2=25的圆心O2（1，0），半径r2=5．设动圆C的圆心C（x，y），半径R．∵动圆C与圆（x+1）2+y2=1及圆（x﹣1）2+y2=25都内切，∴|O1C|=R﹣1，|O2C|=5﹣R．∴|O1C|+|O2C|=5﹣1=4＞|O1O2|=2，因此动点C的轨迹是椭圆，2a=4，2c=2，解得a=2，c=1，∴b2=a2﹣c2=3．因此动圆圆心C的轨迹方程是．故答案为：．点评：本题考查了两圆相内切的性质、椭圆的定义，属于中档题．14．若直线l：xcosθ+ysinθ﹣1=0与圆（x﹣cosθ）2+（y﹣1）2=相切，且θ为锐角，则直线l的斜率是﹣．考点：直线与圆相交的性质．专题：计算题；直线与圆．分析：由条件利用直线和圆相切的性质，点到直线的距离公式求得sinθ=．再结合θ为锐角，可得θ=，从而求得直线xcosθ+ysinθ﹣1=0的斜率的值．解答：解：由题意可得圆心（cosθ，1）到直线xcosθ+ysinθ﹣1=0的距离等于半径，即=，化简可得|sinθ﹣sin2θ|=，即sinθ﹣sin2θ=，求得sinθ=．再结合θ为锐角，可得θ=，故直线xcosθ+ysinθ﹣1=0的斜率为﹣，故答案为：﹣．点评：本题主要考查直线和圆相切的性质，点到直线的距离公式的应用，体现了转化的数学思想，属于基础题．15．设非零向量与的夹角是，且||=|+|，则的最小值是．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由已知利用模的等式两边平方得到||=||，将所求平方利用此关系得到关于t的二次函数解析式，然后求最小值．解答：解：因为非零向量与的夹角是，且||=|+|，所以||2=|+|2=||2+2+||2，所以||=||，则（）2==t2+2t+=（t+1）2+，所以当t=﹣1时，的最小值是；故答案为：．点评：本题考查了向量的数量积以及向量的平方与模的平方相等的运用．三、解答题（共5小题，共74分．解答时应写出必要的文字说明、证明过程或演算步骤）16．设△ABC的内角A、B、C所对的边分别为a、b、c，已知a=1，b=2，cosC=（Ⅰ）求△ABC的周长；（Ⅱ）求cos（A﹣C）的值．考点：余弦定理；两角和与差的余弦函数．专题：计算题．分析：（I）利用余弦定理表示出c的平方，把a，b及cosC的值代入求出c的值，从而求出三角形ABC的周长；（II）根据cosC的值，利用同角三角函数间的基本关系求出sinC的值，然后由a，c及sinC 的值，利用正弦定理即可求出sinA的值，根据大边对大角，由a小于c得到A小于C，即A为锐角，则根据sinA的值利用同角三角函数间的基本关系求出cosA的值，然后利用两角差的余弦函数公式化简所求的式子，把各自的值代入即可求出值．解答：解：（I）∵c2=a2+b2﹣2abcosC=1+4﹣4×=4，∴c=2，∴△ABC的周长为a+b+c=1+2+2=5．（II）∵cosC=，∴sinC===．∴sinA===．∵a＜c，∴A＜C，故A为锐角．则cosA==，∴cos（A﹣C）=cosAcosC+sinAsinC=×+×=．点评：本题主要考查三角函数的基本公式和解斜三角形的基础知识，同时考查学生的基本运算能力，是一道基础题．17．已知公差不为0的等差数列{a n}的前n项和为S n，满足a2，a3，a5成等比数列，S6=45．（Ⅰ）求数列{a n}的通项公式及前n项和S n；（Ⅱ）令p n=+，是否存在正整数M，使不等式p1+p2+…+p n﹣2n≤M 恒成立，若存在，求出M的最小值；若不存在，说明理由．考点：数列的求和；等差数列的性质．专题：等差数列与等比数列．分析：（1）通过设公差为d，利用=a2a5、S6=45得a2=d=3，进而可得结论；（2）由（1）计算可得p n=2+﹣，并项相加可得p1+p2+…+p n﹣2n=2﹣，进而可得结论．解答：解：（1）设公差为d，由已知，得=a2a5，即=a2（a2+3d），解得a2=d，由S6=45得2a2+3d=15，∴a2=d=3，∴数列{a n}的通项a n=3n﹣3，前n项和S n=；（2）结论：存在最小的正整数M=2，使不等式p1+p2+…+p n﹣2n≤M恒成立．理由如下：p n=+=+=2+﹣，∴p1+p2+…+p n﹣2n=2（1﹣+﹣+﹣+…+﹣）=2﹣．由n为整数，可得p1+p2+…+p n﹣2n＜2，故存在最小的正整数M=2，使不等式p1+p2+…+p n﹣2n≤M恒成立．点评：本题考查求数列的通项及前n项和，判定和的取值范围，注意解题方法的积累，属于中档题．18．如图，四边形ABCD为平行四边形，AB=5，AD=4，BD=3，将△BCD沿着BD翻折到平面BC1D处，E，F分别为边AB，C1D的中点．（Ⅰ）求证：EF∥平面BCC1；（Ⅱ）若异面直线EF，BC1所成的角为30°，求直线C1D与平面ABCD所成角的正弦值．考点：直线与平面所成的角；直线与平面平行的判定．专题：空间位置关系与距离；空间角．分析：（Ⅰ）先连接CC1，取CC1的中点G，并连接FG，BG，从而可说明四边形FGBE为平行四边形，从而得到EF∥BG，根据线面平行的判定定理即可得到EF∥平面BCC1；（Ⅱ）容易说明∠C1BG=30°，从而得到∠C1BC=60°，从而△BCC1为等边三角形，能够说明直线AB⊥平面BCC1，从而得到平面ABCD⊥平面BCC1．取BC中点H，连接C1H，从而有C1H⊥BC，根据面面垂直的性质定理即知C1H⊥平面ABCD，连接DH，∠C1DH便是直线C1D和平面ABCD所成的角，根据已知边的长度即可求C1D，C1H，从而能求出sin∠C1DH．解答：解：（Ⅰ）证明：连接CC1，取CC1的中点G，连接FG，BG，则：∵四边形ABCD是平行四边形，E，F分别为AB，C1D的中点；∴FG∥BE，且FG=BE；∴四边形BEFG是平行四边形；∴EF∥BG，BG⊂平面BCC1，EF⊄平面BCC1；∴EF∥平面BCC1；（Ⅱ）由（Ⅰ）可知，∠C1BG为异面直线EF，BC1所成的角，∴∠C1BG=30°，∠C1BC=60°；又BC=BC1，∴△C1BC为等边三角形；AB=5，AD=4，BD=3，∴∠ADB=∠CBD=∠C1BD=90°；∴BD⊥BC，BD⊥BC1，且BC∩BC1=B；∴BD⊥平面BCC1；∴平面ABCD⊥平面BCC1，平面ABCD∩平面BCC1=BC；取BC中点H，连接C1H，则C1H⊥平面ABCD；连接DH，则∠C1DH即为直线C1D和平面ABCD所成的角；∴；∴直线C1D与平面ABCD所成角的正弦值为．点评：考查三角形中位线的性质，平行四边形的定义，线面平行的判定定理，异面直线所成角的定义，线面垂直、面面垂直的判定定理，以及面面垂直的性质定理，线面角的定义及求法．19．如图，已知抛物线y2=4x的焦点为F，过F的直线交抛物线于M、N两点，其准线l与x轴交于K点．（1）求证：KF平分∠MKN；（2）O为坐标原点，直线MO、NO分别交准线于点P、Q，求|PQ|+|MN|的最小值．考点：直线与圆锥曲线的关系．专题：综合题；圆锥曲线的定义、性质与方程．分析：（1）设KM和KN的斜率分别为k1，k2，证明KF平分∠MKN，只需证k1+k2=0即可；（2）设M、N的坐标分别为，利用三点共线可得P、Q点的坐标．设直线MN的方程为x=my+1，代入抛物线方程，结合韦达定理，求出|PQ|，|MN|，从而可求|PQ|+|MN|的最小值．解答：（1）证明：抛物线焦点坐标为F（1，0），准线方程为x=﹣1…．设直线MN的方程为x=my+1，M、N的坐标分别为由，∴y1+y2=4m，y1y2=﹣4…..设KM和KN的斜率分别为k1，k2，显然只需证k1+k2=0即可．∵K（﹣1，0）∴k1+k2==0…（2）解：设M、N的坐标分别为，由M，O，P三点共线可得P点的坐标为，同理可由N，O，Q三点共线可求出Q点坐标为，…设直线MN的方程为x=my+1．由∴y1+y2=4m，y1y2=﹣4，则=…又直线MN的倾斜角为θ，则∴…．同理可得…..∴（时取到等号）…..点评：本题考查直线与抛物线的位置关系，考查韦达定理的运用，考查学生分析解决问题的能力，考查学生的计算能力，综合性强．20．已知二次函数f（x）=x2+bx+c，其中常数b，c∈R．（Ⅰ）若任意的x∈[﹣1，1]，f（x）≥0，f（2+x）≤0，试求实数c的取值范围；（Ⅱ）若对任意的x1，x2∈[﹣1，1]，有|f（x1）﹣f（x2）|≤4，试求实数b的取值范围．考点：二次函数的性质．专题：函数的性质及应用．分析：（Ⅰ）若任意的x∈[﹣1，1]，f（x）≥0，f（2+x）≤0，可得是f（1）=0，即1为函数函数f（x）的一个零点．由韦达定理，可得函数f（x）的另一个零点，进而可得实数c的取值范围；（Ⅱ）若对任意的x1，x2∈[﹣1，1]，有|f（x1）﹣f（x2）|≤4，f（x）max﹣f（x）min≤4，结合二次函数的图象和性质分类讨论，可得实数b的取值范围．解答：解：（Ⅰ）因为x∈[﹣1，1]，则2+x∈[1，3]，由已知，有对任意的x∈[﹣1，1]，f（x）≥0恒成立，任意的x∈[1，3]，f（x）≤0恒成立，故f（1）=0，即1为函数函数f（x）的一个零点．由韦达定理，可得函数f（x）的另一个零点，又由任意的x∈[1，3]，f（x）≤0恒成立，∴[1，3]⊆[1，c]，即c≥3（Ⅱ）函数f（x）=x2+bx+c对任意的x1，x2∈[﹣1，1]，有|f（x1）﹣f（x2）|≤4恒成立，即f（x）max﹣f（x）min≤4，记f（x）max﹣f（x）min=M，则M≤4．当||＞1，即|b|＞2时，M=|f（1）﹣f（﹣1）|=|2b|＞4，与M≤4矛盾；当||≤1，即|b|≤2时，M=max{f（1），f（﹣1）}﹣f（）=﹣f（）=（1+）2≤4，解得：|b|≤2，即﹣2≤b≤2，综上，c的取值范围为﹣2≤b≤2．点评：本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质是解答的关键．。
浙江省2018届高三“五校联考”第二次考试数学试题(含答案)(2018.05)
A. a 1
第Ⅱ卷（非选择题部分，共 110 分）
二、填空题:本大题共 7 小题,多空题每题 6 分,单空题每题 4 分，共 36 分．
11．已知 2 log 6 x 1 log 6 3 ，则 x 的值是 12．若实数 x ， y 满足 为 ▲ ．
▲
． ，x
2
x y 1 ，则 x y 的最大值为 y | 2 x 1|
D.
3 1
8. 若 cos sin tan 0 A． (0,
，则 （ ▲ ） 2
C． (
) 6
B． (
, ) 6 4
, ) 4 3
D． (
, ) 3 2
9．已知 ABC 的三边长分别为 a、b、c，有以下四个命题： （1）以 （2）以 2 （3）以 a （4）以
1 MC 的最小值 3
三、解答题：本大题共 5 小题，共 74 分．解答应写出文字说明、证明过程或演算步骤． 18． （本题满分 14 分）在 ABC 中，角 A 、 B 、 C 的对边分别为 a 、 b 、 c ， 且 (b c) a (2
8 ，则 P ( X 2) 3
C.
8 3
B.
8 27
2 3
D.
4 9
4．设 a , b 是两条直线， , 是两个平面，则“ a b ”的一个充分条件是 （ ▲ ）
A. a , b ∥ , C. a , b , ∥
B. a , b , ∥ D. a , b ∥ ,
2 ( x a ) 1 a, x 0 10．已知函数 f ( x ) 的最小值为 2a 1 ，则实数 a 的取值范围是 x a 2 a 1, x 0
浙江省五校联考2018年高考模拟数学理科试卷及答案解析
浙江省五校联考2018年高考模拟数学理科试卷（总分：150分 时间：120分钟）一、选择题：本题共12小题，每小题5分，共60分． 1. 已知集合(){},|1A x y y x ==-，(){},|1B x y y x ==-+，则A B =I( )A.∅B.{}1C.{}0,1D.(){}1,02.已知复数z= 201821i i++（i 为虚数单位），则复数z 的共轭复数．．．．在复平面内对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩（单位：分），已知甲组数据的中位数为17，乙组数据的平均数为17.4，则x 、y 的 值分别为（ ）A. 7、8B. 5、7C. 8、5D. 7、74. 设向量a ，b 满足，()3-=g a a b ，则a 与b 的夹角为5若123)(23++-=x x a x x f 在区间⎪⎭⎫⎝⎛3,21上有极值点,则实数的取值范围是( )A. B. C. D.6. 执行如图所示的程序框图，若输出的57S =，则判断框内应填入的条件是（ ） A ．4k > B ．5k > C.6k > D ．7k >7. 已知ABCD 为正方形，其内切圆I 与各边分别切于E ，F ，G ，H ，连接EF ，FG ，GH ，HE ．现向正方形ABCD 内随机抛掷一枚豆子，记事件A ：豆子落在圆I 内，事件B ：豆子落在四边形EFGH 外，则(|)P B A =（ ）A ．14π-B ．4π C ．21π-D ．2π8. 已知函数⎪⎩⎪⎨⎧≥<≤=1,4sin 10,2)(x x x x f x π，则=-+)7log 3()2(2f fA ．87 B ． 227 C ．158 D ． 1579.我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中，有5架“歼— 15”飞机准备着舰，如果乙机不能最先着舰，而丙机必须在甲机之前着舰（不一定相邻），那么不同的着舰方法种数为（ ） A. 24 B. 36 C.48 D. 9610．已知抛物线C ：24y x =的焦点为F ，直线24y x =-与C 交于A ，B 两点．则cos AFB ∠=( )A ．45B ．35C ．35-D ．45-11. 中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖b i e．如图为一个阳马与一个鳖臑的组合体，已知三棱锥P ADE -为鳖臑,且PA ⊥平面ABCE ，2AB AD ==，1ED =，该鳖臑．．的外接球的表面积为9π，则阳马．．的外接球的体积为A． B． C． D．12．已知函数()(1)(2)e e xf x m x x =----，若关于x 的不等式0)(>x f 有且只有一个正整数解，则实数m 的最大值为A ．3e e 2+B ．2e e 2+C ．3e e 2-D ．2e e2-第Ⅱ卷（非选择题，共90分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答．作图题可先用2B 铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚，在试题卷上作答无效． 二、填空题：本大题共4个小题，每小题5分，共20分．13. 已知平面向量(==m ,n ，则m 在n 上的投影=_______.14. 已知6260126(2)(1)(1)...(1)x a a x a x a x +=+++++++，则3a = ．（结果用数值表示）．15．在ABC △中，AB BC =，7cos 18B =-．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．16．对1x R ∀∈，[]23,4x ∃∈，使得不等式2211221223x x x x x mx ++≥++成立，则实数m 的取值范围是 ．三、解答题：共70分．解答应写出文字说明、证明过程和演算步骤．第17～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答． 17. （本小题满分12分）已知数列{a n }满足a l =﹣2，a n+1=2a n +4． （I ）证明数列{a n +4}是等比数列；（Ⅱ）求数列{|a n |}的前n 项和S n ．18. （本小题满分12分）如图，已知长方形ABCD 中，22AB =，2AD =，M 为DC 的中点.将∆ADM 沿AM 折起，使得平面ADM ⊥平面ABCM.（1）求证：AD BM ⊥；（2若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为519. （本小题满分12分）四川省阆中中学某部根据运动场地的影响，但为尽大可能让学生都参与到运动会中来，在2018春季运动会中设置了五个项目，其中属于跑步类的两项，分别是200米和400米，另外三项分别为跳绳、跳远、跳高．学校要求每位学生必须参加，且只参加其中一项，学校780名同学参加各运动项目人数统计如下条形图：其中参加跑步类的人数所占频率为713，为了了解学生身体健康与参加运动项目之间的关系，用分层抽样的方法从这780名学生中抽取．．13．．人进行分析．．．．．．．（Ⅰ）求条形图中m 和n 的值以及抽取的13人中参加200米的学生人数；（Ⅱ）现从抽取的参加400米和跳绳两个项目中随机抽取4人，记其中参加400米跑的学生人数为X ，求离散型随机变量X 的分布列与数学期望．20.（本小题满分12分）已知椭圆C ：22221x y a b+=（0a b >>）的左右焦点分别为1F ，2F ，离心率为12，点A 在椭圆C 上，1||2AF =，1260F AF ∠=︒，过2F 与坐标轴不垂直的直线l 与椭圆C 交于P ，Q 两点．（Ⅰ）求椭圆C 的方程；（Ⅱ）若P ，Q 的中点为N ，在线段2OF 上是否存在点(,0)M m ，使得MN PQ ⊥？若存在，求实数m 的取值范围；若不存在，说明理由． 21.（本小题满分12分）已知函数()()R a a x x a x x x f ∈+--=22ln 在其定义域内有两个不同的极值点. （1）求a 的取值范围；（2）记两极值点分别为.,,2121x x x x <且已知0>λ，若不等式112e x x λλ+<⋅恒成立，求λ的范围.请考生在第22,23,三题中任选一题作答，如果多做，则按所做的第一题给分.作答时请写清题号22. （本小题满分10分）已知曲线C ： 21sin ρθ=-，直线cos :sin x t l y t αα=⎧⎨=⎩（t 为参数，0απ≤<）. （Ⅰ）求曲线C 的直角坐标方程；（Ⅱ）设直线 与曲线C 交于A 、B 两点（A 在第一象限），当30OA OB +=时，求α的值. 23. （本小题满分10分）已知函数f （x ）=﹣x 2+ax+4，g （x ）=|x+1|+|x ﹣1|． （1）当a=1时，求不等式f （x ）≥g （x ）的解集；（2）若不等式f （x ）≥g （x ）的解集包含[﹣1，1]，求a 的取值范围．理科数学答案一、选择题（每小题5分，共计60分）二．填空题（每小题5分，共计20分）13． -1 14． 20 15． 3816．(],3-∞ 三、解答题17.（I ）证明：∵数列{a n }满足a l =﹣2，a n+1=2a n +4，∴a n+1+4=2（a n +4）..................3分 ∴数列{a n +4}是等比数列，公比与首项为2．...............................................................6分 （II ）解：由（I ）可得：a n +4=2n ， ∴a n =2n ﹣4，...............................................8分∴当n=1时，a 1=﹣2；n≥2时，a n ≥0，..........................................................................9分 ∴n≥2时，S n =﹣a 1+a 2+a 3+…+a n =2+（22﹣4）+（23﹣4）+…+（2n ﹣4） =﹣4（n ﹣1）=2n+1﹣4n+2．n=1时也成立．............................................11分∴S n =2n+1﹣4n+2．n ∈N * ．.............................................................................................12分 18. 【答案】（1）解：证明：∵长方形ABCD 中，AB=，AD=，M 为DC 的中点，∴AM=BM=2，∴BM ⊥AM.....................................3分∵平面ADM ⊥平面ABCM ，平面ADM∩平面ABCM=AM ，BM ⊂平面ABCM ∴BM ⊥平面ADM ∵AD ⊂平面ADM∴AD ⊥BM.......................................................5分 （2）解：建立如图所示的直角坐标系设，则平面AMD 的一个法向量 ，...................................7分，设平面AME 的一个法向量 则 取y=1，得所以，............................................10分因为 ，求得 ，所以E 为BD 的中点 .......................11分19..（Ⅱ）由题意，得抽取的13人中参加400米的学生人数有240134780⨯=，参加跳绳的学生人数有3人，所以X 的所有可能取值为1、2、3、4，………………6分()134347C C 41C 35P X ===，()224347C C 182C 35P X ===，()314347C C 123C 35P X ===，()4447C 14C 35P X ===，………………9分所以离散型随机变量X 的分布列为：……………………………………………………………………………11分 所以41812116()1234353535357E X =⨯+⨯+⨯+⨯=．………………12分 20．解：（Ⅰ）由12e =得2a c =，1||2AF =，2||22AF a =-， 由余弦定理得，222121212||||2||||cos ||AF AF AF AF A F F +-⋅=，解得1c =，2a =，2223b a c =-=，所以椭圆C 的方程为22143x y +=． (5)分（Ⅱ）存在这样的点M 符合题意. 设11(,)P x y ，22(,)Q x y ，00(,)N x y ， 由2(1,0)F ，设直线PQ 的方程为(1)y k x =-，由221,43(1),x y y k x ⎧+=⎪⎨⎪=-⎩得2222(43)84120k x k x k +-+-=，…………………7分 由韦达定理得2122843k x x k +=+，故212024243x x k x k +==+， 又点N 在直线PQ 上，02343k y k -=+，所以22243(,)4343k kN k k -++. …………………9分 因为MN PQ ⊥，所以22230143443MNk k k k k m k --+==--+，整理得22211(0,)34344k m k k==∈++， 所以存在实数m ，且m 的取值范围为1(0,)4．...12分21.I 依题意得函数)(x f 得定义域为(0,+∞)，所以方程0)('=x f 在(0,+∞)有两个不同的根， 即方程0ln =-ax x 在(0,+∞)有两个不同的根. 问题转化为函数xx x g ln )(=与ay =的图象(0,+∞)有两个不同的交点. 又,ln 1)('2xxx g -=即当e x <<0时，0)('>x g ；当e x >时，0)('<x g ， 所以)(x g 在),0(e 上单调递增，在),(+∞e 上单调递减.从而ee g x g 1)()(==极大值 ………………3分 又)(x g 有且只有一个零点是1，且当0→x 时，-∞→)(x g ；当+∞→x 时，0)(→x g . 所以，要想函数xxx g ln )(=与函数a y =的图象(0,+∞)有两个不同的交点， 只需e a 10<<.…6分 (II )因为λλ+⋅<211x x e 等价于21ln ln 1x x λ+<λ+，由(I )知21,x x 是方程0ln =-ax x 的两个根，即2211ln ,ln ax x ax x ==，所以原式等价于)(ln ln 12121x x a x x λ+=λ+<λ+，因为2100x x <<>λ，，所以原式等价于211x x a λ+λ+>. …………8分又由2211ln ,ln ax x ax x ==作差得)(ln2121x x a x x -=，即2121ln x x x x a -=.所以原式等价于2121211lnx x x x x x λ+λ+>-，因为210x x <<时，原式恒成立，即212121)()1(ln x x x x x x λλ+-+〈恒成立. 令)1,0(,21∈=t x x t ，则不等式)1()1(ln -++<t t t λλ在)1,0(∈t 上恒成立. 令λλ+-+-=t t t t h )1()(1ln )(，又2222)()()1()()(11)('λ+λ--=λ+λ+-=t t t t t t t h ，当12≥λ时，可见)(0,1∈t 时，0)('>t h ，所以)(0,1)(∈t t h 在上单调递增, 又)(0,10)(,0)(1∈<=t t h h 在上恒成立，符合题意. …………10分当12<λ时，可见当)(0,2λ∈t 时，0)('>t h ，当)1(2，λ∈t 时，0)('<t h 所以)(0,)(2λ∈t t h 在上单调递增, 在),1(2λ∈t 上单调递减，又)(0,10)(,0)(1∈<=t t h h 在上不恒成立，不符合题意，舍去.综上所述，若不等式λλ+⋅<211x x e 恒成立，只需12≥λ，又0>λ，所以1≥λ…………12分22解：（Ⅰ）由 ，得 ，................................................................2分 所以曲线C 的直角坐标方程为 ................................................................................5分（Ⅱ）将直线l 的参数方程代入，得 ，.......7分设A ，B 两点对应的参数分别为 ，由韦达定理及 得 ，故 (10)分23.（1）解：（1）当a=1时，f （x ）=﹣x 2+x+4，是开口向下，对称轴为x=的二次函数，g （x ）=|x+1|+|x ﹣1|= ，................................................................................2分当x ∈（1，+∞）时，令﹣x 2+x+4=2x ，解得x=，g （x ）在（1，+∞）上单调递增，f （x ）在（1，+∞）上单调递减，∴此时f （x ）≥g （x ）的解集为（1，]； (3)分当x ∈[﹣1，1]时，g （x ）=2，f （x ）≥f （﹣1）=2．当x ∈（﹣∞，﹣1）时，g （x ）单调递减，f （x ）单调递增，且g （﹣1）=f （﹣1）=2． 综上所述，f （x ）≥g （x ）的解集为[﹣1，]；...........................................................5分（2）依题意得：﹣x 2+ax+4≥2在[﹣1，1]恒成立，即x 2﹣ax ﹣2≤0在[﹣1，1]恒成立，则只需，解得﹣1≤a≤1，故a 的取值范围是[﹣1，1]． ...............................................................................................10分。
2018届浙江省五校高三第二次联考文科数学试题及答案
2018学年浙江省第二次五校联考数学（文科）试题卷第Ⅰ卷一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合{}1A x x =>，{}B x x m =<，且A B =R ，那么m 的值可以是（ ）A ．1-B ．0C ．1D ．2 2．已知,a b R ∈，则“222a b +<”是 “1ab <”的( ) A ．必要而不充分条件 B ．充要条件C ．充分而不必要条件D ．既不充分也不必要条件3．如图是某班50位学生期中考试数学成绩的频率分布直方图，其中成绩分组区间是：[)4050，，[)5060，，[)6070，，[)7080，，[)8090，，[]90100，，则图中x 的值等于A ．0.12B ．0.18C ．0.012D ．0.0184．已知()cos()3f x x πω=+的图像与1=y 的图象的两相邻交点间的距离为,π要得到()y f x =的图像，只需把sin y x ω=的图像 （ ）A ．向右平移127π个单位 B ．向左平移127π个单位 C ．向右平移56π个单位 D ． 向左平移56π个单位5．下列命题正确的是( )A ．若平面α不平行于平面β，则β内不存在直线平行于平面αB ．若平面α不垂直于平面β，则β内不存在直线垂直于平面αC ．若直线l 不平行于平面α，则α内不存在直线平行于直线lD ．若直线l 不垂直于甲面α，则α内不存在直线垂直于直线l6．执行如图所示的程序框图，输出的S 值为（ ）A ．126B ．105C ．91D ．667．若(,),4παπ∈且3cos 24sin(),4παα=-则α2sin 的值为 （ ）A ．79B ．79- C ．19- D ．198．已知双曲线2222:1x y C a b-=的左、右焦点分别是12,F F ，正三角形12AF F 的一边1AF 与双曲线左支交于点B ，且114AF BF =，则双曲线C 的离心率的值是（ ） A ．123+ B． C ．1313+ D9．已知函数32()69f x x x x abc =-+-， 其中a b c <<，且0)()()(===c f b f a f ，现给出如下结论：①0)1()0(>f f ；②0)1()0(<f f ；③(0)(3)0f f >；④0)3()0(<f f . 其中正确结论的个数是（ ）A ．1B ．2C ．3D ．410．用()n A 表示非空集合A 中的元素个数，定义()(),()(),()(),()()n A n B n A n B A B n B n A n A n B -≥⎧*=⎨-<⎩当当若22{|140,},{||2014|2013,}A x x ax a RB x x bx b R =--=∈=++=∈，设{|1}S b A B =*=，则()n S 等于（ ） A ．4B ．3C ．2D ．1第Ⅱ卷二、填空题（本大题共7小题，每小题4分，共28分）11．分别在集合{1,2,4}A =和{3,5,6}B =中随机的各取一个数，则这两个数的乘积为偶数的概率为 ；12．一个几何体的三视图如图所示，侧视图是一个等边三角形，俯视图是半圆和正方形，则这个几何体的体积为 .13．过点(11,2)A 作圆22241640x y x y ++--=的弦，其中弦长为整数的共有 条。
2018年浙江省“五校联考”高考数学二模试卷
2018年浙江省“五校联考”高考数学二模试卷一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 设集合A={x||x−1|≤1}，B={x|log2x≤2}，则B∩∁R A=()A.[2, 4]B.(2, 4]C.[0, 4]D.(2, 4]∪(−∞, 0)2. 若复数z满足z(1+i)=|1−i|+i（其中i为虚数单位），则z的虚部为（）A.1−√22B.√2−12C.−√2+12i D.√2−12i3. 已知随机变量X∼B(4, p)，若EX=83，则P(X=2)=()A.8 3B.827C.23D.494. 设a，b是两条直线，α，β是两个平面，则a⊥b的一个充分条件是（）A.a⊥α，b // β，α⊥βB.a⊥α，b⊥β，α // βC.a⊂α，b⊥β，α // βD.a⊂α，b // β，α⊥β5. 如图，设A、B是半径为2的圆O上的两个动点，点C为AO中点，则CO→∗CB→的取值范围是（）A.[−1, 3]B.[1, 3]C.[−3, −1]D.[−3, 1]6. (1−√x)6(1+√x)4的展开式中x的系数是（）A.−4B.−3C.3D.47. 点D是△ABC的边AB的中点，∠ABC=120∘，|CD||AB|=√32，若以A、B为焦点的双曲线恰好经过点C，则该双曲线的离心率为（）A.√7+13B.√5+12C.√2+1D.√3+18. 若cosα+sinα=tanα(0<α<π2)，则α∈()A.(0,π6) B.(π6,π4) C.(π4,π3) D.(π3,π2)9. 已知△ABC的三边长分别为a、b、c，有以下四个命题：（1）以√a，√b，√c为边长的三角形一定存在；（2）以2a ，2b ，2c 为边长的三角形一定存在；（3）以a 3，b 3，c 3为边长的三角形一定存在；（4）以|a −b|+c ，|b −c|+a ，|c −a|+b 为边长的三角形一定存在，其中正确命题的个数为（ ） A.1个 B.2个 C.3个 D.4个10. 已知函数f(x)={|(x −a)2−1|+a,x ≥0|x −a|+2a −1,x <0 的最小值为2a −1，则实数a 的取值范围是（ ） A.a =±1 B.0≤a ≤1 C.a ≤0或a =1 D.a ≤0或a ≥1二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．已知2log 6x =1−log 63，则x 的值是________．若实数x ，y 满足{−x +y ≤1y ≥|2x −1| ，则x +y 的最大值为________，x 2+y 2的取值范围为________．一个三棱锥的三视图如图所示，则其表面积为________．点G 是△ABC 的重心，过G 作直线与AB 、AC 两边分别交于M 、N 两点，且AM →=xAB →，AN →=yAC →．若x =12，则y =________，若S △AMN =23S △ABC ，则x +y =________．已知正项等比数列{a n }的前n 项和为S n ，若−1，S 5，S 10成等差数列，则S 10−2S 5=________，S 15−S 10的最小值为________．将一个4×4正方形棋盘中的8个小正方形方格染成红色，使得每行、每列都恰有两个红色方格，则有________种不同的染色方法．棱长为36的正四面体A−BCD的内切球球面上有一动点M，则MB+13MC的最小值为________．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．在△ABC中，角A、B、C的对边分别为a、b、c，且(b+c)2−a2=(2+√2)bc，sinAsinB=cos2C2．(Ⅰ)求角A和角B的大小；(Ⅱ)已知当x∈R时，函数f(x)=sinx(cosx+asinx)的最大值为32，求a的值．如图，四棱锥P−ABCD的底面是梯形．BC // AD，AB=BC=CD=1，AD=2，PB=√132，PA=PC=√3(Ⅰ)证明；AC⊥BP；(Ⅱ)求直线AD与平面APC所成角的正弦值．(Ⅰ)求证：lnx<√x>1)；(Ⅱ)设函数f(x)=1lnx −1x−1(x>1)(ⅰ)求证：f(x)是减函数；(ⅱ)若不等式(1+1n)n+a<e对任意n∈N∗恒成立（e是自然对数的底数），求实数a的取值范围．如图，已知椭圆C:x2a2+y2b2=1(a>b>0)离心率为12，焦距为2．(Ⅰ)求椭圆C的方程；(Ⅱ)直线l与椭圆切于点P，OQ⊥l，垂足为Q，其中O为坐标原点．求△OPQ面积的最大值．已知正项数列{a n}满足a1=4，lna n+1=1na n2−a n+3，n∈N∗．(Ⅰ)求证：a n≥4n；(Ⅱ)求证：16≤12+a1+12+a2+..+12+a n≤14参考答案与试题解析2018年浙江省“五校联考”高考数学二模试卷一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.【答案】 B【考点】交、并、补集的混合运算 【解析】解不等式求得集合A 、B ，根据交集与补集的定义计算即可． 【解答】集合A ={x||x −1|≤1}={x|−1≤x −1≤1}={x|0≤x ≤2}=[0, 2]， B ={x|log 2x ≤2}={x|0<x ≤4}=(0, 4]， ∴ ∁R A =(−∞, 0)∪(2, +∞)， ∴ B ∩∁R A =(2, 4]． 2.【答案】 A【考点】 复数的运算 【解析】复数z 满足z(1+i)=|1−i|+i ，则(a +bi)(1+i)=a −b +(b +a)i =√2+i ，列方程组能求出z 的虚部． 【解答】设z =a +bi ，∵ 复数z 满足z(1+i)=|1−i|+i （其中i 为虚数单位）， ∴ (a +bi)(1+i)=√2+i ，∴ a +bi +ai +bi 2=a −b +(b +a)i =√2+i ， ∴ {a −b =√2a +b =1 ，解得a =√2+12，b =1−√22．∴ z 的虚部为1−√22．3.【答案】 B【考点】离散型随机变量的期望与方差 【解析】根据数学期望值求出p ，再利用公式计算概率P(X =2)的值． 【解答】由随机变量X ∼B(4, p)， 且EX =83，即np =4p =83，解得p =23；∴ P(X =2)=C 42⋅(23)2⋅(1−23)2=827． 4.【答案】 C【考点】空间中直线与直线之间的位置关系 充分条件、必要条件、充要条件 【解析】根据题意分别画出错误选项的反例图形即可． 【解答】A 、B 、D 的反例如图．5.【答案】 A【考点】平面向量数量积的性质及其运算律 【解析】如图所示，可得O(0, 0)，A(−2, 0)，C(−1, 0)，设B(2cosθ, 2sinθ)．θ∈[0, 2π)．利用数量积运算性质与三角函数的单调性可得CO →∗CB →范围．【解答】 如图所示，可得O(0, 0)，A(−2, 0)，C(−1, 0)，设B(2cosθ, 2sinθ)．θ∈[0, 2π)． CO →∗CB →=(1, 0)⋅(2cosθ+1, 2sinθ)=2cosθ+1∈[−1, 3]． 6.【答案】 B【考点】二项式定理的应用 【解析】展开式中x 的系数由三部分和组成：(1−√x)6的常数项与(1+√x)4展开式的x 的系数积；(1−√x)6的展开式的x 的系数与(1+√x)4的常数项的积；(1−√x)6的√x 的系数与(1+√x)4的√x 的系数积．利用二项展开式的通项求得各项系数． 【解答】(1−√x)6的展开式的通项为T r+1=C 6r (−√x)r =(−1)rC 6rx r2∴ (1−√x)6展开式中常数项为C 60，含x 的项的系数为C 62，含√x 的项的系数为−C 61 (1+√x)4的展开式的通项为T r+1=C 4r(√x)r∴(1+√x)4的展开式中的x的系数为C42，常数项为C40，含√x的项的系数为C41故(1−√x)6(1+√x)4的展开式中x的系数是C60C42+C62C40−C61C41=6+15−24=−37.【答案】A【考点】双曲线的特性【解析】设AB=2，根据余弦定理计算BC，AC，从而得出离心率．【解答】不妨设AB=2，则CD=√3，BD=12AB=1，在△BCD中，由余弦定理可得：cos∠ABC=BC2+1−32BC =−12，解得BC=1，在△ABC中，由余弦定理得AC=√4+1−2∗2∗1∗cos120∘=√7，不妨设以AB为焦点的双曲线方程为x2a2−y2b2=1，则2a=AC−BC=√7−1，2c=AB=2，∴离心率e=ca =√7−1=√7+13．8.【答案】C【考点】三角函数的恒等变换及化简求值【解析】把等式左边利用辅助角公式化积，结合α的范围求出cosα+sinα的范围进一步得到tanα的范围，则答案可求．【解答】cosα+sinα=√2sin(α+π4)，当0<α<π2时，π4<α+π4<3π4，则√2sin(α+π4)∈(1, √2]⊂(1, √3)，∴tanα∈(1, √3)．得α∈(π4,π3 )．9.【答案】∵(√b+√c)2−(√a)2=b+c−a+2√bc>0，∴√b+√c>√a，∴以√a，√b，√c为边长的三角形一定存在；当b=3，c=2，a=4时，22+23>24不成立，因此以2a，2b，2c为边长的三角形不一定存在；当b=3，c=2，a=4时，a3>b3+c3不成立，因此以a3，b3，c3为边长的三角形不一定存在； B【考点】 三角形求面积 【解析】三角形ABC 的三边长分别为a ，b ，c ，不妨设a ≥b ≥c ，则b +c >a ．通过作差或平方作差，利用绝对值不等式的性质及其三角形三边大小关系即可判断出结论． 【解答】∵ (√b +√c)2−(√a)2=b +c −a +2√bc >0，∴ √b +√c >√a ，∴ 以√a ，√b ，√c 为边长的三角形一定存在；当b =3，c =2，a =4时，22+23>24不成立，因此以2a ，2b ，2c 为边长的三角形不一定存在；当b =3，c =2，a =4时，a 3>b 3+c 3不成立，因此以a 3，b 3，c 3为边长的三角形不一定存在；∵ |a −b|+c +|b −c|+a ≥|a −c|+c +a >|c −a|+b ，∴ 以|a −b|+c ，|b −c|+a ，|c −a|+b 为边长的三角形一定存在； 其中正确命题的个数为2个． 故选：B ． 10.【答案】 A【考点】分段函数的应用函数的最值及其几何意义 【解析】讨论a =0，a =1，求得f(x)的解析式，运用二次函数、绝对值函数的值域，可得最值，即可得到结论． 【解答】解：若a =0，则f(x)={|x 2−1|,x ≥0|x|−1,x <0 ， 可得x <0时，f(x)>−1； x ≥0时，f(x)≥0，可得f(x)的值域为(−1, +∞)，无最小值； 当a =1时，f(x)={|(x −1)2−1|+1,x ≥0|x −1|+1,x <0 ， 当x <0时，f(x)=|x −1|+1>2，当x ≥0时，f(x)=|(x −1)2−1|+1≥1， 当x =0时，取得最小值1，则f(x)的最小值为1，满足题意，当a =−1时，f(x)={|(x +1)2−1|−1,x ≥0|x +1|−3,x <0， 当x <0时，f(x)≥−3；当x ≥0时，f(x)=x 2+2x −1的值域为[−1, +∞)， 可得f(x)的最小值为−1． 故排除B ，C,D. 故选A .二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分． 【答案】 √2【考点】对数的运算性质 【解析】由对数的性质分别化简等号两边，再根据对数函数的定义域和单调性求值． 【解答】原式等价于log 6x 2=log 66−log 63=log 62， 所以x 2=2， 又x >0， ∴ x =√2， 【答案】 5,[0, 13] 【考点】 简单线性规划 【解析】画出不等式组表示的平面区域，由图形求出目标函数z =x +y 的最大值，再根据z =x 2+y 2表示区域内的点到原点的距离的平方，求出x 2+y 2的取值范围． 【解答】不等式组{−x +y ≤1y ≥|2x −1| 可化为 {x −y ≥−1y ≥2x −1y ≥0 或{x −y ≥−1y ≥−2x +1y ≥0， 在同一坐标系中画出两个不等式组表示的平面区域，如图所示；则由图形知，目标函数z =x +y 过点C 时，z 取得最大值， 由{x −y =−1y =2x −1 ，解得C(2, 3)， ∴ x +y 的最大值为5；又z =x 2+y 2表示区域内的点到原点的距离的平方， 由图形知，x 2+y 2的最小值为0， 最大值为22+32=13，∴ x 2+y 2的取值范围是[0, 13]． 【答案】26+2√34，其外接球的体积是125√23π【考点】由三视图求体积 【解析】判断几何体的形状，利用所使用的数据求解三棱锥的表面积以及外接球体积即可． 【解答】如图：PA ⊥平面ABC ，AB ⊥BC ，PA =5，AB =3，BC =4，三棱锥的表面积为：12×3×5+12×3×4+12×4×√25+9+12×5×√9+16=26+2√34 三棱锥的外接球就是长方体三度为：5，4，3的外接球，所以外接球的半径为：12√32+42+52=5√22．外接球的体积为：4π3×(5√22)3=125√23π． 【答案】 1,2【考点】平面向量的基本定理 【解析】用AM →,AN →表示出AG →，根据三点共线求出x ，y 的关系，根据三角形的面积比得出xy =23，从而可求出x +y 的值． 【解答】根据条件：AC →=1y AN →，AB →=1x AM →；又AG →=13AB →+13AC →；∴ AG →=13x AM →+13y AN →； 又M ，G ，N 三点共线； ∴ 13x +13y =1； ∵ x =12，∴ y =1； ∵ S △AMN =23S △ABC ， ∴12AM∗AN∗sin∠MAN 12AB∗AC∗sin∠BAC =AM AB∗AN AC =xy =23，又1x +1y =3，即x+yxy =3， ∴ x +y =2．【答案】1,4【考点】等比数列的前n项和【解析】由题意和等差数列易得第一问；再根据S5，S10−S5，S15−S10为等比数列，可得S15−S10为S5的式子，由基本不等式可得第二问．【解答】∵−1，S5，S10成等差数列，∴2S5=S10−1，∴S10−2S5=1，又由等比数列的性质可得S5，S10−S5，S15−S10为等比数列，∴S5(S15−S10)=(S10−S5)2，∴S15−S10=(S10−S5)2S5=(1+2S5−S5)2S5=S5+1S5+2≥2√S5∗1S5+2=4，当且仅当S5=1S5即S5=1时取等号，∴S15−S10的最小值为4，【答案】90【考点】排列、组合及简单计数问题【解析】根据题意，先分析第一行的染法数目，进而分类讨论第一行染好后的3种情况，①第二行的红色方格均与第一行的红色方格同列，②第二行染的红色方格与第一行的红色方格均不同列，③第二行染的红色方格恰有一个与第一行的红色方格同列，依次分析第三、四行的染法数目，综合可得第二、三、行的染法数目，由分步计数原理可得答案．【解答】第一行染2个红色方格有C42种染法；第一行染好后，有如下三种情况：①第二行的红色方格均与第一行的红色方格同列，这时其余行都只有1种染法；②第二行染的红色方格与第一行的红色方格均不同列，这时第三行有C42种染法，第四行的染法随之确定；③第二行染的红色方格恰有一个与第一行的红色方格同列，而第一、第二这两行染好后，第三行的红色方格必然有一个与上面的红色方格均不同列，这时第三行的染法有2种，第四行染法随之确定．因此，共有染法为：6×(1+6+4×2)=90（种）．【答案】4√33【考点】球内接多面体【解析】由阿波罗尼斯球得内切球球心O是线段CH上以C，E为定点空间中满足PCPE=λ(λ≠1)的点P的集合，连结CO并延长交平面ABD于H，交内切球上方的点设为K，过M作ME⊥CH，交CH于E，连结BM，CM，设OE=x，由已知得CO=9√6，OH=3√6，KCKE=HC HE ，推导出x=√6，λ=3，从而13MC=ME，进而MB+13MC=MB+ME≥BE，由此能求出MB+13MC的最小值．【解答】由阿波罗尼斯球得内切球球心O是线段CH上以C，E为定点，空间中满足PCPE=λ(λ≠1)的点P的集合，连结CO并延长交平面ABD于H，交内切球上方的点设为K，过M作ME⊥CH，交CH于E，连结BM，CM，设OE=x，由已知得CO=9√6，OH=3√6，KC KE =HCHE，∴√63√6−x=√63√6+x，解得x=√6，∴λ=KCKE =√62√6=3，∴MCME =3，∴13MC=ME，∴MB+13MC=MB+ME≥BE，在△BOE中，BO=CO=9√6，OE=√6，cos∠BOE=−cos∠BOH=−13，∴BE=√(9√6)2+(√6)2−2×9√6×√6×(−13)=4√33．∴MB+13MC的最小值为4√33．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．【答案】(Ⅰ)由(b+c)2−a2=(2+√2)bc，可得：b2+c2−a2=√2bc，所以cosA=b2+c2−a22bc =√2bc2bc=√22，又0<A<π，可得：A=π4，由sinAsinB=cos2C2，可得：√22sinB=1+cosC2，√2sinB=1+cosC，∴B+C=3π4，则√2sin(3π4−C)=1+cosC，∴可得：sinC=1，解得C=π2，∴B=π4．(Ⅱ)f(x)=sinx(cosx+asinx)=12sin2x+a2(1−cos2x)=a2+√1+a22sin(2x−θ)，tanθ=a，∵函数f(x)=sinx(cosx+asinx)的最大值为32，∴a2+√1+a22=32，∴解得a=43．．【考点】余弦定理【解析】(Ⅰ)由已知可得：b2+c2−a2=√2bc，利用余弦定理可求cosA，结合范围0<A<π，可求A=π4，由已知可得sinB=1+cosC，由B+C=3π4，则利用三角函数恒等变换的应用可求sinC=1，解得C=π2，利用三角形内角和定理解得B=π4．(Ⅱ)利用恒等变换公式对f(x)=sinx(cosx+asinx)化简得到f(x)=a2+√1+a22sin(2x−θ)，再由最大值，建立方程即可求出a的值．【解答】(Ⅰ)由(b+c)2−a2=(2+√2)bc，可得：b2+c2−a2=√2bc，所以cosA=b2+c2−a22bc =√2bc2bc=√22，又0<A<π，可得：A=π4，由sinAsinB=cos2C2，可得：√22sinB=1+cosC2，√2sinB=1+cosC，∴B+C=3π4，则√2sin(3π4−C)=1+cosC，∴可得：sinC=1，解得C=π2，∴B=π4．(Ⅱ)f(x)=sinx(cosx+asinx)=12sin2x+a2(1−cos2x)=a2+√1+a22sin(2x−θ)，tanθ=a，∵函数f(x)=sinx(cosx+asinx)的最大值为32，∴a2+√1+a22=32，∴解得a=43．．【答案】则A(0, −√32, 0)，C(0, √32, 0)，P(−34, 0, 3√34)，D(−1, √32, 0)，∴AD→=(−1, √3, 0)，AC→=(0, √3, 0)，AP→=(−34, √32, 3√34)，设平面ACP 的法向量为n →=(x, y, z)，则{n →∗AC →=0n →∗AP →=0 ，即{√3y =0−34x +√32y +3√34z =0 ， 令x =√3得n →=(√3, 0, 1)， ∴ cos <n →，AD →>=n →∗AD →|n →||AD →|=−√34， ∴ 直线AD 与平面APC 所成角的正弦值为|cos <n →，AD →>|=√34．【考点】直线与平面垂直 直线与平面所成的角 【解析】（I ）取AC 的中点M ，连接PM ，BM ，通过证明AC ⊥平面PBM 得出AC ⊥BP ； (II)以M 为原点建立坐标系，求出平面APC 的法向量n →，通过计算n →与AD →的夹角得出AD 与平面APC 所成角． 【解答】（I ）证明：取AC 的中点M ，连接PM ，BM ， ∵ AB =BC ，PA =PC ，∴ AC ⊥BM ，AC ⊥PM ，又BM ∩PM =M ， ∴ AC ⊥平面PBM ， ∵ BP ⊂平面PBM ， ∴ AC ⊥BP ．(II)∵ 底面ABCD 是梯形．BC // AD ，AB =BC =CD =1，AD =2， ∴ ∠ABC =120∘，∵ AB =BC =1，∴ AC =√3，BM =12，∴ AC ⊥CD ， 又AC ⊥BM ，∴ BM // CD ．∵ PA =PC =√3，CM =12AC =√32，∴ PM =32，∵ PB =√132，∴ cos∠BMP =PM 2+BM 2−BP 22PM∗BM=−12，∴ ∠PMB =120∘，以M 为原点，以MB ，MC 的方向为x 轴，y 轴的正方向，以平面ABCD 在M 处的垂线为z 轴建立坐标系M −xyz ， 【答案】（1）证明：令g(x)=lnx −√x>1)，则g′(x)=1x −√x−(x−1)⋅12√xx=1−√x+x−12√xx=(√x−1)⋅1−√x 2√xx=√x−1)22x √x<0，∴ g(x)在(1, +∞)上单调递减， ∴ g(x)<g(1)=0，即lnx √x<0．∴ lnx <x>1)．（2）证明：(i)f′(x)=−1x(lnx)2+1(x−1)2=x(lnx)2−(x−1)2(x−1)2(lnx)2，由(I)可知lnx <√x，∴ (lnx)2<(x−1)2x，∴ x(lnx)2<(x −1)2，∴ f′(x)<0，∴ f(x)=1lnx −1x−1(x >1)是减函数． (ii)由(1+1n )n+a <e 得(n +a)ln(1+1n )<1， ∵ ln(1+1n )>ln1=0，∴ n +a <1ln(1+1n)，即a <1ln(1+1n)−n ，令1+1n =t ，则n =1t−1(1<t ≤2)． ∴ a <1lnt −1t−1=f(t)，由(i)可知f(t)在(1, 2]上单调递减， ∴ f(t)的最小值为f(2)=1ln2−1． ∴ a <1ln2−1．【考点】不等式的证明 【解析】（I ）作差求导，根据单调性和最值得出结论；(II)(i)根据(I)的结论判断f′(x)<0，从而结论得证；(ii)分离参数可得a <1ln(1+1n)−n ，使用换元法和(i)的单调性求出函数的最小值即可得出a 的范围． 【解答】（1）证明：令g(x)=lnx −√x>1)，则g′(x)=1x−√x−(x−1)⋅12√xx=1−√x+x−12√xx=(√x−1)⋅1−√x 2√xx=√x−1)22x √x<0，∴ g(x)在(1, +∞)上单调递减， ∴ g(x)<g(1)=0，即lnx √x<0．∴ lnx <x>1)．（2）证明：(i)f′(x)=−1x(lnx)2+1(x−1)2=x(lnx)2−(x−1)2(x−1)2(lnx)2，由(I)可知lnx <√x，∴ (lnx)2<(x−1)2x，∴ x(lnx)2<(x −1)2，∴ f′(x)<0，∴ f(x)=1lnx −1x−1(x >1)是减函数． (ii)由(1+1n )n+a <e 得(n +a)ln(1+1n )<1， ∵ ln(1+1n )>ln1=0，∴ n +a <1ln(1+1n)，即a <1ln(1+1n)−n ，令1+1n =t ，则n =1t−1(1<t ≤2)． ∴ a <1lnt −1t−1=f(t)，由(i)可知f(t)在(1, 2]上单调递减， ∴ f(t)的最小值为f(2)=1ln2−1． ∴ a <1ln2−1． 【答案】（1）由椭圆的离心率e =ca =12，则2c =2，c =1， 则a =2，b =√a 2−b 2=3， ∴ 椭圆C 的方程：x 24+y 23=1；（2）方法一：设P(x 0, y 0)，(x 0≠0, y 0≠0)由椭圆在P 的切线方程：x 0x 4+y 0y 3=1，即3x 0x +4y 0y −12=0，则直线OQ 的方程：y =4y3x 0x ，即3x 0y −4y 0x =0，则|OQ|=√9x 0+16y 0，|PQ|=0000√9x 0+16y 0=00√9x 0+16y 0，则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12√9x 0+16y 0×00√9x 0+16y 0=6|x 0y 0|9x 02+16y 02≤6|x 0y 0|2×3×4|x 0y 0|=14，当且仅当9x 02=16y 02，即x 02=167，y 02=97时取等号， △OPQ 面积的最大值14．方法二：设切线方程：y =kx +m ，(k ≠0)切点P(x 0, y 0)，(x 0≠0, y 0≠0)， O 到切线的距离：|OQ|=√1+k 2，联立{y =kx +m x 24+y 23=1，整理得：(3+4k 2)x 2+8kmx +4m 2−12=0，△=(8km)2−4×(3+4k 2)(4m 2−12)=0，整理得：m 2=3+4k 2， 代入解得：x 0=√3+4k 2，y 0=k 0x +m =√3+4k 2， 直线OQ 的方程：y =−1k x ，即ky +x =0，则|PQ|=|√3+4k 2−√3+4k 2|√1+k 2=√3+4k 2√1+k 2，则则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12×|PQ|⋅|OQ|=12√3+4k 2√1+k 2⋅√1+k 2=12×|k|1+k 2≤12×|k|2|k|=14， 当且仅当k 2=1时，即x 02=167，y 02=97时取等号， △OPQ 面积的最大值14．【考点】椭圆的标准方程 椭圆的应用直线与椭圆的位置关系 【解析】(Ⅰ)根据椭圆的离心率公式及c =1，即可求得a 和c 的值，即可求得椭圆方程；(Ⅱ)方法一：根据椭圆的切线方程，求得直线OQ 的方程，根据点到直线的距离公式即可求得|OQ|及|PQ|，利用三角形的面积公式和基本不等式即可求得△OPQ 面积的最大值；方法二：设切线方程y =kx +m ，求得直线OQ 方程，将切线方程代入椭圆方程，由△=0，即可求得m 2=3+4k 2，利用点到直线的距离公式分别求得|OQ|及|PQ|，根据三角形的面积公式及基本不等式的性质，即可求得△OPQ 面积的最大值． 【解答】（1）由椭圆的离心率e =ca =12，则2c =2，c =1， 则a =2，b =√a 2−b 2=3， ∴ 椭圆C 的方程：x 24+y 23=1；（2）方法一：设P(x 0, y 0)，(x 0≠0, y 0≠0)由椭圆在P 的切线方程：x 0x 4+y 0y 3=1，即3x 0x +4y 0y −12=0，则直线OQ 的方程：y =4y3x 0x ，即3x 0y −4y 0x =0，则|OQ|=√9x 0+16y 0，|PQ|=0000√9x 0+16y 0=00√9x 0+16y 0，则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12√9x 0+16y 0×00√9x 0+16y 0=6|x 0y 0|9x 02+16y 02≤6|x 0y 0|2×3×4|x 0y 0|=14， 当且仅当9x 02=16y 02，即x 02=167，y 02=97时取等号，△OPQ 面积的最大值14．方法二：设切线方程：y =kx +m ，(k ≠0)切点P(x 0, y 0)，(x 0≠0, y 0≠0)， O 到切线的距离：|OQ|=√1+k 2，联立{y =kx +mx 24+y 23=1，整理得：(3+4k 2)x 2+8kmx +4m 2−12=0，△=(8km)2−4×(3+4k 2)(4m 2−12)=0，整理得：m 2=3+4k 2， 代入解得：x 0=√3+4k 2，y 0=k 0x +m =√3+4k 2， 直线OQ 的方程：y =−1k x ，即ky +x =0，则|PQ|=|√3+4k 2−√3+4k 2|√1+k 2=√3+4k 2√1+k 2，则则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12×|PQ|⋅|OQ|=12√3+4k 2√1+k 2⋅√1+k 2=12×|k|1+k 2≤12×|k|2|k|=14， 当且仅当k 2=1时，即x 02=167，y 02=97时取等号， △OPQ 面积的最大值14． 【答案】证明：(Ⅰ)首先利用lnx ≤x −1，可得1n a n 2+a n −3=lna n+1≤a n+1−1，即a n+1≥1na n 2+a n −4，以下用数学归纳法证明a n ≥4n ， ①当n =1时显然成立；②假设当n =k 时，不等式成立，即a k ≥4k ，则当n =k +1时，由函数f(x)=1k x 2−x +4的单调性可得，a k+1≥1k ⋅a k 2−a k +4≥1k(4k)2−4k +4=12k +4>4(k +1)，也就是说，当n =k +1时，不等式也成立；由①②可知，a n ≥4n 对任意的n ∈N ∗成立； （2）易知12+a 1+12+a 2+⋯+12+a n>12+a 1=16，由a n+1≥1n a n2−a n +4=a n (an n−1)+4≥3a n +4，则a n+1+2≥3(a n +2)， 所以，a n +2≥3(a n−1+2)≥32(a n−2+2)≥⋯≥3n−1(a 1+2)=3n−1⋅6=2⋅3n ，则12+a n≤12⋅13，因此，12+a 1+12+a 2+⋯+12+a n≤12(13+132+⋯+13n )=12⋅13(1−13n )1−13=14(1−13n )=14，所以，16≤12+a 1+12+a 2+⋯+12+a n≤14．【考点】数列与不等式的综合 【解析】(Ⅰ)由lnx ≤x −1，得a n+1≥1n a n2−a n +4，然后利用数学归纳法证明不等式a n ≥4n 成立；(Ⅱ)先由12+a 1+12+a 2+⋯+12+a n>12+a 1=16成立，再由a n+1≥1n a n2−a n +4≥3a n +4成立，于是得到a n+1+2≥3(a n +2)成立，进而得到a n +2≥2⋅3n ，于是得到12+a n≤12⋅13n，然后利用不等式的可加性与等比数列求和公式可证明12+a 1+12+a 2+⋯+12+a n≤14成立．【解答】证明：(Ⅰ)首先利用lnx ≤x −1，可得1n a n 2+a n −3=lna n+1≤a n+1−1，即a n+1≥1na n 2+a n −4，以下用数学归纳法证明a n ≥4n ， ①当n =1时显然成立；②假设当n =k 时，不等式成立，即a k ≥4k ，则当n =k +1时，由函数f(x)=1k x 2−x +4的单调性可得，a k+1≥1k ⋅a k 2−a k +4≥1k(4k)2−4k +4=12k +4>4(k +1)，也就是说，当n =k +1时，不等式也成立；由①②可知，a n ≥4n 对任意的n ∈N ∗成立； （2）易知12+a 1+12+a 2+⋯+12+a n>12+a 1=16，由a n+1≥1n a n2−a n +4=a n (an n −1)+4≥3a n +4，则a n+1+2≥3(a n +2)， 所以，a n +2≥3(a n−1+2)≥32(a n−2+2)≥⋯≥3n−1(a 1+2)=3n−1⋅6=2⋅3n ，则12+a n≤12⋅13n ，因此，12+a 1+12+a 2+⋯+12+a n≤12(13+13+⋯+13)=12⋅13(1−13n )1−13=14(1−13)=14，所以，16≤12+a 1+12+a 2+⋯+12+a n≤14．。
2018届浙江省高三第二次五校联考文科数学试题及答案 精品
2018学年浙江省五校联考第二次考试数学（文科）试题卷本试题卷分选择题和非选择题两部分．全卷共4页, 选择题部分1至2页, 非选择题部分3至4页．满分150分, 考试时间120分钟．请考生按规定用笔将所有试题的答案涂、写在答题纸上．参考公式：柱体的体积公式V =Sh 其中S 表示柱体的底面积，h 表示柱体的高锥体的体积公式 V =13Sh 其中S 表示锥体的底面积，h 表示锥体的高台体的体积公式1()123V h S S =++ 其中S 1,S 2分别表示台体的上,下底面积球的表面积公式S =4πR 2其中R 表示球的半径，h 表示台体的高球的体积公式V =43πR3其中R 表示球的半径第Ⅰ卷（选择题 共40分）一、选择题（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 在C ∆AB 中，“C 0AB⋅A =”是“C ∆AB 为直角三角形”的（ ▲ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件2. 已知数列{}n a 满足：21n a n n =+，且910n S =，则n 的值为（ ▲ ） A ．7 B ．8 C ．9 D ．103．要得到函数sin 2y x =的图象，只需将函数πcos(2)3y x =-的图象（ ▲ ）A ．向右平移π6个单位长度B ．向左平移π6个单位长度C ．向右平移π12个单位长度D ．向左平移π12个单位长度4．若αβ、是两个相交平面，则在下列命题中，真命题的序号为（ ▲ ）①若直线m α⊥，则在平面β内，一定不存在与直线m 平行的直线． ②若直线m α⊥，则在平面β内，一定存在无数条直线与直线m 垂直． ③若直线m α⊂，则在平面β内，不一定存在与直线m 垂直的直线． ④若直线m α⊂，则在平面β内，一定存在与直线m 垂直的直线． A ．①③ B．②③ C．②④ D．①④ 5．已知菱形ABCD 的对角线AC 长为1，则ADAC =（ ▲ ）A ．4B ．2C ．1D ．216．设x R ∈, 对于使22x x M -+≤成立的所有常数M 中，我们把M 的最小值1叫做22x x -+ 的上确界. 若,a b R +∈，且1a b +=，则122a b--的上确界为（ ▲ ） A ．5-B ．4-C ．92D ．92-7．如图，已知椭圆C 1：112x +y 2=1，双曲线C 2：22a x —22by =1（a >0，b >0），若以C 1的长轴为直径的圆与C 2的一条渐近线交于A 、B 两点，且C 1与该渐近线的两交点将线段AB 三等分，则C 2的离心率为（ ▲ ） A ．5 B ．5 C ．17 D ．71428. 如图，正ABC ∆的中心位于点G (0,1)，A (0,2)，动点P 从A 点出发沿ABC ∆的边界按逆时针方向运动，设旋转的角度(02)AGP x x π∠=≤≤，向量OP 在(1,0)a =方向的投影为y （O 为坐标原点），则y 关于x 的函数()y f x =的图像是（ ▲ ）非选择题部分（共110分）二、填空题（本大题共7小题，前4题每题6分，后3题每空4分，共36分．）9．设全集U R =，集合2{|340}A x x x =--<，2{|log (1)2}B x x =-<，则A B =▲ ，AB = ▲ ，RC A = ▲ .10．若变量,x y 满足202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩，则2x y+的最大值为 ▲ ，_____21的取值范围-+x y ▲ . 11. 已知命题p ：R x ∈∃，x-1>lnx ．命题q ：R x ∈∀，0>x ，则⌝p ： ▲ ，命题p∧（⌝q ）是 ▲ （填真命题或假命题）。
浙江省五校联盟2023-2024学年高三下学期3月联考试题 数学含答案
浙江省五校联盟2023-2024学年高三下学期3月联考数学试卷（答案在最后）命题:一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.若全集U ,集合A,B 及其关系如图所示,则图中阴影部分表示的集合是()A.()U A B ⋂ðB.()U A B ⋃ðC.()U A B⋂ð D.()U A B⋂ð2.已知(1,2),||2a b == ,且a b ⊥ ,则a b - 与a的夹角的余弦值为()A.5B.3C.4D.63.设b ,c 表示两条直线,,αβ表示两个平面,则下列说法中正确的是()A.若//,b c αα⊂,则//b cB.若//,b c b α⊂,则//c αC.若,//c αβα⊥,则c β⊥ D.若//,c c αβ⊥,则αβ⊥4.已知角α的终边过点(3,2cos )P α-,则cos α=()A.2B.2-C.2±D.12-5.设等比数列{}n a 的公比为q ,前n 项和为n S ,则“2q =”是“{}1n S a +为等比数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知实数x ,y 满足3x >,且2312xy x y +-=,则x y +的最小值为()A.1+B.8C. D.1+7.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ,点A 为双曲线的左顶点,以12F F 为直径的圆交双曲线的一条渐近线于P ,Q 两点,且23PAQ π∠=,则该双曲线的离心率为()C.2138.在等边三角形ABC 的三边上各取一点D ,E ,F ,满足3,90DE DF DEF ︒==∠=,则三角形ABC 的面积的最大值是()A. B.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.在学校组织的《青春如火,初心如炬》主题演讲比赛中,有8位评委对每位选手进行评分(评分互不相同),将选手的得分去掉一个最低评分和一个最高评分,则下列说法中正确的是()A.剩下评分的平均值变大B.剩下评分的极差变小C.剩下评分的方差变小D.剩下评分的中位数变大10.在三棱锥A BCD -中,已知3,2AB AC BD CD AD BC ======,点M ,N 分别是AD ,BC 的中点，则()A.MN ⊥ADB.异面直线AN ,CM 所成的角的余弦值是78C.三棱锥A BCD -的体积为3D.三棱锥A BCD -的外接球的表面积为11π11.已知函数()(sin cos )xf x e x x =⋅+,则()A.()f x 的零点为,4x k k Z ππ=-∈B.()f x 的单调递增区间为32,2,22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦C.当0,2x π⎡⎤∈⎢⎣⎦时,若()f x kx ≥恒成立,则22k e ππ≤⋅D.当10031005,22x ππ⎡⎤∈-⎢⎥⎣⎦时,过点1,02π-⎛⎫⎪⎝⎭作()f x 的图象的所有切线,则所有切点的横坐标之和为502π三、填空题:本题共3小题,每小题5分,共15分.12.直线3430x y -+=的一个方向向量是.13.甲、乙两人争夺一场羽毛球比赛的冠军,比赛为“三局两胜”制.如果每局比赛中甲获胜的概率为23,乙获胜的概率为13,则在甲获得冠军的情况下,比赛进行了三局的概率为.14.已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=,若(21),(2)f x g x --均为偶函数,且当[1,2]x ∈时,3()2f x mx x =-,则(2024)g =.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,斜三棱柱111ABC A B C -的底面是直角三角形,90ACB ︒∠=,点1B 在底面ABC 内的射影恰好是BC 的中点,且2BC CA ==.(I)求证:平面11ACC A ⊥平面11B C CB ;(II),求平面1ABB 与平面11AB C 夹角的余弦值.16.(本小题满分15分)己知函数()ln f x x ax =-,其中a R ∈.(I)若曲线()y f x =在1x =处的切线在两坐标轴上的截距相等,求a 的值;(II)是否存在实数a ,使得()f x 在(0,]x e ∈上的最大值是-3?若存在,求出a 的值;若不存在,说明理由.17.(本小题满分15分)记复数的一个构造:从数集中随机取出2个不同的数作为复数的实部和虚部.重复n 次这样的构造,可得到n 个复数,将它们的乘积记为n z .已知复数具有运算性质:|()()||()||()|a bi c di a bi c di +⋅+=+⋅+,其中,,,a b c d R ∈.(I)当2n =时,记2z 的取值为X ,求X 的分布列;(II)当3n =时,求满足32z ≤的概率;(III)求5n z <的概率n P .18.(本小题满分17分)在平面直角坐标系xOy 中,我们把点*(,),,x y x y N ∈称为自然点.按如图所示的规则,将每个自然点(,)x y 进行赋值记为(,)P x y ,例如(2,3)8P =,(4,2)14,(2,5)17P P ==.(I)求(,1)P x ;(II)求证:2(,)(1,)(,1)P x y P x y P x y =-++;(III)如果(,)P x y 满足方程(1,1)(,1)(1,)(1,1)2024P x y P x y P x y P x y +-+++++++=,求(,)P x y 的值.19.(本小题满分17分)在平面直角坐标系xOy 中,过点(1,0)F 的直线l 与抛物线2:4C y x =交于M ,N 两点(M在第一象限).(I)当||3||MF NF =时,求直线l 的方程;(II)若三角形OMN 的外接圆与曲线C 交于点D (异于点O ,M ,N ),(i)证明:△MND 的重心的纵坐标为定值，并求出此定值;(ii)求凸四边形OMDN 的面积的取值范围.参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.题号12345678答案CBDBCACA二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.题号91011答案BCABDACD三、填空题:本题共3小题,每小题5分,共15分.12.31,4⎛⎫⎪⎝⎭(答案不唯一)13.2514.-6四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)(第I 问,6分;第II 问,7分)解:(I)取BC 中点为M ,连接11,B M B 在底面内的射影恰好是BC 中点,1B M ∴⊥平面ABC ,又AC ⊂ 平面1,ABC B M AC ∴⊥,又90,ACB AC BC ︒∠=∴⊥ ,1,B M BC ⊂ 平面111,,B C CB B M BC M AC ⋂=∴⊥平面11B C CB ,又AC ⊂ 平面11,ACC A ∴平面11ACC A ⊥平面11B C CB .(II)以C 为坐标原点,建立如图所示空间直角坐标系,2BC CA == ,11(2,0,0),(0,2,0),(0,1,0),(0,A B M B C ∴-,111((2,2,0),(0,2,0)AB AB B C =-=-=-,设平面1BAB 的法向量为(,,)n x y z =,100n AB n AB ⎧⋅=⎪∴⎨⋅=⎪⎩则有20220x y x y ⎧-++=⎪⎨-+=⎪⎩,令z =,则3,x y n ==∴= ,设平面1BAB 的法向量为(,,)m a b c =,11100m AB m B C ⎧⋅=⎪∴⎨⋅=⎪⎩则有2020a b b ⎧-++=⎪⎨-=⎪⎩,令a =则0,2,b c n ==∴=,||5|cos ,||||7| n m n m n m ⋅∴<〉==,平面1ABB 与平面11AB C 夹角的余弦值为57.16.(本小题满分15分)(第I 问,6分;第II 问,9分)(I)1()f x a x'=-,则(1)1,(1)f a f a '=-=-,故曲线()y f x =在1x =处的切线为(1)(1)y a a x +=--,即(1)1y a x =--,当1a =时,此时切线为1y =-,不符合要求当1a ≠时,令0x =,有1y =-,令0y =,有11x a =-,故111a=--,即2a =,故2a =(II)11()ln ,()axf x x ax f x a x x-=-∴=-= ,①当0a ≤时,()f x 在(0,e]上单调递增,()f x ∴的最大值是(e)1e 3f a =-=-,解得40ea =>,舍去;②当0a >时,由11()0ax f x a x x -=-==,得1x a=,当10e a <<,即1a e >时,10,a x ⎛⎫∴∈ ⎪⎝⎭时,1()0;,e f x x a ⎛⎫>∈ ⎪⎝⎭时,()0f x <,()f x ∴的单调递增区间是10,a ⎛⎫ ⎪⎝⎭,单调递减区间是1,e a ⎛⎫ ⎪⎝⎭,又()f x 在(0,e]上的最大值为2max 13,()1ln 3,e f x f a a a ⎛⎫-∴==--=-∴= ⎪⎝⎭;当1e a ≤,即10ea <≤时,()f x 在(0,e]上单调递增,max ()(e)1e 3f x f a ∴==-=-,解得41e ea =,舍去.综上,存在a 符合题意,此时2e a =17.(本小题满分15分)(第I 问,6分;第II 问,4分;第III 问,5分)(I)由题意可知,可构成的复数为{1,,1}i i +,|1|||1,||||||| 2.i i =====+=且X的可能取值为,111111224242111111666666122(1),(,(2)999C C C C C C P X P X P X C C C C C C ⋅⋅⋅=========⋅⋅⋅，112211661(3)9C C P X C C ⋅===⋅111142221111666621(,(4)99C C C C P X P X C C C C ⋅⋅======⋅⋅，所以分布列为:(II)共有111666216CC C ⋅⋅=种,满足32z ≤的情况有:①3个复数的模长均为1,共有1112228C C C ⋅⋅=种;②3个复数中,2个模长均为1,1或者2,共有2111322448C C C C ⋅⋅⋅=种;所以()38487221627P z +≤==.(III)当1n =或2时,显然都满足,此时1n P =;当3n ≥时,满足5n z <共有三种情况:①n 个复数的模长均为1,则共有()122nn C =;②1n -个复数的模长为1,剩余1或者2,则共有()11111242n n n n C C C n --+⋅⋅=⋅;③2n -个复数的模长为1,剩余2个模长为2,则共有()221111244(1)2n n n nCCC C n n --+⋅⋅⋅=-⋅.故()()()2112621222(1)212563n n n n n nn nn n n n n P z C ++++⋅+-⋅+<===,此时当1,2n =均成立.所以()21253n nn P z +<=.18.(本小题满分17分)(第I 问,4分;第II 问,7分;第III 问,6分)解:(I)根据图形可知(1)(,1)1232x x P x x +=++++=,(II)固定x ,则(,)P x y 为一个高阶等差数列,且满足(,1)(,)1,(1,)(,),P x y P x y x y P x y P x y x y +-=+-+-=+所以(1)(,1)(,1)12(1)(1)2y y P x y P x y y x y x ++-=++++-=+- (1)(1)(,1)(1)22y y x x P x y y x +++=+-+所以(1)(1)(,)(1)(1)22x x y y P x y x y +-=++--,(1)(1)(1,)(2)(1)22x x y y P x y x y ---=++--,所以(1)(1)(1)(1)(,1)(1,)(2)(1)(1)2222x x y y y y x x P x y P x y x y y x --++++-=++--++-+222322(,)x y xy y x P x y =++--+=(III)P(x +1,y -1)+P(x ,y +1)+P(x +1,y )+P(x +1,y +1)=2024等价于(,)(,1)(1,)(1,1)2023P x y P x y P x y P x y +++++++=,等价于(,1)3(1,)2023P x y P x y +++=即13[(1)(21)][(1)(2)(1)(2)]202322x x y y x x x y y x +++-++++-+=,化简得2221010(1)()21010y xy x y x x y x y x ++-+=⇔+-++=,由于x y +增大,(1)()x y x y +-+也增大,当31x y +=时,(1)()29921010x y x y x +-++<<,当33x y +=时,(1)()210561010x y x y x +-++>>,故当32x y +=时,(1)()210109,23x y x y x x y +-++=⇒==,即9102322(9,23)82247422P ⨯⨯=++⨯=19.(本小题满分17分)(第I 问,4分;第II 问,5分;第III 问,8分)解:(I)设直线()()1122:1,,,,MN X my M x y N x y =+联立214x my y x=+⎧⎨=⎩,消去x ,得2440y my --=,所以12124,4y y m y y +=⋅=-,||3||MF NF =,则123y y =-122212224,34y y y m y y y +=-=∴⋅=-=-,则213m =,又由题意0,3m m >∴=,直线的方程是y =;(II)(i)方法1:设()()()112233,,,,,M x y N x y D x y 因为O ,M ,D ,N 四点共圆,设该圆的方程为220x y dx ey +++=,联立22204x y dx ey y x⎧+++=⎨=⎩,消去x ,得42(416)160y d y ey +++=,即()3(416)160y y d y e +++=，所以123,,y y y 即为关于y 的方程3(416)160y d y e +++=的3个根,则()()()3123(416)16y d y e y y y y y y +++=---,因为()()()()()32123123122313123y y y y y y y y y y y y y y y y y y y y y ---=-+++++-,由2y 的系数对应相等得,1230y y y ++=,所以MND 的重心的纵坐标为0.方法2:设()()()112233,,,,,M x y N x y D x y ,则1213234444,,,OM ON MD ND k k k k y y y y y y ====++,因为O,M,C,N 四点共圆,所以MON MDN π∠+∠=,即tan tan 0MON MDN ∠+∠=,()21124tan 116OM ONOM ON y y k k MON k k y y --∠==+⋅+()()()1213234tan ,116ND MDND MD y y k k MDN k k y y y y --∠==+⋅+++化简可得:312y y y =--,所以MND 的重心的纵坐标为0.(ii)记,OMN MND 的面积分别为12,S S ,由已知得直线MN 的斜率不为0设直线:1MN x my =+,联立214x my y x=+⎧⎨=⎩,消去x ,得2440y my --=,所以12124,4y y m y y +=⋅=-,所以11211||22S OF y y =⋅⋅-==由(i)得,()3124y y y m =-+=-,所以2223311(4)444x y m m ==⨯-=,即()24,4D m m -,因为()21212||2444MN x x m y y m =++=++=+,点D 到直线MN的距离d =所以()22211||448122S MN d m m =⋅⋅=⋅+⋅-,所以)221281181S S S m m =+=+-=+-M 在第一象限,即1230,0,40y y y m ><=-<,依次连接O,M,D,N 构成凸四边形OMDN ,所以()3122y y y y =-+<,即122y y -<,又因为122244,2y y y y ⋅=-<,即222y <,即20y <<,所以122244m y y y y =+=->+=,即24m >,即218m >,所以)218116S m m =+-=,设t =,则4t >,令()2()161f t t t =-,则()()222()1611614816f t t t t t ''=-+-=-,因为4t >,所以2()48160f t t '=->,所以()f t在区间4⎛⎫+∞⎪⎝⎭上单调递增,所以()42f t f ⎛⎫>=⎪⎝⎭,所以S的取值范围为,2⎛⎫+∞ ⎪⎝⎭.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
浙江省2018年五校联考试题
数学(文史类)答案
11.
()⎪⎪⎩
⎪⎪⎨
⎧⎪
⎭⎫ ⎝⎛
<-⎪⎭⎫ ⎝⎛≥-21121122x x x 12.(]4,∞- 13.1- 14.()2,0 三、解答题：本大题共6小题，每小题14分，共84分。
解答应写出文字说明，证明过程或演算步骤。
15．解：设()11,y x =，()22,y x =………………………………………………（2分） 则023211=+-=⋅y x c a ；
423222-=+-=⋅y x c b ；………………………………………………（
6分） 82
121=+=y x ；
42
22
2=+=y x ．………………………………………………（10分）
解得⎩⎨⎧==6211y x ，或⎩⎨⎧-=-=6211y x ，对应的b 分别为⎩⎨⎧-==2022y x ，或⎩⎨⎧==1
322y x ，
分别代入()
2,32-=+=n m ，解得6,4±=-=m n ……………（14分）
16．解：()(
)cos 1sin sin 4f x a x x b x a b π⎛
⎫=+++=+++ ⎪⎝
⎭……………（2分）
（Ⅰ）当1a =时，()14f x x b π⎛
⎫==+++ ⎪⎝
⎭
∴当()222
4
2
k x k k Z π
π
π
ππ-
≤+
≤+
∈时，()f x 是增函数，
∴函数()f x 的单调增区间为()32,244k k k Z ππππ⎡
⎤-+∈⎢⎥⎣
⎦……………（8分） （Ⅱ）由0x π≤≤得5444
x πππ
≤+≤
∴sin 14x π⎛
⎫≤+≤ ⎪⎝
⎭………………………………………………（10分）
∵0a <
∴当sin 14x π⎛
⎫+= ⎪⎝
⎭时，()f x 取最小值33a b ++=……………（※）
当sin 4x π⎛
⎫+= ⎪⎝⎭
时， ()f x 取最大值4，即4b =
将4b =代入（※）式得1a =5a b +=（14分） 17．解：（Ⅰ）3P =
3
1
………………………………………………（4分） （Ⅱ）由于第n 次到顶点A 是从D C B ,,三个顶点爬行而来，从其中任何一个顶点
到达A 的概率都是3
1
，而第1-n 次在顶点A 与小虫在D C B ,,是对立事件． 因此，第n 次到顶点A 的概率为()113
1
--=n n P P ………………（8分）
即⎪⎭⎫
⎝⎛--=-
-4131411n n P P ………………………………………（11分） ⎭
⎬⎫⎩
⎨⎧-∴=41,11n P P 是以43411=-P
为首项，公比为3
1
-的等比数列， ()N n n P n n ∈≥+⎪
⎭
⎫
⎝⎛-=∴-,2 4
1
31431
………………………………（14分） 18．
（Ⅰ）取1CC 的中点G ，则DG 为AE 在面1DC 内的射影，11D F DG AE D F ⊥∴⊥ 又1AD AE A D F ⋂=∴⊥面ADE ………………………………（5分） （Ⅱ）不成立………………………………（7分） 设1CC 、F D 1与平面ADE 的交点分别为G 、H, 在菱形11C CDD 中，可得DG DD ⊥1 又 平面⊥ABCD 平面11C CDD ，
且平面⋂ABCD 平面11C CDD =CD ，CD AD ⊥
1DD AD ⊥∴，因此AED DD 平面⊥1
所以1DHD ∠为直线ADE F D 与平面1所成的角………………………………（10分） 在菱形11C CDD 内，因为CD C 1∠=0
60，所以0
1120=∠DE D
可求得a F D 271=
，所以14
7
5arccos
1=∠F D D ， 在H DD Rt 1∆中，2
11π
=
∠+∠HD D H DD ，∴1DHD ∠=14
7
5arcsin
所以直线ADE F D 与平面1所成的角为14
7
5arcsin
．………………………（14分） 19．解：
（Ⅰ）88a b +=⇒
设12(0,2),(0,2)F F -，则128MF MF +=
因此，点M 的轨迹是以12F F 、为焦点，长轴长为8的椭圆，其方程为：22
11216
x y +=
…………………………………………………（6分） （Ⅱ）假设存在这样的直线，使得OAPB 为矩形，并设:3l y kx =+
与椭圆方程联立得：2(324)18210(*)k x kx ++-= 设1122(,),(,)A x y B x y ，则12x x 、是（*）的两根，
且121222
1821
,3434
k x x x x k k +=-
=-++………………………………（8分） 因为OAPB 为矩形，故OB OA ⊥ 则02121=+y y x x ，()()0332121=+++kx kx x x
()
()093121212
=++++x x k x x k
……………………（11分）
由此可得：()
094
31834312122
22=++
⨯-++-
k k k k 解得：25
16
k k =
∴=因此，当直线的斜率为时，可使OAPB 为矩形． ………………………………（14分）
20．解：（Ⅰ）()x f 为非奇非偶函数．
()()3
32x m x x f ++-=- ，而33)(2)(x m x x f -+=
()()x f x f --∴()3
32x m x ++-=33)(2x m x ---=x m x 2362+-不恒为零，
同样，()()x f x f +-也不恒为零．………………………………（6分）
y
x
l
B
A
O
P
Ⅱ） 33)(2)(x m x x f -+= ()22'363m mx x x f -+=∴
又 )(x f 在),5[+∞上单调递增，()036322'≥-+=∴m mx x x f 在),5[+∞上恒成立．
因此⎩⎨
⎧
≥-+≤-0
3307552
m m m ，得255255+≤≤-m ，又因为0>m ， 所以2550+≤<m ．………………………………（14分）。