化工原理正交试验报告模板
正交试验设计常用正交表分析报告

2
2
1
2
2
6
2
2
1
2
2
2
1
1
2
1
1
7
2
3
2
1
1
1
2
2
2
1
1
8
2
4
2
1
1
2
1
1
1
2
2
9
3
1
2
1
2
2
1
2
2
1
2
10
3
2
2
1
2
1
2
1
1
2
1
11
3
3
1
2
1
2
1
2
1
2
1
12
3
4
1
2
1
1
2
1
2
1
2
13
4
1
2
2
1
2
2
1
2
2
1
14
4
2
2
2
1
1
1
2
1
1
2
15
4
3
1
1
2
2
2
1
1
1
2
16
4
4
1
1
2
1
1
2
2
2
1
(8)L16(43×26)
1
1
1
2
2
2
2
1
1
1
1
2
2
2
正交实验报告

正交实验报告正交实验报告一、引言正交实验是一种常用的实验设计方法,用于确定多个因素对某个结果的影响程度及其相互作用关系。
在工程、科学研究和市场调研等领域中,正交实验被广泛应用于寻找最佳参数组合、提高产品质量和降低成本等方面。
二、实验目的本次实验旨在通过正交实验设计,研究不同因素对某个结果的影响,并确定最佳的因素组合,以实现优化目标。
三、实验设计1. 因素选择根据实验目的,我们选择了A、B和C三个因素,分别代表产品材料、工艺参数和环境条件。
这三个因素的水平分别设定为A1、A2、B1、B2、C1和C2,共计6个水平。
2. 正交表设计我们使用L9正交表进行实验设计。
L9正交表是一个9行4列的表格,每一行代表一个试验,每一列代表一个因素,表格中的数字表示该因素在该试验中的水平。
通过正交表设计,可以保证各个因素在不同试验中均匀分布,从而减少误差。
3. 实验过程根据正交表的设计,我们依次进行了9个试验。
在每个试验中,我们按照正交表中指定的因素水平设置实验条件,并记录结果。
四、实验结果在每个试验中,我们记录了某个结果的数值,并进行了统计分析。
以下是实验结果的总结:1. 因素A对结果的影响通过分析实验结果,我们发现因素A对结果的影响较为显著。
在A1水平下,结果的数值较低;而在A2水平下,结果的数值明显提高。
这表明在产品材料的选择上,A2水平更适合实现优化目标。
2. 因素B对结果的影响实验结果显示,因素B对结果的影响较小。
在B1和B2水平下,结果的数值相差不大。
这说明在工艺参数的选择上,B1和B2水平的差异对结果影响较小。
3. 因素C对结果的影响在实验中,我们发现因素C对结果的影响较为复杂。
在C1水平下,结果的数值较低;而在C2水平下,结果的数值明显提高。
然而,我们还观察到在A1水平下,C1水平的结果较好;在A2水平下,C2水平的结果较好。
这表明因素C 的影响与其他因素的交互作用有关。
五、结论与建议通过正交实验的设计与分析,我们得出以下结论与建议:1. 最佳因素组合根据实验结果,我们可以确定最佳因素组合为A2B1C2。
化工原理含实验报告(3篇)

第1篇一、实验目的1. 理解并掌握化工原理中的基本概念和原理。
2. 通过实验验证理论知识,提高实验技能。
3. 熟悉化工原理实验装置的操作方法,培养动手能力。
4. 学会运用实验数据进行分析,提高数据处理能力。
二、实验内容本次实验共分为三个部分:流体流动阻力实验、精馏实验和流化床干燥实验。
1. 流体流动阻力实验实验目的:测定流体在圆直等径管内流动时的摩擦系数与雷诺数Re的关系,将测得的~Re曲线与由经验公式描出的曲线比较;测定流体在不同流量流经全开闸阀时的局部阻力系数。
实验原理:流体在管道内流动时,由于摩擦作用,会产生阻力损失。
阻力损失的大小与流体的雷诺数Re、管道的粗糙度、管道直径等因素有关。
实验中通过测量不同流量下的压差,计算出摩擦系数和局部阻力系数。
实验步骤:1. 将水从高位水槽引入光滑管,调节流量,记录压差。
2. 将水从高位水槽引入粗糙管,调节流量,记录压差。
3. 改变流量,重复步骤1和2,得到一系列数据。
4. 根据数据计算摩擦系数和局部阻力系数。
实验结果与分析:通过实验数据绘制~Re曲线和局部阻力系数曲线,与理论公式进行比较,验证了流体流动阻力实验原理的正确性。
2. 精馏实验实验目的:1. 熟悉精馏的工艺流程,掌握精馏实验的操作方法。
2. 了解板式塔的结构,观察塔板上汽-液接触状况。
3. 测定全回流时的全塔效率及单板效率。
4. 测定部分回流时的全塔效率。
5. 测定全塔的浓度分布。
6. 测定塔釜再沸器的沸腾给热系数。
实验原理:精馏是利用混合物中各组分沸点不同,通过加热使混合物汽化,然后冷凝分离各组分的方法。
精馏塔是精馏操作的核心设备,其结构对精馏效率有很大影响。
实验步骤:1. 将混合物加入精馏塔,开启加热器,调节回流比。
2. 记录塔顶、塔釜及各层塔板的液相和气相温度、压力、流量等数据。
3. 根据数据计算理论塔板数、全塔效率、单板效率等指标。
4. 绘制浓度分布曲线。
实验结果与分析:通过实验数据,计算出了理论塔板数、全塔效率、单板效率等指标,并与理论值进行了比较。
最新正交实验报告

最新正交实验报告实验目的:本实验旨在通过正交实验方法,优化产品生产过程中的关键参数,以达到提高产品质量和生产效率的目的。
实验材料:1. 生产原料A、B、C2. 生产设备D型机3. 测量工具E实验设计:根据前期研究和生产经验,选取影响产品质量和效率的四个主要因素:原料A的添加量、原料B的添加温度、原料C的混合时间和设备D的运行速度。
每个因素设定三个水平,形成L9(3^4)正交表进行实验设计。
实验过程:1. 按照正交表的安排,对每个实验组进行相应的参数设置。
2. 每个实验组的生产过程进行三次重复,以减少随机误差。
3. 生产后对产品进行质量检测,记录数据。
实验结果与分析:通过对9组实验的数据进行分析,发现原料A的添加量对产品质量影响最大,其次是原料B的添加温度,原料C的混合时间和设备D的运行速度影响相对较小。
通过方差分析确定各因素的显著性水平,并据此调整最佳参数组合。
最佳参数组合推荐:1. 原料A的添加量:水平22. 原料B的添加温度:水平33. 原料C的混合时间:水平14. 设备D的运行速度:水平2结论:根据正交实验结果,推荐采用上述最佳参数组合进行生产,预期能够显著提升产品质量和生产效率。
建议在实际生产中进一步验证该参数组合的效果,并根据实际情况进行微调优化。
建议:1. 对推荐的参数组合进行小规模的生产验证。
2. 持续监控生产过程和产品质量,以便及时发现并解决可能出现的问题。
3. 考虑其他可能影响生产的因素,如环境温度、湿度等,并在必要时纳入后续的正交实验中。
正交试验2012
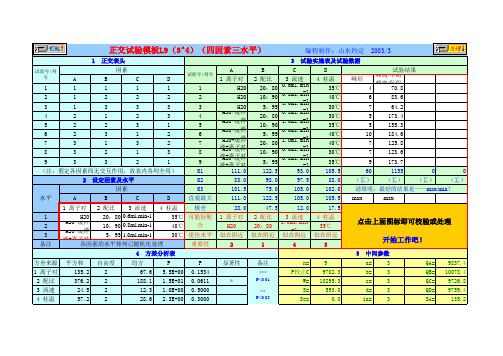
H2O+缓冲液+离子对 3 5:95 1.0ml.min-1 各因素的水平排列已随机化处理 备注 4 方差来源 1 离子对 2 配比 3 流速 4 柱温 平方和 135.2 376.2 24.5 57.2 自由度 2 2 2 2 均方 67.6 188.1 12.3 28.6 F
30℃ 更佳水平 重要性 P 0.1534 0.0611 0.5000 0.3000
93.0 97.5 105.0 105.0 12.0 3 流速 似在附近 4
(∑) (∑) (∑) (∑) 请填明:最好的结果是——max/min? max max
直观最大 极差 可能好配合
20:80 1.0ml.min-1
点击上面图标即可校验或处理 开始工作吧!
中间参数 a= b= c= d= ia= 3 3 3 3 3 QA= QB= QC= QD= SA= 9837.4 10078.4 9726.8 9759.4 135.2
1 2 3 4 5 6 7 8
1 2 3 4 5 6
20:80 0.6ml.min-1 10:90 0.8ml.min-1 5:95 1.0ml.min-1 20:80 0.8ml.min-1 10:90 1.0ml.min-1 5:95 0.6ml.min-1 20:80 1.0ml.min-1 10:90 0.6ml.min-1 5:95 0.8ml.min-1 122.5 98.0 75.0 122.5 47.5 2 配比 似在附近 1 备注
正交试验模板L9(3^4)(四因素三水平)
1
试验号\列号
编程制作:山水约定
3 试验实施表及试验数据 D 4 柱温 35℃ 40℃ 30℃ 30℃ 35℃ 40℃ 40℃ 30℃ 35℃ 105.5 88.0 102.0 105.5 17.5 4 柱温 35℃ 似在附近 3 5 n= P校正C W= S= Se= 9 9702.3 10295.3 593.0 0.0 C 3 流速
化工原理实验报告【范本模板】

实验一 伯努利实验一、实验目的1、熟悉流体流动中各种能量和压头的概念及相互转化关系,加深对柏努利方程式的理解。
2、观察各项能量(或压头)随流速的变化规律。
二、实验原理1、不可压缩流体在管内作稳定流动时,由于管路条件(如位置高低、管径大小等)的变化,会引起流动过程中三种机械能——位能、动能、静压能的相应改变及相互转换.对理想流体,在系统内任一截面处,虽然三种能量不一定相等,但能量之和是守恒的(机械能守恒定律)。
2、对于实际流体,由于存在内磨擦,流体在流动中总有一部分机械能随磨擦和碰撞转化为热能而损失。
故而对于实际流体,任意两截面上机械能总和并不相等,两者的差值即为机械损失。
3、以上几种机械能均可用U 型压差计中的液位差来表示,分别称为位压头、动压头、静压头。
当测压直管中的小孔(即测压孔)与水流方向垂直时,测压管内液柱高度(位压头)则为静压头与动压头之和。
任意两截面间位压头、静压头、动压头总和的差值,则为损失压头。
4、柏努利方程式∑+++=+++f h pu gz W e p u gz ρρ2222121122式中:1Z 、2Z ——各截面间距基准面的距离 (m ) 1u 、2u ——各截面中心点处的平均速度(可通过流量与其截面积求得) (m/s)1P 、2p ——各截面中心点处的静压力(可由U 型压差计的液位差可知) (Pa )对于没有能量损失且无外加功的理想流体,上式可简化为ρρ2222121122p u gz p u gz ++=++ 测出通过管路的流量,即可计算出截面平均流速ν及动压g 22ν,从而可得到各截面测管水头和总水头。
三、实验流程图泵额定流量为10L/min,扬程为8m,输入功率为80W。
实验管:内径15mm。
四、实验操作步骤与注意事项1、熟悉实验设备,分清各测压管与各测压点,毕托管测点的对应关系.2、打开开关供水,使水箱充水,待水箱溢流后,检查泄水阀关闭时所有测压管水面是否齐平,若不平则进行排气调平(开关几次)。
正交实验验证实验报告
正交实验验证实验报告正交实验验证实验报告一、引言正交实验是一种常用的实验设计方法,通过对多个因素的组合进行测试,可以有效地分析因素对结果的影响程度,从而优化产品设计或工艺流程。
本报告旨在通过正交实验验证的方式,对某产品的多个因素进行测试,以确定最佳的因素组合。
二、实验目的本实验旨在通过正交实验验证的方法,确定某产品的最佳因素组合,以提高产品的性能和质量。
具体目标如下:1. 确定影响产品性能的关键因素;2. 通过正交实验验证,确定最佳的因素组合;3. 分析不同因素对产品性能的影响程度。
三、实验设计1. 实验因素本实验选取了三个主要因素进行测试,分别是温度、湿度和时间。
这三个因素对产品的性能有着重要影响,因此需要对其进行详细的测试和分析。
2. 正交实验设计为了有效地测试和分析这三个因素的影响,我们采用了正交实验设计。
通过正交表的设计,将三个因素分别设置为三个水平,以全面覆盖可能的因素组合。
具体的实验设计如下:温度(A):低温(-10℃)、常温(25℃)、高温(40℃)湿度(B):低湿(30% RH)、中湿(60% RH)、高湿(90% RH)时间(C):短时间(10分钟)、中时间(30分钟)、长时间(60分钟)四、实验过程1. 实验设备与材料本实验使用了温湿度控制仪、计时器、测试样品等设备和材料。
2. 实验步骤(1)将温湿度控制仪设置为所需的温度和湿度水平。
(2)将测试样品放置于温湿度控制仪中,确保样品受到相同的环境条件。
(3)根据正交实验设计,依次设置不同的因素组合,并记录下每组实验的温度、湿度和时间。
(4)在每组实验结束后,对测试样品进行性能测试,并记录测试结果。
(5)重复以上步骤,直至完成所有实验。
五、实验结果与分析1. 实验结果通过对所有实验数据的整理和分析,得到了各个因素对产品性能的影响结果。
具体的实验结果如下所示:温度(A)湿度(B)时间(C)性能指标-10℃ 30% RH 10分钟优秀-10℃ 60% RH 30分钟良好-10℃ 90% RH 60分钟一般25℃ 30% RH 30分钟良好25℃ 60% RH 60分钟一般25℃ 90% RH 10分钟优秀40℃ 30% RH 60分钟一般40℃ 60% RH 10分钟优秀40℃ 90% RH 30分钟良好2. 分析与讨论通过对实验结果的分析,可以得出以下结论:(1)温度对产品性能有着显著影响。
正交实验设计及结果分析报告
正交试验设计对于单因素或两因素试验,因其因素少,试验的设计、实施与分析都比较简单。
但在实际工作中,常常需要同时考察3个或3个以上的试验因素,若进行全面试验,则试验的规模将很大,往往因试验条件的限制而难于实施。
正交试验设计就是安排多因素试验、寻求最优水平组合的一种高效率试验设计方法。
1 正交试验设计的概念及原理1.1 正交试验设计的基本概念正交试验设计是利用正交表来安排与分析多因素试验的一种设计方法。
它是由试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验的,通过对这部分试验结果的分析了解全面试验的情况,找出最优的水平组合。
例如:设计一个三因素、3水平的试验A因素,设A1、A2、A33个水平;B因素,设B1、B2、B33个水平;C因素,设C1、C2、C33个水平,各因素的水平之间全部可能组合有27种。
全面试验:可以分析各因素的效应,交互作用,也可选出最优水平组合。
但全面试验包含的水平组合数较多(图示的27个节点),工作量大,在有些情况下无法完成。
若试验的主要目的是寻求最优水平组合,则可利用正交表来设计安排试验。
全面试验法示意图三因素、三水平全面试验方案正交试验设计的基本特点是:用部分试验来代替全面试验,通过对部分试验结果的分析,了解全面试验的情况。
正因为正交试验是用部分试验来代替全面试验的,它不可能像全面试验那样对各因素效应、交互作用一一分析;当交互作用存在时,有可能出现交互作用的混杂。
虽然正交试验设计有上述不足,但它能通过部分试验找到最优水平组合,因而很受实际工作者青睐。
如对于上述3因素3水平试验,若不考虑交互作用,可利用正交表L9(34)安排,试验方案仅包含9个水平组合,就能反映试验方案包含27个水平组合的全面试验的情况,找出最佳的生产条件。
1.2 正交试验设计的基本原理正交设计就是从选优区全面试验点(水平组合)中挑选出有代表性的部分试验点(水平组合)来进行试验。
上图中标有试验号的九个“(·)”,就是利用正交表L9(34)从27个试验点中挑选出来的9个试验点。
正交实验报告
《实验设计与分析》课程作业——正交试验报告学院机电工程学院专业机械工程年级班级 2013级(1)班学号 211301014 学生姓名罗志强任课教师郭钟宁2014年 9 月一、实验基本原理与方法1.1正交试验设计的基本概念正交试验设计是利用正交表来安排与分析多因素试验的一种设计方法。
它是由试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验的,通过对这部分试验结果的分析了解全面试验的情况,找出最优的水平组合。
正交试验设计的基本特点是:用部分试验来代替全面试验,通过对部分试验结果的分析,了解全面试验的情况。
1.2正交表正交表是利用“均衡搭配”与“整齐可比”这两条基本原理,从大量的全面实验方案(点)中,为挑选出少量具有代表性的试验点,所制成的排列整齐的规格化表格。
正交表用 L为正交表的代号,n为试验的次数,t为水平数,c为列数,也就是可能安排最多的因素个数。
正交表的基本性质为:(1)正交性:任一列中,各水平都出现,而且出现次数相等;任两列之间各种不同水平的所有可能组合都出现,且对出现的次数相等。
(2)代表性:任一列的各水平都出现,使得部分试验中包括了所有因素的所有水平;任两列的所有水平组合都出现,使任意两因素间的试验组合为全面试验。
(3)综合可比性:任一列的各水平出现的次数相等;任两列间所有水平组合出现次数相等,使得任一因素各水平的试验条件相同。
这就保证了在每列因素各水平的效果中,最大限度地排除了其他因素的干扰。
从而可以综合比较该因素不同水平对试验指标的影响情况。
1.3正交试验的结果分析1、直观分析法-极差分析法:计算简便,直观,简单易懂,是正交试验结果分析最常用方法。
2、正交试验结果的方差分析:方差分析基本思想是将数据的总变异分解成因素引起的变异和误差引起的变异两部分,构造F统计量,作F检验,即可判断因素作用是否显著。
二、实验内容及要求本试验数据为本人实验所得,运用正交试验来分析335nm激光对钛酸锶陶瓷的划切工艺,并通过共聚焦三维显微镜来对切槽进行观测与测量。
正交实验报告模板
竭诚为您提供优质文档/双击可除正交实验报告模板篇一:正交实验设计及结果分析正交试验设计对于单因素或两因素试验,因其因素少,试验的设计、实施与分析都比较简单。
但在实际工作中,常常需要同时考察3个或3个以上的试验因素,若进行全面试验,则试验的规模将很大,往往因试验条件的限制而难于实施。
正交试验设计就是安排多因素试验、寻求最优水平组合的一种高效率试验设计方法。
1正交试验设计的概念及原理1.1正交试验设计的基本概念正交试验设计是利用正交表来安排与分析多因素试验的一种设计方法。
它是由试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验的,通过对这部分试验结果的分析了解全面试验的情况,找出最优的水平组合。
例如:设计一个三因素、3水平的试验A因素,设A1、A2、A33个水平;b因素,设b1、b2、b33个水平;c因素,设c1、c2、c33个水平,各因素的水平之间全部可能组合有27种。
全面试验:可以分析各因素的效应,交互作用,也可选出最优水平组合。
但全面试验包含的水平组合数较多(图示的27个节点),工作量大,在有些情况下无法完成。
若试验的主要目的是寻求最优水平组合,则可利用正交表来设计安排试验。
全面试验法示意图三因素、三水平全面试验方案正交试验设计的基本特点是:用部分试验来代替全面试验,通过对部分试验结果的分析,了解全面试验的情况。
正因为正交试验是用部分试验来代替全面试验的,它不可能像全面试验那样对各因素效应、交互作用一一分析;当交互作用存在时,有可能出现交互作用的混杂。
虽然正交试验设计有上述不足,但它能通过部分试验找到最优水平组合,因而很受实际工作者青睐。
如对于上述3因素3水平试验,若不考虑交互作用,可利用正交表L9(34)安排,试验方案仅包含9个水平组合,就能反映试验方案包含27个水平组合的全面试验的情况,找出最佳的生产条件。
1.2正交试验设计的基本原理正交设计就是从选优区全面试验点(水平组合)中挑选出有代表性的部分试验点(水平组合)来进行试验。
