第5讲 系统方框图
第5讲 系统方框图
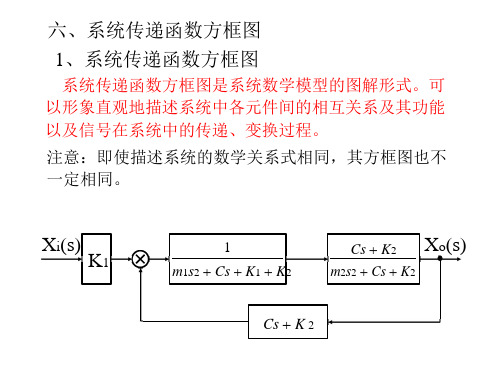
六、系统传递函数方框图1、系统传递函数方框图系统传递函数方框图是系统数学模型的图解形式。
可以形象直观地描述系统中各元件间的相互关系及其功能以及信号在系统中的传递、变换过程。
注意:即使描述系统的数学关系式相同,其方框图也不一定相同。
X i(s)K1 1m1s2 + Cs + K1 + K2Cs + K2m2s2 + Cs + K2X o(s)Cs + K 2方框图的结构要素 信号线带有箭头的直线,箭头表示信号的传 递方向,直线旁标记信号的时间函数 或象函数。
X (s ),x (t )信号线信号引出点(线)表示信号引出或测量的位置和传递方向。
同一信号线上引出的信号,其性质、大小完全一样。
X (s )X (s )X (s )X (s )X (s )X (s )引出线函数方框(环节)X1(s) G(s) X2(s) 传递函数的图解表示。
函数方框函数方框具有运算功能,即:X2(s)=G(s)X1(s)求和点(比较点、综合点)信号之间代数加减运算的图解。
用符号“ ”及相应的信号箭头表示,每个箭头前方的“+”或“-”表示加上此信号或减去此信号。
±X 1(s )X 1(s )±X 2(s )相邻求和点可以互换、合并、 分解,即满足代数运算的交换律、结合律和分配律。
B AA -BA -B+CCAB AA -B+CA+CA+C -B +CC 求和点可以有多个输入,但输出是唯一的。
任何系统都可以由信号线、函数方框、信号 引出点及求和点组成的方框图来表示。
函数方框函数方框U i (s )求和点U (s )1 RI (s )1Cs引出线U o (s )方框图示例系统方框图的建立步骤建立系统各元部件的微分方程,明确信号的因果关系(输入/输出)。
对上述微分方程进行拉氏变换,绘制各部件的方框图。
按照信号在系统中的传递、变换过程,依次将各部件的方框图连接起来,得到系统的方框图。
+ i(t)dt u o (t) =U o (s) =[U i o (s)] I (s) = (s) U U o (s) =示例无源RC网络RRi(t ) = u i (t ) u o (t )1C拉氏变换得:u i(t)Ci(t)无源RC电路网络u o(t)RI (s) = U i (s) U o (s)1I (s)Cs 1R1CsI (s)从而可得系统各方框单元及其方框图。
2.3系统的方框图及其简化
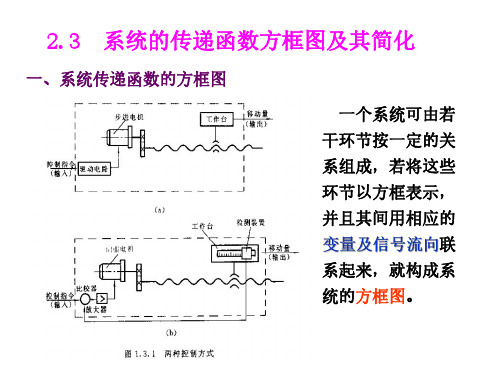
例:求系统传递函数。
Xi(s) + E(+s)
分
+
支
B(s)
点
前
移 Xi(s) + E(+s)
+
B(s)
G1 +
H2
G2
G3
H1
H2G3
G1 +
G2
G3
H1
Xo(s) Xo(s)
Xi(s) + E(+s)
+
B(s)
G1 +
H2G3 G2
H1
Xo(s) G3
Xi(s) + E(+s) G1
+
B(s)
纲也要相同。 相加点可以有多个输入,
但输出是唯一的。
C
A + A-B+C +
B
(3) 分支点
分支点表示同一信号向不同方向的传递。只传递信号, 不传递能量。
在分支点引出的信号不仅量纲相同,而且数值也相 等。
X(s) X(s) X(s)
2、系统方框图的建立步骤
(1) 建立系统(或元件)的
;
(2) 对这些原始微分方程进行
函数无量纲,而且H(s)的量纲是G(s)的量纲的倒数。
小小总结:
前述三种基本连接形式:串联、并联、反馈
G(s)
①两个环 Xi(s)
节相串联
G1(Gs) 1 ( sX)1G(s)2 (Gs)2(s)
Xo(s)
②两个环节 G(s)
相并联
G1(s) Xo1(s)
Xi(s)
G1(s)
G2
+
(s) +_
G2 (s) Xo2(s)
控制系统方块图 ppt课件

•方块图的绘制 •方块图的化简
PPT课件
1
引言
• 求系统的传递函数时,需要对微分方程组或 经拉氏变换后的代数方程组进行消元。而采 用结构图,更便于求取系统的传递函数,还 能直观地表明输入信号以及各中间变量在系 统中的传递过程。因此,结构图作为一种数 学模型,在控制理论中得到了广泛的应用。
G1 ( s)
R1 R2C1C2 s 2
1 (R1C1
R2C2
R1C2 )s
1
G2 (s)
1 R1C1s 1
1 R2C2s 1
1
R1R2C1C2s2 (R1C1 R2C2 )s 1
G1(s)中的 R1C2s 项是由负载效应产生的,因此不能按照 两个RC网络串联来处理,若需要按串联使用,需在两级
C(s) G(s)E(s) B(s) H (s)C(s) E(s) R(s) B(s)
消去E(s)和B(s),得:
C(s) G(s)[R(s) H (s)C(s)] [1 G(s)H(s)]C(s) G(s)R(s)
C(s) R(s)
GB
(s)
1
G(s) G(s)H
综合点后移
PPT课件
16
(2) 综合点之间的移动 下图为相邻两个综合点前后移动的等效变换。
挪动前,总输出信号 : 挪动后,总输出信号 :
可以互换
CR X Y
CRY X
PPT课件
17
(3) 引出点前后移 在图中给出了引出点后移的等效变换。
挪动后的支路上的信号为:
R 1 G(s)R R G(s)
PPT课件
高考生物一轮复习第5讲 细胞器与生物膜系统课件

叶绿体 椭球形、球形
成分
内膜:与有氧呼吸有关的酶 类囊体薄膜:①与光反应有关
基质:①与有氧呼吸有关的 的酶;②叶绿素和类胡萝卜素
酶;
基质:①与暗反应有关的酶;
②少量DNA和RNA
②少量DNA和RNA
增大膜面积方式 内膜向内凹陷形成嵴 囊状结构堆叠形成基粒
功能
有氧呼吸的主要场所 光合作用的场所
共同点
合作用进行的酶
正常生理状态下,溶酶体不会分解细胞自身结构
④
:将多肽再加工为成熟的蛋白质,并以囊泡的方式运输到细胞
膜。
具有该标志的蛋白质能被高尔基体膜上的M6
P受体识别,经高尔基体膜包裹形成囊泡,在囊泡逐渐转化为溶酶体的过程中,
带有M6P标志的蛋白质转化为溶酶体酶;不能发生此识别过程的蛋白质经囊
泡运往细胞膜。
2.归类比较各种细胞器
[提醒] (1)真核细胞中的核糖体有两类:附着核糖体主要合成分泌蛋白(如抗 体等);游离核糖体主要合成细胞自身所需要的蛋白质。 (2)内质网有两类:粗面内质网与分泌蛋白的合成、加工、运输有关;滑面内 质网与脂质(如某些激素)的合成有关。 (3)动物细胞内的高尔基体与分泌物的形成有关,是各种膜成分相互转化中的 “枢纽”。植物细胞内的高尔基体与细胞壁的形成有关。 (4)液泡中的色素是花青素,与花和果实的颜色有关;叶绿体中的色素是叶绿 素等,与光合作用有关。
解析 有氧呼吸的第二阶段在线粒体基质中进行,可产生[H],但不会发 生[H]的还原反应,[H]的还原反应发生在有氧呼吸的第三阶段,在线粒体内膜 上进行,A错误;在低等植物细胞的有丝分裂过程中,中心体在前期参与纺锤体 的形成,核糖体在间期参与蛋白质合成,B正确;溶酶体内含有多种水解酶,能 分解衰老、损伤的细胞器,吞噬并杀死侵入细胞的病毒或病菌,被溶酶体分解 后的产物如氨基酸、核苷酸等对细胞有用的物质,细胞可以再利用,C正确;液 泡主要存在于植物细胞中且细胞液具有一定的浓度,D正确。
第5讲 制造执行系统(MES)

质
量
管
理
数
据
采
集
数
据
接
口
昆明理工大学工业工程系 余开朝 2010
《制造业管理信息化》讲义
第五讲 制造执行系统(MES)
二、 MES的功能
3. MES 的功能简介
理
数
据
采
集
数
据
接
口
昆明理工大学工业工程系 余开朝 2010
《制造业管理信息化》讲义
第五讲 制造执行系统(MES)
二、 MES的功能
3. MES 的功能简介
工序详细调度
资源分配和状态管理
生产单元分配
文
档
控
制
产品跟踪和产品清单管理
通过监视工件在任意时刻的位置 和状态来获取每一个产品的历史纪录, 该记录向用户提供产品组及每个最终 产品使用情况的可追溯性。
人力资源管理
过
程
管
理
质
量
管
理
数
据
采
集
数
据
接
口
昆明理工大学工业工程系 余开朝 2010
《制造业管理信息化》讲义
第五讲 制造执行系统(MES)
二、 MES的功能
3. MES 的功能简介
工序详细调度
资源分配和状态管理
生产单元分配
文
档
控
制
产品跟踪和产品清单管理
提供按分钟级更新的员工状态信 息数据(工时,出勤等),基于人员 资历,工作模式,业务需求的变化来 指导人员的工作。
信号与系统 系统框图ppt课件

+
2/s 2/(8+s) +
Y(s)
-4X1(s)
+
1/s
-2X2(s)=-2Y(s)+2X1(s)
第四步:按信息流向从左向右写出输出与输入之间的函数关
系式。
X1(s)+[ 1-2X2(s)](1/s)=Y(s)
将X1(s)=2/(8+s)代入:
得到 Y(s)=
3s 12 s2 10s 16
15
总结
7
Mason公式
Mason公式为
M
H (s)
Y (s)
Pk (s)k (s)
k 1
X (s)
(s)
其中
H (s) (s) Pk (s) k (s)
从输入节点到输出节点之间的系统函数
特征式 (s) 1 Li Li Lj Li Lj Lk L
从输入节点到输出节点的第k条前向通路增益
在(s) 中,将与第k条前向通路相接触
通过设系统输入函数X(S)=1,求输出的单位脉冲响应的 拉普拉斯变换而确定系统函数的方法,称为脉冲响应法。
9
1 + ×+ ×
_+
H2Y(S)
_
H2
G1
+
×
X1(s)
G2
×
×
G3
Y(S)
×
H1
H1X1(s)
Y(S)
1.将反馈环节于信号引出点处切断,并且在引出点处用某变量标明。 2.将反馈环挪开,但在比较器(加法器)的输入端保留反馈信号,并且将各反馈信号 用引出点处信号与反馈通道传递函数之乘积表示。
5.求输出函数的拉氏变换形式:
Y(S) =
系统方框图和系统传递函数市公开课获奖课件省名师示范课获奖课件

C(s)
H3(s)
H1(s)
例2 (解题措施一之环节2)
R(s) 1
G1 ( s )
-
G2 ( s )
3
-
-2
H1(s)
?
G3 ( s ) H3(s)
C(s)
G4 ( s )
例2 (解题措施一之环节3)
R(s)
1
G1(s)
-
G2 ( s )
3
G2 ( s) H 2 ( s )
-
-2
G3 ( s )
G(s)
C(s) G(s)
引出点之间旳移动
B R(s) A
B
R(s)
A
引出点之间旳移动
B R(s) A
B
R(s)
A
相邻引出点互换位置,不变化信号旳性质。
五 举例阐明(例1)
例1:利用构造图变换法,求位置随动系 统旳传递函数Qc(s)/Qr(s) 。
r
Ks
Ka
-
1
-
Ra
ML
-
1
Cm
Js2 fs
C(s)
1 G2 (s)G3 (s)H2 (s) G3G4 H3 G1G2G3G4 H1
引出点后移等效变换图
R(s)
C(s)
G(s)
R(s)
R(s)
G(s)
C(s)
R(s) 1/G(s)
引出点前移
R(s)
C(s)
G(s)
C(s)
R(s)
C(s)
G(s)
?
C(s)
问题: 要保持原来旳信号传递关系不变, ?等于什么。
引出点前移等效变换 图
R(s)
C(s)
系统方框图及系统传递函数分解课件

系统传递函数对方框图的影响
系统传递函数决定了系统的动态特性,通过调整传递 函数可以改变系统的性能。
传递函数的数学表达式可以转化为方框图,通过对方 框图的调整可以实现传递函数的优化,进而改善系统 性能。
04
系统方框图的分解
方框图分解的方法与步骤
简化系统分析
对于复杂系统,方框图能够简化 分析过程,方便进行系统性能分 析和优化。
指导控制器设计
根据系统方框图,可以设计合适 的控制器,实现系统对特定性能 指标的优化。
传递函数在控制系统分析中的应用
数学建模基础
传递函数是控制系统数学建模的基本工具,用于描述系统的动态 行为。
稳定性分析
通过分析传递函数的极点和零点,可以判断系统的稳定性。
03
系统方框图与系统传递 函数的关系
方框图与传递函数的关系
方框图是系统传递函数的图形表示, 通过方框图可以直观地了解系统内部 各环节的信号传递关系。
传递函数是描述系统动态特性的数学 模型,通过传递函数可以计算系统的 频率响应、稳定性等性能指标。
系统方框图对系统性能的影响
系统方框图反映了系统的结构组成和信号传递关系,通过分析方框图可以了解系统性能的优劣。
控制系统分析
通过传递函数分解,分析控制系统的稳定 性、动态性能和稳态性能,为控制系统的
优化提供依据。
控制系统校正
通过传递函数分解,对控制系统的开环传 递函数进行修改,以改善控制系统的性能 指标。
06
系统方框图与系统传递函 数在控制系统中的应用
方框图在控制系统设计中的应用
描述系统动态特性
通过方框图可以直观地表示系统 的动态过程,明确各环节的输入 和输出关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[
FK1(s) Fi(s)
⊗
FC(s)
1 X(s) m1 s 2
X(s)
⊗
K1 Cs
FK1(s) FC(s)
Xo(s)
1 X ( s) = Fi (s) − FC (s) − FK1 (s) 2 m1s
[
]
FK1 ( s ) = K1 [X ( s ) − X o ( s )]
(b)
FC ( s ) = Cs[X ( s ) − X o ( s )]
FK2(s) FK1(s)
K1 Cs
K2
⊗
FC(s)
1 X(s) m1s 2
⊗
Xo(s
)
⊗ ⊗
FC(s)
+
1 m2 s 2
Xo(s)
机械系统方框图
系统方框图的简化 方框图的运算法则 串联连接(传递函数相乘)
Xi(s)
G1(s)
X1(s)
G2(s)
X2(s) ...Xn-1(s) Gn(s)
Xo(s)
m2 K2 m1 xi(t) K1 C
xo(t)
x(t)
简化的悬挂系统(垂直方向单轮模型)
(a)
FK2(s
)
FK1(s)
⊗ ⊗
+
FC(s)
1 2 m2 s
Xo(s)
Xo(s)
K2
FK2(s)
1 X o (s) = FK1 ( s ) + FC ( s ) − FK 2 ( s ) 2 m2 s (c)
[
]
FK 2 ( s ) = K 2 X o ( s )
(d)
FK1(s) Fi(s)
Cs + K2
Xo(s)
m2s2 + Cs + K2
Cs + K 2
方框图的结构要素 信号线
带有箭头的直线,箭头表示信号的传 递方向,直线旁标记信号的时间函数 或象函数。
X(s), x(t)
信号线
信号引出点(线)
表示信号引出或测量的位置和传递方向。 同一信号线上引出的信号,其性质、大小完全一样。 X(s) X(s)
示例 无源RC网络
Ri (t ) = ui (t ) − uo (t )
ui(t)
R
C i(t)
1 uo (t ) = ∫ i (t )dt C
拉氏变换得:
RI ( s ) = U i ( s ) − U o ( s ) 1 Uo ( s) = I ( s) Cs
uo(t)
无源RC电路网络
1 I ( s ) = [U i ( s ) − U o ( s )] R 1 U o ( s) = I ( s) Cs
函数方框 函数方框
Ui(s)求和点U(s)
⊗
1 R
I(s)
1 Cs
引出线 Uo(s)
方框图示例
系统方框图的建立 步骤 建立系统各元部件的微分方程,明确信号 的因果关系(输入/输出)。 对上述微分方程进行拉氏变换,绘制各部 件的方框图。 按照信号在系统中的传递、变换过程, 依次将各部件的方框图连接起来,得到系统 的方框图。
Xi(s)
⊗ ⊗
+
G1(s)
G2 ( s ) 1 + G2 ( s )G3 ( s ) H 2 ( s )
G3(s)
Xo(s)
H1(s) H3(s)
3、消去H1(s) 反馈回路
Xi(s)
⊗
G1 ( s)G2 ( s)G3 ( s) 1 − G1 ( s)G2 ( s) H1 ( s) + G2 ( s)G3 ( s) H 2 ( s)
Xo(s)
H3(s)
4、消去H3(s) 反馈回路
Xi(s) Xo(s) G1(s)G2 (s)G3(s) 1− G1(s)G2 (s)H1(s) + G2 (s)G3(s)H2 (s) + G1(s)G2 (s)G3(s)H3(s)
例:系统传递函数方框图简化
求和点 前移
引出点 后移
例:汽车悬挂系统的传递函数
(m s + Cs + K )X (s) = (Cs + K )X (s) (m s + Cs + K + K )X (s) = (Cs + K )X
2 2 2 o 2 2 1 1 2 2
o ( s ) + K1 X i ( s )
Xi(s)
K1
1 m1s2 + Cs + K1 + K2
X(s)
Cs + K2
Xi(s)
G(s)=G1(s)G2(s)···Gn(s)
Xo(s)
并联连接(传递函数相加)
G1(s) + G2(s) . . . Gn(s) +
Xi(s)
+
⊗
Xo(s)
Xi(s)
G1(s)+ G2(s)+⋅ ⋅ ⋅ + Gn(s)
Xo(s)
反馈连接(很重要)
Xi(s)
±
⊗
E(s)
G(s) H(s)
X1(s)
⊗
X1(s)±X2(s) 相邻求和点可以互换、合并、
分解,即满足代数运算的交换 律、结合律和分配律。
B A
±
X2(s)
⊗
A-B
⊗
C
A-B+C
B A
⊗
C
A+C
⊗
A+C-B
A
B
⊗
C
A-B+C A-B +C
求和点可以有多个输入,但输出是唯一的。
任何系统都可以由信号线、函数方框、信号 引出点及求和点组成的方框图来表示。
X(s)
X(s)
引出线
X(s)
X(s)
函数方框(环节) 传递函数的图解表示。
X1(s)
G(s)
函数方框
X2(s)
函数方框具有运算功能,即:
X2(s)=G(s)X1(s)
求和点(比较点、综合点) 信号之间代数加减运算的图解。用符号“⊗” 及相应的信号箭头表示,每个箭头前方的 “+”或“-”表示加上此信号或减去此信号。
从而可得系统各方框单元及其方框图。 1 Ui(s) Ui-Uo I(s) I(s) 1 Uo(s) ⊗ R Cs
Uo(s)
(a) I ( s ) =
1 [U i ( s ) − U o ( s ) ] R
(b)U o (s) =
1 I ( s) Cs
Ui(s)
⊗
U(s) 1 R
I(s)
1 Cs
Uo(s)
Xo(s)
m2s2 + Cs + K2
Cs + K 2
X o ( s) K1 (Cs + K 2 ) = X i ( s ) m1m2 s 4 + (m1 + m2 )Cs 3 + [K1m2 + (m1 + m2 ) K 2 ]s 2 + K1Cs + K1K 2
作业:用解析法求简化汽车悬挂系统(垂直方向) 的传递函数,并作出该系统的方框图。
六、系统传递函数方框图 1、系统传递函数方框图
系统传递函数方框图是系统数学模型的图解形式。可 以形象直观地描述系统中各元件间的相互关系及其功能 以及信号在系统中的传递、变换过程。 注意:即使描述系统的数学关系式相同,其方框图也不 一定相同。
Xi(s)
K1
1 m1s 2 + Cs + K1 + K2
X(s)
分别做拉氏变换,有:
FC ( s ) = Cs[X ( s ) − X o ( s )]
FK1 ( s ) = K1 [X ( s ) − X o ( s )]
1 X (s) = Fi ( s ) − FC ( s ) − FK1 ( s ) 2 m1s
[
] ]
1 X o (s) = FK1 ( s ) + FC ( s ) − FK 2 ( s ) 2 m2 s FK 2 ( s ) = K 2 X o ( s )
Xo(s)
方框图的等效变换法则 求和点的移动
A
⊗ ±
B
G(s)
C
A
G(
A B
G(s) G(s) 求和点后移
⊗
C
A
⊗
G(s)
1 G (s)
C B
±
±
求和点前移
引出点的移动
A
G(s)
C C
A
G(s)
C A
A
G(s) G(s) 引出点前移
C C
A
G(s)
C
1 A G (s)
引出点后移
一般系统方框图简化方法: 1)明确系统的输入和输出。对于多输入多输出系 统,针对每个输入及其引起的输出分别进行化简; 2)若系统传递函数方框图内无交叉回路,则根据 环节串联,并联和反馈连接的等效运算法则从里 到外进行简化; 3)若系统传递函数方框图内有交叉回路,则根据 相加点、分支点等移动规则消除交叉回路,然后 按每2)步进行化简; 注意:分支点和相加点之间不能相互移动。
车体 质心 当汽车行驶时,轮胎 的垂直位移作用于汽 车架 车悬挂系统上,系统 的运动由质心的平移 运动和围绕质心的旋 转运动组成。 汽车悬挂系统(垂直方向)
m2 K2 m1 xi(t) K1 C
xo(t)
x(t)
简化的悬挂系统(垂直方向单轮模型)
′′ ′ m2 xo (t ) = − K 2 [xo (t ) − x(t )] − C [xo (t ) − x′(t )] ′ m1 x′′(t ) = K 2 [xo (t ) − x(t )] + C [xo (t ) − x′(t )] + K1[xi (t ) − x(t )]
