匀变速直线运动的四个基本公式
匀变速直线运动总结

2.2 匀变速直线运动的一、匀变速直线运动1、定义:在变速直线运动中,如果在任意相等的时间内速度的改变相等,即加速度不变的运动。
2、v-t图象是一条倾斜直线3、匀加速直线运动:速度随时间均匀增加匀减速直线运动:速度随时间均匀减小二、速度与时间的关系式:1、v=v0+at只适用于匀变速直线运动速度.v-t图的斜率=a.2、通常取初速度v0方向为正方向,加速度a可正可负(正、负表示方向),在匀变速直线运动中a恒定.(1)当a与v0同方向时,a>0表明物体的速度随时间均匀增加,如下图.(2)当a与v0反方向时,a<0表明物体的速度随时间均匀减少,如下图3、速度公式是矢量式: v=v0+at (矢量式)注意:在具体运算中必须规定正方向来简化一直线上的矢量运算。
若初速度v0=0,则v=at三、v-t图1、v-t图象中一条倾斜直线表示匀变速直线运动,若是一条曲线则表示非匀变速直线运动。
2、若是曲线,则某点切线的斜率表示该时刻的加速度。
2.3匀变速直线运动的位移与时间的关系一、匀速直线运动的位移公式法:x=vt图像法:结论:匀速直线运动的位移等于v – t 图线与t 轴所夹的矩形“面积”面积也有正负,面积为正,表示位移的方向为正方向,面积为负值,表示位移的方向为负方向.匀变速直线运动的位移也可用图线与坐标轴所围的面积表示。
二、匀变速直线运动的位移1.位移公式:2.对位移公式的理解:⑴反映了位移随时间的变化规律。
⑵因为υ0、α、x 均为矢量,使用公式时应先规定正方向。
(一般以υ0的方向为正方向)若物体做匀加速运动,a 取正值,若物体做匀减速运动,则a 取负值. (3)若v 0=0,则x=(4)特别提醒:t 是指物体运动的实际时间,要将位移与发生这段位移的时间对应起来.2012x v t at=+221t 0v at x +=(5)代入数据时,各物理量的单位要统一.(用国际单位制中的主单位) 二.匀变速直线运动重要推论1.任意两个连续相等的时间间隔T 内的位移之差是一个恒量, s 2-s 1=s 3-s 2=… 即Δs=aT 22.在一段时间t 内,中间时刻的瞬时速度v 等于这段时间的平均速度3.一段时间t 内的平均速度等于这段时间的初、末速度的算术平均值3.位移与加速度、速度的关系2.4 匀变速直线运动的位移与速度的关系 匀变速直线运动位移与速度的关系:速度公式: v =v 0+at 和位移公式两式消去t,得(不涉及到时间t ,用这个公式方便)一、匀变速直线运动的规律(4基本公式) 1、速度公式:v =v 0+at2、位移公式:3、平均速度:4、位移与速度关系:匀变速直线运动的推论(3推论)ax v v 2202=-ax v v 222=-2tvv v +=txv v v =+=)(2101、中间时刻的瞬时速度:2>3、任意连续相等时间内的位移差相等:通式22ttv v xv vt+===232BDCx xv vT+==23123424BD AECx x x x x xv v vT T++++====2sv2tv2)(aTnmssnm-=-tvvt vx t2+==(5)代入数据计算时不用代单位,但最后结果要有单位,且运算过程需把其它单位转化成国际单位。
匀变速直线运动公式总结

匀变速直线运动公式1.瞬时速度与时间的关系:atv v t +=02.位移与时间的关系: 2021at t v x += 3.瞬时速度与位移的关系:axv v t 2202+=4.位移与初、末速度和时间的关系: t v v x t )(210+= 5.平均速度与初、末速度的关系:)(210t v v v +=6.平均速度与这段时间中间时刻的瞬时速度的关系:01()2t v v v v ==+中间时刻7.一段位移中点位置的瞬时速度与初、末速度的关系:v v ==中点位置8.在相邻、相等时间内,位移之差的关系:相等21321n n x x x x x x -∆-∆=∆-∆==∆-∆9.在相邻、相等时间(T )内,位移的差值与加速度和每一个时间间隔(T )的关系: 221321n n x x x x x x aT -∆-∆=∆-∆==∆-∆=10.在相隔、相等时间(T )内,位移的差值与加速度和时间间隔(T )的关系: 21)1()(aT n x x x n -=∆-∆=∆∆11.在初速度为零的匀加速运动中,第1秒内、第2秒内、第3秒内、┅┅┅第n 秒内的位移之比(平均速度之比)是:1:3:5:┅┅┅:(2n -1)12.在初速度为零的匀加速运动中,前1秒内、前2秒内、前3秒内、┅┅┅前n 秒内的位移之比(平均速度之比)是1:4:9:┅┅┅:(n 2)13.在初速度为零的匀加速运动中,头1个x 米、头2个x 米、头3个x 米、┅┅┅头n 个x 米内所用时间之比(速度改变量之比)是1::::14.在初速度为零的匀加速运动中,第1个x 米、第2个x 米、第3个x 米、┅┅┅第n 个x 米内所用时间之比(速度改变量之比)是1:1):::---。
高一物理匀变速直线运动规律推论

2
两个连续相等的时间T内的位移之差:
x x2 x1 (v1 v0 )T aT 2
因为T是个恒量,小车加速度也是恒量,因此 △x也是个恒量。 即:只要物体做匀变速直线运动,它在任意两 个连续相等的时间内的位移之差等于一个常数.
匀变速直线运动推论公式:
1、任意两个连续相等时间间隔T内,位移之差 是常数,即△x=x2-x1=aT2。 拓展:△xMN=xM-xN=(M-N)aT2
思考:物体拉动的条件?
(拉力大于最大静摩擦力) 说明:最大静摩擦力大于滑动摩擦力
思考:1只有静止的物体才受到静摩擦力的作用? 2静摩擦力一定是阻力?
二 滑动摩擦力 1定义:两个接触的物体,当一个物体在另一个物 体表面滑动的时候,会受到另一个物体阻碍它滑动 的力
2产生条件:①接触面粗糙②接触并挤压③ 发生相对滑动 3作用点:接触面间
支持力与压力属于弹力
4、绳的弹力:
A A
B
总结:绳的弹力方向总是 沿着绳并指向绳的收缩方向。 绳的弹力处处相等
拉力属于弹力
三、弹力有无判断
方法:撤去支撑物法
FN
假设法+共点力平衡法
FN
F
F
FN FN G FN FN G FNLeabharlann F不平衡G
不平衡
不平衡
四、弹力的大小
弹力的大小与物体 的形变有关,形变越大, 弹力越大,形变消失, 弹力随着消失
探究:探究静摩擦力的变化
器材:木块,砝码一盒,弹簧测力计,木板。
实验结论:静摩擦力随拉力的增大而增大,当拉力 达到某一数值时木块开始移动,拉力突然减小。
补充:静摩擦力是个聪明的力,不但大小随外力而 变化,方向也随外力方向变化而变,且有最大值。 6最大静摩擦力:(在数值上等于物体刚刚开始运动时的拉力) 静摩擦力的范围: 0<F≤Fmax
匀变速直线运动十个基本公式

匀变速直线运动十个基本公式匀变速直线运动是我们在物理学中经常遇到的一种运动形式。
在描述这种运动时,我们常常会用到十个基本公式。
这些公式能够帮助我们计算物体的位移、速度和加速度等关键参数。
下面,我将为大家详细介绍这十个基本公式,并给出一些实际应用的例子。
1. 位移公式:s = v0t + 1/2at^2这个公式用来计算物体的位移,其中s代表位移,v0代表初速度,t代表时间,a代表加速度。
例如,在赛车比赛中,我们可以用这个公式计算出赛车在特定时间内的位移。
2. 速度公式:v = v0 + at这个公式用于计算物体的速度,其中v代表速度,v0代表初速度,t代表时间,a代表加速度。
例如,我们可以用这个公式计算一辆汽车在特定时间内的速度。
3. 加速度公式:a = (v - v0) / t这个公式用于计算物体的加速度,其中a代表加速度,v代表速度,v0代表初速度,t代表时间。
比如,在自行车竞赛中,我们可以使用这个公式计算出车手的加速度。
4. 时间公式:t = (v - v0) / a这个公式可以帮助我们计算物体的运动时间,其中t代表运动时间,v代表速度,v0代表初速度,a代表加速度。
举个例子,当我们知道一个物体的速度、加速度和初速度时,我们可以利用这个公式来计算出物体运动所需的时间。
5. 初速度公式:v0 = v - at这个公式用于计算物体的初速度,其中v0代表初速度,v代表速度,a代表加速度,t代表时间。
比如,在保龄球比赛中,我们可以利用这个公式计算出撞击木瓶之前球的初速度。
6. 加速度时间公式:a = (v - v0) / t这个公式可以用来计算物体的加速度,其中a代表加速度,v代表速度,v0代表初速度,t代表时间。
例如,在火箭发射过程中,我们可以使用这个公式计算出火箭的加速度。
7. 末速度公式:v = v0 + at末速度公式可以用来计算物体的末速度,其中v代表末速度,v0代表初速度,a代表加速度,t代表时间。
匀变速直线运动公式、推论推导、及规律总结
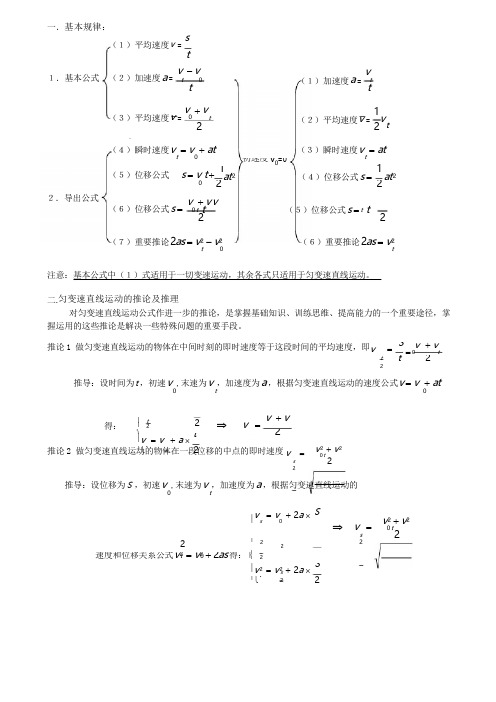
1.基本公式 (2)加速度 a = v - v初速度 v 0=0(5)位移公式 s = v t + 122推论 1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即v= St 2⇒ v = v + v ⎪ t 2 ⎪ 2 ⎨ 2 ⎪v = v + a ⨯ t ⎪⎩ t2 ⎧2速度和位移关系公式 v 2 = v 2 + 2as 得: ⎪ 2⎪v 2 = v 2+ 2 a ⨯ S⎪⎩ t 22一.基本规律:(1)平均速度 v =stvt 0(1)加速度 a = ttt(3)平均速度 v = v 0 +v2t1(2)平均速度 v = v2 t(4)瞬时速度 v = v + at(3)瞬时速度 v = attt1at 2(4)位移公式 s = at 22.导出公式(6)位移公式 s = v + v v0 t t (5)位移公式 s = t t2 2(7)重要推论 2as = v 2 - v 2t(6)重要推论 2as = v 2t注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
t v + v = 0t2推导:设时间为 t ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的速度公式 v = v + at0 t得:推论 2 做匀变速直线运动的物体在一段位移的中点的即时速度v=sv 2 + v 20 t22推导:设位移为 S ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的0 t⎪vs = v 0+ 2 a ⨯2t 0 ⎨ s 2 S⇒ v =s2v 2 + v 20 t2经过第二个时间 t 后的速度为 v =2v +at ,这段时间内的位移为 S = v t + at 2 = v t + at 22 2 经过第三个时间 t 后的速度为 v =3v +at ,这段时间内的位移为 S = v t + at 2 = v t+ at 2 2 2 2 2 3 2 32 2 2 2t推论 3 做匀变速直线运动的物体,如果在连续相等的时间间隔 t 内的位移分别为 S 、 S 、 S …… S123n ,加速度为 a,则 ∆S =S 2- S 1 = S 3 - S 2= …… = S n - S推导:设开始的速度是 vn -1= at2经过第一个时间 t 后的速度为 v = v + a t ,这一段时间内的位移为 S = v t + 1 0 1 0 1 2 at 2,1 32 0 2 1 0 1 52 032…………………经过第 n 个时间 t 后的速度为 v =nv +at ,这段时间内的位移为 S =v t +1 a t 2 =v t + n 0 n n -1 02n -1 2at 2则 ∆S = S 2 - S 1 = S 3 - S 2 = …… = S n - Sn -1= at 2点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度 a 与时间 “有关的恒量”.这也提供了一种加速度的测量的方法: 即 a =∆S,只要测出相邻的相同时间内的位移之差 ∆S 和 t ,就容易测出加速度 a 。
匀变速运动的公式、证明及简单应用

a3 = (x6 – x3 ) / 3 T2
(3T ) 2 ?(m s 2 )
( x4 x5 x6 ) ( x1 x2 x3 )
九、初速为零的匀变速直线运动的特殊规律
①1T末、2T末、3T末……的速度比为1∶2∶3∶4…… 证明:由速度公式得: 1T末的速度v1=aT; 2T末的速度v2=a· 2T=2aT ; 3T末的速度为v3=a· 3T=3aT …… ∴v1∶v2∶v3∶…… =aT∶2aT∶3aT∶…… =1∶2∶3∶……
t1 : t 2 : t3 : 1 : ( 2 1) : ( 3 2 ) :
例题
一物体从五楼楼顶上开始做自由落体运动,已知通过 顶层用时为1s, 估算通过底层的时间。
例题
一物体在足够高的地方做自由落体运动。g=10m/s2 求:
(1)1s末、2s末、3s末、4s末、……的速度。 (2)1s内、2s内、3s内、4s内、……的位移。 (3)第1s内、第2s内、第3s内、第4s内、……的位移。
纸带分析:加速度的求解
A B
x1 x2
C
x3
D
x4
E
x5
F x6
G
逐差法求加速度
Δ x1 = x4 - x1 = 3a1 T2 Δ x2 = x5 – x2 = 3a2 T2 a1 = (x4 - x1 ) / 3 T2 a2 = (x 5 – x2 ) / 3 T2
Δ x3 = x6 – x3 = 3a3 T2
xm xm1 xm1 xm2 xn 2 xn 1 xn 1 xn ( m n) a T 2
例如:5 x1 (5 1)a T 2 4a T 2 x 证明:5 x1 x5 x 4 x 4 x3 x3 x 2 x 2 x1 4a T 2 x
匀变速运动的基本公式

匀变速运动的基本公式1.三个基本公式速度公式:v t=v0+at;位移公式:s=v0t+12at2;位移速度关系式:v t2-v02=2as.2.三个推论(1)连续相等的相邻时间间隔T内的位移差等于恒量,即s2-s1=s3-s2=…=s n-s(n-1)=aT2.(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初末时刻速度矢量和的一半,还等于中间时刻的瞬时速度.平均速度公式:v=v0+v t2=vt2.(3)匀变速直线运动的某段位移中点的瞬时速度v s2=v02+v t22.3.初速度为零的匀加速直线运动的特殊规律(1)在1T末,2T末,3T末,…nT末的瞬时速度之比为v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n.(2)在1T内,2T内,3T内,…,nT内的位移之比为s1∶s2∶s3∶…∶s n=12∶22∶32∶…∶n2.(3)在第1个T内,第2个T内,第3个T内,…,第n个T内的位移之比为sⅠ∶sⅡ∶sⅢ∶…∶s n=1∶3∶5∶…∶(2n-1).(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶t n=1∶(2-1)∶(3-2)∶…∶(n-n-1).(5)从静止开始通过连续相等的位移时的速度之比为v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n.一.匀变速直线运动规律公式的三性(1)条件性:速度公式和位移公式的适应条件必须是物体做匀变速直线运动.(2)矢量性:位移公式和速度公式都是矢量式.(3)可逆性:由于物体运动条件的不同,解题时可进行逆向转换.限时训练1.(2009·江苏单科)图1-2-3如图1-2-3所示,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s就熄灭,此时汽车距离停车线18 m.该车加速时最大加速度大小为2 m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5 m/s.下列说法中正确的有().①如果立即以最大加速度做匀加速运动,在绿灯熄灭前汽车可能通过停车线②如果立即以最大加速度做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速③如果立即以最大加速度做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线④如果距停车线5 m处以最大加速度减速,汽车能停在停车线处A.①②B.③④C.①③D.②④2.(2010·课标全国,24)短跑名将博尔特在北京奥运会上创造了100 m和200 m短跑项目的新世界纪录,他的成绩分别是9.69 s和19.30 s.假定他在100m比赛时从发令到起跑的反应时间是0.15 s,起跑后做匀加速运动,达到最大速率后做匀速运动.200 m比赛时,反应时间及起跑后加速阶段的加速度和加速时间与100 m比赛时相同,但由于弯道和体力等因素的影响,以后的平均速率只有跑100 m时最大速率的96%.求:(1)加速所用时间和达到的最大速率;(2)起跑后做匀加速运动的加速度.(结果保留两位小数)3.(2011·重庆卷,14)某人估测一竖直枯井深度,从井口静止释放一石头并开始计时,经 2 s听到石头落底声.由此可知井深约为(不计声音传播时间,重力加速度g取10 m/s2)().A.10 m B.20 mC.30 m D.40 m4.(2011·安徽卷,16)一物体做匀加速直线运动,通过一段位移Δx所用的时间为t1,紧接着通过下一段位移Δx所用的时间为t2,则物体运动的加速度为().A.2Δx(t1-t2)t1t2(t1+t2)B.Δx(t1-t2)t1t2(t1+t2)C.2Δx(t1+t2)t1t2(t1-t2)D.Δx(t1+t2)t1t2(t1-t2).5.(2011·天津卷)质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位),则该质点().A.第1 s内的位移是5 mB.前2 s内的平均速度是6 m/sC.任意相邻的1s内位移差都是1 mD.任意1 s内的速度增量都是2 m/s答案 1 C 2.(1)1.29S 11.24M/S (2)8.71 3.B 4.A 5.D。
匀变速直线运动公式规律总结

匀变速直线运动公式、规律总结一.基本规律:v =ts 1. 公式 a =t v v t 0- a =tv tv =20t v v + v =t v 21 at v v t +=0 at v t =021at t v s +=221at s = t v v s t 20+= t v s t 2= 2022v v as t -= 22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动..................................。
二.匀变速直线运动的两个重要规律:1.匀变速直线运动中某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:即2t v =v ==t s 20t v v + 2.匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量:设时间间隔为T ,加速度为a ,连续相等的时间间隔内的位移分别为S 1,S 2,S 3,……S N ;则∆S=S 2-S 1=S 3-S 2= …… =S N -S N -1= aT 2注意:设在匀变速直线运动中物体在某段位移中初速度为0v ,末速度为t v ,在位移中点的瞬时速度为2s v ,则中间位置的瞬时速度为2s v =2220t v v + 无论匀加速还是匀减速总有2t v =v =20t v v +<2s v =2220t v v +三.自由落体运动和竖直上抛运动:v=2tvgtvt=s=212gt22tvgs=总结:自由落体运动就是初速度v=0,加速度a=g的匀加速直线运动.gtvvt-=2.竖直上抛运动2021gttvs-=222vvgst-=-总结:竖直上抛运动就是加速度ga-=的匀变速直线运动.四.初速度为零的匀加速直线运动规律:设T为时间单位,则有:(1)1s末、2s末、3s末、……ns末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n同理可得:1T末、2T末、3T末、……nT末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n(2)1s内、2s内、3s内……ns内位移之比为:S1∶S2∶S3∶……:S n=12∶22∶32∶……∶n2同理可得:1T内、2T内、3T内……nT内位移之比为:S1∶S2∶S3∶……:S n=12∶22∶32∶……∶n2(3)第一个1s内,第二个2s内,第三个3s内,……第n个1s内的位移之比为:SⅠ∶SⅡ∶SⅢ∶……:S N=1∶3∶5∶……∶(2n-1)同理可得:第一个T内,第二个T内,第三个T内,……第n个T内的位移之比为:SⅠ∶SⅡ∶SⅢ∶……:S N=1∶3∶5∶……∶(2n-1)(4)通过连续相等的位移所用时间之比为:t1∶t2∶t3∶……:t n=1∶(12-)∶(23-)∶………∶(1--nn)课时4:匀速直线运动、变速直线运动基本概念(例题)一.变速直线运动、平均速度、瞬时速度:例1:一汽车在一直线上沿同一方向运动,第一秒内通过5m,第二秒内通过10m,第三秒内通过20m,第四秒内通过5m,则最初两秒的平均速度是_________m/s,则最后两秒的平均速度是_________m/s,全部时间的平均速度是_________m/s.例2:做变速运动的物体,若前一半时间的平均速度为4m/s,后一半时间的平均速度为8m/s,则全程内的平均速度是_________m/s;若物体前一半位移的平均速度为4m/s,后一半位移的平均速度为8m/s,则全程内的平均速度是_________m/s.二.速度、速度变化量、加速度:提示:1、加速度:是表示速度改变快慢的物理量,是矢量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 匀变速直线运动的研究 一、四个基本公式
1、 匀变速直线运动速度随时间变化规律公式:at v v +=0
2、匀变速直线运动位移随时间变化规律公式:202
1at t v x +
= 【例1】以10 m/s 的速度匀速行驶的汽车,刹车后做匀减速直线运动。
若汽车刹车后第2 s 内的位移为6.25 m(刹车时间超过2 s),则刹车后6 s 内汽车的位移是多大?
3、匀变速直线运动位移与速度的关系:ax v v 22
02=-
【例2】身高为2 m 的宇航员,用背越式跳高,在地球上能跳2 m ,在另一星球上能跳5 m ,若只考虑重力因素影响,地球表面重力加速度为g ,则该星球表面重力加速度约为( ) A.5
2g B.25g C.1
5
g D.14
g 【例7】一辆车由静止开始作匀变速直线运动,在第8 s 末开始刹车,经4 s 停下来,汽车刹车过程也是匀变速直线运动,那么前后两段加速度的大小之比和位移之比x 1 ׃ x 2分别是( )
A 、=1:4 ,x 1 ׃ x 2=1:4
B 、=1:2,x 1 ׃ x 2=1:4
C 、=1:2 ,x 1 ׃ x 2=2:1 C 、
=4:1 ,x 1 ׃ x 2=2:1
【例6】一只小球自屋檐自由下落,在Δt =0.25 s 内通过高度为Δh =2 m 的 窗口,求窗口的顶端距屋檐多高?(取g =10 m/s2)
4、匀变速直线运动平均速度公式:(v0+v1)/2 通过图像关系证明
二、 匀变速直线运动的三个推论
1、 某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:
试证明此结论:
2、
某段位移内中间位置的瞬时速度2
x v 与这段位移的初、末速度0v 与t v 的关
系为:()
22
02
2
1t x v v v +=
试证明此结论:
【例3】一列从车站开出的火车,在平直轨道上做匀加速直线运动,已知这列火车的长度为l , 火车头经过某路标时的速度为v 1,而车尾经过这个路标时的速度为v 2,求: (1)火车的加速度a ;
(2)火车中点经过此路标时的速度v ; (3)整列火车通过此路标所用的时间t 。
【例4】做匀加速直线运动的列车驶出车站,车头经过站台上的工作人员面前时,速度大小为s m /1,车尾经过该工作人员时,速度大小为s m /7。
若该工作人员一直站在原地没有动,则车身的正中部经过他面前时的速度大小为多少?
3、在连续相等的时间(T )内的位移之差为一恒定值,即:2
aT x =∆2
02
t
t v v v v +=
=
(又称匀变速直线运动的判别式)
推证: 设物体以初速v 0、加速度a 做匀加速直线运动,
自计时起时间T 内的位移:
在第2个T 内的位移
即2aT x =∆ 进一步推证可得=∆=
2T
x a 【例5】一质点做匀加速直线运动,在连续相等的两个时间间隔内通过的位移分别为24m 和64m ,每个时间间隔是2S ,求加速度a 。
三、初速度为零的匀加速运动的几个比例式
v 0=0设t=0开始计时,以T 为时间单位,则
1、 1T 末、2T 末、3T 末…瞬时速度之比为1v ׃2v ׃3v ׃…= 推证
2、 第一个T 内,第二个T 内,第三个T 内……位移之比 x I ׃ x II ׃ x III ׃ … ׃ x N =
推证
3、 1T 内、2T 内、3T 内…位移之比x 1 ׃ x 2 ׃ x 3 ׃ … ׃ x n = 推证
4、通过连续相同的位移所用时间之比t 1 ׃ t 2 ׃ t 3 ׃ … ׃ t n = 推证 由2
2
1at x =
知t 1= 通过第二段相同位移所用时间t 2=
同理t 3=
则t 1 ׃ t 2 ׃ t 3 ׃ … ׃ t n =
【例5】完全相同的三个木块,固定在水平地面上,一颗子弹以速度v 水平射入,子弹穿透三块木块后速度恰好为零,设子弹在木块内做匀减速直线运动,则子弹穿透三木块所用的时间之比是 ;如果木块厚度不同,子弹穿透三木块所用的时间相同,则三木块的厚度之比是 (子弹在三木块中做匀减速直线运动的加速度是一样的)
【例6】对于做初速度为零的匀加速直线运动的物体,以下叙述中不正确的是( ). A .相邻的相等时间间隔内的位移之差为常数
B .相邻的相等时间间隔内的位移之差为最初的那个等时间间隔内位移的两倍
C .该物体运动过程中任意两个相等的时间间隔内速度的改变量均相等
D .该物体运动过程中任意两个相等的时间间隔内位移大小之比一定是奇数比
【例7】一质点做匀加速直线运动,第三秒内的位移2m ,第四秒内的位移是2.5m ,那么以下说法中不正确的是( ) A .这两秒内平均速度是2.25m/s B .第三秒末即时速度是2.25m/s C .质点的加速度是0.125m/s 2 D .质点的加速度是0.5m/s 2
【例8】一个物体做匀变速直线运动,若运动的时间之比为t 1:t 2:t 3:…=1:2:3:…,下面说法中正确的是( )
A .相应的运动距离之比一定是x 1 ׃ x 2 ׃ x 3:…=1:4:9: …
B .相邻的相同时间内的位移之比一定是x I ׃ x II ׃ x III ׃ …=1:3:5: …
C .相邻的相同时间内位移之差值一定是2aT x =∆,其中T 为相同的时间间隔.
D .以上说法正确都是不正确的
(【例9】骑自行车的人沿着直线从静止开始运动,运动后,在第1 s 、2 s 、3 s 、4 s 内,通过的路程分别为1 m 、2 m 、3 m 、4 m ,有关其运动的描述正确的是( ) A .4 s 内的平均速度是2.5 m/s
B .在第3、4 s 内平均速度是3.5 m/s
C .第3 s 末的瞬时速度一定是3 m/s
D .该运动一定是匀加速直线运动
【例10】一列火车作匀变速直线运动驶来,一人在轨道旁观察火车的运动,发现在相邻的两个10s 内,火车从他面前分别驶过8节车厢和6节车厢,每节车厢长8m (连接处长度不计)。
求:
⑴火车的加速度a ;
⑵人开始观察时火车速度的大小。
【例11】从斜面上某位置,每隔0.1 s释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得s BC=15 cm,s CD =20 cm,试求
(1)小球的加速度.
(2)拍摄时B球的速度v B=?
(4)A球上面滚动的小球还有几个?。
