高中物理竞赛讲义-静电场的能量
高二物理竞赛课件:电场的能量(共14张PPT)

球内场强:
球外场强:
Qa
解二:
电场能是以体密度定域分布在空间内的静电能。 思考: 半径为R、带电量为Q的均匀带电球面,其 静电能与球体的静电能相比,哪个大?
四维时空——洛仑兹变换的几何化
坐标变量: x, y, z, ict w
与x, y, z,量纲一致,并反映S中的符号差异 时空间隔:
P
不同惯性系——对应四维时空的 转动操作(投影变化,但时空间 隔不变),其变换关系即洛仑兹 变换。
1.0103m处,从S观察到这两事件相距2.0103m。试问 由S 系测得此两事件的时间间隔为多少?
解:由洛仑兹变换得
解法二
E
2 0
1
(R2
x x2 )1/ 2
1.当 R x
2.当 R x
E 2 0
(R2
x x2 )1/ 2
1
R2 x2
1
2
1
1 R 2 2 x
E
2 0
1 1
1 2
R x
2
q
4 0x2
电场的能量
电场的能量
带电系统带电: 电荷相对移动外力克服电场力做功电场
能量。
一、点电荷系统的能量
q1
r
q2
电能:
n个点电荷系统的电能: 连续分布带电体的电能:
有电介质时静电场的计算 1. 根据介质中的高斯定理计算出电位移矢量
2. 根据电场强度与电位移矢量的关系计算场强
本课程只要 求特殊情况
电介质一点 —— 事件 ——“世界点” 四维时空中的线 —— 事件的进程 ——“世界线”
光锥:离开和到达某世界点的所有世界线 组成的三维曲面
光锥把xy — ct曲面分成了四个区:
高二物理竞赛电场能量和电磁场理论简介课件(共18张PPT)

I q 则 FtD 与qt I等c 也量具值有,并电流量纲 d d d 在气体动理论方面,他还提出了气体分子按速率分布的统计规律。
现对其充电,使电路上的传导电流
,若略去边缘效应, 求(1)两极板间的位移电流;(2)两极板间离开轴线的距离为
d 的点 处的磁感强度 .
1888 年赫兹的实验证实了他的预言,麦克斯韦理论奠定了经典动力学的基础,为无线电技术和现代电子通讯技术发展开辟了广阔前景。
r 注意该式右方无负号. 应如何判断
H 的方向? H
麦克斯韦方程组的积分形式
含四大方程
sD ds
B
s
ds
l E dl
l H dl
r dV
V 0
电场 高斯定理
磁场
-
B
s t ds
电场 环路定理
s( jc+ Dt ) ds 磁场
麦克斯韦认为 了解
麦克斯韦方程组的积分形式
推广后的
-
空间任一点 极板上电量从 0 —Q 作的总功为 从球心到无穷远处的电场能量 各方程的 经典电磁理论的奠基人 , 气体动理论创始人之一 . 麦克斯韦将恒定磁场的安培环路定理
0C
2C
A
q(t)
q(t)
+
B
W A Q2 Q CU 1 CU 2 1 QU
2C
2
2
忽略边缘效应,对平行板电容器有
U Ed
C 0s
d
W
1 2
0
E
2
sd
1 2
0
E
2V
能量密度
wW V
1 2
0
E
2
(适用于所有电场)
不均匀电场中 dW wdV
高中物理奥林匹克竞赛专题---静电场能量与能量密度(共13张PPT)

§9. 4 静电场能量与能量密度
·1 ·
Chapter 9. 静电场中的导体与电介质 §9. 4 静电场能量与能量密度
一、静电场能量密度及能量
保持 Q 不变!板间的静电引力:
Fe
0 20
Q
1 2
EQ
Q
缓慢下移A板,外力做功: Q
dW dV
e
E2Q Sddxx
EQ 2S
E
0 0
Q 0S
,
Q S
0E
dWe dV
120E2
若充满电介质 εr ,则:
ddW Ve 12r0E2
Q Q
0 0
固定金属板 B
S
0
dV A
缓 0
F
慢
S
B
E
0 0
F
dx A
·3 ·
Chapter 9. 静电场中的导体与电介质
We
Q2 2C
1 2
QU
1 2
CU
2
☻电容器的能量是指存储在电容器内部的电场能量。
☻当 Q 一定时,We ∝ 1/C ; 当 U 一定时,We ∝ C 。
C 1 C 2
We1 We2
C 1 C2
C2
We1 We2
·10 ·
Chapter 9. 静电场中的导体与电介质 §9. 4 静电场能量与能量密度
归纳
1. 静电场能量密度:
weddW V e 1 2r0E2 E2
高二物理竞赛静电场的能量课件

把dq从无穷远处搬移到带电体上的过程.
电场力所做元功: dA电 (0 U)dq Udq
外力克服电场力所做元功: dA Udq
Q
外力克服电场力所做总功: A dA Udq 0
外力的功转化为带电体的能量:
Q
W A 0 Udq
例:平板电容器,两极板间距为d,面积为S,其中放有一层
厚度为t的均匀电介质,其相对电容率为εr,求其电容C。
解一:
A + --++ --++ - B
+
-
+ - + --++ -
+
-
+ - + --++ -
S
t
d
注意:可应用电容器的串并联规律计算电容
d S
C1
1S
d1
,
C2
2S
d2
C1
1S1
d
,
C2
2S2
d
解:
11 1
C C1 C2
放入电介质后电容增加:
C S
d
C 2L
ln RB RA
C C1 C2
C 4 RARB
RB RA
能量
We
1 2
Q2 C
1 CU 2 2
1 UQ 2
we
1 2
E 2
1 2
DE
1 2
D2
We V wedV
dV 4r2dr
dV 2rldr
且d R , 求单位长度的电容 .
解 设两金属线的电荷线密度为
E E E 2π 0 x 2π 0 (d x)
高中物理奥林匹克竞赛专题---电容-电容器-静电场的能量(共22张PPT)

Q
Q
VB
VA
步骤 1)设两极板分别带电 Q; 2)求 E;
3)求 V ;4)求 C .
上页 下页 返回 帮助
6-5 电容 电容器 静电场的能量
第六章 静电场
1 平板电容器
d
(1)设两导体板分别带电 Q
(2)两带电平板间的电场强度
+
-
+
-
E Q 0 0S
S
&#(3)两带电平板间的电势差
r
+
+
上页 下页 返回 帮助
6-5 电容 电容器 静电场的能量
第六章 静电场
U Q ( 1 1)
4π0 R1 R2
CU Q4π0
R1R2 R2R1
R2
C4π0R1
孤立导体球电容
+
+
+
R2
+
+
R 1 +
r
+
+
上页 下页 返回 帮助
6-5 电容 电容器 静电场的能量
UR Edx
2R
dR 1 1
2π0 R
( )dx x dx
E
π0lnd RRπ0lnR d
oP
xdx
x
C π ε0
U ln d R
d
上页 下页 返回 帮助
6-5 电容 电容器 静电场的能量
四、静电场的能量
1.电容器的电能
第六章 静电场
6-5 电容 电容器 静电场的能量
第六章 静电场
一 孤立导体的电容
单位
C Q V
1F1C/V
1μF106F
1pF1012F
例如 孤立的导体球的电容
南师附中物理竞赛讲义 11.4静电场的能量

11.4静电场的能量一、电容器的静电能研究电容器的充电过程。
一开始电容器的电势差很小,搬运电荷需要做的功也很小,充电后两板间电势差增加,搬运电荷越来越困难,需要做的功变多。
可以看成是一个变力(变电势差)做功问题。
图像法用面积表示做功。
画Q -U 图像还是U -Q 图像?22111222Q E QU CU C=== 电容器充电过程中,电荷和能量均由电源提供。
在电源内部,可以看成是正电荷从负极移动到正极。
由于电源电动势(即电压)不变,克服电场力做功为:W QU =在电容器充电过程中电源消耗的能量和电容器增加的静电能不相等!思考:两者是否一定是两倍的关系?多余的电能消耗在电路中(定性解释)例1、极板相同的两个平行板电容器充以相同的电量,第一个电容器两极板间的距离是第二个电容器的两倍。
如果将第二个电容器插在第一个电容器的两极板间,并使所有极板都相互平行,问系统的静电能如何改变。
例2、平行板电容器C 接在如图所示电路中,接通电源充电,当电压达到稳定值U 0时,就下列两种情况回答,将电容C 的两极板的距离从d 拉到2d ,电容器的能量变化为多少?外力做功各是多少?并说明做功的正负(1)断开电源开关.(2)闭合电源开关.例3、图中所示ad为一平行板电容器的两个极板,bc是一块长宽都与a 板相同的厚导体板,平行地插在a、d之间,导体板的厚度bc=ab=cd.极板a、d与内阻可忽略电动势为E的蓄电池以及电阻R相连如图.已知在没有导体板bc时电容器a、d的电容为C0 ,现将导体板bc抽走,设已知抽走导体板bc的过程中所做的功为A,求该过程中电阻R上消耗的电能.例4、如图所示,电容器C可用两种不同的方法使其充电到电压U=NE。
(1)开关倒向B位置,依次由1至2至3∙∙∙∙∙∙至N。
(2)开关倒向A位置一次充电使电容C的电压达到NE。
试求两种方式充电的电容器最后储能和电路上损失的总能量。
(电源内阻不计)例5、在图所示电路中,三个电容器C 1、C 2、C 3,的电容值均为C ,电源的电动势为E,R 1、R 2为电阻,S 为双掷开关.开始时,三个电容器都不带电,先接通S a .再接通S b .再接通S a ,再接通S b ……如此多次换向,并使每次接通前都已达到静电平衡.试求:(1)当S 第n 次接通b 并达到平衡后,每个电容器两端的电压各是多少?(2)当反复换向的次数无限增多时,在所有电阻上消耗的总电能是多少?二、能量与能量密度注意:电能是分布在空间中的电场所具有的,而不是带电体具有的。
2020年高中物理竞赛辅导课件:电磁学(静电场中的导体和电介质)05静电场的能量(共13张PPT)

全国高中生物理学奥林匹克竞赛
普通物理学
(含竞赛真题练习)
§2.6 静电场的能量(Energy of Electrostatic Field) 1.带电电容器的能量
充电时,电源做功→电容器的静电能;放电 时,能量C
B
放电: t=0
+Q (-Q)
t—t+t
Note: W → C , 也是计算电容的一种方法.
[例2-9] 电容为C的电容器,极板上带电量Q. 将
其与另一不带电的相同电容器并联,则
该电容器组的静电能W=
.
解:
C
+Q -Q
并联后, 总带电量为 C Q, 总电容为 2C
W=Q2/4C
[思考] 为什么静电能变小了?
+q -dq
(-q)
电场力做功:
dA (dq)(V V )
(dq) q C
A 1
0
qdq
Q2
CQ
2C
带电电容器的静电能:
W
Q2 A
1 CU 2
1 QU
2C 2
2
2.静电场的能量 充电与放电→极板间电场产生与消失 场的观点:静电能储存于电场中
W 1 CU 2 1 0r S (Ed )2 DE Sd
2
2d
2
电场的能量密度(单位体积中的能量):
w DE 2
电场的能量:
(对任何电场都成立)
W wdV
[例2-8] 金属球半径R,带电量Q,求其静电能. 解: [解法一] 视为带电电容器:
W Q2 Q2
2C 80R
[例2-8] 金属球半径R,带电量Q,求其静电能. 解: [解法二]计算静电场的能量:
静电场的能量课件高中物理竞赛
12 0r E2Sd
1 2
DE
V
能量储存在电场中
(1) 电场能量密度
单位体积内所储存电场能量:
w
W e
eV
1 DE 2
1
D
E
2
对任意电场成立
(2) 电场能量
任W 何 带电V系1 2统E 的2d 电场V 中V 所储1 2D 存的E 总d能量V为:
V 为电场占据的整个空间体积
例1 如图,一带电量为q的球形导体置
为电场占据的整个空间体积 板极上带电± Q时所储的电能为
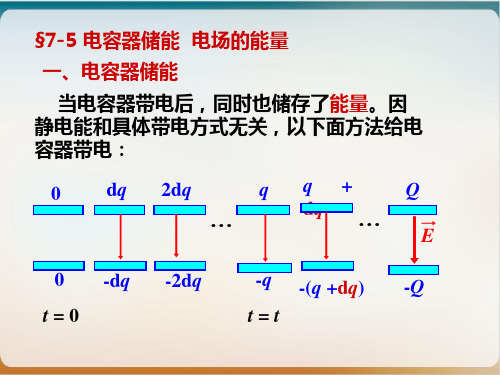
场能量减少. 至t时刻,电容器已带电q,此时若再移动dq,外力作功为
当电容器带电后,同时也储存了能量。
答案为(B)
例2 为电容器充电. 在电源保持连接的情况下, 把电介质插入, 则静电能 . (填增大、减小、不变)
解:电源保持连接 V一定
插入介质后,C增大
dWe wedV8πQ2r2dr
电容器贮存的电场能量
We
dWe8Q π2
R2 dr R1 r2
Q2 ( 1 1 )
8π R1 R2
与 We
1比Q较2得 2C
C4π R2R1 球形电容器电容
R2 R1
得电量增加
CU 2 W
2
思考
W
若将“电源保持连接”改为“电源断开”, 结果?
例3 一平行板电容器的极板面积s,间距d,充满
电容率的介质,用电源充电后,两极板上带电
分别为+Q和-Q,如图所示。断开电源,把左极
板固定,向外拉动右极板,使极板间距增大到2d。
求:
dd
(1)外力克服两极板间的吸引力
所做的功。
.若在两球壳间充以电容率为 的电介质,问此电容
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静电场的能量
一、电容器的静电能
研究电容器的充电过程。
一开始电容器的电势差很小,搬运电荷需要做的功也很小,
充电后两板间电势差增加,搬运电荷越来越困难,需要做的功变
多。
可以看成是一个变力(变电势差)做功问题。
图像法用面积表示做功。
画Q -U 图像还是U -Q 图像?
2
2111222Q E QU CU C
=== 电容器充电过程中,电荷和能量均由电源提供。
在电源内部,可以看成是正电荷从负极移动到正极。
由于电源电动势(即电压)不变,克服电场力做功为:
W QU =
在电容器充电过程中电源消耗的能量和电容器增加的静电能不相等!
思考:两者是否一定是两倍的关系?
多余的电能消耗在电路中(定性解释)
例1、极板相同的两个平行板电容器充以相同的电量,第一个电容器两极板间的距离是第二个电容器的两倍。
如果将第二个电容器插在第一个电容器的两极板间,并使所有极板都相互平行,问系统的静电能如何改变。
例2、平行板电容器C 接在如图所示电路中,接通电源充电,当电压达到稳定值U 0时,就下列两种情况回答,将电容C 的两极板的距离从d 拉到2d ,电容器的能量变化为多少?外力做功各是多少?并说明做功的正负
(1)断开电源开关.
(2)闭合电源开关.
例3、图中所示ad为一平行板电容器的两个极板,bc是一块长宽都与a 板相同的厚导体板,平行地插在a、d之间,导体板的厚度bc=ab=cd.极板a、d与内阻可忽略电动势为E的蓄电池以及电阻R相连如图.已知在没有导体板bc时电容器a、d的电容为C0 ,现将导体板bc抽走,设已知抽走导体板bc的过程中所做的功为A,求该过程中电阻R上消耗的电能.
例4、如图所示,电容器C可用两种不同的方法使其充电到
电压U=NE。
(1)开关倒向B位置,依次由1至2至3∙∙∙∙∙∙
至N。
(2)开关倒向A位置一次充电使电容C的电压达到
NE。
试求两种方式充电的电容器最后储能和电路上损失的
总能量。
(电源内阻不计)
例5、在图所示电路中,三个电容器C 1、C 2、C 3,的电容值均为C ,电源的电动势为E,R 1、R 2为电阻,S 为双掷开关.开始时,三个电容器都不带电,先接通S a .再接通S b .再接通S a ,再接通S b ……如此多次换向,并使每次接通前都已达到静电平衡.试求:
(1)当S 第n 次接通b 并达到平衡后,每个电容器两端的电压各是多少?
(2)当反复换向的次数无限增多时,在所有电阻上消耗的总电能是多少?
二、能量与能量密度
注意:电能是分布在空间中的电场所具有的,而不是带电体具有的。
平行板电容器(空气介质)的能量为:
2
2221111222424S E W QU CU E d V kd k
ππ==== 上式也可以写为:
W wV =
其中w 为能量密度:
2
124E w k
π= 此公式是普适的,对任何电场适用。
(证明略)
对于非匀强电场,w 不是定值
W w V =∆∑
例6、半径为R 的球面均匀带电,总电量为Q ,求整个空间内的静电能。
例7、已知球面均匀带电量Q,半径为R,试计算带电球面上的表面张力系数。
