标准大气参数推算
标准大气参数计算公式

标准大气参数计算公式该套计算公式摘自“杨炳尉 标准大气参数的公式表示 宇航学报1983年1月”,以美标1976标准大气为对照,采用拟合方法,在利用流体静力学得到的大气数据解析计算公式的基础上加上适当的修正因子,缩小公式的计算误差。
计算方法如下:几何高度Z 与重力位势高度H 之间的转换:)/1/(0R Z Z H +=km R 3010356766.6⨯=为地球半径km Z 0191.110≤≤2559.42559.5)(15.2883308.441W W P P K W T HW SLSL===-=ρρ km Z 0631.200191.11≤<W W P P K T H W SLSL11105898.1101953.1)(650.2163416.69647.14exp --⨯=⨯==⎪⎭⎫ ⎝⎛-=ρρ km Z 1619.320631.20≤<1629.3521629.342102722.3105158.2)(552.221552.2219021.241----⨯=⨯==-+=W W P P K W T H W SLSLρρ km Z 3501.471619.32≤<2011.1332011.123102618.3108338.2)(350.2504107.897499.391----⨯=⨯==-+=W W P P K W T H W SLSLρρ km Z 4125.513501.47≤<W W P P K T H W SLSL44104920.9109155.8)(650.2709223.76252.48exp --⨯=⨯==⎪⎭⎫ ⎝⎛-=ρρ km Z 8020.714125.51≤<2011.1142011.124105280.2101671.2)(021.2472218.884390.591W W P P K W T H W SLSL--⨯=⨯==--=ρρ km Z 0000.868020.71<<0816..1650816.175107632.1102274.1)(590.2002950.1000303.781W W P P K W T H W SLSL--⨯=⨯==--=ρρ km Z 0000.910000.86≤≤()W W H P P K T H W SLSL 663106411.31010042.12730.2)(87.1864700.52848.87exp ---⨯=⨯⨯+==⎪⎭⎫ ⎝⎛-=ρρ音速、重力加速度、粘度的计算公式对0至90公里范围内各段通用,分别为: 音速:)(0468.20K T a = s m /重力加速度:()2310356766.6/180665.9⨯+=Z g 2/s m 粘度(Sutherland 公式): ⎪⎭⎫ ⎝⎛⋅+⨯=⎪⎭⎫ ⎝⎛⋅+⨯=--32373236sec 4.11010487.1sec 4.11010458.1m kg T T m N T T g s m / 海平面大气参数值22242324252/1040294.3/80665.9/12492.0/2250.1/1003323.1/1001325.1108815.2s m a s m g m s kg m kg m kg m N P KT SL SL SL SL SL ⨯==⋅==⨯=⨯=⨯=ρ。
海拔和气压转换公式

海拔和气压转换公式你知道吗,海拔和气压之间有着很有趣的关系呢。
一般来说,随着海拔的升高,气压是会降低的。
这就像是住在高楼大厦的顶层,空气好像都变得稀薄了一些,其实就是气压变小了。
那具体的转换公式呢,比较常用的一个近似公式是这样的。
气压随海拔高度的变化可以用指数函数来近似表示。
比如说,在标准大气条件下,气压和海拔高度的关系大致可以表示为:P = P₀ * (1 - (Lh / T₀))^(gM / (RL))。
这里面的字母都代表着不同的含义哦。
P₀是海平面的标准大气压,大概是1013.25百帕;L是温度垂直递减率,一般取0.0065 K/m;h就是我们要求的海拔高度啦;T₀是海平面的标准温度,大概是288.15 K;g是重力加速度,约等于9.80665 m/s²;M是空气的摩尔质量,大概是0.0289644 kg/mol;R是理想气体常数,等于8.31447 J/(mol·K)。
这个公式看起来是不是有点复杂呀?其实只要你耐心一点,把每个字母的含义都搞清楚,就会发现它还是很有逻辑的。
不过呢,这个公式也只是一个近似的计算哦。
在实际的情况中,大气的情况是非常复杂的。
比如说,不同的地理位置,大气的温度、湿度、气流等等都会有很大的差异。
就像在海边和在高山上,大气的状况就完全不一样。
海边的空气湿度比较大,这也会对气压产生影响。
而在高山上,地形复杂,气流的运动也很复杂,这都会让实际的气压和按照这个公式计算出来的结果有一些偏差。
但是呢,这个公式在很多情况下还是很有用的。
比如说,气象学家在做天气预报的时候,就会用到这个公式的原理。
他们通过测量不同地方的气压,然后根据这个公式来推测海拔高度,或者反过来,根据海拔高度来预估气压的情况。
这样就能更好地了解大气的运动和变化,从而做出更准确的天气预报。
还有哦,对于那些喜欢登山或者飞行的小伙伴来说,这个公式也很有意义。
登山的时候,随着海拔不断升高,你能明显感觉到气压的变化,身体也会有一些反应。
标准大气
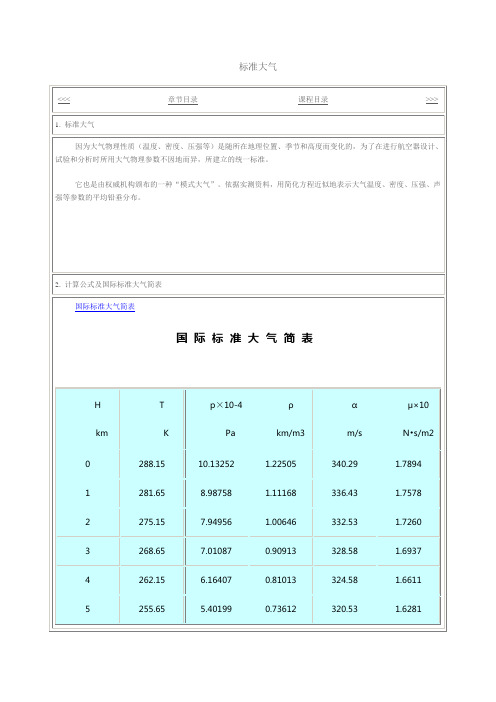
0.16542
295.07
1.4216
17
216.65
0.87867
0.14128
295.07
1.4216
18
216.65
0.75048
0.12068
295.07
1.4216
19
216.65
0.64100
0.10307
295.07
1.4216
20
216.65
0.54749
0.08803
295.07
1.4216
21
217.65
0.46779
0.07487
295.75
1.4271
22
218.65
0.39997
0.06373
296.43
1.4326
23
219.65
0.34224
0.05428
297.11
1.4381
24
220.65
0.29305
0.04627
297.78
1.4435
25
301.14
1.4706
30
226.65
0.11719
0.01801
301.80
1.4760
31
227.65
0.10082
0.01548
302.47
1.4814
32
228.65
0.08680
0.01323
303.13
1.4868
表中a为在流体介质中声音传播的速度,简称音速。
1.4216
12
216.65
1.93309
0.31083
295.07
标准大气压推导

标准大气压推导全文共四篇示例,供读者参考第一篇示例:标准大气压是指海平面上的大气压力,通常定义为1013.25毫巴(1毫巴≈100帕)或者1013.25千帕。
标准大气压是气象学和大气科学中常用的一个重要参数,用于描述大气中空气的密度、温度和湿度等变化。
标准大气压的推导涉及到气体压强的计算和大气层的结构。
根据理想气体的状态方程PV=nRT,大气压力可以用气体的分子数目、温度和体积等参数来表示。
在海平面上,大气内的气体受地球引力的影响,会受到大气柱的重力作用,因此气体在不同高度上受到的压力会有所不同。
大气的密度随着海拔的增加而递减,这也导致了大气层内气压的不同。
根据气压与海拔的关系公式P=P0*exp(-Mgh/RT),可以推导出不同海拔高度处的大气压力。
其中P为海拔高度处的气压,P0为海平面上的标准大气压,M为气体的平均分子质量,g为重力加速度,h为海拔高度,R为气体常数,T为温度。
综合考虑气体的状态方程和海拔高度对气压的影响,可以得出不同海拔高度处的标准大气压。
在海平面上,标准大气压通常被定义为1013.25毫巴或者1013.25千帕,但随着海拔的增加,实际气压会有所不同。
例如在珠穆朗玛峰的顶峰处,由于海拔高度极高,大气压远低于标准大气压,这也是登山者需要携带氧气瓶来补充氧气的原因之一。
标准大气压的推导对于气象学、气候学和航空航天等领域都具有重要意义。
在天气预报和气候研究中,标准大气压可以用来描述大气层的结构和变化,帮助科学家们更好地理解和预测气候变化。
在航空航天领域,标准大气压可以用来计算飞行器在不同高度上的气动力学特性,以确保飞行安全。
标准大气压的推导是一个涉及到气体物理学和气象学等多个学科知识的综合性问题。
通过对气体状态方程和大气层结构的深入研究,科学家们可以更加准确地描述和理解大气压力的变化规律,为气象预测、气候研究和航空航天技术的发展提供重要参考。
【注:本文共计663字】第二篇示例:标准大气压推导是气象学中一个重要的概念,它在天气预报、航空航天等领域起着至关重要的作用。
大气计算

L Hu / v s 1.5 0.25 8.8(m) 0.0428
取沉降室内气体流速 u=0.25m/s,H=1.5m,有沉降室长度 相应的,沉降室宽度为
W
Q 2800 2.07 (m) 3600 H u 3600 1.5 0.25
计算所得沉降室尺寸为:长 L=8.8m 宽 W=2.07m 高 H=1.5m 其中高 H 为设定的数据,据此设计出的沉降室比较庞大,应考虑改进: 已知: P=101.325kPa,t=20℃ 管式电除尘器圆筒形集尘极直径 D=0.3m;管长 L=2.0m 气体流量 Q=0.075m3/s 集尘器附近的平均场强 Ep=100kV/m 粒径为 1.0μ m 的粉尘荷电量 q=0.3×10-15C 求:该粉尘的驱进速度和捕集效率
设计锅炉烟气重力沉降室。 已知:烟气量:2800m3/h;烟气温度 t=150℃ ; 烟气真密度ρ p=2100kg/m3 要求:能除去 Dp≥30μ m 的烟尘
查表得 t=150℃时粘性系数μ =2.4×10-4Pa.s 有:尘粒沉降速率
vs
2 dp p g
18
(30106 ) 2 2100 9.8 0.0428(m / s) 4 18 2.4 10
u u1 ( z )m z1
其中:
u
、u 1
分别为 z、z1 高度处的平均风速
国际标准大气和飞行高度的确定一

飞机一般在以上高度范围内活动。
第一节 大气层
2、密度 地球外层空气的存在是因为地球的引力 将其包围在自己的周围
• 随高度的增加,空气的密度就会越小
第一节 大气层
3、压力 大气压力是物体单位面积上所承受的大气
柱的重量
• 随高度的增加,大气压力降低。
第一节 大气层
4、对飞行的影响 • 飞行高度太高,空气密度很小,发动机
•
2、公式
:
m v
第一节 大气层
• 3、单位 :标准单位为 工程单位为
kg / m3
kg s2 / m4
• 4、对概念的理解(与人口密度比较理解)
第一节 大气层
• (二)、空气的温度(T) • 1、概念:空气的温度指空气的冷热程度。 • 2、定理:布朗运动
气体的温度越高,空气分子不规则运 动的越快,分子的平均动能越大。
第三章 航空器活动的环境 及导航
大气层基本介绍 空中导航
EXIT
第一节 大气层
本节内容: 一、大气物理参数 二、大气各物理参数随高度的变化 三、大气的分层 四、国际标准大气和飞行高度的确定
ห้องสมุดไป่ตู้
m
v
第一节 大气层
一、大气物理参数
• (一)、空气的密度()
• 1、概念:单位体积内的空气质量
• 起飞和降落阶段使用
第一节 大气层
2、海平面气压高度(QNH) • 以当地实际海平面的气压数据作为高度
的基准面,飞机高度表上表示出来的高 度就是飞机的实际海拔高度
• 爬升和下降阶段使用
第一节 大气层
3、标准气压高度(ISA) • 以国际标准大气的基准面得到的高度称
标准大气条件
标准大气条件标准大气条件是指在一定的气压和温度下,大气的密度、温度和声速等参数的标准值。
在地球上,标准大气条件通常指的是在海平面上的大气条件,这也是工程技术设计和科学研究中常用的参考条件。
在标准大气条件下,大气的压强约为101.325千帕,温度约为15摄氏度。
在这样的条件下,空气的密度约为1.225千克/立方米,声速约为340.29米/秒。
这些数值为工程设计和科学研究提供了重要的参考依据。
标准大气条件的确定对于航空航天、气象学、环境科学等领域具有重要意义。
在航空航天领域,飞行器的设计和性能计算需要考虑大气条件的影响。
在气象学和环境科学领域,大气条件的变化与气候变化、空气污染等问题密切相关。
除了在地球上的海平面上,标准大气条件也可以根据不同的要求进行调整。
例如,在高海拔地区,由于气压较低,大气的密度和温度会有所变化。
在这种情况下,需要根据实际情况对标准大气条件进行修正,以保证工程设计和科学研究的准确性。
在工程设计中,标准大气条件的使用可以帮助工程师进行设计计算和性能预测。
例如在飞机设计中,需要考虑飞机在不同大气条件下的飞行性能,包括爬升率、巡航速度、燃料消耗等。
在这种情况下,标准大气条件可以作为设计的基准,帮助工程师进行性能预测和优化设计。
在科学研究中,标准大气条件的使用可以帮助科学家进行实验设计和数据分析。
例如在气候模拟研究中,需要考虑不同大气条件对气候变化的影响。
在这种情况下,标准大气条件可以作为实验的基准,帮助科学家进行数据分析和模型验证。
总之,标准大气条件是工程设计和科学研究中不可或缺的重要参考条件。
它的准确确定和合理应用对于推动工程技术和科学研究的发展具有重要意义。
希望本文对标准大气条件的理解和应用能够有所帮助。
标准大气压海拔
标准大气压海拔标准大气压是理想气体状态下,在海平面上的压强。
它是巴里定律所得的结果,即将一个压缩空气的容器加热至同温度下保持不变的体积,会得到一个设定的大气压力。
在物理学中,标准大气压的数值为101.325千帕斯卡(kPa),用来作为大气压的标准计量单位。
标准大气压随着海拔的高度而下降。
这是由于大气的压力是由地球表面上的重力引起的,随着海拔的高度逐渐变弱。
这种下降的趋势并不是线性的,而是指数式的。
也就是说,离开海平面越高,每上升一定的高度,标准大气压的变化量就会越大。
为了方便计算和比较,国际上采用了一组标准大气压的值。
这组值是基于一个理想的标准大气的假设情况所得出的。
这个理想的标准大气假设为一束干燥的气体,其中气压按照指数规律随海拔增加而下降,温度随着高度的增加而保持恒定。
根据这个假设,国际上规定了在海平面上的标准大气压为1013.25毫巴(mb),1毫巴相当于 100帕斯卡(Pa)。
这个值还可以通过将功率为1.85的指数函数用于一个海拔中任意高度计算的方法来推算得出。
然而,在真实情况下,大气是非常复杂的。
它包含了水蒸气、氮气、氧气等各种气体的混合物。
而且大气中水蒸气和其他气体的含量和分布也会随着地理位置、时间和季节的变化而变化,在这些因素的影响下,标准大气压也会发生变化。
在气象学中,标准大气压是指在一定的时间和地点下测定的平均大气压值。
总之,标准大气压是大气压的标准计量单位,根据巴里定律,标准大气压在海平面上为101.325kPa,随着海拔的变化而下降,但是这种下降的趋势并不是线性的,是指数式的,国际上有一组标准的大气压值以便于科学计算和比较。
标准大气压计算公式
标准大气压计算公式
在标准大气压的计算中,我们可以使用以下的公式:
P=P0*(1-(L*h)/T0)^(gM/RL)
其中:
-P是标准大气压
-L是温度随高度变化的率(一般取为0.0065摄氏度/米)
-h是海拔高度
-T0是参考高度上的温度(一般取为288.15摄氏度)
-g是重力加速度(一般取为9.8米/秒^2)
-RL是气体常数(一般取为8.314千焦耳/(摩尔·开尔文))
这个公式的推导基于气体力学原理,这里给出了一个简化的版本。
在
实际应用中,还需要考虑其他因素,例如地球自转带来的惯性力等。
此外,温度、湿度等因素对气压的影响也需要考虑。
这个公式的基本思想是根据海拔高度的变化和重力加速度的作用,推
导出气压随着高度的变化规律。
当海拔高度变化时,温度和压力都会相应
发生改变,而这些因素又会影响到大气的密度和体积。
因此,通过这个公
式可以计算出不同高度上的标准大气压。
需要注意的是,这个公式是一个推导公式,在实际应用中可能会存在
误差。
因为气象条件的变化是很复杂的,无法完全用一个简化的公式来描述。
因此,在实际应用中,我们往往需要结合气象观测和实际数据,通过
数学建模等方法来计算气压的变化规律。
标准大气压的计算公式为我们理解气压变化提供了一个基本框架,它能够帮助我们理解气象现象、解释天气变化以及进行气象预测等工作。
在气象学、航空航天等领域,对气压变化的研究和预测是非常重要的。
通过不断地发展研究,我们可以更好地理解和预测气象现象,提高气象预报的准确性,为人们的生活和工作提供更好的保障。
海拔与大气密度和温度间的换算关系
海拔与大气密度和温度间的换算关系Revised by Hanlin on 10 January 2021海拔高度与大气密度和温度间的换算关系1、根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气密度、湿度与海拔高度的关系。
注:标准状态下大气压力为1,相对空气密度为1,绝对湿度为11g/m3。
从表中可以看出,海拔高度每升高1000m,相对大气压力大约降低12%,空气密度降低约10%,绝对湿度随海拔高度的升高而降低。
绝对湿度是指每单位容积的气体所含水分的重量,用mg/L或g/m3表示;相对湿度是指绝对湿度与该温度饱和状态水蒸气含量之比用百分数表达。
2、空气温度与海拔高度的关系在无热源、无遮护的情况下,空气温度随海拔高度的增高而降低。
一般研究所采集的温度与海拔高度的关系:从表中可以看出:空气温度在一般情况下,海拔高度每升高1000m,最高温度会降低5℃,平均温度也会降低5℃。
大气密度(atmosphericdensity)单位容积的大气质量。
空气密度在标准状况(0℃(273k),101KPa)下为1.293g·L-1。
空气的密度大小与气温等因素有关,我们一般采用的空气密度是指在0摄氏度、绝对标准指标下,密度为1.297千克每立方米(1.297kg/m3).大气压力随海拔高度而变化,由经验公式P=P0(1-0.02257h)5.256(kPa)式中h一海拔高度(km).用上面公式,算出压力,然后根据密度=P*29/(8314*T),其中P的单位是帕,T的单位是K,通常也就是273.15+t不同温度下干空气算公式:空气密度=1.293(实际压力/标准物理大气压)*(273/实际绝对温度),绝对温度=+273通常情况下,即30摄氏度时,取1.165KG/M3-60摄氏度时,取1.65KG/M3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
The International Standard Atmosphere (ISA)Mustafa Cavcar*Anadolu University, 26470 Eskisehir, TurkeyNomenclaturea= speed of sound, m/secg= acceleration of gravity, m/sec2h= altitude, m or ftp= pressure, N/m2 or hPaR= real gas constant for air, 287.04 m2/°Ksec2T= temperature, °K or °Cρ= density, kg/m3Subscripts0= standard sea level conditions11= tropopause caonditionsAbbreviationsICAO = International Civil Aviation OrganizationISA = International Standard AtmosphereMSL = Mean Sea LevelPA = Pressure Altitude1. Standard Atmosphere ModelingFor purposes of pressure altimeter calibrations, aircraft and rocket performance and their design, and so forth, knowledge of the vertical distribution of such quantities as pressure, temperature, density, and speed of sound is required. Since the real atmosphere never remains constant at any particular time or place, a hypothetical model must be employed as an approximation to what may be expected. This model is known as the standard atmosphere. The air in the model is assumed to be devoid of dust, moisture, and water vapor and to be at rest with respect to the Earth (that is, no winds or turbulence). [1]The first standard atmospheric models were developed in the 1920's in both Europe and the United States. The slight differences between the models were reconciled and an internationally accepted model was introduced in 1952 by the International Civil Aviation Organization (ICAO). [1] The International Standard Atmosphere is defined in ICAO Document 7488/2. The ISA assumes the mean sea level (MSL) conditions as given in Table 1.* Professor, School of Civil Aviation; mcavcar@.tr.Table 1 International Standard Atmosphere, Mean Sea Level ConditionsPressure =0p 101 325 N/m 2 = 1013.25 hPa Density =0ρ 1.225 kg/m 3 Temperature =0T 288.15°K (15°C) Speed of sound=0a 340.294 m/secAcceleration of gravity =0g 9.80665 m/sec 21.1. Temperature ModelingThe following diagram (Figure 1) illustrates the temperature variations in the standard atmosphere:Figure 1 International Standard Atmosphere temperature variation [2].Temperature decreases with altitude at a constant rate of -6.5°C/1000m (-1.98°C/1000ft) up to the tropopause. The standard tropopause altitude is 11,000 m (36,089 ft). Therefore, the air which is considered as a perfect gas in the ISA model presents the following characteristics within the troposphere:1000(m)5.60h T T −= (1) or1000(ft)98.10h T T −= (2)For simple estimations, Equation (2) can be assumed1000(ft)20h T T −= (3)The temperature remains at a constant value of -56.5°C (216.65°K) from the tropopause up to 20,000 m (65,600 ft).This ISA model is used as a reference to compare real atmospheric conditions and the corresponding engine/aircraft performance. The atmospheric conditions will therefore be expressed as ISA +/- ∆ISA at a given flight level [2].Example:Let’s consider a flight in the following conditions:Altitude = 31,000 feetActual Temperature = -37ºCThe standard temperature at 31,000 feet is: 4731215−=×−=T ºC, whereas the actual temperature is -37ºC, i.e. 10ºC above the standard.Conclusion: The flight is operated in ISA+10 conditions1.2. Pressure ModelingTo calculate the standard pressure p at a given altitude, the temperature is assumed standard, and the air is assumed as a perfect gas. The altitude obtained from the measurement of the pressure is called pressure altitude (PA). Both Table 2 and Figure 2 show variation of the pressure altitude as a function of the pressure. The last column of Table 2 shows corresponding flight levels for the given pressure altitudes. The flight level is the altitude expressed in hundreds of feet.Table 2 Pressure altitude versus pressure [2].Figure 2 Pressure altitude versus pressure [2].The pressure variations for the International Standard Atmosphere can be calculated by using the hydrostatic equation, perfect gas law and the temperature lapse rate equation. The hydrostatic equation for a column of air (Figure 3):=(4)dpρ−gdhThe equation of state for the perfect gas:RT p ρ=(5)where R is the real gas constant for the air. Dividing the hydrostatic equation by the equation of state gives:dh RT g RT gdh p dp−=−=ρρ (6)The relationship between the pressure at a troposphere altitude and sea level pressure can be obtained by integrating equation (1) between 00=h and h :∫∫=−−=p p h h h T dh R g p dp 00000065.0Performing the above integration, we obtain:2561.5000065.01−=T h p p (7)In equation (7), the unit of 0T is °K, and h is in meters.Pressure above the tropopauseFor the altitudes above the tropopause, the temperature is constant, so that integrating equation (6) from the tropopause to an altitude above the tropopause:∫∫=−=p p h h dh RT g p dp 11111100011results in)(111111h h RT gep p −−=(8)where the parameters with subscript “11” correspond to the values at the tropopause, and =11p 226.32 hPa, =11T 216.65 °K, and =11h 11,000 m1.3. Density ModelingSince the pressure and standard temperature are known for a given altitude, the standard density can easily be calculated from the perfect gas equation (5):RTp =ρ (9)2. International Standard Atmosphere (ISA) Table [2]The International Standard Atmosphere parameters (temperature, pressure, density) can be provided as a function of the altitude under a tabulated form, as given in Table 3:Table 3 International Standard Atmosphere [2]References[1] Talay, T.A., Introduction to the Aerodynamics of Flight, NASA SP-367, NationalAeronautics and Space Administration, Washington, D.C., 1975, p. 6-9.[2] Airbus, Getting to Grips with Aircraft Performance, Airbus Industrie, CustomerServices, Blagnac, 2000, p. 11-16.。
