基于时频分析的欠定信号盲分离与微弱特征提取_李宏坤
声学信号处理的盲源分离算法研究

声学信号处理的盲源分离算法研究声学信号处理是一个广泛的研究领域,其目标是从混合的声音中分离出源自不同信号源的声音。
盲源分离是声学信号处理中的一项重要任务,它不依赖于事先对混合信号的了解,而是通过分析混合信号的统计特性来分离源信号。
近年来,随着深度学习和人工智能的发展,盲源分离算法得到了很大的突破。
以下将介绍几种常见的盲源分离算法及其研究进展。
1. 独立成分分析(ICA)独立成分分析是一种常用的盲源分离方法,它的基本假设是混合信号是由相互独立的源信号线性组合而成的。
ICA通过最大化信号的非高斯性,选取合适的分离矩阵,将混合信号分离成相互独立的源信号。
然而,ICA在面对多源信号和非线性混合模型时存在一定的局限性。
2. 时间频率分析时间频率分析是一种基于信号的时频特性的盲源分离方法。
它通过对混合信号进行时频分析,将源信号的时频特性提取出来。
时间频率分析常用的算法有短时傅里叶变换(STFT)、小波变换和强度比谱(IPS)等。
这些方法在分离语音信号、音乐信号和环境噪声等方面取得了一定的成效。
3. 贝叶斯源分离贝叶斯源分离是一种基于贝叶斯统计推断的盲源分离算法。
它通过建立源信号和混合信号的统计模型,利用贝叶斯推断的方法推导出源信号的分布参数,从而实现分离。
贝叶斯源分离算法在处理高斯噪声和非线性混合模型时具有一定的优势。
除了上述几种算法,还有很多其他的盲源分离方法,如基于狄利克雷分布的盲源分离、盲源分离的最大似然估计算法等。
这些方法在不同的应用场景下具有各自的优缺点。
然而,盲源分离算法仍然存在一些挑战和难题。
首先,多源信号的盲源分离是一个复杂的问题,需要在保证分离效果的同时,尽量减少源信号的干扰。
其次,盲源分离算法在非线性混合模型和非高斯噪声环境下的性能较差,需要进一步研究改进。
此外,盲源分离算法在实时性、稳定性和适应性等方面还需要进一步提升。
为了解决上述问题,研究者们正在不断探索新的盲源分离算法。
其中,结合深度学习的方法是近年来的热点之一。
欠定盲源分离混合矩阵的时频分析估计方法

欠定盲源分离混合矩阵的时频分析估计方法摘要:在盲源分离信号处理中,尤其在欠定条件下(观测信号数目大于源信号数目),精确的估计混合矩阵是具有挑战性的问题。
现存部分方法利用信号的稀疏性进行求解,并假设在时域或者时频域中源信号不重叠,然而这类方法在假设条件不满足,即源信号部分重叠情况下随着信号稀疏性降低性能恶化明显。
本文针对具有较弱稀疏性的源信号,提出了一种基于时频分析的欠定盲源分离的混合矩阵估计方法。
首先,利用源信号时频变换后系数实部与虚部比值的差异性选择单源点;其次,运用经典的聚类方法估计解混合矩阵的各向量。
仿真结果表明:提出的方法简易可行并具有较好的估计性能。
关键词:盲源分离;时频分析;矩阵估计1、引言盲源分离(Blind Source Separation)技术在过去20年里发展迅速,其较强的信号处理能力使其在各信号处理领域得到了广泛的应用。
给定混合系统,盲源分离的目的就是在未知源信号和混合系统的情况下估计出源信号。
欠定盲源分离(UBSS,Underdetermined Blind Source Separation)就是指输入的源信号个数多于观测信号个数,在这种情况下,通常方法无法寻找混合矩阵的逆矩阵,所以一类基于信号稀疏性的求解方法应运而生。
这类方法利用源信号的稀疏性来估计混合矩阵并且恢复源信号,信号的稀疏性指的是在一定的范围内大部分信号值为零,只有极小部分信号值存在。
欠定盲分离问题一般由两步法解决:第一步估计混合矩阵,第二步恢复源信号。
现有的部分算法利用了信号时域稀疏性,假设源信号是具有拉普拉斯分布的稀疏信号从而解决欠定盲分离问题。
当信号不具有时域稀疏性,部分学者利用信号在变换域的稀疏特性来解决欠定问题,例如时频变换。
最早利用时频域稀疏性来解决适定问题,DUET算法来解决欠定问题,Linh-Trung et al.运用聚类算法[13]处理欠定问题, 此类算法基于信号在时频域的正交假设。
然而在实际中,正交假设过于严格,准正交条件下利用子空间估计方法解决欠定问题,此方法同时假设在任一时频点上的源信号数目少于观测信号数目;放宽了正交条件并且假设任一时频点上的源信号数目小于等于观测信号数目。
一种基于时间相关度的盲分离方法

一种基于时间相关度的盲分离方法
刘彦;舒勤
【期刊名称】《信号处理》
【年(卷),期】2009(025)002
【摘要】本文从信号的相关性出发,提出信号时间相关度的定义,并证明了时间相关度定义具有如下性质:一组独立源信号的线性混合信号其时间相关度介于源信号中时间相关度的最小值和最大值之间.本文根据这一定义及性质,利用矩阵广义特征值理论,建立时间相关度的广义特征值问题,通过求解此广义特征值问题的特征矢量,从而达到分离信号的目的.本文算法适用于瞬时混合模型,仿真结果证明本算法可以应用与灰度图像的分离及复杂混合环境中声音的分离,计算简单,性能良好,效果真实可靠.
【总页数】6页(P204-209)
【作者】刘彦;舒勤
【作者单位】四川大学电气信息学院,成都,610065;四川大学电子信息学院,成都,610065;四川大学电气信息学院,成都,610065
【正文语种】中文
【中图分类】TP391
【相关文献】
1.一种时变信道下基于粒子滤波的同频混合信号盲分离方法 [J], 马欢;江桦
2.一种基于自然梯度的循环平稳信号盲分离方法及其应用 [J], 郭彬;张永祥;柯维
3.一种基于二阶锥约束克服信道不匹配的盲分离方法 [J], 骆忠强;谢伟;李成杰
4.一种动量因子自适应自然梯度的盲分离方法 [J], 谭骏;刘辉
5.一种基于独立分量分析的变速跳频信号盲分离方法 [J], 王淼; 蔡晓霞; 雷迎科因版权原因,仅展示原文概要,查看原文内容请购买。
基于循环平稳特性的时频分析法欠定盲源分离

基于循环平稳特性的时频分析法欠定盲源分离张良俊;杨杰;卢开旺;孙亚东【摘要】基于二次时频分布的算法是解决欠定盲源分离问题的一种有效方法.不同于传统算法,针对循环平稳信号,借助分段平均的周期图法求解谱相关密度函数,并利用其实现Wigner-Ville时频分布的重构.计算信号时频分布矩阵并找出自源时频点,利用自源时频点对应的时频分布矩阵构建新的3阶张量模型.利用平行因子分解,直接实现源信号的分离.该算法不需要假设任意时频点的源数目,不大于混合信号数目.仿真实验结果表明,所提出的方法可以有效地抑制噪声,并且只需要一步即可实现源信号的恢复,避免“两步法”造成的误差叠加,提高了盲源分离的效率和性能.【期刊名称】《兵工学报》【年(卷),期】2015(036)004【总页数】7页(P703-709)【关键词】信息处理技术;欠定盲源分离;循环平稳;二次时频分布;Wigner-Ville分布;平行因子分解【作者】张良俊;杨杰;卢开旺;孙亚东【作者单位】武汉理工大学光纤传感技术与信息处理教育部重点实验室,湖北武汉430070;武汉理工大学光纤传感技术与信息处理教育部重点实验室,湖北武汉430070;空军军械通用装备军事代表局,北京100071;武汉理工大学光纤传感技术与信息处理教育部重点实验室,湖北武汉430070【正文语种】中文【中图分类】TN911.7盲源分离(BSS)的目标在于仅仅利用接收到的混合信号,实现对所有源信号的分离,被广泛应用于语音、生物医学和阵列信号处理等领域[1-2]。
然而,源信号的数目极有可能大于混合信号的数目,此时的盲源分离被称为欠定盲源分离(UBSS)[3]。
目前,传统解决UBSS问题主要采用“两步法”,即首先估计出混合矩阵,再进行源信号的分离。
基于二次时频分布的方法被广泛地应用于混合矩阵的估计[4],其基本思想是首先构建混合信号的时频分布矩阵,然后利用所有自源点的时频分布矩阵构建新的高维矩阵,最后进行联合对角化和特征值分解等方法实现信号分离。
一种基于l~1范数的欠定盲源分离算法

一
种 基 于 范 数 的欠 定 盲 源 分 离算 法
谢 忠德
( 广东工业大学 应用数学 学院 , 广东 广州 5 0 2 ) 150
摘要 : 出了一种基 于两步法的欠定盲源分离新算 法. 提 在混 叠矩 阵估 计 阶段 , 采用 基于势 函数 的聚类方法 , 源信 在
号恢复 阶段 , 出一种快速 的稀疏 信号重构算法 . 提 系统方程 A () () s t =x £ 的任 一解 ,由它 的一 个特解 与其相对 应的 齐次线性方程组 的一组 基的线性组合之 和表示 , 从而使原来 直接估计有 /个独立 变量的源信号 S t 转化为估 计只 ' t () 有 n—m个 独立变量的系数 向量 Z再借助稀疏 表示实现盲源信号 的分离. 真实 验验证了新算法容易实现 , . 仿 分离速 度快 , 能够很好地满 足盲分离 对速度的要求. 关键词 : 欠定 盲源分离 ; 函数 ; 势 z 范数优化模型 ; 稀疏表示
中 图 分 类 号 : N 1 . T 9 23 文 献 标 志码 :A 文 章 编 号 :10 -12 2 1 )20 8 —5 0 77 6 ( 0 2 0 —0 9 0
An Al o ihm o de de e m i d Bl o r e S p r to s d o 1n r g rt f r Un r t r ne i nd S u c e a a i n Ba e n 1- o m
0 mn
叠 矩 阵 , 表示传 感 器数 目, m n表示 源 信 号 数 目, 是 t
离 散 时刻 , 是 观 测 样 本 数 . S B S问 题 的 目的就 是 , 对 任何 时刻 t根据 已知 的观测 信 号 ( ) 在 混 叠矩 , t, 阵 A 未 知 的情 况 下 , 复 出未 知 的 源 信 号 ( ) 当 恢 t. m<n时 , 个 问题就 是大 家熟 知 的 U S . 这 B S 在欠 定条 件 下 , 叠矩 阵 A 是 不 可 逆 的 , 实 现 欠 定 盲 分 离 混 要
时频分析的欠定盲源分离算法

时频分析的欠定盲源分离算法佚名【摘要】随着跳频通信系统性能的不断提升,传统信号处理方式无法适应跳频信号载频时变的特性,提出一种改进思想,采用时频分析方法对多跳频欠定盲源分离问题进行研究分析.由于线性时频分析方法满足线性叠加原理并且信号间没有交叉项干扰的影响,采用短时傅里叶变换对多跳频信号进行处理分析;利用自适应时频支撑点阈值设定的方法,剔除低能量噪点对时频单源点的影响,并结合改进的k-均值算法对混合矩阵进行估计;在不同时问段短时傅里叶变换的窗函数中,通过判断频率聚类数的不同,确定跳频信号频率跳变点的时刻及位置;通过时频单源点的时频比矩阵对时变混合矩阵进行估计.仿真实验验证了改进算法对混合矩阵具有较好的估计特性,算法改进的效果也比较明显.【期刊名称】《哈尔滨商业大学学报(自然科学版)》【年(卷),期】2018(034)006【总页数】5页(P706-710)【关键词】跳频信号;欠定盲源分离;时频单源点;短时傅里叶变换【正文语种】中文【中图分类】TN914跳频(Frequence Hopping,FH)通信是最常用的扩频方式之一,由于自我保护能力强,不易被干扰,在军事通信领域备受关注[1].跳频信号是最具代表性的非平稳信号,而时频分析方法可以对非平稳信号进行描述[2-3].在现实复杂的电磁环境中,由于无法预先获知先验信息,因此只能通过盲处理来获取更多的信息,对多跳频信号进行估计分析.1 跳频信号数学模型假设N个跳频源信号在一段时间内发生了K次频率跳变,设定源信号为sn(t)时,可以得到sn(t)的表达式,如式(1)所示:(1)其中:an(t)表示信号sn(t)的基带复包络;ωnk和φnk分别表示为第n个跳频信号在跳频源信号第k跳的载频和初始相位;Thn表示跳频源信号的跳周期;g(t)表示升余弦函数.为了方便表达,采用均匀线型天线阵,将N个源信号入射到M个阵元数的天线阵上,可以得到调频信号的解析形式,如式(2)所示:sn(t)=an(t)ej[ωn(t)+φn(t)](2)其中:ωn(t)、φn(t)分别表示时变的源信号频率和相位.当有噪声存在时,观测信号x(t)可表示为源信号和噪声的叠加,如式(3)所示:x(t)=A(t)s(t)+n(t)=(3)其中:x(t)=[x1(t),…,xM(t)]T为观测信号;A(t)是一个M×N的复数混合时变矩阵,用列矢量的形式可以将混合矩阵A(t)表示为A(t)=[a1(t),…,aN(t)]T,混合矩阵中各元素可以表示为amn(t)=e(-j2πfn(t)τmn);s(t)=[s1(t),…,sN(t)]T为跳频源信号;n(t)=[n1(t),…,nM(t)]T为均值为0,方差为δ2的加性高斯白噪声.2 单源点聚类2.1 线性时频分析为了更好的对跳频信号进行分析,引入线性时频分析方法对跳频信号进行稀疏化处理,既可以满足线性叠加原理,又没有交叉项的干扰[4-7].由于短时傅立叶变换(Short Time Fourier Transform,STFT)计算复杂度低且实时性较好[8-11].采用STFT对观测信号进行时频分析,如式(4)所示:(4)对式(3)进行STFT变换,变换后为:X(t,f)=A(t)S(t,f)+N(t,f)(5)其中:X(t,f)=[X1(t,f),…,XM(t,f)]T表示观测信号,S(t,f)=[S1(t,f),…,SN(t,f)]T以及N(t,f)=[N1(t,f),…,NM(t,f)]T分别表示源信号sn(t)以及噪声n(t)的STFT变换. 2.2 自适应时频支撑点复杂电磁环境夹杂着很多的噪声点,可以针对跳频信号的特点,通过对阀值εa的讨论,减少外界因素的干扰,令随机选取的时频单源点Pl=(tl,fl),皆满足‖Xm(Pl)‖2>εa.通过对阈值的设定,不但可以很好的保留信息量大的时频点,剔除可能受噪声影响信息量提取困难的时频点,而且为后续的工作节省了运算量[12].文献[13]中指出,噪声能量阀值εa的选取与噪声水平有关,通常情况下设置噪声阀值文献[13]由于在噪声方差σ2未知的情况下,将噪声阀值设置为不具有时变性.当阈值εa设定较小时,将会引入噪声;如果阈值εa设置过大时,将会有信息点被误剔除,造成信息的丢失.通过上述讨论,本文采用了自适应时频支撑点阈值筛选的方法.通过求时频点频率模值FTF的Fmin和Fmax的均值作为筛选值的初始值ε1.ε1=(Fmin+Fmax)/2(6)以ε1为分类标准,对所有时频点分为TFH1、TFH2两类,并分别统计每类中时频点聚集的个数为NTFR1、NTFR2,并求出各类平均值,如式(7)所示.(7)通过对式(6)中频率模值的更新,重新估计阈值.εk=(FTFR1+FTFR2)/2(8)采用迭代的思想,对阈值重复估计变换,当第k+1次与第k次阈值不再变化时,即εk+1=εk,操作结束.2.3 k-means聚类算法由于k-means聚类算法具有效率高、复杂度低的特点,被广泛应用于观测信号的聚类[14].若有M个观测信号,x=[x1,x2,…,xM]为m维列矢量.采用欧氏距离来对观测信号点进行分类处理,即观测信号点与某一个选取的聚类中心间欧氏距离最小,则该观测信号归属于此聚类中心.欧氏距离的计算规则如式(9)所示.(9)令观测信号点分为k组,随机在观测信号点中选取k个点作为初始聚类中心,根据式(9)分别计算出每个观测信号点同这k个聚类中心之间的欧氏距离,如果计算出来的欧氏距离小于设定的阀值,则该观测信号归属于距离最近的聚类中心.对每类观测信号点进行求均值,将计算出来的均值作为新的聚类中心,利用新的聚类中心重新计算欧氏距离,直到聚类中心不再改变.k-means聚类算法缺陷是需要提前估计跳频信号的聚类数目,但在盲源分离条件下,并没有先验知识,所以无法获得聚类数.本文采用DB Index聚类评估准则(Davies-Bouldin Index)[15],在没有任何先验知识的条件下,准确获取跳频信号的聚类数k,从而完成聚类分析DB Index准则基本模型如下所示:(10)其中:K是聚类数目,Di为Ci类中的所有样本点到其聚类中心的平均距离,Dj为Ci类中的所有样本点到Cj类中心的平均距离,Cij为Ci类和Cj类中心之间的距离.可以看出,DB越小表示类与类之间的相似度越低,分离效果越好,从而对应越佳的聚类结果.2.4 时频比矩阵模型为了便于叙述算法原理,令混合信号观测时频矩阵可以表示为(11)对于某个时频单源点Pl=(tl,fl)来说,假设该单源点只有源信号S1存在,即Sl(tl,fl)≠0,且S2(tl,fl)=S3(tl,fl)=0,将该点的观测数据X1(tl,fl)与X2(tl,fl)相比所得到的比值为(12)令某一时刻的源信号Sn的单源点个数为L,那么该单源时频点集合令m∈{1,…M},根据式(12)计算单源时频比矩阵可以表示为(13)由于时频比矩阵每列都与混合矩阵的每列一一相对应,从而可以得出混合矩阵列矢量的估计值,如式(14)所示.(14)综上分析,要想对混合矩阵进行估计,需要对跳频信号进行稀疏化处理,通过在时频域的聚类特性,采用k-means算法对时频点聚类分析,再通过时频比矩阵的分析,完成混合矩阵的估计.2.5 频率跳变点检测通过STFT对跳频信号的稀疏化处理,很容易观测到跳频信号发生了频率的跳变,跳频信号频率跳变点检测原理如图1所示.图1 跳频信号频率跳变点检测示意图从图1可以看出,当所选时间t=t1时,跳频信号的频率值为f1,因此时频点(t1,f1)周围具有能量;当所选时间t=t2时,跳频信号的频率值由f2和f3组成,我们可以在时频点(t2,f2)和(t2,f3)附近找到相应的能量分布.通过上述分析,当跳频信号发生跳变的瞬间,在时频域频率跳变点前后,都会有能量的聚集,但窗函数滑动步长以及窗函数长度的影响,不同窗函数的频率值会在跳变时刻附近同时存在.因此,可以根据k-means聚类算法在不同时刻、不同频率值产生的聚类数的不同,来判断跳变时刻,进而得到跳变点的位置.下面将对基于单源点聚类的混合矩阵估计算法步骤进行具体描述:1)傅里叶变换通过汉明窗作为窗函数,对观测信号xm(t)作稀疏化处理,得到时频域矩阵;2)采用自适应时频支撑点阈值的设定对时频点进行筛选,删除信息携带较少的点;3)k-均值聚类算法结合DB Index聚类评估准则在聚类数未知的条件下对混合矩阵进行估计;4)通过单源点对时频域中时频比矩阵X(Ωn)的估计,结合公式(14)可以获得混合矩阵列矢量的估计值并由各个列矢量估计值构建混合矩阵估计值5)根据各个时刻聚类数的比较,寻找N(t)≠N的时刻tn,即混合矩阵发生跳变的时刻,可以对时变混合矩阵进行估计.3 仿真分析仿真实验采用天线阵元数目M=2的均匀线性阵列,各阵元间距d=10,信号采样频率为20 MHz,跳频源信号数目N=4.各跳频源信号的参数如表1所示.表1 同步正交网台跳频信号参数跳频源信号跳频频率/MHzS17.5,7.2,6.6,8.4,7.8S24.5,8,5.5,5,6.5S33.5,5,4.5,6.1,4S46.5,6,7.5,7,5.5 通过阈值εa对低能量噪点的剔除,以及通过STFT变换稀疏化处理,跳频信号仿真如图2所示.选用混合矩阵估计误差EA(dB)对估计性能进行衡量,混合矩阵估计误差EA的具体定义如下:图2 跳频信号仿真分析图(15)其中:为算法估计值,N为初始信号个数,‖·‖F为F-范数,EA数值越低则的值越接近A,即准确度越高.本文通过改进的k-means聚类算法结合时频比矩阵对时变混合矩阵进行估计,仿真对比可以看出,本文算法具有更好的性能.见图3.图3 混合矩阵估计误差随信噪比变化曲线4 结语基于通信对抗在战场环境中的重要作用,如何保证通信网络系统抗干扰、保密、高效运行,成为了研究的重点,欠定条件下的多跳频信号网台分选在实际作战中十分关键.本文基于时频单源点的研究,针对跳频信号中时频域支撑点阈值的分析,以及改进的k-means聚类方法的结合,实现了多跳频时变混合矩阵的估计.通过仿真验证了算法的有效性,并在低信噪比条件下显示出良好的性能.参考文献:【相关文献】[1] 陈利虎. 跳频信号的侦察技术研究[D]. 长沙: 国防科学技术大学, 2009.[2] 吕晨杰, 王斌. 采用纹理特征的跳频信号盲检测算法[J]. 信号处理, 2015, 31(4): 453-460.[3] 冯涛, 袁超伟. 基于时频分布的跳频信号盲分离方法[J]. 系统工程与电子技术, 2010, 32(5): 900-903.[4] 彭天亮. 时频域欠定盲分离研究[D]. 南京: 东南大学, 2016.[5] 付卫红, 李爱丽, 黄坤, 等. 欠定盲分离时变混合矩阵的估计[J]. 电子科技大学学报, 2015, 44(4): 508-512.[6] 齐昶, 王斌. 低信噪比下跳频信号参数盲估计[J]. 计算机工程与应用, 2012, 48(3): 153-155.[7] 陈利虎. 基于空时频分析的多分量跳频信号DOA估计[J]. 系统工程与电子技术, 2011, 33(12): 2587-2592.[8] 武少豪. 基于欠定盲分离的跳频信号恢复与分选技术研究[D]. 西安: 西安电子科技大学, 2014.[9] 高瑞涛. 基于时频分析的跳频信号参数估计方法研究[D]. 西安: 西安电子科技大学, 2011.[10] 张曦, 杜兴民, 朱礼亚. 基于Gabor谱方法的跳频信号时频分析[J]. 数据采集与处理, 2007, 22(2): 150-154.[11] 张曦, 王星, 杜兴民. 基于小波变换的跳频信号参数盲估计[J]. 电路与系统学报, 2009, 14(4): 60-65.[12] 于欣永, 郭英, 张坤峰, 等. 基于盲源分离的多跳频信号网台分选算法[J]. 信号处理, 2017 (8): 1082-1089.[13] 宁晓鹏. 基于时频分析的跳频信号盲分离算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.[14] 李爱丽. 欠定盲源分离混合矩阵估计算法的研究[D]. 西安: 西安电子科技大学, 2014.[15] 张莉, 孙钢, 郭军. 基于K-均值聚类的无监督的特征选择方法[J]. 计算机应用研究, 2005,22(3): 23-24.。
基于广义S变换地震剖面数据时频分析及分频显示

基于广义S变换地震剖面数据时频分析及分频显示
李宏伟;姜镭
【期刊名称】《内蒙古石油化工》
【年(卷),期】2009(000)019
【摘要】地震信号是一种非平稳信号,时频分析法是非平稳信号分析的有效方法,用时频分析技术处理地震信号,可以较为精确地分析数据时间和频率特征。
现阶段应用于地震数据处理方面的时频分析方法有很多种,本文选取广义S变换作为时频分析工具,对地震数据进行处理,并提取不同频率剖面进行对比。
实际资料处理表明,广义S变换在地震高分辨率处理方面是行之有效的,具有较强的抗干扰能力。
通过时频分解,我们可以根据需求提取不同的单频剖面,细致研究局部层位,识别地震剖面中特征信息。
【总页数】3页(P57-59)
【作者】李宏伟;姜镭
【作者单位】成都理工大学信息工程学院,四川成都610059
【正文语种】中文
【中图分类】P631.443
【相关文献】
1.广义S变换域低照度图像时频分析及滤波
2.时频分析在地震剖面数据的分频显示中的应用
3.基于物理小波时频分析及RGB分频混色的高精度频谱成像技术优势分
析及应用4.广义S变换时频分析在广域电磁法数据处理中的应用5.基于广义S变换时频滤波的MT数据去噪
因版权原因,仅展示原文概要,查看原文内容请购买。
【国家自然科学基金】_盲源信号分离_基金支持热词逐年推荐_【万方软件创新助手】_20140801
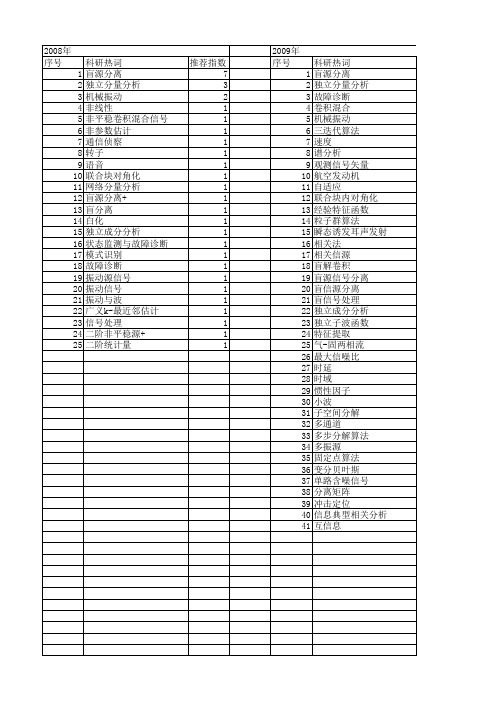
科研热词 盲源分离 独立分量分析 故障诊断 非平稳信号 盲信源分离 振动与波 高阶累积量 频谱分析 频域 非负矩阵分解 非线性盲源提取 非线性盲源分离 非平稳 雅克比方法 阈值函数 重盲源分离 近似联合块对角化 跳频信号 贝叶斯推论 语音信号处理 船舶 航空发动机 联合对角化 线性聚类 第二代小波 稀疏成分分析 相合束广义特征分解 相关系数分析 盲解卷积 盲源信号分离 盲信号处理 盖尔圆理论 白化 滚动轴承 源数估计 测向 波束形成 水下航行器 歌曲数据库 次序不确定性 最小输出能量 最大比合并 时频比 时频分析 时频分布 时差估计 旨源分离 旋转机械 排列模糊 振源 投影梯度算法 小波多分辨率分析
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 科研热词 盲源分离 独立分量分析 飞机 脑电信号 独立成分分析 梯度算法 循环累积量 信息处理 雅可比旋转 跳频信号 超定 负熵 贝叶斯推论 舱音 舱青 稀疏表示 稀疏分量分析 矩阵联合对角化 盲信号分离 独立变量分析 熵估计 涡扇发动机 波恩-约旦分布 欠定盲源分离 欠定盲分离 欠定混合 模糊聚类 机械振源 最大信噪比 故障诊断 振动信号处理 振动信号 循环平稳信号 广义hough变换 局域均值分解 小波重构 小波变换 小波分解 参考源信号 压缩感知 半盲分离 信源估计 信号源噪声 交流电机调速系统 互相关系数 主成分分析 fast ica 推荐指数 12 3 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练晓婷
(大连理工大学机械工程学院
116023)
摘要:盲源分离对于多振源信号的故障诊断与识别是一种有效的方法,但是传统的盲源分离算法都是针对观察信号大于或等 于源信号的情况,但对于观察信号小于源信号的欠定盲分离问题,这在很大程度上制约了盲源分离的实际应用。通过应用经 验模式分解和时频分析对非平稳信号分析的优势,提出基于时频分析的欠定盲源分离方法进行设备微弱特征提取。对振动信 号进行经验模式分解,并根据分解得到的内蕴模式分量估计源信号个数并选择最优的观察信号,将振动信号与选择的最优观 察信号组成新的观察信号进行基于时频分析的盲源分离,通过对仿真信号和齿轮箱实测信号进行验证分析。并与基于独立分 量分析的盲源分离算法进行对比,研究表明基于时频分析的盲源分离对混合信号具有更好的分离效果,能够较好地对微弱特 征进行提取。 关键词:盲源分离;欠定信号;时频分析;经验模式分解;微弱特征提取 中图分类号:TH165
* 国家自然科学基金 (51175057) 和中央高校基本科研业务费专项资金 (DUT14ZD204)资助项目。20131004 收到初稿,20140210 收到修改稿
情况,因此目前采用的正定盲源分离方法不能满足 实际要求,急需研究一种新的针对观察信号小于源 信号的多振源信号分析方法。 现有的基于时频分析和独立变量分析的盲源 分离方法都是针对正定的盲源分离,适用的都是观 察信号大于或等于源信号的盲源分离问题,艾延廷 [1] 等 基 于 独 立 成 分 分 析 (Independent component analysis, ICA)对航空发电机和低压转子的振动信号 [2] 进行正定的盲源分离,ADEL 等 提出了基于时频 分析的盲源分离算法。在实际的工程应用中的,由 于采集通道数有限而振动源比较多,导致观察信号 数目没有源信号的个数多, 而形成欠定盲分离问题,
第 50 卷第 18 期 2014 年 9 月
机
械工程ຫໍສະໝຸດ 学 报Vol.50 Sep.
No.18 2014
JOURNAL OF MECHANICAL ENGINEERING
DOI:10.3901/JME.2014.18.014
基于时频分析的欠定信号盲分离与微弱特征提取*
李宏坤 张学峰 徐福健 刘洪轶
大连
式中
f (t ) ——源信号; imfi (t ) ——分解后的第 i 个内蕴模式分量; rn ——趋势项;
n ——分解后得到的内蕴模式分量的个数。 在机械故障诊断中,往往故障信息都隐藏在背 景噪声中,而为了对故障信息进行分析,经常需要 通过滤波来分离噪声,但是一般的滤波是将信号的 高频部分当作是噪声信号去除,这样可能导致高频 的故障信息被忽略,而 EMD 分解是对信号进行从 高频到低频的分解,从频域上看 EMD 分解相当于
[5]
n
i i 1
n
(3)
前 k (1 k n) 个虚拟观察信号的累计方差贡献 率可以表示为
C j j i
j 1 j 1 i 1
k
k
n
(4)
f (t ) imfi (t ) rn
i 1
(1)
通过式 (3) 可以估计得到一个满足条件的最小 值 k1 ,即可初步估计源信号个数。同时,由于平均 特征值可以反映特征值分布的集中趋势,那么可以 利用平均特征值进一步估计源信号的个数,即将所 有的特征值中大于平均特征值的个数记为 k2 。最 后,结合累计方差贡献率方法和平均特征值方法估 计的源信号个数,取两者中较大的数作为最后的源 信号个数,即 k max(k1 , k2 ) 。图 1 所示为估计源信 号个数的流程图。 1.3 最优观察信号选取 在进行欠定盲源分离时,首先在估计出了源信 号的个数之后,就要选择相同数目的观察信号,把 欠定盲分离转换为正定的盲分离,但是从经验模式
[4]
对信号进行一系列的倍频程带通滤波,故障信息将 会在不同的 IMF 中得以体现。EMD 在对信号进行 分离时,具有频带自适应性和对信号结构的自适应 性, 频带自适应性是指带通滤波器在高频处频带窄, EMD 即 滤波随着信号的频谱的变化而发生变化; 对信号结构自适应性是指 EMD 滤波随着信号时域 结构和相位的变化而变化,也就是说即使频谱很接 近的信号,经过 EMD 分解的结果包含有原信号的 [6-7] 故障信息 。 1.2 源信号个数估计 在对振动信号 x1 (t ) 进行欠定盲源分离时,为了 保证信号分析的精度,需要根据 EMD 分解结果估 计源信号个数并构造多通道的观察信号。将观察信 号与 EMD 分解结果构成虚拟的多通道观察信号 x(t),如式(2)所示
0
前言
盲源分离可以将振动信号中的众多振动源信 号分离出来,从而对机械设备进行故障诊断,是在 20 世纪 80 年代中后期发展起来的一种功能强大的 信号处理方法,为机械设备多故障复合诊断提供了 一种新的方法,已成为很多领域研究和发展的重要 课题,同时也具有十分重要的实用价值。测试通道 有限而振动源较多的信号分析,是属于欠定盲分离
x (t ) [ x1 (t ), imf1 (t ), imf 2 (t ),, rn1 (t )]
(2)
本 文 利 用 主 元 分 析 (Principal component analysis, PCA)中主元个数的确定的方法来估计源信 号,使用的是基于平均特征值的累计方差贡献率的 [8-9] 方法来估计源信号个数 。 首先要保证虚拟多通道观察信号的累计方差 贡献率要大于某一阈值,一般根据专家经验阈值 取值为 85%。计算虚拟多通道观察信号 x(t)的协方 T 差矩阵 Rx=(x(t)x(t) ) 的特征值,从大到小排列为 1 , 2 ,, n ,则第 j 个虚拟观察信号的方差贡献率
16
机
械
工
程
学
报
第 50 卷第 18 期期
(2) 计算协方差矩阵 Rxx ( ) 按降序排列的特征 值 1 , 2 ,, m 和对应的特征矢量 h1 , h2 ,, hm ,并估 ˆ 计噪声方差 σ ˆ 2 和白化矩阵 W
ˆ2
m 1 i m n i n1
(6)
ˆ [( ˆ 2 )1/ 2 h1 ,(1 ˆ 2 )1/ 2 h2 , ,(n ˆ 2 )1/ 2 hn ] W 1
Investigation on Blind Source Separation for Under-determined Mixtures Based on Time-frequency Analysis and Weak Feature Extraction
LI Hongkun ZHANG Xuefeng XU Fujian LIU Hongyi LIAN Xiaoting
1
1.1
经验模式分解
经验模式分解定义
Cj j
经验模式分解(Empirical mode decomposition, EMD)是 HUANG 在 1998 年提出来的,是用来处理 非线性、非平稳的信号,能将信号分解为一系列的 表征信号特征时间尺度的内蕴模式分量 (Intrinsic mode function, IMF)和一个趋势项之和, 分解结果可 以表示为如下形式
月 2014 年 9 月
李宏坤等:基于时频分析的欠定信号盲分离与微弱特征提取
15
用传统的盲分离算法不能解决问题,需要研究新的 算法,欠定盲源分离目前已经成为盲信号处理领域 中的热点研究问题,得到很多人的关注。毋文峰 [3] 等 提出了对单通道信号进行基于快速 ICA(Fast independent component analysis, FastICA)算法的盲 分离,利用的是奇异值估计源信号个数;刘佳等 也提出了对单通道信号地声信号的盲分离问题,利 用 集 合 经 验 模 分 解 (Ensemble empirical mode decomposition,EEMD)将信号从一维转换为多维, 将欠定的盲分离问题转换为正定盲分离问题。基于 时频分析的盲源分离方法虽然对混合信号的分离有 很好的效果,但是对于观察信号个数小于源信号的 欠定盲分离问题仍然不能解决,并且基于时频分析 的盲分离方法得到的估计源信号的顺序和幅值是不 确定的,并不能完全准确地分离出振动源信号,对 估计得到的源信号需要对其幅值进行归一化处理。 本文根据经验模式分解的结果估计源信号个 数并且选择最优的观察信号,将欠定的盲分离转换 为正定盲分离,然后进行基于时频分析的盲分离来 处理欠定观察信号的盲分离问题,获取表征信号微 弱故障的信号,从而实现故障诊断与状态识别。并 以仿真信号与实际测试的齿轮箱微弱故障特征提取 进行方法的有效性验证。
(School of Mechanical Engineering, Dalian University of Technology, Dalian 116023)
Abstract:Blind source separation(BSS) is an effective method for the fault diagnosis and classification of mixture signals with multiple vibration sources. The traditional BSS algorithm is applicable to the number of observed signals is no less to the source signals. BSS performance is limit for the under-determined condition that the number of observed signals is less than source signals. An under-determined BSS method is provided based on the advantage of time-frequency analysis and empirical mode decomposition (EMD). It is suitable for weak feature extraction and pattern recognition. The vibration signal is decomposed by using EMD. The number of source signals are estimated and the optimal observed signals are determined according to the EMD result. Then, the vibration signal and the optimal observed signals are used to construct the multi-channel observed signals. In the end, blind source separation based on time-frequency analysis are used to the constructed signals. Simulation signal and gearbox signals are used to verify the effectiveness of this method. Compared with independent component analysis, BSS based on time-frequency analysis has good performance on signal separation. It is more suitable for weak feature extraction. Key words:blind source separation;under-determined mixtures;time-frequency analysis;empirical mode decomposition;weak feature extraction *
