2020年郑州大学高等数学考试题(完整版)
2020年河南省高考数学试卷(理科)(新课标ⅰ)

2020年河南省高考数学试卷(理科)(新课标Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)若z=1+i,则|z2﹣2z|=()A.0B.1C.D.22.(5分)设集合A={x|x2﹣4≤0},B={x|2x+a≤0},且A∩B={x|﹣2≤x≤1},则a=()A.﹣4B.﹣2C.2D.43.(5分)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为()A.B.C.D.4.(5分)已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p=()A.2B.3C.6D.95.(5分)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(x i,y i)(i=1,2,…,20)得到下面的散点图:由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是()A.y=a+bx B.y=a+bx2C.y=a+be x D.y=a+blnx 6.(5分)函数f(x)=x4﹣2x3的图象在点(1,f(1))处的切线方程为()A.y=﹣2x﹣1B.y=﹣2x+1C.y=2x﹣3D.y=2x+17.(5分)设函数f(x)=cos(ωx+)在[﹣π,π]的图象大致如图,则f(x)的最小正周期为()A.B.C.D.8.(5分)(x+)(x+y)5的展开式中x3y3的系数为()A.5B.10C.15D.209.(5分)已知α∈(0,π),且3cos2α﹣8cosα=5,则sinα=()A.B.C.D.10.(5分)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π11.(5分)已知⊙M:x2+y2﹣2x﹣2y﹣2=0,直线l:2x+y+2=0,P为l上的动点.过点P 作⊙M的切线P A,PB,切点为A,B,当|PM|•|AB|最小时,直线AB的方程为()A.2x﹣y﹣1=0B.2x+y﹣1=0C.2x﹣y+1=0D.2x+y+1=0 12.(5分)若2a+log2a=4b+2log4b,则()A.a>2b B.a<2b C.a>b2D.a<b2二、填空题:本题共4小题,每小题5分,共20分。
郑州大学网络教育高等数学期末考试复习题及参考答案

正确 错误
回答错误!正确答案: A
收藏
正确 错误
回答错误!正确答案: B
收藏
错误 正确
回答错误!正确答案: B
收藏
正确 错误
回答错误!正确答案: B
收藏
错误 正确
回答错误!正确答案: B
函数的极值点一定是函数的驻点。 收藏
正确 错误
回答错误!正确答案: B
连续周期函数的原函数为周期函数。
收藏
B.
仅有水平渐近线
C. 仅有铅直渐近线
D. 既有水平渐近线,又有铅直渐近线
回答错误!正确答案: D
收藏
A.
B.
C.
D.
回答错误!正确答案: A
收藏
A.
2
B.
0
C.
1
D.
3
回答错误!正确答案: A
收藏
A.
B.
C.
D.
回答错误!正确答案: D
收藏
A.
B. C. D.
回答错误!正确答案: B
收藏
A. B.
C.
D.
回答错误!正确答案: B
收藏A.1来自B.0C.-2
D.
2
回答错误!正确答案: D
收藏
A. 充分必要条件
B. 必要条件
C. 既非充分也不必要条件
D. 充分条件
回答错误!正确答案: B
收藏
A. B.
C.
D.
回答错误!正确答案: A
收藏
A.
B.
C.
D.
回答错误!正确答案: A
收藏
A.
B. C. D.
错误 正确
回答错误!正确答案: A
2020年全国大学高等数学考试及答案解析
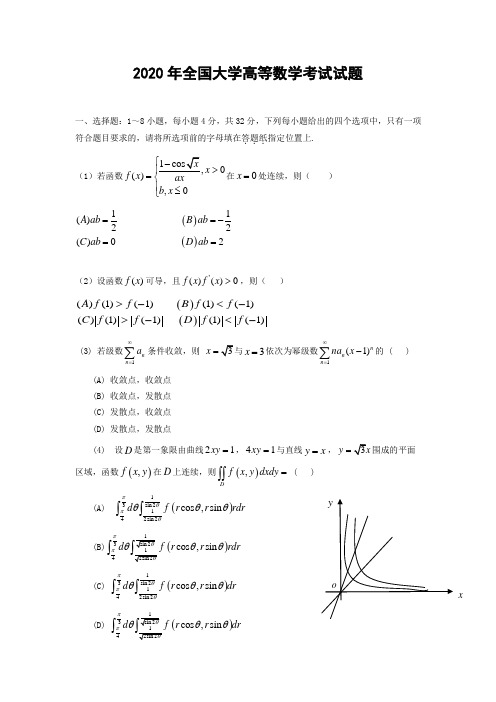
2020年全国大学高等数学考试试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)若函数1,0(),0x f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续,则( ) ()()11()22()02A abB abC abD ab ==-==(2)设函数()f x 可导,且'()()0f x f x >,则( )()()()(1)(1)(1)(1)()(1)(1)(1)(1)A f fB f fC f fD f f >-<->-<-(3) 若级数1∞=∑nn a条件收敛,则=x 3=x 依次为幂级数1(1)∞=-∑n n n na x 的 ( )(A) 收敛点,收敛点 (B) 收敛点,发散点 (C) 发散点,收敛点 (D) 发散点,发散点(4) 设D 是第一象限由曲线21xy =,41xy =与直线y x =,y =围成的平面区域,函数(),f x y 在D 上连续,则(),Df x y dxdy =⎰⎰ ( )(A)()13sin 2142sin 2cos ,sin d f r r rdr πθπθθθθ⎰⎰(B)()34cos ,sin d f r r rdr ππθθθ⎰(C)()13sin 2142sin 2cos ,sin d f r r dr πθπθθθθ⎰⎰(D)()34cos ,sin d f r r dr ππθθθ⎰x(5)设α是n 维单位列向量,E 为n 阶单位矩阵,则( )()()()()22T T TT A E B E C E D E αααααααα-++-不可逆不可逆不可逆不可逆(6)设矩阵200210100021,020,020*********A B C ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,则( ) ()()(),,(),,A A C B C B A C B C C A C B C D A C B C 与相似与相似与相似与不相似与不相似与相似与不相似与不相似(7) 若A,B 为任意两个随机事件,则 ( )(A) ()()()≤P AB P A P B (B) ()()()≥P AB P A P B (C) ()()()2≤P A P B P AB (D) ()()()2≥P A P B P AB(8)设随机变量,X Y 不相关,且2,1,3===EX EY DX ,则()2+-=⎡⎤⎣⎦E X X Y ( )(A) 3- (B) 3 (C) 5- (D) 5二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (1) 已知函数21()1f x x=+,则(3)(0)f =__________ (2) 微分方程'''230y y y ++=的通解为y =_________(3) 若曲线积分221L xdx aydy x y -+-⎰在区域{}22(,)|1D x y x y =+<内与路径无关,则 a =__________(4)设Ω是由平面1++=x y z 与三个坐标平面平面所围成的空间区域,则(23)__________.x y z dxdydz Ω++=⎰⎰⎰(5)设二维随机变量(,)x y 服从正态分布(1,0;1,1,0)N ,则{0}________.P XY Y -<=三、解答题:15—23小题,共94分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤. (1)(本题满分10分)设函数(,)f u v 具有2阶连续偏导数,(,cos )xy f e x =,求0x dy dx=,22x d y dx=(2)(本题满分10分)求21lim ln 1nn k kk nn →∞=⎛⎫+ ⎪⎝⎭∑(3)(本题满分10分)已知函数()y x 由方程333320x y x y +-+-=确定,求()y x 的极值(4)(本题满分 10 分)(I )设函数()()u x ,v x 可导,利用导数定义证明u x v x u x v x u x v x '''=+[()()]()()()()(II )设函数()()()12n u x ,u x ,,u x 可导,n f x u x u x u x =12()()()(),写出()f x 的求导公式.(5)(本题满分 10 分)已知曲线L的方程为,z z x ⎧=⎪⎨=⎪⎩起点为()A,终点为()0,B ,计算曲线积分()()2222d d ()d LI y z x z x y y x y z =++-+++⎰.(6) (本题满11分)设向量组1,23,ααα内3R 的一个基,113=2+2k βαα,22=2βα,()313=++1k βαα.(I )证明向量组1β2β3β为3R 的一个基;(II )当k 为何值时,存在非0向量ξ在基1,23,ααα与基1β2β3β下的坐标相同,并求所有的ξ.(7)(本题满分11分)设二次型222123123121323(,,)2282f x x x x x ax x x x x x x =-++-+在正交变换X QY =下的标准型221122y y λλ+,求a 的值及一个正交矩阵Q(8)(本题满分11分)设随机变量,X Y 相互独立,且X 的概率分布为1(0)(2)2P X P X ====,Y 的概率密度为201()0,y y f y <<⎧=⎨⎩,其他()I 求()P Y EY ≤()∏求Z X Y =+的概率密度。
2020年全国大学高等数学考试试题及解析

2020年全国大学高等数学考试试题一、填空题(本题共5分,每小题3分,满分15分.把答案在题中横线上.)(1) 2013sin coslim(1cos )ln(1)x x x x x x →+=++ . (2) 设幂级数nn n a x∞=∑的收敛半径为3,则幂级数11(1)n nn na x ∞+=-∑的收敛区间为 .(3) 对数螺线e θρ=在点2(,)(,)2e ππρθ=处的切线的直角坐标方程为 .(4)函数ln(u x =在(1,0,1)A 点处沿A 点指向(3,2,2)B -点方向的方向导数为___________.(5) 设A 是43⨯矩阵,且A 的秩()2r A =,而102020103B ⎛⎫ ⎪= ⎪ ⎪-⎝⎭,则()r AB =___________.二、选择题(本题共5个小题,每小题3分,满分15分.在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1) 已知2()()x ay dx ydyx y +++为某函数的全微分,则a 等于 ( )(A) -1 (B) 0 (C) 1 (D) 2 (2) 设()f x 有二阶连续导数,且(0)0f '=,0()lim 1||x f x x →''==,则 ( ) (A) (0)f 是()f x 的极大值 (B) (0)f 是()f x 的极小值(C) (0,(0))f 是曲线()y f x =的拐点(D) (0)f 不是()f x 的极值,(0,(0))f 也不是曲线()y f x =的拐点(3) 设0(1,2,)n a n >=,且1n n a ∞=∑收敛,常数(0,)2πλ∈,则级数21(1)(tan )n n n n a n λ∞=-∑( )(A) 绝对收敛 (B) 条件收敛 (C) 发散 (D) 收敛性与λ有关(4) 设111122232333,,,a b c a b c a b c ααα⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦则三条直线1110a x b y c ++=,2220a x b y c ++=,3330a x b y c ++=(其中220,1,2,3i i a b i +≠=)交于一点的充要条件是 ( )(A) 123,,ααα线性相关 (B) 123,,ααα线性无关(C) 秩123(,,)r ααα=秩12(,)r αα (D) 123,,ααα线性相关,12,αα线性无关(5) 设两个相互独立的随机变量X 和Y 的方差分别为4和2,则随机变量32X Y -的方差是( )(A) 8 (B) 16 (C) 28 (D) 44三、(本题共3小题,每小题5分,满分15分.)(1) 计算22(),I x y dV Ω=+⎰⎰⎰其中Ω为平面曲线22,0y z x ⎧=⎨=⎩绕z 轴旋转一周形成的曲面与平面8z =所围成的区域.(2) 计算曲线积分()()()Cz y dx x z dy x y dz -+-+-⎰,其中C 是曲线221,2,x y x y z ⎧+=⎨-+=⎩从z轴正向往z 轴负向看,C 的方向是顺时针的.(3) 在某一人群中推广新技术是通过其中已掌握新技术的人进行的.设该人群的总人数为N ,在0t =时刻已掌握新技术的人数为0x ,在任意时刻t 已掌握新技术的人数为()x t (将()x t 视为连续可微变量),其变化率与已掌握新技术人数和未掌握新技术人数之积成正比,比例常数0,k >求()x t .四、(本题共2小题,每小题6分,满分12分.) (1) 计算曲面积分(2)Sx z dydz zdxdy ++⎰⎰,其中S 为有向曲面22(01)z x y z =+≤≤,其法向量与z 轴正向的夹角为锐角.(2) 设变换2,u x y u x ay=-⎧⎨=+⎩可把方程2222260z z zx x y y ∂∂∂+-=∂∂∂∂化简为20z u v ∂=∂∂,求常数a ,其中(,)z z x y =有二阶连续的偏导数.五、(本题满分6分)设()f x 连续,1()(),x f xt dt ϕ=⎰且0()limx f x A x→=(A 为常数),求()x ϕ'并讨论()x ϕ'在0x =处的连续性.六、(本题满分7分)设对任意0x >,曲线()y f x =上点(,())x f x 处的切线在y 轴上的截距等于01()xf t dt x⎰,求()f x 的一般表达式.七、(本题共2小题,第(1)小题5分,第(2)小题6分,满分11分.)(1) 设B 是秩为2的54⨯矩阵,123(1,1,2,3),(1,1,4,1),(5,1,8,9)T T Tααα==--=--是齐次线性方程组0Bx =的解向量,求0Bx =的解空间的一个标准正交基.(2) 已知111ξ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦是矩阵2125312A a b -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦的一个特征向量.(Ⅰ) 试确定参数,a b 及特征向量ξ所对应的特征值; (Ⅱ) 问A 能否相似于对角阵?说明理由.八、(本题满分6分)设TA E ξξ=-,其中E 是n 阶单位矩阵,ξ是n 维非零列向量,Tξ是ξ的转置,证明:(1) 2A A =的充要条件是1Tξξ=;(2) 当1Tξξ=时,A 是不可逆矩阵.九、(本题满分7分)从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是25.设X 为途中遇到红灯的次数,求随机变量X 的分布律、分布函数和数学期望.十、填空题(本题共2小题,每小题3分,满分6分.)(1) 设工厂A 和工厂B 的产品的次品率分别为1%和 2%,现从由A 和B 的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属A 生产的概率是__________. (2) 设ξ、η是两个相互独立且均服从正态分布2)N 的随机变量,则随机变量 ξη-的数学期望()E ξη-=__________.2020年全国大学高等数学考试试题及解析一、填空题(本题共5分,每小题3分,满分15分.把答案在题中横线上.) (1)【答案】32【分析】这是00型极限.注意两个特殊极限00sin ln(1)lim 1,lim 1x x x x x x→→+==.【解析】将原式的分子、分母同除以x ,得2001sin 13sin cos 3cos3limlim .ln(1)(1cos )ln(1)2(1cos )x x x x x x x x x x x x x x→→++==++++ 评注:使用洛必达法则的条件中有一项是0()lim()x x f x g x →''应存在或为∞,而本题中, []200111(3sin cos )3cos 2cos sinlimlim 1cos (1cos )ln(1)sin ln(1)1x x x x x x x x x xx x x x x→→'+++=+'++-+++ 极限不存在,也不为∞,不满足使用洛必达法则的条件,故本题不能用洛必达法则.【相关知识点】1.有界量乘以无穷小量为无穷小量. (2)【答案】(2,4)-【解析】考察这两个幂级数的关系.令1t x =-,则()1212111n n n nnnn n n na ttna tta t ∞∞∞+-==='==∑∑∑.由于逐项求导后的幂级数与原幂级数有相同的收敛半径,1nn n a t∞=∑的收敛半径为3⇒()1nn n a t ∞='∑的收敛半径为 3.从而()2111n n n n n n t a t na t ∞∞+=='=∑∑的收敛半径为3,收敛区间即(-3,3),回到原幂级数11(1)n nn na x ∞+=-∑,它的收敛区间为313x -<-<,即(2,4)-.评注:幂级数的收敛区间指的是开区间,不考虑端点. 对于n n n a x ∞=∑,若1limn n na a ρ+→+∞=⇒它的收敛半径是1R ρ=.但是若只知它的收敛半径为R ,则⇒11limn n n a a R +→+∞=,因为1lim n n naa +→+∞可以不存在(对于缺项幂级数就是这种情形).(3)【答案】2x y e π+=【解析】求切线方程的主要问题是求其斜率x k y '=,而x y '可由e θρ=的参数方程cos cos ,sin sin x e y e θθρθθρθθ⎧==⎪⎨==⎪⎩求得: 2sin cos sin cos ,1cos sin cos sin x x y e e y y x e e θθθπθθθθθθθθθθθθ='++''====-'--, 所以切线的方程为2(0)y e x π-=--,即2x y e π+=.评注:本题难点在于考生不熟悉极坐标方程与直角坐标方程之间的关系.(4)【答案】12【分析】先求方向l 的方向余弦和,,u u ux y z∂∂∂∂∂∂,然后按方向导数的计算公式 cos cos cos u u u u l x y zαβγ∂∂∂∂=++∂∂∂∂求出方向导数. 【解析】因为l 与AB 同向,为求l 的方向余弦,将{}{}31,20,212,2,1AB =----=-单位化,即得 {}{}12,2,1cos,cos ,cos 3||AB l AB αβγ==-=. 将函数ln(u x =+分别对,,x y z 求偏导数得12Au x ∂==∂,0Au y∂==∂,12Au z∂==∂, 所以cos cos cos AA AA u u u ulx y z αβγ∂∂∂∂=++∂∂∂∂ 1221110()233232=⨯+⨯-+⨯=. (5)【答案】2【解析】因为10220100103B ==≠-,所以矩阵B 可逆,故()()2r AB r A ==.【相关知识点】()min((),())r AB r A r B ≤.若A 可逆,则1()()()[()]()r AB r B r EB r A AB r AB -≤==≤.从而()()r AB r B =,即可逆矩阵与矩阵相乘不改变矩阵的秩.二、选择题(本题共5个小题,每小题3分,满分15分.在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1)【答案】(D)【解析】由于存在函数(,)u x y ,使得 22()()()x ay dx ydydu x y x y +=+++, 由可微与可偏导的关系,知2()u x ay x x y ∂+=∂+,2()u yy x y ∂=∂+, 分别对,y x 求偏导数,得2243()()2()(2)()()u a x y x ay x y a x ayx y x y x y ∂+-+⋅+--==∂∂++, 232()u yy x x y ∂-=∂∂+. 由于2u y x ∂∂∂与2u x y∂∂∂连续,所以22u uy x x y ∂∂=∂∂∂∂,即 33(2)2()()a x ay y x y x y ---=++2a ⇒=,故应选(D).(2)【答案】(B)【解析】因为()f x 有二阶连续导数,且0()lim10,||x f x x →''=>所以由函数极限的局部保号性可知,在0x =的空心领域内有()0||f x x ''>,即()0f x ''>,所以()f x '为单调递增. 又由(0)0f '=,()f x '在0x =由负变正,由极值的第一充分条件,0x =是()f x 的极小值点,即(0)f 是()f x 的极小值.应选(B).【相关知识点】极限的局部保号性:设0lim ().x x f x A →=若0A >(或0A <)⇒0,δ∃>当00x x δ<-<时,()0f x >(或()0f x <).(3)【答案】(A)【解析】若正项级数1nn a∞=∑收敛,则21nn a∞=∑也收敛,且当n →+∞时,有tanlim (tan )limn n n n n nλλλλλ→+∞→+∞=⋅=. 用比较判别法的极限形式,有22tanlim0nn nn a na λλ→+∞=>.因为21n n a ∞=∑收敛,所以2lim tann x n a nλ→+∞也收敛,所以原级数绝对收敛,应选(A).【相关知识点】正项级数比较判别法的极限形式:设1n n u ∞=∑和1n n v ∞=∑都是正项级数,且lim,nn nv A u →∞=则(1) 当0A <<+∞时,1nn u∞=∑和1nn v∞=∑同时收敛或同时发散;(2) 当0A =时,若1nn u∞=∑收敛,则1nn v∞=∑收敛;若1nn v∞=∑发散,则1nn u∞=∑发散;(3) 当A =+∞时,若1nn v∞=∑收敛,则1nn u∞=∑收敛;若1nn u∞=∑发散,则1nn v∞=∑发散.(4)【答案】(D)【解析】方法1:三条直线交于一点的充要条件是方程组111111222222333333000a x b y c a x b y c a x b y c a x b y c a x b y c a x b y c++=+=-⎧⎧⎪⎪++=⇒+=-⎨⎨⎪⎪++=+=-⎩⎩ 有唯一解.将上述方程组写成矩阵形式:32A X b ⨯=,其中112233a b A a b a b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦是其系数矩阵,123c b c c -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦.则AX b =有唯一解⇔[]()2r A r A b ==(方程组系数矩阵的秩与增广矩阵的秩相等且等于未知量的个数),即A 的列向量组12,αα线性相关.所以应选(D). 方法2:用排除法.(A)123,,ααα线性相关,当123ααα==时,方程组的系数矩阵与增广矩阵的秩相等且小于未知量的个数,则①式有无穷多解,根据解的个数与直线的位置关系.所以三条直线重合,相交有无穷多点,(A)不成立.(B)123,,ααα线性无关,3α不能由12,αα线性表出,方程组的系数矩阵与增广矩阵的秩不相等,方程组无解,根据解得个数与直线的位置关系,所以一个交点也没有,(B)不成立.(C)秩123(,,)r ααα=秩12(,)r αα,当123(,,)r ααα=12(,)1r αα=时,三条直线重合,不只交于一点,与题设条件矛盾,故(C)不成立.由排除法知选(D).评注:应重视线性代数中的几何背景.空间直线方程及平面方程其在空间的位置关系应与线性代数中的线性相关性、秩及方程组的解及其充要条件有机的结合起来. (5)【答案】(D)【解析】因X 与Y 独立,故3X 和2Y 也相互独立.由方差的性质,有(32)(3)(2)9()4()44D X Y D X D Y D X D Y -=+-=+=.【相关知识点】方差的性质:X 与Y 相互独立时,22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数.三、(本题共3小题,每小题5分,满分15分.)(1)【分析】三重积分的计算有三种方法:直角坐标中的计算,柱面坐标中的计算,球面坐标中的计算,其中柱面坐标中又可分先z 后(,)r θ,或先(,)r θ后z 两种方法.本题的区域Ω为绕z 轴旋转的旋转体,用柱面坐标先(,)r θ后z 方便.【解析】方法1:采用柱面坐标,先(,)r θ后z ,为此,作平面z z =.{}22(,,)|2,,z D x y z x y z z z =+≤=82220()zD I x y dv dz r rdrd θΩ=+=⋅⎰⎰⎰⎰⎰⎰(将直角坐标化为柱面坐标)82301024.3dz d dr ππθ==⎰⎰ 方法2:将Ω投影到xOy 平面,得圆域{}22(,)|16,D x y x y =+≤用柱面坐标先z 后(,)r θ,有22248422330021024()2(8).23r r I x y dv d dr r dz r dr ππθπΩ=+==-=⎰⎰⎰⎰⎰⎰评注:做二次积分或三次积分时,如果里层积分的结果不含外层积分变量,那么里、外层积分可以分别积分然后相乘即可.如本例方法2中20d πθ⎰可以单独先做.(2)【解析】方法1:写出C 的参数方程,然后用曲线积分化为定积分的公式. 由平面上圆的参数方程易写出C 的参数方程为:()cos ,()sin ,()2cos sin x x t t y y t t z z t t t ======-+,其中2z x y =-+.由C 的方向知,C 在Oxy 平面上的投影曲线相应地也是顺时针的,于是t 从π2到0. 在把参数方程代入被积表达式之前,先用C 的方程将被积表达式化简,有222022220()()()(2)()(2)(2())()[cos (2cos sin )]cos (2())()0[2cos sin cos 2cos ]02cos 2.C CI z y dx x z dy x y dzx dx x z dy z dzx t dx t t t t tdt z t dz t t t t t dt tdt ππππππ=-+-+-=-+-+-=-+--++-=+--+=-=-⎰⎰⎰⎰⎰⎰⎰方法2:用斯托克斯公式来计算.记S 为平面2x y z -+=上C 所围有限部分,由L 的定向,按右手法则S 取下侧.原积分2SS dydzdzdx dxdy dxdy x y z z yx zx y∂∂∂==∂∂∂---⎰⎰⎰⎰. S 在xy 平面上的投影区域xy D 为221x y +≤.将第二类曲面积分化为二重积分得原积分22xyD dxdy π=-=-⎰⎰.这里因S 取下侧,故公式取负号.(3)【解析】已掌握新技术人数()x t 的变化率,即dxdt,由题意可立即建立初值问题 0(),(0).dxkx N x dtx x ⎧=-⎪⎨⎪=⎩ 把方程分离变量得,()dx kdt x N x =-111()dx kdt N x N x+=-.积分可得 11ln xkt c N N x=+-,1kNt kNtcNe x ce =+.xyz 1O xyOyOz 1以0(0)x x =代入确定00x c N x =-,故所求函数为000.kNt kNtNx e x N x x e=-+四、(本题共2小题,每小题6分,满分12分.)(1)【分析一】见下图所示,S 在xOy 平面与yOz 平面上的投影均易求出,分别为22:1xy D x y +≤;2:11,1yz D y y z -≤≤≤≤,或01,z z y z ≤≤≤≤ 图1求Szdxdy ⎰⎰,自然投影到xOy 平面上.求(2)Sx z dydz +⎰⎰时,若投影到xOy 平面上,被积函数较简单且可利用对称性.【分析二】令(,,)2,(,,)0,(,,)P x y z x z Q x y z R x y z z =+==,则SI Pdydz Rdxdy =+⎰⎰.这里,213P Q R x y z∂∂∂++=+=∂∂∂,若用高斯公式求曲面积分I ,则较简单.因S 不是封闭曲面,故要添加辅助曲面.【解析】方法一:均投影到平面xOy 上,则22(2)[(2)()()]xySD zI x z dydz zdxdy x z x y dxdy x∂=++=+-++∂⎰⎰⎰⎰, 其中22z x y =+,22:1xy D x y +≤.把2zx x∂=∂代入,得 2222242()()xyxyxyD D D I x dxdy x x y dxdy x y dxdy =--+++⎰⎰⎰⎰⎰⎰,由对称性得222()0xyD x xy dxdy +=⎰⎰,22242()xyxyD D x dxdy x y dxdy =+⎰⎰⎰⎰,所以 22()xyD I x y dxdy =-+⎰⎰. 利用极坐标变换有121340001242I d r dr r ππθπ⎡⎤=-=-=-⎢⎥⎣⎦⎰⎰.方法二:分别投影到yOz 平面与xOy 平面.投影到yOz 平面时S要分为前半部分1:S x =2:S x =(见图1),则12(2)(2)S S SI x z dydz x z dydz zdxdy =++++⎰⎰⎰⎰⎰⎰.由题设,对1S 法向量与x 轴成钝角,而对2S 法向量与x 轴成锐角.将I 化成二重积分得2222)()()4().yzyzxyyzxyD D D D D I z dydz z dydz x y dxdyx y dxdy =-+-++=-++⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰2213111221131242200sin 2()344(1)cos 3343,34224yzz y D z y y t dy z y dyy dy tdt πππ=--====-=-=⋅⋅=⋅⎰⎰⎰⎰⎰⎰⎰或21101.24yzD dz dz ππ===⎰⎰⎰⎰(这里的圆面积的一半.)22()2xyD x y dxdy π+=⎰⎰(同方法一).因此, 4.422I πππ=-⋅+=-方法三:添加辅助面221:1(1)S z x y =+≤,法方向朝下,则11(2)1S S Dx z dydz zdxdy dxdy dxdy π++==-=-⎰⎰⎰⎰⎰⎰,其中D 是1S 在平面xy 的投影区域:221x y +≤.S 与1S 即22z x y =+与1z =围成区域Ω,S 与1S 的法向量指向Ω内部,所以在Ω上满足高斯公式的条件,所以1(2)3S S x z dydz zdxdy dV Ω++=-⎰⎰⎰⎰⎰11()3332D z dz dxdy zdz ππ=-=-=-⎰⎰⎰⎰, 其中,()D z 是圆域:22x y z +≤,面积为z π. 因此,133(2)()222S I x z dydz zdxdy ππππ=--++=---=-⎰⎰. (2)【解析】由多元复合函数求导法则,得z z u z v z zx u x v x u v∂∂∂∂∂∂∂=+=+∂∂∂∂∂∂∂, 2z z u z v z z a y u y v y u v∂∂∂∂∂∂∂=+=-+∂∂∂∂∂∂∂, 所以 22222222()()z z z z u z v z v z ux x u x v u x u v x v x v u x∂∂∂∂∂∂∂∂∂∂∂∂∂=+=⋅+⋅+⋅+⋅∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ 222222z z zu u v v∂∂∂=++∂∂∂∂, 2222222()()z z z z u z v z v z u x y y u y v u y u v y v y v u y∂∂∂∂∂∂∂∂∂∂∂∂∂=+=⋅+⋅+⋅+⋅∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ 222222(2)z z za a u u v v∂∂∂=-+-+∂∂∂∂,222222222222222()()2()()44.z z z a y y u y vz u z v z v z ua u y u v y v y v u yz z z a a u u v v∂∂∂∂∂=-+∂∂∂∂∂∂∂∂∂∂∂∂∂=-⋅+⋅+⋅+⋅∂∂∂∂∂∂∂∂∂∂∂∂∂=-+∂∂∂∂代入2222260z z zx x y y ∂∂∂+-=∂∂∂∂,并整理得 2222222226(105)(6)0z z z z z a a a x x y y u v v∂∂∂∂∂+-=+++-=∂∂∂∂∂∂∂. 于是,令260a a +-=得3a =或2a =-.2a =-时,1050a +=,故舍去,3a =时,1050a +≠,因此仅当3a =时化简为20zu v∂=∂∂. 【相关知识点】多元复合函数求导法则:若(,)u u x y =和(,)v v x y =在点(,)x y 处偏导数存在,函数(,)z f u v =在对应点(,)u v 具有连续偏导数,则复合函数[(,),(,)]z f u x y v x y =在点(,)x y 处的偏导数存在,且,z f u f v z f u f v x u x v x y u y v y∂∂∂∂∂∂∂∂∂∂=+=+∂∂∂∂∂∂∂∂∂∂.五、(本题满分6分)【分析】通过变换将()x ϕ化为积分上限函数的形式,此时0x ≠,但根据0()limx f x A x→=,知 (0)0f =,从而1(0)(0)0f dt ϕ==⎰,由此,利用积分上限函数的求导法则、导数在一点处的定义以及函数连续的定义来判定()x ϕ'在0x =处的连续性. 【解析】由题设0()limx f x A x→=知,(0)0,(0),f f A '==且有(0)0ϕ=.又 10()()()(0),xf u du x f xt dtu xtx xϕ==≠⎰⎰于是 02()()()(0),xxf x f u dux x xϕ-'=≠⎰由导数定义,有0200()()(0)()(0)limlimlim22xx x x f u du x f x Axx x ϕϕϕ→→→-'====⎰. 而 022000()()()()lim ()limlim lim x xx x x x xf x f u duf u du f x x xx xϕ→→→→-'==-⎰⎰ (0)22A AA ϕ'=-==, 从而知()x ϕ'在0x =处连续.评注:对1()()x f xt dt ϕ=⎰作积分变量变换xt u =时,必附加条件0x ≠.因此,由01()()xx f u du xϕ=⎰得到的()x ϕ'也附加有条件0x ≠.从而(0)ϕ'应单独去求.六、(本题满分7分)【解析】曲线()y f x =上点(,())x f x 处的切线方程为()()()Y f x f x X x '-=-.令0X =得y 轴上的截距()()Y f x f x x '=-.由题意,01()()()xf t dt f x f x x x' =-⎰. 为消去积分,两边乘以x ,得 20()()()xf t dt xf x f x x ' =-⎰, (*)将恒等式两边对x 求导,得2()()()2()()f x f x xf x xf x x f x ''''=+--,即 ()()0xf x f x '''+=.在(*)式中令0x =得00=自然成立.故不必再加附加条件.就是说()f x 是微分方程0xy y '''+=的通解.下面求解微分方程0xy y '''+=.方法一:()100xy y xy xy C ''''''+=⇒=⇒=, 因为0x >,所以1C y x'=, 两边积分得 12()ln y f x C x C ==+.方法二:令()y P x '=,则y P '''=,解0xP P '+=得1C y P x'==. 再积分得12()ln y f x C x C ==+.七、(本题共2小题,第(1)小题5分,第(2)小题6分,满分11分.)【分析】要求0Bx =的解空间的一个标准基,首先必须确定此解空间的维数以及相应个数的线性无关的解.【解析】(1)因秩()2r B =,故解空间的维数()422n r B -=-=,又因12,αα线性无关,12,αα是方程组0Bx =的解,由解空间的基的定义,12,αα是解空间的基.用施密特正交化方法先将其正交化,令:[][][][]1121221111,1,2,3,(,)521,1,4,11,1,2,32,1,5,3.(,)153TT T T βααββαβββ===-=---=--将其单位化,有]]1212121,1,2,3,2,1,5,3T T ββηηββ====--, 即为所求的一个标准正交基.评注:此题是一个基本计算题,只要求得一个齐次方程组的基础解系再标准正交化即可. 由于解空间的基不唯一,施密特正交化处理后标准正交基也不唯一.已知条件中12,,αα3α是线性相关的(注意12323ααα-=),不要误认为解空间是3维的.(2)(I)设ξ是矩阵A 的属于特征值0λ的特征向量,即0,A ξλξ=021*******,1211a b λ-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦即 0002125312a b λλλ--=⎧⎪+-=⎨⎪-++=-⎩0130,a ,b λ⇒=-=-=. (II)将(1)解得的30a ,b =-=代入矩阵A ,得212533102A -⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦. 其特征方程为3212533(1)0,12E A λλλλλ---=-+-=+=+知矩阵A 的特征值为1231λλλ===-.由于 312()5232101r E A r --⎡⎤⎢⎥--=--=⎢⎥⎢⎥⎣⎦, 从而1λ=-只有一个线性无关的特征向量,故A 不能相似对角化. 评注:A 相似于对角阵⇔A 的每个i r 重特征值有i r 个线性无关的特征向量.八、(本题满分6分)【解析】(1)因为TA E ξξ=-,Tξξ为数,Tξξ为n 阶矩阵,所以2()()2()(2)T T T T T T T A E E E E ξξξξξξξξξξξξξξ=--=-+=--,因此, 2(2)(1)0TTTTTA A E E ξξξξξξξξξξ=⇔--=-⇔-= 因为ξ是非零列向量,所以0Tξξ≠,故210,TA A ξξ=⇔-=即1Tξξ=. (2)反证法.当1Tξξ=时,由(1)知2A A =,若A 可逆,则121A A A A A E --===. 与已知T A E E ξξ=-≠矛盾,故A 是不可逆矩阵.九、(本题满分7分) 【分析】首先需要清楚二项分布的产生背景.它的背景是:做n 次独立重复试验,每次试验的结果只有两个(要么成功,要么失败),每次试验成功的概率都为p ,随机变量X 表示n 次试验成功的次数,则~(,)X B n p .这道题中经过三个交通岗,在各个交通岗遇到红灯的事件是独立的,概率都为25,相当于做了3次独立重复试验,试验的结果只有两个(要么遇到红灯(成功),要么不遇到(失败)),每次成功的概率都为25,X 表示遇到红灯的次数,相当于做了3次试验成功的次数,故2~(3,)5X B .【解析】由题意知:2~(3,)5X B ,由二项分布的分布律的定义,有{}33(1),0,1,2,3.k kk p X k C p p k -==-=再由离散型随机变量分布函数的定义,有()kk xF x p≤=∑,(1)当0x <时,()0kk xF x p≤==∑;(2)当01x ≤<,{}300300322327()0()(1)555125k k xF x p p P X C -≤⎛⎫=====-==⎪⎝⎭∑; (3)当12x ≤<,{}{}1131013272281()01()(1)12555125k k xF x p p p P X P X C -≤==+==+==+-=∑; (4)当23x ≤<, {}{}{}012()012kk xF x pp p p P X P X P X ≤==++==+=+=∑223238122117()(1)12555125C -=+-=; (5)当3x ≥时{}{}{}{}0123()01231k k xF x p p p p p P X P X P X P X ≤==+++==+=+=+==∑.因此X 的分布函数为:0,0,27,01,12581(),12,125117,23,1251,3.x x F x x x x <⎧⎪⎪≤<⎪⎪⎪=≤<⎨⎪⎪≤<⎪⎪≥⎪⎩ 2~(3,)5X B 的数学期望为26355EX np ==⋅=.【相关知识点】1.二项分布分布律的定义:{}(1),0,1,,k kn k n P X k C p p k n -==-=.2.离散型随机变量分布函数的定义:{}()i ix xF x P X x p ≤=≤=∑.3.二项分布~(,)X B n p 的期望为EX np =.十、填空题(本题共2小题,每小题3分,满分6分.) (1)【答案】37【解析】设事件C =“抽取的产品是次品”,事件D =“抽取的产品是工厂A 生产的”,则事件D 表示“抽取的产品是工厂B 生产的”,依题意有()0.60,()0.40,(|)0.01,(|)0.02P D P D P C D P C D ====.应用贝叶斯公式可以求得条件概率(|)P D C :()(|)0.60.013(|)0.60.010.40.027()(|)()(|)P D P C D P D C P D P C D P D P C D ⨯===⨯+⨯+.【相关知识点】贝叶斯公式:设试验E 的样本空间为S .A 为E 的事件,12,,,n B B B 为S的一个划分,且()0,()0(1,2,,)i P A P B i n >>=,则1()(|)(|),1,2,,.()(|)i i i njjj P B P A B P B A i n P B P A B ===∑ (*)(*)式称为贝叶斯公式.(2)【解析】由于ξ与η相互独立且均服从正态分布2)N ,因此它们的线性函数U ξη=-服从正态分布,且()0,EU E E E ξηξη=-=-=()11122DU D D D ξηξη=-=+=+=, 所以有 (0,1)UN .代入正态分布的概率密度公式,有22()u f u du +∞--∞=⎰. 应用随机变量函数的期望公式有22(||)(||)||u E E U u du ξη+∞--∞-= =⎰222u du +∞-=⎰由凑微分法,有222(||)2()2u uE d ξη+∞--=--⎰22u +∞-==.【相关知识点】对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ++=++,22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数.。
河南省2020年专升本《高等数学》考试试题

河南省2020年普通高等学校专科毕业生进入本科阶段学习考试《高等数学》注意事项:答题前,考生务必将自己的姓名、考场号、座位号、考生号填写在答题卡上。
本卷的试题答案必须答在答题卡上,答在卷上无效。
一、选择题(每小题2分,共60分)在每小题的四个备选答案中选出一个正确答案,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标。
1.当0→x 时,x x 632-是x 的()A.高阶无穷小B.低阶无穷小C.同阶非等价无穷小D.等价无穷小2.设()x f 是在R 上奇函数,则()()x x x f -++21ln sin 在R 上是()A.奇函数B.偶函数C.非奇非偶D.无法判断3.求极限xx x 411lim ⎪⎭⎫⎝⎛-∞→()A.4eB.4-eC.eD.14.设()121+=+x x f ,则()51--x f =()A.92-x B.112-x C.32-xD.22-x 5.设函数()()⎪⎪⎩⎪⎪⎨⎧>-=<--=1,11,21,122sin 2x x x x x x x f ,则()x f 在1=x 处的极限()A.0B.1C.2D.不存在6.函数()xx y -++=311ln 的定义域是()A.[]3,1- B.()3,1- C.[)3,1- D.(]3,1-7.xe x xx ln lim 11-→-=()A.0B.1C.2D.38.设()x f 在区间内是连续函数,且()()()6lim3=--→a x a f x f ax ,则()x f 在a x =处()A.()x f ax →lim 存在,()0≠'a f B.不可导C.()x f 有极大值 D.无极值9.844lim 2+--∞→x x x x ()A.1-B.0C.1D.∞10.设()212='f ,则极限()()()h f h f h +-+→1ln 222lim 0=()A.21 B.1 C.21-D.1-11.下列式子成立的是()A.⎪⎭⎫⎝⎛+=a x ad adx 2 B.22221dx e dx xe x x =题号一二三四五总分分值602050146150班级:姓名:准考证号:C.36πC.xd dx x = D.⎪⎭⎫⎝⎛=x d xdx 1ln 12.设函数()x f 满足()1=-xde x df ,则()x f ''=()A.xxe-- B.xe-- C.xxe D.xe-13.设xx y 33⋅=在0x 处取得极小值,则0x =()A.3ln 1-B.3ln - C.3ln 1 D.3ln 14.设函数x x y ln =在点M 处的切线平行于12+=x y ,则点M 的坐标是()A.()0,1 B.()0,e C.()1,e D.()e e ,15.函数()x y y =是由方程1332=+-x xy y 所确定的隐函数,则='y ()A.x y y x 32332-- B.xy x y 32332-- C.yx x y 33322-- D.y x y x 33232--16.函数()()xx x x f sin 12-=有()个间断点A.0B.1C.2D.无数17.若不定积分()c xdx x f +=⎰1,则()x f '=()A.xln B.x1 C.21x -D.32x 18.()=-⎰dx x 21sin ()A.()c x +-21cosB.()c x +--21cosC.()c x +-21cos 21D.()c x +--21cos 2119.已知()()dt ex f x t⎰+=21为连续函数,则当2≥n 时,()()x f n =()A.xe2 B.xn e22 C.xn e 212- D.xn e212+20.由曲线x y 2=,直线x y =以及直线1=x 所围成的平面图形绕x 轴旋转所形成旋转体的体积是()A.π517 B.πC.π1D.π17521.下列广义积分收敛的是()A.⎰∞++021dx x xB.⎰∞+1sin xdxC.dx xe⎰∞+1 D.dx x ⎰∞+-424122.平面013=++-z y x 和平面022=++y x 的位置关系是()A.垂直B.斜交C.平行不重合D.重合23.曲面方程022=++z y x 在空间直角坐标系中表示的是()A.椭圆面B.圆锥面C.旋转抛物面D.柱面24.已知()2sin xy z =,则22xz∂∂=()A.()24cos xyy B.()24cos xyy - C.()24sin xyy D.()24sin xyy -25.已知xye z -=在点()1,0-处在方向→l 上取得最大方向导数,则→l =()A.→→--ji B.→→+ji C.→→+-j i D.→→-j i 26.设函数()x y y =参数方程⎩⎨⎧+=-=tet y t t x sin cos 所确定,则0=t dxdy =()A.0 B.1 C.1- D.2-27.下列级数收敛的是()A.∑∞=11n neB.nn ∑∞=⎪⎭⎫ ⎝⎛123 C.∑∞=⎪⎭⎫ ⎝⎛-13132n n n D.∑∞=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛1132n n n 28.设L 为正向圆周622=+y x ,则()()dy x x dx y y xL42332++-⎰=()A.π6 B.π6- D.π36-29.级数∑∞=0!n nn kx 在0>k 时的收敛区间是()A.()1,1- B.⎪⎭⎫⎝⎛-k k 1,1 C.()k k ,- D.()+∞∞-,30.二阶常系数非齐次微分x e y y y xsin 862=+'-''用待定系数法时,特解方程设为*y =()A.xce 2 B.()x c x c excos sin 212+C.()x c x c xexcos sin 212+ D.()x c x c ex xcos sin 2122+二、填空题(每小题2分,共20分)31.已知()x x f arctan 1=+,()[]2-=x x g f ,则()2+x g =___________32.已知()()⎪⎩⎪⎨⎧≤+>+=0,cos 50,2sin 2x x e x x x a xx f x ,在0=x 处连续,则a =_____________33.设函数()()dt t x f x ⎰+=203ln 的单调递增区间为________________34.已知()x f x 2lim →的极限存在,且()()x f x x x f x 23lim 3→+=,则()x f '=________________35.dx x x ⎰--2224=________________36.设()()c x F dx x f +=⎰,则()⎰xdx x f cos sin =___________________37.设平面区域(){}10,0,≤≤≤≤=x x y y x D ,则⎰⎰Dxdxdy =____________38.已知()y x z +=2ln ,则dz =_________________39.已知幂级数()()!210n x nn n∑∞=-的和函数是____________40.二阶常系数齐次方程0=+'+''y y y 的通解是____________________三、计算题(每小题5分,共50分)41.求极限()2311431321211lim -∞→⎪⎪⎭⎫⎝⎛+⨯++⨯+⨯+⨯n n n n 42.已知函数xxy ln =,求导数y '43.已知()()x e x x x f x +--+=1ln 1111sin,求其水平渐近线和垂直渐近线44.求函数()5683234++-=x x x x f 的凹凸区间及拐点45.求不定积分()dxx x ⎰+12146.求定积分dx x ⎰+4023cos 1π47.已知向量()()()6,0,18,2,30,4,4===→→→c b a ,求→→→⋅⎪⎭⎫ ⎝⎛⨯cb a 48.已知函数()y x z z ,=,且123232=+++z xyz y x (其中026≠+zxy ),求yzx z ∂∂∂∂,49.计算二重积分⎰⎰Dydxdy ,其中D 为122=+y x,且0,0>>y x 50.将函数()252412-+=x x x f 展开成x 的幂级数四、应用题(每小题7分,共14分)51.已知函数21x y -=与x 轴有两个交点分别为B A ,,在曲线上存在D C ,两点,以AB 为底边的等腰梯形ABCD ,试求C 点的纵坐标为多少时,等腰梯形ABCD 的面积最大?52.某文物于1972年8月发掘出土,经研究测算该文物出土时C 14(放射性同位素碳—14)标本存量为初始量0R 的0.7761倍。
2020年全国大学高数考试试题及解析

2020年全国大学高等数学考试试题一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)(1)曲线上与直线垂直的切线方程为__________ . (2)已知,且,则=__________ . (3)设为正向圆周在第一象限中的部分,则曲线积分的值为__________.(4)设是由锥面与半球面围成的空间区域,是的整个边界的外侧,则_________.(5)设均为3维列向量,记矩阵,,如果,那么 .(6)从数1,2,3,4中任取一个数,记为, 再从中任取一个数,记为, 则=____________.二、选择题(本题共8小题,每小题4分,满分32分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)(1)设函数,则在内( )(A)处处可导 (B)恰有一个不可导点 (C)恰有两个不可导点 (D)至少有三个不可导点(2)设是连续函数的一个原函数,表示的充分必要条件是则必有( )(A)是偶函数是奇函数 (B)是奇函数是偶函数ln y x =1=+y x (e )e x x f x -'=(1)0f =()f x L 222=+y x ⎰-Lydx xdy 2Ω22y x z +=222y x R z --=∑Ω⎰⎰∑=++zdxdy ydzdx xdydz 123,,ααα123(,,)=A ααα123123123(,24,39)=++++++B ααααααααα1=A =B X X ,,2,1 Y }2{=Y P n nn xx f 31lim )(+=∞→()f x ),(+∞-∞()F x ()f x ""N M ⇔"M ",N ()F x ()f x ⇔()F x ()f x ⇔(C)是周期函数是周期函数 (D)是单调函数是单调函数(3)设函数, 其中函数具有二阶导数, 具有一阶导数,则必有( )(A)(B)(C)(D)(4)设有三元方程,根据隐函数存在定理,存在点的一个邻域,在此邻域内该方程( )(A)只能确定一个具有连续偏导数的隐函数(B)可确定两个具有连续偏导数的隐函数和 (C)可确定两个具有连续偏导数的隐函数和 (D)可确定两个具有连续偏导数的隐函数和(5)设是3阶方阵,将的第1列与第2列交换得,再把的第2列加到第3列得,则满足的可逆矩阵为( )(A) (B)(C)(D)()F x ()f x ⇔()F x ()f x ⇔⎰+-+-++=yx y x dt t y x y x y x u )()()(),(ψϕϕϕψ2222y ux u ∂∂-=∂∂2222yu x u ∂∂=∂∂222y uy x u ∂∂=∂∂∂222xuy x u ∂∂=∂∂∂ln e 1xz xy z y -+=(0,1,1)(,)z z x y =(,)x x y z =(,)z z x y =(,)y y x z =(,)z z x y =(,)x x y z =(,)y y x z =A A B B C =AQ C Q ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100101010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100001110(6)设为满足的任意两个非零矩阵,则必有( )(A)的列向量组线性相关的行向量组线性相关 (B)的列向量组线性相关的列向量组线性相关 (C)的行向量组线性相关的行向量组线性相关 (D)的行向量组线性相关的列向量组线性相关(7)设随机变量服从正态分布对给定的,数满足,若,则等于() (A)(B)(C) (D)(8)设随机变量独立同分布,且其方差为 令,则( )(A)(B) (C)(D)三、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤)1、(本题满分12分)设,证明.,A B =AB O A ,B A ,B A ,B A ,B X (0,1),N )10(<<αααu αα=>}{u X P α=<}{x X P x 2αu 21α-u21α-u α-1u )1(,,,21>n X X X n .02>σ∑==ni i X n Y 1121Cov(,)X Y nσ=21Cov(,)X Y σ=212)(σnn Y X D +=+211)(σnn Y X D +=-2e e a b <<<2224ln ln ()e b a b a ->-某种飞机在机场降落时,为了减少滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下.现有一质量为9000kg 的飞机,着陆时的水平速度为700km/h 经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为 问从着陆点算起,飞机滑行的最长距离是多少?(注:kg 表示千克,km/h 表示千米/小时)3、(本题满分12分)计算曲面积分其中是曲面的上侧.4、(本题满分12分)已知函数在上连续,在内可导,且. 证明: A 存在 使得.B 存在两个不同的点,使得5、(本题满分12分)设函数具有连续导数,在围绕原点的任意分段光滑简单闭曲线上,曲线积分的值恒为同一常数.(1)证明:对右半平面内的任意分段光滑简单闭曲线有.(2)求函数的表达式.).100.66⨯=k ,)1(322233dxdy z dzdx y dydz x I ⎰⎰∑-++=∑)0(122≥--=z y x z ()f x [0,1](0,1)(0)0,(1)1f f ==),1,0(∈ξξξ-=1)(f )1,0(,∈ζη.1)()(=''ζηf f )(y ϕL 24()22Ly dx xydyx yφ++⎰0x >,C 24()202Cy dx xydyx y φ+=+⎰)(y ϕ已知二次型的秩为2. (1)求的值;(2)求正交变换,把化成标准形. (3)求方程=0的解.7、(本题满分9分)设矩阵的特征方程有一个二重根,求的值,并讨论是否可相似对角化.8、(本题满分9分)设为随机事件,且,令求:(1)二维随机变量的概率分布. (2)和的相关系数9、(本题满分9分)设为来自总体的简单随机样本,为样本均值,记求:(1)的方差. (2)与的协方差21232221321)1(22)1()1(),,(x x a x x a x a x x x f +++-+-=a x y =Q ),,(321x x x f ),,(321x x x f 12314315a -⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦A a A ,AB 111(),(|),(|)432P A P B A P A B ===;,,0,1不发生发生A A X ⎩⎨⎧=.,,0,1不发生发生B B Y ⎩⎨⎧=(,)X Y X Y .XY ρ)2(,,,21>n X X X n (0,1)N X .,,2,1,n i X X Y i i =-=i Y n i DY i ,,2,1, =1Y n Y 1Cov(,).n Y Y2020年全国大学高等数学考试试题解析一、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线)(1)曲线y=lnx 上与直线1=+y x 垂直的切线方程为 1-=x y . 【分析】 本题为基础题型,相当于已知切线的斜率为1,由曲线y=lnx 的导数为1可确定切点的坐标。
2020年河南省高考数学试卷(文科)(新课标Ⅰ)

2020年河南省髙考数学试卷(文科)(新课标I )一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
1.已知集合Λ = {%∣X 2-3X -4<0}, B={-4, 1, 3, 5},则AC ∖B=() A.{-4, 1}B.{l, 5}C.{3, 5}D.{l, 3}【答案】D【考点】 交集及其运算 【解析】求解一元二次不等式得到集合4,再由交集运算得答案• 【解答】集⅛4={%∣%2-3X -4 <0} = (-l, 4), B={-4, 1,3,5}, 则AnB=(1, 3}, 2.若z=l +2i + iS 则IZl=()A.0B.lC.√2D.2【答案】C【考点】 复数的模 【解析】根据复数的定义化简原式,并通过模长公式求解即町. 【解答】z=l + 2i + i 3= l + 2i - i = l + i, .∙. IZI =√12÷ I 2= ∖[2.3•埃及胡夫金字塔是占代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四 棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面枳,则其侧面三角形 底边上的高与底面正方形的边长的比值为()【答案】A. √5-lD.√5+lB •导C【考点】棱柱、棱锥、棱台的侧面积和表面积【解析】先根据正四棱锥的几何性质列出等量关系,进而求解结论.【解答】设正四棱锥的高为/1,底面边长为6侧面三角形底边上的高为∕Λ则依题意有:h2 = ^ah h2 = h2-φ2'因此有护-φ2 = lαΛ,=> 4(》2 _ 2(》一1 =O » =字(负值舍去);4・设O为正方形ABCD的中心,在O, A9 B、C9 D中任取3点,则取到的3点共线的概率为()【答案】A【考点】占典概型及其概率计算公式【解析】根据古典概率公式即可求出.【解答】O, A f B, C, D中任取3点,共有屈=10种, 其中共线为4,O, C和B, O, D两种,故取到的3点共线的概率为P =5.某校一个课外学习小组为研究某作物种子的发芽率y和温度%(单位:9)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(X it y i Xi = I t 220)得到下面的散点图:由此散点图,在10。
河南专升本高等数学试题(含答案)

高数试题练习一、函数、极限连续1.函数)(x f y 的定义域是()A .变量x 的取值范围B .使函数)(x f y 的表达式有意义的变量x 的取值范围C .全体实数D .以上三种情况都不是2.以下说法不正确的是()A .两个奇函数之和为奇函数B .两个奇函数之积为偶函数C .奇函数与偶函数之积为偶函数D .两个偶函数之和为偶函数3.两函数相同则()A .两函数表达式相同B .两函数定义域相同C .两函数表达式相同且定义域相同D .两函数值域相同4.函数42y x x 的定义域为()A .(2,4)B .[2,4]C .(2,4]D .[2,4)5.函数3()23sin f x x x 的奇偶性为()A .奇函数B .偶函数C .非奇非偶D .无法判断6.设,121)1(x xx f 则)(x f 等于( )A .12x xB .xx212C .121x xD .xx2127.分段函数是()A .几个函数B .可导函数C .连续函数D .几个分析式和起来表示的一个函数8.下列函数中为偶函数的是()A .xey B .)ln(x yC .xx y cos 3D .xy ln 9.以下各对函数是相同函数的有()A .xx g x x f )()(与B .x x g x x f cos )(sin 1)(2与C .1)()(x g x x x f 与D .2222)(2)(xxx xx g xx f 与10.下列函数中为奇函数的是()A .)3cos(x y B .xx y sin C .2xxe eyD .23xxy 11.设函数)(x f y的定义域是[0,1],则)1(x f 的定义域是( )A .]1,2[B .]0,1[ C .[0,1]D .[1,2]12.函数20200022)(2xxx x xx f 的定义域是( )A .)2,2(B .]0,2(C .]2,2(D .(0,2]13.若)1(,23321)(f xxx xx f 则( )A .3B .3C .1D .114.若)(x f 在),(内是偶函数,则)(x f 在),(内是()A .奇函数B .偶函数C .非奇非偶函数D .0)(x f 15.设)(x f 为定义在),(内的任意不恒等于零的函数,则)()()(x f x f x F 必是()A .奇函数B .偶函数C .非奇非偶函数D .)(x F 16.设42,021,1211,1)(2xx x x x x f 则)2(f 等于( )A .12B .182C .D .无意义17.函数x x ysin 2的图形()A .关于ox 轴对称B .关于oy 轴对称C .关于原点对称D .关于直线x y 对称18.下列函数中,图形关于y 轴对称的有()A .xx ycos B .13xx y C .2xxe eyD .2xxe ey19.函数)(x f 与其反函数)(1x f的图形对称于直线( )A .y B .x C .xy D .xy 20. 曲线)1,0(log aax y a y a x与在同一直角坐标系中,它们的图形()A .关于x 轴对称B .关于y 轴对称C .关于直线x y 轴对称D .关于原点对称21.对于极限)(lim 0x f x ,下列说法正确的是()A .若极限)(lim 0x f x存在,则此极限是唯一的B .若极限)(lim 0x f x 存在,则此极限并不唯一C .极限)(lim 0x f x 一定存在D .以上三种情况都不正确22.若极限A )(lim 0x f x存在,下列说法正确的是()A .左极限)(lim 0x f x不存在B .右极限)(lim 0x f x不存在C .左极限)(lim 0x f x和右极限)(lim 0x f x存在,但不相等D .A)(lim )(lim )(lim 0x f x f x f x xx23.极限ln 1limxex xe的值是()A .1B .1eC .0D .e24.极限ln cot lim ln x x x+0的值是().A .0B . 1C .D .125.已知2sin lim2xx bax x,则()A .,2ba B .1,1ba C .1,2b a D .,2b a 26.设b a,则数列极限limn nnnab是A .aB .bC .1D .ba 27.极限x x1321lim的结果是A .0B .21C .51D .不存在28.xlim xx 21sin为()A .2B .21C .1 D .无穷大量29.nm nxmxx ,(sin sin lim 0为正整数)等于()A .n mB .m n C .nm nm )1(D .mn mn )1(30.已知1tan lim23xx bax x,则()A .0,2b a B .,1b aC .,6b a D .1,1b a 31.极限xxx x xcos cos lim()A .等于 1B .等于0C .为无穷大D .不存在32.设函数10001sin )(xexx x x f x则)(lim 0x f x( )A .1B .0C .1D .不存在33.下列计算结果正确的是()A .ex xx1)41(lim B .41)41(lim ex xxC .41)41(lim ex xxD .4110)41(lim e x x x34.极限xx xtan 0)1(lim 等于()A . 1B .C .0D .2135.极限xxxx xsin 11sinlim 0的结果是A .1B .1C .0D .不存在36.1sinlim k kxx x为()A .kB .k1C .1 D .无穷大量37.极限xxsin lim 2=()A .0B .1C .1D .238.当x 时,函数xx)11(的极限是( )A .eB .eC .1D .139.设函数1cos 0001sin )(xx x x x x f ,则)(lim 0x f xA .1B .0C .1D .不存在40.已知a xax xx 则,516lim 21的值是()A .7B .7C . 2D .341.设20tan )(xxx xaxx f ,且)(lim 0x f x 存在,则a 的值是( )A .1B .1C .2D .242.无穷小量就是()A .比任何数都小的数B .零C .以零为极限的函数D .以上三种情况都不是43.当0x 时,)2sin(3x x与x 比较是()A .高阶无穷小B .等价无穷小C .同阶无穷小,但不是等价无穷小D .低阶无穷小44.当0x时,与x 等价的无穷小是()A .xxsin B .)1ln(x C .)11(2x x D .)1(2x x45.当0x 时,)3tan(3x x 与x 比较是()A .高阶无穷小B .等价无穷小C .同阶无穷小,但不是等价无穷小D .低阶无穷小46.设,1)(,)1(21)(x x g x x x f 则当1x 时()A .)(x f 是比)(x g 高阶的无穷小B .)(x f 是比)(x g 低阶的无穷小C .)(x f 与)(x g 为同阶的无穷小D .)(x f 与)(x g 为等价无穷小47.当x时,11)(ax x f 是比x 高阶的无穷小,则( )A .1aB .aC .a 为任一实常数D .1a 48.当0x时,x 2tan 与2x比较是()A .高阶无穷小B .等价无穷小C .同阶无穷小,但不是等价无穷小D .低阶无穷小49.“当0x x,A x f )(为无穷小”是“A x f x x)(lim”的()A .必要条件,但非充分条件B .充分条件,但非必要条件C .充分且必要条件D .既不是充分也不是必要条件50.下列变量中是无穷小量的有()A .)1ln(1limx xB .)1)(2()1)(1(lim1x xx x xC .x x x1cos 1limD .xx x1sincos lim51.设时则当0,232)(x x f xx()A .)(x f 与x 是等价无穷小量B .)(x f 与x 是同阶但非等价无穷小量C .)(x f 是比x 较高阶的无穷小量D .)(x f 是比x 较低阶的无穷小量52.当0x时,下列函数为无穷小的是( )A .xx 1sinB .xe1C .xln D .xxsin 153.当0x时,与2sin x等价的无穷小量是( )A .)1ln(x B .xtan C .xcos 12D .1xe54.函数,1sin)(xx x f y当x时)(x f ( )A .有界变量B .无界变量C .无穷小量D .无穷大量55.当0x时,下列变量是无穷小量的有( )A .xx3B .xx cos C .x ln D .xe56.当0x 时,函数xx ysec 1sin 是( )A .不存在极限的B .存在极限的C .无穷小量D .无意义的量57.若0x x 时, )(x f 与)(x g 都趋于零,且为同阶无穷小,则()A .)()(limx g x f x xB .)()(limx g x f x xC .)1,0()()(limc c x g x f x xD .)()(limx g x f x x不存在58.当0x时,将下列函数与x 进行比较,与x 是等价无穷小的为( ) A .x 3tan B .112xC .xx cot csc D .xx x 1sin259.函数)(x f 在点0x 有定义是)(x f 在点0x 连续的()A .充分条件B .必要条件C .充要条件D .即非充分又非必要条件60.若点0x 为函数的间断点,则下列说法不正确的是()A .若极限A )(lim 0x f xx 存在,但)(x f 在0x 处无定义,或者虽然)(x f 在0x 处有定义,但)(A0x f ,则0x 称为)(x f 的可去间断点B .若极限)(lim 0x f x x与极限)(lim 0x f x x都存在但不相等,则0x 称为)(x f 的跳跃间断点C .跳跃间断点与可去间断点合称为第二类的间断点D .跳跃间断点与可去间断点合称为第一类的间断点61.下列函数中,在其定义域内连续的为()A .xx x f sin ln )(B .00sin )(x ex x x f xC .10101)(xx x x x x f D .01)(xx x x f 62.下列函数在其定义域内连续的有()A .x x f 1)(B .0cos 0sin )(x x x x x f C .10001)(xx x x xx f D .01)(xx x x f 63.设函数21ar c t an)(xx x x f 则)(x f 在点0x 处()A .连续B .左连续C .右连续D .既非左连续,也非右连续64.下列函数在0x处不连续的有( )A .0)(2xx e x f x B .1sin )(21xx x x x f C .0)(2x xx x x f D .0)1ln()(2xxx x x f 65.设函数12111)(2xx x xx f , 则在点)(1x f x 处函数()A .不连续B .连续但不可导C .可导,但导数不连续D .可导,且导数连续66.设分段函数101)(2xx x xx f ,则)(x f 在0x 点()A .不连续B .连续且可导C .不可导D .极限不存在67.设函数)(x f y,当自变量x 由0x 变到y x x 相应函数的改变量时,0=()A .)(0x x f B .xx f )('0C .)()(00x f x x f D .xx f )(068.已知函数12000)(xxxx ex f x,则函数)(x f ( )A .当0x 时,极限不存在B .当0x 时,极限存在C .在0x处连续D .在0x 处可导69.函数)1ln(1x y的连续区间是( )A .),2[]2,1[B .),2()2,1(C .),1(D .),1[70.设nxnx x f x13lim)(,则它的连续区间是()A .),(B .处为正整数)(1n nx C .)()0,(D .处及n xx1071.设函数31011)(xx xx x f ,则函数在0x 处()A .不连续B .连续不可导C .连续有一阶导数D .连续有二阶导数72.设函数0xx x xy,则)(x f 在点0x 处()A .连续B .极限存在C .左右极限存在但极限不存在D .左右极限不存在73.设11cot)(2x arc xx f ,则1x 是)(x f 的()A .可去间断点B .跳跃间断点C .无穷间断点D .振荡间断点74.函数2xy e x zy的间断点是( )A .)1,1(),1,1(),0,1(B .是曲线yey 上的任意点C .)1,1(),1,1(),0,0(D .曲线2xy上的任意点75.设2)1(42xx y,则曲线( )A .只有水平渐近线2y B .只有垂直渐近线x C .既有水平渐近线2y ,又有垂直渐近线0x D .无水平,垂直渐近线76.当0x 时, xx y1sin()A .有且仅有水平渐近线B .有且仅有铅直渐近线C .既有水平渐近线,也有铅直渐近线D .既无水平渐近线,也无铅直渐近线二、一元函数微分学77.设函数)(x f 在点0x 处可导,则下列选项中不正确的是()A .xy x f x 00lim )('B .xx f x x f x f x)()(lim)('000C .00)()(lim)('0x xx f x f x f x xD .hx f h x f x f h )()21(lim )('00078.若e cos xy x ,则'(0)y ( )A .0B .1C .1D .279.设x x g e x f xsin )(,)(,则)]('[x g f ()A .xesin B .xecos C .xecos D .xesin 80.设函数)(x f 在点0x 处可导,且2)('0x f ,则hx f h x f h)()21(lim00等于()A .1B .2C .1D .2181.设)(x f 在a x处可导,则xx af x a f x)()(lim=()A .)('a f B .)('2a f C .0D .)2('a f 82.设)(x f 在2x 处可导,且2)2('f ,则hh f h f h)2()2(lim()A .4B .0C .2D .383.设函数)3)(2)(1()(xx x x x f ,则)0('f 等于()A .0B .6C .1D .384.设)(x f 在0x 处可导,且1)0('f ,则hh f h f h )()(lim 0()A .1B .0C .2D .385.设函数)(x f 在0x 处可导,则0limhhx f f )()h - x (00( )A .与0x ,h 都有关B .仅与0x 有关,而与h 无关C .仅与h 有关,而与0x 无关D .与0x ,h 都无关86.设)(x f 在1x处可导,且21)1()21(lim 0h f h f h ,则)1('f ()A .21B .21C .41D .4187.设)0('')(2f ex f x则( ) A .1B .1C .2D .288.导数)'(log x a 等于( )A .a x ln 1B .a x ln 1C .xxa log 1D .x189.若),1()2(249102x xx xy则)29(y=()A .30B .29!C .0D .30×20×1090.设',)(',)()(y x f ee f y x f x 则存在且=( )A .)()()()('x f xx f xee f e e f B .)(')(')(x f ee f x f xC .)(')()(')()(x f ee f ee f x f x x f x xD .)()('x f xee f 91.设)0('),100()2)(1()(f x xx x x f 则()A .100B .100!C .!100D .10092.若',y x yx则( )A .1x xx B .xx xln C .不可导D .)ln 1(x x x93.处的导数是在点22)(xx x f ( ) A .1 B .0C .1D .不存在94.设',)2(y x yx则()A .)1()2(x x x B .2ln )2(xx C .)2ln 21()2(x x xD .)2ln 1()2(x x x95.设函数)(x f 在区间],[b a 上连续,且,0)()(b f a f 则( )A .)(x f 在),(b a 内必有最大值或最小值B .)(x f 在),(b a 内存在唯一的0)(,f 使C .)(x f 在),(b a 内至少存在一个0)(,f 使D .)(x f 在),(b a 内存在唯一的)(',f 使96.设,)()(x g x f y则dx dy ( )A .])()(')()('[2x g x g x f x f y B .])(1)(1[2x g x f yC .)()('21x g x f yD .)()('2x g x f y 97.若函数)(x f 在区间)b a,(内可导,则下列选项中不正确的是()A .若在)b a,(内0)('x f ,则)(x f 在)b a,(内单调增加B .若在)b a,(内0)('x f ,则)(x f 在)b a,(内单调减少C .若在)b a,(内0)('x f ,则)(x f 在)b a,(内单调增加D .)(x f 在区间)b a,(内每一点处的导数都存在98.若)(yx f 在点0x 处导数存在,则函数曲线在点))(,(00x f x 处的切线的斜率为()A .)('0x f B .)(0x f C .0 D .199.设函数)(y x f 为可导函数,其曲线的切线方程的斜率为1k ,法线方程的斜率为2k ,则1k 与2k 的关系为()A .211k k B .121k k C .121k k D .21k k 100.设0x 为函数)(x f 在区间b a,上的一个极小值点,则对于区间ba,上的任何点x ,下列说法正确的是()A .)()(0x f x fB .)()(0x f x f C .)()(0x f x f D .)()(0x f x f 101.设函数)(x f 在点0x 的一个邻域内可导且0)('0x f (或)('0x f 不存在),下列说法不正确的是()A .若0x x 时, 0)('x f ;而0x x 时, 0)('x f ,那么函数)(x f 在0x 处取得极大值B .若0x x 时, 0)('x f ;而0x x 时, 0)('x f ,那么函数)(x f 在0x 处取得极小值C .若0x x时, 0)('x f ;而0x x时, 0)('x f ,那么函数)(x f 在0x 处取得极大值D .如果当x 在0x 左右两侧邻近取值时,)('x f 不改变符号,那么函数)(x f 在0x 处没有极值102.0)('0x f ,0)(''0x f ,若0)(''0x f ,则函数)(x f 在0x 处取得()A .极大值B .极小值C .极值点D .驻点103.b x a时,恒有0)(x f ,则曲线)(x f y在ba,内()A .单调增加B .单调减少C .上凹D .下凹104.数()exf x x 的单调区间是() .A .在),(上单增B .在),(上单减C .在(,0)上单增,在(0,)上单减D .在(,0)上单减,在(0,)上单增105.数43()2f x xx的极值为().A .有极小值为(3)f B .有极小值为(0)f C .有极大值为(1)f D .有极大值为(1)f 106.xey 在点(0,1)处的切线方程为()A .x y1B .xy 1C .xy 1D .xy 1107.函数x xxxx f 处的切线与的图形在点)1,0(162131)(23轴交点的坐标是()A .)0,61(B .)0,1(C .)0,61(D .)0,1(108.抛物线x y 在横坐标4x 的切线方程为()A .44yx B .44yxC .184y x D .184y x 109.线)0,1()1(2在x y 点处的切线方程是()A .1x yB .1x y C .1x y D .1x y 110.曲线)(x f y在点x 处的切线斜率为,21)('x x f 且过点(1,1),则该曲线的方程是( )A .12x xy B .12x x y C .12x xy D .12xxy111.线22)121(x ey x上的横坐标的点0x处的切线与法线方程()A .063023y x y x 与B .63023y x y x 与C .063023yxy x与D .063023yxy x与112.函数处在点则0)(,)(3xx f x x f ( )A .可微B .不连续C .有切线,但该切线的斜率为无穷D .无切线113.以下结论正确的是( )A .导数不存在的点一定不是极值点B .驻点肯定是极值点C .导数不存在的点处切线一定不存在D .0)('0x f 是可微函数)(x f 在0x 点处取得极值的必要条件114.若函数)(x f 在0x 处的导数,0)0('f 则0x称为)(x f 的()A .极大值点B .极小值点C .极值点D .驻点115.曲线)1ln()(2xx f 的拐点是()A .)1ln ,1(与)1ln ,1(B .)2ln,1(与)2ln ,1(C .)1,2(ln 与)1,2(ln D .)2ln ,1(与)2ln ,1(116.线弧向上凹与向下凹的分界点是曲线的()A .驻点B .极值点C .切线不存在的点D .拐点117.数)(x f y 在区间[a,b]上连续,则该函数在区间[a,b]上()A .一定有最大值无最小值B .一定有最小值无最大值C .没有最大值也无最小值D .既有最大值也有最小值118.下列结论正确的有()A .0x 是)(x f 的驻点,则一定是)(x f 的极值点B .0x 是)(x f 的极值点,则一定是)(x f 的驻点C .)(x f 在0x 处可导,则一定在0x 处连续D .)(x f 在0x 处连续,则一定在0x 处可导119.由方程yx exy确定的隐函数)(x y y dxdy ( )A .)1()1(x y y x B .)1()1(y x x y C .)1()1(y x x y D .)1()1(x y y x 120.xyy xe y',1则()A .yyxee 1B .1yyxee C .yy xee 11D .yex)1(121.设x x g e x f xsin )(,)(,则)]('[x g f ()A .xesin B .xecos C .xecos D .xesin 122.设x x g e x f xcos )(,)(,则)]('[x g f A .xesin B .xecos C .xecos D .xesin 123.设)(),(x t t f y 都可微,则dyA .dtt f )('B .)('x dxC .)('t f )('x dtD .)('t f dx124.设,2sin xey则dy()A .xd e x2sin B .xd ex2sinsin 2C .xxd exsin 2sin 2sin D .xd exsin 2sin 125.若函数)(x f y 有dy x xxx f 处的微分该函数在时则当00,0,21)('是()A .与x 等价的无穷小量B .与x 同阶的无穷小量C .比x 低阶的无穷小量D .比x 高阶的无穷小量126.给微分式21xxdx ,下面凑微分正确的是( )A .221)1(xx d B .221)1(xx d C .2212)1(xx d D .2212)1(xx d 127.下面等式正确的有( )A .)(sin sin xxxx e d e dxe e B .)(1x d dx xC .)(222x d e dx xex x D .)(cos sin cos cos x d exdx exx128.设)(sin x f y,则dy()A .dx x f )(sin 'B .xx f cos )(sin 'C .xdxx f cos )(sin 'D .xdxx f cos )(sin '129.设,2sin xey则dyA .xd e x2sinB .x d ex2sinsin2C .xxd exsin 2sin 2sin D .xd exsin 2sin 三、一元函数积分学130.可导函数)(F x 为连续函数)(x f 的原函数,则( )A .)('x f B .)()(F'x f x C .)(F'x D .)(x f 131.若函数)(F x 和函数)(x 都是函数)(x f 在区间I 上的原函数,则有()A .I x x x ),(F )('B .I x x x ),()(F C .Ix x x ),()(F'D .IxC x x ,)()(F 132.有理函数不定积分2d 1x x x等于().A .2ln 12xx x CB .2ln 12xx x CC .2ln 12xx x CD .2ln 122xx x C133.不定积分22d 1x x等于().A .2arcsin x CB .2arccosx C C .2arctan x CD .2cot arc x C134.不定积分2e e (1)d x xx x等于().A .1e xC xB .1e xC x C .1exC xD .1exCx135.函数xe xf 2)(的原函数是( )A .4212xeB .xe22C .3312xeD .xe231136.xdx 2sin 等于()A .cx2sin 21B .cx 2sin C .cx2cos 2D .cx 2cos 21137.若xdx x x dx x xf sin sin )(,则)(x f 等于()A .xsin B .xx sin C .xcos D .xx cos 138.设xe是)(x f 的一个原函数,则dxx xf )('()A .cx e x)1(B .cx e x)1(C .cx e x)1(D .cx e x)1(139.设,)(xe xf 则dxx x f )(ln '()A .cx1B .cx1C .cx ln D .cx ln 140.设)(x f 是可导函数,则')(dxx f 为()A .)(x f B .cx f )(C .)('x f D .cx f )('141.以下各题计算结果正确的是( )A .xxdx arctan 12B .cxdxx 21C .cx xdx cos sin D .cx xdx 2sec tan142.在积分曲线族dx x x 中,过点(0,1)的积分曲线方程为( )A .12x B .1)(525x C .x2D .1)(255x 143.dx x31=()A .cx 43B .cx221C .cx221D .cx221144.设)(x f 有原函数x xln ,则dx x xf )(=()A .cx x )ln 4121(2B .cx x )ln 2141(2C .cx x )ln 2141(2D .cx x )ln 4121(2145.xdxxcos sin ()A .c x 2cos 41B .cx 2cos 41C .cx2sin 21D .cx2cos 21146.积分dxx]'11[2()A .211xB .cx211C .xtan arg D .cx arctan 147.下列等式计算正确的是()A .cx xdx cos sin B .cx dx x 43)4(C .cxdxx 32D .cdxxx22148.极限xx xxdxtdt00sin lim的值为()A .1B .0C .2D .1149.极限xxxdxx tdt202sin lim的值为()A .1B .0C .2D .1150.极限403sin limxdtt xx=( )A .41B .31C .21D .1151.2ln 01x t dte dxd ()A .)1(2xe B .exC .ex2D .12xe152.若xtdt dx dx f 0sin )(,则()A .x x f sin )(B .x x f cos 1)(C .cx x f sin )(D .xx f sin 1)(153.函数xdt t t tx213在区间]10[,上的最小值为()A .21B .31C .41D .0154.若xtxc dt te xf e x xg 02122213)(,)(,且23)(')('lim x g x f x则必有()A .0cB .1cC .1cD .2c155.x dt t dxd 14)1(()A .21xB .41xC .2121xxD .xx121156.]sin [2dt t dxd x ( )A .2cos xB .2cos 2xx C .2sin xD .2cost157.设函数0sin )(2xa x x tdtx f x在0x 点处连续,则a 等于()A .2B .21C .1D .2158.设)(x f 在区间],[b a 连续, ),()()(b xadt t f x F x a则)(x F 是)(x f 的( )A .不定积分B .一个原函数C .全体原函数D .在],[b a 上的定积分159.设则为连续函数其中,)(,)()(2x f dt t f axx x F xa)(lim x F ax=()A .2a B .)(2a f a C .0 D .不存在160.函数x2sin 1的原函数是()A .cx tan B .cxcot C .cxcot D .xsin 1161.函数)(x f 在[a,b]上连续, x adt t f x )()(,则()A .)(x 是)(x f 在[a,b]上的一个原函数B .)(x f 是)(x 的一个原函数C .)(x 是)(x f 在[a,b]上唯一的原函数D .)(x f 是)(x 在[a,b]上唯一的原函数162.广义积分dxe x( ) A .0 B .2C .1D .发散163.dxx 02cos 1( )A .0B .2C .22D .2164.设)(x f 为偶函数且连续,又有等于则)(,)()(0x F dt t f x F x( )A .)(x F B .)(x F C .0D .2)(x F 165.下列广义积分收敛的是()A .1xdx B .1xx dx C .dxx 1D .132xdx166.下列广义积分收敛的是()A .13xdx B .1cosxdxC .dxx 1ln D .1dxe x167.apxp dx e)0(等于()A .paeB .paea1C .paep1D .)1(1paep168.ex x dx2)(ln ( )A .1B .e1C .eD .(发散)169.积分dx e kx收敛的条件为()A .kB .0k C .0k D .k 170.下列无穷限积分中,积分收敛的有()A .dxe xB .1x dxC .dxe xD .cos xdx171.广义积分edx xxln 为()A .1B .发散C .21D .2172.下列广义积分为收敛的是( )A .edxxxln B .exx dxlnC .edxx x 2)(ln 1D .edxx x 21)(ln 1173.下列积分中不是广义积分的是()A .0)1ln(dxx B .42211dxx C .11-21dxxD .3-11dxx174.函数()f x 在闭区间[a,b]上连续是定积分badx x f )(在区间[a,b]上可积的().A .必要条件B .充分条件C .充分必要条件D .既非充分又飞必要条件175.定积分121sin 1x dx x等于().A .0B .1C .2D .1176.定积分122d ||xx x 等于().A .0B . 1C .174D .174177.定积分x x xd e )15(45等于().A .0B .5eC .5-eD .52e178.设)(x f 连续函数,则22)(dxx xf ()A .4)(21dx x f B .20)(21dxx f C .40)(2dxx f D .4)(dxx f 179.积分11sin 2xdxx e exx()A .0B .1C .2D .3180.设)(x f 是以T 为周期的连续函数,则定积分Tl ldx x f I)(的值()A .与l有关B .与T 有关C .与l ,T 均有关D .与l ,T 均无关181.设)(x f 连续函数,则2)(dxxx f ()A .21)(21dxx f B .210)(2dxx f C .20)(dxx f D .2)(2dxx f 182.设)(x f 为连续函数,则1)2('dx x f 等于()A .)0()2(f f B .)0()1(21f f C .)0()2(21f f D .)0()1(f f 183.C 数)(x f 在区间[a,b]上连续,且没有零点,则定积分b adx x f )(的值必定()A .大于零B .大于等于零C .小于零D .不等于零184.下列定积分中,积分结果正确的有()A .cx f dx x f ba )()('B .)()()('a f b f dxx f baC .)]2()2([21)2('a f b f dxx f baD .)2()2()2('a f b f dx x f ba185.以下定积分结果正确的是()A .2111dx xB .21112dx xC .211dx D .211xdx 186.adxx 0)'(arccos ()A .211xB .cx211C .ca2arccos D .arccos arccosa 187.下列等式成立的有( )A .0sin 11xdx x B .11dxe xC .abxdx abtan tan ]'tan [D .xdxxdxdxsin sin 0188.比较两个定积分的大小()A .213212dx x dx x B .213212dx x dx x C .213212dxx dxx D .213212dxx dxx 189.定积分22221sin dx xx x 等于()A .1B .-1C .2D .0190.11-x dx( )A .2B .2C .1D .1191.下列定积分中,其值为零的是()A .22-sin xdx x B .20cos xdx x C .22-)(dx x e xD .22-)sin (dxx x192.积分21dxx ()A .0B .21C .23D .25193.下列积分中,值最大的是()A .12dx x B .13dxx C .14dxx D .15dxx 194.曲线x y42与y 轴所围部分的面积为()A .2224dyy B .224dyy C .44dxx D .444dxx 195.曲线xey 与该曲线过原点的切线及y 轴所围形的为面积()A .e xxdxxe e1B .10ln ln dyy y y C .1dxex exD .edyy y y 1ln ln 196.曲线2xyx y 与所围成平面图形的面积( )A .31B .31C .1 D .-1四、常微分方程197.函数y c x (其中c 为任意常数)是微分方程1x y y 的().A .通解B .特解C .是解,但不是通解,也不是特解D .不是解198.函数23xy e是微分方程40y y 的().A .通解B .特解C .是解,但不是通解,也不是特解D .不是解199.2()sin y y x y x 是().A .四阶非线性微分方程B .二阶非线性微分方程C .二阶线性微分方程D .四阶线性微分方程200.下列函数中是方程0y y 的通解的是().A .12sin cos y C x C xB .xy Ce C .yCD .12xyC eC 专升本高等数学综合练习题参考答案1.B2.C3.C4.B 在偶次根式中,被开方式必须大于等于零,所以有40x 且20x ,解得24x ,即定义域为[2,4].5.A 由奇偶性定义,因为33()2()3sin()23sin ()f x x x xx f x ,所以3()23sin f x xx 是奇函数.6.解:令t x 1,则tt tt t f 21212211)(,所以xx x f 212)(,故选 D 7.解:选D8.解:选D 9.解:选B 10.解:选C11.解:110x ,所以01x ,故选 B 12.解:选C13.解:选 B14.解:选 B15.解:选 B16.解:)(x f 的定义域为)4,1[,选D17.解:根据奇函数的定义知选 C18.解:选 C19. 解:选 C20.解:因为函数)1,0(log a ax ya ya x与互为反函数,故它们的图形关于直线x y 轴对称,选 C 21.A 22.D23.解:这是00型未定式ln 1l 1limlimx exex x exe,故选B .24.解:这是型未定式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学模拟题
第一部分 客观题
一、判断题
1、 函数x x x f sin )(=在),(+∞-∞上有界。
( 错 B)
2、错B
3、函数的极值点一定是函数的驻点。
( 错 B )
4、对A
5、设)(x f 是一个连续的奇函数,则0)(11=⎰
-dx x f 。
( 对A ) 二、单项选择题
6、 、定积分 dx x ⎰--2
/2/2sin 1ππ的值是: ( D )
(A )0; (B) 1; (C) 2-; (D) 2;
7、在下列指定的变化过程中,( C )是无穷小量. (A) )(1sin ∞→x x x (B) )0(1sin →x x (C) )0()1ln(→+x x (D) )(e 1
∞→x x 8、设(ln )1f x x '=+,则()f x =( C ).
(A) 22x x c ++ (B)22x x e e c ++ (C)x x e c ++ (D)ln (2ln )2
x x + 9、.曲线2211x x
e e y ---+=( D )
(A) 无渐近线 (B) 仅有水平渐近线
(C) 仅有铅直渐近线 (D)既有水平渐近线,又有铅直渐近线
10 、 C
第二部分 主观题
一、求解下列各题
1
2、设()y y x =由方程组cos sin sin cos x t t t y t t t
=+⎧⎨=-⎩确定,求dy dx 。
解:
3、求曲线 2(1)y x x =- 的凹凸区间。
解:Y=(x-1)²x 求二阶导数,再找零点 x= - (1/2) ,以所找零点将定义域区间划分为2个区间,(-∞,-(1/2))和((-1/2),+∞),在前一个区间,f ' ' <0 ,为凹区间,后一个区间为凸区间。
在 x= - (1/2) 的左右,其二阶导数变号,故拐点为(-(1/2), 7/8)
4、 求
4
0e ⎰。
5、 设222()()4x x f t dt F x x =
-⎰,其中)(x f 为连续函数,求2
lim ()x F x →。
二、应用题 1、求由曲线2y x =与直线2y x =+所围成的平面图形的面积。
解:y=x²与y=x+2的交点为:(-1,1), (2,4)
则由曲线y=x²与y=x+2围成图形的面积等于y=x+2-x²在[-1,2]上的定积分. 所以:S=∫[-1,2](x+2-x²)dx
=x²/2+2x-x³/3,l[-1,2]
=(2+4-8/3)-(1/2-2+1/3)
=(6-8/3+2-5/6)
=8-21/6 =27/6 =4.5
三、证明题。
