材料力学弯曲变形(强度)
合集下载
材料力学课件第5章
M
zM
x
等截面梁
y
注意 当梁为变截面梁时, max 并不一定
发生在|M|max 所在面上.
22
5.3 横力弯曲时梁横截面上的正应力 弯曲正应力强度条件
h
常用图y形Wz
c b
Wz =Iz /ymax
z
Wz
Iz h
bh3 2 12 h
bh2 6
2
h2
h1
y
c
z
Wz
Iz h1
1 ( b1h13 h1 6
z
于是
M
E
Iz
M
得
1 M
EIz
y
x
代入
E
y得
My
Iz
15
5.2 纯弯曲时梁横截面上的正应力
常用图形y、Iz
h
y
1.矩形
dy
c
y z
Iz
Ay2 d A
h 2
y2b d y bh3
h 2
12
b
y
同理：
Iy
hb3 12
z
Iz
b1h13 12
b2h23 12
c
b2 b1
同理： I y
h1b13 12
y
12 rp
mn
x2
x
x1
12
dx
'=
x2 FN1
FN2
'=
38
5.4 横力弯曲时梁横截面上的切应力 弯曲切应力强度条件
F
Fx 0
FN 2 FN1 dx b
x1
y
12 rp mn
x2
x
12
dx
材料力学第6章弯曲变形
Fb M2 x2 F ( x2 a ) l
M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下，弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时，梁截面上有弯矩也有剪力，对于跨 度远大于截面高度的梁，剪力对弯曲变形的影响可以 省略，(a)式便可以作为横力弯曲变形的基本方程。其 中，M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合， 造成磨损不匀，产生噪音， 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大，会 使梁上小车行走困难， 出现爬坡现象，还会引 起较严重的振动。
变形超过允许数值，即 使在弹性范围内，也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为： 3 1 Fb 2 2 wmax l b 9 3 EIl
M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下，弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时，梁截面上有弯矩也有剪力，对于跨 度远大于截面高度的梁，剪力对弯曲变形的影响可以 省略，(a)式便可以作为横力弯曲变形的基本方程。其 中，M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合， 造成磨损不匀，产生噪音， 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大，会 使梁上小车行走困难， 出现爬坡现象，还会引 起较严重的振动。
变形超过允许数值，即 使在弹性范围内，也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为： 3 1 Fb 2 2 wmax l b 9 3 EIl
材料力学-第7章 弯曲变形
引言
梁弯曲问题的近似和简化
q( x)
M0
ML
Q0
QL
弯曲问题中，不考虑轴向拉伸。因此，梁内力只有弯矩和剪力 下面，我们分别考虑弯矩和剪力引起的弯曲变形效果
材料力学－第7章 弯曲变形
挠度曲线 垂直于轴线的横截面弯曲后仍为平面，仍 垂直于轴线，只是相互间转动一个角度
M
弯矩引起的弯曲变形
M
剪力引起的弯曲变形
例题
2
已知：简支梁受力如 图所示。FP、EI、l均为已 知。 求：加力点B的挠度和 支承A、C处的转角。
材料力学－第7章 弯曲变形
§7- 3 计算梁位移的积分法
解：1． 确定梁约束力 首先，应用静力学方法求得 梁在支承A、C二处的约束力分别 如图中所示。 解：2． 分段建立梁的弯矩方程 因为B处作用有集中力FP，所以需要分为AB和BC两段 建立弯矩方程。 在图示坐标系中，为确定梁在0～l/4范围内各截面上的 弯矩，只需要考虑左端A处的约束力3FP/4；而确定梁在l/4～ l范围内各截面上的弯矩，则需要考虑左端A处的约束力 3FP/4和荷载FP。
Q
垂直于轴线的横截面弯曲后不垂直于轴线
Q
材料力学中一般考虑细长梁，顾而可以忽略剪力引起的变形，只 考虑弯矩引起的变形。因为所有横截面始终与轴线垂直，所以，梁的 弯曲变形可以仅用轴线来表征。空间的梁简化成一轴线。
材料力学－第7章 弯曲变形
挠度曲线
问题1： 如何表征梁的弯曲变形
－用什么物理量来描述梁的变形
( x)
w
x
x
( x)
w( x)
材料力学－第7章 弯曲变形
挠度曲线
* 弯曲变形的表征
梁在弯曲变形后，横截面的位置将发生改变，这种位置 的改变称为位移 (displacement) 。梁的位移包括三部分：
梁弯曲问题的近似和简化
q( x)
M0
ML
Q0
QL
弯曲问题中，不考虑轴向拉伸。因此，梁内力只有弯矩和剪力 下面，我们分别考虑弯矩和剪力引起的弯曲变形效果
材料力学－第7章 弯曲变形
挠度曲线 垂直于轴线的横截面弯曲后仍为平面，仍 垂直于轴线，只是相互间转动一个角度
M
弯矩引起的弯曲变形
M
剪力引起的弯曲变形
例题
2
已知：简支梁受力如 图所示。FP、EI、l均为已 知。 求：加力点B的挠度和 支承A、C处的转角。
材料力学－第7章 弯曲变形
§7- 3 计算梁位移的积分法
解：1． 确定梁约束力 首先，应用静力学方法求得 梁在支承A、C二处的约束力分别 如图中所示。 解：2． 分段建立梁的弯矩方程 因为B处作用有集中力FP，所以需要分为AB和BC两段 建立弯矩方程。 在图示坐标系中，为确定梁在0～l/4范围内各截面上的 弯矩，只需要考虑左端A处的约束力3FP/4；而确定梁在l/4～ l范围内各截面上的弯矩，则需要考虑左端A处的约束力 3FP/4和荷载FP。
Q
垂直于轴线的横截面弯曲后不垂直于轴线
Q
材料力学中一般考虑细长梁，顾而可以忽略剪力引起的变形，只 考虑弯矩引起的变形。因为所有横截面始终与轴线垂直，所以，梁的 弯曲变形可以仅用轴线来表征。空间的梁简化成一轴线。
材料力学－第7章 弯曲变形
挠度曲线
问题1： 如何表征梁的弯曲变形
－用什么物理量来描述梁的变形
( x)
w
x
x
( x)
w( x)
材料力学－第7章 弯曲变形
挠度曲线
* 弯曲变形的表征
梁在弯曲变形后，横截面的位置将发生改变，这种位置 的改变称为位移 (displacement) 。梁的位移包括三部分：
材料力学--弯曲正应力及其强度条件
C
E
15 106 200 109
7.5 105
q 40 kN / m
A
C
1.5 m
1.5 m
B 300 200
例21：图示木梁，已知下边缘纵向总伸
长为 10 mm，E=10GPa，求载荷P的大小。
P
300
A
C
B 200
2m
2m
解： AC
l/2
(x) dx
0
l/2 (x) d x l/2 M ( x) d x
1m
例20：简支梁受均布荷载，在其Ｃ截面
的下边缘贴一应变片，已知材料的 E=200GPa，试问该应变片所测得的应变 值应为多大？
q 40 kN / m
A
C
1.5 m
1.5 m
B 300 200
解：C截面的弯矩
ql2 MC 8 45kN m
C截面下边缘的应力 C
MC Wz
15MPa
应变值
P
y1
y2
Cz
解：
max
M max y1 Iz
[ ]
(1)
max
M max y2 Iz
[ ]
(2)
(1) 得： y1 [ ]
(2)
y2 [ ]
例16：图示外伸梁，受均布载荷作用，
材料的许用应力［σ］=160 MPa，校核 该梁的强度。
10 kN / m
2m
4m
200 100
10 kN / m
变形几何关系 从三方面考虑： 物理关系
静力学关系
1、变形几何关系
m
mn
m
aa
bb
mn
m
m
观察到以下变形现象: (1)aa、bb弯成弧线，aa缩短，bb伸长 (2)mm、nn变形后仍保持为直线，且仍与变为
知识资料材料力学知识资料弯曲变形应力状态分析和强度理论(一)(新版)
需要课件请或弯曲变形粱的挠度与转角（一）挠曲线在外力作用下，梁的轴线由直线变为光洁的弹性曲线，梁弯曲后的轴线称为挠曲线。
在平面弯曲下，挠曲线为梁形心主惯性平面内的一条平面曲线v=f(x)(见图5-8-1)。
（二）挠度与转角梁弯曲变形后，梁的每一个横截面都要产生位移，它包括三部分：1. 挠度梁横截面形心在垂直于轴线方向的线位移，称为挠度，记作v。
沿梁轴各横截面挠度的变化规律，即为梁的挠曲线方程。
v=f(x)2．转角横截面相对本来位置绕中性轴所转过的角度，称为转角，记作θ。
小变形情况下，3．此外，横截面形心沿梁轴线方向的位移，小变形条件下可忽略不计。
(三)挠曲线近似微分方程在线弹性范围、小变形条件下，挠曲线近似微分方程为上式是在图5—8—l所示坐标系下建立的。
挠度w向下为正，转角θ顺时针转为正。
积分法计算梁的位移按照挠曲线近似微分方程(5—8—1)，积分两次，即得梁的转角方程和挠度方程，即由第1 页/共6 页式中积分常数C、D，可由梁的边界条件来决定。
当梁的弯矩方程需分段列出时，挠曲线微分方程也需分段建立，分段积分。
于是全梁的积分常数数目将为分段数目的两倍。
为了决定所有积分常数，除利用边界条件外，还需利用分段处挠曲线的延续条件(在分界点处左、右两段梁的转角和挠度均应相等)。
用叠加法求梁的位移（一）叠加原理几个荷载同时作用下梁的任一截面的挠度或转角等于各个荷载单独作用下同一截面挠度或转角的总和。
（二）叠加原理的适用条件叠加原理仅适用于线性函数。
要求挠度、转角为梁上荷载的线性函数，必须满意： 1．材料为线弹性材料；2．梁的变形为小变形；3．结构几何线性。
（三）叠加法的特征1．各荷载同时作用下挠度、转角等于单独作用下挠度、转角的总和，应该是几何和，同一方向的几何和即为代数和。
2．梁在容易荷载作用下的挠度、转角应为已知或可查手册。
3．叠加法相宜于求梁某一指定截面的挠度和转角。
[例 5—8—1] 用积分法求图5—8—3所示各梁的挠曲线方程时，试问应分为几段?将浮上几个积分常数? 并写出各梁的边界条件和延续条件。
中职机械计算梁的弯曲变形强度
知识链接 任务5 计算梁的弯曲变形强度
3、采用等强度梁
本模块小结
◇静力学介绍了物体的受力分析、力系的等效替换（或 简化）、建立各种力系的平衡条件等。
◇将工程结构和机械中的简单构件简化为一维杆件，计 算杆中的应力、变形，以保证结构能承受预定的载荷。
◇选择适当的材料、截面形状和尺寸，以便设计出既安 全又经济的结构构件和机械零件。
任务5 计算梁的弯曲变形强度
一、梁纯弯曲时横截面上的正应力
2 .梁纯弯曲时的变形特点，如图2-2-31。 可得出平面假设：两横截面变形前为平面，变形后仍为平
面；横截面始终垂直于轴线；横截面无相对错动。 由平面假设可以判断纯弯曲梁横截面上只有正应力 ， 无 剪
应力。 中性层：梁内既不缩短也不伸长(不受压不受拉)的一层。中
任务5 计算梁的弯曲变形强度
一、梁纯弯曲时横截面上的正应力 4 .梁纯弯曲时正应力的计算公式
在弹性范围内，梁纯弯曲时横截面上任意一点的正 应力为:
任务5 计算梁的弯曲变形强度
一、梁纯弯曲时横截面上的正应力 4 . 梁纯弯曲时正应力的计算公式
在中性轴上y=0，所以σ=0；当y=ymax 时，σ=σmax。最大正 应力产生在离中性轴最远的边缘处。
性层是梁上拉伸区与压缩区的分界面。 中性轴：中性层与横截面的交线。变形时横截面绕中性轴
旋转。
任务5 计算梁的弯曲变形强度
一、梁纯弯曲时横截面上的正应力 3 .梁纯弯曲时横截面上正应力的
分布规律
如图2-2-32所示，正应力分布规 律为：横截面上各点正应力的大小， 与该点到中性轴的距离成正比。中 性轴处正应力为零。
任务实施 任务5 计算梁的弯曲变形强度
(1)确定最大弯矩，由图2-30可知梁的最大弯矩为: (2)确定抗弯截面模量。 (3)校核强度。
材料力学教程-7.弯曲变形
数据处理
根据需要，对数据进行计算、 绘图等处理，以便更好地理解 和分析实验结果。
结果分析
结合实验数据和理论分析，评 估材料的弯曲性能，并探讨影 响材料弯曲性能的因素。
结论总结
总结实验结果，得出结论，并 提出改进和优化材料弯曲性能
的建议。
04
弯曲变形的工程应用实例
桥梁的弯曲变形分析
总结词
桥梁的弯曲变形分析是确保桥梁安全的重要环节，通过分析桥梁在不同载荷下的弯曲变形程度，可以评估桥梁的 承载能力和安全性。
转角
梁在弯曲变形后，其横截 面绕其中性轴旋转的角度 称为转角。转角是衡量梁 横截面旋转程度的量。
弯曲变形的物理关系
弯矩
由于外力作用在梁上，使梁产生弯曲变形的力矩 称为弯矩。弯矩是引起梁弯曲变形的力。
剪力
在梁弯曲变形过程中，垂直于轴线的横向剪切力 称为剪力。剪力使梁产生剪切变形。
扭矩
当外力作用在梁的某一侧时，会使梁产生扭转变 形，这种使梁产生扭转变形的力矩称为扭矩。
详细描述
高层建筑由于其高度和规模，对风载和地震等外部载荷非常敏感。因此，在高层建筑设 计阶段，需要进行详细的弯曲变形分析。这包括对建筑物的整体结构和各个楼层在不同 载荷下的弯曲变形进行模拟和分析，以确保建筑物在各种外部载荷下的安全性和稳定性。
机械零件的弯曲变形分析
要点一
总结词
机械零件的弯曲变形分析是确保机械系统正常运行的关键 环节。通过对机械零件在不同工作载荷下的弯曲变形进行 分析，可以优化零件的设计和加工工艺，提高其工作性能 和寿命。
通过实例分析和习题练习，学生可以加深对弯曲 变形的理解，提高解决实际问题的能力。
弯曲变形的未来研究方向
弯曲变形的非线性行为
根据需要，对数据进行计算、 绘图等处理，以便更好地理解 和分析实验结果。
结果分析
结合实验数据和理论分析，评 估材料的弯曲性能，并探讨影 响材料弯曲性能的因素。
结论总结
总结实验结果，得出结论，并 提出改进和优化材料弯曲性能
的建议。
04
弯曲变形的工程应用实例
桥梁的弯曲变形分析
总结词
桥梁的弯曲变形分析是确保桥梁安全的重要环节，通过分析桥梁在不同载荷下的弯曲变形程度，可以评估桥梁的 承载能力和安全性。
转角
梁在弯曲变形后，其横截 面绕其中性轴旋转的角度 称为转角。转角是衡量梁 横截面旋转程度的量。
弯曲变形的物理关系
弯矩
由于外力作用在梁上，使梁产生弯曲变形的力矩 称为弯矩。弯矩是引起梁弯曲变形的力。
剪力
在梁弯曲变形过程中，垂直于轴线的横向剪切力 称为剪力。剪力使梁产生剪切变形。
扭矩
当外力作用在梁的某一侧时，会使梁产生扭转变 形，这种使梁产生扭转变形的力矩称为扭矩。
详细描述
高层建筑由于其高度和规模，对风载和地震等外部载荷非常敏感。因此，在高层建筑设 计阶段，需要进行详细的弯曲变形分析。这包括对建筑物的整体结构和各个楼层在不同 载荷下的弯曲变形进行模拟和分析，以确保建筑物在各种外部载荷下的安全性和稳定性。
机械零件的弯曲变形分析
要点一
总结词
机械零件的弯曲变形分析是确保机械系统正常运行的关键 环节。通过对机械零件在不同工作载荷下的弯曲变形进行 分析，可以优化零件的设计和加工工艺，提高其工作性能 和寿命。
通过实例分析和习题练习，学生可以加深对弯曲 变形的理解，提高解决实际问题的能力。
弯曲变形的未来研究方向
弯曲变形的非线性行为
吉林大学考研材料力学题型二：弯曲强度及变形
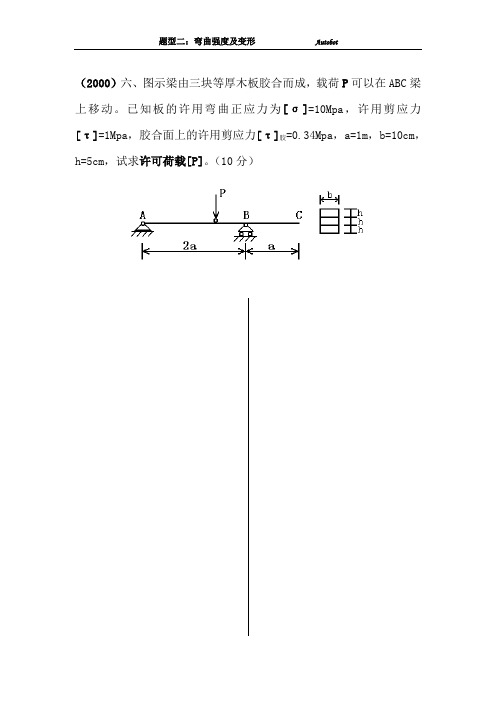
（2000）六、图示梁由三块等厚木板胶合而成，载荷P可以在ABC梁上移动。
已知板的许用弯曲正应力为[σ]=10Mpa，许用剪应力[τ]=1Mpa，胶合面上的许用剪应力[τ]胶=0.34Mpa，a=1m，b=10cm，h=5cm，试求许可荷载[P]。
（10分）
（2001）八、已知如图，（1）、试列出求解AB梁弯曲变形所需的挠曲线近似微分方程。
（不必积分）（2）、列出确定积分常数所需的全部条件。
（6分）
（2002）三、铸铁梁上作用有可移动的荷载P，已知：y1=52mm，y2=88mm，I z=763cm4，铸铁拉伸时的σb=120Mpa，压缩时的σb=640Mpa，安全系数n=4。
试确定铸铁梁的许可荷载P；并求τmax（10分）
（2003）八、列出求解AB梁弯曲变形所需的挠曲线近似微分方程（不必积分）；写出确定积分常数所需的全部条件；画出挠曲线的大致形状。
已知：q、a、弹簧刚度K，EI为常数。
（10分）
（2006）三、有一长L=10M，直径D=40CM的原木，[σ]=6MP A,欲加工成矩形截面梁，且梁上作用有可移动荷载F，试问：1、当H、B和X 为何值时，梁的承载能力最大？2、求相应的许用荷载[F]。
（15分）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
弯曲变形
F
1.绘制压板简图，如右图所示： 2.计算压板所受外力：
A
C
B
FNA 3.6kN
3.计算最大弯矩：
FNB 2.4kN
40 FNA
60 FNB
M max FNAl 3.6 103 40 10 3 144 N m y
4.计算截面C处的抗弯截面系数：
δ
W b 2 / 6 d 2 / 6 3 2
弯曲变形
56
机械基础-材料力学-弯曲变形
2021/3/3
思考与联系-2.校核梁的强度
弯曲变形
1.计算梁所受外力：
FA FB F 2
2.计算最大弯矩：
l Fl M max FA 2 4
3.计算抗弯截面系数：
W bh2 6
4.计算最大正应力：
F
A
B
l/2
l/2
7
机械基础-材料力学-弯曲变形
2021/3/3
相关知识
弯曲变形
❖一、梁纯弯曲时横截面上的正应力 ▪ 梁纯弯曲的概念 ▪ 梁纯弯曲时的变形特点 ▪ 梁纯弯曲时横截面上正应力的分布规律 ▪ 梁纯弯曲时正应力的计算公式
▪ 常用截面的I、W计算公式
❖二、梁纯弯曲时的强度条件
8
机械基础-材料力学-弯曲变形
2021/3/3
q=60kN弯/曲m变形
A
B
3m
+
67.5(kNm)
M
最大弯矩下降了：
67.5671.51.560.82 8 2%
梁内最大正应力同样 下降了82%。
27
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
28
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
29
机械基础-材料力学-弯曲变形
2021/3/3
10
机械基础-材料力学-弯曲变形
22002211//33//33
相关知识
弯曲变形
❖一、梁纯弯曲时横截面上的正应力 ▪ 梁纯弯曲的概念 ▪ 梁纯弯曲时的变形特点 ▪ 梁纯弯曲时横截面上正应力的分布规律 ▪ 梁纯弯曲时正应力的计算公式
▪ 常用截面的I、W计算公式
❖二、梁纯弯曲时的强度条件
11
机械基础-材料力学-弯曲变形
相关知识-梁纯弯曲的概念
内力
弯矩M 剪力F
正应力 切应力
M
纯弯曲: F =0 ， M≠0
横力弯曲：F≠0， M≠0
9
机械基础-材料力学-弯曲变形
弯曲变形
F
2021/3/3
相关知识-梁纯弯曲的概念
弯曲变形
Fa
C A
F F
- -F
a F 纯弯曲(Pure Bending)
D B
F+
x
M
x
-
-Fa
AB段纯弯曲(Pure Bending)
▪ 常用截面的I、W计算公式
❖二、梁纯弯曲时的强度条件
21
机械基础-材料力学-弯曲变形
2021/3/3
相关知识-梁纯弯曲时的强度条件 弯曲变形
弯矩最大的截
F
面就是危险截
面
A
h
其上下边缘各点的弯曲正 应力即为最大工作应力，
B
该点称为危险点。
l
max≤
M
max
max
M max Wz
≤
22
纵向线的伸长区，梁的宽度减少。
m a b n
m a b
n
12
机械基础-材料力学-弯曲变形
m a
b n
m
M
a
b
n
2021/3/3
相关知识-纯弯曲时的变形特点
弯曲变形
2、平面假设：
① 横截面变形后仍为平面。
② 横截面始终垂直于轴线。
③ 横截面无相对错动。
断定：纯弯曲梁横截面上只有 正应力，无剪应力。
M
① 纯弯曲时梁横截面上的正应力
➢ 利②用强正度应条力件强进度行条强件度校核并设计构件 ③ 提高梁的弯曲强度的一些措施
5
机械基础-材料力学-弯曲变形
2021/3/3
任务描述
❖ 确定压板厚度δ ▪ 已知：
• F=6kN • [σ]=110MPa
φ14
32 δ
弯曲变形
F
A
C
B
40 FNA
60 FNB
y
z 14 32
2021/3/3
弯曲变形
48
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
49
机械基础-材料力学-弯曲变形
2021/3/3
蔡甸汉江公路大桥 弯曲变形
110m+180m+110m预应力混凝土连续刚构桥
50
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
51
机械基础-材料力学-弯曲变形
6
机械基础-材料力学-弯曲变形
22002211//33//33
任务一 计算梁的弯曲变形内力
弯曲变形
❖知识目标 ❖能力目标 ❖任务描述 ❖任务分析 ❖相关知识 ❖任务实施 ❖知识链接 ❖思考与练习
① 将压板简化为受集中力作用的简支梁。 ② 作剪力图和弯矩图，确定危险截面。
③ 计算最大弯曲正应力，通过强度计算来确 定压板厚度。
机械基础-材料力学-弯曲变形
2021/3/3
任务一 计算梁的弯曲变形内力
弯曲变形
❖知识目标 ❖能力目标 ❖任务描述 ❖任务分析 ❖相关知识 ❖任务实施 ❖知识链接 ❖思考与练习
确定压板厚 度。
F
A
C
B
40 FNA
60 FNB
δ
y
z 14 32
23
机械基础-材料力学-弯曲变形
2021/3/3
任务实施
矩形
b
实心圆
空心圆
z
d
z
Dd
z
y
I
z
bh3 12
ym
a
x
h 2
y
I
z
d 4
64
y
m
a
x
d 2
y
I
z
D 4
64
(1
4
)
D ymax 2
bh2 Wz 6
20
Wz
d 3
32
Wz
D3
32
(1
4
)
d D
机械基础-材料力学-弯曲变形
2021/3/3
相关知识
弯曲变形
❖一、梁纯弯曲时横截面上的正应力 ▪ 梁纯弯曲的概念 ▪ 梁纯弯曲时的变形特点 ▪ 梁纯弯曲时横截面上正应力的分布规律 ▪ 梁纯弯曲时正应力的计算公式
弯曲变形
考虑弯曲切应力强度，则梁高的最小值为：
max
3FS 2bhm
in
≤
[ ]
F
hmin
3F
2b[
]
x
F F
x
x l
40
机械基础-材料力学-弯曲变形
2021/3/3
400kN
弯曲变形
5m
900
200
400kN 5m
300
900
200
41
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
42
2021/3/3
弯曲变形
38
机械基础-材料力学-弯曲变形
2021/3/3
知识链接-采用等强度梁
F b
M (x)
h
max(x) W (x) [ ]
M (x) Fx
M
又 W (x) bh2 (x) 6
F
h(x)
6Fx
b[ ]
x
弯曲变形
l － Fl
39
机械基础-材料力学-弯曲变形
2021/3/3
中性层
中性轴
14
机械基础-材料力学-弯曲变形
2021/3/3
相关知识
弯曲变形
❖一、梁纯弯曲时横截面上的正应力 ▪ 梁纯弯曲的概念 ▪ 梁纯弯曲时的变形特点 ▪ 梁纯弯曲时横截面上正应力的分布规律 ▪ 梁纯弯曲时正应力的计算公式
▪ 常用截面的I、W计算公式
❖二、梁纯弯曲时的强度条件
15
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
内蒙古磴口黄河大桥
52
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
53
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
54
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
55
机械基础-材料力学-弯曲变形
2021/3/3
任务一 计算梁的弯曲变形内力
❖知识目标 ❖能力目标 ❖任务描述 ❖任务分析 ❖相关知识 ❖任务实施 ❖知识链接 ❖思考与练习
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
43
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
44
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
45
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
46
机械基础-材料力学-弯曲变形
2021/3/3
弯曲变形
47
机械基础-材料力学-弯曲变形
弯曲变形
在面积相等的情况下，选择抗弯截面系数大的截面
z
h
b
z
z