材料力学 弯曲变形分析
弯曲变形实验报告

弯曲变形实验报告弯曲变形实验报告引言:弯曲变形是材料力学中的重要研究内容之一,它涉及到材料的强度、刚度和韧性等性能参数。
本实验旨在通过对不同材料进行弯曲变形实验,探究材料在受力情况下的变形特性,并对实验结果进行分析和总结。
实验装置与方法:本次实验使用了一台弯曲试验机,试验样品选取了铝合金、钢材和塑料等不同材料的试样。
首先,将试样固定在试验机上,调整试验机的参数,如加载速度和加载方式等。
然后,通过试验机施加不同的弯曲载荷,记录下试样在不同载荷下的变形情况。
实验结果与分析:实验结果显示,不同材料在受力下表现出不同的变形特性。
首先,铝合金试样在受力后出现较为明显的塑性变形,这是由于铝合金具有较高的韧性和良好的可塑性。
其次,钢材试样在受力后呈现出较小的变形,这是由于钢材具有较高的强度和刚性。
最后,塑料试样在受力后出现较大的变形,并且不能恢复原状,这是由于塑料具有较低的强度和刚性,易于发生永久性变形。
进一步分析发现,不同材料的变形特性与其微观结构密切相关。
铝合金由于晶粒细小且均匀,因此在受力时更容易发生塑性变形;而钢材由于晶粒较大且排列有序,因此在受力时更难发生塑性变形。
塑料由于分子链之间的相对滑动性较高,因此在受力时更容易发生形变。
实验结果的应用:弯曲变形实验结果对工程领域具有重要的应用价值。
例如,在建筑设计中,通过对不同材料的弯曲变形特性进行研究,可以选择合适的材料用于不同的结构部件。
对于需要承受较大变形的结构,可以选择具有较高韧性的材料,如铝合金;对于需要承受较大载荷的结构,可以选择具有较高强度和刚性的材料,如钢材。
此外,弯曲变形实验结果还可以用于材料性能的评估和质量控制。
通过对材料在受力下的变形情况进行观察和分析,可以判断材料的强度、刚度和韧性等性能是否符合设计要求,从而确保产品的质量。
结论:通过弯曲变形实验,我们对不同材料在受力下的变形特性进行了研究和分析。
实验结果表明,不同材料在受力下表现出不同的变形特性,这与其微观结构密切相关。
材料力学(赵振伟)梁的弯曲变形2

3. 应用叠加原理的若干情况 1 ) 荷载的分解或重组
q m
q
L/2 L/2
L
F
q
q
m L/2 L/2
F
例
q0
EI
A 求图示自由端的挠度。
L2
L2
q0
L
w1
q0
w3
B
w2
L2
L2
w1
q0 L4 8EI
w2
q0 L 24
8EI
q0 L4 128EI
w3
B
L 2
q0 L 23
6EI
L 2
q0 L4 96EI
wA
w1
w2
w3
41q0 L4 384EI
2) 逐段刚化法
依据: 若结构可分为若干部分,且各部分在荷载作用下的 变形不是相互独立的,那么,结构中 A 点的位移是各个部 分在这一荷载作用下的变形在 A 点所引起的位移的叠加。
A EI a
变形刚体
F
F
Fa 2
B
C
a/2
wwww1122
B (F1, F2,, Fn ) B1(F1) B2 (F2 ) Bn(Fn )
yB (F1, F2,, Fn ) yB1(F1) yB2 (F2 ) yBn(Fn )
叠加法的特征: 1、梁在简单载荷作用下挠度、转角应为已知或有变形表可查; 2、叠加法适用于求梁个别截面的挠度或转角值。
分析和讨论
q
在下列不同的支承方 式中,哪一种刚度最高?
q
q
分析和讨论
q
梁由混凝土材料制成,如果横截面从左图改为右图,能 够改善强度吗?能够改善刚度吗?
梁的材料由普通钢改为优质钢,能够改善强度吗? 梁的材料由普通钢改为优质钢,能够改善刚度吗?
材料力学-弯曲变形

(向下)
qB
qmax
w(l)
Pl 2 2EI
(顺时针)
例题2
图示的等截面简支梁长为l,抗弯刚度为
EI,在右端受有集中力偶M0的作用,求梁任
一截面的转角和挠度。
y
解:
由整体平衡得 FAx=0, FAy= FBy= M0/l 从而,截面的弯矩为
M(x)= xFAy= xM0/l
FAx A x o
FAy
横截面变形:
线位移:长度变化
水平方向—小变形假定,挠曲轴平坦,忽略不计 垂直方向—挠度 w= w(x)
转角:角度变化
横截面相对于原位置转过的夹角,
一般用q (x)表示截面转角,并且以逆时针为正
q'
对于细长梁,略去剪力对变形影响 平截面假设成立: 变形的横截面与挠曲轴垂直
q q tan q dw
(l 2
a2)
y
例题3
P x
A
C
于是,梁的挠曲线方程为 FAx
l
w
w1 w2
(x) (x)
0 xa a xb
FAy
a
b
Pb
6 EIl
Pa
6 EIl
x3 (b2 l2 )x (l x)3 (a2 l2
)(l
x)
0 xa a xl
转角方程为
q w ww12((xx))
0 xa a xb
Pb 2EIl
x2
C1
ቤተ መጻሕፍቲ ባይዱdx
Pb 6EIl
x3
C1x
D1
同理,对CB段
w2
w2dx C2
Pa EIl
(l
x)dx
C2
材料力学:第七章 弯曲变形

(1) 挠度w大小取决于M, E, I三个参数 应该取较小的M, 较大的E, I
(2) 弯矩M大小取决于载荷\约束分布及梁跨度大小
(3) 截面惯性矩I 大小和截面形状有关,
弹性模量E大小和材料有关
Iz =
y2dA,
A
当A大小一定时, y越大, I 越大
梁的合理刚度设计
选择I 较大的薄壁横截面形状
1 度静不定 选 FBy 为多余力, 去约 束, 写出位移边界条件
-变形协调条件 -物理方程
利用边界条件 解出未知力
列平衡方程,求其他约束力:
-补充方程
分析方法与步骤:
判断梁的静不定度
用多余力代替多余约
束的作用,得相当系统
相当系统
相当系统有多种选择:
计算相当系统在多余约
束处的位移,并根据变形 协调条件建立补充方程。
例题
解:
()
()
例题
例题
解:
()
()
()
例题
图示组合梁,EI=常数,求 wB 与qA
例题
解:
P378, 情况8
()
P377, 情况1,2
()
例题
图示刚架,求截面 C 的铅垂位移
例题
解:
位移w1包括AB弯曲 和AB扭转两部分
例题
矩形截面梁, 自由端承受集中载荷F作用, 该载荷与对 称轴y的夹角为θ, 用叠加法计算自由端求自由端截面形心C
的位移d
解:
例题
一般情况下
挠曲轴与外力作用面一般不重合
§6 简单静不定梁
静不定度与多余约束 简单静不定梁分析方法
静不定度与多余约束
静不定度 4-3= 1
材料弯曲试验方法

材料弯曲试验方法材料弯曲试验是一种常用的材料力学性能测试方法,用于评估材料的抗弯强度、弹性模量等力学性能指标。
在弯曲试验中,材料在外力的作用下发生变形,并在达到一定程度时发生破坏。
本文将介绍材料弯曲试验的基本原理、试验步骤、仪器设备以及数据处理方法。
材料弯曲试验的基本原理是根据材料在受力时的弯曲变形,通过施加力矩或力对材料进行弯曲。
在弯曲试验中,通常使用三点弯曲或四点弯曲的方式施加力矩。
在三点弯曲试验中,材料样品的两端固定,施加一个垂直于样品平面的力在中间部位。
在四点弯曲试验中,材料样品的两端固定,施加两个对称的力作用在中间部位。
通过施加不同大小的力矩,观察材料的弯曲变形和破碎情况,并测量相关的试验数据。
进行材料弯曲试验时,首先需要准备试验样品。
样品的尺寸和几何形状应符合相应的标准要求。
样品的准备通常包括切割、打磨和清洗等步骤。
亲用曲率计量R 和荷载R,曲率计与荷载计从机械静力学中得到,公式为:M=PL/4R=1/L样品准备完成后,将样品放置在弯曲试验机的弯曲支撑上,并将力施加在样品的中间部位。
在加载过程中,需要保持加载速度均匀,并逐渐增加加载的力大小。
通过逐渐增加的力加载,可以观察样品的变形情况,并记录相关的试验数据。
在加载过程中,可以使用压电应变片或应变计来测量材料的变形量,以进一步计算材料的弯曲应力和弹性模量。
在试验完成后,需要对试验数据进行处理和分析。
常用的试验数据包括弯曲应力-应变曲线、弯曲强度和弹性模量等参数。
弯曲应力-应变曲线是表示材料在弯曲过程中应力和应变的关系曲线。
通过绘制应力-应变曲线,可以评估材料的弹性和塑性变形特性。
弯曲强度表示材料在弯曲过程中承受的最大弯曲应力,可以用于比较不同材料的弯曲性能。
弹性模量表示材料的刚度和变形能力,是评估材料在受力下的抵抗能力的重要参数。
总结起来,材料弯曲试验是一种常用的材料力学性能测试方法,可以评估材料的抗弯强度、弹性模量等力学性能指标。
通过施加力矩对材料进行弯曲,并测量相关的试验数据,可以得到材料的弯曲应力-应变曲线、弯曲强度和弹性模量等参数。
材料力学第5章弯曲变形ppt课件
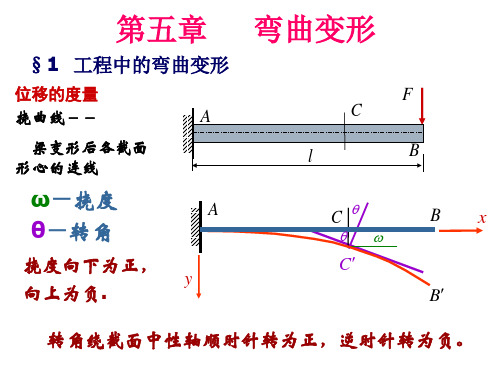
qL
4.22kNm
4.22kNm
M
max
32 M
max
76.4MPa
WZ
d 3
例题
20kN m
A
4m
FA
20kN m
A
MA
4m
试求图示梁的支反力
40kN
B
D
2m
2m
B
B1 FB
FB 40kN
B
D
B2
2m
2m
在小变形条件下,B点轴向力较小可忽略不
计,所以为一次超静定.
C
B1 B2
FBBBMF12AA2383qFEqELBqqLI84LI2LLZZ32F35BFF4FEFB83PBPLIEL7Z3L12IZ.218352.k75N5kFkN2PNmEL2IZ2
x
边界条件
A
L2
B
L2
C
y
连续条件
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
全梁仅一个挠曲线方程
C
q
EA
共有两个积分常数 边界条件
L1
A
x
B
EI Z
L
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
q
a
B C LBC
B
2a
FN
B
q2a4
8EIZ
FN 2a3
3EIZ
C
FN
a
D
弯曲变形知识点总结

弯曲变形知识点总结一、弯曲变形的原理1.1 弯曲应力和弯曲应变在外力作用下,梁或梁状结构会发生弯曲变形。
在梁上的任意一点,都会受到弯曲应力的作用。
弯曲应力是指由于梁在受力下产生的内部应力,它的大小和方向取决于梁的截面形状、受力方向和大小等因素。
弯曲应力与梁的截面形状呈二次关系,通常情况下,弯曲应力最大值出现在梁的截面中性轴附近。
随着梁的弯曲,材料内部会产生弯曲应变。
弯曲应变也是和梁的截面形状有关的,并且与弯曲应力呈线性关系。
弯曲应变可以用来描述梁在受力下的变形情况,对于计算梁的弯曲变形非常重要。
1.2 理想弹性梁的弯曲变形对于理想弹性梁而言,其弯曲变形可以通过弯曲方程来描述。
弯曲方程可以根据梁的几何形状和外力作用来得到,通过求解弯曲方程可以得到梁的变形情况。
理想弹性梁的弯曲变形遵循胡克定律,即弯曲应力和弯曲应变成正比。
1.3 破坏弯曲当外力作用到一定程度时,梁会发生破坏弯曲。
在破坏弯曲阶段,梁的抵抗力不足以克服外力作用,导致梁发生不可逆的变形。
在此阶段,梁的弯曲应力和弯曲应变将迅速增大,直至梁失去稳定性。
二、弯曲变形的计算方法2.1 弯曲方程弯曲方程是描述梁弯曲变形的重要工具,可以根据弯曲方程来求解梁的弯曲应力和弯曲应变。
通常情况下,弯曲方程是一种二阶微分方程,需要求解出合适的边界条件,才能得到梁的变形情况。
弯曲方程的求解与梁的截面形状直接相关,对于不同形状的梁,需要采用不同的弯曲方程。
2.2 梁的截面性质对于计算梁的弯曲变形而言,了解梁的截面性质非常重要。
梁的截面性质包括截面面积、截面惯性矩等参数,这些参数会直接影响弯曲方程的求解。
在实际工程中,可以通过截面性质来选择合适的梁截面形状,以满足结构设计的需求。
2.3 数值计算方法为了解决复杂梁的弯曲变形问题,通常需要采用数值计算方法。
数值计算方法可以通过数学模型来描述梁的变形行为,然后通过计算机仿真来得到梁的变形情况。
在工程实践中,有限元方法是一种常用的数值计算方法,可以对复杂结构的弯曲变形问题进行有效求解。
材料力学-第7章 弯曲变形

梁弯曲问题的近似和简化
q( x)
M0
ML
Q0
QL
弯曲问题中,不考虑轴向拉伸。因此,梁内力只有弯矩和剪力 下面,我们分别考虑弯矩和剪力引起的弯曲变形效果
材料力学-第7章 弯曲变形
挠度曲线 垂直于轴线的横截面弯曲后仍为平面,仍 垂直于轴线,只是相互间转动一个角度
M
弯矩引起的弯曲变形
M
剪力引起的弯曲变形
例题
2
已知:简支梁受力如 图所示。FP、EI、l均为已 知。 求:加力点B的挠度和 支承A、C处的转角。
材料力学-第7章 弯曲变形
§7- 3 计算梁位移的积分法
解:1. 确定梁约束力 首先,应用静力学方法求得 梁在支承A、C二处的约束力分别 如图中所示。 解:2. 分段建立梁的弯矩方程 因为B处作用有集中力FP,所以需要分为AB和BC两段 建立弯矩方程。 在图示坐标系中,为确定梁在0~l/4范围内各截面上的 弯矩,只需要考虑左端A处的约束力3FP/4;而确定梁在l/4~ l范围内各截面上的弯矩,则需要考虑左端A处的约束力 3FP/4和荷载FP。
Q
垂直于轴线的横截面弯曲后不垂直于轴线
Q
材料力学中一般考虑细长梁,顾而可以忽略剪力引起的变形,只 考虑弯矩引起的变形。因为所有横截面始终与轴线垂直,所以,梁的 弯曲变形可以仅用轴线来表征。空间的梁简化成一轴线。
材料力学-第7章 弯曲变形
挠度曲线
问题1: 如何表征梁的弯曲变形
-用什么物理量来描述梁的变形
( x)
w
x
x
( x)
w( x)
材料力学-第7章 弯曲变形
挠度曲线
* 弯曲变形的表征
梁在弯曲变形后,横截面的位置将发生改变,这种位置 的改变称为位移 (displacement) 。梁的位移包括三部分:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a)3
C2 x2
D2
目录
B B x
FBy
§6.3 用积分法求弯曲变形
4)由边界条件确定积分常数
位移边界条件
x1 0, y1(0) 0 x2 l, y2(l) 0 光滑连续条件
x1 x2 a, 1(a) 2 (a)
x1 x2 a, y1(a) y2 (a)
代入求解,得
C1
C2
y M (x) > 0
M (x) > 0
d2y
dx 2 > 0
x
O
y M (x) < 0
M (x) < 0
d2y
dx 2 < 0
x
O
目录
§6.2 挠曲线的微分方程
由弯矩的正负号规定可得,弯矩的符号与挠曲线的二阶 导数符号一致,所以挠曲线的近似微分方程为:
d 2 y M (x) dx2 EI z
由上式进行积分,求出梁横截面的转角和挠度。
目录
§6.3 用积分法求弯曲变形
挠曲线的近似微分方程为:
d2y dx2
M(x) EI z
EI z
d2y dx2
M(x)
积分一次得转角方程为:
EI z
dy dx
EI z
M( x)dx C
再积分一次得挠度方程为:
EIz y M( x)dxdx Cx D
7-3
目录
§6.3 用积分法求弯曲变形
材料力学
龚峰 gongfeng@
第6章 弯曲变形
§6.1 工程中的弯曲变形问题 §6.2 挠曲线的微分方程 §6.3 用积分法求弯曲变形 §6.4 用叠加法求弯曲变形 §6.5 简单超静定梁 §6.6 提高弯曲刚度的一些措施
目录
目录
§6.1 工程中的弯曲变形问题
7-1
目录
§6.1 工程中的弯曲变形问题
7-2
目录
§6.2 挠曲线的微分方程
2. 挠曲线的近似微分方程
推导弯曲正应力时,得到:
1M
EIz
忽略剪力对变形的影响
1 M (x)
(x) EIz
目录
§6.2 挠曲线的微分方程
由数学知识可知:
1
d2y dx2 [1 ( dy )2 ]3
dx
略去高阶小量,得
1 d2y
dx2
d2 y M(x) 所以 dx2 EIz
积分常数C、D 由梁的位移边界条件和光滑连续条件确定。
位移边界条件
光滑连续条件
AA
A AA A A AA A A
A AA AA A AAA A
A AAA A
~ ~
~~ ~
~
~ ~ ~ ~
~
~ ~~~ ~ ~ ~~~
yA 0
yA 0
A 0
yA
-弹簧变形
yAL yAR
AL AR
yAL yAR
目录
§6.3 用积分法求弯曲变形
例题6.1:求梁的转角方程和挠度方程,并求最大转角和最大挠度,
梁的EI已知。
解 1)由梁的整体平衡分析可得:
y
F
FAx 0, FAy F(), M A Fl( ) A
2)写出x截面的弯矩方程
x
yB
l
Bx
B
M(x) F(l x) F(x l)
3)列挠曲线近似微分方程并积分
目录
§6.1 工程中的弯曲变形问题
目录
§6.2 挠曲线的微分方程
1. 基本概念
y
x
转角
挠度
y
挠曲线
x
挠曲线方程:
y y(x)
挠度y:截面形心在y 方向的位移
y 向上为正
转角θ:截面绕中性轴转过的角度。
逆时针为正
由于小变形,截面形心在x方向的位移忽略不计
挠度转角关系为:
tan dy
dx
CB 段: a x2 l
y
F
A
A
DC
F Ay x1
x2
a
ymax b
E I 2
Fb 2l
x22
F 2
( x2
a)2
Fb (l 2 6l
b2 )
B B x
FBy
EIy2
Fb 6l
x23
F 6
( x2
a)3
Fb (l 2 6l
b2 )x2
目录
§6.3 用积分法求弯曲变形
6)确定最大转角和最大挠度
d2y
EI dx2 积分一次
M(x) F(x l)
EI dy EI 1 F(x l)2
C
dx
2
再积分一次 EIy 1 F (x l)3 Cx D
6
目录
§6.3 用积分法求弯曲变形
4)由位移边界条件确定积分常数
x 0, A 0
x 0, yA 0
y
代入求解 C 1 Fl 2 ,
3l 2 4b2
(a>b)
令 d 0 得,
dx
x
l,max
B
Fab 6EIl
(l
a)(
)
令 dy 0 得, dx
y
F
A
A
DC
F Ay x1
x2
a
ymax b
x
l2 b2 ,
3
Fb (l 2 b2 )3 ymax 9 3EIl ( )
而梁中点 C 处的挠度为:
B B x
FBy
Fb
yC
y1
x1 l 2
48EI
D 1 Fl 3
A
x
yB
2
6
l
5)确定转角方程和挠度方程
EI 1 F ( x l)2 1 Fl 2
2
2
EIy 1 F ( x l)3 1 Fl 2 x 1 Fl 3
6
2
6
6)确定最大转角和最大挠度
x l,
max
B
Fl 2 , 2EI
ymax
yB
Fl 3 3EI
目录
F
Bx
B
§6.3 用积分法求弯曲变形
1 6
Fbl
Fb 3 6l
D1 D2 0
y
F
A
A
DC
F Ay x1
x2
a
ymax b
B B x
FBy
目录
§6.3 用积分法求弯曲变形
5)确定转角方程和挠度方程
AC 段: 0 x1 a
EI1
Fb 2l
x2 1
Fb 6l
(l 2
b2 )
EIy 1
Fb 6l
x3 1
Fb 6l
(l 2
b2 )x1
x1 ,0
x1
a
Mx2
FAy
x2
ห้องสมุดไป่ตู้
F( x2
a)
Fb l
x2
F( x2
a),
a x2 l
目录
§6.3 用积分法求弯曲变形
3)列挠曲线近似微分方程并积分
AC 段: 0 x1 a
EI
d 2 y1 dx12
M( x1 )
Fb l
x1
EI dy1 dx1
EI ( x1 )
Fb 2l
x2 1
C1
EIy 1
Fb 6l
x3 1
C1 x1
D1
CB 段:
a x2 l
y
F
A
A
DC
F Ay x1
x2
a
ymax b
EI
d 2 y2 dx22
M(x2 )
Fb l
x2
F(x2
a)
EI
dy2 dx2
EI ( x2 )
Fb 2l
x2 2
F 2
( x2
a)2
C2
EIy 2
Fb 6l
x3 2
F 6
( x2
例题6.2:求梁的转角方程和挠度方程,并求最大转角和最大挠度,
梁的EI已知,l=a+b,a>b。
y
F
解 1)由梁整体平衡分析得:
Fb
Fa
FAx 0, FAy l , FBy l
2)弯矩方程
AC 段:
A
A
DC
F Ay x1
x2
a
ymax b
B B x
FBy
M x1 FAy
CB 段:
x1
Fb l
