最新河海大学材料力学习题库
材料力学复习题

材料力学复习题河海大学材料力学复习题目录目录 ..................................................................... ... 1 复习题二 ......................................................................2 复习题三 ......................................................................4 复习题四 ......................................................................5 复习题五 ......................................................................711 复习题六 .....................................................................复习题八 .....................................................................14 复习题九 .....................................................................18 复习题十 .....................................................................21 复习题十一 ...................................................................24 复习题十四 ...................................................................26 复习题十五 ...................................................................27 答案 ..................................................................... . (29)第 1 页共 35 页河海大学材料力学复习题复习题二2-1 试求出图示各杆件中?—?截面上的内力。
河海大学材料力知识学习题集册规范标准答案解析
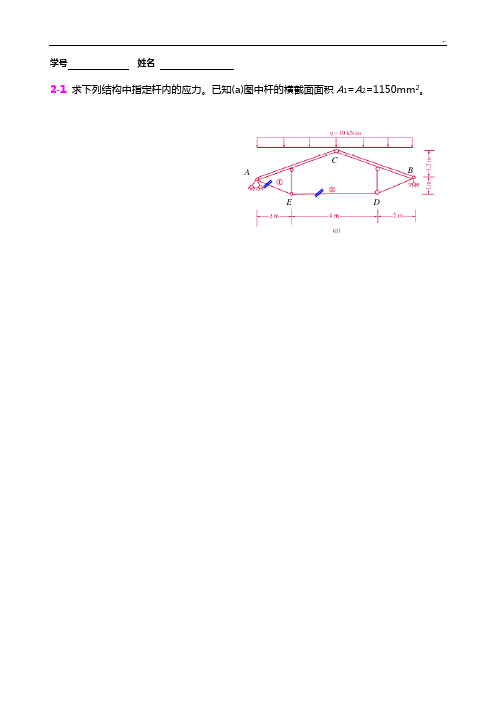
学号姓名2-1求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A1=A2=1150mm2。
AE CDB2-2求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB的横截面积为40mm2,下段BC的横截面积为30mm2,杆材料的ρg=78kN/m3。
2-4一直径为15mm,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm,直径缩小了0.022mm,确定材料的弹性模量E、泊松比ν。
2-6图示短柱,上段为钢制,长200mm,截面尺寸为100×100mm2;下段为铝制,长300mm,截面尺寸为200×200mm2。
当柱顶受F力作用时,柱子总长度减少了0.4mm,试求F值。
已知E钢=200GPa,E铝=70GPa。
,.2-7图示等直杆AC,材料的容重为ρg,弹性模量为E,横截面积为A。
求直杆B截面的位移ΔB。
学号姓名2-8图示结构中,AB可视为刚性杆,AD为钢杆,面积A1=500mm2,弹性模量E1=200GPa;CG为铜杆,面积A2=1500mm2,弹性模量E2=100GPa;BE为木杆,面积A3=3000mm2,弹性模量E3=10GPa。
当G点处作用有F=60kN时,求该点的竖直位移ΔG。
2-11图示一挡水墙示意图,其中AB杆支承着挡水墙,各部分尺寸均已示于图中。
若AB杆为圆截面,材料为松木,其容许应力[σ]=11MPa,试求AB杆所需的直径。
2-12图示结构中的CD杆为刚性杆,AB杆为钢杆,直径d=30mm,容许应力[σ]=160MPa,弹性模量E=2.0×105MPa。
试求结构的容许荷载F。
2-14图示AB为刚性杆,长为3a。
A端铰接于墙壁上,在C、B两处分别用同材料、同面积的①、②两杆拉住,使AB杆保持水平。
在D点作用荷载F后,求两杆内产生的应力。
设弹性模量为E,横截面面积为A。
学号 姓名2-15 两端固定,长度为l ,横截面面积为A ,弹性模量为E 的正方形杆,在B 、C 截面处各受一F 力作用。
河海大学材料力学考研练习题

学号姓名2-1求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A1=A2=1150mm2。
CBAE D2-2求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB的横截面积为40mm2,下段BC的横截面积为30mm2,杆材料的ρg=78kN/m3。
2-4一直径为15mm,标距为200mm的合金钢杆,比例极限内荷载从零缓慢地增加58.4kN时,杆伸长了0.9mm,直径缩小了0.022mm,确定材料的弹性模量E、泊松比ν。
2-6图示短柱,上段为钢制,长200mm,截面尺寸为100×100mm2;下段为铝制,长300mm,截面尺寸为200×200mm2。
当柱顶受F力作用时,柱子总长度减少了0.4mm,试求F值。
已知E钢=200GPa,E铝=70GPa。
2-7图示等直杆AC,材料的容重为ρg,弹性模量为E,横截面积为A。
求直杆B截面的位移ΔB。
学号姓名2-8图示结构中,AB可视为刚性杆,AD为钢杆,面积A1=500mm2,弹性模量1E1=200GPa;CG为铜杆,面积A2=1500mm2,弹性模量E2=100GPa;BE为木杆,面积A3=3000mm2,弹性模量E3=10GPa。
当G点处作用有F=60kN时,求该点的竖直位移ΔG。
2-11图示一挡水墙示意图,其中AB杆支承着挡水墙,各部分尺寸均已示于图中。
若AB杆为圆截面,材料为松木,其容许应力[σ]=11MPa,试求AB杆所需的直径。
2-12图示结构中的CD杆为刚性杆,AB杆为钢杆,直径d=30mm,容许应力[σ]=160MPa,弹性模量E=2.0×105MPa。
试求结构的容许荷载F。
2-14图示AB为刚性杆,长为3a。
A端铰接于墙壁上,在C、B两处分别用同材料、同面积的①、②两杆拉住,使AB杆保持水平。
在D点作用荷载F后,求两杆内产生的应力。
设弹性模量为E,横截面面积为A。
学号姓名2-15两端固定,长度为l,横截面面积为A,弹性模量为E的正方形杆,在B、C截面处各受一F力作用。
(完整版)河海大学材料力学期末考试

河海大学《材料力学》期末考试卷〈考试时间:120分钟)一、填空(每题2分,共20分)3.为了求解静不定问题,必须研究构件的娈形 ,从而寻找出补充方程。
4.______________________________________ 材料力学中求内力的基本方法是截面法____________________________________________ o5 •矩形截面梁的弯曲軻力为Fs,横截面积为人则梁上的最大切应力为______ 3匚/2A_________________________________________________________________ 。
7.________________________ 第四强度理论认为_____ 畸变能密Jt 是引起屈服的主要因素'S .挠曲线的近似徹分方程是_____________ N:w/必:三M [E1 ___________________ °9.求解组合变形的基本步屋是,(1)对外力进行分析或简化,使之对应基本变形,C2)求解每一种基本变形的内力、应力及应支等,(3)将所得结果进行叠加。
10.压杆稳走问题中,欧拉公式成立的条件是: ________ z _______________ o11・II轴扭转时的强度条件为_ — = 兀<[i]—刚度条件为心M TJGI, S0]。
13.莫尔强度理论的强度条件为 _____ 6 - {0J/9』巳____________ o14 •进行应力分析时,单元体上切应力等于零的面称为主平面'其上应力称/ 主应力。
二、单项迭择题(每題2分,共20分)1-所有脆性材科,它与塑性材料相比,其拉伸力学性能的最大特点是(C )。
A强度低,对应力集中不敢感$B.相同拉力作用T7变形小3C.断裂前几乎没有塑性变形jD.应力•应变关系严格遵循胡克走律。
2.在美国事件中,恐怖分子的飞机撞击国贸大J1后,该大原起火燃烧,然后坍埸。
河海大学材料力学习题册答案解析
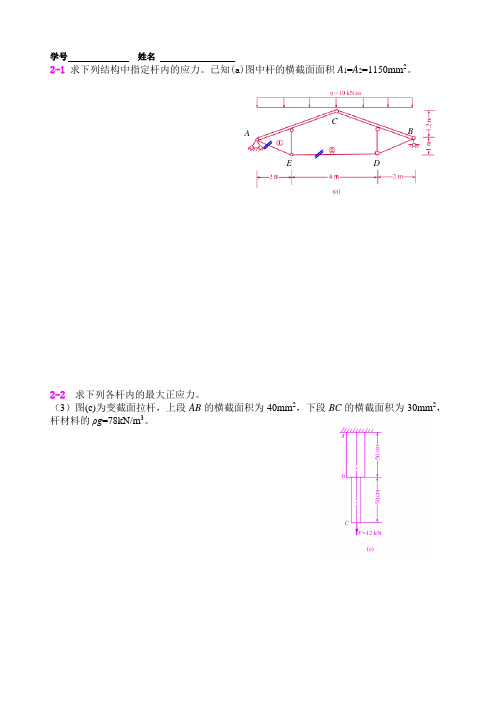
学号姓名2-1求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A1=A2=1150mm2。
2-2求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB的横截面积为40mm2,下段BC的横截面积为30mm2,杆材料的ρg=78kN/m3。
AECDB-2-2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比ν。
2-6图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm 2;下段为铝制,长300mm ,截面尺寸为200×200mm 2。
当柱顶受F 力作用时,柱子总长度减少了0.4mm ,试求F 值。
已知E 钢=200GPa ,E 铝=70GPa 。
2-7 图示等直杆AC ,材料的容重为ρg ,弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
-3-学号 姓名2-8 图示结构中,AB 可视为刚性杆,AD 为钢杆,面积A 1=500mm 2,弹性模量E 1=200GPa ;CG 为铜杆,面积A 2=1500mm 2,弹性模量E 2=100GPa ;BE 为木杆,面积A 3=3000mm 2,弹性模量E 3=10GPa 。
当G 点处作用有F =60kN 时,求该点的竖直位移ΔG 。
2-11 图示一挡水墙示意图,其中AB 杆支承着挡水墙,各部分尺寸均已示于图中。
若AB 杆为圆截面,材料为松木,其容许应力[σ]=11MPa ,试求AB 杆所需的直径。
-4-2-12 图示结构中的CD 杆为刚性杆,AB 杆为钢杆,直径d =30mm ,容许应力[σ]=160MPa ,弹性模量E =2.0×105MPa 。
试求结构的容许荷载F 。
2-14 图示AB 为刚性杆,长为3a 。
A 端铰接于墙壁上,在C 、B 两处分别用同材料、同面积的①、②两杆拉住,使AB 杆保持水平。
河海大学材料力学习题册答案解析.
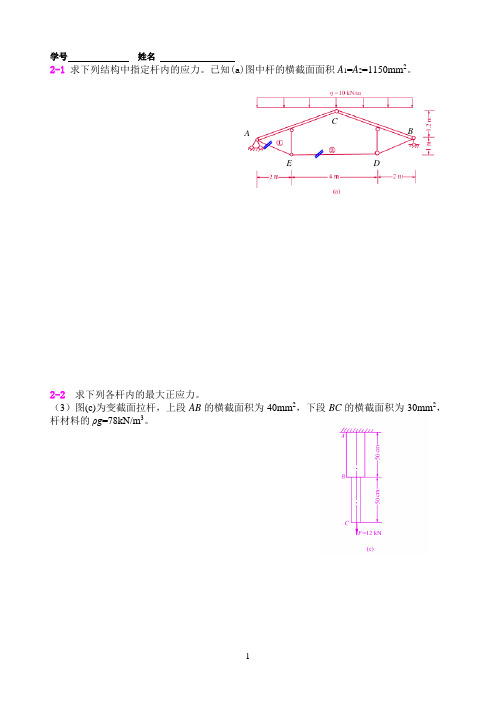
学号姓名2-1求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A1=A2=1150mm2。
2-2求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB的横截面积为40mm2,下段BC的横截面积为30mm2,杆材料的ρg=78kN/m3。
AECDB2-4一直径为15mm,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm,直径缩小了0.022mm,确定材料的弹性模量E、泊松比ν。
2-6图示短柱,上段为钢制,长200mm,截面尺寸为100×100mm2;下段为铝制,长300mm,截面尺寸为200×200mm2。
当柱顶受F力作用时,柱子总长度减少了0.4mm,试求F值。
已知E钢=200GPa,E铝=70GPa。
2-7图示等直杆AC,材料的容重为ρg,弹性模量为E,横截面积为A。
求直杆B截面的位移ΔB。
学号姓名2-8图示结构中,AB可视为刚性杆,AD为钢杆,面积A1=500mm2,弹性模量E1=200GPa;CG为铜杆,面积A2=1500mm2,弹性模量E2=100GPa;BE为木杆,面积A3=3000mm2,弹性模量E3=10GPa。
当G点处作用有F=60kN时,求该点的竖直位移ΔG。
2-11图示一挡水墙示意图,其中AB杆支承着挡水墙,各部分尺寸均已示于图中。
若AB 杆为圆截面,材料为松木,其容许应力[σ]=11MPa,试求AB杆所需的直径。
2-12图示结构中的CD杆为刚性杆,AB杆为钢杆,直径d=30mm,容许应力[σ]=160MPa,弹性模量E=2.0×105MPa。
试求结构的容许荷载F。
2-14图示AB为刚性杆,长为3a。
A端铰接于墙壁上,在C、B两处分别用同材料、同面积的①、②两杆拉住,使AB杆保持水平。
在D点作用荷载F后,求两杆内产生的应力。
设弹性模量为E,横截面面积为A。
学号姓名2-15两端固定,长度为l,横截面面积为A,弹性模量为E的正方形杆,在B、C截面处各受一F力作用。
河海大学材料力学习题库
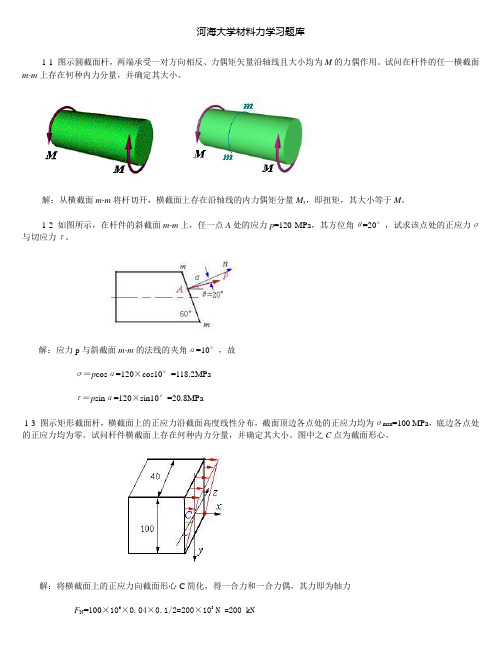
河海大学材料力学习题库1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力ζ与切应力η。
解:应力p与斜截面m-m的法线的夹角α=10°,故ζ=p cosα=120×cos10°=118.2MPaη=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为ζmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m返回1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:返回第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
河海大学出版社 材料力学 习题解答word

第二章 拉压变形2-11 图示一挡水墙示意图,其中AB 杆支承着挡水墙,各部分尺寸均已示于图中。
若AB 杆为圆截面,材料为松木,其容许应力[σ]=11MPa ,试求AB 杆所需的直径。
解:2-16 试校核图示销钉的剪切强度。
已知F =120kN ,销钉直径d =30mm ,材料的容许应力[τ]=70MPa 。
若强度不够,应改用多大直径的销钉?解:MPa A F 88841049210120243./=⨯⨯⨯==-πτ 不满足强度条件46324110571810702101202-⨯=⨯⨯⨯=≥=.][τπF d A F NP3m4m2mkN b h P 40221==γkNF P F F MN N i O111104060032...:)(==⨯-⨯⨯=∑强度条件:cmd m d AF N583102861101110111142363..)/(.][≥⨯=⨯⋅⨯⨯≥≤=-πσσ以上解不合理: 柔度:7557451.)//(/=⨯==d i l μλ3.d3cm第三章 扭转变形3-3 图示组合圆轴,内部为钢,外圈为铜,内、外层之间无相对滑动。
若该轴受扭后,两种材料均处于弹性范围,横截面上的切应力应如何分布?两种材料各承受多少扭矩?dxd φργ= γτG =80120 5050F AB Cc x c r 1r 2 r 3 F M 3-10(b) F=40kN, d=20mm 解:中心c 位置 380/=c x 等效后:kNF M 936103802003.)/(=⨯-=-由F 引起的切应力MPa d kN A F 442403243.)/()/(==='πτ由M 引起的剪切力满足321r F r F r F B A c ///==Mr F r F r F B A C =++321解得kNF C 839.=C 铆钉切应力最大MPa d kN A F C 712683924.)/(./===''πτMpac 1169.=''+'=ττττγ第四章弯曲变形4-12 切应力流4-12 试画出图示各截面的弯曲中心的大致位置,并画出切应力流的流向,设截面上剪力F Q 的方向竖直向下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河海大学材料力学习题库1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m返回1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:返回第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
如欲使BC与AB段的正应力相同,试求BC段的直径。
解:因BC与AB段的正应力相同,故2-3 图示轴向受拉等截面杆,横截面面积A=500 mm2,载荷F=50 kN。
试求图示斜截面m-m上的正应力与切应力,以及杆内的最大正应力与最大切应力。
解:返回2-4(2-11)图示桁架,由圆截面杆1与杆2组成,并在节点A承受载荷F=80kN作用。
杆1、杆2的直径分别为d1=30mm和d2=20mm,两杆的材料相同,屈服极限σs=320MPa,安全因数n s=2.0。
试校核桁架的强度。
解:由A点的平衡方程可求得1、2两杆的轴力分别为由此可见,桁架满足强度条件。
2-5(2-14)图示桁架,承受载荷F作用。
试计算该载荷的许用值[F]。
设各杆的横截面面积均为A,许用应力均为[σ]。
解:由C点的平衡条件由B点的平衡条件1杆轴力为最大,由其强度条件返回2-6(2-17)图示圆截面杆件,承受轴向拉力F作用。
设拉杆的直径为d,端部墩头的直径为D,高度为h,试从强度方面考虑,建立三者间的合理比值。
已知许用应力[σ]=120MPa,许用切应力[τ]=90MPa,许用挤压应力[σbs]=240MPa。
解:由正应力强度条件由切应力强度条件由挤压强度条件式(1):式(3)得式(1):式(2)得故D:h:d=1.225:0.333:12-7(2-18)图示摇臂,承受载荷F1与F2作用。
试确定轴销B的直径d。
已知载荷F1=50kN,F2=35.4kN,许用切应力[τ]=100MPa,许用挤压应力[σbs]=240MPa。
解:摇臂ABC受F1、F2及B点支座反力F B三力作用,根据三力平衡汇交定理知F B的方向如图(b)所示。
由平衡条件由切应力强度条件由挤压强度条件故轴销B的直径第三章轴向拉压变形3-1 图示硬铝试样,厚度δ=2mm,试验段板宽b=20mm,标距l=70mm。
在轴向拉F=6kN的作用下,测得试验段伸长Δl=0.15mm,板宽缩短Δb=0.014mm。
试计算硬铝的弹性模量E与泊松比μ。
解:由胡克定律返回3-2(3-5) 图示桁架,在节点A处承受载荷F作用。
从试验中测得杆1与杆2的纵向正应变分别为ε1=4.0×10-4与ε2=2.0×10-4。
试确定载荷F及其方位角θ之值。
已知杆1与杆2的横截面面积A1=A2=200mm2,弹性模量E1=E2=200GPa。
解:杆1与杆2的轴力(拉力)分别为由A点的平衡条件(1)2+(2)2并开根,便得式(1):式(2)得返回3-3(3-6) 图示变宽度平板,承受轴向载荷F作用。
试计算板的轴向变形。
已知板的厚度为δ,长为l,左、右端的宽度分别为b1与b2,弹性模量为E。
解:返回3-4(3-11) 图示刚性横梁AB,由钢丝绳并经无摩擦滑轮所支持。
设钢丝绳的轴向刚度(即产生单位轴向变形所需之力)为k,试求当载荷F作用时端点B的铅垂位移。
解:设钢丝绳的拉力为T,则由横梁AB的平衡条件钢丝绳伸长量由图(b)可以看出,C点铅垂位移为Δl/3,D点铅垂位移为2Δl/3,则B点铅垂位移为Δl,即返回3-5(3-12) 试计算图示桁架节点A的水平与铅垂位移。
设各杆各截面的拉压刚度均为EA。
解:(a) 各杆轴力及伸长(缩短量)分别为因为3杆不变形,故A点水平位移为零,铅垂位移等于B点铅垂位移加2杆的伸长量,即(b) 各杆轴力及伸长分别为A点的水平与铅垂位移分别为(注意AC杆轴力虽然为零,但对A位移有约束) 返回3-6(3-14) 图a所示桁架,材料的应力-应变关系可用方程σn=Bε表示(图b),其中n和B为由实验测定的已知常数。
试求节点C的铅垂位移。
设各杆的横截面面积均为A。
(a) (b)解:2根杆的轴力都为2根杆的伸长量都为则节点C的铅垂位移3-7(3-16) 图示结构,梁BD为刚体,杆1、杆2与杆3的横截面面积与材料均相同。
在梁的中点C承受集中载荷F作用。
试计算该点的水平与铅垂位移。
已知载荷F=20kN,各杆的横截面面积均为A=100mm2,弹性模量E=200GPa,梁长l=1000mm。
解:各杆轴力及变形分别为梁BD作刚体平动,其上B、C、D三点位移相等3-8(3-17) 图示桁架,在节点B和C作用一对大小相等、方向相反的载荷F。
设各杆各截面的拉压刚度均为EA,试计算节点B和C间的相对位移ΔB/C。
解:根据能量守恒定律,有3-9(3-21) 由铝镁合金杆与钢质套管组成一复合杆,杆、管各载面的刚度分别为E1A1与E2A2。
复合杆承受轴向载荷F作用,试计算铝镁合金杆与钢管横载面上的正应力以及杆的轴向变形。
解:设杆、管承受的压力分别为F N1、F N2,则F N1+F N2=F(1)变形协调条件为杆、管伸长量相同,即联立求解方程(1)、(2),得杆、管横截面上的正应力分别为杆的轴向变形返回3-10(3-23) 图示结构,杆1与杆2的弹性模量均为E,横截面面积均为A,梁BC为刚体,载荷F=20kN,许用拉应力[σt]=160MPa,许用压应力[σc]=110MPa。
试确定各杆的横截面面积。
解:设杆1所受压力为F N1,杆2所受拉力为F N2,则由梁BC的平衡条件得变形协调条件为杆1缩短量等于杆2伸长量,即联立求解方程(1)、(2)得因为杆1、杆2的轴力相等,而许用压应力小于许用拉应力,故由杆1的压应力强度条件得返回3-11(3-25) 图示桁架,杆1、杆2与杆3分别用铸铁、铜和钢制成,许用应力分别为[σ1]=40MPa,[σ2]=60MPa,[σ3]=120MPa,弹性模量分别为E1=160GPa,E2=100GPa,E3=200GPa。
若载荷F=160kN,A1=A2=2A3,试确定各杆的横截面面积。
解:设杆1、杆2、杆3的轴力分别为F N1(压)、F N2(拉)、F N3(拉),则由C点的平衡条件杆1、杆2的变形图如图(b)所示,变形协调条件为C点的垂直位移等于杆3的伸长,即联立求解式(1)、(2)、(3)得由三杆的强度条件注意到条件A1=A2=2A3,取A1=A2=2A3=2448mm2。
返回3-12(3-30) 图示组合杆,由直径为30mm的钢杆套以外径为50mm、内径为30mm的铜管组成,二者由两个直径为10mm 的铆钉连接在一起。
铆接后,温度升高40°,试计算铆钉剪切面上的切应力。
钢与铜的弹性模量分别为E s=200GPa与E c=100GPa,线膨胀系数分别为αl s=12.5×10-6℃-1与αl c=16×10-6℃-1。
解:钢杆受拉、铜管受压,其轴力相等,设为F N,变形协调条件为钢杆和铜管的伸长量相等,即铆钉剪切面上的切应力返回3-13(3-32) 图示桁架,三杆的横截面面积、弹性模量与许用应力均相同,并分别为A、E与[σ],试确定该桁架的许用载荷[F]。
为了提高许用载荷之值,现将杆3的设计长度l变为l+Δ。
试问当Δ为何值时许用载荷最大,其值[F max]为何。
解:静力平衡条件为变形协调条件为联立求解式(1)、(2)、(3)得杆3的轴力比杆1、杆2大,由杆3的强度条件若将杆3的设计长度l变为l+Δ,要使许用载荷最大,只有三杆的应力都达到[σ],此时变形协调条件为返回4-1(4-3) 图示空心圆截面轴,外径D=40mm,内径d=20mm,扭矩T=1kN•m。
试计算横截面上的最大、最小扭转切应力,以及A点处(ρA=15mm)的扭转切应力。
解:因为τ与ρ成正比,所以返回4-2(4-10) 实心圆轴与空心圆轴通过牙嵌离合器连接。
已知轴的转速n=100 r/min,传递功率P=10 kW,许用切应力[τ]=80MPa,d1/d2=0.6。
试确定实心轴的直径d,空心轴的内、外径d1和d2。
解:扭矩由实心轴的切应力强度条件由空心轴的切应力强度条件返回4-3(4-12) 某传动轴,转速n=300 r/min,轮1为主动轮,输入功率P1=50kW,轮2、轮3与轮4为从动轮,输出功率分别为P2=10kW,P3=P4=20kW。
(1) 试求轴内的最大扭矩;(2) 若将轮1与轮3的位置对调,试分析对轴的受力是否有利。
解:(1) 轮1、2、3、4作用在轴上扭力矩分别为轴内的最大扭矩若将轮1与轮3的位置对调,则最大扭矩变为最大扭矩变小,当然对轴的受力有利。
返回4-4(4-21) 图示两端固定的圆截面轴,承受扭力矩作用。
试求支反力偶矩。
设扭转刚度为已知常数。
解:(a) 由对称性可看出,M A=M B,再由平衡可看出M A=M B=M(b)显然M A=M B,变形协调条件为解得(c)(d)由静力平衡方程得变形协调条件为联立求解式(1)、(2)得返回4-5(4-25) 图示组合轴,由套管与芯轴并借两端刚性平板牢固地连接在一起。
