立体几何证明方法总结及经典3例(可编辑修改word版)

合集下载

立体几何常见证明方法

立体几何常见证明方法1、线线平行①利用相似三角形或平行四边形②利用公理4：平行于同一直线的两条直线互相平行③线面平行⇒线线平行即////a a a l l αβαβ⎫⎪⊂⇒⎬⎪=⎭ ④面面平行⇒线线平行即b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα即b a b a //⇒⎭⎬⎫⊥⊥αα2、线线垂直①两条直线所成角为90︒②线面垂直⇒线线垂直即b a b a ⊥⇒⎭⎬⎫⊂⊥αα ③三垂线定理及其逆定理三垂线定理：l AC l BC AB ⊥⇒⎭⎬⎫⊥⊥α 三垂线逆定理：l BC l AC AB ⊥⇒⎭⎬⎫⊥⊥α ④两直线平行，其中一条垂直于第三条直线，则另一条也垂直于这条直线。

3、线面平行①定义：若一条直线和一个平面没有公共点，则它们平行；②线线平行⇒线面平行若平面外的一条直线平行于平面内的一条直线，则它与这个平面平行。

即ααα////a a b b a ⇒⎪⎭⎪⎬⎫⊄⊂③面面平行⇒线面平行若两平面平行，则其中一个平面内的任一条直线平行于另一个平面。

即βαβα////a a ⇒⎭⎬⎫⊂4、线面垂直①线线垂直⇒线面垂直若一条直线垂直平面内两条相交直线，则这条直线垂直这个平面。

即ααα⊥⇒⎪⎭⎪⎬⎫=⊂⊂⊥⊥a O c bc b c a b a ,,②面面垂直⇒线面垂直两平面垂直，其中一个平面内的一条直线垂直于它们的交线，则这条直线垂直于另一个平面。

即βαβαβα⊥⇒⎪⎭⎪⎬⎫⊥⊂=⊥a l a a l ,,即αββα⊥⇒⎭⎬⎫⊥l l //即αα⊥⇒⎭⎬⎫⊥b a b a // 5、面面平行①线面平行⇒面面平行若一个平面内两条相交直线都平行于另一个平面，则这两个平面平行。

即βαααββ//,//,//⇒⎪⎭⎪⎬⎫=⊂⊂O b a b a b a②平行于同一平面的两个平面平行即βαγβγα//////⇒⎭⎬⎫即βαβα//⇒⎭⎬⎫⊥⊥l l 6、面面垂直①依定义，二面角的平面角为90︒； ②βαα⊥⇒⎬⎫⊂a l。

立体几何证明定理及性质总结

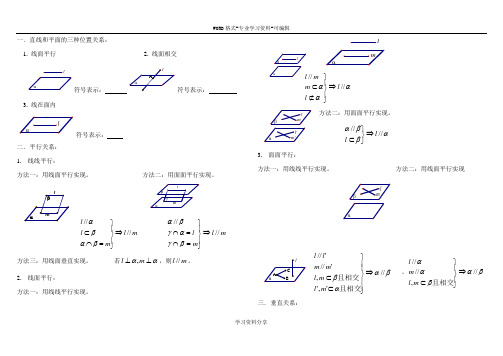
一．直线和平面的三种位置关系：1. 线面平行2. 线面相交l符号表示：符号表示：3. 线在面内符号表示：二．平行关系：1.线线平行：方法一：用线面平行实现。

方法二：用面面平行实现。

mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβαmlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三：用线面垂直实现。

若αα⊥⊥ml,，则ml//。

2.线面平行：方法一：用线线平行实现。

ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二：用面面平行实现。

αββα////ll⇒⎭⎬⎫⊂3.面面平行：方法一：用线线平行实现。

方法二：用线面平行实现βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll。

βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三．垂直关系：l学习资料分享学习资料分享1. 线面垂直：方法一：用线线垂直实现。

方法二：用面面垂直实现。

αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥l AB AC A AB AC AB l AC l ,αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m , 2. 面面垂直：方法一：用线面垂直实现。

方法二：计算所成二面角为直角。

βαβα⊥⇒⎭⎬⎫⊂⊥l l3. 线线垂直：方法一：用线面垂直实现。

m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二：三垂线定理及其逆定理。

PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭。

立体几何证明方法总结

五、线面垂直的证明方法：
1、定义法：直线与平面内任意直线都垂直。
2、如果一条直线和一个平面内的两条相交直线垂直，那么
这条直线垂直于这个平面。（线面垂直的判定定理） 3、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。（面面垂直的性质定理） 4、两条平行直线中的一条垂直于平面，则另一条也垂直于
1 (2)a=1 2
(3)a=
(4)a=4.
3
当BC边上存在点Q,使PQ┴QD时，可以取____
P
A
D
B
Q
C
作业：1.两个平面分别垂直于两条互相垂直的直线，则这两个平面互相垂直。（以两条直线相交为例，写出已知、求证，并画出图形）
A1B1C1D1 中，底面 ABCD 是直角梯 2. 如图，直棱柱 ABCD形，∠ BAD＝∠ ADC＝ 90° ， AB＝2AD＝ 2CD＝2.
(1)求证： AC⊥平面 BB1C1C； (2)在 A1B1 上是否存在一点 P，使得 DP 和平面 BCB1，平面 ACB1 都平行？证明你的结论．
5.分别和两条异面直线平行的两个平面平行。
四、线线垂直的证明方法：
1、勾股定理。 2、等腰三角形，三线合一
3、菱形对角线，等几何图形
4、直径所对的圆周角是直角。
5、如果一条直线和一个平面垂直，那么这条直线就和这个
平面内任意的直线都垂直。
6、如果两条平行线中的一条垂直于一条直线，则另一条也
垂直于这条直线。
2、如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。（面面垂直的判定定理）
3、一条直线垂直于一个平面，平行于另一个平面，则这两个平面垂直。
4、若两个平行平面中的一个垂直于第三个平面，则另一个平面也垂直于第三个平面。

立体几何常见证明方法

立体几何方法归纳小结一、线线平行的证明方法1、根据公理4，证明两直线都与第三条直线平行。

2、根据线面平行的性质定理，若直线a平行于平面A ，过a的平面B与平面A相交于b ，则a//b。

3、根据线面垂直的性质定理，若直线a与直线b都与平面A垂直，则a//b 。

4、根据面面平行的性质定理，若平面A//平面B，平面C与平面A和平面B的交线分别为直线a与直线b，则a//b 。

二、线面平行的证明方法1、根据线面平行的定义，证直线与平面没有公共点。

2、根据线面平行的判定定理，若平面A内存在一条直线b与平面外的直线a平行，则a//A 。

(用相似三角形或平行四边形)3、根据平面与平面平行的性质定理，若两平面平行，则一个平面内的任一直线与另一个平面平行。

三、面面平行的证明方法1、根据定义，若两平面没有公共点，则两平面平行。

2、根据两平面平行的判定定理，一个平面内有两相交直线与另一平面平行，则两平面平行。

或根据两平面平行的判定定理的推论，一平面内有两相交直线与另一平面内两相交直线平行，则两平面平行。

3、垂直同一直线的两平面平行。

4、平行同一平面的两平面平行。

四、两直线垂直的证明方法1、根据定义,证明两直线所成的角为90°2、一直线垂直于两平行直线中的一条,也垂直于另一条.3、一直线垂直于一个平面,则它垂直于平面内的所有直线.4、根据三垂线定理及逆定理,若平面内的直线垂直于平面的一条斜线(或斜线在平面内的射影),则它垂直于斜线在平面内的射影(或平面的斜线).五、线面垂直的证明方法1、根据定义,证明一直线与平面内的任一(所有)直线垂直,则直线垂直于平面.2、根据判定定理,一直线垂直于平面内的两相交直线,则直线垂直于平面.3、一直线垂直于两平行平面中的一个,也垂直于另一个.4、两平行直线中的一条垂直于一个平面,另一条也垂直于这个平面.5、根据两平面垂直的性质定理,两平面垂直,则一个平面内垂直于它们交线的直线垂直于另一个平面.六、面面垂直的证明方法1、根据面面垂直的定义，两平面相交所成的二面角为直二面角，则两平面垂直。

立体几何判定方法和性质汇总

四、直线系方程有几种？都怎样设出？怎样求一直线系过定点？
例 1 、求直线 (m+1)x+(m1)y2=0 所通过的定点P的坐标.
五、两点间距离公式是什么？
推导此公式时的重要思想方法是什么？中点坐标公式？
点到直线的距离、两条平行直线间的距离公式？
六、有哪些常见的对称问题？各如何解决？
例5．在正四棱柱AC1中，底面边长为1，侧棱长为2 ，⑴求D1B1与平面A1BCD1所成的角 ⑵求B1到平面A1BC1的距离
D1
C1
A1
B1
DE
C
平面解析几何的公式与方法
一、直线的斜率定义（两种）二、直线的方程的四种特殊形式和一般式
三、已知两条直线l1：A1x+B1y+C1=0与 l2：A2x+B2y+C2=0(A1,B1不全为零，A2,B2 不全为零).则: (1) l1∥l2 (2) l1⊥l2
4.已知一直线被两条已知直线A1x+B1y+C1=0、： A2x+B2y+C2=0所截得的线段中点P的坐标为（x0,y0），求这条直线的方程如图所示。
解：设直线与直线相交于A(x1,y1), 因为P(x0,y0) 是线段AB的中点，所以直线与直线的交点B的坐标
为(2x0- x1, 2y0 -y1).将点A(x1,y1)、交点B(2x0x1, 2y0 -y1) 的坐标分别代入直线： A1x+B1y+C1=0、：A2x+B2y+C2得方程组
(2)用斜率公式。分别计算一个点与另两个点连线的斜率，若两斜率相等或者两斜率都不存在，则这三点共线，否则不共线；
(3)用直线方程。计算经过其中两个点的直线方程，再判断另一个点的坐标是否满足该直线方程，若满足则这三点共线，否则不共线。

立体几何证明方法总结及例题复习课程

这条直线垂直于这个平面。（线面垂直的判定定理） 4、如果两个平面互相垂直，那么在一个平面内垂直于它们
交线的直线垂直于另一个平面。（面面垂直的性质定理） 5、两条平行直线中的一条垂直于平面，则另一条也垂直于
这个平面。 6、一条直线垂直于两平行平面中的一个平面，则必垂直于
另一个平面。 7、两相交平面同时垂直于第三个平面，那么两平面交线垂
(3)解 ∵EF⊥FB，∠BFC＝90° ∴BF⊥平面 CDEF． ∴BF 为四面体 B－DEF 的高．又 BC＝AB＝2，∴BF＝FC＝ 2． VB－DEF＝13×12×1× 2× 2＝31．
此课件下载可自行编辑修改，仅供参考！感谢您的支持，我们努力做得更好！谢谢
1、勾股定理。 2、等腰三角形，三线合一 3、菱形对角线，等几何图形 4、直径所对的圆周角是直角。 5、点在线上的射影。 6、如果一条直线和一个平面垂直，那么这条直线就和这个
平面内任意的直线都垂直。 7、如果两条平行线中的一条垂直于一条直线，则另一条也
垂直于这条直线。
五、线面垂直的证明方法：
1、定义法：直线与平面内任意直线都垂直。2、点在面内的射影。 3、如果一条直线和一个平面内的两条相交直线垂直，那么
直于第三个平面。（小题用） 8、过一点，有且只有一条直线与已知平面垂直。（小题用） 9、过一点，有且只有一个平面与已知直线垂直。（小题用）
六、面面垂直的证明方法：
1、定义法：两个平面的二面角是直二面角。 2、如果一个平面经过另一个平面的一条垂线，那么这两个
平面互相垂直。（面面垂直的判定定理） 3、如果一个平面与另一个平面的垂线平行，那么这两个平面互相垂直。
• (1)证明如图，设AC与BD交于点G，则G为AC 的中点．连接EG，GH，由于H为BC的中点，

立体几何证明方法总结及经典3例(推荐文档)

立体几何证明方法总结及典例例1：平行类证明【平行类证明方法总结】线线平行的证明方法：三线间平行的传递性，三角形中位线，平行四边形对边平行且相等，梯形的上下底平行，棱柱圆柱的侧棱平行且相等，两平行面被第三面所截交线平行，成比例（相似）证平行等等。

线面平行的证明方法：面外线与面内线平行，两面平行则面内一线与另面平行等等面面平行的证明方法：面内相交线与另面平行则面面平行，三面间平行的传递性等等。

【例】正方形ABCD 与正方形ABEF 所在平面相交于AB ，在AE 、BD 上各有一点P 、Q ，且AP=DQ.求证：PQ ∥面BCE.证法一：如图（1），作PM ∥AB 交BE 于M ，作QN ∥AB 交BC 于N,连接MN, 因为面ABCD ∩面ABEF=AB, 则AE=DB. 又∵AP=DQ, ∴PE=QB.又∵PM ∥AB ∥QN, ∴AE PE AB PM =,BD BQDC QN =. ∴DCQNAB PM =. ∴PM ∥QN.四边形PMNQ 为平行四边形. ∴PQ ∥MN.又∵MN ⊂面BCE ，PQ ⊄面BCE ， ∴PQ ∥面BCE. 证法二：如图(2)，连结AQ 并延长交BC 或BC 的延长线于点K ，连结EK. ∵AD ∥BC, ∴QKAQQB DQ =. 又∵正方形ABCD 与正方形ABEF 有公共边AB ，且AP=DQ ， ∴PEAPQK AQ =.则PQ ∥EK. ∴EK ⊂面BCE ，PQ ⊄面BCE. ∴PQ ∥面BCE. 例2：垂直类证明【垂直类证明方法总结】证垂直的几种方法：勾股定理、等腰（边）三角形三线合一、菱形对角线、矩形（含正方形）、90o 、相似三角形（与直角三角形）、圆直径对的圆周角、平行线、射影定理（三垂线定理）、线面垂直、面面垂直等【例】如图所示，ABCD 为正方形，SA ⊥平面ABCD ，过A 且垂直于SC 的平面分别交SB SC SD ，，于E F G ，，．求证：AE SB ⊥，AG SD ⊥．证明：∵SA ⊥平面ABCD ，∴SA BC ⊥． ∵AB BC ⊥，∴BC ⊥平面SAB ．又∵AE ⊂平面SAB ， ∴BC AE ⊥． ∵SC⊥平面AEFG ，∴SC AE ⊥．∴AE ⊥平面SBC ． ∴AE SB ⊥．同理证AG SD ⊥．例3：向量法解立体几何类【量法解立体几何类公式总结】基本公式若),,(),,,(222111z y x b z y x a ==，则①212121z z y y x x b a ++=⋅；②222222212121||,||z y x b z y x a ++=++=；③212121z z y y x x b a ++=⋅④222222212121212121,cos z y x z y x z z y y x x b a ++⋅++++>=<夹角公式：.||||cos 2121n n n n ⋅⋅-=θ距离公式：||||||n n AB CD d ⋅== 【例】已知两个正四棱锥P －ABCD 与Q －ABCD 的高都为2，AB ＝4．（1）证明：PQ ⊥平面ABCD ；（2）求异面直线AQ 与PB 所成的角；（3）求点P 到面QAD 的距离．简解：（1）略；（2）由题设知，ABCD 是正方形，且AC ⊥BD ．由（1），PQ ⊥平面ABCD ，故可分别以直线CA DB QP ，，为x ，y ，z 轴建立空间直角坐标系（如图1），易得(2202)(0222)AQ PB =--=-，，，，，，1cos 3AQ PB AQ PB AQ PB<>==，．所求异面直线所成的角是1arccos3．（3）由（2）知，点(0220)(22220)(004)D AD PQ -=--=-，，，，，，，，设n =（x ，y ，z ）是平面QAD 的一个法向量，则00AQ AD ⎧=⎪⎨=⎪⎩，，n n 得200x z x y ⎧+=⎪⎨+=⎪⎩，，取x ＝1，得(112)--，，n =．点P到平面QAD 的距离22PQ d==n n．立体几何证明经典习题平行题目1、P是平行四边形ABCD所在平面外一点,Q是PA的中点.求证：PC∥面BDQ.2、如图（1），在直角梯形P1DCB中，P1D//BC，CD⊥P1D，且P1D=8，BC=4，DC=46，A是P1D的中点，沿AB把平面P1AB折起到平面PAB的位置（如图（2）），使二面角P—CD—B成45°，设E、F分别是线段AB、PD的中点.求证：AF//平面PEC；垂直题目3、如图2，P是△ABC所在平面外的一点，且PA⊥平面ABC，平面PAC⊥平面PBC．求证：BC⊥平面PAC．4、如图2，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD向量法解立体几何题目5、在三棱柱ABC －A 1B 1C 1中，AB ⊥侧面BB 1C 1C ，E 为棱CC 1上异于C 、C 1的一点，EA ⊥EB 1．已知2AB =，BB 1＝2，BC ＝1，∠BCC 1＝3π．求二面角A －EB 1－A 1的平面角的正切值．立体几何证明经典习题答案1、证明：如图，连结AC 交BD 于点O . ∵ABCD 是平行四边形，∴A O =O C.连结O Q ，则O Q 在平面BDQ 内，且O Q 是△APC 的中位线， ∴PC ∥O Q.∵PC 在平面BDQ 外， ∴PC ∥平面BDQ.2、证明：如图，设PC 中点为G ，连结FG ，则FG//CD//AE ，且FG=21CD=AE ， ∴四边形AEGF 是平行四边形 ∴AF//EG ，又∵AF ⊄平面PEC ，EG ⊂平面PEC ， ∴AF//平面PEC3、证明：在平面PAC 内作AD ⊥PC 交PC 于D ． ∵平面PAC ⊥平面PBC ，且两平面交于PC ，AD ⊂平面PAC ，且AD ⊥PC ，∴AD ⊥平面PBC ．又∵BC ⊂平面PBC ， ∴AD ⊥BC ．∵PA ⊥平面ABC ，BC ⊂平面ABC ， ∴PA ⊥BC ． ∵AD ∩PA =A ， ∴BC ⊥平面PAC ．4、证明：取AB 的中点Ｆ，连结CF ，DF ． ∵ACBC =， ∴CFAB ⊥．∵AD BD =，（等腰三角形三线合一）∴DF AB ⊥．又CFDF F =，∴AB ⊥平面CDF ．∵CD ⊂平面CDF ，∴CD AB ⊥．又CD BE ⊥，BEAB B =，∴CD ⊥平面ABE ，CD AH ⊥．∵AH CD ⊥，AH BE ⊥，CD BE E =，∴ AH ⊥平面BCD ．5、以B 为原点，分别以BB 1、BA 所在直线为y 轴、z 轴，过B 点垂直于平面AB 1的直线为x 轴建立空间直角坐标系．由于BC ＝1，BB 1＝2，AB ＝2，∠BCC 1＝3π， ∴在三棱柱ABC －A 1B 1C 1中，有B （０，０，０）、A （０，０，2）、B 1（０，2，０）、31022c ⎛⎫-⎪ ⎪⎝⎭，，、133022C ⎛⎫ ⎪ ⎪⎝⎭，，．设302E a ⎛⎫ ⎪ ⎪⎝⎭，，且1322a -<<，由EA ⊥EB 1，得10EA EB =，即3322022a a ⎛⎫⎛⎫---- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭，，，， 233(2)2044a a a a =+-=-+=，∴13022a a ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭，即12a =或32a =（舍去）．故31022E ⎛⎫ ⎪ ⎪⎝⎭，，．由已知有1EA EB ⊥，111B A EB ⊥，故二面角A －EB 1－A 1的平面角θ的大小为向量11B A 与EA 的夹角．因11(002)B A BA ==，，，31222EA ⎛⎫=-- ⎪ ⎪⎝⎭，，故11112cos 3EA B A EA B A θ==，即2tan 2θ=。

立体几何证明方法总结及经典3例

∴ PA⊥ BC ．
∵ AD ∩ PA= A， ∴BC ⊥平面 PAC ． 4 、证明：取 AB 的中点Ｆ，连结 CF ， DF ．
∵ AC BC ， ∴ CF AB ．
∵ AD BD ，（等腰三角形三线合一）
∴ DF AB ．又 CF DF F ， ∴ AB 平面 CDF ． ∵ CD 平面 CDF ， ∴ CD AB ．又 CD BE ， BE AB B ， ∴ CD 平面 ABE ， CD AH ． ∵ AH CD ， AH BE ， CD BE E ， ∴ AH 平面 BCD ．
∴ AF// 平面 PEC
3 、证明：在平面 PAC 内作 AD ⊥ PC 交 PC 于 D ．
∵平面 PAC⊥平面 PBC ，且两平面交
于 PC， AD 平面 PAC，且 AD ⊥ PC，
∴ AD ⊥平面 PBC ．
又∵ BC 平面 PBC ，
∴ AD ⊥ BC ．
∵ PA⊥平面 ABC ， BC 平面 ABC ，
∴ PQ ∥面 BCE.
证法二：
如图 (2) ，连结 AQ 并延长交 BC 或 BC 的延长线于点 K ，连结 EK.
∵ AD ∥ BC,
DQ AQ
∴
.
QB QK
又∵正方形 ABCD 与正方形 ABEF 有公共边 AB ，且 AP=DQ ，
AQ AP
∴
.则 PQ ∥EK.
QK PE
∴ EK 面 BCE ， PQ 面 BCE.
A 是 P1 D 的中点，沿 AB 把平面 P 1AB 折起到平面 PAB 的位置（如图（ 2）），使二面角 P— CD — B 成 45 °，设 E 、 F 分别是线段 AB 、 PD 的中点 . 求证： AF// 平面 PEC ；

立体几何证明方法汇总

GPABCDF EABC DEF① 中位线定理例题：已知如图：平行四边形ABCD 中，6BC =，正方形ADEF 所在平面与平面ABCD 垂直，G ，H 分别是DF ，BE 的中点．（１）求证：GH ∥平面CDE ；（２）若2,42CD DB ==，求四棱锥F-ABCD 的体积．练习：1、如下图所示：在直三棱柱ABC —A 1B 1C 1中，AC=3，BC=4，AB=5，AA 1=4，点D 是AB 的中点。

求证：AC 1∥平面CDB 1；2. 如图，1111D C B A ABCD -是正四棱柱侧棱长为1，底面边长为2，E是棱BC 的中点。

（1）求证：//1BD 平面DE C 1；（2）求三棱锥BCD D 1-的体积.3、如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，4,3PD DC ==，E 是PC 的中点。

（1）证明：//PA BDE 平面；（2）求PAD ∆以PA 为轴旋转所围成的几何体体积。

例2、如图, 在矩形ABCD 中,2AB BC = , ,P Q 分别为线段,AB CD 的中点, EP ⊥平面ABCD .求证: AQ ∥平面CEP ；（利用平行四边形）练习：①如图，PA 垂直于矩形ABCD 所在的平面，E 、F 分别是AB 、PD 的中点。

求证：AF ∥平面PCE ；②如图，已知P 是矩形ABCD 所在平面外一点，ABCD 平面PD ⊥，M ，N 分别是AB ，PC 中点。

求证：//PAD MN 平面③ 如图，已知AB ?平面ACD ，DE 求证：AF 1111D C B A O ABCD 证：//1O C 面11AB D ．③比例关系例题3、P 是平行四边形ABCD 平面外一点，M 、N 分别是PB BC 上的点，且NCBNPM BM =,求证：MN ABCD ⊥EA ABCD //EF AB =4,=2,=1AB AE EF Ⅱ）若点M 在线段AC 上，且满足14CM CA =, 求证：//EM 平面FBC ；E A 1B 1C 1D 1DC BA_ H_ G_ D_ A_ B_ CEFD ABEFMA BCDEF1A 1C 1B E FGACBEBACNDFM④面面平行-线面平行例题4、如图,矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∠∠︒903P ABCD -ABCD PD ⊥ABCD 2PD AB ==E F G PC PD BCEFG PA 面//P EFG-111ABC A B C -090ACB ∠=,,E F G 11,,AA AC BB 1CG C G⊥(Ⅰ)求证：//CG BEF 平面；3、如图所示,正方形ADEF 与梯形ABCD 所在的平面互相垂直,,//,22AD CD AB CD CD AB AD ⊥==. 在EC 上找一点M ,使得//BM 平面ADEF ,请确定M点的位置,并给出证明．4、（2012山东文）如图，几何体E ABCD -是四棱锥，△ABD 为正三角形，,CB CD EC BD =⊥.(Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =︒，M 为线段AE 的中点，求证：DM ∥平面BEC .例题：如图，已知四棱锥ABCD P -。

立体几何证明定理归纳

立体几何证明定理归纳立体几何是几何学的一个重要分支，研究的是三维空间中的图形和物体。

在立体几何中，定理归纳是一种常用的证明方法。

通过对特定情况的证明，推导出一般情况的结论。

本文将以立体几何证明定理归纳为主题，探讨该证明方法的应用。

定理归纳是一种基于数学归纳法的证明方法，通过先证明一个特定情况的结论，再通过归纳推理得出一般情况的结论。

在立体几何中，定理归纳常被用于证明与体积、表面积、角度等相关的定理。

我们来看一个简单的例子，证明一个等腰直角三角形的斜边长度等于两直角边长度之和。

我们假设等腰直角三角形的两直角边长度分别为a，那么根据勾股定理，斜边的长度为：c = √(a² + a²) = a√2这是特定情况下的结论。

接下来，我们假设等腰直角三角形的两直角边长度分别为k和k，其中k为任意正实数。

同样使用勾股定理，我们可以得出：c = √(k² + k²) = k√2由此可见，在特定情况下的结论成立的情况下，一般情况下的结论也成立。

这就是定理归纳的基本思想。

在立体几何中，定理归纳的应用非常广泛。

下面我们将通过几个具体的例子，进一步探讨定理归纳的方法。

例一：证明正方体的体对角线长度等于边长的平方根乘以√3。

我们假设正方体的边长为a，那么根据勾股定理，体对角线的长度为：d = √(a² + a² + a²) = √(3a²) = a√3这是特定情况下的结论。

接下来，我们假设正方体的边长为k，其中k为任意正实数。

同样使用勾股定理，我们可以得出：d = √(k² + k² + k²) = √(3k²) = k√3由此可见，在特定情况下的结论成立的情况下，一般情况下的结论也成立。

例二：证明一个圆锥的侧面积等于底面积的一半乘以斜高。

我们假设圆锥的底面积为A，斜高为h，那么根据圆锥的侧面积公式，侧面积为：S = 1/2 * A * l其中l为斜高。

立体几何中平行与垂直证明方法归纳

a ∥
a∥
α
a a
β
3) 利用定义：直线在平面外，且直线与平面没有公共点
（三）平面与平面平行的证明
常见证明方法：
1) 利用平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。
3
a ⊂ b ⊂
a ∩b P
a // b //
⇒ /性：如正方体的上下底面互相平行等
一条直线与一个平面内的两条相交直线都垂直，则该直线垂直于此平面。
a
b
ab
A
l
l a l b
l
b
Aa
4) 利用平面与平面垂直的性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
5
l
a
a
a l
l
5) 利用常用结论：
① 一条直线平行于一个平面的一条垂线，则该直线也垂直于此平面。
在同一个平面内，垂直于同一条直线的两条直线互相平行。
8) 利用定义：在同一个平面内且两条直线没有公共点
（二）直线与平面平行的证明
1) 利用直线与平面平行的判定定理：
平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行。
a
a
b a∥
a∥b
b
2) 利用平面与平面平行的性质推论：
两个平面互相平行，则其中一个平面内的任一直线平行于另一个平面。
a b ba
b a
α
4) 利用平面与平面垂直的性质推论：
如果两个平面互相垂直，在这两个平面内分别作垂直于交线的直线，则这
两条直线互相垂直。
4
l a b al
bl
ab
β b

立体几何中的证明

立体几何中的证明：1.直线、平面平行的判定2.两个平面平行的判定3直线与直线垂直的判定4.判定直线和平面垂直的方法5.平面与平面垂直的判定方法6．能求线线角1.如图2.在直棱柱ABC-A 1B1C1中,∠BAC=90°,AB=AC=,AA1=3,D是BC的中点,点E在菱BB1上运动.(I) 证明:AD⊥C1E;(II) 当异面直线AC,C1E 所成的角为60°时,求三棱锥C1-A2B1E的体积.E P B C DA 2.如图，四棱锥P －ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，点E 在线段AD 上，CE ∥AB 。

（Ⅰ）求证：CE ⊥平面PAD ；（Ⅱ）若PA ＝AB ＝1，AD ＝3，CD ＝2，∠CDA ＝45°，求四棱锥P －ABCD 的体积3.如图,在四棱锥P ABCD -中,//AB CD ,AB AD ⊥,2CD AB =,平面PAD ⊥底面ABCD ,PA AD ⊥,E 和F 分别是CD 和PC 的中点,求证:(1)PA ⊥底面ABCD ;(2)//BE 平面PAD ;4.如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=. (Ⅰ)证明:1AB AC ⊥; (Ⅱ)若2AB CB ==,1AC =求三棱柱111ABC A B C -的体积.15.（2013年高考江西卷（文））如图,直四棱柱ABCD –A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=,AA1=3,E为CD上一点,DE=1,EC=3(1) 证明:BE⊥平面BB1C1C;(2) 求棱锥B1 -EA1C1的体积6.如图，四边形ABCD为正方形，QA⊥平面ABCD，PD．PD∥QA，QA=AB=12（I）证明：PQ⊥平面DCQ；（II）求棱锥Q—ABCD的的体积与棱锥P—DCQ的体积的比值．7.。

立体几何证明方法总结

、线线平行的证明方法1 、利用平行四边形。

2 、利用三角形或梯形的中位线。

3 、如果一条直线与一个平面平行,经过这条直线的平面与这个平面相交, 那么这条直线就与交线平行。

（线面平行的性质定理）4 、如果两个平行平面同时与第三个平面相交,那么它们的交线平行。

（面面平行的性质定理）5 、如果两条直线垂直于同一个平面,那么这两条直线平行。

（线面垂直的性质定理）6 、平行于同一条直线的两条直线平行。

7 、夹在两个平行平面之间的平行线段相等。

（需证明）二、线面平行的证明方法:1 、定义法:直线与平面没有公共点。

2 、如果平面外一条直线与这个平面内的一条直线平行,那么这条直线与这个平面平行。

（线面平行的判定定理）3 、两个平面平行,其中一个平面内的任何一条直线必平行于另一个平面。

三、面面平行的证明方法:1 、定义法:两平面没有公共点。

2 、如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。

（面面平行的判定定理）3 、平行于同一平面的两个平面平行。

4 、经过平面外一点,有且只有一个平面与已知平面平行。

5 、垂直于同一直线的两个平面平行。

四、线线垂直的证明方法:1 、勾股定理。

2 、等腰三角形。

3 、菱形对角线。

圆所对的圆周角就是直角点在线上的射影。

如果一条直线与一个平面垂直 ,那么这条直线就与这个平面内任意的直线都垂直。

在平面内的一条直线 ,如果与这个平面一条斜线的射影垂直 ,那么它也与这条斜线垂直。

（三垂线定理 ,需证明）在平面内的一条直线 ,如果与这个平面一条斜线垂直 ,那么它也与这条斜线的射影垂直。

（三垂线逆定理 ,需证如果两条平行线中的一条垂直于一条直线 ,则另一条也垂直于这条直线。

线面垂直的证明方法 :定义法 : 直线与平面内任意直线都垂直。

点在面内的射影。

如果一条直线与一个平面内的两条相交直线垂直 ,那么这条直线垂直于这个平面。

（线面垂直的判定定理）如果两个平面互相垂直 ,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

立体几何知识归纳+典型例题+方法总结

立体几何知识归纳+典型例题+方法总结一、知识归纳1．平面平面的基本性质：掌握三个公理及推论，会说明共点、共线、共面问题.（1）证明点共线的问题，一般转化为证明这些点是某两个平面的公共点（依据：由点在线上，线在面内，推出点在面内），这样可根据公理2证明这些点都在这两个平面的公共直线上.（2）证明共点问题，一般是先证明两条直线交于一点，再证明这点在第三条直线上，而这一点是两个平面的公共点，这第三条直线是这两个平面的交线.（3）证共面问题一般先根据一部分条件确定一个平面，然后再证明其余的也在这个平面内，或者用同一法证明两平面重合.2. 空间直线（1）空间直线位置关系三种：相交、平行、异面. 相交直线：共面有且仅有一个公共点；平行直线：共面没有公共点；异面直线：不同在任一平面内，无公共点（2）平行公理：平行于同一条直线的两条直线互相平行.等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等（如右图）.（直线与直线所成角]90,0[︒︒∈θ）（向量与向量所成角])180,0[οο∈θ推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成锐角（或直角）相等.（3）两异面直线的距离：公垂线段的长度.空间两条直线垂直的情况：相交（共面）垂直和异面垂直.[注]：21,l l 是异面直线，则过21,l l 外一点P ，过点P 且与21,l l 都平行平面有一个或没有，但与21,l l 距离相等的点在同一平面内. （1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面）3. 直线与平面平行、直线与平面垂直（1）空间直线与平面位置分三种：相交、平行、在平面内.（2）直线与平面平行判定定理：如果平面外一条直线和这个平面内一条直线平行，那么这条直线和这个平面平行.（“线线平行⇒线面平行”）（3）直线和平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.（“线面平行⇒线线平行”）（4）直线与平面垂直是指直线与平面任何一条直线垂直，过一点有且只有一条直线和一个平面垂直，过一点有且只有一个平面和一条直线垂直. 若PA⊥α，a ⊥AO ，得a ⊥PO （三垂线定理），三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一：如果一条直线和一个平面内的两条相PO A a交直线都垂直，那么这两条直线垂直于这个平面.（“线线垂直⇒线面垂直”）直线与平面垂直的判定定理二：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面.性质：如果两条直线同垂直于一个平面，那么这两条直线平行.（5）a.垂线段和斜线段长定理：从平面外一点．．向这个平面所引的垂线段和斜线段中，①射影相等的两条斜线段相等，射影较长的斜线段较长；②相等的斜线段的射影相等，较长的斜线段射影较长；③垂线段比任何一条斜线段短.b.射影定理推论：如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上.4. 平面平行与平面垂直（1）空间两个平面的位置关系：相交、平行.（2）平面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行.（“线面平行⇒面面平行”）推论：垂直于同一条直线的两个平面互相平行；平行于同一平面的两个平面平行.[注]：一平面内的任一直线平行于另一平面.（3）两个平面平行的性质定理：如果两个平面平行同时和第三个平面相交，那么它们交线平行.（“面面平行⇒线线平行”）（4两个平面垂直判定一：两个平面所成的二面角是直二面角，则两个平面垂直.两个平面垂直判定二：如果一条直线与一个平面垂直，那么经过这条直线的平面垂直于这个平面.（“线面垂直⇒面面垂直”）注：如果两个二面角的平面分别对应互相垂直，则两个二面角没有什么关系.（5）两个平面垂直性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论：如果两个相交平面都垂直于第三平面，则它们交线垂直于第三平面.简证：如图，在平面内过O 作OA 、OB 分别垂直于21,l l ，因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.所以结论成立 b.最小角定理的应用（∠PBN 为最小角）简记为：成角比交线夹角一半大，且又比交线夹角补角一半长，一定有4条.成角比交线夹角一半大，又比交线夹角补角小，一定有2条.成角比交线夹角一半大，又与交线夹角相等，一定有3条或者2条. 成角比交线夹角一半小，又与交线夹角一半小，一定有1条或者没有.5. 棱柱. 棱锥（1）棱柱a.①直棱柱侧面积：Ch S =（C 为底面周长，h 是高）该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积：l C S 1=（1C 是斜棱柱直截面周长，l 是斜棱柱的侧棱长）该公式是利用斜棱柱的侧面展开图为平行四边形得出的.b.{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱PαβθM A B O柱}⊃{正方体}.{直四棱柱}I {平行六面体}={直平行六面体}.c.棱柱具有的性质：①棱柱的各个侧面都是平行四边形，所有的侧棱都相等；直棱柱的各．个侧面都是矩形．．．．．．．；正棱柱的各个侧面都是全等的矩形．．．．．. ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等．．多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.d.平行六面体：定理一：平行六面体的对角线交于一点．．．．．．．．．．．．．，并且在交点处互相平分. [注]：四棱柱的对角线不一定相交于一点.定理二：长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一：长方体一条对角线与同一个顶点的三条棱所成的角为γβα,,，则 1cos cos cos 222=++γβα.推论二：长方体一条对角线与同一个顶点的三各侧面所成的角为γβα,,，则2cos cos cos 222=++γβα. （2）棱锥：棱锥是一个面为多边形，其余各面是有一个公共顶点的三角形.[注]：①一个三棱锥四个面可以都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥；所以棱柱棱柱3V S h V ==. a.①正棱锥定义：底面是正多边形；顶点在底面的射影为底面正多边形的中心.[注]：i. 正四棱锥的各个侧面都是全等的等腰三角形.（不是等边三角形）ii. 正四面体是各棱相等，而正三棱锥是底面为正三角形，侧棱与底棱不一定相等iii. 正棱锥定义的推论：若一个棱锥的各个侧面都是全等的等腰三角形（即侧棱相等）；底面为正多边形. ②正棱锥的侧面积：'Ch 21S =（底面周长为C ，斜高为'h ） ③棱锥的侧面积与底面积的射影公式：αcos 底侧S S =（侧面与底面成的二面角为α）附：以知c ⊥l ，b a =⋅αcos ，α为二面角b l a --.则l a S ⋅=211①，b l S ⋅=212②，b a =⋅αcos ③ ⇒①②③得αcos 底侧S S =.注：S 为任意多边形的面积（可分别求多个三角形面积和的方法）. b.棱锥具有的性质：①正棱锥各侧棱相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高相等（它叫做正棱锥的斜高）.②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形，正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.c.特殊棱锥的顶点在底面的射影位置：①棱锥的侧棱长均相等，则顶点在底面上的射影为底面多边形的外心. ②棱锥的侧棱与底面所成的角均相等，则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等，则顶点在底面上的射影为底面l abc多边形内心.④棱锥的顶点到底面各边距离相等，则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直，则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直，则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球，球心0是各条棱的中垂面的交点，此点到各顶点的距离等于球半径；⑧每个四面体都有内切球，球心I 是四面体各个二面角的平分面的交点，到各面的距离等于半径.（3）球：a.球的截面是一个圆面.①球的表面积公式：24R S π=.②球的体积公式：334R V π=. b.纬度、经度：①纬度：地球上一点P 的纬度是指经过P 点的球半径与赤道面所成的角的度数.②经度：地球上B A ,两点的经度差，是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数，特别地，当经过点A 的经线是本初子午线时，这个二面角的度数就是B 点的经度.附：①圆柱体积：h r V 2π=（r 为半径，h 为高） ②圆锥体积：h r V 231π=（r 为半径，h 为高） ③锥体体积：Sh V 31=（S 为底面积，h 为高）（1）. ①内切球：当四面体为正四面体时，设边长为a ，a h 36=，243a S =底，243a S =侧，得R a R a a a ⋅⋅+⋅=⋅2224331433643a a a R 46342334/42=⋅==⇒. 注：球内切于四面体：h S R S 313R S 31V 底底侧ACD B ⋅=⋅+⋅⋅⋅=-. ②外接球：球外接于正四面体，可如图建立关系式.6. 空间向量（1）a.共线向量：共线向量亦称平行向量，指空间向量的有向线段所在直线互相平行或重合.b.共线向量定理：对空间任意两个向量)0(≠a ， ∥的充要条件是存在实数λ（具有唯一性），使b a λ=.c.共面向量：若向量a 使之平行于平面α或a 在α内，则a 与α的关系是平行，记作∥α.d.①共面向量定理：如果两个向量b a ,不共线，则向量与向量b a ,共面的充要条件是存在实数对x 、y 使y x +=.②空间任一点．．．O ．和不共线三点．．．．．．A ．、．B ．、．C ．，则)1(=++++=z y x OC z OB y OA x OP 是PABC 四点共面的充要条件. （简证：→+==++--=AC z AB y AP OC z OB y OA z y OP )1(P 、A 、B 、C 四点共面）注：①②是证明四点共面的常用方法.（2）空间向量基本定理：如果三个向量．．．．c b a ,,不共面．．．，那么对空间任一向量P ，存在一个唯一的有序实数组x 、y 、z ，使c z b y a x p ++=.推论：设O 、A 、B 、C 是不共面的四点，则对空间任一点P , 都存在唯一的有序实数组x 、y 、z 使 z y x ++=(这里隐含x+y+z≠1). O BDO R注：设四面体ABCD 的三条棱，,,,d AD c AC b AB ===其中Q 是△BCD 的重心，则向量)(31c b a AQ ++=用MQ AM AQ +=即证.对空间任一点O 和不共线的三点A 、B 、C ，满足OP xOA yOB zOC =++u u u r u u u r u u u r u u u r ，则四点P 、A 、B 、C 是共面⇔1x y z ++=（3）a.空间向量的坐标：空间直角坐标系的x 轴是横轴（对应为横坐标），y 轴是纵轴（对应为纵坐标），z 轴是竖轴（对应为竖坐标）. ①令=(a 1,a 2,a 3),),,(321b b b =，则),,(332211b a b a b a b a ±±±=+，))(,,(321R a a a a ∈=λλλλλ，332211b a b a b a b a ++=⋅ ，a ∥)(,,332211Rb a b a b a b ∈===⇔λλλλ332211b a b a b a ==⇔ 0332211=++⇔⊥b a b a b a .222321a a a ++==(向量模与向量之间的转化：a a =⇒•=空间两个向量的夹角公式232221232221332211||||,cos b b b a a a b a b a b a b a b a b a ++⋅++++=⋅•>=<ρρρρρρ（a ＝123(,,)a a a ，b ＝123(,,)b b b ）. ②空间两点的距离公式：212212212)()()(z z y y x x d -+-+-=.b.法向量：若向量a 所在直线垂直于平面α，则称这个向量垂直于平面α，记作α⊥a ，如果α⊥a 那么向量a 叫做平面α的法向量.c.向量的常用方法：①利用法向量求点到面的距离定理：如图，设n 是平面α的法向量，AB 是平面α的一条射线，其中α∈A ，则点B 到平面α||n . ②异面直线间的距离d = (12,l l 是两异面直线，其公垂向量为n r ，C D 、分别是12,l l 上任一点，d 为12,l l 间的距离).③直线AB 与平面所成角的正弦值sin ||||AB m AB m β⋅=u u u r u r u u u r u r (m u r 为平面α的法向量). ④利用法向量求二面角的平面角定理：设21,n n 分别是二面角βα--l 中平面βα,的法向量，则21,n n 所成的角就是所求二面角的平面角或其补角大小（21,n n 方向相同，则为补角，21,n 反方，则为其夹角）.d.证直线和平面平行定理：已知直线⊄a 平面α，α∈∈D C a B A ,,,，且C 、D 、E 三点不共线，则a ∥α的充要条件是存在有序实数对μλ,使μλ+=.（常设μλ+=求解μλ,若μλ,存在即证毕，若μλ,不存在，则直线AB 与平面相交）.AB二、经典例题考点一空间向量及其运算1. 已知,,A B C 三点不共线，对平面外任一点，满足条件122555OP OA OB OC =++u u u r u u u r u u u r u u u r ，试判断：点P 与,,A B C 是否一定共面？解析：要判断点P 与,,A B C 是否一定共面，即是要判断是否存在有序实数对,x y 使AP xAB y AC =+u u u r u u u r u u u r 或对空间任一点O ，有OP OA x AB y AC =++u u u r u u u r u u u r u u u r .答案：由题意：522OP OA OB OC =++u u u r u u u r u u u r u u u r ，∴()2()2()OP OA OB OP OC OP -=-+-u u u r u u u r u u u r u u u r u u u r u u u r ，∴22AP PB PC =+u u u r u u u r u u u r ，即22PA PB PC =--u u u r u u u r u u u r ，所以，点P 与,,A B C 共面．点评：在用共面向量定理及其推论的充要条件进行向量共面判断的时候，首先要选择恰当的充要条件形式，然后对照形式将已知条件进行转化运算．2.如图，已知矩形ABCD 和矩形ADEF 所在平面互相垂直，点M ，N 分别在对角线BD ，AE 上，且13BM BD =，13AN AE =．求证：//MN 平面CDE ．解析：要证明//MN 平面CDE ，只要证明向量NM u u u u r 可以用平面CDE 内的两个不共线的向量DE u u u r 和DC u u u r 线性表示．答案:证明：如图，因为M 在BD 上，且13BM BD =，所以111333MB DB DA AB ==+u u u r u u u r u u u r u u u r ．同理1133AN AD DE =+u u u r u u u r u u u r ，又CD BA AB ==-u u u r u u u r u u u r ，所以MN MB BA AN =++u u u u r u u u r u u u r u u u r 1111()()3333DA AB BA AD DE =++++u u u r u u u r u u u r u u u r u u u r 2133BA DE =+u u u r u u u r 2133CD DE =+u u u r u u u r ．又CD uuu r 与DE u u u r 不共线，根据共面向量定理，可知MN u u u u r ，CD uuu r ，DE u u u r 共面．由于MN 不在平面CDE 内，所以//MN 平面CDE ．点评：空间任意的两向量都是共面的．与空间的任两条直线不一定共面要区别开.考点二证明空间线面平行与垂直3. 如图, 在直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AA 1＝4，点D 是AB 的中点，（I ）求证：AC ⊥BC 1；（II ）求证：AC 1//平面CDB 1；解析：（1）证明线线垂直方法有两类：一是通过三垂线定理或逆定理证明，二是通过线面垂直来证明线线垂直；（2）证明线面平行也有两类：一是通过线线平行得到线面平行，二是通过面面平行得到线面平行. 答案:解法一：（I ）直三棱柱ABC －A 1B 1C 1，底面三边长AC =3，BC =4AB =5，∴ AC ⊥BC ，且BC 1在平面ABC 内的射影为BC ，∴ AC ⊥BC 1；（II ）设CB 1与C 1B 的交点为E ，连结DE ，∵ D 是AB 的中点，E 是BC 1的中点，∴ DE//AC 1，∵ DE ⊂平面C D B 1，AC 1⊄平面C D B 1，∴ AC 1//平面C D B 1；解法二：∵直三棱柱ABC －A 1B 1C 1底面三边长AC ＝3，BC ＝4，AB ＝5，∴AC 、BC 、C 1C 两两垂直，如图，以C 为坐标原点，直线CA 、CB 、C 1C 分别为x 轴、y轴、z 轴，建立空间直角坐标系，则C （0,0，0），A （3,0，0），C 1（0,0，4），B （0,4，0），B 1（0,4，4），D （23，2,0）（1）∵AC ＝（－3,0，0），1BC ＝（0，－4,0），∴AC •1BC ＝0，∴AC ⊥BC 1. （2）设CB 1与C 1B 的交战为E ，则E （0,2，2）.∵DE ＝（－23，0,2），1AC ＝（－3,0，4），∴121AC DE =，∴DE ∥AC 1.A B C A B C E x yz4. 如图所示，四棱锥P —ABCD 中，AB ⊥AD ，CD ⊥AD ，PA ⊥底面ABCD ，PA=AD=CD=2AB=2，M 为PC 的中点.(1)求证：BM ∥平面PAD ；(2)在侧面PAD 内找一点N ，使MN ⊥平面PBD ；(3)求直线PC 与平面PBD 所成角的正弦.解析：本小题考查直线与平面平行，直线与平面垂直，二面角等基础知识，考查空间想象能力和推理论证能力.答案：（1）ΘM 是PC 的中点，取PD 的中点E ，则 ME CD 21，又AB CD 21 ∴四边形ABME 为平行四边形∴BM ∥EA ，PAD BM 平面⊄，PAD EA 平面⊂∴BM ∥PAD 平面（2）以A 为原点，以AB 、AD 、AP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系，如图，则())0,0,1B ，()0,2,2C ，()0,2,0D ，()2,0,0P ，()1,1,1M ，()1,1,0E在平面PAD 内设()z y N ,,0，()1,1,1---=→--z y MN ，()2,0,1-=→--PB ，()0,2,1-=→--DB 由→--→--⊥PB MN ∴0221=+--=⋅→--→--z PB MN ∴21=z由→--→--⊥DB MN ∴0221=+--=⋅→--→--y DB MN ∴21=y∴⎪⎭⎫ ⎝⎛21,21,0N ∴N 是AE 的中点，此时BD MN P 平面⊥（3）设直线PC 与平面PBD 所成的角为θ()2,2,2-=→--PC ，⎪⎭⎫ ⎝⎛---=→--21,21,1MN ，设→--→--MN PC ,为α 3226322cos -=⋅-=⋅=→--→--→--→--MN PC MNPC α 32cos sin =-=αθ 故直线PC 与平面PBD 所成角的正弦为32解法二：（1）ΘM 是PC 的中点，取PD 的中点E ，则ME CD 21，又AB CD 21 ∴四边形ABME 为平行四边形∴BM ∥EA ，PAD BM 平面⊄PAD EA 平面⊂∴BM ∥PAD 平面（2）由（1）知ABME 为平行四边形ABCD PA 底面⊥∴AB PA ⊥，又AD AB ⊥∴PAD AB 平面⊥ 同理PAD CD 平面⊥，PAD 平面⊂AE∴A E A B ⊥ ∴AB ME 为矩形 CD ∥ME ，PD CD ⊥，又A E PD ⊥ ∴PD ⊥ME ∴ABME 平面⊥PD PBD PD 平面⊂∴ABME PBD 平面平面⊥ 作EB ⊥MF 故PBD 平面⊥MFMF 交AE 于N ，在矩形ABME 内，1==ME AB ，2=AE∴32=MF ，22=NE N 为AE 的中点 ∴当点N 为AE 的中点时，BD MN P 平面⊥（3）由（2）知MF 为点M 到平面PBD 的距离，MPF ∠为直线PC 与平面PBD 所成的角，设为θ，32sin ==MP MF θ ∴直线PC 与平面PBD 所成的角的正弦值为32点评：（1）证明线面平行只需证明直线与平面内一条直线平行即可；（2）求斜线与平面所成的角只需在斜线上找一点作已知平面的垂线，斜线和射影所成的角，即为所求角；（3）证明线面垂直只需证此直线与平面内两条相交直线垂直变可.这些从证法中都能十分明显地体现出来考点三求空间图形中的角与距离根据定义找出或作出所求的角与距离，然后通过解三角形等方法求值，注意“作、证、算”的有机统一.解题时注意各种角的范围：异面直线所成角的范围是0°＜θ≤90°，其方法是平移法和补形法；直线与平面所成角的范围是0°≤θ≤90°，其解法是作垂线、找射影；二面角0°≤θ≤180°，其方法是：①定义法；②三垂线定理及其逆定理；③垂面法另外也可借助空间向量求这三种角的大小.5. 如图，四棱锥P ABCD -中，侧面PDC 是边长为2的正三角形，且与底面垂直，底面ABCD 是60ADC ∠=o 的菱形，M 为PB 的中点.(Ⅰ)求PA 与底面ABCD 所成角的大小；(Ⅱ)求证：PA ⊥平面CDM ；(Ⅲ)求二面角D MC B --的余弦值.解析：求线面角关键是作垂线，找射影，求异面直线所成的角采用平移法求二面角的大小也可应用面积射影法，比较好的方法是向量法答案：(I)取DC 的中点O ，由ΔPDC 是正三角形，有PO ⊥DC ．又∵平面PDC ⊥底面ABCD ，∴PO ⊥平面ABCD 于O ．连结OA ，则OA 是PA 在底面上的射影．∴∠PAO 就是PA 与底面所成角．∵∠ADC =60°，由已知ΔPCD 和ΔACD 是全等的正三角形，从而求得OA =OP =3∴∠PAO =45°．∴PA 与底面ABCD 可成角的大小为45°．(II)由底面ABCD 为菱形且∠ADC =60°，DC =2，DO =1，有OA ⊥DC ．建立空间直角坐标系如图，则(3,0,0),(0,0,3),(0,1,0)A P D -, (3,2,0),(0,1,0)B C ．由M 为PB 中点，∴33(1,M ． ∴33((3,0,3),DM PA ==u u u u r u u u r (0,2,0)DC =u u u r ． ∴333203)0PA DM ⋅=⨯-=u u u r u u u u r ，03200(3)0PA DC ⋅=⨯+⨯-=u u u r u u u r ．∴PA ⊥DM ，PA ⊥DC ． ∴PA ⊥平面DMC ．(III)33(),(3,1,0)CM CB ==u u u u r u u u r ．令平面BMC 的法向量(,,)n x y z =r ，则0n CM ⋅=u u u u r r ，从而x +z =0； ……①, 0n CB ⋅=u u u r r 30x y +=． ……②由①、②，取x =−1，则3,1y z =． ∴可取(3,1)n=-r ．由(II)知平面CDM 的法向量可取(3,0,3)PA =u u u r ， ∴2310cos ,||||56n PA n PA n PA ⋅-<>=⋅u u u r r u u u r r u u u r r 10法二：（Ⅰ）方法同上（Ⅱ）取AP 的中点N ，连接MN ，由（Ⅰ）知，在菱形ABCD 中，由于60ADC ∠=o ，则AO CD ⊥，又PO CD ⊥，则CD APO ⊥平面，即CD PA ⊥，又在PAB ∆中，中位线//MN 12AB ，1//2CO AB ，则//MN CO ，则四边形OCMN 为Y ，所以//MC ON ，在APO ∆中，AO PO =，则ON AP ⊥，故AP MC ⊥而MC CD C =I ，则PA MCD ⊥平面（Ⅲ）由（Ⅱ）知MC PAB ⊥平面，则NMB ∠为二面角D MC B --的平面角，在Rt PAB ∆中，易得PA=PB ===，cos AB PBA PB ∠===，cos cos()5NMB PBA π∠=-∠=-故，所求二面角的余弦值为5-点评：本题主要考查异面直线所成的角、线面角及二面角的一般求法，综合性较强用平移法求异面直线所成的角，利用三垂线定理求作二面角的平面角，是常用的方法.6. 如图，在长方体1111ABCD A B C D -中，11,2,AD AA AB ===点E 在线段AB 上. （Ⅰ）求异面直线1D E 与1A D 所成的角；（Ⅱ）若二面角1D EC D --的大小为45︒，求点B 到平面1D EC 的距离.解析：本题涉及立体几何线面关系的有关知识, 本题实质上求角度和距离,在求此类问题中，要将这些量归结到三角形中,最好是直角三角形,这样有利1D A B CD E 1A 1B 1C于问题的解决，此外用向量也是一种比较好的方法.答案：解法一：（Ⅰ）连结1AD .由已知，11AA D D 是正方形，有11AD A D ⊥.∵AB ⊥平面11AA D D ，∴1AD 是1D E 在平面11AA D D 内的射影.根据三垂线定理，11AD D E ⊥得，则异面直线1D E 与1A D 所成的角为90︒. 作DF CE ⊥，垂足为F ，连结1D F ，则1CE D F ⊥所以1DFD ∠为二面角1D EC D --的平面角，145DFD ∠=︒.于是111,DF DD D F ==易得Rt Rt BCE CDF ∆≅∆，所以2CE CD ==，又1BC =，所以BE =. 设点B 到平面1D EC 的距离为h .∵1,B CED D BCE V V --=即1111113232CE D F h BE BC DD ⋅⋅⋅=⋅⋅⋅，∴11CE D F h BE BC DD ⋅⋅=⋅⋅，即=，∴4h =.故点B 到平面1D EC 解法二：分别以1,,DA DB DD 为x 轴、y 轴、z 轴，建立空间直角坐标系.（Ⅰ）由1(1,0,1)A ，得1(1,0,1)DA =u u u u r设(1,,0)E a ，又1(0,0,1)D ，则1(1,,1)D E a =-u u u u r .∵111010DA D E ⋅=+-=u u u u r u u u u r ∴11DA D E ⊥u u u u r u u u u r则异面直线1D E 与1A D 所成的角为90︒.（Ⅱ）(0,0,1)=m 为面DEC 的法向量，设(,,)x y z =n 为面1CED 的法向量，则(,,)x y z =n|||cos ,|cos 45||||2⋅<>===︒=m n m n m n ∴222z x y =+. ①由(0,2,0)C ，得1(0,2,1)DC =-u u u u r ，则1D C ⊥u u u u r n ，即10DC ⋅=u u u u r n ∴20y z -= ② 由①、②，可取(3,1,2)=n 又(1,0,0)CB =u u u r ，所以点B 到平面1D EC 的距离||36422CB d ⋅===u u u r n |n |. 点评：立体几何的内容就是空间的判断、推理、证明、角度和距离、面积与体积的计算，这是立体几何的重点内容,本题实质上求角度和距离,在求此类问题中,尽量要将这些量归结于三角形中,最好是直角三角形,这样计算起来,比较简单,此外用向量也是一种比较好的方法,不过建系一定要恰当,这样坐标才比较容易写出来.考点四探索性问题7. 如图所示：边长为2的正方形ABFC 和高为2的直角梯形ADEF 所在的平面互相垂直且DE=2，ED//AF 且∠DAF =90°.（1）求BD 和面BEF 所成的角的余弦；（2）线段EF 上是否存在点P 使过P 、A 、C 三点的平面和直线DB 垂直，若存在，求EP 与PF 的比值；若不存在，说明理由.解析：1.先假设存在，再去推理，下结论： 2.运用推理证明计算得出结论，或先利用条件特例得出结论，然后再根据条件给出证明或计算. 答案：（1）因为AC 、AD 、AB 两两垂直，建立如图坐标系，则B （2，0，0），D （0，0，2），E （1，1，2），F （2，2，0），则)0,2,0(),2,1,1(),0,0,2(=-==BF BE DB设平面BEF 的法向量x z y x n -=则),,,(0,02==++y z y ，则可取)0,1,2(=n ，∴向量)1,0,2(=n DB 和所成角的余弦为1010)2(21220222222=-++-+⋅. 即BD 和面BEF 所成的角的余弦1010. （2）假设线段EF 上存在点P 使过P 、A 、C 三点的平面和直线DB 垂直，不妨设EP 与PF 的比值为m ，则P 点坐标为),12,121,121(m m m m m +++++ 则向量=),12,121,121(m m m m m +++++，向量=CP ),12,11,121(mm m m ++-++ 所以21,012)2(12101212==+-++++++m m m m m m 所以. 点评：本题考查了线线关系，线面关系及其相关计算，本题采用探索式、开放式设问方式，对学生灵活运用知识解题提出了较高要求.8. 如图，在三棱锥V ABC -中，VC ABC ⊥底面，AC BC ⊥，D 是AB 的中点，且AC BC a ==，π02VDC θθ⎛⎫=<< ⎪⎝⎭∠．（I ）求证：平面VAB ⊥平面VCD ；（II ）试确定角θ的值，使得直线BC 与平面VAB 所成的角为π6．解析：本例可利用综合法证明求解，也可用向量法求解.答案:解法1：（Ⅰ）AC BC a ==∵，ACB ∴△是等腰三角形，又D 是AB 的中点，CD AB ⊥∴，又VC ⊥底面ABC ．VC AB ⊥∴．于是AB ⊥平面VCD ．又AB ⊂平面VAB ，∴平面VAB ⊥平面VCD ．（Ⅱ）过点C 在平面VCD 内作CH VD ⊥于H ，则由（Ⅰ）知CD ⊥平面VAB ．连接BH ，于是CBH ∠就是直线BC 与平面VAB 所成的角．依题意π6CBH ∠=，所以在CHD Rt △中，sin 2CH a θ=；在BHC Rt △中，πsin 62a CH a ==，sin θ=∴． π02θ<<∵，π4θ=∴．故当π4θ=时，直线BC 与平面VAB 所成的角为π6．解法2：（Ⅰ）以CA CB CV ，，所在的直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系，则(000)(00)(00)000tan 222a a C A a B a D V a θ⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭，，，，，，，，，，，，，，，于是，tan 222a a VD θ⎛⎫=- ⎪ ⎪⎝⎭u u u r ，，，022a a CD ⎛⎫= ⎪⎝⎭u u u r ，，，(0)AB a a =-u u u r ，，．从而2211(0)0002222a a ABCD a a a a ⎛⎫=-=-++= ⎪⎝⎭u u u r u u u r ，，，，··，即AB CD ⊥．同理2211(0)tan 02222a a AB VD a a a a θ⎛⎫=-=-++ ⎪ ⎪⎝⎭u u u r u u u r ，，，，··即AB VD ⊥．又CD VD D =I ，AB ⊥∴平面VCD ．又AB ⊂平面VAB ．∴平面VAB ⊥平面VCD ．（Ⅱ）设平面VAB 的一个法向量为()x y z =，，n ，则由00AB VD ==u u u r，··nn ．得0tan 0222ax ay a a x y θ-+=⎧⎪⎨+-=⎪⎩，．可取(11)θ=n ，又(00)BC a =-u u u r，，，于是πsin 62BC BC θ===u u u r u u u r n n ··，即sin 2θ=π02θ<<∵，π4θ∴=．故交π4θ=时，直线BC 与平面VAB 所成的角为π6．解法3：（Ⅰ）以点D 为原点，以DC DB ，所在的直线分别为x 轴、y 轴，建立如图所示的空间直角坐标系，则(000)000000222D A a B a C a ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，，，，，，，，，，，0tan 22V a θ⎛⎫- ⎪ ⎪⎝⎭，，，于是0tan 22DV a a θ⎛⎫=- ⎪ ⎪⎝⎭u u u r ，，，002DC ⎛⎫=- ⎪ ⎪⎝⎭u u u r ，，，(00)AB =u u u r ，．从而(00)AB DC =u u u r u u u r ，·0002a ⎛⎫-= ⎪ ⎪⎝⎭，，·，即AB DC ⊥．同理(00)0tan 0AB DV θ⎛⎫== ⎪ ⎪⎝⎭u u u r u u u r ，，·，即AB DV ⊥．又DC DV D =I ， AB ⊥∴平面VCD ．又AB ⊂平面VAB ， ∴平面VAB ⊥平面VCD ．（Ⅱ）设平面VAB 的一个法向量为()x y z =，，n ，则由00AB DV ==u u u r u u u r ，··n n ，得2022tan 022ay ax az θ⎧=⎪⎨-+=⎪⎩，．可取(tan 01)n θ=，，，又220BC a a ⎛⎫=-- ⎪ ⎪⎝⎭u u u r ，，，于是22tan π22sin sin 61tan a BC BC a θθθ===+u u u r u u u r n n ···，即πππsin 0224θθθ=<<，，∵∴=．故角π4θ=时，即直线BC 与平面VAB 所成角为π6．点评：证明两平面垂直一般用面面垂直的判定定理,求线面角一是找线在平面上的射影在直角三角形中求解,但运用更多的是建空间直角坐标系,利用向量法求解考点五折叠、展开问题9．已知正方形ABCD E 、F 分别是AB 、CD 的中点,将ADE V 沿DE 折起,如图所示,记二面角A DE C --的大小为(0)θθπ<<(I) 证明//BF 平面ADE ;(II)若ACD V 为正三角形,试判断点A 在平面BCDE 内的射影G 是否在直线EF 上,证明你的结论,并求角θ的余弦值分析:充分发挥空间想像能力，重点抓住不变的位置和数量关系，借助模型图形得出结论，并给出证明.解: (I)证明:EF 分别为正方形ABCD 得边AB 、CD 的中点,ADBCVxyAEB CF DG∴EB//FD,且EB=FD,∴四边形EBFD 为平行四边形∴BF//ED.,EF AED BF AED ⊂⊄Q 平面而平面,∴//BF 平面ADE(II)如右图,点A 在平面BCDE 内的射影G 在直线EF 上,过点A 作AG 垂直于平面BCDE,垂足为G,连结GC,GDQ ∆ACD 为正三角形,∴AC=AD. ∴CG=GD. Q G在CD 的垂直平分线上, ∴点A 在平面BCDE 内的射影G 在直线EF 上,过G 作GH 垂直于ED 于H,连结AH,则AH DE ⊥,所以AHD ∠为二面角A-DE-C 的平面角即G AH θ∠=.设原正方体的边长为2a,连结AF,在折后图的∆AEF中,EF=2AE=2a,即∆AEF 为直角三角形, AG EF AE AF ⋅=⋅.2AG a ∴=在Rt ∆ADE 中, AH DE AE AD ⋅=⋅AH ∴=.GH ∴=,1cos 4GH AH θ== 点评：在平面图形翻折成空间图形的这类折叠问题中，一般来说，位于同一平面内的几何元素相对位置和数量关系不变：位于两个不同平面内的元素，位置和数量关系要发生变化，翻折问题常用的添辅助线的方法是作棱的垂线.关键要抓不变的量.考点六球体与多面体的组合问题10．设棱锥M-ABCD 的底面是正方形，且MA ＝MD ，MA ⊥AB ，如果ΔAMD 的面积为1，试求能够放入这个棱锥的最大球的半径.分析：关键是找出球心所在的三角形，求出内切圆半径. 解： ∵AB ⊥AD ，AB ⊥MA ， ∴AB ⊥平面MAD ，由此，面MAD ⊥面AC.记E 是AD 的中点，从而ME ⊥AD. ∴ME ⊥平面AC ，ME ⊥EF.设球O 是与平面MAD 、平面AC 、平面MBC 都相切的球. 不妨设O ∈平面MEF ，于是O 是ΔMEF 的内心. 设球O 的半径为r ，则r ＝MFEM EF S MEF++△2设AD ＝EF ＝a,∵S ΔAMD ＝1. ∴ME ＝a 2.MF ＝22)2(aa +, r ＝22)2(22aa a a +++≤2222+＝2-1. 当且仅当a ＝a2，即a ＝2时，等号成立.∴当AD ＝ME ＝2时，满足条件的球最大半径为2-1.点评：涉及球与棱柱、棱锥的切接问题时一般过球心及多面体中的特殊点或线作截面，把空间问题化归为平面问题，再利用平面几何知识寻找几何体中元素间的关系.注意多边形内切圆半径与面积和周长间的关系；多面体内切球半径与体积和表面积间的关系. 三、方法总结1．位置关系：（1）两条异面直线相互垂直证明方法：○1证明两条异面直线所成角为90º；○2证明两条异面直线的方向量相互垂直.（2）直线和平面相互平行证明方法：○1证明直线和这个平面内的一条直线相互平行；○2证明这条直线的方向向量和这个平面内的一个向量相互平行；○3证明这条直线的方向向量和这个平面的法向量相互垂直.（3）直线和平面垂直证明方法：○1证明直线和平面内两条相交直线都垂直，○2证明直线的方向量与这个平面内不共线的两个向量都垂直；○3证明直线的方向量与这个平面的法向量相互平行.（4）平面和平面相互垂直证明方法：○1证明这两个平面所成二面角的平面角为90º；○2证明一个平面内的一条直线垂直于另外一个平面；○3证明两个平面的法向量相互垂直.2．求距离：求距离的重点在点到平面的距离，直线到平面的距离和两个平面的距离可以转化成点到平面的距离，一个点到平面的距离也可以转化成另外一个点到这个平面的距离.（1）两条异面直线的距离。

立体几何证明方法总结(教师)

一、线线平行的证明方法：1、利用平行四边形。

2、利用三角形或梯形的中位线。

3、如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行。

（线面平行的性质定理）4、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

（面面平行的性质定理）5、如果两条直线垂直于同一个平面，那么这两条直线平行。

（线面垂直的性质定理）6、平行于同一条直线的两条直线平行。

7、夹在两个平行平面之间的平行线段相等。

（需证明）二、线面平行的证明方法：1、定义法：直线与平面没有公共点。

2、如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

（线面平行的判定定理）3、两个平面平行，其中一个平面内的任何一条直线必平行于另一个平面。

三、面面平行的证明方法：1、定义法：两平面没有公共点。

2、如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

（面面平行的判定定理）3、平行于同一平面的两个平面平行。

4、经过平面外一点，有且只有一个平面和已知平面平行。

5、垂直于同一直线的两个平面平行。

四、线线垂直的证明方法：1、勾股定理。

2、等腰三角形。

3、菱形对角线。

4、圆所对的圆周角是直角。

5、点在线上的射影。

6、如果一条直线和一个平面垂直，那么这条直线就和这个平面内任意的直线都垂直。

7、在平面内的一条直线，如果和这个平面一条斜线的射影垂直，那么它也和这条斜线垂直。

（三垂线定理，需证明）8、在平面内的一条直线，如果和这个平面一条斜线垂直，那么它也和这条斜线的射影垂直。

（三垂线逆定理，需证明）9、如果两条平行线中的一条垂直于一条直线，则另一条也垂直于这条直线。

五、线面垂直的证明方法：1、定义法：直线与平面内任意直线都垂直。

2、点在面内的射影。

3、如果一条直线和一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面。

（线面垂直的判定定理）4、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

(完整word)高中数学立体几何证明公式

线线平行→线面平行如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

线面平行→线线平行如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行。

线面平行→面面平行如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

面面平行→线线平行如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

线线垂直→线面垂直如果一条直线和一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面。

线面垂直→线线平行如果连条直线同时垂直于一个平面，那么这两条直线平行。

线面垂直→面面垂直如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

线面垂直→线线垂直线面垂直定义：如果一条直线a与一个平面α内的任意一条直线都垂直，我们就说直线a垂直于平面α。

面面垂直→线面垂直如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

三垂线定理如果平面内的一条直线垂直于平面的血现在平面内的射影，则这条直线垂直于斜线。

立体几何常见证明方法

立体几何常见证明方法第一篇：立体几何常见证明方法立体几何方法归纳小结一、线线平行的证明方法1、根据公理4，证明两直线都与第三条直线平行。

2、根据线面平行的性质定理，若直线a平行于平面A，过a的平面B与平面A相交于b，则 a//b。

3、根据线面垂直的性质定理，若直线a与直线b都与平面A垂直，则a//b。

4、根据面面平行的性质定理，若平面A//平面B，平面C与平面A和平面B的交线分别为直线 a与直线 b，则a//b。

υυυρυυυρ5、由向量共线定理，若AB=xCD，且AB、CD不共线，则向量AB所在的直线a与向量cd所在的直线b平行，即a//b。

二、线面平行的证明方法1、根据线面平行的定义，证直线与平面没有公共点。

2、根据线面平行的判定定理，若平面 A内存在一条直线b与平面外的直线a平行，则a//A。

(用相似三角形或平行四边形)3、根据平面与平面平行的性质定理，若两平面平行，则一个平面内的任一直线与另一个平面平行。

4、向量法，向量c与平面A法向量垂直，且向量c所在直线c不在平面内，则c//A。

三、面面平行的证明方法1、根据定义，若两平面没有公共点，则两平面平行。

2、根据两平面平行的判定定理，一个平面内有两相交直线与另一平面平行，则两平面平行。

或根据两平面平行的判定定理的推论，一平面内有两相交直线与另一平面内两相交直线平行，则两平面平行。

3、垂直同一直线的两平面平行。

4、平行同一平面的两平面平行。

5、向量法，证明两平面的法向量共线。

四、两直线垂直的证明方法1、根据定义,证明两直线所成的角为90°2、一直线垂直于两平行直线中的一条,也垂直于另一条.3、一直线垂直于一个平面,则它垂直于平面内的所有直线.4、根据三垂线定理及逆定理,若平面内的直线垂直于平面的一条斜线(或斜线在平面内的射影),则它垂直于斜线在平面内的射影(或平面的斜线).5、向量法.五、线面垂直的证明方法1、根据定义,证明一直线与平面内的任一(所有)直线垂直,则直线垂直于平面.2、根据判定定理,一直线垂直于平面内的两相交直线,则直线垂直于平面.3、一直线垂直于两平行平面中的一个,也垂直于另一个.4、两平行直线中的一条垂直于一个平面,另一条也垂直于这个平面.5、根据两平面垂直的性质定理,两平面垂直,则一个平面内垂直于它们交线的直线垂直于另一个平面.6、向量法,证明平面的法向量与表示该直线的向量共线.六、面面垂直的证明方法1、根据面面垂直的定义，两平面相交所成的二面角为直二面角，则两平面垂直。

立体几何证明汇总

立体几何1.空间多边形不在同一平面内的若干线段首尾相接所成的图形叫做空间折线. 若空间折线的最后一条线段的尾端与最初一条线段的首端重合，则叫做封闭的空间折线. 若封闭的空间折线各线段彼此不相交，则叫做这空间多边形平面，平面是一个不定义的概念，几何里的平面是无限伸展的. 平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ…或拉丁字母M 、N 、P 来表示，也可用表示平行四边形的两个相对顶点字母表示，如平面AC.在立体几何中，大写字母A ，B ，C ，…表示点，小写字母，a,b,c,…l,m,n,…表示直线，且把直线和平面看成点的集合，因而能借用集合论中的符号表示它们之间的关系，例如： a) A ∈l —点A 在直线l 上；A ∉α—点A 不在平面α内； b) l ⊂α—直线l 在平面α内； c) a ⊄α—直线a 不在平面α内； d) l ∩m=A —直线l 与直线m 相交于A 点； e) α∩l=A —平面α与直线l 交于A 点； f)α∩β=l —平面α与平面β相交于直线l.2.平面的基本性质公理1 如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. 公理2 如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线. 公理3 经过不在同一直线上的三个点，有且只有一个平面. 根据上面的公理，可得以下推论.推论1 经过一条直线和这条直线外一点，有且只有一个平面. 推论2 经过两条相交直线，有且只有一个平面. 推论3 经过两条平行直线，有且只有一个平面. 3.证题方法典型例题（一）点共线。

证题方法间接证法直接证法反证法同一法例已知：四边形ABCD 中，AB ‖DC ，AB 、BC 、DC 、AD分别与平面相交于点E 、F 、G 、H 。

求证：点E 、F 、G 、H 在同一条直线上。

（二）线共点例已知：四边形ABCD 是空间四边形，E 、F 、G 、H 分别为AB 、BC 、CD 、DA 上的点，且直线EH 和FG 相交于点P 。