8梯形-等腰梯形的性质基础题和培优题
八年级数学下册22.5(1)等腰梯形的性质

A 15
D
∴BE=AD=15 ,DE=AB=20 20
20
∵AB=DC
∴DE=DC ∵四边形ABCD是等腰梯形
B
15 E
C
∴∠C=∠B=60°(等腰梯形同一底边上的两内角相等)
∴△DEC是等边三角形. ∴EC=DE=20
∴BC=BE+EC=15+20=35
练一练:
如图,在等腰梯形ABCD中,AD∥BC,AB=DC,对角线
AC⊥BD于点O,AD=4,BC=8,求BD。求S梯形ABCD
解:过点D作DE∥AC交BC的延长线于点E
∴∠1=∠AOD=90°
A4 D
∵AD∥BC
∴四边形ACED是平行四边形
(平行四边形的定义)
∴DE=AC CE=AD=4
(平行四边形的对边相等)
1 O
∵在等腰梯形ABCD中,
AC=BD(等腰梯形的两条B对角线相等) 8
用一个等腰三角形纸片过两腰在三角
形内部用尺裁出一个梯形,并判断这个梯形 是否为等腰梯形.
E
A \ B
D /
C
A
D
等腰梯形
B
C
探索
折一折你手中的等腰梯形纸片
A B
(1) 两腰相等
AB=CD D (2)是轴对称图形
对称轴:两底中点的连 线所在的直线
C (3)同底上两内角相等 ∠A= ∠D, ∠B= ∠C 如何说明?
AB=DC,若AC=3cm,则BD= 3 cm
x+x
B
C
第1,3题图
A
D
3.已知等腰梯形的一个内角等于70°, B
第2题图 C
则其他三个内角的度数是 110°,110 °,70 ° 。
等腰梯形(练习)

等腰梯形(练习)《等腰梯形》基础训练姓名班级学号成绩【知识要点】1、等腰梯形的性质定理和判定定理,并能应⽤进⾏计算和证明;2、通过添加适当的辅助线,将等腰梯形问题转化成三⾓形、平⾏四边形等熟知的⼏何图形来解决问题;3、⽅法:梯形问题⼀般通过添加平⾏线,或作⾼,将梯形问题转化为平⾏四边形、矩形、直⾓三⾓形的问题来解决的.等腰梯形性质:⑴边:;⑵⾓:;⑶对⾓线:;(3)对称性:___________________________. 等腰梯形判定:⑴定义:;⑵⾓:;⑶对⾓线:;⼀.填空题 (3分×10 = 30分)1.等腰梯形的上、下底长分别为6、8,且有⼀个⾓是60°,则它的腰长为.2.如果等腰梯形的⾼等于腰长的⼀半,则它的四个⾓分别等于.3.已知等腰梯形的上、下底长分别为2㎝和6㎝,且它的两条对⾓线互相垂直,则这个梯形的⾯积为.4.若梯形⾯积为144,且两底的⽐为4:5,⾼为16,则梯形的上、下底分别为.5.直⾓梯形的⾼为6㎝,有⼀个⾓是30°,则这个梯形的两腰分别为_____ _____㎝.6.如图1,在梯形ABCD 中,AD ∥BC ,AB =CD ,∠B =60°,AC ⊥AB ,则∠D = _ __°,∠ACD =_________°.7.如图2,在梯形ABCD 中,BC ∥AD ,DE ∥AB ,DE =DC ,∠A=100°,∠EDC =_______°.图1 图2 图38.如图3,在等腰梯形ABCD 中,相等的线段共有对.B A DC E B AD C B D CA9.等腰梯形的锐⾓是60°,它的两底分别是15㎝、49㎝,则腰为=㎝.10.在梯形ABCD中,AD∥BC,∠B=90°,AB=12,BC=10,AD=5,则CD= .⼆.选择题(3分×6 = 18分)1.有两个⾓相等的梯形是( )(A)等腰梯形(B)直⾓梯形(C)⼀般梯形(D)直⾓梯形或等腰梯形2.在四边形ABCD中,AD∥BC,AC=BD,则四边形ABCD中( )(A)平⾏四边形(B)等腰梯形(C)矩形(D)等腰梯形或矩形3.下列命题正确的是( )(A)凡是梯形对⾓线都相等(B)⼀组对边平⾏,另⼀组对边相等的四边形是梯形(C)同⼀底上的两个⾓相等的梯形是等腰梯形(D)只有两个⾓相等的梯形是等腰梯形4.已知梯形的中位线长为24㎝,上、下底的⽐为1:3,则梯形的上、下底之差是( ) (A)24㎝(B)12㎝(C)36㎝(D)48㎝5.已知梯形的两个对⾓分别是78°和120°,则另两个⾓分别是( )(A)78°或120°(B)102°或60°(C)120°或78°(D)60°或120°6.下列关于等腰梯形的判断,正确的是( )(A)两底相等(B)同底上的两底⾓互补(C)每两个⾓相等(D)对⾓线交点在对称轴上三.解答题(6分×6 + 8分×2 = 52分)1.在梯形ABCD中,AB∥CD,∠D=2∠B,AD与CD的长度分别为a和b.(1)求AB的长.(2)若AD⊥AB于点A,求梯形的⾯积.2.如图,已知等腰梯形ABCD 中,AB ∥DC ,其中∠A =72°,AD =DC =CB ,你能说明为什么A 、B 、C 、D 中任意三点都能构成等腰三⾓形吗?3.如图,在等腰梯形ABCD 中,BC ∥AD .(1)画出线段AB 平移后的线段DE ,其平移的⽅向为射线AD 的⽅向,平移的距离为线段AD 的长;(2)若AD =3,AB =4,BC =7,求线段EC 的长和∠B 的度数.4.如图,已知梯形ABCD 中,AB ∥CD ,AD =BC ,点E 是底边AB 的中点.求证:DE =CE .5.如图,梯形ABCD 中,AD ∥BC ,对⾓线AC ⊥BD,且AC =5cm ,BD =12cm ,求该梯形的⾯积.BA D C CB E B6.如图,在梯形ABCD 中,AD ∥BC ,DE ∥AB ,△CDE 的周长为36cm ,AD=6cm .求梯形ABCD 的周长.7.如图所⽰,在梯形ABCD 中,AB ∥CD ,AD ⊥AC ,AD =AC ,DB =DC ,AC ,BD 交于点E ,试问CE 与CB 相等吗,为什么?8.如图,已知△ABC 中,AH ⊥BC 于H ,D 、E 、F 、分别为AB 、BC、CA 的中点.四边EFGH 是等腰梯形吗?为什么?H A BED C A。
等腰梯形的性质判定复习

B
C
E
例5 : 如图, 梯形ABCD中,AD//BC,EF//AB 2.5cm 且E为CD中点,AB=5cm,则EF=_________
A B M F D E C
例6 : 如图, 梯形ABCD中,AD//BC,B C 90 AD 1
0
1 BC 3, E, F分别为AD, BC的中点, 则EF __________
C
• 答:梯形的面积为6.8.
• 误点剖析 要注意灵活应用梯形面积的求 法. • 评注(1)当梯形(或任意四边形)对角线 互相垂直时,它们的面积等于对角线乘积 的一半. • (2)本题也可以利用等量关系 D A • S梯形ABCD=S△ABC+S△ADC来解答.
如图,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个 动点(E与A、D不重合),G、F、H分别是BE、BC、CE的 中点. (1)试探索四边形EGFH的形状,并说明理由; (2)当点E运动到什么位置时,四边形EGFH是菱形? 并加以证明; (3)若(2)中的菱形EGFH是正方形,请探索线段EF与 线段BC的关系,并证明你的结论.
距离叫做梯形的高.
两腰不相等的梯形; 等腰梯形:两腰相等的梯形叫做等腰梯形; (2)分类:梯形: 直角梯形:一腰与底垂直的梯形叫做直角 梯形.
1 (3)面积:S 梯形= (上底+下底)×高=中位线×高. 2
2.梯形的中位线 定义:连接梯形两腰中点的线段叫做梯形中位线. 判定: (1)经过梯形一腰中点与底平行的直线必平分另一腰; (2)定义法. 性质:梯形的中位线平行于两底,并且等于两底和的一半.
A
E
D
B
M
F
N
C
例7 : 梯形ABCD中, AD / / BC, AB 7, BC 8
初二梯形性质及判定练习题

初二梯形性质及判定练习题梯形的定义梯形是指两边是平行线段的四边形。
梯形的性质* 对于同一梯形,上底和下底两边平行。
* 对于同一梯形,左右两边相等。
* 对于同一梯形,上下两边长度之和等于对角线长度之和。
梯形判定方式* 同一四边形,两边平行,另两边不平行,就是梯形。
* 一般判定定理:如果一个四边形的两对角线互相等长,那么这个四边形是梯形。
梯形的分类* 直角梯形:梯形中有个直角。
* 等腰梯形:左右两边相等的梯形。
练题设梯形ABCD中,AB // CD,AB = 8cm,BC = CD = 6cm,AD = 4cm。
1. 求梯形ABCD的面积。
2. 过点D作线段AD的平行线与AB交于E点,求三角形CDE 的面积。
3. 过线段AD中点O作BC的垂线,交与BC于点P,求三角形AOP的面积。
分析解答1. 梯形面积公式:$S_{ABCD} = \frac{AB+CD}{2} \times AD = \frac{8+6}{2} \times 4 = 28$ (平方厘米)。
2. 因为AD // BE,所以三角形CDE与梯形ABCD面积相同,而梯形ABCD的面积为28平方厘米,所以三角形CDE的面积为28平方厘米。
3. 因为AO与BC垂直,所以 $\angle AOP = 90°$,所以三角形AOP为直角三角形,而AO = $\frac{AD}{2} = 2$,OP = BC - BP = BC - $\frac{AD}{2}$ = 6 - 2 = 4,所以三角形AOP的面积为$\frac{AO \times OP}{2} = 4$ (平方厘米)。
以上是初二梯形性质及判定练习题的内容。
2019-2020学年八年级数学上学期期末复习《梯形、等腰梯形》 苏科版

2019-2020学年八年级数学上学期期末复习《梯形、等腰梯形》 苏科版一、知识点:1. 梯形的有关概念:2. 梯形中的常用辅助线的添法:3. 等腰梯形的性质:①等腰梯形的两腰 ;两底 。
②等腰梯形同一底上的 相等。
③等腰梯形的 相等。
4.等腰梯形的判定:① 相等的梯形是等腰梯形。
② 两个角相等的梯形是等腰梯形。
③ 相等的梯形是等腰梯形。
二、基础训练:1.下列结论正确的是( )A .梯形可分为直角梯形和等腰梯形两类B .四边形可以分成平行四边形和梯形两类C .平行四边形是梯形的特殊形式D .直角梯形和等腰梯形都是梯形的特殊形式2、已知等腰梯形的一个底角等于600,它的两底分别为13cm 和37cm ,它的周长为_______; 3.等腰梯形ABCD 对角线交于O 点,∠BOC =120°,∠BDC=80°,则∠DAB= . 4.在梯形ABCD 中,AD ∥BC ,∠B =50°,∠C =80°,BC =5, AD =3,则CD =____.5、如图,在等腰梯形ABCD 中,AD ∥BC ,AB = AD ,BD = BC ,则∠C= 0。
三、例题讲解 1、已知,如图,梯形ABCD 中,AD∥BC,∠B=60°,∠C=30°, AD=2,BC=8.求梯形两腰AB 、CD 的长.2、如图,等腰梯形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O . 试说明:AO =DO .3、如图,在梯形ABCD 中,AB //DC ,∠D =90o,AD =DC =4,AB =1,F 为AD 的中点, 求点F 到BC 的距离。
C AD CBA B CDD A CBA 'D CA BO第1题图DEPBA第3题图C4、如图,在梯形ABCD 中,AD BC ∥,AB AC ⊥,45B ∠=,AD =,BC =DC 的长.5、如图,在等腰梯形A BCD 中,AD ∥BC ,AB=CD ,M 为BC 中点,则: (1)点M 到两腰AB 、CD 的距离相等吗?请说出你的理由。
等腰梯形的性质专项练习30题(有答案)ok
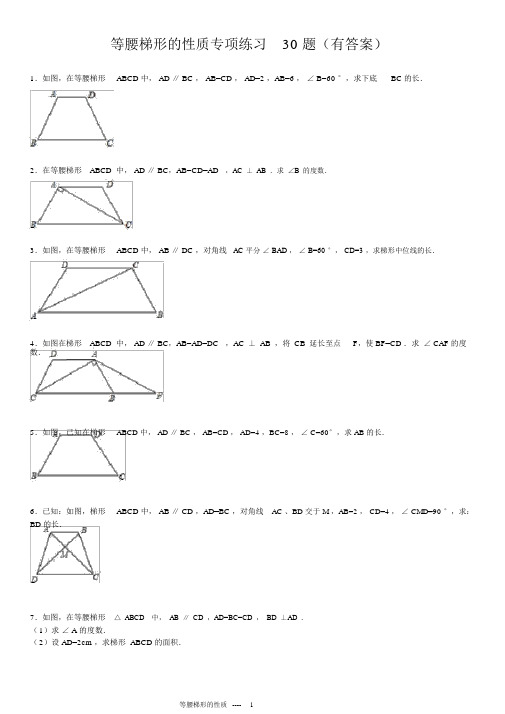
等腰梯形的性质专项练习30 题(有答案)1.如图,在等腰梯形ABCD 中, AD ∥ BC , AB=CD , AD=2 ,AB=6 ,∠ B=60 °,求下底BC 的长.2.在等腰梯形ABCD 中, AD ∥ BC,AB=CD=AD,AC⊥AB.求∠B的度数.3.如图,在等腰梯形ABCD 中, AB ∥ DC ,对角线AC 平分∠ BAD ,∠ B=60 °, CD=3 ,求梯形中位线的长.4.如图在梯形ABCD 中, AD ∥ BC,AB=AD=DC,AC⊥AB,将CB延长至点F,使 BF=CD .求∠ CAF 的度数.5.如图,已知在梯形ABCD 中, AD ∥ BC , AB=CD , AD=4 ,BC=8 ,∠ C=60°,求 AB 的长.6.已知:如图,梯形ABCD 中, AB ∥ CD ,AD=BC ,对角线AC 、BD 交于 M ,AB=2 , CD=4 ,∠ CMD=90 °,求:BD 的长.7.如图,在等腰梯形△ ABCD中,AB∥ CD,AD=BC=CD,BD⊥AD.(1)求∠ A 的度数.(2)设 AD=2cm ,求梯形 ABCD 的面积.8.如图,在等腰梯形 ABCD 中,AD ∥ BC ,AB=CD ,∠ B=60 °.AE ⊥BC 于 E;EF⊥ CD 于 F,点 F 是 CD 的中点.求证: AD=BE .9.如图,在等腰梯形ABCD 中,已知AD ∥BC, AB=CD , AE ⊥BC 于 E,∠ B=60 °,∠ DAC=45 °,,求梯形 ABCD 的周长?10.如图示,在等腰梯形 ABCD 中, AD ∥BC,∠ B=45 °,中位线长为 5cm,高为 2cm,求梯形底边 BC 的长及梯形的面积.11.如图,在梯形ABCD 中, AD ∥ BC ,AB=DC=6cm , BD ⊥ CD 于 D ,∠ C=60°.(1)求∠ DBC 的度数;(2)求 AD 的长.12.如图,等腰梯形 ABCD 中, AB ∥ CD ,AB=2AD ,梯形周长为 40,对角线 BD 平分∠ABC ,求梯形的腰长及两底边的长.13.如图,在等腰梯形 ABCD 中, AD ∥ BC, AC 平分∠ BCD ,已知 AD=5cm , BC=9cm ,求等腰梯形 ABCD 的周长.14.如图,在梯形ABCD 中, AD ∥BC , AB=DC ,点 E 在 BC 的延长线上,DE=DB .求证: AD=CE .15.如图,等腰梯形ABCD 中, AD ∥ BC, BD ⊥DC ,点 E 是 BC 边的中点, DE ∥AB .(1)求∠ BCD 的度数;(2)若 AB=4 ,求等腰梯形 ABCD 的面积.16.如图,在等腰梯形 ABCD 中, AB=CD ,∠ D=120 °, AC 平分∠ BCD ,梯形的中位线长为 6,求 AC 的长及梯形的面积?17.如图, E 是等腰梯形ABCD 底边 AB 上的中点,求证:DE=CE .18.如图,在等腰梯形 ABCD 中, AB ∥ CD ,AD=BC ,E、F 是 AB 上的两点且 AE=BF ,DF 与 CE 相交于点 O.问 OE 与OF 相等吗?为什么?19.如图,在等腰梯形ABCD 中, AD ∥ BC,∠ A=2 ∠ B , BC=3, AB=2 .求 AD 的长.20.如图,等腰梯形ABCD 中, AD ∥ BC, BD ⊥CD ,∠ A=2 ∠ C, BC=8cm ,求腰 DC 的长.21.如图所示,在等腰梯形ABCD 中,已知AD ∥ BC, AB=DC ,∠ ACB=42 °,∠ ACD=27 °.(1)∠ BAC= _________ °;(2)如果 BC=10cm ,连接 BD ,求 BD 的长度.22.如图,在等腰梯形ABCD 中, AD ∥ BC, M 是 AD 的中点, MB=MC吗?为什么?23.如图,在梯形ABCD 中, AB=DC=AD , AC=BC ,求∠ B 的度数.24.如图, E 是等腰梯形ABCD 底边 AB 上的中点, DE 和 CE 相等吗,为什么?25.如图,等腰梯形ABCD 中, AD ∥ BC, AB=CD ,两条对角线AC ⊥BD , AE ⊥ BC .(1)求证: AE= ( AD+BC );(2)若 AC=10cm ,求等腰梯形 ABCD 的面积.26.如图,已知在等腰梯形ABCD 中, CD ∥ AB , AD=BC ,四边形 AEBC 是平行四边形.求证:∠ ABD=∠ ABE.27.如图,等腰梯形ABCD 中, AD ∥ BC, AB=CD ,对角线BD 平分∠ABC ,且 BD ⊥ DC ,上底 AD=3cm .(1)求∠ ABC 的度数;(2)求梯形 ABCD 的周长.28.已知等腰梯形 ABCD 中, AD ∥BC , AB=CD ,BD 平分∠ABC , BD ⊥CD,若梯形的周长为 25cm,求梯形各边的长.29.如图,已知四边形ABCD 是等腰梯形, AD ∥ BC ,对角线AC ⊥BD ,延长 BC 至 E 点,使 CE=AD ,连接 DE .(1)求∠ ACE 的度数;(2)若 AD+BC=10cm ,求△BDE 的面积.30.如图所示:在等腰梯形ABCD 中, AB ∥ DC, AD=DC=CB ,∠ ADC=120 °.(1)试探讨线段 AC 与 BC 的位置关系;(2)若 AD=4 ,求梯形 ABCD 的面积.参考答案:1.过点 D 作 DE∥ AB ,则可得 DE=AB=CD ,又∵ ∠ B=∠ DEC=60 °,∴ △ DEC 为等边三角形,∴CE=AB=6cm ,故可得 BC=BE+EC=AD+EC=8cm.2.在等腰梯形ABCD 中,∵AD ∥ BC , AB=CD ,∴∠B=∠BCD .(1 分)∵AD=CD ,∴∠ACD= ∠CAD .(1 分)又∵AD ∥ BC,∴∠ACB= ∠CAD .(1 分)∴∠ACB= ∠ACD .(1 分)∵AC⊥AB ,∴ ∠ B+∠ ACB=90 °.(1 分)∴∠B+∠B=90°.∴ ∠ B=60 °.3.∵四边形 ABCD 是等腰梯形,∠ B=60 °,∴ ∠ BAD= ∠ B=60 °, AD=BC ,∵AC 平分∠BAD ,∴ ∠ BAC= ∠ DAC=30 °,∴ ∠ ACB=90 °,又∵AB ∥DC,∴∠ACD= ∠BAC ,∴∠ACD= ∠DAC ,∴DC=AD=3 ,∴BC=AD=3 ,在 Rt△ ACB 中,∵∠BAC=30 °,∴ AB=2BC=6 ,∴所求中位线的长是(AB+DC)=(6+3)=4.54.∵AD ∥BC ,∴∠DAC= ∠ACB ,∵AD=DC ,∴∠DCA= ∠DAC ,∴ ∠ ACD= ∠ ACB=∠DCB,∵AB=DC ,∴ ∠ ABC= ∠ DCB=2 ∠ ACB ,∵AC⊥AB ,∴ ∠ CAB=90 °,∴ ∠ ABC=60 °,∵AB=BF ,∴∠BAF= ∠F,∵ ∠ ABC= ∠ BAF+ ∠ F,∴ ∠ BAF=30 °,∴ ∠ CAF= ∠ CAB+ ∠ BAF=90 °+30°=120 °.5.分别过点 A , D 作 AE ⊥ BC, DF⊥ BC .∵在梯形 ABCD 中,AD ∥ BC ,AB=CD ,AD=4 ,BC=8 ,∴AD=EF=4 ,BE=CF= ( 8﹣ 4) =2,∵ ∠ C=60 °,∴ ∠ CDF=30 °,∴CD=4 ,∵AB=CD ,∴ AB=4 .6.如图,过点 B 作 BE ∥AC 交 DC 的延长线于点 E,∴ ∠ EBD= ∠ CMD=90 °,∵AB ∥CD ,∴四边形 ACEB 是平行四边形,∴AC=BE ,CE=AB ,∵ AB=2 ,CD=4 ,∴DE=DC+CE=DC+AB=4+2=6 ,∵梯形 ABCD 中, AB ∥ CD , AD=BC ,∴AC=BD ,∴BD=BE ,在 Rt△BDE 中,由勾股定理得, BD2+BE2=DE2,即 BD2+BD2=62,解得 BD=3.故答案为: 3 .7. 1)解:∵ AD=BC=DC ,∴∠CDB= ∠ CBD,∵DC ∥BA ,∴∠CDB= ∠ DBA ,∴ ∠ CBA=2 ∠ DBA ,∵DC ∥AB , AD=BC ,∴∠A= ∠ABC=2 ∠DBA ,∵DB ⊥AD ,∴ ∠ ADB=90 °,∵AD ∥BC,AE⊥BC,DF⊥BC,∴ ∠ A= ×90°=60°,∴AE ∥DF,∴四边形 ADFE 是平行四边形,答:∠ A=60 °.∴,∴梯形 ABCD 的周长为: AD+DC+BC+AB=﹣( 2)解:作 DE ⊥ AB 于 E,1+2+2+2+ ﹣ 1=4+2 .∵ ∠ A=60 °,∠ DEA=90 °,答:梯形 ABCD 的周长是 4+2 .∴ ∠ ADE=30 °,∴ AE= AD=1cm ,由勾股定理得: DE= cm,同理 AB=2AC=4cm ,10.取两腰 AB ,CD 的中点分别为 E 和 F,连接 EF,∴梯形 ABCD 的面积是( CD+AB )×DE= (×2cm+4cm )根据梯形中位线定理得:EF= ( AD+BC ),× cm=3 cm 2,cm2∵ EF=5cm ,∴ AD+BC=10cm ,答:梯形 ABCD 的面积是过 A, D 作出梯形的两条高 AM 和 DN ,∵梯形 ABCD ,∴AD ∥BC,∴ ∠ MAD= ∠ AMN= ∠MND=90 °,∴四边形 AMND 为矩形,∴ AD=MN ,8.连接 ED.又 Rt△ABM 和 Rt△ DCN 中,∵AD ∥BC,AB=CD ,AM=DN , AB=AC ,∴ ∠ B=∠ C=60°,∴ Rt△ABM ≌ Rt△ DCN ,∵ EF⊥CD , F 是 CD 中点,∴ BM=CN ,∴ ED=EC ( 3 分)由∠ AMB=90 °,∠ B=45 °,得△ ABM 为等腰直角三角形,∴ ∠ DEC= ∠C=60°∴ MB=AM=2cm ,同理 CN=DN=2cm ,∴ △ ECD 是等边三角形,( 4 分)设 AD=MN=xcm ,∴ ∠ B=∠ DEC 则 AD+BC=AD+BM+MN+NC=2x+4=10 ,∴AB ∥DE(5 分)解得: x=3,∴四边形 ABED 是平行四边形( 6 分)∴ BC=2+x+2=7 ;∴ AD=BE ( 7 分)∴梯形的面积 S= = =10cm 2.9.∵ AD ∥BC ,∠ DAC=45 °,∴ ∠ ACB=45 °∵AE⊥BC,,∴,∵ ∠ B=60 °,∴BE=1 , AB=2 ,∴DC=2 ,作 DF⊥ BC 于点 F,∴四边形 AEFD 是矩形,∴AE=DF ,∵ ∠ B=∠ C,∠AEB= ∠DFC=90 °,∴ △ ABE ≌△ DCF (AAS ),∴BE=FC=1 ,∴,答: BC=7cm ,梯形的面积10cm2.11.(1)∵BD⊥ CD 于 D,∴ ∠ BDC=90 °,∵ ∠ C=60 °,∴ ∠ DBC=180 °﹣ 90°﹣60°=30°;(2)如图,过 D 作 DE ∥ AB 交 BC 于点 E,∵AD ∥BC,∴四边形 ABED 是平行四边形,∴AD=BE ,AB=DE ,∵ AB=DC ,∴DC=DE ,∵ ∠ C=60 °,∴ △ CDE 是等边三角形,∴CE=DC=6cm ,在 Rt△ BCD 中,∵∠ DBC=30 °,DC=6cm ,∴BC=2DC=2 ×6=12cm,∴BE=BC ﹣ CE=12 ﹣ 6=6cm,∴AD 的长为 6cm.12.∵四边形 ABCD 是等腰梯形, AB ∥ DC,∴AD=BC ,∠DBA= ∠CDB ,又 BD 平分∠ABC ,∴∠ CBD= ∠ DBA ,∴∠ CDB= ∠ CBD ,∴CD=BC ,又 AB=2AD ,AB+AD+CD+BC=40,∴2AD+AD+AD+AD=40 ,5AD=40 ,AD=8 ,∴CD=8 , AB=16 ,即梯形腰长为8,两底边长为8 和 16,答:梯形的腰长是8,两底边的长分别是8, 16 13.∵ AD ∥BC,∴∠DAC= ∠ACB ,∵AC 平分∠BCD ,∴∠DCA= ∠ACB ,∴∠DAC= ∠DCA ,∴AD=CD=AB=5cm ,∴等腰梯形 ABCD 的周长是AB+BC+CD+AD=5cm+5cm+5cm+9cm=24cm ,答:等腰梯形 ABCD 的周长是 24cm.14.法一:在梯形ABCD 中,∵AD ∥BC,AB=AC ,∴ ∠ ABC= ∠ DCB (等腰梯形同一底上的内角相等),∠A+ ∠ABC=180 °,又∵ ∠ DCE+ ∠ DCB=180 °,∴∠A=∠DCE ,∵DB=BE ,∴∠DBC= ∠E,∵∠ADB= ∠DBC,∴∠ADB= ∠E,在△ABD 和△CDE 中,,∴△ABD ≌△CDE(AAS ),∴AD=CE ;证法二:连接AC ,在梯形 ABCD 中,∵ AD ∥ BC, AB=AC ,∴ AC=BD (等腰梯形的对角线相等),∠ ABC= ∠DCB (等腰梯形同一底上的内角相等),在△ABC 和△DCB 中,,∴ △ ABC ≌ △DCB ( SAS),∴∠ACB= ∠ DBC,∵DB=BE ,∴∠DBC= ∠ E,∴∠ACB= ∠ E,∴AC ∥DE ,又∵ DE=BD ,∴DE=AC ,∴四边形 ACED 是平行四边形(一组对边平行的四边形是平行四边形),∴AD=CE .(平行四边形的对边相等).15.( 1)∵梯形 ABCD 是等腰梯形,∴AB=CD ,∵AD ∥BC , DE∥ AB ,∴四边形 ABED 是平行四边形,∴AB=CD=DE ,∵BD ⊥DC,∴∠ BDC=90 °,∵点 E 是 BC 边的中点,∴BE=DE=CE ,∴DE=DE=CE ,即△ CDE 是等边三角形,∴∠ BCD=60 °;(2)过点 D 作 DF⊥BC 于点 F,∵ △ CDE 是等边三角形,AB=CD=4 ,∴ DF=CD ?sin60°=4 × =2,∵AB=BE=CE=4 ,∴ BC=2AB=8 ,∴ S 梯形ABCD = ( AD6BC )?DF= ×( 4+8)×2 =1216.∵四边形 ABCD 是等腰梯形,∠ D=120°,∴ ∠ B= ∠ BCD=60 °,∵AC 平分∠BCD,∴ ∠ BCA= ∠ ACD=30 °,则∠ BAC=90 °,又∠ CAD= ∠BCA ,∴ ∠ CAD= ∠ACD ,则 AD=CD=AB ,在 Rt△ ABC 中,∵∠ BCA=30 °,∴BC=2AB=2AD ,∵中位线长为 6,∴AD+BC=3AD=12 ,∴AD=4 , BC=2AD=8 ,在 Rt△ ABC 中,由勾股定理,得,作 AE⊥BC 于 E,则,∴ 梯形的面积为,答: AC 的长是 4,梯形的面积是12.17.∵等腰梯形ABCD ,∴BC=AD ,∠CBE= ∠ DAE .∵ E 是 AB 上的中点,∴BE=AE .∴△ CBE ≌△ DAE (SAS).∴DE=CE .18. OE=OF .理由:∵AE=BF ,∴AE+EF=BF+EF ,即 AF=BE .∵等腰梯形 ABCD 中, AB ∥ CD ,∴AD=CB ,∠A= ∠B .∴△ADF ≌△BCE .∴∠ DFE= ∠ CEF.∴OE=OF19.过点 A 作 AE ⊥BC 于 E,过点 D 作 DF⊥ BC 于 F,则四边形 AEFD 是矩形,所以 AD=EF , BE=FC因为∠ A=2 ∠ B,又∠ BAD+ ∠B=180 °,所以∠ B=60 °在 Rt△ AEB 中,因为∠ BAE=90 °﹣60°=30°,AB=2 ,所以 BE= AB=所以 AD=BC ﹣ 2BE=3 ﹣ 1×2=1.20.因为四边形 ABCD 是等腰梯形, AD ∥ BC,所以∠ A= ∠ ADC ,∠ ADC+ ∠C=180 °( 2 分)又∠ A=2 ∠ C,则 2∠ C+∠ C=180°,故∠ C=60°( 4 分)因为 BD ⊥ CD,BC=8cm ,所以,∠ DBC=180 °﹣90°﹣60°=30°(6 分)则 DC= BC=4cm ,即为所求.21.( 1)∵∠ ACB=42 °,∠ ACD=27 °,∴ ∠ BCD= ∠ BCA+ ∠ ACD=69 °;(2)∵∠ ABC= ∠ BAC=69 °,∴AC=BC=10cm ,又∵四边形 ABCD 是等腰梯形,∴BD=AC=10cm .22.∵四边形 ABCD 是等腰梯形,∴AB=DC ,∠ A= ∠ D.∵M 是 AD 的中点,∴AM=DM .在△ABM 和△ DCM 中,,∴ △ ABM ≌△ DCM ( SAS).∴MB=MC23.∵四边形 ABCD 是等腰梯形,∴∠B=∠BCD.∵AD ∥BC ,∴ ∠ DAC= ∠ACB ,∵AD=CD ,∴ ∠ ACD= ∠DAC ,∴∠ACB= ∠ DCA ,设∠ ACD=x ,则得到∠DAC= ∠ACB=x ,∠B= ∠ BAC=2x ,∴ ∠ B+ ∠ ACB+ ∠ BAC=180 °,即x+2x+2x=180 °,解得 x=36°,∴∠B=72°24. DE=CE .理由是:∵等腰梯形ABCD ,AB ∥ CD,∴∠A= ∠B,∵E 为 AB 的中点,∴AE=BE ,在△CBE 和△DAE 中,∴△CBE≌△DAE (SAS),∴DE=CE .25. 1)证明:过点 D 作 DF∥ AC ,交 BC 的延长线于点F,过点 D 作 DH ⊥BC 于点 H,∵AD ∥BC ,∴四边形 ACFD 是平行四边形,∴CF=AD ,DF=AC ,∵AC ⊥BD ,AE⊥BC,∴DH=AE , DF ⊥BD ,∵ AB=CD ,∴AC=BD ,∴BD=DF ,∴△ BDF 是等腰直角三角形,∴BH=FH ,∴DH= BF= ( BC+CF )= (AD+BC ),∴AE= (AD+BC );(2)解:∵AC=10cm ,∴BD=DF=10cm ,在 Rt△ BDF 中, BF==10(cm),∴ AD+BC=BF=10cm,∴AE= BF=5 ( cm),∴ S 梯形ABCD = ( AD+BC )?AE=×10×5=50(cm2).26.∵四边形 AEBC 是平行四边形,AD=BC ,∴AD=BC=AE , BD=AC=BE ,在△AEB 和△ ADB 中,,∴△AEB ≌△ADB ,∴∠ABD= ∠ABE .27.( 1)等腰梯形 ABCD 中, AD ∥BC , AB=CD ,∴∠C=∠ABC ,∵BD 平分∠ABC ,∴ ∠ C=∠ ABC=2 ∠ DBC ,∵BD⊥DC,∴ ∠BDC=90 °,∴3∠ DBC=90 °,∴ ∠ DBC=30 °,∴ ∠ ABC= ∠ C=2∠ DBC=60 °;(2)∵AD ∥BC,∴∠ADB= ∠DBC,∵BD 平分∠ABC ,∴∠ABD= ∠DBC,∴∠ABD= ∠ADB ,∴ AB=AD=DC ,∵AD=3cm ,∴AB=DC=3cm ,在 Rt△ BDC 中,∠BDC=90 °,∠DBC=30 °, DC=3cm ,∴BC=2DC=6cm ,∴梯形 ABCD 的周长是AD+AB+BC+CD=3cm+3cm+6cm+3cm=15cm.28.∵在等腰梯形ABCD 中, AB=CD ,∴∠ABC= ∠ C,∵对角线 BD 平分∠ABC ,∴ ∠ DBC=∠ ABC=∠ C,∵AD ∥BC ,∴∠DBC= ∠ ADB ,∴ ∠ C=2∠ DBC ,∵BD ⊥CD ,∴∠ DBC=30 °,∴ BC=2CD ,∵梯形的周长 =AD+AB+BC+CD=5AB=30cm ,∴AB=AD=CD=6cm , BC=12cm29.( 1)∵ AD ∥BC, CE=AD ,∴四边形 ACED 为平行四边形∴DE ∥ AC ,DE=AC∵四边形 ABCD 是等腰梯形,∴AC=BD ,∴BD=DE ,∴∠ E=∠ DBE ,∵AC ⊥BD , AC ∥DE,∴DE⊥BD ,∴ ∠BDE=90 °,∴∠E=45°∵DE∥AC ,∴ ∠ E+∠ ACE=180 °,∴ ∠ ACE=135 °(2)∵ AD=CE ,∴BE=BC+CE=BC+AD=10cm ,∴ Rt△BDE 中,由勾股定理得:BD2+DE2=BE2,又∵ BD=DE ,∴ BD2=50,∴ S△BDE =cm2.30.( 1)线段 AC 与 BC 的位置关系是:AC ⊥ BC ,理由是:∵等腰梯形ABCD ,∠ ADC=120 °,∴ ∠ DAB= ∠CBA=60 °,又由 AD=DC ,∠ADC=120 °,∴ ∠ DAC=30 °,∴ ∠ CAB=30 °,∴ ∠ ACB=90 °,即 AC⊥BC .(2)过 C 作 CE∥AD 交 AB 于 E,∵DC ∥AB , CE∥ AD ,AD=DC ,∴四边形 ADCE 是菱形,又∠ CBA=60 °,△ CBE 为等边三角形,作 CF⊥AB 于 F,∴,则梯形 ABCD 的面积为cm2,答:梯形 ABCD 的面积是 12 cm 2.等腰梯形的性质---11。
等腰梯形的性质定理和判定定理及其证明同步练习教师

等腰梯形性质和判定定理及其证明水平测试第1题.如图,在梯形ABCD 中,AD BC ∥,AB DC AD ==,60C ∠=°,AE BD ⊥于点1E AE =,,求梯形ABCD 的高.答案:解:作DF BC ⊥于点F . 因为AD BC ∥,所以12∠=∠. 因为AB AD =,所以23∠=∠. 所以13∠=∠.又因为AB DC =,60C ∠=,所以11133022ABC C ∠=∠=∠=∠=.又因为AE BD ⊥于点E ,1AE =,所以2AB DC ==. 在Rt CDF △中,由正弦定义,可得DF = 所以梯形ABCD第2题.下列命题中,错误的是( ) 答案:B A .矩形的对角线互相平分且相等 B .对角线互相垂直的四边形是菱形 C .等腰梯形的两条对角线相等D .等腰三角形底边上的中点到两腰的距离相等第3题. 如图,45AOB ∠=,过OA 上到点O 的距离分别为1357911,,,,,,的点作OA 的垂线与OB 相交,再按一定规律标出一组黑色梯形的面积(如图所示1234S S S S ,,,,)写出第10个黑色梯形的面积10S = .答案:76第4题.用含30角的两块同样大小的直角三角板拼图形,下列四种图形:①平行四边形,②菱形,③矩形,④直角梯形.其中可以被拼成的图形是( )答案:B A .①② B .①③ C .③④ D .①②③第5题.顺次连接等腰梯形四边中点所得到的四边形是( ) 答案:D A.等腰梯形B.直角梯形C.矩形D.菱形BCBC第6题.已知梯形的两底边长分别为6和8,一腰长为7,则另一腰长a 的取值范围是 .答案:5<a <9第7题.如图,在等腰梯形ABCD 中,AD BC ∥,60B ∠=,AD AB =.点E F ,分别在AD ,AB 上,AE BF =,DF 与CE 相交于P ,则DPE ∠=。
答案:120第8题.如图,在等腰梯形ABCD 中,AD ∥BC ,AB=DC ,点E 是BC 边的中点,EM ⊥AB ,EN ⊥CD ,垂足分别为M 、N . 求证:EM=EN答案:因为AD ∥BC ,AB=DC ,所以B C ∠=∠……………………………2分 因为,,EM AB EN CD ⊥⊥所以90BME CNE ∠=∠=︒……………3分在Rt △BME 和Rt △CNE 中,BME CNE B C BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,所以Rt △BME ≌ Rt △CNE ………………………7分 所以EM =EN …………………………………8分 第9题.如图,在直角梯形A B中,1c m A B C D A D C D A B A D ==∥,⊥,,,4c CD =,则BC = cm .第10题. 如图,在平行四边形ABCD 中,点E F ,分别在AB CD ,上移动,且AE CF =,则四边形BFDE 不可能...是( )答案:C A .矩形 B .菱形C .梯形D .平行四边形第11题. 如图,四边形ABCD 是矩形,F 是AD 上一点,E 是CB 延长线上一点,且四边形AECF 是等腰梯形.下列结论中不一定...正确的是( ) A.AE FC =B.AD BC = C.AEB CFD ∠=∠ D.BE AF =答案:D第12题.下列说法正确的是( )答案:C A .有两个角为直角的四边形是矩形 B .矩形的对角线互相垂直 C .等腰梯形的对角线相等D .对角线互相垂直的四边形是菱形ENMDCBABCDA第13题. 如图,将一张等腰直角三角形纸片沿中位线剪开可以拼成不同形状的四边形,请写出其中一种四边形的名称.答案:平行四边形、矩形、等腰梯形(三种中任选一种均给满分)第14题. 如图,将一张等腰直角三角形纸片沿中位线DE 剪开后,可以拼成的四边形是( )答案:DA .矩形或等腰梯形B .矩形或平行四边形C .平行四边形或等腰梯形D .矩形或等腰梯形或平行四边形第15题.已知:如图,在等腰ABC △中,AB AC =,BD AC ⊥,CE AB ⊥, 垂足分别为点D ,E ,连接DE .求证:四边形BCDE 是等腰梯形.答案:证明:在等腰ABC △中,AB AC =,ABC ACB ∴∠=∠.CE AB ⊥,BD AC ⊥,90BEC CDB ∴∠=∠=.又BC CB =,BEC CDB ∴△≌△. 3分BE CD ∴=.AE AD ∴=.AED ADE ∴∠=∠.AED ABC ∴∠=∠.ED BC ∴∥. 5分 又BE CD ,不平行,∴四边形BCDE 是梯形.7分∴四边形BCDE 是等腰梯形.(理由:同一底上的两底角相等的梯形是等腰梯形,或两腰相等的梯形是等腰梯形) 8分第16题.如图,在正六边形ABCDEF 中,对角线AE 与BF 相交于点M ,BD 与CE 相交于点N . (1)观察图形,写出图中两个不同形状....的特殊四边形; (2)选择(1)中的一个结论加以证明. 答案:解:(1)矩形ABDE ,矩形BCEF ; 或菱形BNEM ;或直角梯形BDEM ,AENB 等. 4分(2)选择ABDE 是矩形. 证明:ABCDEF 是正六边形,120AFE FAB ∴==∠∠,30EAF ∴=∠,90EAB FAB FAE ∴=-=∠∠∠.5分同理可证90ABD BDE ==∠∠.∴四边形ABDE 是矩形.7分选择四边形BNEM 是菱形.ADECBAD CB E证明:同理可证:90FBC ECB ==∠∠,90EAB ABD ==∠∠,BM NE ∴∥,BN ME ∥.∴四边形BNEM 是平行四边形.BC DE =,30CBD DEN ==∠∠,BNC END =∠∠, BCN EDN ∴△≌△. BN NE ∴=.∴四边形BNEM 是菱形.7分选择四边形BCEM 是直角梯形.证明:同理可证:BM CE ∥,90FBC =∠,又由BC 与ME 不平行, 得四边形BCEM 是直角梯形. 7分第17题.下列三角形纸片,能沿直线剪一刀得到等腰梯形的是( )第18题.把长为8cm 的矩形按虚线对折,按图中的虚线剪出一个直角梯形,打开得到一个等腰梯形,剪掉部分的面积为6cm 2,则打开后梯形的周长是( )答案:AA .(cm B .(cm C .22cm D .18cm第19题. (内蒙呼和浩特课改,3分)如图在梯形ABCD 中,AD BC ∥,BC BD =,120A ∠=.则C ∠=度.答案:755070A .50 80B .50100C .50 D .C第20题. 如图1,ABC △是直角三角形,如果用四张与ABC △全等的三角形纸片恰好拼成一个等腰梯形,如图2,那么在Rt ABC △中,ACAB的值是.答案:2第21题.如图,在等腰梯形ABCD 中,AB CD ∥,对角线AC 平分602cm BAD B CD ∠∠==,,,则梯形ABCD 的面积为( )2cm A.B .6C.D .12答案:A第22题.如图,在梯形ABCD 中,AD BC ∥,对角线BD 平分ABC ∠,BAD ∠的平分线AE 交BC 于E F G ,,分别是AB AD ,的中点. (1)求证:EF EG =;(2)当AB 与EC 满足怎样的数量关系时,EG CD ∥?并说明理由. 答案:(1)证明:AD BC ∥DBC ADB ∴∠=∠又ABD DBC ∠=∠ABD ADB ∴∠=∠ AB AD ∴=2分又12AF AB =,12AG AD = AF AG ∴=3分又BAE DAE ∠=∠,AE AE =AFE AGE ∴△≌△EF EG ∴=5分 (2)当2AB EC =时,EG CD ∥6分2AB EC =2AD EC ∴=12GD AD EC ∴== 7分又GD EC ∥∴四边形GECD 是平行四边形EG CD ∴∥8分AC B图1图2BE C DGA FBECDGAF第23题. 如图,梯形ABCD 中,AD BC ∥,45B =∠,120D =∠,8cm AB =,则DC 的长为( ) A.3B.3C.D .8cm 答案:A第24题.在等腰梯形ABCD 中,5AB DC AD BC ==∥,,713DC AB ==,,点P 从点A 出发,以3个单位/s 的速度沿AD DC →向终点C 运动,同时点Q 从点B 出发,以1个单位/s 的速度沿BA 向终点A 运动.在运动期间,当四边形PQBC 为平行四边形时,运动时间为( )答案:AA .3sB .4sC .5sD .6s第25题.如图,在等腰梯形ABCD 中,AB CD ∥,E F ,是边AB 上两点,且AE BF =,DE 与CF 相交于梯形ABCD 内一点O .(1)求证:OE OF =;(2)当EF CD =时,请你连接DF CE ,,判断四边形DCEF 是什么样的四边形,并证明你的结论. 答案:(1)证明:梯形ABCD 为等腰梯形,AB CD ∥,∴AD BC =,A B ∠=∠.2分AE BF =,∴ADE BCF △≌△.3分 ∴DEA CFB ∠=∠.∴OE OF =.4分(2)当DC EF =时,四边形DCEF 是矩形. 5分证明:DC EF ∥且DC EF =.∴四边形DCEF 是平行四边形.6分 又由(1)得ADE BCF △≌△,∴CF DE =.7分 ∴四边形DCEF 是矩形.8分评分说明:判断四边形DCEF 为平行四边形,并说理正确的,得2分第26题. 如图,已知等腰梯形ABCD 中,AD BC ∥,110A =∠,则C =∠( ) A.90 B.80C.70D.60 答案:C第27题. 如图,梯形ABCD 中,AB ∥CD ,AD = CD ,E 、F 分别是AB 、BC 的中点,若∠1 = 35︒,则∠D = .答案:110︒ABCDABQAB CDOFEB FEA D CB第28题.如图,等腰梯形ABCD 中,AD BC ∥,点E 是AD 延长线上一点,DE BC =.(1)求证:E DBC ∠=∠;(2)判断ACE △的形状(不需要说明理由). 答案:(1)AD BC ∵∥,BCD EDC ∠=∠∴. 1分B C D E =∵,BCD EDC ∠=∠,CD DC =,B C D E D ∴△≌△.3分 E D B C∠=∠∴. 2分 另证:DE BC ∵∥,DE BC =, 2分 B C E D∴是平行四边形. 2分 E DBC ∠=∠∴.2分(2)ACE △是等腰三角形. 2分第29题.我们学习了四边形和一些特殊的四边形,右图表示了在某种条件下它们之间的关系. 如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行. 那么请你对标上的其他6个数字序号写出相对应的条件.答案:③——相邻两边垂直; ④——相邻两边相等; ⑤——相邻两边相等; ⑥——相邻两边垂直; ⑦——两腰相等;⑧——一条腰垂直于底边.D A BC E。
等腰梯形的性质与判定 试题

等腰梯形的性质与判定 试题一、选择题1 .下列命题错误的是( )A.矩形是平行四边形;B.相似三角形一定是全等三角形C.等腰梯形的对角线相等D.两直线平行,同位角相等2 .顺次连结等腰梯形各边中点得到的四边形是A 矩形B 菱形C 正方形D 平行四边形 3 .如图,锐角三角形ABC 中(AB>AC),AH⊥BC,垂足为H,E 、D 、F 分别是各边的中点,则四边形EDHF 是( )A.梯形B.等腰梯形C.直角梯形D.矩形4 .等腰梯形的下底是上底的3倍,高与上底相等,这个梯形的腰与下底所夹角的度数为A.30°B.45°C.60°D.135°5 .若等腰梯形的两底差等于一腰长,那么它的腰与下底的夹角为A.︒30B.︒45C.︒60D.︒756 .等腰梯形的腰长为13cm,两底差为10cm,则高为 ( )A 、69cmB 、12cmC 、69cmD 、144cm7 .在等腰梯形ABCD 中,AD∥BC,AD=3,BC=7,AB=CD,E 为CD 的中点,四边形ABED 的周长与△BCE 的周长之差为2,则AB 的长为( ).A.8B.3C.6D.78 .如图8,等腰梯形ABCD 中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD 的面积是(•)二、填空题9 .如图1,请写出等腰梯形ABCD(AB∥CD)特有而一般梯形不具有的三个特征: ________,________,________.10.等腰梯形ABCD 中,AD∥BC,AB=6,AD=5,BC=8,且AB∥DE,则△DEC 的周长是____________.11.等腰梯形的对角线互相垂直,若高为8,则梯形的面积是_______.12.如图 2所示,在等腰梯形ABCD 中,∠B=450,已知腰长是3cm,则∠ADC=______度,高DE=_____。13.等腰梯形ABCD 中,AB∥CD,对角线AC 与BD 相交与O,请写出图中一对相等的线段___________。14.顺次连结等腰梯形四边的中点,所得四边形是____________;15.等腰梯形的一个锐角为60°, 一腰长为24cm,•一底长为39cm,•则另一底长为_______. 16.若等腰梯形ABCD 的上、下底之和为4,并且两条对角线所夹锐角为60,则该等腰梯形的面积为___________(结果保留根号的形式).三、解答题17.如图,在等腰梯形ABCD 中,AB ∥CD ,延长底边AB 到E ,使得BE =DC .求证:AC =CE.18.如图,将等腰梯形ABCD 的一条对角线BD 平移到CE 的位置,(1)试猜猜线段AE 与AD 、BC有怎样的数量关系?为什么?(2)ΔACE 是等腰三角形吗?为什么?19.如图,等腰梯形ABCD 中,AB∥CD,AD=BC,对角线AC⊥BD 于O,若DC=4cm,AB=9cm 。求梯形的高。O DCB A A B CDE答案一、选择题1 .B点拨:两三角形全等是两三角形,相似的一种特例,所以全等一定相似,但相似不一定全等.2 .B3 .B4 .B5 .C6 .A;7 .C 解析:如图所示,四边形ABCD的周长=AB+BE+DE+AD,△BCE的周长=BC+EC+BE,两者之差为2,即AB+BE+DE+AD-(BC+EC+BE)=AB+AD-BC=AB+3-7=2,所以AB=6.BEDC A8 .A二、填空题9 .略10.15 ;11.解析:如图所示,过点D分别作DF⊥BC于F点,DE∥AC交BC•延长线于点E.∵梯形ABCD,AD∥BC,∴四边形ACED是平行四边形,∴DE=AC,AD=CE.∵AB=CD,∴AC=BD(等腰梯形对角线相等),∴BD=DE.∵BD⊥AC,∴BD⊥DE,∴∠DBF=∠DEF=45°,∴DF=BF=FE.∴S梯形ABCD=12(AD+BC)DF=12BE×DF=12(2DF)×DF=DF2.∵DF=8,∴S梯形ABCD=64. 答案:64BE DC A F 12.323 13.AC=BD 等;14.菱形15.如图所示,过D 点作DE∥AB 交BC 于点E.∵AD∥BC,∴四边形ABED 是平行四边形,∴∠DEC=∠B,∴AB=ED,AD=BE.∵∠B=∠C=60°,AB=DC=24cm,∴△ECD 是等边三角形,∴CD=ED=E C=24cm.若AD=39cm,则BC=BE+EC=AD+EC=63cm;若BC=39cm,则AD=BE=BC-EC=15cm,且均符合三边关系定理,∴另一底长应为63cm 或15cm.答案:63cm 或15cmBE DC A 16.三、解答题 17.证明:在等腰梯形ABCD 中∵ AB ∥CD AD =CB ,∴ ∠DAB =∠CBA又 ∵∠CDA +∠DAB =180°∠CBA +∠CBE =180°∴∠CDA=∠CBE又∵ BE=DC∴△ADC ≌△CBE∴AC =CE18.(1) AE=AD+BC ∵BD平移到CE ∴ 四边形DBCE是平行四边形∴ DE=BC ∴AE=AD+DE=AD+BC 。(2) ∵ BD=CE AC=BD ∴AC=CE ∴△ACE是等腰三角形。19.解:过C作CE∥BD交AB的延长线于E,过C作CF⊥AB于FAB∥CD, CE∥BD∴CE=BD , BE=CD=4等腰梯形ABCD中,AC=BD ∴CE=ACAC⊥BD, CE∥BD ∴CE⊥AC∴△ACE是等腰直角三角形∴CF=12AE=12(AB+BE)∵AB=9cm ∴CF=12(9+4)=132cm即梯形的高为132cm。。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形等腰梯形等腰梯形的性质【基础练习】1.等腰梯形中,下面判断正确的是()A.两底角相等B.两个角相等C.同底上两底角互补D.对角线交点在对称轴上2.对角线互相垂直平分的四边形一定是()A.矩形B.菱形C.等腰梯形D.直角梯形3.等腰梯形的上底、下底、高之比为1∶3∶1,则下底角的度数是()A. 30°B. 45°C. 60°D. 75°4.在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AD,则∠B等于()A. 30°B. 45°C. 60°D. 135°AD//,AC与BD交于O点,图中全等三角形有()5.等腰梯形ABCD中,BCA. 两对B. 四对C一对 D. 三对6.等腰梯形中,下列判断正确的是()A. 两底相等B. 两个角相等C. 同底上两底角互补D. 对角线交点在对称轴上7.下列命题中:①有两个角相等的梯形是等腰梯形②有两条边相等的梯形是等腰梯形③两条对角线相等的梯形是等腰梯形④等腰梯形上、下底中点连线,把梯形分成面积相等的两部分其中真命题有()A. 1个B. 2个C. 3个D. 4个8.若等腰梯形两底之差等于一腰的长, 那么这个梯形一内角是()A. 90°B. 60°C. 45°D. 30°9. 若等腰梯形的三边长分别是3、4、11,则这个等腰梯形的周长是( )A .21B .29C .21或29D .21或22或29 10. 若等腰梯形两底之差的一半等于它的高,那么这个梯形一底角是( )A .30° B.45° C. 60° D. 75°11. 在课外活动课上,老师让同学们做一个对角线互相垂直的等腰梯形状的风筝,其面积是450cm 2,则对角线所用的竹条至少需要( )A.230 B.30 C.60 D.26012. 如图,把长为8cm 的矩形按虚线对折,按图中的虚线剪出一个直角梯形,打开得到一个等腰梯形,剪掉部分的面积为6cm 2,则打开后梯形的周长是( )A .(10+213)cmB .(10+13)cmC .22cmD .18cm 13. 若等腰梯形的两底差等于一腰长,那么它的腰与下底的夹角为( )A.︒30B.︒45C.︒60D.︒75 14. 等腰梯形的腰长为13cm,两底差为10cm,则高为 ( )A 、69cmB 、12cmC 、69cmD 、144cm15. 在等腰梯形ABCD 中,AD ∥BC,AD=3,BC=7,AB=CD,E 为CD 的中点,四边形ABED 的周长与△BCE 的周长之差为2,则AB 的长为( ). A.8 B.3 C.6 D.716. 如图8,等腰梯形ABCD 中,AB ∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD 的面积是( A.1615 B.165 C.3215 D.16173cm3cm(12题图)17. 如图,等腰梯形ABCD 中,AB ∥CD ,AC ⊥BC ,点E 是AB 的中点,EC ∥AD ,则∠ABC等于( )A. 75°B. 70°C. 60°D. 30°18. 如图,已知等腰梯形ABCD 中,AD ∥BC ,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( ) A. 19B. 20C. 21D. 2219. 如图,在等腰梯形ABCD 中,AB ∥CD ,对角线AC 平分∠BAD ,∠B ︒=60,CD=2cm ,则梯形ABCD 的面积为A. 2cm 33B. 2cm 6C. 2cm 36D. 2cm 1220. 等腰梯形的上底、下底和腰长分别为4cm 、10cm 、6cm ,则等腰梯形的下底角为_____. 21. 如图,在等腰梯形ABCD 中,AD ∥BC ,AB≠AD ,对角线AC ,BD 相交于点O ,如下四个结论:①梯形ABCD 是轴对称图形;②∠DAC=∠DCA ;③△AOB ≌△DOC.请把其中正确结论的序号填在横线上:________.22. 在四边形ABCD 中,AD ∥BC ,AD≠BC ,若使它成为等腰梯形,则可添加的条件是_________(只写一个即可)23. 等腰梯形ABCD 中,对角线AC 、BD 相交于点O ,那么图中的全等三角形最多有________对.24. 等腰梯形的腰与上底相等且等于下底的一半,则梯形的对角线与下底的夹角是________.25. 等腰梯形的腰长是5cm ,上、下底的长分别是6cm 和12cm ,则它的面积是________cm 2. 26. 如图,在梯形ABCD 中,AD ∥BC ,AB=DC=4cm ,BD 平分∠ABC ,∠C=60°,则梯形的周长是___________cm.27. 如图1,请写出等腰梯形ABCD(AB ∥CD)特有而一般梯形不具有的三个特征:________,________,________.28. 等腰梯形的对角线互相垂直,若高为8,则梯形的面积是_______.29. 如图 2所示,在等腰梯形ABCD 中,∠B=450,已知腰长是3cm,则∠ADC=______度,高DE=_____。30. 等腰梯形ABCD 中,AB ∥CD,对角线AC 与BD 相交与O,请写出图中一对相等的线段___________。C BAD(8题图)AB CDEAB CDODCBA31.顺次连结等腰梯形四边的中点,所得四边形是____________;32.等腰梯形的一个锐角为60°,一腰长为24cm,一底长为39cm,则另一底长为_______.33.若等腰梯形ABCD的上、下底之和为4,并且两条对角线所夹锐角为60o,则该等腰梯形的面积为___________(结果保留根号的形式).34.等腰梯形的腰长为5cm,上、下底的长分别为6cm和12cm,则它的面积为_______.35.如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠ADC=120°.求证:(1)BD⊥DC;(2)若AB=4,求梯形ABCD的面积.36.已知等腰梯形的一个底角为60°,它的两底分别是6 cm、16 cm.求这个等腰梯形的周长.37.如图,等腰梯形ABCD中,AD∥BC,AB=CD=AD,BD⊥CD,试求这个等腰梯形的各个内角的度数。
38.如图,等腰梯形ABCD,对角线AC与BD互相垂直,且AC=12,求梯形ABCD的面积.39. 如图,等腰梯形ABCD 中,AD ∥BC ,AB=DC ,AC ⊥BD ,过D 点作DE ∥AC 交BC的延长线于E 点。
(1)求证:四边形ACED 是平行四边形;(4分)(2)若AD=3,BC=7,求梯形ABCD 的面积;(8分)40. 如图,在等腰梯形ABCD 中,AD ∥BC ,∠C=60°,AD=CD.E 、F 分别在AD 、CD 上,DE=CF ,AF 、BE 交于点P ,求∠BPF 的度数.【培优练习】41. 在等腰梯形ABCD 中,AD//BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别是E 、F ,AD=4,BC=8,则AE+EF 等于( ) A .9 B .10 C .11 D .12B PF DC AEFE CBDAA DCCDB A42. 如图,在梯形ABCD 中,AB ∥CD ,AD=BC ,点E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,则下列结论一定正确的是( ) A .∠HGF=∠GHEB .∠GHE=∠HEFC .∠HEF=∠EFGD .∠HGF=∠HEF43. 如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别为E 、F ,AD=4,BC=8,则AE+EF 等于( ) A .9B .10C .11D .1244. 如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别为E ,F ,设AD=a ,BC=b ,则四边形AEFD 的周长是( ) A .3a+bB .2(a+b )C .2b+aD .4a+b45. 已知:如图,梯形ABCD 是等腰梯形,AB ∥CD ,AD=BC ,AC ⊥BC ,BE ⊥AB 交AC的延长线于E ,EF ⊥AD 交AD 的延长线于F ,下列结论:①BD ∥EF ;②∠AEF=2∠BAC ;③AD=DF ;④AC=CE+EF .其中正确的结论有( ) A .1个B .2个C .3个D .4个46. 等腰梯形的一个底角是65°,则它的其余三个角是_________. 47. 如图,在等腰梯形ABCD 中,AD ∥BC ,AD=5,BC=9,∠C=60°⑴AB= ;⑵梯形ABCD 的周长= .48.用下面的方法来证明:在同一底上的两个角相等的梯形是等腰梯形.(1)如图1,分别延长梯形ABCD的腰BA,CD,设它们相交于点E. 通过证明△EAD 和△EBC都是________三角形来证明.图1图2(2)如图2,作梯形ABCD的高AE,DF,通过证明Rt△ABE≌Rt△DCF来证明定理.49.已知等腰梯形的锐角等于60°,它的两底分别为15 cm,49 cm,求它的腰长. 在研究等腰梯形时,常常通过辅助线,使等腰梯形与等腰三角形联系起来. 想一想,用怎样的辅助线可以在等腰梯形中划出等腰三角形.50.如图,将等腰梯形ABCD的一条对角线BD平移到CE的位置,(1)试猜猜线段AE与AD、BC有怎样的数量关系?为什么?(2)ΔACE是等腰三角形吗?为什么?51.如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)求证:四边形EFGH是正方形;(2)若AD=2,BC=4,求四边形EFGH的面积.52.如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE.(1)求证:AF=DE;(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长.53.如图,在等腰梯形ABCD中,AD=4,BC=9,∠B=45°.动点P从点B出发沿BC向点C运动,动点Q同时以相同速度从点C出发沿CD向点D运动,其中一个动点到达端点时,另一个动点也随之停止运动.(1)求AB的长;(2)设BP=x,问当x为何值时△PCQ的面积最大,并求出最大值;(3)探究:在AB边上是否存在点M,使得四边形PCQM为菱形?请说明理由.54.如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.(1)求证:△MDC是等边三角形;(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值?如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.11。
