高二空间几何练习题
高中必修二空间几何练习题及讲解

高中必修二空间几何练习题及讲解### 高中必修二空间几何练习题及讲解#### 练习题一:点、线、面的位置关系题目:在空间直角坐标系中,设点A(2, 3, 4),点B(-1, -2, 1),求证线段AB与平面x+y+z=6垂直。
解答:首先,我们需要找到线段AB的方向向量。
设向量\(\vec{AB} =\vec{b} - \vec{a}\),其中\(\vec{a} = (2, 3, 4)\),\(\vec{b} = (-1, -2, 1)\)。
计算得到\(\vec{AB} = (-3, -5, -3)\)。
接下来,我们观察平面x+y+z=6的法向量。
由平面方程可知,其法向量为\(\vec{n} = (1, 1, 1)\)。
要证明线段AB与平面垂直,需要证明\(\vec{AB} \cdot \vec{n} =0\)。
计算点积:\((-3) \times 1 + (-5) \times 1 + (-3) \times 1 = -3 - 5 - 3 = -11\)。
由于点积不为零,线段AB与平面x+y+z=6不垂直。
题目中的结论是错误的。
#### 练习题二:空间几何体的体积计算题目:已知一个正四面体的高为h,求其体积。
解答:正四面体的体积公式为\(V = \frac{1}{3}Bh\),其中B是底面积。
正四面体的底面是一个正三角形,设正四面体的边长为a,则底面积B 可以通过公式\(B = \frac{\sqrt{3}}{4}a^2\)计算。
由于正四面体的高h与边长a有如下关系:\(h =\frac{\sqrt{2}}{2}a\)。
将h代入体积公式,得到\(V = \frac{1}{3} \times\frac{\sqrt{3}}{4}a^2 \times \frac{\sqrt{2}}{2}a =\frac{\sqrt{2}}{12}a^3\)。
#### 练习题三:空间直线与平面的交点题目:已知直线l: \(x = 2t + 1\), \(y = 1 - t\), \(z = 3 - 4t\),平面π: \(2x - y + z - 5 = 0\),求直线l与平面π的交点。
高二数学提升练习题 (空间立体几何)1

A B 主视图 C 左视图 俯视图3 4 2 俯视图主视图 左视图空间立体几何三视图专题1一个三棱锥的三视图是三个直角三角形,如左图所示,那么该三棱锥的外接球的外表积为2.一个几何体的三视图如右图所示,其中,主视图中△ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为3.知一个空间几何体的三视图如下图,根据图中标出的尺寸〔单位:cm 〕,可得这个几何体的体积是___________cm 3.〔第4题〕4〔山东卷6〕右图是一个几何体的三视图,根据图中数据,可得该几何体的外表积是 5四棱锥P ABCD -的顶点P 在底面ABCD 中的投影恰好是A ,其三视图如右图,那么四棱锥P ABCD - 的外表积为__ .〔第6题〕6一个三棱锥的三视图是三个直角三角形,如下图那么该三棱锥的外接球的外表积为 .7一个几何体的三视图如下图,其中主视图、左视图均为上底为2,下底为4,腰为5 的等腰梯形,俯视图为一圆环,那么该几何体的体积为 .8.〔课本改编题,新增内容〕右图为一个几何体的三视图,尺寸如下图,那么该几何体的体积为 9据图中尺寸〔单位:cm 〕,可知这个几何体的外表积是342 俯视图 主视图 左视图2 2 主视图 2 4左视图俯视图〔第3图〕〔第9题〕〔第8题〕10图是一个空间几何体的三视图,其主视图、左视图均为正三角形,俯视图为圆,那么该几何体的侧面积为 .广东高考文科数学分类汇编--立体几何2021年广东高考文科数学左视图俯视图〔第7题222 C2313主视图左视图俯视图 2 2 〔10题〕18.〔本小题总分值14分〕如图4,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BED,FB=a5〔1〕证明:EB⊥FD〔2〕求点B到平面FED的距离.2021年广东高考文科数学6.给定以下四个命题:①假设一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②假设一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④假设两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是A.①和② B.②和③ C.③和④ D.②和④17.〔本小题总分值13分〕某高速公路收费站入口处的平安标识墩如图4所示,墩的上半局部是正四棱锥P -EFGH,下半局部是长方体ABCD -EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.〔1〕请画出该平安标识墩的侧(左)视图〔2〕求该平安标识墩的体积 〔3〕证明:直线BD ⊥平面PEG2021年广东高考文科数学7.将正三棱柱截去三个角〔如图1所示,A B C ,,分别是GHI △三边的中点〕得到几何体如图2,那么该几何体按图2所示方向的侧视图〔或称左视图〕为〔 〕18.〔本小题总分值14分〕如图5所示,四棱锥P ABCD -的底面ABCD 是半径为R 的圆的内接四边形,其中BD 是圆的直径,60ABD ∠=,45BDC ∠=,ADP BAD △∽△.〔1〕求线段PD 的长;〔2〕假设11PC R =,求三棱锥P ABC -的体积.E F DIA H GBC EF D AB C侧视 图1图2 BEA .BEB . BEC .BED .PAD2007年广东高考文科数学6.假设l m n ,,是互不一样的空间直线,αβ,是不重合的平面,那么以下命题中为真命题的是〔 〕 A.假设l n αβαβ⊂⊂,,∥,那么l n ∥B.假设l αβα⊥⊂,,那么l β⊥ C.假设l nm n ⊥⊥,,那么l m ∥D.假设l l αβ⊥,∥,那么αβ⊥17.〔本小题总分值12分〕某几何体的俯视图是如图5所示的矩形,正视图〔或称主视图〕是一个底边长为8,高为4的等腰三角形,侧视图〔或称左视图〕是一个底边长为6,高为4的等腰三角形. 〔1〕求该几何体的体积V ; 〔2〕求该几何体的侧面积S .图52021年广东高考文科数学 一、D二、 18.〔1〕证明: 点E 为弧AC 的中点2021年广东高考文科数学6.D7. 17.【解析】(1)侧视图同正视图,如右图所示. 〔2〕该平安标识墩的体积为:P EFGH ABCD EFGH V V V --==221406040203200032000640003=⨯⨯+⨯=+=()2cm 〔3〕如图,连结EG,HF 及 BD ,EG 与HF 相交于O,连结PO. 由正四棱锥的性质可知,PO ⊥平面EFGH ,PO HF ∴⊥ 又EG HF ⊥ HF ∴⊥平面PEG 又BD HF BD ∴⊥平面PEG ;2021年广东高考文科数学 7.A 18.解:〔1〕BD 是圆的直径ADP BAD △∽△90BAD ∴∠=,又ADP BAD △∽△,AD DP BA AD ∴=,22234(sin 60)431(sin 30)22R AD BD DP R BA BD R ⨯====⨯; 〔2〕在Rt BCD △中,cos 452CD BD R ==2222229211PD CD R R R PC +=+==PD CD ∴⊥,又90PDA ∠= PD ∴⊥底面ABCD2113211sin(6045)22222224ABC S AB BC R R R ⎛⎫=+=⨯+⨯= ⎪ ⎪⎝⎭△ 三棱锥P ABC -的体积为2311313133344P ABC ABC V S PD R R R -++===△ 2007年广东高考文科数学二、D17解: 由可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥V -ABCD;(1) ()1864643V =⨯⨯⨯= (2) 该四棱锥有两个侧面VAD 、VBC 是全等的等腰三角形,且BC 边上的高为1h ==另两个侧面VAB. VCD 也是全等的等腰三角形,AB 边上的高为 25h ==因此 112(685)4022S =⨯⨯⨯⨯=+.C PA B 图5D,,,A B A x B y f B A B x y x f y y x y →映射定义:设,是两个非空的集合,如果按某一个确定的对应关系,使对于集合中的任意一个元素, 在集合中都有唯一确定的元素与之对应,那么就称对应:为从集合到集合的一个映射传统定义:如果在某变化中有两个变量并且对于在某个范围内的每一个确定的值,定义 按照某个对应关系都有唯一确定的值和它对应。
高二数学空间几何体试题答案及解析

高二数学空间几何体试题答案及解析1.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有( )A.20B.15C.12D.10【答案】D【解析】由图可知对于上底面的每一个顶点,在下底面有两个顶点与其连线可成为五棱柱的对角线,故五棱柱的对角线的条数共有条.【考点】正五棱柱的几何特征.2.顶点在同一球面上的正四棱柱体ABCD-A1B1C1D1中,,,则两点间的球面距离为()A.B.C.D.【答案】B【解析】已知正四棱柱ABCD-A1B1C1D1的底面ABCD边长为1,高,它的八个顶点都在同一球面上,那么,正四棱柱ABCD-A1B1C1D1的对角线长为球的直径,中点O为球心.正四棱柱对角线AC1=2,则球的半径为1.根据题中所给数据,可得∠AOC=,则A,C两点的球面距离为。
选B.【考点】正四棱柱及其外接球的几何特征,球面距离的概念。
点评:简单题,关键是认识到:正四棱柱ABCD-A1B1C1D1的八个顶点都在同一球面上,得到正四棱柱ABCD-A1B1C1D1的对角线长即为球的直径。
3.设长方体的三条棱长分别为、、,若长方体所有棱长度之和为,一条对角线长度为,体积为,则等于( ).A.B.C.D.【答案】A【解析】设长方体的长、宽、高分别为a,b,c,由题意可知,a+b+c=6…①,abc=2…②,a2+b2+c2=25…③,由①式平方-②可得ab+bc+ac=…④,④÷②得: =,故选A【考点】本题考查了长方体的有关知识点评:此类问题主要考查了点、线、面间的距离计算,考查空间想象能力、运算能力,是基础题.4.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于.【答案】【解析】设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,则OO1EO2为矩形,于是对角线O1O2=OE,而OE=,∴两圆心的距离O1O2=【考点】本题考查了球的有关概念,两平面垂直的性质.点评:求解本题,可以从三个圆心上找关系,构建矩形利用对角线相等即可求解出答案.5.(本题12分)如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,⑵证:平面A1CB⊥平面BDE;⑵求A1B与平面BDE所成角的正弦值。
(完整版)空间几何体练习题含答案
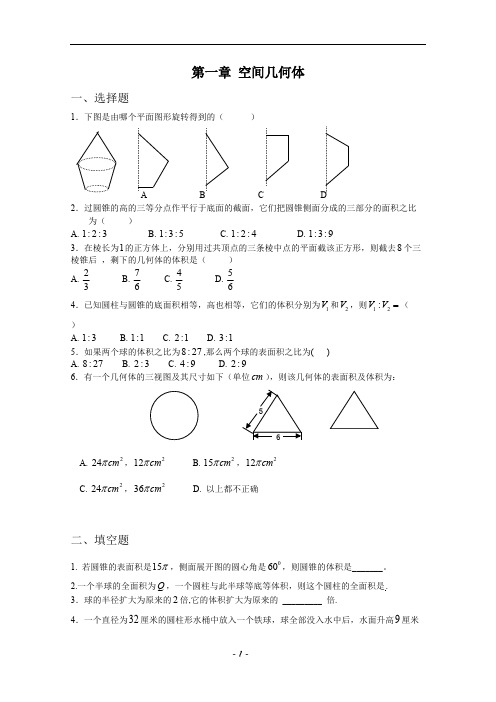
第一章空间几何体一、选择题1.下图是由哪个平面图形旋转得到的()A B C D2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A. B. C. D.1:2:31:3:51:2:41:3:93.在棱长为的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去个三18棱锥后,剩下的几何体的体积是()A. B. C. D.237645564.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为和,则(1V2V12:V V=)A. B. C. D.1:31:12:13:15.如果两个球的体积之比为,那么两个球的表面积之比为( )8:27A. B. C. D.8:272:34:92:96.有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及体积为:cmA. ,B. ,224cmπ212cmπ215cmπ212cmπC. ,D. 以上都不正确224cmπ236cmπ二、填空题1. 若圆锥的表面积是,侧面展开图的圆心角是,则圆锥的体积是_______。
15π0602.一个半球的全面积为,一个圆柱与此半球等底等体积,则这个圆柱的全面积是.Q3.球的半径扩大为原来的倍,它的体积扩大为原来的_________ 倍.24.一个直径为厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高厘米329则此球的半径为_________厘米.5.已知棱台的上下底面面积分别为,高为,则该棱台的体积为___________。
4,163三、解答题1. (如图)在底半径为,母线长为的圆柱,求圆柱的表面积242.如图,在四边形中,,,,,ABCD 090DAB ∠=0135ADC ∠=5AB =CD =,求四边形绕旋转一周所成几何体的表面积及体积.2AD =ABCD AD参考答案一、选择题1.A 几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得2.B 从此圆锥可以看出三个圆锥,123123::1:2:3,::1:2:3,r r r l l l == 12312132::1:4:9,:():()1:3:5S S S S S S S S =--=3.D 111115818322226V V -=-⨯⨯⨯⨯⨯=正方体三棱锥4.D 121:():()3:13V V Sh Sh ==5.C 121212:8:27,:2:3,:4:9V V r r S S ===6.A 此几何体是个圆锥,23,5,4,33524r l h S πππ====⨯+⨯⨯=表面 2134123V ππ=⨯⨯=二、填空题1. 设圆锥的底面半径为,母线为,则,得,r l 123r l ππ=6l r =,得,圆锥的高226715S r r r r ππππ=+⋅==r =h =21115337V r h ππ==⨯=2. 109Q 22223,S R R R Q R πππ=+===全 32222221010,,2233339V R R h h R S R R R R Q πππππ==⋅==+⋅==3. 821212,8r r V V ==4. 12234,123V Sh r h R R ππ=====5. 28'11()(416)32833V S S h =++=⨯+⨯= 三、解答题1.解:圆锥的高,h ==1r =22(2S SS πππ=+=+=侧面表面底面 2.解:S S S S=++表面圆台底面圆台侧面圆锥侧面25(25)2πππ=⨯+⨯+⨯⨯⨯1)π=+ V V V=-圆台圆锥222112211()331483r r r r h r h πππ=++-=。
高二空间几何练习题

练习1一、选择题:1.a 、b 是两条异面直线,以下结论正确的选项是〔〕 A .过不在a 、b 上的任一点,可作一个平面与a 、b 都平行 B .过不在a 、b 上的任一点,可作一条直线与a 、b 都相交 C .过不在a 、b 上的任一点,可作一条直线与a 、b 都平行 D .过a 可以且只可以作一个平面与b 平行2.空间不共线的四点,可以确定平面的个数为 ( )A.0B.1C.1或4D.无法确定3.在正方体1111ABCD A B C D -中,M 、N 分别为棱1AA 、1BB 的中点,那么异面直线CM 和1D N 所成角的正弦值为 ( ) A.19B.23C.459D.2594.平面α⊥平面β,m 是α内的一直线,n 是β内的一直线,且m n ⊥,那么:①m β⊥;②n α⊥;③m β⊥或n α⊥;④m β⊥且n α⊥。
这四个结论中,不正确...的三个是( ) A.①②③B.①②④C.①③④D.②③④5.一个简单多面体的各个面都是三角形,它有6个顶点,那么这个简单多面体的面数是 ( ) A. 4 B. 5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,那么甲、乙两地最短距离为〔设地球半径为R 〕 ( )A.R π42B. R 3πC. R 2πD. 3R7. 直线l ⊥平面α,直线m ⊂平面β,有以下四个命题: (1)m l ⊥⇒βα// (2)m l //⇒⊥βα(3)βα⊥⇒m l // (4)βα//⇒⊥m l 其中正确的命题是 ( ) A. (1)与(2) B. (2)与(4) C. (1)与(3) D. (3)与(4)8. 正三棱锥的侧面均为直角三角形,侧面与底面所成角为α,那么以下不等式成立的是 ( ) A. 60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9.ABC ∆中,9AB =,15AC =,120BAC ∠=︒,ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14,那么P 到平面α的距离为 ( ) A.7B.9C.11D.1310.在一个45︒的二面角的一个平面内有一条直线与二面角的棱成角45︒,那么此直线与二面角的另一个平面所成角的大小为 ( )A.30︒B.45︒C.60︒D.90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点,沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作D.给出以下位置关系: ①SD ⊥面DEF; ②SE ⊥面DEF; ③DF ⊥SE; ④EF ⊥面SED, 其中成立的有: () A. ①与② B. ①与③ C. ②与③ D. ③与④12. 某地球仪的北纬60度圈的周长为6πcm,那么地球仪的外表积为( )A. 24πcm 2B. 48πcm 2C. 144πcm 2D. 288πcm 2 二、填空题13. 直二面角α—MN —β中,等腰直角三角形ABC 的斜边BC ⊂α,一直角边AC ⊂β,BC 与β所成角的正弦值是46,那么AB 与β所成角大小为__________。
(完整版)高中数学必修2空间立体几何大题

必修2空间立体几何大题一.解答题(共18小题)1.如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB(3)求三棱锥V﹣ABC的体积.2.如图,三棱锥P﹣ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.(1)求三棱锥P﹣ABC的体积;(2)证明:在线段PC上存在点M,使得AC⊥BM,并求的值.3.如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.4.如图,直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面B1BCC1;(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F﹣AEC的体积.5.如图,在直三棱柱ABC﹣A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.6.如题图,三棱锥P﹣ABC中,平面PAC⊥平面ABC,∠ABC=,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥BC.(Ⅰ)证明:AB⊥平面PFE.(Ⅱ)若四棱锥P﹣DFBC的体积为7,求线段BC的长.7.如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;(Ⅱ)求三棱锥P﹣ABC体积的最大值;8.如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(Ⅰ)证明:平面AEC⊥平面BED;(Ⅱ)若∠ABC=120°,AE⊥EC,三棱锥E﹣ACD的体积为,求该三棱锥的侧面积.9.如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2,AA1=,BB1=2,点E和F分别为BC和A1C的中点.(Ⅰ)求证:EF∥平面A1B1BA;(Ⅱ)求证:平面AEA1⊥平面BCB1;(Ⅲ)求直线A1B1与平面BCB1所成角的大小.10.如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.(1)求证:MN∥平面BCD;(2)求证:平面BCD⊥平面ABC.11.如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.(1)求证:BF⊥AC;(2)若CE=1,∠CBE=30°,求三棱锥F﹣BCE的体积.12.如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.求证:(Ⅰ)EC⊥CD;(Ⅱ)求证:AG∥平面BDE;(Ⅲ)求:几何体EG﹣ABCD的体积.13.如图,已知三棱锥A﹣BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.(1)求证:DM∥平面APC;(2)若BC=4,AB=20,求三棱锥D﹣BCM的体积.14.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=,O为AC 与BD的交点,E为棱PB上一点.(Ⅰ)证明:平面EAC⊥平面PBD;(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.15.已知正四棱柱ABCD﹣A1B1C1D1,底面边长为,点P、Q、R分别在棱AA1、BB1、BC上,Q是BB1中点,且PQ∥AB,C1Q⊥QR(1)求证:C1Q⊥平面PQR;(2)若C1Q=,求四面体C1PQR的体积.16.如图,直三棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点.(1)证明BC1∥平面A1CD(2)设AA1=AC=CB=2,AB=2,求三菱锥C﹣A1DE的体积.17.如图甲,⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,且∠CBA=∠DAB=.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:(Ⅰ)求证:CB⊥DE;(Ⅱ)求三棱锥C﹣BOD的体积;(Ⅲ)在劣弧上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.18.如图:是直径为的半圆,O为圆心,C是上一点,且.DF⊥CD,且DF=2,,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.(Ⅰ)求证:面BCE⊥面CDF;(Ⅱ)求证:QR∥平面BCD;(Ⅲ)求三棱锥F﹣BCE的体积.必修2空间立体几何大题参考答案与试题解析一.解答题(共18小题)1.(2015?北京)如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB(3)求三棱锥V﹣ABC的体积.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定;平面与平面垂直的判定.专题:综合题;空间位置关系与距离.分析:(1)利用三角形的中位线得出OM∥VB,利用线面平行的判定定理证明VB∥平面MOC;(2)证明:OC⊥平面VAB,即可证明平面MOC⊥平面VAB(3)利用等体积法求三棱锥V﹣ABC的体积.解答:(1)证明:∵O,M分别为AB,VA的中点,∴OM∥VB,∵VB?平面MOC,OM?平面MOC,∴VB∥平面MOC;(2)∵AC=BC,O为AB的中点,∴OC⊥AB,∵平面VAB⊥平面ABC,OC?平面ABC,∴OC⊥平面VAB,∵OC?平面MOC,∴平面MOC⊥平面VAB(3)在等腰直角三角形ACB中,AC=BC=,∴AB=2,OC=1,∴S△VAB=,∵OC⊥平面VAB,∴V C﹣VAB=?S△VAB=,∴V V﹣ABC=V C﹣VAB=.点评:本题考查线面平行的判定,考查平面与平面垂直的判定,考查体积的计算,正确运用线面平行、平面与平面垂直的判定定理是关键.2.(2015?安徽)如图,三棱锥P﹣ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.(1)求三棱锥P﹣ABC的体积;(2)证明:在线段PC上存在点M,使得AC⊥BM,并求的值.考点:棱柱、棱锥、棱台的体积;点、线、面间的距离计算.专题:综合题;空间位置关系与距离.分析:(1)利用V P﹣ABC=?S△ABC?PA,求三棱锥P﹣ABC的体积;(2)过B作BN⊥AC,垂足为N,过N作MN∥PA,交PA于点M,连接BM,证明AC⊥平面MBN,可得AC⊥BM,利用MN∥PA,求的值.解答:(1)解:由题设,AB=1,AC=2,∠BAC=60°,可得S△ABC==.因为PA⊥平面ABC,PA=1,所以V P﹣ABC=?S△ABC?PA=;(2)解:过B作BN⊥AC,垂足为N,过N作MN∥PA,交PC于点M,连接BM,由PA⊥平面ABC,知PA⊥AC,所以MN⊥AC,因为BN∩MN=N,所以AC⊥平面MBN.因为BM?平面MBN,所以AC⊥BM.在直角△BAN中,AN=AB?cos∠BAC=,从而NC=AC﹣AN=.由MN∥PA得==.点评:本题考查三棱锥P﹣ABC的体积的计算,考查线面垂直的判定与性质的运用,考查学生分析解决问题的能力,属于中档题.3.(2015?黑龙江)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.考点:棱柱、棱锥、棱台的体积;平面的基本性质及推论.专题:综合题;空间位置关系与距离.分析:(Ⅰ)利用平面与平面平行的性质,可在图中画出这个正方形;(Ⅱ)求出MH==6,AH=10,HB=6,即可求平面a把该长方体分成的两部分体积的比值.解答:解:(Ⅰ)交线围成的正方形EFGH如图所示;(Ⅱ)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为EFGH为正方形,所以EH=EF=BC=10,于是MH==6,AH=10,HB=6.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.点评:本题考查平面与平面平行的性质,考查学生的计算能力,比较基础.4.(2015?湖南)如图,直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面B1BCC1;(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F﹣AEC的体积.考点:棱柱、棱锥、棱台的体积;平面与平面垂直的判定.专题:空间位置关系与距离.分析:(Ⅰ)证明AE⊥BB1,AE⊥BC,BC∩BB1=B,推出AE⊥平面B1BCC1,利用平面余平米垂直的判定定理证明平面AEF⊥平面B1BCC1;(Ⅱ)取AB的中点G,说明直线A1C与平面A1ABB1所成的角为45°,就是∠CA1G,求出棱锥的高与底面面积即可求解几何体的体积.解答:(Ⅰ)证明:∵几何体是直棱柱,∴BB1⊥底面ABC,AE?底面ABC,∴AE⊥BB1,∵直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E分别是BC的中点,∴AE⊥BC,BC∩BB1=B,∴AE⊥平面B1BCC1,∵AE?平面AEF,∴平面AEF⊥平面B1BCC1;(Ⅱ)解:取AB的中点G,连结A1G,CG,由(Ⅰ)可知CG⊥平面A1ABB1,直线A1C与平面A1ABB1所成的角为45°,就是∠CA1G,则A1G=CG=,∴AA1==,CF=.三棱锥F﹣AEC的体积:×==.点评:本题考查几何体的体积的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.5.(2015?江苏)如图,在直三棱柱ABC﹣A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.考点:直线与平面平行的判定;直线与平面垂直的性质.专题:证明题;空间位置关系与距离.分析:(1)根据中位线定理得DE∥AC,即证DE∥平面AA1C1C;(2)先由直三棱柱得出CC1⊥平面ABC,即证AC⊥CC1;再证明AC⊥平面BCC1B1,即证BC1⊥AC;最后证明BC1⊥平面B1AC,即可证出BC1⊥AB1.解答:证明:(1)根据题意,得;E为B1C的中点,D为AB1的中点,所以DE∥AC;又因为DE?平面AA1C1C,AC?平面AA1C1C,所以DE∥平面AA1C1C;(2)因为棱柱ABC﹣A1B1C1是直三棱柱,所以CC1⊥平面ABC,因为AC?平面ABC,所以AC⊥CC1;又因为AC⊥BC,CC1?平面BCC1B1,BC?平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1;又因为BC1?平面BCC1B1,所以BC1⊥AC;因为BC=CC1,所以矩形BCC1B1是正方形,所以BC1⊥平面B1AC;又因为AB1?平面B1AC,所以BC1⊥AB1.点评:本题考查了直线与直线,直线与平面以及平面与平面的位置关系,也考查了空间想象能力和推理论证能力的应用问题,是基础题目.6.(2015?重庆)如题图,三棱锥P﹣ABC中,平面PAC⊥平面ABC,∠ABC=,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥BC.(Ⅰ)证明:AB⊥平面PFE.(Ⅱ)若四棱锥P﹣DFBC的体积为7,求线段BC的长.考点:直线与平面垂直的判定;棱柱、棱锥、棱台的体积.专题:开放型;空间位置关系与距离.分析:(Ⅰ)由等腰三角形的性质可证PE⊥AC,可证PE⊥AB.又EF∥BC,可证AB⊥EF,从而AB与平面PEF内两条相交直线PE,EF都垂直,可证AB⊥平面PEF.(Ⅱ)设BC=x,可求AB,S△ABC,由EF∥BC可得△AFE≌△ABC,求得S△AFE=S△ABC,由AD=AE,可求S△AFD,从而求得四边形DFBC的面积,由(Ⅰ)知PE为四棱锥P﹣DFBC的高,求得PE,由体积V P﹣DFBC=S DFBC?PE=7,即可解得线段BC的长.解答:解:(Ⅰ)如图,由DE=EC,PD=PC知,E为等腰△PDC中DC边的中点,故PE⊥AC,又平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PE?平面PAC,PE⊥AC,所以PE⊥平面ABC,从而PE⊥AB.因为∠ABC=,EF∥BC,故AB⊥EF,从而AB与平面PEF内两条相交直线PE,EF都垂直,所以AB⊥平面PEF.(Ⅱ)设BC=x,则在直角△ABC中,AB==,从而S△ABC=AB?BC=x,由EF∥BC知,得△AFE≌△ABC,故=()2=,即S△AFE=S△ABC,由AD=AE,S△AFD==S△ABC=S△ABC=x,从而四边形DFBC的面积为:S DFBC=S△ABC﹣S AFD=x﹣x=x.由(Ⅰ)知,PE⊥平面ABC,所以PE为四棱锥P﹣DFBC的高.在直角△PEC中,PE===2,故体积V P﹣DFBC=S DFBC?PE=x=7,故得x4﹣36x2+243=0,解得x2=9或x2=27,由于x>0,可得x=3或x=3.所以:BC=3或BC=3.点评:本题主要考查了直线与平面垂直的判定,棱柱、棱锥、棱台的体积的求法,考查了空间想象能力和推理论证能力,考查了转化思想,属于中档题.7.(2015?福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;(Ⅱ)求三棱锥P﹣ABC体积的最大值;(Ⅲ)若BC=,点E在线段PB上,求CE+OE的最小值.考点:直线与平面垂直的判定;棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:(Ⅰ)由题意可证AC⊥DO,又PO⊥AC,即可证明AC⊥平面PDO.(Ⅱ)当CO⊥AB时,C到AB的距离最大且最大值为1,又AB=2,即可求△ABC面积的最大值,又三棱锥P﹣ABC的高PO=1,即可求得三棱锥P﹣ABC体积的最大值.(Ⅲ)可求PB===PC,即有PB=PC=BC,由OP=OB,C′P=C′B,可证E为PB中点,从而可求OC′=OE+EC′==,从而得解.解答:解:(Ⅰ)在△AOC中,因为OA=OC,D为AC的中点,所以AC⊥DO,又PO垂直于圆O所在的平面,所以PO⊥AC,因为DO∩PO=O,所以AC⊥平面PDO.(Ⅱ)因为点C在圆O上,所以当CO⊥AB时,C到AB的距离最大,且最大值为1,又AB=2,所以△ABC面积的最大值为,又因为三棱锥P﹣ABC的高PO=1,故三棱锥P﹣ABC体积的最大值为:.(Ⅲ)在△POB中,PO=OB=1,∠POB=90°,所以PB==,同理PC=,所以PB=PC=BC,在三棱锥P﹣ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示,当O,E,C′共线时,CE+OE取得最小值,又因为OP=OB,C′P=C′B,所以OC′垂直平分PB,即E为PB中点.从而OC′=OE+EC′==.亦即CE+OE的最小值为:.点评:本题主要考查了直线与直线、直线与平面的位置关系、锥体的体积的求法等基础知识,考查了空间想象能力、推理论证能力、运算求解能力,考查了数形结合思想、化归与转化思想,属于中档题.8.(2015?河北)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(Ⅰ)证明:平面AEC⊥平面BED;(Ⅱ)若∠ABC=120°,AE⊥EC,三棱锥E﹣ACD的体积为,求该三棱锥的侧面积.考点:平面与平面垂直的判定;棱柱、棱锥、棱台的侧面积和表面积.专题:空间位置关系与距离.分析:(Ⅰ)根据面面垂直的判定定理即可证明:平面AEC⊥平面BED;(Ⅱ)根据三棱锥的条件公式,进行计算即可.解答:证明:(Ⅰ)∵四边形ABCD为菱形,∴AC⊥BD,∵BE⊥平面ABCD,∴AC⊥BE,则AC⊥平面BED,∵AC?平面AEC,∴平面AEC⊥平面BED;解:(Ⅱ)设AB=x,在菱形ABCD中,由∠ABC=120°,得AG=GC=x,GB=GD=,∵AE⊥EC,△EBG为直角三角形,∴BE=x,∵三棱锥E﹣ACD的体积V===,解得x=2,即AB=2,∵∠ABC=120°,∴AC2=AB2+BC2﹣2AB?BCcosABC=4+4﹣2×=12,即AC=,在三个直角三角形EBA,EBG,EBC中,斜边AE=EC=ED,∵AE⊥EC,∴△EAC为等腰三角形,则AE2+EC2=AC2=12,即2AE2=12,∴AE2=6,则AE=,∴从而得AE=EC=ED=,∴△EAC的面积S==3,在等腰三角形EAD中,过E作EF⊥AD于F,则AE=,AF==,则EF=,∴△EAD的面积和△ECD的面积均为S==,故该三棱锥的侧面积为3+2.点评:本题主要考查面面垂直的判定,以及三棱锥体积的计算,要求熟练掌握相应的判定定理以及体积公式.9.(2015?天津)如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2,AA1=,BB1=2,点E和F 分别为BC和A1C的中点.(Ⅰ)求证:EF∥平面A1B1BA;(Ⅱ)求证:平面AEA1⊥平面BCB1;(Ⅲ)求直线A1B1与平面BCB1所成角的大小.考点:平面与平面垂直的判定;直线与平面平行的判定;直线与平面所成的角.专题:空间位置关系与距离.分析:(Ⅰ)连接A1B,易证EF∥A1B,由线面平行的判定定理可得;(Ⅱ)易证AE⊥BC,BB1⊥AE,可证AE⊥平面BCB1,进而可得面面垂直;(Ⅲ)取BB1中点M和B1C中点N,连接A1M,A1N,NE,易证∠A1B1N即为直线A1B1与平面BCB1所成角,解三角形可得.解答:(Ⅰ)证明:连接A1B,在△A1BC中,∵E和F分别是BC和A1C的中点,∴EF∥A1B,又∵A1B?平面A1B1BA,EF?平面A1B1BA,∴EF∥平面A1B1BA;(Ⅱ)证明:∵AB=AC,E为BC中点,∴AE⊥BC,∵AA1⊥平面ABC,BB1∥AA1,∴BB1⊥平面ABC,∴BB1⊥AE,又∵BC∩BB1=B,∴AE⊥平面BCB1,又∵AE?平面AEA1,∴平面AEA1⊥平面BCB1;(Ⅲ)取BB1中点M和B1C中点N,连接A1M,A1N,NE,∵N和E分别为B1C和BC的中点,∴NE平行且等于B1B,∴NE平行且等于A1A,∴四边形A1AEN是平行四边形,∴A1N平行且等于AE,又∵AE⊥平面BCB1,∴A1N⊥平面BCB1,∴∠A1B1N即为直线A1B1与平面BCB1所成角,在△ABC中,可得AE=2,∴A1N=AE=2,∵BM∥AA1,BM=AA1,∴A1M∥AB且A1M=AB,又由AB⊥BB1,∴A1M⊥BB1,在RT△A1MB1中,A1B1==4,在RT△A1NB1中,sin∠A1B1N==,∴∠A1B1N=30°,即直线A1B1与平面BCB1所成角的大小为30°点评:本题考查线面垂直与平行关系的证明,涉及直线与平面所成的角,属中档题.10.(2015?醴陵市)如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.(1)求证:MN∥平面BCD;(2)求证:平面BCD⊥平面ABC.考点:平面与平面垂直的判定;直线与平面平行的判定.专题:空间位置关系与距离.分析:(1)由中位线定理和线面平行的判定定理,即可得证;(2)由线面垂直的性质和判定定理,可得CD⊥平面ABC,再由面面垂直的判定定理,即可得证.解答:证明:(1)因为M,N分别是AC,AD的中点,所以MN∥CD.又MN?平面BCD且CD?平面BCD,所以MN∥平面BCD;(2)因为AB⊥平面BCD,CD?平面BCD,所以AB⊥CD.又CD⊥BC,AB∩BC=B,所以CD⊥平面ABC.又CD?平面BCD,所以平面BCD⊥平面ABC.点评:本题考查线面平行的判定和面面垂直的判定,考查空间直线和平面的位置关系,考查逻辑推理能力,属于中档题.11.(2015?葫芦岛一模)如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.(1)求证:BF⊥AC;(2)若CE=1,∠CBE=30°,求三棱锥F﹣BCE的体积.考点:旋转体(圆柱、圆锥、圆台).专题:计算题;空间位置关系与距离.分析:(1)欲证BF⊥AC,先证BF⊥平面AEC,根据线面垂直的判定定理可知只需证CE⊥BF,BF⊥AE且CE∩AE=E,即可证得线面垂直;(2)V F﹣BCE=V C﹣BEF=?S△BEF?CE=??EF?BF?CE,即可求出三棱锥F﹣BCE的体积.解答:(1)证明:∵AB⊥平面BEC,CE?平面BEC,∴AB⊥CE∵BC为圆的直径,∴BE⊥CE.∵BE?平面ABE,AB?平面ABE,BE∩AB=B∴CE⊥平面ABE,∵BF?平面ABE,∴CE⊥BF,又BF⊥AE且CE∩AE=E,∴BF⊥平面AEC,∵AC?平面AEC,∴BF⊥AC…(6分)(2)解:在Rt△BEC中,∵CE=1,∠CBE=30°∴BE=,BC=2又∵ABCD为正方形,∴AB=2,∴AE=,∴BF?AE=AB?BE,∴BF=,∴EF=∴V F﹣BCE=V C﹣BEF=?S△BEF?CE=??EF?BF?CE=????1=…(12分)点评:本小题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力,考查三棱锥F﹣BCE的体积的计算,属于中档题.12.(2015?商丘三模)如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.求证:(Ⅰ)EC⊥CD;(Ⅱ)求证:AG∥平面BDE;(Ⅲ)求:几何体EG﹣ABCD的体积.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定.专题:综合题;空间位置关系与距离.分析:(Ⅰ)利用面面垂直的性质,证明EC⊥平面ABCD,利用线面垂直的性质证明EC⊥CD;(Ⅱ)在平面BCEG中,过G作GN⊥CE交BE于M,连DM,证明四边形ADMG为平行四边形,可得AG∥DM,即可证明AG∥平面BDE;(Ⅲ)利用分割法即可求出几何体EG﹣ABCD的体积.解答:(Ⅰ)证明:由平面ABCD⊥平面BCEG,平面ABCD∩平面BCEG=BC,CE⊥BC,CE?平面BCEG,∴EC⊥平面ABCD,…(3分)又CD?平面BCDA,故EC⊥CD…(4分)(Ⅱ)证明:在平面BCEG中,过G作GN⊥CE交BE于M,连DM,则由已知知;MG=MN,MN∥BC∥DA,且,∴MG∥AD,MG=AD,故四边形ADMG为平行四边形,∴AG∥DM…(6分)∵DM?平面BDE,AG?平面BDE,∴AG∥平面BDE…(8分)(Ⅲ)解:…(10分)=…(12分)点评:本题考查面面垂直、线面平行,考查几何体体积的计算,考查学生分析解决问题的能力,正确运用面面垂直、线面平行的判定定理是关键.13.(2015?南昌模拟)如图,已知三棱锥A﹣BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB 为正三角形.(1)求证:DM∥平面APC;(2)若BC=4,AB=20,求三棱锥D﹣BCM的体积.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定.专题:空间位置关系与距离.分析:(1)可由三角形的中位线定理得到线线平行,进而得到线面平行.(2)先证明MD⊥底面BCD,进而可计算出体积.解答:(1)证明:∵M为AB的中点,D为PB的中点,∴MD为△PAB的中位线,∴MD∥AP.而AP?平面PAC,MD?平面PAC,∴MD∥平面PAC.(2)解:∵△PMB为正三角形,PD=DB,∴MD⊥PB.∵MD∥AP,AP⊥PC,∴MD⊥PC.又PC∩PB=P,∴MD⊥平面PBC.即MD为三棱锥M﹣BCD的高.由AB=20,∴MB=10,BD=5,∴MD=5.在Rt△PCB中(因为AC⊥BC,所以PC⊥BC),由勾股定理得PC==2.于是S△BCD=S△BCP×==.∴V三棱锥D﹣BCM=V三棱锥M﹣BCD==10.点评:利用三角形的中位线定理证明线线平行是证明线面平行常用的方法之一.先证明线面垂直是求体积的关键.14.(2015?沈阳模拟)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=,O为AC与BD的交点,E为棱PB上一点.(Ⅰ)证明:平面EAC⊥平面PBD;(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.考点:棱柱、棱锥、棱台的体积;平面与平面垂直的判定.专题:空间位置关系与距离.分析:(Ⅰ)由已知得AC⊥PD,AC⊥BD,由此能证明平面EAC⊥平面PBD.(Ⅱ)由已知得PD∥OE,取AD中点H,连结BH,由此利用,能求出三棱锥P﹣EAD的体积.解答:(Ⅰ)证明:∵PD⊥平面ABCD,AC?平面ABCD,∴AC⊥PD.∵四边形ABCD是菱形,∴AC⊥BD,又∵PD∩BD=D,AC⊥平面PBD.而AC?平面EAC,∴平面EAC⊥平面PBD.(Ⅱ)解:∵PD∥平面EAC,平面EAC∩平面PBD=OE,∴PD∥OE,∵O是BD中点,∴E是PB中点.取AD中点H,连结BH,∵四边形ABCD是菱形,∠BAD=60°,∴BH⊥AD,又BH⊥PD,AD∩PD=D,∴BD⊥平面PAD,.∴(还可以用VP-ABD-VE-ABD)==.点评:本题考查平面与平面垂直的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.15.(2015?上海模拟)已知正四棱柱ABCD﹣A1B1C1D1,底面边长为,点P、Q、R分别在棱AA1、BB1、BC上,Q是BB1中点,且PQ∥AB,C1Q⊥QR(1)求证:C1Q⊥平面PQR;(2)若C1Q=,求四面体C1PQR的体积.考点:棱柱、棱锥、棱台的体积;直线与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(1)由已知得AB⊥平面B1BCC1,从而PQ⊥平面B1BCC1,进而C1Q⊥PQ,又C1Q⊥QR,由此能证明C1Q⊥平面PQR.(2)由已知得B1Q=1,BQ=1,△B1C1Q∽△BQR,从而BR=,QR=,由C1Q、QR、QP两两垂直,能求出四面体C1PQR 的体积.解答:(1)证明:∵四棱柱ABCD﹣A1B1C1D1是正四棱柱,∴AB⊥平面B1BCC1,又PQ∥AB,∴PQ⊥平面B1BCC1,∴C1Q⊥PQ,又已知C1Q⊥QR,且QR∩QP=Q,∴C1Q⊥平面PQR.(2)解:∵B1C1=,,∴B1Q=1,∴BQ=1,∵Q是BB1中点,C1Q⊥QR,∴∠B1C1Q=∠BQR,∠C1B1Q=∠QBR,∴△B1C1Q∽△BQR,∴BR=,∴QR=,∵C1Q、QR、QP两两垂直,∴四面体C1PQR 的体积V=.点评:本小题主要考查空间线面关系、线面垂直的证明、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.16.(2015?凯里市校级模拟)如图,直三棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点.(1)证明BC1∥平面A1CD(2)设AA1=AC=CB=2,AB=2,求三菱锥C﹣A1DE的体积.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定.专题:空间位置关系与距离.分析:(1)连结AC1交A1C于点F,连结DF,则BC1∥DF,由此能证明BC1∥平面A1CD.(2)由已知得AA1⊥CD,CD⊥AB,从而CD⊥平面ABB1A1.由此能求出三菱锥C﹣A1DE的体积.解答:(1)证明:连结AC1交A1C于点F,则F为AC1中点又D是AB中点,连结DF,则BC1∥DF.因为DF?平面A1CD,BC1不包含于平面A1CD,所以BC1∥平面A1CD.(2)解:因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥CD.由已知AC=CB,D为AB的中点,所以CD⊥AB.又AA1∩AB=A,于是CD⊥平面ABB1A1.由AA1=AC=CB=2,得∠ACB=90°,,,,A1E=3,故A1D2+DE2=A1E2,即DE⊥A1D.所以三菱锥C﹣A1DE的体积为:==1.点评:本题考查直线与平面平行的证明,考查三菱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.17.(2015?东城区一模)如图甲,⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,且∠CBA=∠DAB=.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:(Ⅰ)求证:CB⊥DE;(Ⅱ)求三棱锥C﹣BOD的体积;(Ⅲ)在劣弧上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.考点:棱柱、棱锥、棱台的体积;直线与平面平行的性质.专题:综合题;空间位置关系与距离.分析:(Ⅰ)利用等边三角形的性质可得DE⊥AO,再利用面面垂直的性质定理即可得到DE⊥平面ABC,进而得出结论.(Ⅱ)由(Ⅰ)知DE⊥平面ABC,利用转换底面的方法,即可求三棱锥的体积;(Ⅲ)存在,G为劣弧的中点.连接OG,OF,FG,通过证明平面OFG∥平面ACD,即可得到结论.解答:(Ⅰ)证明:在△AOD中,∵,OA=OD,∴△AOD为正三角形,又∵E为OA的中点,∴DE⊥AO…(1分)∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,∴DE⊥平面ABC.…(3分)又CB?平面ABC,∴CB⊥DE.…5分(Ⅱ)解:由(Ⅰ)知DE⊥平面ABC,∴DE为三棱锥D﹣BOC的高.∵D为圆周上一点,且AB为直径,∴,在△ABD中,由AD⊥BD,,AB=2,得AD=1,.…(6分)∵,∴==.…(8分)(Ⅲ)解:存在满足题意的点G,G为劣弧的中点.…(9分)证明如下:连接OG,OF,FG,易知OG⊥BD,又AD⊥BD∴OG∥AD,∵OG?平面ACD,∴OG∥平面ACD.…(10分)在△ABC中,O,F分别为AB,BC的中点,∴OF∥AC,OF?平面ACD,∴OF∥平面ACD,…(11分)∵OG∩OF=O,∴平面OFG∥平面ACD.又FG?平面OFG,∴FG∥平面ACD.…(12分)点评:本题考查线线、线面、面面关系,考查线线垂直的判定、面面垂直的性质、线面平行的判定及几何体高与体积的计算,考查空间想象能力、推理论证能力、运算求解能力及分析探究问题和解决问题的能力.18.(2015?威海模拟)如图:是直径为的半圆,O为圆心,C是上一点,且.DF⊥CD,且DF=2,,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.(Ⅰ)求证:面BCE⊥面CDF;(Ⅱ)求证:QR∥平面BCD;(Ⅲ)求三棱锥F﹣BCE的体积.考点:棱柱、棱锥、棱台的体积;直线与平面平行的判定;平面与平面垂直的判定.专题:空间位置关系与距离.分析:(Ⅰ)证明BD⊥DF,DF⊥BC,利用直线与平面垂直的判定定理证明BC⊥平面CFD,然后证明面BCE⊥面CDF.(Ⅱ)连接OQ,通过证明RQ∥OM,然后证明QR∥平面BCD.(Ⅲ)利用v F﹣BCE=v F﹣BCD﹣v E﹣BCD求解几何体的体积即可.解答:(本小题满分12分)证明:(Ⅰ)∵DF=2,,,∴BF2=BD2+DF2,∴BD⊥DF﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)又DF⊥CD,∴DF⊥平面BCD﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)∴DF⊥BC,又BC⊥CD,∴BC⊥平面CFD,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)∵BC?面BCE∴面BCE⊥面CDF.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)(Ⅱ)连接OQ,在面CFD内过R点做RM⊥CD,∵O,Q为中点,∴OQ∥DF,且﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∵DF⊥CD∴RM∥FD,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)又FR=3RC,∴,∴,∵E为FD的中点,∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)∴OQ∥RM,且OQ=RM∴OQRM为平行四边形,∵RQ∥OM﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)又RQ?平面BCD,OM?平面BCD,∴QR∥平面BCD.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)(Ⅲ)∵,∴∠DBC=30°,∴在直角三角形BCD中有,,∴﹣﹣﹣﹣﹣﹣﹣﹣(12分)(或求VB-FCE 1/3*1/2*FE*CD*BC)点评:本题考查直线与平面垂直的判定定理的应用直线与平面平行的判定定理以及几何体的体积的求法,考查空间想象能力以及逻辑推理计算能力.。
高二数学-空间向量与立体几何测试题及答案

高二数学空间向量与立体几何测试题第1卷(选择题,共50分)一、选择题:(本大题共10个小题每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 在下列命题中:CD若a、b共线则a、b所在的直线平行;@若a、b所在的直线是异面直线,则a、b一定不共面;@若a、b、c三向量两两共面,则a、b、c三向量一定也共面;@已知三向量a、b、c,则空间任意一个向量p总可以唯一表示为p=a+yb+zc,, y, z R.其中正确命题的个数为( )A. 0B. 1C. 2D. 32. 若三点共线为空间任意一点且则的值为()A. lB.C.D.3. 设,且,则等千()A. B. 9 C. D4. 已知a=(2, —1, 3) , b= C—1, 4, —2) , c= (7, 5, 入),若a、b、c三向量共面,则实数入等千()A. B. C.5.如图1,空间四边形的四条边及对角线长都是,点分别是的中点则等千()D.A.C...BD6. 若a、b均为非零向量,则是a与b共线的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件7. 已知点0是LABC所在平面内一点满足• = • = • '则点0是LABC的()A. 三个内角的角平分线的交点B. 三条边的垂直平分线的交点C. 三条中线的交点8. 已知a+b+c=O,al =2, bl =3,A. 30°B. 45°D.三条高的交点l e = , 则向量a与b之间的夹角为()C. 60°D. 以上都不对9. 已知, ' ,点Q在直线OP上运动,则当取得最小值时,点Q的坐标为()A.B.10. 给出下列命题:CD已知,则C. D.@为空间四点若不构成空间的一个基底,那么共面;@已知则与任何向量都不构成空间的一个基底;@若共线则所在直线或者平行或者重合.正确的结论的个数为()C. 3A.1B.2D.4 第II卷(非选择题,共100分)二、填空题(本大题共6小题,每小题5分,共30分)11.已知LABC的三个顶点为A(3, 3, 2) , B (4, —3, 7) , C (0, 5, 1) , 则BC边上的中线长为12. 已知三点不共线为平面外一点若由向量确定的点与共面,那么13. 已知a,b,c是空间两两垂直且长度相等的基底,m=a+b,n=b-c,则m,n的夹角为14. 在空间四边形ABC D中,AC和B D为对角线G为L:.ABC的重心,E是B D上一点BE=3E D, 以{, , }为基底,则=15. 在平行四边形ABCD中,AB=AC=l,乙ACD=90, 将它沿对角线AC折起,使AB与CD成60角,则B,D两点间的距离为16. 如图二面角a-t -B的棱上有A,B两点直线AC,B D分别在这个二面角的两个半平面内,且都垂直千AB,已知AB=4,AC=6, B D=8, C D= ,二面角Q—t—B的大小三、解答题(本大题共5小题,满分70分),17. C lo分)设试问是否存在实数,使成立?如果存在,求出;如果不存在,请写出证明.18. (12分)如图在四棱锥中,底面ABC D是正方形,侧棱底面ABC D,, 是PC的中点,作交PB千点F.(1)证明PAIi平面EDB:(2)证明PB上平面E F D:(3)求二面角的大小.、、、、、、、、.、19. (12分)如图在直三棱柱ABC—AlBlCl中,底面是等腰直角三角形,乙ACB=90°.侧棱AA1=2, D. E 分别是CCl与AlB的中点点E在平面ABO上的射影是DAB D的重心G.(1)求AlB与平面ABO所成角的大小.(2)求Al到平面ABO的距离1) 20. 12分)如图在三棱柱ABC-AlBlCl中,AB上AC,顶点Al在底面ABC上的射影恰为点B,且AB=AC=A1B=2.2)求棱AA1与BC所成角的大小;在棱BlCl上确定一点P,使AP=, 并求出二面角P—AB—Al的平面角的余弦值A1C1B21. (12分)如图直三棱柱ABC-AlBlCl中AB上AC,D.E分别为AAl.B lC的中点DEl_平面BCCl.C I)证明:A B=ACC II)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小c,22. (12分)P是平面ABC D外的点四边形ABC D是平行四边形,AP= (-1, 2, -1)(1)求证:PA 平面ABC D.(2)对千向量,定义一种运算:,试计算的绝对值;说明其与几何体P—ABC D的体积关系,并由此猜想向量这种运算的绝对值的几何意义(几何体P-ABC D叫四棱锥,锥体体积公式:V= ) .一、选 1 2 择题(本大题土2上、10小题,每3 4空间向量与立体几何(2)参考答案5 6 7 8 9 10小题5/刀\.让,/、50分)题号答案D D D A B C A 二、填空题(本大题共4小题,每小题6分,共24分)11. (0, ,) 12. 0 13. 1, —3 14. 90° l厮—15。
高二几何练习题大全

高二几何练习题大全几何学是数学中重要的分支之一,它研究的是空间和形状的性质。
对于高中学生来说,几何学是一个重要的课程内容。
为了帮助高二学生巩固和提升他们的几何知识水平,本文为大家收集了一些高二几何练习题,供同学们参考和练习。
1. 难度:简单已知△ABC中,∠C = 90°,AC = 5 cm,BC = 12 cm。
求AB的长度。
2. 难度:中等已知△ABD中,∠B = 45°,BD = 10 cm。
若BD与AC垂直,并且AD = 2BD,求AC的长度。
3. 难度:中等已知△ABC中,∠A = 90°,BC = 8 cm,AC = 10 cm。
点D在AC 上,且BD的长度为4 cm。
求△BDC的面积。
4. 难度:困难已知菱形ABCD,对角线AC与BD相交于点E,且∠AEC = 60°,AE = 6 cm。
求菱形ABCD的面积。
5. 难度:困难已知正方形ABCD的边长为8 cm,以点A为圆心,以AC为半径画一个圆,圆与正方形的边BC相交于点E。
求三角形BEA的面积。
6. 难度:简单已知△ABC中,∠A = 60°,AC = 6 cm。
点D在BC边上,且BD的长度为4 cm。
求△ACD的面积。
7. 难度:中等已知△ABC为等腰直角三角形,AB = BC = 5 cm。
点D在边AC上,且AD的长度为4 cm。
求△ABD的面积。
8. 难度:中等已知△ABC为等边三角形,边长为10 cm。
点D在边AB上,且BD的长度为4 cm。
求△ACD的面积。
9. 难度:困难已知正方形ABCD的边长为10 cm,以点A为圆心,以AC为半径画一个圆,圆与正方形的边BC相交于点E。
连接AE和DE,求△AED的面积。
10. 难度:困难已知△ABC为等边三角形,边长为8 cm。
点D在边AB上,且BD的长度为3 cm。
点E在边AC上,且AE的长度为5 cm。
求四边形BCDE的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习1一、选择题:1.a 、b 是两条异面直线,下列结论正确的是( )A .过不在a 、b 上的任一点,可作一个平面与a 、b 都平行B .过不在a 、b 上的任一点,可作一条直线与a 、b 都相交C .过不在a 、b 上的任一点,可作一条直线与a 、b 都平行D .过a 可以且只可以作一个平面与b 平行2.空间不共线的四点,可以确定平面的个数为 ( )A.0 B.1 C.1或4 D.无法确定3.在正方体1111ABCD A B C D -中,M 、N 分别为棱1AA 、1BB 的中点,则异面直线CM 和1D N 所成角的正弦值为 ( ) A.19 B.23C.459 D.2594.已知平面α⊥平面β,m 是α内的一直线,n 是β内的一直线,且m n ⊥,则:①m β⊥;②n α⊥;③m β⊥或n α⊥;④m β⊥且n α⊥。
这四个结论中,不正确...的三个是( ) A.①②③ B.①②④ C.①③④ D.②③④5.一个简单多面体的各个面都是三角形,它有6个顶点,则这个简单多面体的面数是 ( ) A. 4 B. 5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球半径为R ) ( )A.R π42B. R 3πC. R 2πD. 3R7. 直线l ⊥平面α,直线m ⊂平面β,有下列四个命题: (1)m l ⊥⇒βα// (2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l 其中正确的命题是 ( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形,侧面与底面所成角为α,则下列不等式成立的是 ( ) A. 60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9.ABC ∆中,9AB =,15AC =,120BAC ∠=︒,ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14,则P 到平面α的距离为 ( ) A.7 B.9 C.11 D.1310.在一个45︒的二面角的一个平面内有一条直线与二面角的棱成角45︒,则此直线与二面角的另一个平面所成角的大小为 ( )A.30︒ B.45︒ C.60︒ D.90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点,沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作D.给出下列位置关系: ①SD ⊥面DEF; ②SE ⊥面DEF; ③DF ⊥SE; ④EF ⊥面SED, 其中成立的有: ( ) A. ①与② B. ①与③ C. ②与③ D. ③与④12. 某地球仪的北纬60度圈的周长为6πcm,则地球仪的表面积为( )A. 24πcm 2B. 48πcm 2C. 144πcm 2D. 288πcm 2二、填空题13. 直二面角α—MN —β中,等腰直角三角形ABC 的斜边BC ⊂α,一直角边AC ⊂β,BC 与β所成角的正弦值是46,则AB 与β所成角大小为__________。
14. 在底面边长为2的正三棱锥V —ABC 中,E 是BC 中点,若△VAE 的面积是41,则侧棱VA 与底面所成角的大小为15.如图,已知矩形ABCD 中,1AB =,BC a =,PA ⊥面ABCD 。
若在BC 上只有一个点Q 满足PQ QD ⊥,则a 的值等于______. 16. 六棱锥P —ABCDEF 中,底面ABCDEF 是正六边形,PA ⊥底面ABCDEF ,给出下列四个命题:①线段PC 的长是点P 到线段CD 的距离;②异面直线PB 与EF 所成角是∠PBC ;③线段AD 的长是直线CD 与平面PAF 的距离;④∠PEA 是二面角P —DE —A 平面角。
其中所有真命题的序号是_______________。
三.解答题:17.如图,已知直棱柱111ABC A B C -中,90ACB ∠=︒,30BAC ∠=︒,1BC =,16AA =,M 是1CC 的中点。
求证:11AB A M ⊥18.如图,在矩形ABCD 中,33AB =,3BC =,沿对角线BD 将BCD ∆折起,使点C 移到P 点,且P 在平面ABD 上的射影O 恰好在AB 上。
(1)求证:PB ⊥面PAD ; (2)求点A 到平面PBD 的距离; (3)求直线AB 与平面PBD 的成角的大小PA BQ CDABC1B 1A 1C MA BCDA B()P C DO19.如图,已知PA ⊥面,ABC AD BC ⊥,垂足D 在BC 的延长线上,且1BC CD DA ===(1) 记PD x =,BPC θ∠=,试把tan θ表示成x 的函数,并求其最大值. (2) 在直线PA 上是否存在点Q ,使得BQC BAC ∠>∠20.正三棱锥V-ABC 的底面边长是a, 侧面与底面成60°的二面角。
求(1)棱锥的侧棱长; (2)侧棱与底面所成的角的正切值。
21.已知正三棱柱ABC-A 1B 1C 1的底面边长为8,面的对角线B 1C=10,D 为AC 的中点,(1)求证:AB 1//平面C 1BD;(2)求异面直线AB 1与BC 1所成角的余弦值;(3)求直线AB 1到平面C 1BD 的距离。
22. 已知A 1B 1C 1-ABC 为直三棱柱,D 为AC 中点,O 为BC 中点,E 在CC 1上,∠ACB=90°,AC=BC=CE=2,AA 1=6.(1)证明平面BDE ∥AO ;(2)求二面角A-EB-D 的大小;(3)求三棱锥O-AA 1D 体积.PA BCD练习1答案一.选择题:二.填空题:13. 60º 14. 41arctan 15. 2 16. ①④ 三.解答题:17.解:【法一】90ACB ∠=︒1111B C AC ⇒⊥,又三棱柱111ABC A B C -是直三棱柱, 所以11B C ⊥面1A C ,连结1A C ,则1AC 是1AB 在面1A C 上的射影在四边形11AAC C 中,111111AA A C A C C M ==,且11112AAC AC M π∠=∠=, 1111AAC AC M ∴∆∆, 11AC A M ∴⊥ 11AB A M ∴⊥【法二】以11C B 为x 轴,11C A 为y 轴,1C C 为z 轴建立空间直角坐标系由1BC=,1AA =90ACB ∠=︒,30BAC ∠=︒,易得1A ,A ,(0,0,2M ,1(1,0,0)B1(1,AB ∴=,1(0,A M =1103(0AB A M ∴=++= 11AB AM ⇒⊥ 所以11AB A M ⊥ 18.解:(1)P 在平面ABD 上的射影O 在AB 上,PO ∴⊥面ABD 。
故斜线BP 在平面ABD 上的射影为AB 。
又DA AB ⊥,DA BP ∴⊥,又BC CD ⊥,BP PD ∴⊥ AD PD D = BP ⇒⊥面PAD(2)过A 作AE PD ⊥,交PD 于E 。
BP ⊥面PAD ,BP AE ∴⊥,AE ∴⊥面BPD 故AE 的长就是点A 到平面BPD 的距离AD AB ⊥,DA BC ⊥ AD ⇒⊥面ABP AD AP ∴⊥在Rt ABP ∆中,AP ==在Rt BPD ∆中,PD CD ==在Rt PAD ∆中,由面积关系,得323AP AD AE PD ===(3)连结BE ,AE ⊥面BPD ,BE ∴是AB 在平面BPD 的射影ABE ∴∠为直线AB 与平面BPD 所成的角在Rt AEB ∆中,sin 3AE ABEAB ∠==, arcsin 3ABE ∴∠= 19.(1)PA ⊥面ABC ,,BD AD BC PD ⊥∴⊥,即90.PDB ∠=在Rt PDB ∆和Rt PDC ∆中,21tan ,tan BPD CPD x x∠=∠=, 221tan tan tan()2121xx x BPC BPD CPD x x xθ-∴=∠=∠-∠==++⋅(1x >)12x x≤=+当且仅当x =,tan θ.(2)在Rt ADB ∆和Rt DC ∆中,tanBAD ∠=2,tan 1CAD ∠= 211tan tan()12134BACBAD CAD -∴∠=∠-∠==<+⨯故在PA 存在点Q (如1AQ =)满足1tan 34BQC <∠≤,使BQC BAC ∠>∠ 20. (12分)解:(1)过V 点作V0⊥面ABC 于点0,VE ⊥AB 于点E ∵三棱锥V —ABC 是正三棱锥 ∴O 为△ABC 的中心 则OA=a a 332332=⨯,OE=a a 632331=⨯ 又∵侧面与底面成60°角 ∴∠VEO=60° 则在Rt △VEO 中;V0=OE ·tan60°=2363aa =⨯ 在Rt △VAO 中,VA=6211273422222aa a a AO VO ==+=+ 即侧棱长为a 621(2)由(1)知∠VAO 即为侧棱与底面所成角,则tan ∠VAO=23332==a aAO VO 21解:(1)连结BC 1交B 1C 于点E ,则E 为B 1C 的中点,并连结DE∵D 为AC 中点 ∴DE ∥AB 1 而DE ⊂面BC 1D , AB 1⊂面BC 1D ∴AB 1∥面C 1BD(2)由(1)知AB 1∥DE ,则∠DEB 或其补角为异面直线AB 1与BC 1所成的角 由条件知B 1C=10, BC=8 则BB 1=6 ∵E 三棱柱中 AB 1=BC 1 ∴DE=5 又∵BD=34823=⨯ ∴在△BED 中 2515524825252cos 222=⨯⨯-+=•-+=∠DE BD BD DE BE BED故异面直线AB 1与BC 1所成角的余弦值为251(3)由(1)知A 到平面BC 1D 的距离即为直线AB 1到平面BC 1D 的距离设A 到平面BC 1D 的距离为h ,则由ABD C D BC A V V --=11得C C S h S ABD D BC 131311••=••∆∆即h=DBC ABD S CC S 11∆∆• 由正三棱柱性质得BD ⊥C 1D 则D C BD S DBC 1:211=∆ ∴131312522446642121221111==+⨯=•=•••=D C CC AD DC BD CC AD BD h 即直线AB 1到平面的距离为131312 22. 证明: ①设F 为BE 与B 1C 的交点,G 为GE 中点 ∵AO ∥DF ∴AO ∥平面BDE②α=arctan 2-arctan22或arcsin1/3 ③用体积法V=31×21×6×h=1练习2一、选择题1.已知直线a 、b 和平面M ,则a//b 的一个必要不充分条件是 ( )A .a//M, b//MB .a ⊥M ,b ⊥MC .a//M, b ⊂MD .a 、b 与平面M 成等角 2.正四面体P —ABC 中,M 为棱AB 的中点,则PA 与CM 所成角的余弦值为 ( )A .23 B .63 C .43 D .33 3.a , b 是异面直线,A 、B ∈a , C 、D ∈b,AC ⊥b,BD ⊥b,且AB=2,CD=1,则a 与b 所成的角为( )A .30°B .60°C .90°D .45°4.给出下面四个命题:①“直线a 、b 为异面直线”的充分非必要条件是:直线a 、b 不相交; ②“直线l 垂直于平面α内所有直线”的充要条件是:l ⊥平面α;③“直线a ⊥b ”的充分非必要条件是“a 垂直于b 在平面α内的射影”;④“直线a ∥平面β”的必要非充分条件是“直线a 至少平行于平面β内的一条直线”. 其中正确命题的个数是 ( ) A .1个 B .2个 C .3个 D .4个 5.设l 1 、l 2为两条直线,a 、β为两个平面,给出下列四个命题:(1)若l 1α⊂, l 2β⊂,l 1∥β,l 1∥a 则a ∥β. (2)若l 1⊥a ,l 2⊥a ,则l 1∥l 2(3)若l 1∥a ,l 1∥l 2,则l 2∥a (4)若a ⊥β,l 1α⊂,则l 1⊥β其中,正确命题的个数是 ( ) A .0个 B .1个 C .2个 D .3个 6.三棱柱111C B A ABC -中,侧面B B AA 11⊥底面ABC ,直线C A 1与底面成︒60角,2===CA BC AB ,B A AA 11=,则该棱柱的体积为( )A .34B .33C .4D .3 7.已知直线l ⊥面α,直线m ⊂面β,给出下列命题: (1)αβ//⇒⊥l m (2)αβ⊥⇒l m // (3)l m //⇒⊥αβ (4)l m ⊥⇒αβ//其中正确的命题个数是( ) A. 1B. 2C. 3D. 48.正三棱锥S ABC -的底面边长为a ,侧棱长为b ,那么经过底边AC和BC 的中点且平行于侧棱SC 的截面EFGH 的面积为( ) A.abB. ab 2C. ab 4D.22ab 9.已知平面α、β、γ,直线l 、m ,且l m m l==⊥⊥βγαγγα ,,,,给出下列四个结论:①γβ⊥;②α⊥l ;③β⊥m ;④αβ⊥.则其中正确的个数是( )A .0B .1C .2D .310.在正方体ABCD -A 1B 1C 1D 1中,M 是棱DD 1的中点,O 是底面ABCD 的中心,P 是棱A 1B 1上任意一点,则直线OP 与支线AM 所成角的大小为( )A .45ºB .90ºC .60ºD .不能确定ABCA 1B 1C 1AA 1D 1 D OMABCSEFG H11.将边长为1的正方形ABCD 沿对角线BD 折起,使得点A 到点A ’的位置,且A ’C =1,则折起后二面角A ’-DC -B 的大小为 ( ) A.22arctan B.4π C.arctan 2 D. 3π12. 正方体ABCD A B C D -1111,E 、F 分别是AA CC 11、的中点,P 是CC 1上的动点(包括端点),过E 、D 、P 作正方体的截面,若截面为四边形,则P 的轨迹是 ( ) A. 线段C F 1 B. 线段CF C. 线段CF 和一点C 1D. 线段C F 1和一点C二、填空题13.矩形ABCD 的对角线AC ,BD 成60°角,把矩形所在的平面以AC 为折痕,折成一个直二面角D —AC —B ,连结BD ,则BD 与平面ABC 所成角的正切值为 .14.将棱长为1的正方体木块加工成一个体积最大的球,则这个球的体积为 ,球的表面积为π (不计损耗).15. 四面体ABCD 中,有如下命题:①若AC ⊥BD ,AB ⊥CD ,则AD ⊥BC ;②若E 、F 、G 分别是BC 、AB 、CD 的中点,则∠FEG 的大小等于异面直线AC 与BD 所成角的大小;③若点O 是四面体ABCD 外接球的球心,则O 在面ABD 上的射影是△ABD 的外心 ④若四个面是全等的三角形,则ABCD 为正四面体。
