测量计算公式(全)
常用测量计算公式、模型

ZA = ZC −T
4-6
HA = HC −T sinα1
终点 B 的桩号及设计高程为
ZB = ZA +L
4-7
HB = HC +T sinα2
设过变坡点的铅垂线与圆弧的交点为 D,则 D 点的桩
号与设计高程为
ZD
=
ZA
+
L 2
mE
sinδ
4-8
HD = HC mE sec δ
式 4-8 中的“ m”,竖曲线为凸形时取“-”,为凹形 时取“+”。
1-2 y′p=(yp-y0)cosα-( xp- x0)sinα
3.面积计算
日常测量常会遇到面积的计算,测量过程手算
又较为不便,下面介绍按多边形角点坐标计算多边
形面积的方法和公式。如图 2 中 J1、J2、J3、J4 为多
边形角点,Ji 点的平面坐标为 xi,yi。多边形的每一 条边和坐标轴、坐标投影线(图中虚线)组成一个个
HZ
说明: lS 为缓和曲线长度, li 为缓和曲线上任一点 至 ZH 或 HZ 点的长度,式 7-2 中的li 为圆曲线上任一点 至圆曲线起点的长度, R 为曲线半径, βi 为缓和曲线上 任一点的切线与过缓和曲线起点 ZH 或 HZ 点的切线的夹
角,ϕi 为圆曲线上任一点至缓和曲线起点 ZH 或 HZ 点的
一致,便于设计、计算与施工放样。建筑坐标系与
城市或国家坐标系(总称大地坐标系)需要进行联
测,即测定建筑坐标系原点的大地坐标(x0,y0), 以及建筑坐标系纵轴在大地坐标系中的方位角
(α),据此可以进行坐标换算。设 XOY 为大地坐标
系的坐标轴,X′O′Y′为建筑坐标系的坐标轴,如
测量计算公式范文

测量计算公式范文
一、长度测量公式:
1.直线长度公式:
直线长度=,x2-x1
2.曲线长度公式:
曲线长度= ∫(a,b) √(1 + (dy/dx)^2) dx 3.圆周的长度:
圆周的长度=2πr
二、面积测量公式:
1.矩形面积公式:
矩形面积=长×宽
2.圆形面积公式:
圆形面积=πr^2
3.三角形面积公式:
三角形面积=(底边长×高)/2
三、体积测量公式:
1.立方体体积公式:
立方体体积=边长^3
2.圆柱体积公式:
圆柱体积=πr^2×高
3.球体积公式:
球体积=(4/3)πr^3
四、力测量公式:
1.牛顿第二定律:
力=质量×加速度
2.压力公式:
压力=力/面积
3.弹簧力公式:
弹簧力=弹性系数×变形距离
五、速度测量公式:
1.平均速度公式:
平均速度=总位移/总时间2.瞬时速度公式:
瞬时速度 = dx/dt
六、功率计算公式:
1.功率公式:
功率=功/时间
2.电功率公式:
电功率=电压×电流
以上只是一些常见的测量计算公式,实际上,不同领域的测量计算公式还有很多。
它们在科学研究、工程设计、经济统计等各个领域都有着广泛的应用。
通过合理使用测量计算公式,我们可以准确地测量和计算各种物理量,为科学研究和工程设计提供可靠的数据支持。
测量,闭合导线等计算及表格

一.坐标计算以下为基本计算公式:直线上计算公式:已知该条直线的方位角à,已知直线的起点或终点的坐标,顺线路方向时,计算点的里程知道,直线的起点或终点的里程知道,可推算出计算点与直线的起点的直线距离d,(即计算点的里程减去起点的里程,逆线路方向时,为直线终点的里程减去计算点的里程),计算坐标增量:∆x=d×cosà∆y=d×cosà计算点的坐标为,直线的起点或终点坐标加上坐标增量,式中方位角à从直线起点算时,为已知即给定的方位角,而从终点算时,à为该段直线的起始方位角加上180度。
à+180à起点计算点终点第一种曲线为两段直线中加一圆曲线,指仅存在圆曲线,如下第1点。
1.圆曲线上计算点相对于ZY或YZ 点的弦长和偏角D=2 RSinδδ=90×L/(πR)δ---------圆曲线偏角D ---------弦长L --------为弧长α=α(zy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。
α=α(yz)-δα------------为计算点的方位角,此α为逆着线路方向计算时。
α(zy)、α(yz)---------为圆曲线的起始方位角。
一般为已知。
计算点相对与直圆点或圆直点的坐标增量:△x=D*COSα△y=D*SINα坐标增量计算完毕后,要算某一点的坐标,用直圆点或圆直点的坐标加上计算点与直圆点或圆直点的坐标增量,即为计算点的坐标。
缓和曲线同理。
第二种曲线为两段直线中始端加一缓和曲线,末端加一缓和曲线,两段缓和曲线中加一圆曲线,如下第2点。
2.缓和曲线上计算点相对于HY或YH点的弦长和偏角δ=L²/6RL0X1=L-(L^5/40R²L0²)Y1=L³/6RL0D=√(X1²+Y1²)α=α(hy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。
测量常用公式一距离计算公式

测量常用公式一距离计算公式距离计算是在数学和物理学中常见的一个问题。
在现实生活中,我们经常需要测量两点之间的距离,无论是在建筑设计,导航系统,旅行规划,还是其他应用中。
在几何学中,最基本的距离计算公式是勾股定理,即在直角三角形中,直角边的平方和等于斜边的平方。
这个公式可以表示为:c²=a²+b²其中,c表示斜边的长度,a和b分别表示直角边的长度。
这个公式在二维平面中适用于计算两点之间的直线距离。
当我们要计算更复杂的距离时,可以使用欧几里得距离公式。
在二维直角坐标系中,欧几里得距离公式可以表示为:d=√((x₂-x₁)²+(y₂-y₁)²)其中,(x₁,y₁)表示第一个点的坐标,(x₂,y₂)表示第二个点的坐标。
这个公式可以计算两个点之间的直线距离。
除了二维平面,欧几里得距离公式也可以扩展到三维空间。
在三维空间中,欧几里得距离公式可以表示为:d=√((x₂-x₁)²+(y₂-y₁)²+(z₂-z₁)²)其中,(x₁,y₁,z₁)表示第一个点的坐标,(x₂,y₂,z₂)表示第二个点的坐标。
这个公式可以计算三维空间中两个点之间的直线距离。
在地理学和导航系统中,我们通常使用球面距离公式来计算地球上两点之间的距离。
球面距离公式可以根据球的半径来调整,但一般情况下使用地球的平均半径来计算。
球面距离公式可以表示为:d = r * arccos(sin(φ₁) * sin(φ₂) + cos(φ₁) * cos(φ₂) * cos(Δλ))其中,d表示两点之间的距离,r表示地球的半径,φ₁和φ₂表示两个点的纬度,Δλ表示两个点的经度之差。
除了上述常见的距离计算公式,还有其他更复杂的公式用于计算两点之间的距离,例如曼哈顿距离、切比雪夫距离、海明顿距离等。
这些公式根据应用的需求和特定的场景选择使用。
在实际应用中,我们可以利用计算机编程语言来实现这些距离计算公式,例如使用Python的math库来计算勾股定理或欧几里得距离公式。
测量学导线测量常用计算公式

一、方位角的计算公式二、平曲线转角点偏角计算公式三、平曲线直缓、缓直点的坐标计算公式四、平曲线上任意点的坐标计算公式五、竖曲线上点的高程计算公式六、超高计算公式七、地基承载力计算公式八、标准差计算公式九、坐标中线测量与计算十、全站仪的使用方法和坐标测量步骤一、方位角的计算公式1. 字母所代表的意义:x1:QD的X坐标y1:QD的Y坐标x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α 2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角 β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+T cos(A+180°)Y ′=V+T sin(A+180°)缓直(圆直)点的国家坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C-T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosOY m =V+Tsin (A+180°)+G sinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW +90°) Y b =Y m +Bsin(A+MW +90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2 中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW +90°) Y b =Y m +Bsin(O+MW +90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD-MW +90°) Y b =Y m +Bsin(A+MD-MW +90°)5)当P>K 时中桩坐标:X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD +90°) Y b =Y m +Bsin(A+MD +90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
测量坐标计算公式讲解

测量坐标计算公式讲解在测量和制图领域,测量坐标计算公式是非常重要的工具。
它们用于确定物体在二维或三维空间中的位置,并进行精确的测量和定位。
本文将介绍一些常用的测量坐标计算公式,并讲解其原理和应用。
一、二维坐标计算1. 直角坐标系直角坐标系是最常用的坐标系之一。
在直角坐标系中,通过给定的两个坐标轴(通常是x轴和y轴),我们可以准确地确定点的位置。
对于二维平面上的点P(x, y),我们可以使用以下公式计算其坐标:x = x1 + Δxy = y1 + Δy其中,x1和y1表示已知点的坐标,Δx和Δy分别表示点P到已知点的水平和垂直距离。
2. 极坐标系极坐标系是另一种常用的坐标系,它使用极径和极角来确定点的位置。
极坐标系常用于描述圆形或其他具有对称性的图形。
对于极坐标系中的点P(r, θ),我们可以使用以下公式计算其坐标:x = r * cos(θ)y = r * sin(θ)其中,r表示点P到原点的距离,θ表示点P与正x轴之间的夹角。
二、三维坐标计算1. 笛卡尔坐标系笛卡尔坐标系是三维空间中最常用的坐标系之一。
它使用x、y和z轴来确定点的位置。
对于三维空间中的点P(x, y, z),我们可以使用以下公式计算其坐标:x = x1 + Δxy = y1 + Δyz = z1 + Δz其中,x1、y1和z1表示已知点的坐标,Δx、Δy和Δz分别表示点P到已知点的水平、垂直和深度距离。
2. 球坐标系球坐标系也是一种常用的三维坐标系,它使用球半径、极角和方位角来确定点的位置。
球坐标系常用于描述球形物体或球面上的点。
对于球坐标系中的点P(ρ, θ, φ),我们可以使用以下公式计算其坐标:x = ρ * sin(θ) * cos(φ)y = ρ * sin(θ) * sin(φ)z = ρ * cos(θ)其中,ρ表示点P到原点的距离,θ表示点P与正z轴之间的夹角,φ表示点P在x-y平面上的投影与正x轴之间的夹角。
测量常用计算公式

一、 方位角的计算公式1. 字母所代表的意义:x 1:QD 的X 坐标 y 1:QD 的Y 坐标 x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角 2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α 2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角 β:JD 处的偏角 2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+ 2. 计算公式:直缓(直圆)点的坐标:X ′=U+Tcos(A+180°)Y ′=V+Tsin(A+180°)缓直(圆直)点的坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C -T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号 2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C -P)cos(A+180°) Y m =V+(C -P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°) 2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosO Y m =V+Tsin(A+180°)+GsinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°) 3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW+90°) Y b =Y m +Bsin(O+MW+90°) 4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD -MW+90°) Y b =Y m +Bsin(A+MD -MW+90°) 5)当P>K 时中桩坐标:X m =U+(T+P -K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
测量员专用·常用测量公式计算表(excel自动计算)
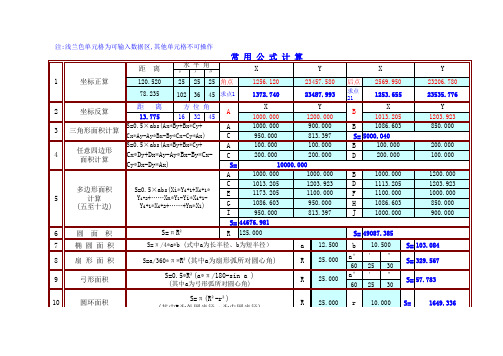
b= 50 13 60
15 一元二次方程求解
公式:ax²+bx+c=0
其中a,b为系数,c为常数项
a 1.00
b
c
此 题 唯 一 解!
X1=
2.00
1.00
X= -1.000
X2=
一元N次方程求解
a1x^N+a2x^N-1+a3x^N-2 +a4x^N-3……+aNx+b=0
a1
a2
0.20 a3
0.50 a4
S= 103.084 S= 329.567 S= 57.783
10
圆环面积
S=π(R²-r²) (其中R为外圆半径,r为内圆半径)
R 25.000 r 10.000 S=
1649.336
10
圆环面积
(其中R为外S圆=π半(径R²,-rr为²)内常圆用半径公) 式 计 算R
25.000
r
10.000 S=
0.009
平距 52.307
所求点高程 351.523
三角形求边 13 已知两角一边
(正弦定理求边)
说明:如右图所示,在角度栏 输任两个角值和在已知边栏 输入任意一边的值即可计算
Sb c
Sa
a
b
Sc
顶角 ° ′ ″
已知边
所求边
a 45 26 35 Sa 100.000 Sa= 100.000
b 82 54 06
(系数)a
a1
1.50
a2
3.50
(系数)b b1 2.50 b2 -1.00
18
三元一次方程组 (X,Y,Z为未知数)
a1*X+b1*Y+c1*Z=d1 a2*X+b2*Y+c2*Z=d2 a3*X+b3*Y+c3*Z=d3 a、b、c为系数,d为常数项
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高速公路的一些线路计算
一、缓和曲线上的点坐标计算
已知:①缓和曲线上任一点离ZH 点的长度:l
②圆曲线的半径:R ③缓和曲线的长度:l 0 ④转向角系数:K(1或-1) ⑤过ZH 点的切线方位角:α ⑥点ZH 的坐标:x Z ,y Z 计算过程:
y y ⑼y x x ⑻x αSsin y ⑺αScos x ⑹90
ααα⑸y x ⑷S 180n x y arctg
α⑶l 3456R l l 40R l l y ⑵)K
R
336l l 6Rl l (x ⑴Z
1Z 11111012
0200
040
49202503307
03
0+=+===-+=+=⋅+=+-=-=
说明:当曲线为左转向时,K=1,为右转向时,K=-1,
公式中n 的取值如下:
⎪⎩
⎪
⎨⎧=<<⎪⎩
⎪
⎨⎧=><⎪⎩
⎪
⎨⎧=<>⎪⎩
⎪
⎨⎧=>>1n 0y 0x 1n 0y 0x 2n 0y 0x 0n 0y 0x 00000000 当计算第二缓和曲线上的点坐标时,则: l 为到点HZ 的长度
α为过点HZ 的切线方位角再加上180° K 值与计算第一缓和曲线时相反 x Z ,y Z 为点HZ 的坐标
切线角计算公式:2Rl l
β0
2
=
二、圆曲线上的点坐标计算
已知:①圆曲线上任一点离ZH 点的长度:l
②圆曲线的半径:R ③缓和曲线的长度:l 0 ④转向角系数:K(1或-1) ⑤过ZH 点的切线方位角:α ⑥点ZH 的坐标:x Z ,y Z 计算过程:
y y ⑿y x x ⑾x αSsin y ⑽αScos x ⑼90α
αα⑻y x ⑺S 180n x y arctg
α⑹m Rsinα'y ⑸p]K )cosα'[R(1x ⑷34560R l 240R l 2l ⑶m 2688R l 24R l ⑵p Rπ)l -90(2l ⑴α'Z
1Z 11111012
0200
0004
5
23003
40
200+=+===-+=+=⋅+=+=+-=+
-=-
==
说明:当曲线为左转向时,K=1,为右转向时,K=-1,
公式中n 的取值如下:
⎪⎩
⎪
⎨⎧=<<⎪⎩
⎪
⎨⎧=><⎪⎩
⎪
⎨⎧=<>⎪⎩
⎪
⎨⎧=>>1n 0y 0x 1n 0y 0x 2n 0y 0x 0n 0y 0x 00000000 当只知道HZ 点的坐标时,则: l 为到点HZ 的长度
α为过点HZ 的切线方位角再加上180° K 值与知道ZH 点坐标时相反 x Z ,y Z 为点HZ 的坐标
三、曲线要素计算公式
β
+∆=+=+=+-=++=++++-=
++++-=-=
-=
+-
=+-==
=
+=+==
D l l :β
R R R
2R P P 2β⒀曲线段长度:l )
l l (21
RαL ⑿圆曲线长度)
l l (21
Rα⑾曲线全长度:L m 2α
2R)tg p p (212α2tg
p p T ⑽第二切线长:m 2α
2R)tg p p (212α2tg
p p T ⑼第一切线长:2688R l 24R l p ⑻第二曲线平移量:2688R l 24R l p ⑺第一曲线平移量:34560R l 240R l 2l m ⑹第二曲线顺移量:34560R l 240R l 2l m ⑸第一曲线顺移量:2R
l β:⑷第二缓曲段总转角值2R l β:⑶第一缓曲段总转角值)l
P P (21l R R 2R
R :β⑵曲线段任意点转角值2Rl l :β⑴缓曲段任意点转角值2
1212121021221212121121
34
222
23
41
2114
52232224
512311
12
21
12121210
2
的边缘曲线长度⒁偏离缓曲:D 公式中各符号说明:
l ——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度) l 1——第一缓和曲线长度 l 2——第二缓和曲线长度 l 0——对应的缓和曲线长度 R ——圆曲线半径 R 1——曲线起点处的半径 R 2——曲线终点处的半径 P 1——曲线起点处的曲率 P 2——曲线终点处的曲率 α——曲线转角值
四、竖曲线上高程计算
已知:①第一坡度:i 1(上坡为“+”,下坡为“-”)
②第二坡度:i 2(上坡为“+”,下坡为“-”) ③变坡点桩号:S Z ④变坡点高程:H Z ⑤竖曲线的切线长度:T ⑥待求点桩号:S
l
E 0
i 1
i 2
H
Hz
S
Sz
R
T
T
计算过程:
)i i T(412R T E ⑷i Ri 2
12R )i i R(21l H ⑶H i i 2T
⑵R (带有符号)
S S l ⑴122
02
1212
Z 1
2Z -==-⎥⎦⎤⎢⎣⎡+++=-=
-=
五、超高缓和过渡段的横坡计算
L x
i1i
i2
过渡段起点
过渡段终点待求点
横坡(+)
(-)
已知:如图,
第一横坡:i
1
第二横坡:i
2
过渡段长度:L
待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i
解:d=x/L
i=(i
2-i
1
)(1-3d2+2d3)+i
1
六、匝道坐标计算 已知:①待求点桩号:K
②曲线起点桩号:K 0 ③曲线终点桩号:K 1 ④曲线起点坐标:x 0,y 0 ⑤曲线起点切线方位角:α0
⑥曲线起点处曲率:P 0(左转为“-”,右转为“+”) ⑦曲线终点处曲率:P 1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:x,y
②待求点的切线方位角:αT 计算过程:
ααα Bcos NAsinT y y BsinT NAcosT x x 42240C
l l 336C l l 6C l l B 3456C l l 40C l l )l (l A /2C l N αT )/2/C
l S(l α P P l C SN l l )P /(P P Nl l K K l )P SGN(P N 时:P P ⑶当αα )/P cosα(cosαy y )/P sinα(sinαx x αSP α 0时:P P ⑵当αα Ssinαy y Scosαx x 0时:P P ⑴当K -K S 1
0T 005
110
1137073034
90
9
250502
00010
1S 0010S 00
1S 01101
T 101010100
11100
T 0000100
+=++=-+=-+---=-+---=-=+=-=
+=-=-=-=≠=--=-+=+=≠==+=+====
T。
