3第三章投入产出核算
合集下载
第3章投入产出核算ppt课件
②产品部门分得越细，其同质性越好；但实际划分 时应兼顾需要与可能。例如，我国的2002年投入产 出表划分123个二级部门，42个一级部门；公布资 料时更简化。
③在现实经济生活中，产品部门无法直接观察到； 但它仍然是一种合理抽象，其资料可用适当方法推 算出来。基本过程为：
实际投入产出资料→产业部门资料→产品部门资料
从使用情况来看，闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ，但在 近些年 的城市 地下工 程施工 中已很 少使用 ，在此 不再说 明。
（二）投入产出法的产生和发
展
法国重农学者魁奈：“经济表”； 马克思：“社会再生产理论”，两大部类比例关系； 瓦尔拉斯：“一般均衡理论模型”，多部门间的比例关系； 1920年代，前苏中央统计局：社会产品棋盘式平衡表； 1930年代，瓦西里•列昂节夫：投入产出表和经济数学模型； 二战后，投入产出法广泛应用于经济管理实践，形成现代经济
➢ [3]刘起运、陈璋、苏汝劼编著：《投入产 出分析》，中国人民大学出版社，2006
从使用情况来看，闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ，但在 近些年 的城市 地下工 程施工 中已很 少使用 ，在此 不再说 明。
§
3.1
产业关联与投入产出
表
一、投入产出法及其产生和发展 （一）产业关联性与投入产出核算 生产过程从产出看，各部门相互提供产品； 生产过程从投入看，各部门相互消耗产品。
（三）投入产出表的两个方向
横表：Ⅰ＋Ⅱ，反映各部门的产出及其使 用去向，即“产品分配”过程；
竖表：Ⅰ＋Ⅲ，反映各部门的投入及其提 供来源，即“价值形成”过程。
“横表”和“竖表”各自存在一定的平衡 关系，彼此之间又在总量上相互制约，构 成投入产出表建模分析的基础框架。
③在现实经济生活中，产品部门无法直接观察到； 但它仍然是一种合理抽象，其资料可用适当方法推 算出来。基本过程为：
实际投入产出资料→产业部门资料→产品部门资料
从使用情况来看，闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ，但在 近些年 的城市 地下工 程施工 中已很 少使用 ，在此 不再说 明。
（二）投入产出法的产生和发
展
法国重农学者魁奈：“经济表”； 马克思：“社会再生产理论”，两大部类比例关系； 瓦尔拉斯：“一般均衡理论模型”，多部门间的比例关系； 1920年代，前苏中央统计局：社会产品棋盘式平衡表； 1930年代，瓦西里•列昂节夫：投入产出表和经济数学模型； 二战后，投入产出法广泛应用于经济管理实践，形成现代经济
➢ [3]刘起运、陈璋、苏汝劼编著：《投入产 出分析》，中国人民大学出版社，2006
从使用情况来看，闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ，但在 近些年 的城市 地下工 程施工 中已很 少使用 ，在此 不再说 明。
§
3.1
产业关联与投入产出
表
一、投入产出法及其产生和发展 （一）产业关联性与投入产出核算 生产过程从产出看，各部门相互提供产品； 生产过程从投入看，各部门相互消耗产品。
（三）投入产出表的两个方向
横表：Ⅰ＋Ⅱ，反映各部门的产出及其使 用去向，即“产品分配”过程；
竖表：Ⅰ＋Ⅲ，反映各部门的投入及其提 供来源，即“价值形成”过程。
“横表”和“竖表”各自存在一定的平衡 关系，彼此之间又在总量上相互制约，构 成投入产出表建模分析的基础框架。
第三章 投入产出核算
Ei
b
j 1 n i 1
n
ij n
（
i 1, 2,, n
）
1 n bij
j 1
第二讲
1 2 …
投入产出核算
j
SNA
n
b12 … 2 b21 b22 … … … … …
1
b11
b1 j
… …
n
b1n
b
j
b2 j b2n j 1 … …
投入产出核算
最终使用 小计 总产出
SNA
n
x11 x21 xn1
x12 x22 xn 2
x1n x2 n xnn
x1 j
j 1 n
n
Y1 Y2 Yn
x2 j
j 1
X1 X2 Xn
x
j 1
n
nj
小 计
xi1
i 1
n
xi 2
i 1
n
xin
二、投入产出的理论基础(P56) 一般均衡理论又称全部均衡理论
第二讲
投入产出核算
SNA
三、列昂惕夫对投入产出分析的贡献 1.将瓦尔拉斯模型体系中多得不可胜数的方程式和变量简 化到可以实际应用和计量的程度。 2.模型中省略了生产资源（生产要素）供给的影响，大大 缩减了一般均衡模型中所包括的联立方程组的数目。 3.从根本上改变了瓦尔拉斯的以论证一般均衡理论为目的 的模型体系，使投入产出分析模型成为以生产技术联系为基础 的研究经济系统各个部分间相互依存数量关系的分析方法，也 使这种方法有了实际应用的可能。
X ( I A)1Y
第二讲
（二）列模型
第三章投入产出核算
五、产业部门之间相互影响程度的分析
通过投入产出模型计算影响力系数和感 应度系数，可以分析产业部门之间的相 互影响程度。 影响力：指某一产业部门对各部门的 影响。 感应度：指某一产业部门受各部门的 影响。
影响力系数
影响力系数：反映某一产业部门对其他各部门 的影响程度。计算公式（第j部门增加单位最终 产品时对各部门的影响力）：
y1
x1
x2n
y2
x2
：：：
xnn
yn
xn
vn
xn
投入产出表的结构
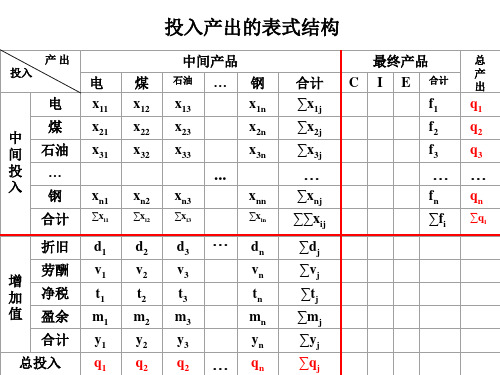
投入产出表由四个象限组成： 第Ⅰ象限：是投入产出表的核心，反映各产业部门 之间的技术经济联系 第Ⅱ象限：反映各产业部门提供的最终产品（规模 和结构） 第Ⅲ象限：反映各产业部门的最初投入（增加值） 第Ⅳ象限：目前未编制
第Ⅰ、Ⅱ象限结合：反映各部门产出的使用去向 第Ⅰ、 Ⅲ象限结合：反映各部门投入的来源和价值形
直接消耗系数矩阵
将第Ⅰ象限每个部门的中间投入数据分 别除以本部门的产出，便得到直接消耗 系数矩阵：
x11 X1
A
x21
X1
xn1 X1
x12 X2 x22 X2
xn 2 X2
x1n Xn x2 n Xn
xn 2 Xn
a11 a21
an1
a12 a22
a1n a2n
为反映某产品的产出与为生产该产品而 完全消耗的各种产品之间的关系，需引 入完全消耗系数。
完全消耗系数的计算
完全消耗=直接消耗+间接消耗
完全消耗系数bij：
n
nn
bij aij aik akj
ais ask akj
k 1
s1 k 1
B bij nn A A2 A3
第三章_投入产出核算习题_答案)
6. 目前我国公布的投入产出表是_A__。
A. 产品部门×产品部门 C. 产业部门×产品部门
B.产品部门×产业部门 B.产业部门×产业部门.
7.B(I A )1 被称为列昂惕夫逆矩阵，它蕴含着丰富的经济意义。下列关于列 昂惕夫逆矩阵说法错误的是__D_。 A. 列昂惕 第Ⅲ象限的行标题包括 ABCD。 A. 固定资产折旧 C. 生产税净额 B. D. 劳动者报酬 营业盈余 E. 存货增加
新疆财经大学
国民经济核算
2.投入产出表的基本平衡关系有 ACE A. 中间投入+最初投入=总投入 B. 中间使用+最终使用+进口=总产出 C. 中间使用+最终使用=总产出 D. 总投入=总产出+进口 E. 总投入=总产出 3. A. B. C. D. E. 关于投入产出表的第Ⅰ象限，下列说法正确的是 ABCE 行标题是中间投入 列标题是中间投入 其含义可以从行向和列向两个方向解读 反映的是最终产品的规模和结构 反映国民经济各产业部门之间的技术经济联系
B. b 表示j部门增加一个单位最终使用时，对i 部门的完全需求量 ij C. 列昂惕夫逆矩阵和完全消耗系数的关系是 B BI
D. 以上说法至少有一个是错误的
新疆财经大学
国民经济核算
8. 在一个三产业投入产出表中，直接消耗系数a 的数值为0.2864， 21 则它所代表的含义是_A__. A. 第一产业生产1单位总产出对第二产业的消耗量 B. 第二产业生产1单位总产出对第一产业的消耗量 C. 第一产业产品分配给第二产业使用部分所占的比例 D. 第二产业产品分配给第一产业使用部分所占的比例
B. 前者只包括主要生产活动也包括次要生产活动，而后者仅包括 一种生产活动 C. 后者既包括主要生产活动也包括次要生产活动，而前者仅包括 一种生产活动
教学课件第三章投入产出核算
12
第一节 投入产出表的基本概念和数据
二、 投入产出表的结构
第Ⅰ、Ⅱ象限连接在一起，通过各横行反 映各产业部门的产品分配和使用去向; 第I、Ⅲ象限连接在一起,各纵行反映各产业 部门在生产中的投入和来源，也反映生产过 程的价值形成。
2007-9-13
13
第一节 投入产出表的基本概念和数据
三、 投入产出表中的基本平衡关系
四、我国的投入产出表
我国现行使用的投入产出表编制使用供给表(V表）和 使用表(U表)方式搜集数据。供给表(V表)和使用表(U 表)，因为第一象限中的中间投入和中间产品使用的部 门分类不一致，而被称为非对称型投入产出表。 在搜集好供给表和使用表后，可以推算出产品部门 x 产品部门的投入产出表。被推算出来的产品部门x产 品部门的投入产出表，因为第一象限中的中间投入和 中间产品都是按照一致的产品部门分类的，因此，也 称为对称型投入产出表。
二、 投入产出表的结构
➢第Ⅰ象限(中间产品象限)
第Ⅰ象限反映按购买者价格计算的中间消耗。 行表示产出，表明每个产业部门的产品提供给各 个产业部门作为生产消耗使用的数量，称为中间产 品或中间使用，行的总计反映了产业部门的中间使 用。 列表示投入，它表明每个产业部门在生产过程中 消耗各个产业部门的产品数量，称为中间投入或中 间消耗。列的总计反映了产业部门的中间投入。
投入产出表种类：教材P45。货币为计量单位的静态宏观
价值型投入产出表（教材P48表3-3、4）。
2007-9-13
3
投入产出表一般格式
产出
投入
1
中
1
x11
间
2
x21
投 ┇┇
入 n xn1
最初投入 v1
总投入 X1
国民经济统计学 第3章中间消耗及投入产出核算
第三章中间消耗与投入产出核算学习目标1.理解中间消耗与投入产出核算的基本原理；2.掌握直接消耗、间接消耗和完全消耗的计算方法；3.了解投入产出表的编制方法；4.掌握投入产出表的应用分析方法。
投入产出核算是国民经济生产总量核算的延伸和发展，它侧重于中间产品的核算，能提供更为丰富、详细的信息，是国民经济核算体系中实物流量核算的一种重要而有效的方法。
本章主要阐述中间消耗与投入产出核算的基本原理，直接消耗、间接消耗和完全消耗系数的计算方法、投入产出表的编制原理和基本方法及其应用分析。
第一节中间消耗与投入产出核算的基本原理一、中间消耗和投入产出的含义中间消耗反映各部门之间的技术经济联系。
在我国以前沿用的物质生产的MPS体系中，只计算物质生产，中间消耗只限于物质消耗。
但现在所采用的SNA体系，不仅包括物质生产还包括了服务生产，从而中间消耗也得到了拓展，既包括了物质消耗，又包括了生产中的各种劳务消耗。
所谓中间消耗由生产过程中所消耗的货物和服务的价值构成，其中不包括固定资产。
这些货物和服务在生产过程中不是被完全用掉了就是被改变了形式。
有些物质投入在生产过程中其物质形式被改变并形成产出之后又会重新出现在新的生产过程中，如：铁矿石在生产中被炼成钢铁之后，又会进入新的生产过程，比如汽车制造。
投入分初始投入，即增加值投入，和中间投入，即中间消耗。
因此，投入具体指生产中投入的各种原材料、燃料、劳务，以及固定资产。
产出指的是生产活动中所生产的产品——货物和服务。
投入产出核算就是应用投入产出方法编制投入产出表，建立投入产出模型来分析国民经济中各部门之间经济和技术关系的宏观数量方法。
它是美国经济学家W.列昂惕夫在1931年开始提出的，1936年，他撰写了《美国经济制度中投入产出数量关系》一文，由此创立了投入产出分析方法，并因此获得了1973年的第五届诺贝尔经济学奖。
整个投入产出核算包括投入产出调查、编制投入产出表、建立投入产出模型和投入产出的分析应用。
3第三章投入产出核算
浙江财经学院
你能准确理解 投入产出表中 数据的实际含
义吗？
6
《国民经济核算》课件
根据投入产出表进行GDP核算
生产法
GDP ＝第一产业总产出－第一产业中间投入合计
＋第二产业总产出－第二产业中间投入合计 ＋第三产业总产出－第三产业中间投入合计
即GDP＝(26448－11152)＋(172970－124517) ＋(58135－29537)
❖ 掌握投入产出核算与国内生产总值核算的关系
❖ 了解编制投入产出表的调查方法
❖ 掌握用非调查方法编表的技术
❖ 掌握运用投入产出表进行经济分析的思路和方法
浙江财经学院
3
《国民经济核算》课件
第一节 投入产出表的结构与内涵
❖ 投入产出表入门 ❖ 根据投入产出表进行GDP核算 ❖ 投入产出表的优势
浙江财经学院
2、由以下五部分数据构成：
总产出、最初投入、中间投入、最终使用、 进出口部分
浙江财经学院
17
《国民经济核算》课件
总产出
1、农业总产出
农业部门总产出加上商业部门代征的农产品税
2、工业总产出
1)现有核算资料是规模以上企业的数据，而 投入产出表中的总产出应包括全部企业的产值；
2)现有核算资料是产业部门口径，而投入产出表 是产品部门口径；
本地区部门对进口品 的中间消耗
n×n
消费
对本地区产品 的消费
对进口品的消 费
最终使用 投资
由本地区产品形成的 固定资产和存货
由进口品形成 的固定资产和存货
出口
本地区产 品
的出口
进口品的 出口
总投入
总产出 本地区总产出
总进口
最初投入
你能准确理解 投入产出表中 数据的实际含
义吗？
6
《国民经济核算》课件
根据投入产出表进行GDP核算
生产法
GDP ＝第一产业总产出－第一产业中间投入合计
＋第二产业总产出－第二产业中间投入合计 ＋第三产业总产出－第三产业中间投入合计
即GDP＝(26448－11152)＋(172970－124517) ＋(58135－29537)
❖ 掌握投入产出核算与国内生产总值核算的关系
❖ 了解编制投入产出表的调查方法
❖ 掌握用非调查方法编表的技术
❖ 掌握运用投入产出表进行经济分析的思路和方法
浙江财经学院
3
《国民经济核算》课件
第一节 投入产出表的结构与内涵
❖ 投入产出表入门 ❖ 根据投入产出表进行GDP核算 ❖ 投入产出表的优势
浙江财经学院
2、由以下五部分数据构成：
总产出、最初投入、中间投入、最终使用、 进出口部分
浙江财经学院
17
《国民经济核算》课件
总产出
1、农业总产出
农业部门总产出加上商业部门代征的农产品税
2、工业总产出
1)现有核算资料是规模以上企业的数据，而 投入产出表中的总产出应包括全部企业的产值；
2)现有核算资料是产业部门口径，而投入产出表 是产品部门口径；
本地区部门对进口品 的中间消耗
n×n
消费
对本地区产品 的消费
对进口品的消 费
最终使用 投资
由本地区产品形成的 固定资产和存货
由进口品形成 的固定资产和存货
出口
本地区产 品
的出口
进口品的 出口
总投入
总产出 本地区总产出
总进口
最初投入
第三章投入产出核算
1.20 0.54 0.60
三、各部门总产量变化对增加值的影响— —列模型
如，表4-1中，假定3个部门的总产出分别增加20、60 、40，各部门增加值增量为：
y (I Aˆc )q
y1 1 0 0 0.3684 0
0 20 12.63
y2 0 1 0 0 0.7111 0 60 17.33
am1
am2
...
amn
m1
m2
...
mn
0
0
...
qn1
完全消耗系数B
B (I A)1 I
完全需求系数：
(I A)1
产品模型（实物模型）(1)
n
j1
xij aij
fi
xij qj
qi
n
aijq j
j 1
fi
qi
（i,j=1,2,…n）
展开为线形方程组：
a11q1 a12q2 ... a1nqn f1 q1
f
n
(I A)q f q (I A)1 f
价值模型(1)
n
xij y j i1
q
j
n
aijq j y j
qj
xij aijq j i1
展开为线形方程组：
（i,j=1,2,…n）
a11q1 a21q1 ... an1q1 y1 q1
a12q2 a22q2 ... an2q2 y2 q2
)
0 ...
0
0 1 ac2
... 0
... 0
...
0
... ...
...
1
acn
n
acj aij
i1
中间流量模型
三、各部门总产量变化对增加值的影响— —列模型
如，表4-1中，假定3个部门的总产出分别增加20、60 、40，各部门增加值增量为：
y (I Aˆc )q
y1 1 0 0 0.3684 0
0 20 12.63
y2 0 1 0 0 0.7111 0 60 17.33
am1
am2
...
amn
m1
m2
...
mn
0
0
...
qn1
完全消耗系数B
B (I A)1 I
完全需求系数：
(I A)1
产品模型（实物模型）(1)
n
j1
xij aij
fi
xij qj
qi
n
aijq j
j 1
fi
qi
（i,j=1,2,…n）
展开为线形方程组：
a11q1 a12q2 ... a1nqn f1 q1
f
n
(I A)q f q (I A)1 f
价值模型(1)
n
xij y j i1
q
j
n
aijq j y j
qj
xij aijq j i1
展开为线形方程组：
（i,j=1,2,…n）
a11q1 a21q1 ... an1q1 y1 q1
a12q2 a22q2 ... an2q2 y2 q2
)
0 ...
0
0 1 ac2
... 0
... 0
...
0
... ...
...
1
acn
n
acj aij
i1
中间流量模型
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二者是中间过渡性核算结果
4）产业部门×产业部门表（很少使用）
2020/6/8
浙江财经学院
12
《国民经济核算》课件
投入产出表中的价格
1）购买者价格
购买者价格是指购买者购买单位货物或服务所实 际支付的价格；
2）生产者价格
生产者价格是购买者价格扣除商业附加费、运输费 后的部分；
3）基本价格
基本价格是生产者价格扣除生产者所支付的产品税 净额后的部分。
2020/6/8
浙江财经学院
4
《国民经济核算》课件
投入产出表入门
表3－1 中国2000年三部门投入产出表 单位：亿元
中间使用
第一 产业
第二 产业
第三 产业
合计
居民 消费
最终使用
政府 消费
固定资本 形成总额
存货 增加
出口
合计
进口 总产出
第一产业
中 间
第二产业
投 入 第三产业
合计
固定资产折旧
劳动者报酬 最 生产税净额 初 投 入 营业盈余
图3-1：投入产出表的四个象限
浙江财经学院
你能准确理解 投入产出表中 数据的实际含
义吗？
6
《国民经济核算》课件
根据投入产出表进行GDP核算
生产法
GDP ＝第一产业总产出－第一产业中间投入合计
＋第二产业总产出－第二产业中间投入合计 ＋第三产业总产出－第三产业中间投入合计
即GDP＝(26448－11152)＋(172970－124517) ＋(58135－29537)
我国的投入产出表采用生产者价格编制 。
2020/6/8
浙江财经学院
13
《国民经济核算》课件
投入产出表的具体部门分类
1、国际标准产业分类(International Standard Industry Classification，ISIC)
2、全球贸易分析项目（GTAP）部门分类 体系（GTAP Sectoral Classification, revision 2，GSC2）
30946 -501 19268 70899 18137 172970
954
-8
3346 28227 -1002
58135
32624 -124 23199 111776 19682 257553
597
8598
5411 14606
13443 20863 15614 49920
415
8889
4108 13412
841 10103
3465 14409
15296 48453 28598 92347
26448 172970 58135 257553
浙江财经学院
5
《国民经济核算》课件
投入产出表入门(续)
第Ⅰ象限 中间投入/中间使用流量
第Ⅱ象限 最终使用流量
第Ⅲ象限 最初投入（收入形成）流量
第Ⅳ象限 ？
2020/6/8
＝92347
2020/6/8
浙江财经学院
7
《国民经济核算》课件
根据投入产出表进行GDP核算
收入法
GDP＝固定资产折旧（14606）＋劳动者报酬（49920） ＋生产税净额 （13412）＋营业盈余（14409）
＝92347
支出法
GDP＝居民消费合计(44372)＋政府消费合计(11705) ＋固定资本形成总额合计（32624）＋存货净变化 合计(-124)＋出口合计(23199)-进口合计(19682)
投入产出表如何揭 示各部门之间的关联 关系？
2020/6/8
浙江财经学院
9
《国民经济核算》课件
第二节 投入产出表的数据口径
❖ 投入产出表中的部门 ❖ 投入产出表的价格 ❖ 投入产出表的具体部门分类 ❖ 进口的处理
2020/6/8
浙江财经学院
10
《国民经济核算》课件
投入产出表中的部门
应用了产业部门，但却不是一般意义上的 产业部门,而是更具有同质性的产品部门。
本地区部门对进口品 的中间消耗 n×n
最
固定资产折旧
初
劳动报酬
投
生产税净额
入
营业盈余
总投入
消费 对本地区产品
的消费
对进口品的消费
最终使用 投资
由本地区产品形成的 固定资产和存货
出口
本地区产品 的出口
3、不同部门分类之间对应关系相当复杂， 不能简单转换。
2020/6进口的处理
两种处理方式：
1）进口品作为一列 2）进口品按使用方向详列成矩阵
中间使用
n个部门
中 间
本地区产品
n 个 部 门
本地区部门对本地区 产品的中间消耗 n×n
投 入
进口品
n 个 部 门
本章学习目标
❖ 掌握投入产出表的基本思想及表中元素的实际意义
❖ 掌握投入产出核算与国内生产总值核算的关系
❖ 了解编制投入产出表的调查方法
❖ 掌握用非调查方法编表的技术
❖ 掌握运用投入产出表进行经济分析的思路和方法
2020/6/8
浙江财经学院
3
《国民经济核算》课件
第一节 投入产出表的结构与内涵
❖ 投入产出表入门 ❖ 根据投入产出表进行GDP核算 ❖ 投入产出表的优势
＝92094
由于数据来源不同，投入产出中支出法的GDP不等于生 产法和收入法的GDP，存在一定的误差，即统计误差为：
92347-92094=253
2020/6/8
浙江财经学院
8
《国民经济核算》课件
投入产出表的优势
❖ 投入产出表在某种意义上就是多部门国内生产 总值核算；
❖ 投入产出表通过其多部门结构,简洁明了地揭示 了各部门之间错综复杂的关联关系。
1）产业部门：基于基层单位来界定 2）产品部门：基于同质生产单位来定义
2020/6/8
浙江财经学院
11
《国民经济核算》课件
投入产出表中的部门（续）
因产业部门与产品部门口径之不同,分为：
1）产品部门×产品部门表
在投入产出表的建模应用中使用最为广泛， 是进行投入产出分析的基础。
2）产品部门×产业部门表（又称U表） 3）产业部门×产品部门表（又称V表）
《国民经济核算》课件
第三章 投入产出核算
2020/6/8
浙江财经学院
1
《国民经济核算》课件
第一节 投入产出表的结构与内涵 第二节 投入产出表的数据口径 第三节 编制投入产出表的调查方法 第四节 编制投入产出表的非调查方法 第五节 投入产出表的应用
2020/6/8
浙江财经学院
2
《国民经济核算》课件
增加值 总投入
2020/6/8
4036
8799
1149 13984
10956
0
5473 1644
97931 17786
16508 119911 11880 31311
21186 12230
0 11705
11152 124517 29537 165206
44372 11705
724 385
585 12649 -543 26448
4）产业部门×产业部门表（很少使用）
2020/6/8
浙江财经学院
12
《国民经济核算》课件
投入产出表中的价格
1）购买者价格
购买者价格是指购买者购买单位货物或服务所实 际支付的价格；
2）生产者价格
生产者价格是购买者价格扣除商业附加费、运输费 后的部分；
3）基本价格
基本价格是生产者价格扣除生产者所支付的产品税 净额后的部分。
2020/6/8
浙江财经学院
4
《国民经济核算》课件
投入产出表入门
表3－1 中国2000年三部门投入产出表 单位：亿元
中间使用
第一 产业
第二 产业
第三 产业
合计
居民 消费
最终使用
政府 消费
固定资本 形成总额
存货 增加
出口
合计
进口 总产出
第一产业
中 间
第二产业
投 入 第三产业
合计
固定资产折旧
劳动者报酬 最 生产税净额 初 投 入 营业盈余
图3-1：投入产出表的四个象限
浙江财经学院
你能准确理解 投入产出表中 数据的实际含
义吗？
6
《国民经济核算》课件
根据投入产出表进行GDP核算
生产法
GDP ＝第一产业总产出－第一产业中间投入合计
＋第二产业总产出－第二产业中间投入合计 ＋第三产业总产出－第三产业中间投入合计
即GDP＝(26448－11152)＋(172970－124517) ＋(58135－29537)
我国的投入产出表采用生产者价格编制 。
2020/6/8
浙江财经学院
13
《国民经济核算》课件
投入产出表的具体部门分类
1、国际标准产业分类(International Standard Industry Classification，ISIC)
2、全球贸易分析项目（GTAP）部门分类 体系（GTAP Sectoral Classification, revision 2，GSC2）
30946 -501 19268 70899 18137 172970
954
-8
3346 28227 -1002
58135
32624 -124 23199 111776 19682 257553
597
8598
5411 14606
13443 20863 15614 49920
415
8889
4108 13412
841 10103
3465 14409
15296 48453 28598 92347
26448 172970 58135 257553
浙江财经学院
5
《国民经济核算》课件
投入产出表入门(续)
第Ⅰ象限 中间投入/中间使用流量
第Ⅱ象限 最终使用流量
第Ⅲ象限 最初投入（收入形成）流量
第Ⅳ象限 ？
2020/6/8
＝92347
2020/6/8
浙江财经学院
7
《国民经济核算》课件
根据投入产出表进行GDP核算
收入法
GDP＝固定资产折旧（14606）＋劳动者报酬（49920） ＋生产税净额 （13412）＋营业盈余（14409）
＝92347
支出法
GDP＝居民消费合计(44372)＋政府消费合计(11705) ＋固定资本形成总额合计（32624）＋存货净变化 合计(-124)＋出口合计(23199)-进口合计(19682)
投入产出表如何揭 示各部门之间的关联 关系？
2020/6/8
浙江财经学院
9
《国民经济核算》课件
第二节 投入产出表的数据口径
❖ 投入产出表中的部门 ❖ 投入产出表的价格 ❖ 投入产出表的具体部门分类 ❖ 进口的处理
2020/6/8
浙江财经学院
10
《国民经济核算》课件
投入产出表中的部门
应用了产业部门，但却不是一般意义上的 产业部门,而是更具有同质性的产品部门。
本地区部门对进口品 的中间消耗 n×n
最
固定资产折旧
初
劳动报酬
投
生产税净额
入
营业盈余
总投入
消费 对本地区产品
的消费
对进口品的消费
最终使用 投资
由本地区产品形成的 固定资产和存货
出口
本地区产品 的出口
3、不同部门分类之间对应关系相当复杂， 不能简单转换。
2020/6进口的处理
两种处理方式：
1）进口品作为一列 2）进口品按使用方向详列成矩阵
中间使用
n个部门
中 间
本地区产品
n 个 部 门
本地区部门对本地区 产品的中间消耗 n×n
投 入
进口品
n 个 部 门
本章学习目标
❖ 掌握投入产出表的基本思想及表中元素的实际意义
❖ 掌握投入产出核算与国内生产总值核算的关系
❖ 了解编制投入产出表的调查方法
❖ 掌握用非调查方法编表的技术
❖ 掌握运用投入产出表进行经济分析的思路和方法
2020/6/8
浙江财经学院
3
《国民经济核算》课件
第一节 投入产出表的结构与内涵
❖ 投入产出表入门 ❖ 根据投入产出表进行GDP核算 ❖ 投入产出表的优势
＝92094
由于数据来源不同，投入产出中支出法的GDP不等于生 产法和收入法的GDP，存在一定的误差，即统计误差为：
92347-92094=253
2020/6/8
浙江财经学院
8
《国民经济核算》课件
投入产出表的优势
❖ 投入产出表在某种意义上就是多部门国内生产 总值核算；
❖ 投入产出表通过其多部门结构,简洁明了地揭示 了各部门之间错综复杂的关联关系。
1）产业部门：基于基层单位来界定 2）产品部门：基于同质生产单位来定义
2020/6/8
浙江财经学院
11
《国民经济核算》课件
投入产出表中的部门（续）
因产业部门与产品部门口径之不同,分为：
1）产品部门×产品部门表
在投入产出表的建模应用中使用最为广泛， 是进行投入产出分析的基础。
2）产品部门×产业部门表（又称U表） 3）产业部门×产品部门表（又称V表）
《国民经济核算》课件
第三章 投入产出核算
2020/6/8
浙江财经学院
1
《国民经济核算》课件
第一节 投入产出表的结构与内涵 第二节 投入产出表的数据口径 第三节 编制投入产出表的调查方法 第四节 编制投入产出表的非调查方法 第五节 投入产出表的应用
2020/6/8
浙江财经学院
2
《国民经济核算》课件
增加值 总投入
2020/6/8
4036
8799
1149 13984
10956
0
5473 1644
97931 17786
16508 119911 11880 31311
21186 12230
0 11705
11152 124517 29537 165206
44372 11705
724 385
585 12649 -543 26448