第一章 信号及其描述练习作业答案
信号与系统课后习题答案—第1章

第1章 习题答案1-1 题1-1图所示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?解: ① 连续信号:图(a)、(c)、(d ); ② 离散信号:图(b ); ③ 周期信号:图(d); ④ 非周期信号:图(a )、(b )、(c); ⑤有始信号:图(a )、(b)、(c ).1-2 已知某系统的输入f (t )与输出y(t )的关系为y(t)=|f(t)|,试判定该系统是否为线性时不变系统。
解: 设T 为此系统的运算子,由已知条件可知: y (t)=T [f (t)]=|f (t)|,以下分别判定此系统的线性和时不变性。
① 线性 1)可加性不失一般性,设f (t )=f 1(t )+f 2(t ),则y 1(t)=T[f 1(t )]=|f 1(t)|,y 2(t )=T [f 2(t)]=|f 2(t )|,y (t )=T [f (t )]=T[f 1(t )+f 2(t )]=|f 1(t )+f 2(t )|,而|f 1(t)|+|f 2(t)|≠|f 1(t )+f 2(t )|即在f 1(t)→y 1(t)、f 2(t)→y 2(t )前提下,不存在f 1(t )+f 2(t )→y 1(t)+y 2(t ),因此系统不具备可加性。
由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性。
2)齐次性由已知条件,y(t )=T[f(t)]=|f (t )|,则T [af(t)]=|af(t )|≠a|f(t )|=ay (t ) (其中a 为任一常数)即在f(t )→y(t )前提下,不存在af (t )→ay(t ),此系统不具备齐次性,由此亦可判定此系统为一非线性系统。
② 时不变特性由已知条件y(t )=T [f(t)]=|f (t)|,则y(t-t 0)=T [f (t —t 0)]=|f (t-t 0)|, 即由f (t)→y(t ),可推出f (t —t 0)→y(t —t 0),因此,此系统具备时不变特性。
信号与系统课后习题与解答第一章

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
信号与系统课后习题与解答第一章
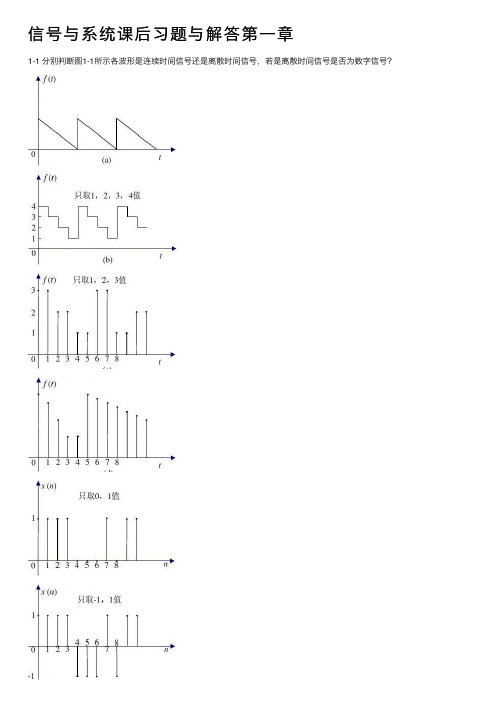
信号与系统课后习题与解答第⼀章1-1 分别判断图1-1所⽰各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解信号分类如下:--???--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所⽰信号分别为(a )连续信号(模拟信号);(b )连续(量化)信号;(c )离散信号,数字信号;(d )离散信号;(e )离散信号,数字信号;(f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所⽰问)(1))sin(t e at ω-;(2)nT e -;(3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221。
解由1-1题的分析可知:(1)连续信号;(2)离散信号;(3)离散信号,数字信号;(4)离散信号;(5)离散信号。
1-3 分别求下列各周期信号的周期T :(1))30t (cos )10t (cos -;(2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解判断⼀个包含有多个不同频率分量的复合信号是否为⼀个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为⾮周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最⼩公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
(3)因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-?=所以周期8162T ππ==。
(精品)信号与系统课后习题与解答第一章

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
信号与系统课后习题与解答第一章

1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21(a )连续信号(模拟信号);(b )连续(量化)信号;(c )离散信号,数字信号;(d )离散信号;(e )离散信号,数字信号;(f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问)(1);)sin(t e at ω-(2);nT e -(3);)cos(πn (4);为任意值)(00)sin(ωωn (5)。
221⎪⎭⎫ ⎝⎛解由1-1题的分析可知:(1)连续信号;(2)离散信号;(3)离散信号,数字信号;(4)离散信号;(5)离散信号。
1-3 分别求下列各周期信号的周期T :(1);)30t (cos )10t (cos -(2);j10t e (3);2)]8t (5sin [(4)。
[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期;对于分量cos (30t ),其周期。
由于5T 1π=15T 2π=为的最小公倍数,所以此信号的周期。
5π21T T 、5T π=(2)由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。
5102T ππ==(3)因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。
信号与系统课后习题与解答第一章

1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21(a )连续信号(模拟信号);(b )连续(量化)信号;(c )离散信号,数字信号;(d )离散信号;(e )离散信号,数字信号;(f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问)(1);)sin(t e at ω-(2);nT e -(3);)cos(πn (4);为任意值)(00)sin(ωωn (5)。
221⎪⎭⎫ ⎝⎛解由1-1题的分析可知:(1)连续信号;(2)离散信号;(3)离散信号,数字信号;(4)离散信号;(5)离散信号。
1-3 分别求下列各周期信号的周期T :(1);)30t (cos )10t (cos -(2);j10t e (3);2)]8t (5sin [(4)。
[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期;对于分量cos (30t ),其周期。
由于5T 1π=15T 2π=为的最小公倍数,所以此信号的周期。
5π21T T 、5T π=(2)由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。
5102T ππ==(3)因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。
信号与系统理论及应用 习题 - 第1章 -作业参考答案

i n2
x(i)
线性
n2
T [1 x1 (n) 2 x2 (n)] 1 y1 (n) 2 y2 (n)
T [ x(n n0 )]
n 2 n0 i n 2 n0
x(i ) y (n n0 )
系统的输出与过去时刻的输入有关,系统为记忆系统。 系统在任何时刻的输出响应与未来有关,系统为非因果系统。 系统输入有界,则系统输出也有界,故系统为稳定系统
1.4 画出下列信号的波形图,注意它们的区别。 (1) x1 (t ) tu(t ) (1)
X(t) tu(t)
(3) x3 (t ) (t 1)u (t )
(5) x5 (t ) t[u(t ) u(t 1)]
0
t
(3)
X(t)
(t+1)u(t)
1 0 t
(5)
X(t) 1 0 t[u(t)-u(t-1)
25(t
P lim
1 T T
T /2
T /2
x(t ) dt lim
2
1 T T
T /2
T /2
5sin 2 t 10sin 3 t dt
2
T T T 1 lim 25 2 [1 cos(4 t )]dt 100 2 [1 cos(6 t )]dt 100 2 sin 2 t sin 3 tdt 0 0 0 T T T T T T 25 sin 4 t 2 100 sin 6 t 2 10 50 2 2 (t ) |0 (t ) |0 sin 5 t |0 sin t |0 T 4 T 6 T T 25 50 25 25 62.5 2
第一章 信号及其描述练习作业答案

20
2、从示波器得到的周期信号x(t)的波形如下图所示,请从图中读出
信号x(t)的峰值XF 、均值μx、绝对均值μ|x|、周期T、频率f、标准差
σx、有效值xr.m.s。
解:
峰值 :xF = 1 均值: μx= 2 绝对均值: μ|x| = 2 周期 : T= 2
xt
3 2 1
0
1
频率 : f = 1/T=0.5
答案:C
9、时域信号持续时间延长,则频域中高频成分 。 A、不变 B、增加 C、减少 D、变化不定
10、时域信号波形变化缓慢,则高频分量 。 A、不变 B、增加 C、减少 D、变化不定
答案:B 答案:C
4
11、如果有 (t) 1 ,根据傅氏变换的 ,则有 (t t0 ) e jt
A、时移性质 B、频移性质 C、相似性质
关系。
×
16
12、 一个在时域有限区间内有值的信号,其频谱可延伸至无 √ 限频谱 13、信号的时域函数变化越缓慢,它包含的高频成分就越多。 ×
14、确定了幅值和频率,就可确定一个单频信号。
×
15、当信号的时间尺度压缩时,其频谱的频带加宽、幅值增高。 ×
17
四、论述题(论述说明下列题目) 1、周期信号的频谱具有的三个特点是什么?
D、 x (t)的自相关函数Rx(τ)的付氏逆变换
答案:B
1
3、下列 信号的频谱是连续的。
A、 x(t) Asin(t 1) B sin(3t 2 )
B、 x(t) 5sin 30t 3sin 50t
C、 x(t) et sin 0t D、 x(t) 5sin t 5cost
答案:C
18、由几个频率不同的正弦信号合成的周期信号,合成信号的周期 是。 A、各信号周期的最小公倍数 B、各信号周期的最大公约数 C、各信号周期的平均值 答案:A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6、如果一个信号的频谱是离散的,则该信号频率成分是
。
A、有限的 是无限的
B、无限的
C、可能是有限的,也可能 答案:C
7、连续周期信号的频谱是 A、离散、周期的 C、连续、非周期的
。 B、离散、非周期的
D、连续、周期的
精品课件
答案:A
3
8、时域信号持续时间压缩,则频域中低频成分
A、不变
B、增加
C、减少
D、 x (t)的自相关函数Rx(τ)的付氏逆变换
精品课件
答案:B D、 。不确
答案:B
1
3、下列
A、 B、 C、 D、
信号的频谱是连续的。
x ( t) A s in (t 1 ) B s in ( 3 t 2 )
x(t)5si3nt03sin5t0
x x((tt)) 5 es itn sitn 5 0c to st
是
。
A、各信号周期的最小公倍数
B、各信号周期的最大公约数
C、各信号周期的平均值
答案:A
精品课件
7
19、周期信号x(t)和y(t)为两个周期信号,T为其共同周期,其互
相
常数
关函数表达式为Rxy(τ) = A、与x(t)同周期的周期信号
。
B、逐步衰减为零 C、 答案:A
20、两个同频正弦信号的互相关函数
变带宽
减小,幅
值 14、已知
x(t) et
则
。 x(t)(t1)dt =
e
。
15、周期信号的频谱具有 离散
特点,瞬变非
周期信号
连续
的频谱具有
特点。
16、X(F)为X(T)的频谱,W(F)为矩形窗函数W(T)的频
谱,二者时域相乘,则频域可表示X(F)*W(F)
为
,连续的
该乘积后的信号的频谱为
频谱。
答案:C
4、信号x (t)和y(t)的互谱Sxy(f )是
。
A、 x (t)和y(t)的卷积的付氏变换
B、 x (t)和y(t)付氏变换的乘积
C、互相关函数Rxy(τ)的付氏变换 D、 x (t)和y(t)的付氏变换
答案:C
精品课件
2
5、傅氏级数中各系数表示各谐波分量的
A、相位
B、周期
C、振幅
。 D、频率 答案:C
。
A、只保留二信号的幅值和频率信息
B、只保留幅值信息
C、保留二信号的幅值、频率和相位差信息
答案:C
精品课件
8
三、填空题(在空白处填写入正确的内容)
1、 某信号能够用明确的数学关系式来描述,可以准确预计其来任
意时刻的值,则该信号称确定性信号
为
。
2、Sx(f)和Sy(f)为系统输入和输出信号的自谱,H(f)为系统频响函
特性。 9、 正弦信号的自相关函数是一个同频的 余弦
函数。
10、周期信号频谱的特点 是
离散的 连续的 ,
瞬变信号频谱的主要特点
是11、周期信号的傅氏三角级数是从 。0
∞到
展开的,
-∞
+∞
傅氏复指数级数是从
到
展开的。
精品课件
11
12、周期信号x(t)的傅氏级数三角函数展开式为:
x(t)a 0 (a nco sn0 tb nsinn0 t) n 1 a 0 A nsin (n0 tn) n 1
A、拉氏变换 B、傅氏变换 乘
来确立彼此的关系。
C、卷积
D、相
答案:B
16、将信号在时域进行扩展,则信号在频域将
A、不变 移
B、扩展
C、压缩
。 D、相
答案:C
精品课件
6
17、两个不同频的简谐信号,其互相关函为
A、周期信号 B、常数τ C、零
。 答案:C
18、由几个频率不同的正弦信号合成的周期信号,合成信号的周期
下面通过做练习来巩固和加深理解“信号及其描述”的概
念
一、单项选择题(请将正确的选择代号填入括号中) 1、工程中常见的周期信号,其谐波的幅值随谐波的频率增加
而
。
2、信号Ax、(t不)的变自功率B谱、密减度小函数Sx(f C)、是 增加 定 A、 x (t)的付立叶变换
B、 x (t)的自相关函数Rx(τ)的付氏变换 C、与x (t) 的幅值频谱x (f )相等的
式中:
a0
1 T
T/2
x(t)dt
T / 2
表示
直流分量
an
2 T
TT//22x(t)cosn0tdt
表示
余弦分量
表示 bn
2 T
TT//22x(t)sinn0tdt
正弦分量
A n 表 各分量的幅值
n 示 ;表示 各分量的相位
0
称为 基频 精品课件
。
(1 ) (2 )
;
;
12
13、对于非周期信号,当时间尺度在压缩时,则其频谱频
精品课件
13
17、从能否用数学公式描述的角度来说,信号可分类
为确定性
非确定性
和18、信号 x ( t ) A 1 c5 t o 1 ) s A 2 c ( 1 t o 2 0 ) s 。A 3 c (3 o t 3 5 ) s(
的频谱是 离散
的,
信号 x ( t) A 1 co 3 t 1 s ) A ( 2 c5 t o 2 ) s A 3 ( c1 o t 1 3 s )
。
ej0t 2(0)
A、频移性质
B、时移性质
C、相似性质 答案:A
,则有
C、相移性质 答案:A
13、随机信号的静态分量在数学上用
A、均值 D、均方根值
B、均方值
精品课件
表示。 C、均方差 答案:A
5
14、表示随机信号中动态分量的统计参数是
。
A、均方值 概率密度函数
B、均值
C、均方差
D、
答案:C
15、信号的时域与频域描述方法是依靠
为
。
余弦函数
5、获得周期性时域信号的频谱用 傅立叶级数
学工具。
6、频谱图反映了信号的 幅值
相位和
频率
的关系。
7、各态历经平稳随机信号的均值Ux表示信号的 静态
量;方差
2 x
描述信号的 动态
分量;
均值Ux 、方差
2 x
和均方值
2 x
三者关系:x2 x2 x2
。
的数 与
分
精品课件
10
8、 周期信号的频谱是离散的,同时周期信号的频谱具有谐波性 和 收敛
。 D、变化不定
答案:C
9、时域信号持续时间延长,则频域中高频成分
A、不变
B、增加
C、减少
。 D、变化不定
答案:B
10、时域信号波形变化缓慢,则高频分量
。
A、不变
B、增加
C、减少
D、变化不
定
答案:C
精ቤተ መጻሕፍቲ ባይዱ课件
4
11、如果有 (t) 1 ,根据傅氏变换的
,则有(tt0)ejt
A、时移性质
B、频移性质
12、如果有 12(),根据傅氏变换的
数,则满足关系Sy(f) =(H(f))2
Sx(f) 。
3、已知某信号的自相关函数
R xx() 1 0 1 5co s3 0
则原信号的均方值
2 x
为
25
方差,
2为
x
15
,
原信号中周期成份的频率
30π(或15)
为原信号中周期成份的幅值为 3 0
,
,
信号的总平均功率为25
。
精品课件
9
4、同频的正弦函数和余弦函数,其互相关函数
